Машинное обучение и Data Science (Часть 25): Прогнозирование временных рядов на форексе с помощью рекуррентных нейросетей (RNN)

MetaTrader 5 — Эксперты | 10 января 2025, 13:44

625

Omega J Msigwa

Содержание

Что такое рекуррентные нейронные сети (RNN)

Рекуррентные нейронные сети (RNN) — это искусственные нейронные сети, предназначенные для распознавания закономерностей в последовательностях данных: временных рядах, языках или видео. В отличие от традиционных нейронных сетей, которые предполагают, что входные данные независимы друг от друга, RNN могут обнаруживать и понимать закономерности из последовательности данных (информации).

Обратите внимание на использование терминов в этой статье. Когда я говорю «Рекуррентная нейронная сеть», я имею в виду простую сеть RNN в виде модели. Рекуррентные нейронные сети (RNN) здесь означают семейство моделей рекуррентных нейронных сетей, куда относятся простая RNN, долговременная краткосрочная память (LSTM) и управляемый рекуррентный блок (GRU).

Для понимания статьи необходимо базовое представление о языке Python, моделях ONNX в MQL5 и машинном обучении с Python.

Разбираем работу RNN

У рекуррентных нейросетей есть так называемая последовательная память, которая означает концепцию сохранения и использования информации из предыдущих временных шагов в последовательности для информирования обработки последующих временных шагов.

Последовательная память похожа на человеческую. Это тот тип памяти, который позволяет нам легче распознавать закономерности в последовательностях, например, при произношении слов.

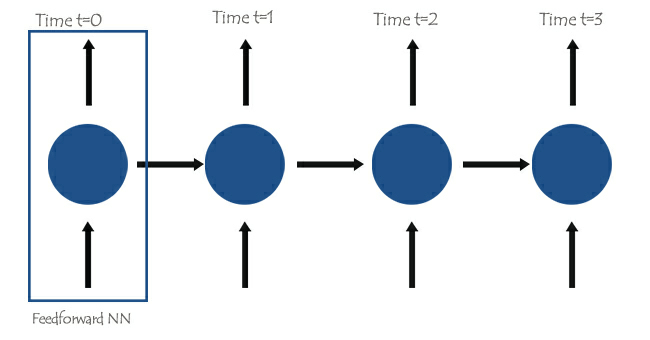
В основе рекуррентных нейронных сетей лежат нейронные сети прямого распространения, соединенные между собой таким образом, что следующий слой получает информацию из предыдущего, что дает простой RNN возможность изучать и понимать текущую информацию на основе предыдущей.

Чтобы лучше это понять, давайте рассмотрим пример с обучением модели RNN для чат-бота. Наш чат-бот должен понимать слова и предложения пользователя. Предположим, получили такое предложение: What time is it?

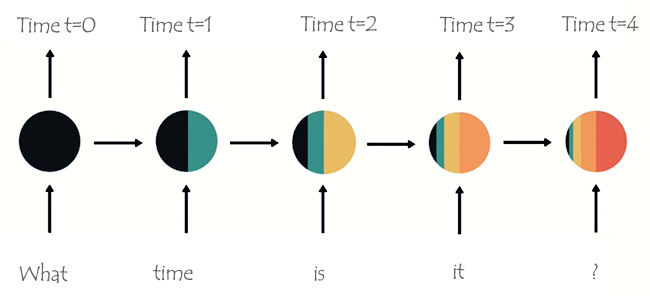
Слова будут разделены на соответствующие им шаги и загружены в RNN одно за другим, как показано на изображении ниже.

На последнем узле сети вы можете заметить странное расположение цветов, обозначающих информацию из предыдущих сетей и текущей. Объем данных из сети в моменты времени t=0 и t=1 в этом последнем узле RNN очень небольшой (эти данные практически не представлены).

По мере того, как RNN обрабатывает всё больше шагов, становится труднее сохранять информацию из предыдущих шагов. Как видно на изображении выше, слова what и time практически отсутствуют в конечном узле сети.

Это и есть кратковременная память. Это вызвано многими факторами, одним из основных из которых является обратное распространение.

Рекуррентные нейросети RNN содержат собственный процесс обратного распространения — обратное распространение ошибки сквозь время. Во время обратного распространения ошибки значения градиента экспоненциально уменьшаются по мере того, как сеть распределяется на каждый временной шаг назад. Градиенты позволяют внести корректировки в параметры нейронной сети (веса и смещения) — именно эта корректировка позволяет нейронной сети обучаться. Небольшие градиенты означают меньшие корректировки. Поскольку на ранние слои воздействуют небольшие градиенты, они обучаются не так эффективно, как хотелось бы. Это называется проблемой исчезающих градиентов.

Из-за проблемы исчезающего градиента простая нейросеть RNN не способна изучать долгосрочные зависимости из разных временных шагов. На изображении выше существует огромная вероятность того, что слова what и time вообще не учитываются, когда модель RNN чат-бота пытается понять предложение пользователя. Сети приходится делать наилучшие предположения, используя половину предложения, состоящего всего из слов is it ? Это делает сеть RNN менее эффективной, поскольку ее память слишком коротка для понимания длинных временных рядов данных, которые часто встречаются в реальных приложениях.

В попытках смягчить проблему кратковременной памяти были разработаны две специализированные рекуррентные нейронные сети: долговременная кратковременная память (LSTM) и управляемый рекуррентный блок (GRU).

LSTM и GRU во многом схожи с RNN, но они способны понимать долгосрочные зависимости, используя механизм вентилей. Мы поговорим о них в следующих статьях, следите за публикациями.

Математика, лежащая в основе рекуррентной нейронной сети

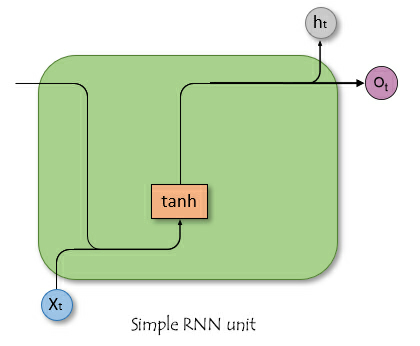
В отличие от нейронных сетей прямого распространения, RNN имеют соединения, которые образуют циклы, что позволяет информации сохраняться. На схематичном изображении ниже показано, как выглядит единица/ячейка сети RNN в разрезе.

где:

— входной сигнал в момент времени t.

— скрытое состояние в момент времени t.

Скрытое состояние

Обозначается как . Это вектор, который хранит информацию из предыдущих временных шагов. Он работает как память сети, позволяя ей фиксировать временные зависимости и закономерности во входных данных с течением времени.

Роли скрытого состояния в сети

Скрытое состояние выполняет несколько важнейших функций в сети RNN:

Оно сохраняет информацию из предыдущих входящих данных. Это позволяет сети обучаться на основе всей последовательности.
Оно обеспечивает контекст для текущих входных данных. Это позволяет сети делать обоснованные прогнозы на основе прошлых данных.
Оно формирует основу для повторяющихся соединений внутри сети. Это позволяет скрытому слою влиять на себя на разных временных этапах.

Возможно, понимание математики в основе сетей RNN не так важно, как знание того, как, где и когда их использовать. Поэтому, если хотите, можете пропустить следующий раздел этой статьи.

Формула

Скрытое состояние на временном шаге вычисляется с использованием входных данных на временном шаге , скрытого состояния из предыдущего временного шага и соответствующих матриц весов и смещений. Формула выглядит следующим образом:

где:

— это матрица весовых коэффициентов для входных данных в скрытое состояние.

— это матрица весовых коэффициентов для скрытого состояния.

— это смещение для скрытого состояния.

σ — функция активации (например, tanh или ReLU).

Выходной слой

Результат на временном шаге вычисляется на основе скрытого состояния на временном шаге .

Где

выход на шаге .

— это матрица весовых коэффициентов от скрытого состояния до выхода.

— смещение выходного слоя.

Расчет потерь

Функция потерь — (здесь может быть любая функция потерь, например, среднеквадратическая ошибка для задач регрессии или перекрестная энтропия для задач классификации).

Общие потери за все временные шаги составляют:

Обратное распространение сквозь время

Чтобы обновить весовые коэффициенты и смещения, необходимо вычислить градиенты потерь относительно каждого веса и смещения соответственно, а затем использовать полученные градиенты для обновления. Все это происходит по шагам.

Шаг	Для весовых коэффициентов	Для смещения
Вычисление градиента выходного слоя	для весовых коэффициентов: Где — градиент потерь относительно выхода.	для смещения: Так как смещение напрямую влияет на выходные данные, имеем: Отсюда
Вычисление градиентов скрытого состояния относительно весовых коэффициентов и смещения	Градиент функции потерь относительно скрытого состояния включает в себя как прямой вклад текущего временного шага, так и косвенный вклад через последующие временные шаги. 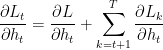Градиент скрытого состояния относительно предыдущего временного шага. Градиент активации скрытого состояния. Градиент весовых коэффициентов скрытого слоя. Общий градиент представляет собой сумму градиентов за все шаги.	Градиент потерь относительно скрытого смещения определяется суммой градиентов потерь относительно скрытого состояния на всех шагах. Смещение влияет на скрытое состояние через функцию активации, поэтому имеем: Используем цепное правило, принимая во внимание, что: Где — производная функции активации. Отсюда: Общий градиент скрытого смещения представляет собой сумму градиентов за все шаги.
Обновление весовых коэффициентов и смещений. Используя вычисленные выше градиенты, мы можем обновить весовые коэффициенты с помощью градиентного спуска или любого из его вариантов (например, Adam) (подробнее здесь).

Несмотря на то, что простые сети RNN не обладают способностью хорошо обучаться на длинных временных рядах, они неплохо подходят для прогнозирования будущих значений на основе недавнего прошлого. Попробуем построить простую рекуррентную нейронную сеть, которая поможет принимать торговые решения.

Создание модели рекуррентной нейронной сети на Python

Построить и скомпилировать модель RNN в Python довольно просто. Это займет всего несколько строк кода с использованием библиотеки Keras.

Python

import tensorflow as tf
from tensorflow.keras.models import Sequential #import sequential neural network layer
from sklearn.preprocessing import StandardScaler
from tensorflow.keras.layers import SimpleRNN, Dense, Input
from keras.callbacks import EarlyStopping
from sklearn.preprocessing import MinMaxScaler
from keras.optimizers import Adam

reg_model = Sequential()

reg_model.add(Input(shape=(time_step, x_train.shape[1]))) # input layer
reg_model.add(SimpleRNN(50, activation='sigmoid')) #first hidden layer
reg_model.add(Dense(50, activation='sigmoid')) #second hidden layer
reg_model.add(Dense(units=1, activation='relu'))  # final layer 

adam_optimizer = Adam(learning_rate = 0.001)

reg_model.compile(optimizer=adam_optimizer, loss='mean_squared_error') # Compile the model
reg_model.summary()

Приведенный выше код предназначен для регрессионной рекуррентной нейронной сети, поэтому у нас есть 1 узел в выходном слое и функция активации Relu в конечном слое. На это есть причина. Об этом мы говорили в статье "Разбираем нейронные сети с прямой связью".

Используя данные, собранные нами в предыдущей статье Прогнозирование временных рядов на форексе с помощью обычных ИИ-моделей (обязательно к прочтению), посмотрим на использование моделей RNN, которые лучше понимают данные временных рядов.

В конце мы оценим результаты модели RNN в сравнении с моделью LightGBM, которую мы построили в предыдущей статье. Бдуем использовать те же данные. Надеюсь, это практический пример поможет закрепить общее представление о прогнозировании временных рядов.

Подготовка данных

В выборке у нас есть 28 столбцов, которые собраны для модели, не являющейся временным рядом.

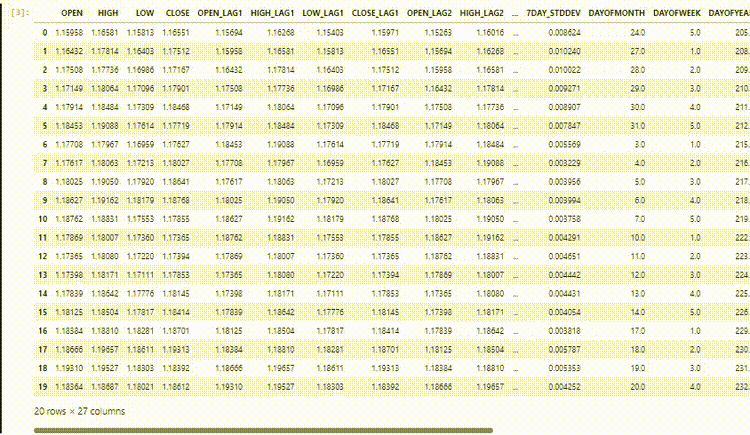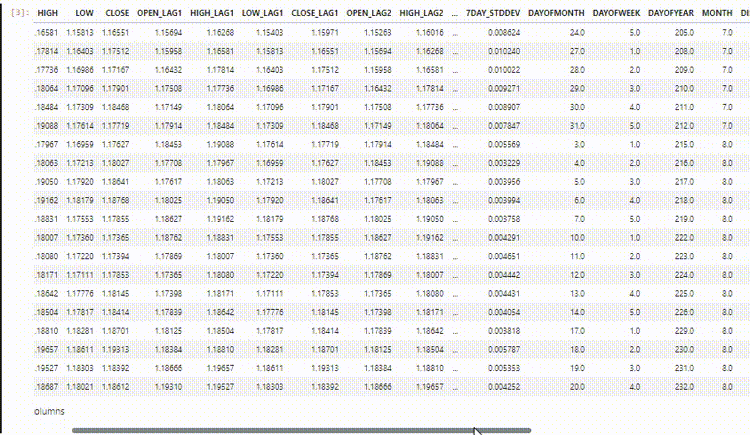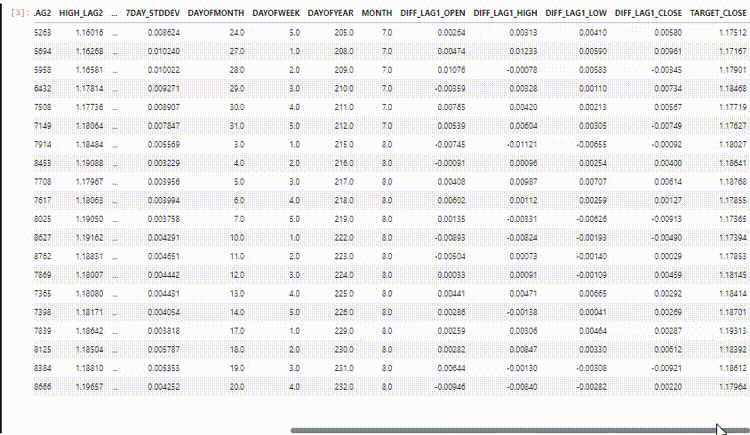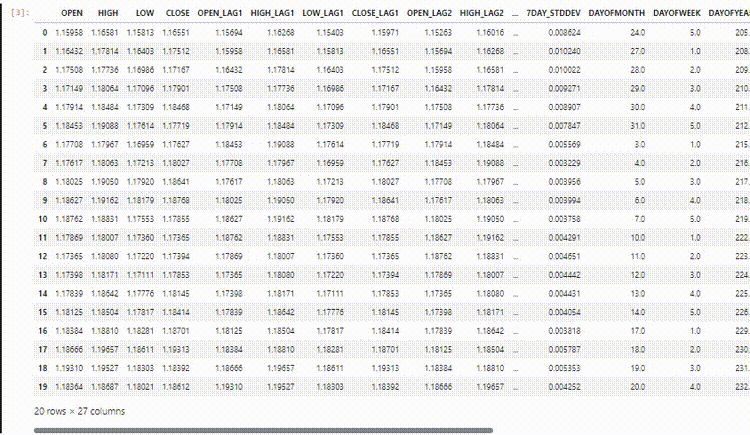
Набор данных для прогнозирования временных рядов

Однако эти данные, которые мы собрали и обработали, имеют много запаздывающих переменных. Такие данные были нудны для предыдущей модели, не являющейся временным рядом. Мы использовали их для поиска зависимых от времени закономерностей. Сети RNN могут распознавать закономерности в пределах заданных временных интервалов.

Поэтоум на данный момент нам не нужны запаздывающие значения, их нужно удалить.

Python

lagged_columns = [col for col in data.columns if "lag" in col.lower()] #let us obtain all the columns with the name lag

print("lagged columns: ",lagged_columns)

data = data.drop(columns=lagged_columns) #drop them

Результаты

lagged columns:  ['OPEN_LAG1', 'HIGH_LAG1', 'LOW_LAG1', 'CLOSE_LAG1', 'OPEN_LAG2', 'HIGH_LAG2', 'LOW_LAG2', 'CLOSE_LAG2', 'OPEN_LAG3', 'HIGH_LAG3', 'LOW_LAG3', 'CLOSE_LAG3', 'DIFF_LAG1_OPEN', 'DIFF_LAG1_HIGH', 'DIFF_LAG1_LOW', 'DIFF_LAG1_CL

Новые данные теперь содержат 12 столбцов.

Новый отфильтрованный набор данных

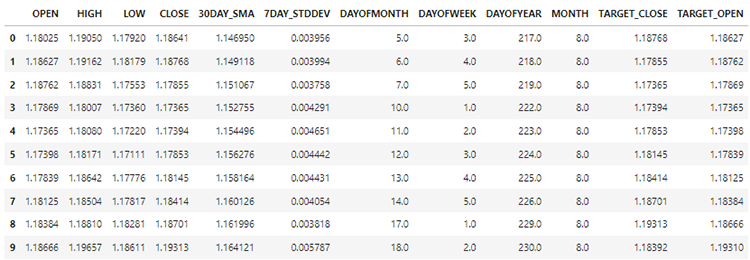
Мы можем разделить данные — 70% обучающие и оставшиеся 30% — данные для тестирования. Если вы используете функцию train_test_split из библиотеки Scikit-Learn, не забудьте установить параметр shuffle=False. Так функция разделит данные, сохранив порядок представленной информации.

Не забывайте, что это прогнозирование временных рядов.

# Split the data

X = data.drop(columns=["TARGET_CLOSE","TARGET_OPEN"]) #dropping the target variables
Y = data["TARGET_CLOSE"]

test_size = 0.3 #70% of the data should be used for training purpose while the rest 30% should be used for testing

x_train, x_test, y_train, y_test = train_test_split(X, Y, shuffle=False, test_size = test_size) # this is timeseries data so we don't shuffle

print(f"x_train {x_train.shape}\nx_test {x_test.shape}\ny_train{y_train.shape}\ny_test{y_test.shape}")

После удаления двух целевых переменных наши данные теперь содержат 10 признаков. Нужно преобразовать эти 10 признаков в последовательные данные, которые сеть RNN сможет обработать.

def create_sequences(X, Y, time_step):
    if len(X) != len(Y):
        raise ValueError("X and y must have the same length")
    
    X = np.array(X)
    Y = np.array(Y)
    
    Xs, Ys = [], []
    
    for i in range(X.shape[0] - time_step):
        Xs.append(X[i:(i + time_step), :])  # Include all features with slicing
        Ys.append(Y[i + time_step])
        
    return np.array(Xs), np.array(Ys)

Приведенная выше функция генерирует последовательность из заданных массивов x и y для указанного временного шага. Чтобы понять, как работает эта функция, посмотрим на следующий пример:

Допустим, у нас есть набор данных с 10 образцами и 2 признаками. Нам нужно создать последовательности с временным шагом 3.

X — матрица формы (10, 2). Y — вектор длины 10.
Функция создаст последовательности следующим образом:
При i=0: Xs будет [0:3, :] X[0:3, :], а Ys — Y[3]. При i=1: Xs будет 𝑋[1:4, :] X[1:4, :], а Ys — Y[4].

И так далее, пока i не станет равным 6.

Полученный Xs будет иметь форму (7, 3, 2), а Ys — иметь длину 7.

После нормализации независимых переменных, которые мы разделили, можно применить функцию create_sequences для генерации последовательных данных.

time_step = 7 # we consider the past 7 days

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()

x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)

x_train_seq, y_train_seq = create_sequences(x_train, y_train, time_step)
x_test_seq, y_test_seq = create_sequences(x_test, y_test, time_step)

print(f"Sequential data\n\nx_train {x_train_seq.shape}\nx_test {x_test_seq.shape}\ny_train{y_train_seq.shape}\ny_test{y_test_seq.shape}")

Результаты

Sequential data

x_train (693, 7, 10)
x_test (293, 7, 10)
y_train(693,)
y_test(293,)

Значение временного шага 7 означает, что в каждом случае сеть RNN будет заполнена данными за последние 7 дней с учетом того, что мы собрали всю информацию, имеющуюся в наборе данных, с дневного таймфрейма. Это похоже на то, как мы вручную получали данные за предыдущие 7 дней из текущего бара в предыдущей статье.

Обучение простой RNN для задач регрессии

early_stopping = EarlyStopping(monitor='val_loss', patience=5, restore_best_weights=True)

history = reg_model.fit(x_train_seq, y_train_seq, epochs=100, batch_size=64, verbose=1, validation_data=(x_test_seq, y_test_seq), callbacks=[early_stopping])

Результаты

Epoch 95/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 6.4504e-05 - val_loss: 4.4433e-05
Epoch 96/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 6.4380e-05 - val_loss: 4.4408e-05
Epoch 97/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 6.4259e-05 - val_loss: 4.4386e-05
Epoch 98/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 6.4140e-05 - val_loss: 4.4365e-05
Epoch 99/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 7ms/step - loss: 6.4024e-05 - val_loss: 4.4346e-05
Epoch 100/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 7ms/step - loss: 6.3910e-05 - val_loss: 4.4329e-05

Кривая потерь обучения регрессора RNN

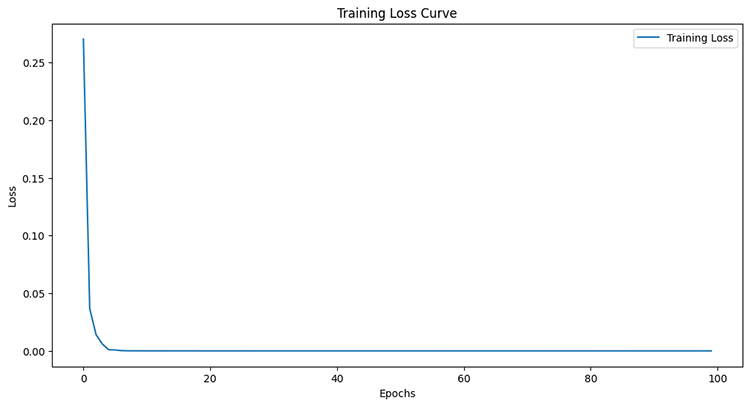
После измерения результатов тестовой выборки.

Python

from sklearn.metrics import r2_score

y_pred = reg_model.predict(x_test_seq) # Make predictions on the test set

# Plot the actual vs predicted values
plt.figure(figsize=(12, 6))
plt.plot(y_test_seq, label='Actual Values')
plt.plot(y_pred, label='Predicted Values')
plt.xlabel('Samples')
plt.ylabel('TARGET_CLOSE')
plt.title('Actual vs Predicted Values')
plt.legend()
plt.show()

print("RNN accuracy =",r2_score(y_test_seq, y_pred))

Точность модели составила 78%.

Регрессор rnn, фактический результат и предсказание

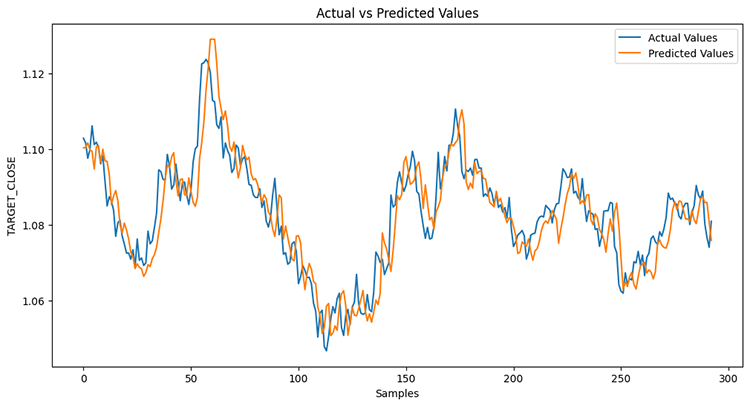
Если вы помните из предыдущей статьи, модель LightGBM показала точность 86,76% при решении задачи регрессии. Таким образом, модель, не основанная на временных рядах, показала себя лучше.

Значимость признаков

Я запускал тесты, чтобы проверить, как переменные влияют на процесс принятия решений модели RNN, используя SHAP.

import shap

# Wrap the model prediction for KernelExplainer
def rnn_predict(data):
    data = data.reshape((data.shape[0], time_step, x_train.shape[1]))
    return reg_model.predict(data).flatten()

# Use SHAP to explain the model
sampled_idx = np.random.choice(len(x_train_seq), size=100, replace=False)
explainer = shap.KernelExplainer(rnn_predict, x_train_seq[sampled_idx].reshape(100, -1))
shap_values = explainer.shap_values(x_test_seq[:100].reshape(100, -1), nsamples=100)

Далее мы строим график значимости признаков.

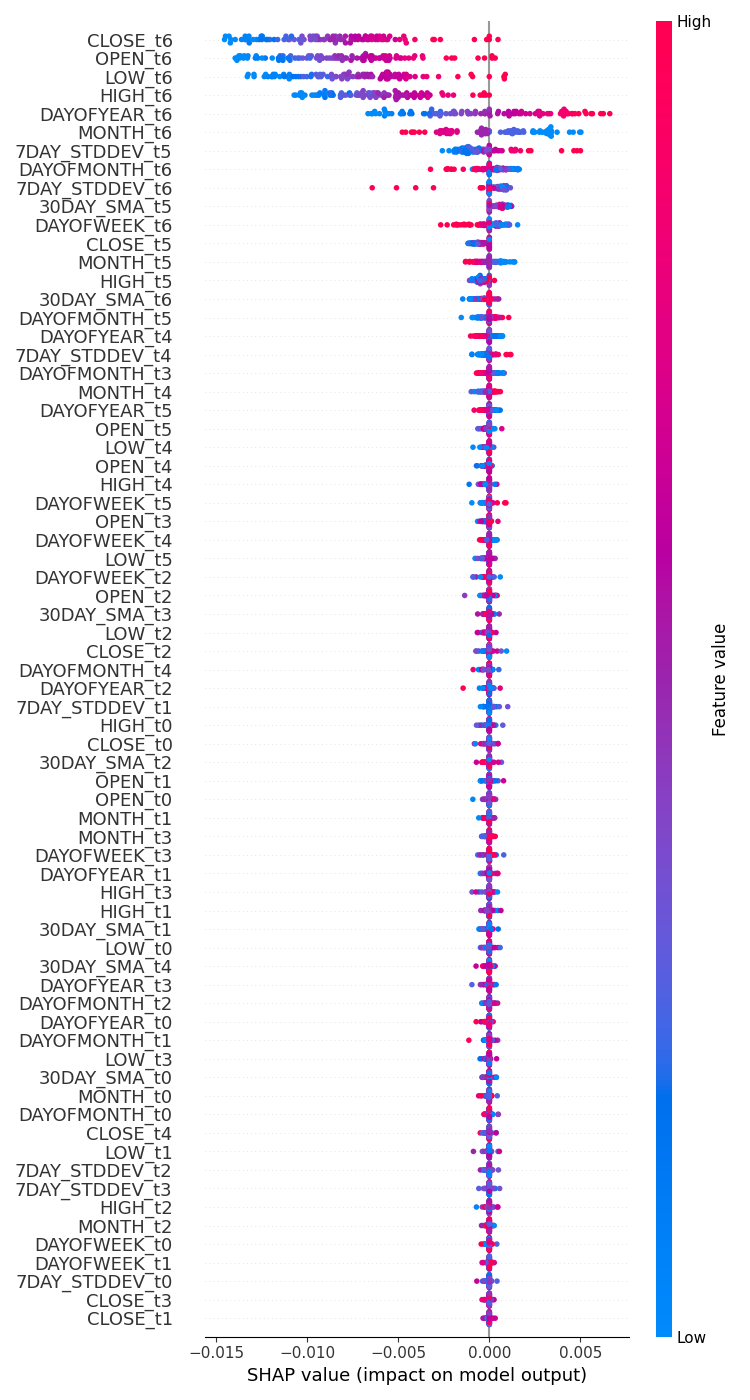
# Update feature names for SHAP
feature_names = [f'{original_feat}_t{t}' for t in range(time_step) for original_feat in X.columns]

# Plot the SHAP values
shap.summary_plot(shap_values, x_test_seq[:100].reshape(100, -1), feature_names=feature_names, max_display=len(feature_names), show=False)

# Adjust layout and set figure size
plt.subplots_adjust(left=0.12, bottom=0.1, right=0.9, top=0.9)  
plt.gcf().set_size_inches(7.5, 14) 
plt.tight_layout()

plt.savefig("regressor-rnn feature-importance.png")
plt.show()

Ниже представлен результат.

Наиболее значимыми переменными являются те, по которым имеется недавняя информация, в то время как наименее значимыми являются переменные с более старыми данными.

Это как будто сказать, что последнее произнесенное в предложении слово несет в себе наибольший смысл во всем предложении.

Это может быть справедливо для модели машинного обучения, но для нас, людей, это мягко говоря странно.

Как было сказано в предыдущей статье, мы не можем доверять только графику значимости признаков, учитывая, что я использовал KernelExplainer вместо рекомендуемого DeepExplainer, потому что получил кучу ошибок, пытаясь заставить последний работать.

Как было сказано в предыдущей статье, наличие регрессионной модели для прогнозирования следующей цены закрытия или открытия не так практично, как использование классификатора — он должен прогнозировать направление движения рынка на следующем баре. Поэтому для этой задачи создадим модель классификатора RNN.

Обучение простой RNN для задачи классификации

Процесс создания в целом повторяет разработку регрессора, но с некоторыми изменениями. Прежде всего, нужно создать целевую переменную для задачи классификации.

Python

Y = []
target_open = data["TARGET_OPEN"]
target_close = data["TARGET_CLOSE"]

for i in range(len(target_open)):
    if target_close[i] > target_open[i]: # if the candle closed above where it opened thats a buy signal
        Y.append(1)
    else: #otherwise it is a sell signal
        Y.append(0)
        
Y = np.array(Y) #converting this array to NumPy


classes_in_y = np.unique(Y) # obtaining classes present in the target variable for the sake of setting the number of outputs in the RNN

Затем нужно обеспечить одно активное состояние для целевой переменной после того создания последовательности, о чем мы говорили при разработки модели регрессии.

from tensorflow.keras.utils import to_categorical

y_train_encoded = to_categorical(y_train_seq)
y_test_encoded = to_categorical(y_test_seq)

print(f"One hot encoded\n\ny_train {y_train_encoded.shape}\ny_test {y_test_encoded.shape}")

Результаты

One hot encoded

y_train (693, 2)
y_test (293, 2)

После этого можно построить модель классификатора RNN и обучить ее.

cls_model = Sequential()

cls_model.add(Input(shape=(time_step, x_train.shape[1]))) # input layer
cls_model.add(SimpleRNN(50, activation='relu'))
cls_model.add(Dense(50, activation='relu'))
cls_model.add(Dense(units=len(classes_in_y), activation='sigmoid', name='outputs')) 


adam_optimizer = Adam(learning_rate = 0.001)

cls_model.compile(optimizer=adam_optimizer, loss='binary_crossentropy') # Compile the model
cls_model.summary()


early_stopping = EarlyStopping(monitor='val_loss', patience=5, restore_best_weights=True)

history = cls_model.fit(x_train_seq, y_train_encoded, epochs=100, batch_size=64, verbose=1, validation_data=(x_test_seq, y_test_encoded), callbacks=[early_stopping])

Для модели классификатора RNN я использовал сигмоиду для последнего слоя сети. Количество нейронов (блоков) в последнем слое должно соответствовать количеству классов, присутствующих в целевой переменной (Y), в этом случае у нас будет два блока.

Model: "sequential_1"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ simple_rnn_1 (SimpleRNN)        │ (None, 50)             │         3,050 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_2 (Dense)                 │ (None, 50)             │         2,550 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ outputs (Dense)                 │ (None, 2)              │           102 │
└─────────────────────────────────┴────────────────────────┴───────────────┘

Для сходимости модели классификатора RNN в процессе обучения понадобилось всего 6 эпох.

Epoch 1/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 2s 36ms/step - loss: 0.7242 - val_loss: 0.6872
Epoch 2/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - loss: 0.6883 - val_loss: 0.6891
Epoch 3/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.6817 - val_loss: 0.6909
Epoch 4/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.6780 - val_loss: 0.6940
Epoch 5/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.6743 - val_loss: 0.6974
Epoch 6/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.6707 - val_loss: 0.6998

Несмотря на более низкую точность в задаче регрессии по сравнению с точностью регрессора LightGBM из предыдущей статьи, модель классификатора RNN оказалась на 3% точнее классификатора LightGBM.

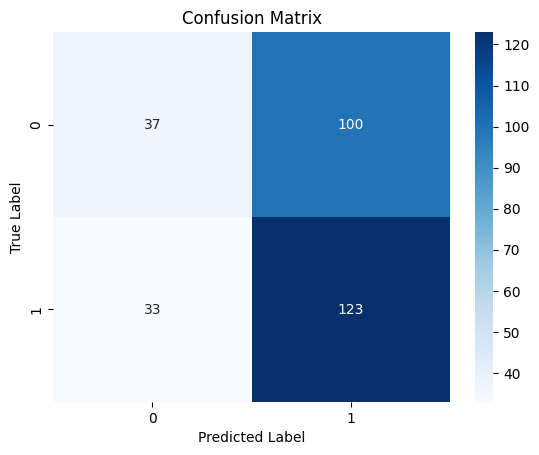
10/10 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
Classification Report
               precision    recall  f1-score   support

           0       0.53      0.27      0.36       137
           1       0.55      0.79      0.65       156

    accuracy                           0.55       293
   macro avg       0.54      0.53      0.50       293
weighted avg       0.54      0.55      0.51       293

Тепловая карта матрицы путаницы

Сохранение рекуррентной модели в ONNX

Созданную модель классификатора RNN мы можем сохранить в формате ONNX для использования в MetaTrader 5.

В отличие от моделей Scikit-learn, сохранить модели глубокого обучения Keras, в нашем случае RNN, не так просто. Также для моделей RNN не очень подходят пайплайны.

В статье Решение проблем интеграции ONNX упоминалось, что можно либо масштабировать данные в MQL5 после сбора или мы сохранить масштабатор, который есть в Python, и загрузить его в mql5 с помощью библиотеки для MQL5.

Сохранение модели

import tf2onnx

# Convert the Keras model to ONNX
spec = (tf.TensorSpec((None, time_step, x_train.shape[1]), tf.float16, name="input"),)
cls_model.output_names=['output']

onnx_model, _ = tf2onnx.convert.from_keras(cls_model, input_signature=spec, opset=13)

# Save the ONNX model to a file
with open("rnn.EURUSD.D1.onnx", "wb") as f:
    f.write(onnx_model.SerializeToString())

Сохранение параметров масштабатора

# Save the mean and scale parameters to binary files

scaler.mean_.tofile("standard_scaler_mean.bin")
scaler.scale_.tofile("standard_scaler_scale.bin")

Сохранение среднего значения и стандартного отклонения, которые являются основными компонентами Стандартного масштабатора, означает успешное сохранение стандартный масштабатора.

Советник на основе рекуррентной нейросети

Первое, что нужно сделать внутри нашего советника, — это добавить модель RNN в формате ONNX и подключить масштабатор в виде ресурсов к советнику.

MQL5 | RNN timeseries forecasting.mq5

#resource "\\Files\\rnn.EURUSD.D1.onnx" as uchar onnx_model[]; //rnn model in onnx format
#resource "\\Files\\standard_scaler_mean.bin" as double standardization_mean[];
#resource "\\Files\\standard_scaler_scale.bin" as double standardization_std[];

Затем загрузим библиотеки для загрузки модели RNN в формате ONNX и для стандартного масштабатора.

MQL5

#include <MALE5\Recurrent Neural Networks(RNNs)\RNN.mqh>
CRNN rnn;

#include <MALE5\preprocessing.mqh>
StandardizationScaler *scaler;

Функция OnInit.

vector classes_in_data_ = {0,1}; //we have to assign the classes manually | it is very important that their order is preserved as they can be seen in python code, HINT: They are usually in ascending order
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
  
//--- Initialize ONNX model
   
   if (!rnn.Init(onnx_model))
     return INIT_FAILED;
   
//--- Initializing the scaler with values loaded from binary files 

   scaler = new StandardizationScaler(standardization_mean, standardization_std);
   
//--- Initializing the CTrade library for executing trades

   m_trade.SetExpertMagicNumber(magic_number);
   m_trade.SetDeviationInPoints(slippage);
   m_trade.SetMarginMode();
   m_trade.SetTypeFillingBySymbol(Symbol());
           
   lotsize = SymbolInfoDouble(Symbol(), SYMBOL_VOLUME_MIN);
   
//--- Initializing the indicators

   ma_handle = iMA(Symbol(),timeframe,30,0,MODE_SMA,PRICE_WEIGHTED); //The Moving averaege for 30 days
   stddev_handle = iStdDev(Symbol(), timeframe, 7,0,MODE_SMA,PRICE_WEIGHTED); //The standard deviation for 7 days
   

   return(INIT_SUCCEEDED);
  }

Прежде чем мы сможем развернуть модель для реальной торговли внутри функции OnTick, необходимо собрать данные так же, как мы собирали данные для обучения. Исключим признаки, которые мы исключали во время обучения.

Напомню, мы обучили модель только с 10 признаками (независимыми переменными).

Новый набор данных для целевых переменных

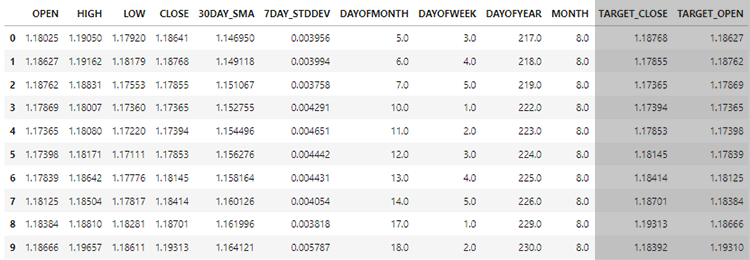
Создадим функцию GetInputData для сбора только эти 10 независимых переменных.

matrix GetInputData(int bars, int start_bar=1)
 {
   vector open(bars), 
          high(bars),
          low(bars), 
          close(bars), 
          ma(bars), 
          stddev(bars), 
          dayofmonth(bars), 
          dayofweek(bars), 
          dayofyear(bars), 
          month(bars);

//--- Getting OHLC values
   
   open.CopyRates(Symbol(), timeframe, COPY_RATES_OPEN, start_bar, bars);
   high.CopyRates(Symbol(), timeframe, COPY_RATES_HIGH, start_bar, bars);
   low.CopyRates(Symbol(), timeframe, COPY_RATES_LOW, start_bar, bars);
   close.CopyRates(Symbol(), timeframe, COPY_RATES_CLOSE, start_bar, bars);
   
   vector time_vector;
   time_vector.CopyRates(Symbol(), timeframe, COPY_RATES_TIME, start_bar, bars);
   
//---

   
   ma.CopyIndicatorBuffer(ma_handle, 0, start_bar, bars); //getting moving avg values 
   stddev.CopyIndicatorBuffer(stddev_handle, 0, start_bar, bars); //getting standard deviation values
   
   string time = "";
   for (int i=0; i<bars; i++) //Extracting time features 
     {
       time = (string)datetime(time_vector[i]); //converting the data from seconds to date then to string
       TimeToStruct((datetime)StringToTime(time), date_time_struct); //convering the string time to date then assigning them to a structure
       
       dayofmonth[i] = date_time_struct.day;
       dayofweek[i] = date_time_struct.day_of_week;
       dayofyear[i] = date_time_struct.day_of_year;
       month[i] = date_time_struct.mon;
     }
   
   matrix data(bars, 10); //we have 10 inputs from rnn | this value is fixed
   
//--- adding the features into a data matrix
   
   data.Col(open, 0);
   data.Col(high, 1);
   data.Col(low, 2);
   data.Col(close, 3);
   data.Col(ma, 4);
   data.Col(stddev, 5);
   data.Col(dayofmonth, 6);
   data.Col(dayofweek, 7);
   data.Col(dayofyear, 8);
   data.Col(month, 9);
   
   return data;
 }

Наконец, можем использовать модель RNN для получения торговых сигналов для нашей простой стратегии.

void OnTick()
  {
//---
   
   if (NewBar()) //Trade at the opening of a new candle
    {
      matrix input_data_matrix = GetInputData(rnn_time_step);
      input_data_matrix = scaler.transform(input_data_matrix); //applying StandardSCaler to the input data
      
      int signal = rnn.predict_bin(input_data_matrix, classes_in_data_); //getting trade signal from the RNN model
     
      Comment("Signal==",signal);
     
   //---
     
      MqlTick ticks;
      SymbolInfoTick(Symbol(), ticks);
      
      if (signal==1) //if the signal is bullish
       {
          if (!PosExists(POSITION_TYPE_BUY)) //There are no buy positions
           {
             if (!m_trade.Buy(lotsize, Symbol(), ticks.ask, ticks.bid-stoploss*Point(), ticks.ask+takeprofit*Point())) //Open a buy trade
               printf("Failed to open a buy position err=%d",GetLastError());
           }
       }
      else if (signal==0) //Bearish signal
        {
          if (!PosExists(POSITION_TYPE_SELL)) //There are no Sell positions
            if (!m_trade.Sell(lotsize, Symbol(), ticks.bid, ticks.ask+stoploss*Point(), ticks.bid-takeprofit*Point())) //open a sell trade
               printf("Failed to open a sell position err=%d",GetLastError());
        }
      else //There was an error
        return;
    }
  }

Тестирование советника на основе рекуррентной нейросети в тестере стратегий

Теперь давайте протестируем все в тестере стратегий. Используем те же значения стоп-лосса и тейк-профита, а также настройки тестирования, которые мы использовали для модели LightGBM.

input group "rnn";
input uint rnn_time_step = 7; 
//this value must be the same as the one used during training in a python script

input ENUM_TIMEFRAMES timeframe = PERIOD_D1;
input int magic_number = 1945;
input int slippage = 50;
input int stoploss = 500;
input int takeprofit = 700;

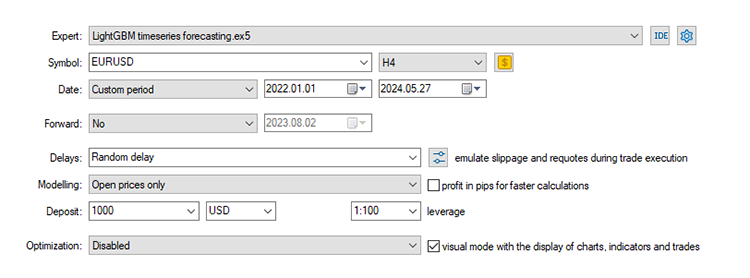
Настройки тестера стратегий:

Настройки тестирования для модели rnn

Советник показал прибыль в 44,56% по 561 сделке.

Отчет советника с rnn

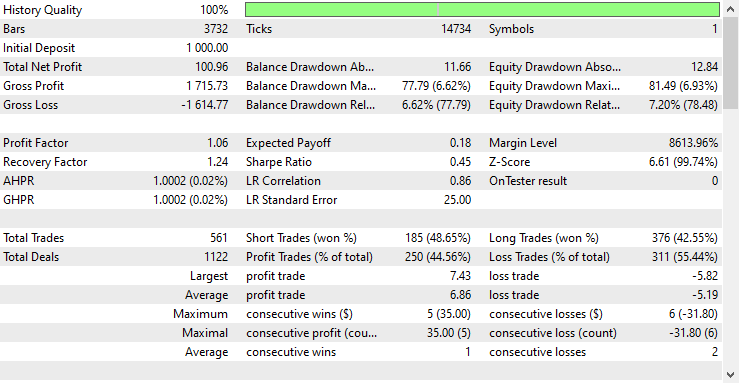
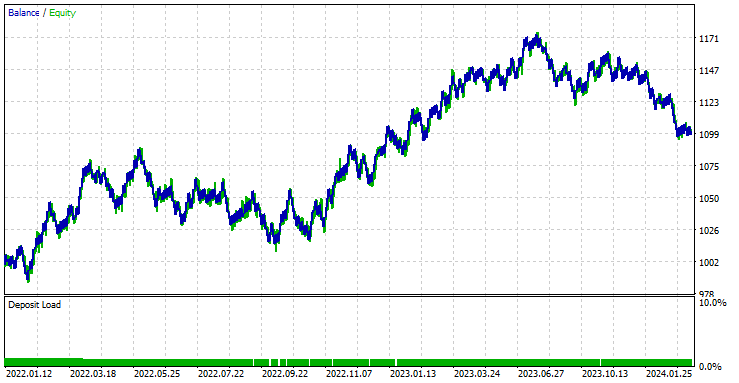
С текущими значениями стоп-лосса и тейк-профита можно справедливо сказать, что модель LightGBM превзошла простую модель RNN при прогнозировании временных рядов, поскольку она показала прибыль в размере $572 по сравнению с прибылью в размере $100 от RNN.

Далее я провел оптимизацию, чтобы найти наилучшие значения стоп-лосса и тейк-профита. Получились значения для стоп-лосса в 1000 пунктов и для тейк-профита в 700 пунктов.

Отчет оптимизированного советника с rnn

Кривая эквити своетника с rnn

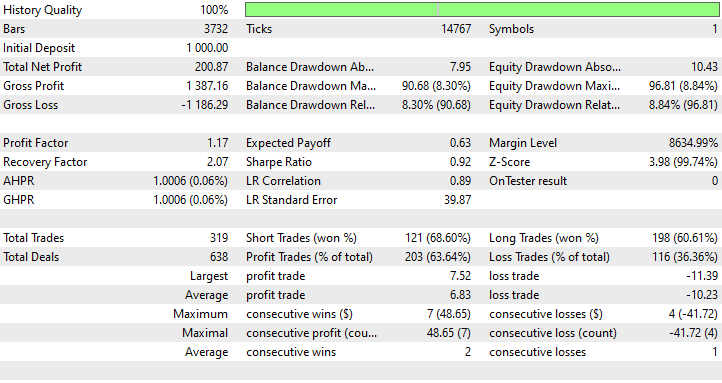
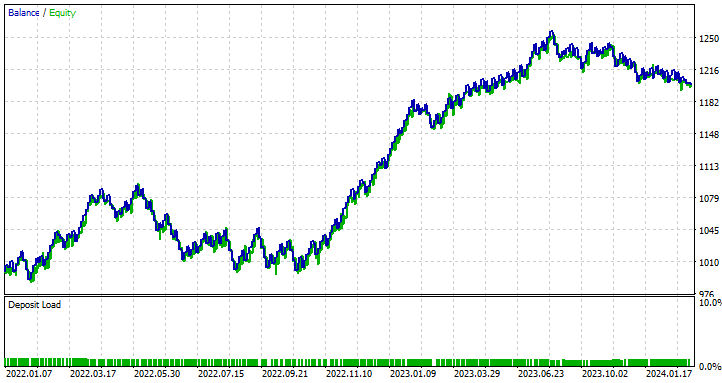
Преимущества использования простых RNN для прогнозирования временных рядов

Они могут обрабатывать последовательные данные.
Простые рекуррентные нейронные сети предназначены для обработки последовательных данных и хорошо подходят для задач, где важен порядок данных. Это прогнозирование временных рядов, моделирование языка и распознавание речи.
Они имеют доступ к параметрам на разных временных шагах.
Это помогает эффективно изучать закономерности во времени. Такой доступ к параметрам делает модель эффективной с точки зрения количества параметров, особенно по сравнению с моделями, которые обрабатывают каждый временной шаг независимо.
Способность фиксировать временные зависимости
Они могут фиксировать зависимости во времени, что необходимо для понимания контекста последовательных данных. Могут эффективно моделировать краткосрочные временные зависимости.
Гибкость в отношении длины последовательности
Простые рекуррентные нейронные сети могут обрабатывать последовательности переменной длины, что делает их гибкими для различных типов последовательных входных данных.
Простота использования и внедрения
Архитектуру простой RNN относительно легко реализовать. Поэтому они более доступны для использования в общем смысле.

Заключительные мысли

В этой статье мы обсудили простые рекуррентные нейросети. мы поговорили о том, как такую сеть реализовать на MQL5. В статья я часто сравнивал результаты модели RNN с моделью LightGBM, которую мы построили в предыдущей статье этой серии. Цель такого сравнения — попытка лучше понять прогнозирование временных рядов с использованием различных моделей.

Сравнение во многих отношениях несправедливо, поскольку эти две модели сильно различаются по структуре и способу прогнозирования. Поэтому не стоит опираться на выводы, сделанные в статье.

Стоит отметить, что модель RNN использовала немного другие данные, чем модель LightGBM. В этой статье мы удалили некоторые параметры, в частности дифференцированные значениями между ценами OHLC (DIFF_LAG1_OPEN, DIFF_LAG1_HIGH, DIFF_LAG1_LOW и DIFF_LAG1_CLOSE).

Можно было бы дополнительно добавить данные, чтобы сделать выборки похожими, но мы решили обойтись без них и использовать только собранную выборку.

С наилучшими пожеланиями.

За развитием этой модели машинного обучения и других из этой серии статей можно следить в моем репозиторий на GitHub.

Таблица вложений

Наименование файла	Тип файла	Описание и использование
RNN timeseries forecasting.mq5	Expert	Торговый робот для загрузки модели RNN в ONNX и тестирования полученной торговой стратегии в MetaTrader 5.
rnn.EURUSD.D1.onnx	ONNX	Модель RNN в формате ONNX.
standard_scaler_mean.bin standard_scaler_scale.bin	Бинарные файлы	Двоичные файлы для стандартного масштабатора
preprocessing.mqh	Включаемый файл	Библиотека стандартного масштабатора
RNN.mqh	Включаемый файл	Библиотека для загрузки и развертывания модели ONNX
rnns-for-forex-forecasting-tutorial.ipynb	Скрипт Python/Блокнот Jupyter	Содержит весь код Python, обсуждаемый в этой статье.

Источники и ссылки

Иллюстрированное руководство по рекуррентным нейронным сетям: понимание интуиции (https://www.youtube.com/watch?v=LHXXI4-IEns)
Рекуррентные нейронные сети - Эпизод 9 (Просто о глубоком обучении) (https://youtu.be/_aCuOwF1ZjU)
Рекуррентные нейронные сети (https://stanford.edu/~shervine/teaching/cs-230/cheatsheet-recurrent-neural-networks#)

Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/15114

Прикрепленные файлы |

Загрузить ZIP

Attachments.zip (34.59 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Нейросети в трейдинге: Мультимодальный агент, дополненный инструментами (Окончание)

Продолжаем работу по реализации алгоритмов мультимодального агента для финансовой торговли FinAgent, предназначенного для анализа мультимодальных данных рыночной динамики и исторических торговых паттернов.

Полиномиальные модели в трейдинге

Эта статья посвящена ортогональным многочленам. Их применение может стать основой для более точного и эффективного анализа рыночной информации, благодаря чему, трейдер сможет принимать более обоснованные решения.

Разработка советника на основе стратегии прорыва диапазона консолидации на MQL5

В статье описываются шаги по созданию торгового советника, который извлекает выгоду из ценовых прорывов после периодов консолидации. Определяя диапазоны консолидации и устанавливая уровни прорыва, трейдеры могут автоматизировать свои торговые решения на основе этой стратегии. Советник призван обеспечить четкие точки входа и выхода, избегая ложных пробоев.

Нейросети в трейдинге: Мультимодальный агент, дополненный инструментами (FinAgent)

Предлагаем познакомиться с фреймворком мультимодального агента для финансовой торговли FinAgent, который предназначен для анализа данных разных типов, отражающих рыночную динамику и исторические торговые паттерны.