Машинное обучение и Data Science (Часть 24): Прогнозирование временных рядов на форексе с помощью обычных ИИ-моделей

MetaTrader 5 — Трейдинг | 28 ноября 2024, 15:53

1 067

Omega J Msigwa

Разделы

Что такое прогнозирование временных рядов?

Прогнозирование временных рядов — это процесс использования прошлых данных для прогнозирования будущих значений в последовательности точек данных. Эта последовательность обычно упорядочена по времени, отсюда и название временной ряд.

Основные переменные во временных рядах

В данных может быть сколько угодно переменных признаков, но все данные для анализа временных рядов или прогнозирования должны содержать вот эти две переменные:

Время

Это независимая переменная, представляющая конкретные моменты времени, когда наблюдались точки данных.
Целевая переменная

Это значение, которое вы пытаетесь предсказать на основе прошлых наблюдений и, возможно, других факторов. (Например, дневная цена закрытия акций, почасовая температура, поминутный трафик веб-сайта).

Целью прогнозирования временных рядов является использование исторических закономерностей и тенденций в данных для составления обоснованных прогнозов относительно будущих значений.

Изображение прогнозирования временных на ядов mql5

В этой статье предполагается, что у вас уже есть базовые знания об ONNX, прогнозировании временных рядов и алгоритме LightGBM. Если нет, рекомендую почитать статьи по ссылкам, чтобы было понятнее.

Где используется прогнозирование временных рядов?

Анализ временных рядов и прогнозирование можно использовать для разных целей:

Прогнозирование будущих значений
Понимание прошлого поведения
Планирование будущего, которое может зависеть от прошлого
Оценка текущих результатов

Классические и современные модели машинного обучения на основе временных рядов

В отличие от классических моделей машинного обучения, таких как линейная регрессия, метод опорных векторов (SVM), нейронные сети (NN) и другие, которые мы обсуждали в прошлых статьях и которые направлены на определение взаимосвязей между переменными признаков и составление будущих прогнозов на основе этих изученных взаимосвязей, модели временных рядов прогнозируют будущие значения на основе ранее наблюдавшихся значений.

Эта разница в подходе означает, что модели временных рядов специально разработаны для обработки временных зависимостей и закономерностей, присущих последовательным данным. Модели прогнозирования временных рядов, такие как ARIMA, SARIMA, экспоненциальное сглаживание, RNN, LSTM и GRU, используют исторические данные для прогнозирования будущих точек ряда, фиксируя тенденции, сезонность и другие временные структуры.

На приведенной ниже блок-схеме показаны различные модели машинного обучения, используемые для прогнозирования временных рядов.

Модели машинного обучения для прогнозирования временных рядов

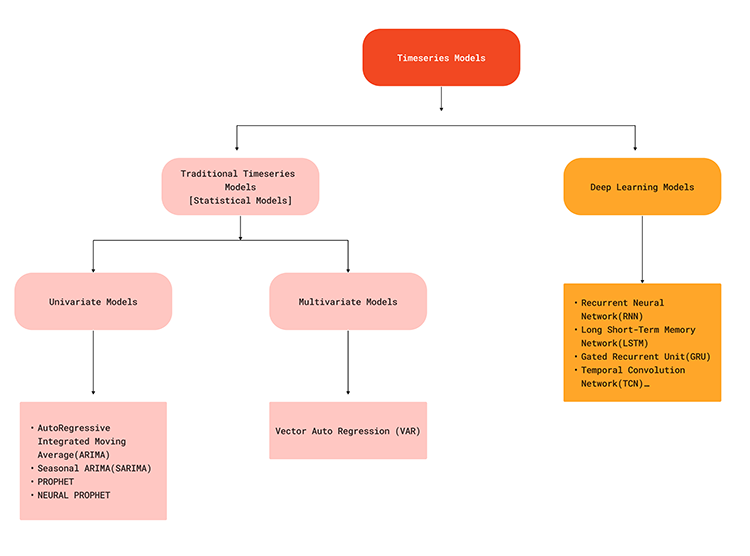
Поскольку модели временных рядов способны фиксировать временные зависимости в данных, их можно использовать для решения щадач прогнозирования на рынке Форекс, ведь все мы знаем, что то, что происходит на рынке в настоящее время, может быть обусловлено некоторыми факторами, которые произошли недавно или когда-то в прошлом. Например, новость по EURUSD, опубликованная 5 минут назад, может стать одним из факторов резкого изменения цены в текущий момент времени. Чтобы лучше это понять, давайте рассмотрим преимущества прогнозирования временных рядов по сравнению с традиционным прогнозированием с использованием моделей машинного обучения.

Характеристики	Прогнозирование временных рядов	Традиционное и современное МО-прогнозирование
Временные зависимости	Способны фиксировать временные закономерности, поскольку учитывают порядок точек данных и зависимости во времени.	Традиционные модели МО рассматривают точки данных как независимые, игнорируя при этом временные зависимости в данных.
Обработка трендов и сезонности	Модели временных рядов, например, ARIMA и другие, имеют встроенные компоненты для обработки тенденций и сезонности.	Требуют ручное извлечение и проектирование функций для учета тенденций и сезонности.
Автокорреляция	Такие модели, как ARIMA и LSTM, могут учитывать автокорреляцию в данных.	Они предполагают, что все признаки независимы, поэтому они не могут учитывать автокорреляцию, если она явно не смоделирована в признаках.
Сложность модели	Модели временных рядов предназначены для задач с использованием последовательных данных.	При работе с традиционными моделями может понадобиться предварительная подготовка признаков для обработки последовательных данных. Это усложняет процесс.
Временные иерархии	Могут распространяться на иерархическое прогнозирование временных рядов (например, ежемесячное, еженедельное).	Традиционные модели могут оказаться неэффективными при прогнозировании в различных временных масштабах без дополнительных разработок.
Прогнозируемая эффективность	Часто обеспечивают лучшую предсказательную эффективность при выполнении временных задач благодаря учету порядка.	Могут не справляться с задачами с временным компонентом.
Вычислительная эффективность	Модели временных рядов можно постепенно обновлять новыми данными.	Традиционным моделям может потребоваться полное переобучение, которое требует больших вычислительных затрат при наличии новых данных.
Интерпретируемые тенденции и сезонность	Такие модели, как ARIMA, предоставляют интерпретируемые компоненты для анализа тенденций и сезонности.	Требуются дополнительные шаги для интерпретации тенденций и сезонности на основе спроектированных признаков.

Несмотря на то, что по умолчанию они не очень хороши для прогнозирования временных рядов, классические и современные модели машинного обучения, такие как LightGBM, XGBoost, CatBoost и пр. можно использовать для прогнозирования временных рядов при условии наличия правильной информации. Все зависит от работы с признаками.

Подготовка признаков для прогнозирования временных рядов

При прогнозировании временных рядов предполагается создание новых и подготовка существующих признаков таким образом, чтобы они содержали важную информацию/компоненты для временных рядов: тренд, сезонность, циклические закономерности, стационарность, автокорреляция и частичная автокорреляция и т.д.

При создании новых признаков для задачи временного ряда следует учитывать множество аспектов. Ниже приведены некоторые из них:

1. Признаки с задержкой

В качестве данных для классического машинного обучения мы часто используем цены OPEN, HIGH, LOW, CLOSE и некоторые другие данные с текущего бара. Данные содержат текущую информацию по каждому конкретному бару и не содержат информации о том, что произошло до этого конкретного бара.

Вводя в наши данные признаки с задержкой, мы охватываем временные зависимости от предыдущих баров, которые определенно имеют отношение к текущей цене бара.

MQL5

//--- getting Open, high, low and close prices
   
   ohlc_struct OHLC;
   
   OHLC.AddCopyRates(Symbol(), timeframe, start_bar, bars);
   time_vector.CopyRates(Symbol(), timeframe, COPY_RATES_TIME, start_bar, bars);
   
//--- Getting the lagged values of Open, High, low and close prices

   ohlc_struct  lag_1;
   lag_1.AddCopyRates(Symbol(), timeframe, start_bar+1, bars);
   
   ohlc_struct  lag_2;
   lag_2.AddCopyRates(Symbol(), timeframe, start_bar+2, bars);
   
   ohlc_struct  lag_3;
   lag_3.AddCopyRates(Symbol(), timeframe, start_bar+3, bars);

В приведенном выше примере мы получаем три признака с задержкой. Поскольку мы собираем эти данные ежедневно, мы получаем информацию за три предыдущих дня для 1000 баров.

Мы копируем MqlRates в векторах начиная с start_bar+1 и получаем бар, идущий перед тем, с которого начинается копирование котировок – start_bar. Если это не совсем понятно, вы можете более подробно почитать об этом в документации https://www.mql5.com/ru/docs/series

MQL5

input int bars = 1000;
input ENUM_TIMEFRAMES timeframe = PERIOD_D1;
input uint start_bar = 2; //StartBar|Must be >= 1

struct ohlc_struct 
{
   vector open;
   vector high;
   vector low;
   vector close;
   
   matrix MATRIX; //this stores all the vectors all-together
   
   void AddCopyRates(string symbol, ENUM_TIMEFRAMES tf, ulong start, ulong size)
    {
      open.CopyRates(symbol, tf, COPY_RATES_OPEN, start, size); 
      high.CopyRates(symbol, tf, COPY_RATES_HIGH, start, size); 
      low.CopyRates(symbol, tf, COPY_RATES_LOW, start, size); 
      close.CopyRates(symbol, tf, COPY_RATES_CLOSE, start, size); 
      
      this.MATRIX.Resize(open.Size(), 4); //we resize it to match one of the vector since all vectors are of the same size
      
      this.MATRIX.Col(open, 0);
      this.MATRIX.Col(high, 1);
      this.MATRIX.Col(low, 2);
      this.MATRIX.Col(close, 3);
    }
};

2. Скользящая статистика

Скользящие статистические данные, такие как среднее значение, стандартное отклонение и другие подобные данные, позволяют обобщить последние тенденции и волатильность в рамках определенного окна. Такие данные можно получить с помощью индикаторов, например скользящей средней за определенный период, стандартного отклонения и т.д.

int ma_handle = iMA(Symbol(),timeframe,30,0,MODE_SMA,PRICE_WEIGHTED); //The Moving averaege for 30 days
int stddev = iStdDev(Symbol(), timeframe, 7,0,MODE_SMA,PRICE_WEIGHTED); //The standard deviation for 7 days
   
vector SMA_BUFF, STDDEV_BUFF;
SMA_BUFF.CopyIndicatorBuffer(ma_handle,0,start_bar, bars);
STDDEV_BUFF.CopyIndicatorBuffer(stddev, 0, start_bar, bars);

Эти скользящие статистические данные дают более широкую картину того, как меняется рынок. Они фиксируют долгосрочные колебания, которые не видны в признаках с задержкой.

3. Признаки даты и времени

Как упоминалось ранее, данные временных рядов имеют временную переменную. Но нужно не просто иметь переменную дата-время, нужно извлечь ее признаки.

Как мы знаем, Форекс демонстрирует определенные закономерности и ведет себя определенным образом в определенные периоды времени. Например, в пятницу обычно нет большой торговой активности, а также рынок становится нестабильным в дни, когда выходят какие-либо важные новости. Кроме того, в некоторые месяцы торговая активность может меняться в лучшую или худшую сторону, то же самое может относиться и к годам. Например, в течение года, когда проходят выборы в определенных странах, например, в США.

Вводя признаки даты и времени, мы явно фиксируем сезонные закономерности, что позволит нашей модели корректировать прогнозы на основе времени года, конкретного дня или месяца и т.д.

Соберем признаки даты и времени в MQL5:

vector time_vector; //we want to add time vector 
time_vector.CopyRates(Symbol(), timeframe, COPY_RATES_TIME, start_bar, bars); //copy the time in seconds


ulong size = time_vector.Size(); 
vector DAY(size), DAYOFWEEK(size), DAYOFYEAR(size), MONTH(size);

MqlDateTime time_struct;
string time = "";
for (ulong i=0; i<size; i++)
  {
    time = (string)datetime(time_vector[i]); //converting the data from seconds to date then to string
    TimeToStruct((datetime)StringToTime(time), time_struct); //convering the string time to date then assigning them to a structure
    
    DAY[i] = time_struct.day;
    DAYOFWEEK[i] = time_struct.day_of_week;
    DAYOFYEAR[i] = time_struct.day_of_year;
    MONTH[i] = time_struct.mon;
  }

4. Дифференцирование

Дифференцирование рядов с сезонными задержками устраняет сезонные закономерности из данных для достижения стационарности, что часто является обязательным требованием для некоторых моделей.

Попробуем вычислить разницу с задержкой lag_1 от текущих цен.

MQL5

vector diff_lag_1_open = OHLC.open - lag_1.open;
vector diff_lag_1_high = OHLC.high - lag_1.high;
vector diff_lag_1_low = OHLC.low - lag_1.low;
vector diff_lag_1_close = OHLC.close - lag_1.close;

На самом деле вы можете вводить сколько угодно задержек, а не только одну, как в примере.

На данный момент у нас имеется 26 независимых переменных/признаков, чего вполне достаточно для наших независимых переменных. Поскольку мы решаем задачу регрессии, давайте соберем цены закрытия в виде окончательной целевой переменной.

vector TARGET_CLOSE;
TARGET_CLOSE.CopyRates(Symbol(), timeframe, COPY_RATES_CLOSE, start_bar-1, bars); //one bar forward

Вы, конечно же, можете создать пользе признаков, если требуется для вашей задачи, учитывая некоторые другие аспекты. Вот несколько примеров:

5. Внешние переменные (экзогенные признаки)

Данные о погоде — попробуйте, может, это поможет
Экономические индикаторы — ВВП, уровень безработицы и т.д. для финансового прогнозирования.

6. Преобразования Фурье и вейвлет-преобразования

Использование преобразований Фурье или вейвлет-преобразований для извлечения циклических закономерностей и тенденций в частотной области.

7. Целевой энкодинг

Вы можете создавать признаки на основе совокупной статистики (среднее, медиана) целевой переменной за различные периоды времени.

Получившийся набор данных содержит 27 столбцов:

Набор данных для прогнозирования временных рядов

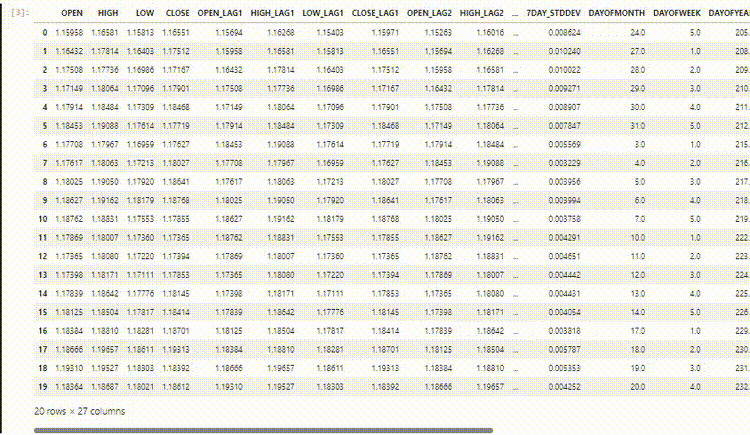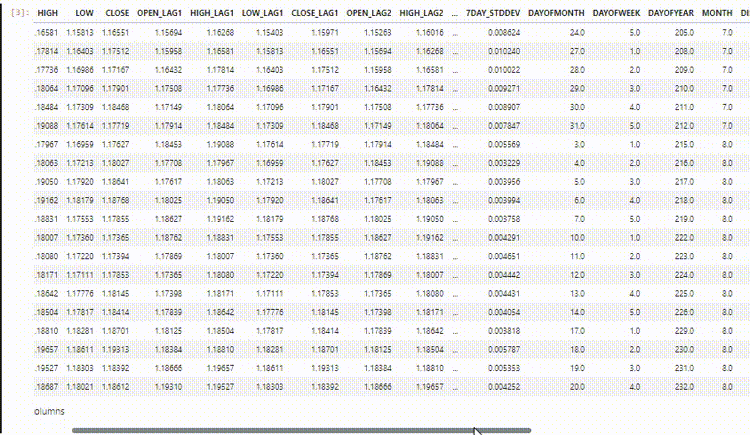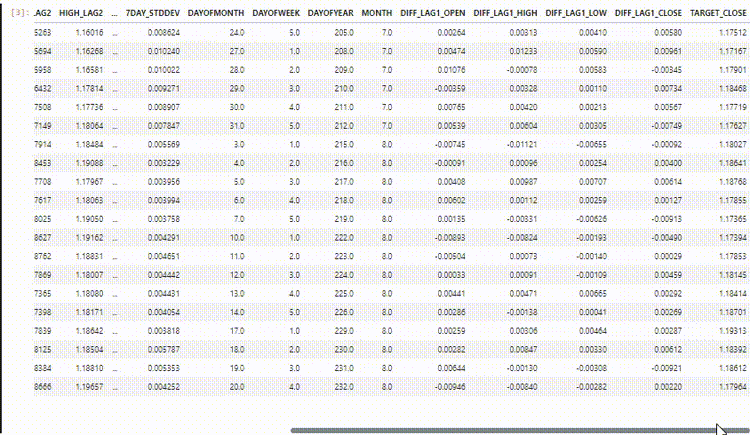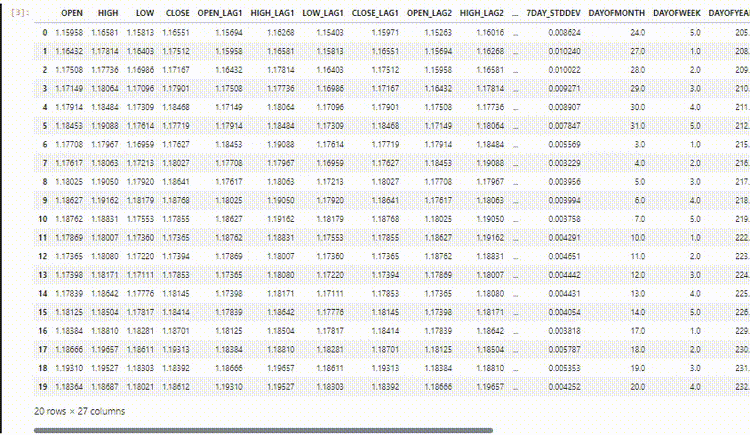
Обучение модели регрессора LightGBM

Теперь, когда у нас есть все необходимые данные, перейдем к Python.

Начнем с разделения данных на обучающую и тестовую выборки.

Python

X = df.drop(columns=["TARGET_CLOSE"])
Y = df["TARGET_CLOSE"]

train_size = 0.7 #configure train size

train_size = round(train_size*df.shape[0])

x_train = X.iloc[:train_size,:]
x_test = X.iloc[train_size:, :]

y_train = Y.iloc[:train_size]
y_test = Y.iloc[train_size:]

print(f"x_train_size{x_train.shape}\nx_test_size{x_test.shape}\n\ny_train{y_train.shape}\ny_test{y_test.shape}")

Результаты

x_train_size(700, 26)
x_test_size(300, 26)

y_train(700,)
y_test(300,)

Обучим модель на обучающих данных.

model = lgb.LGBMRegressor(**params)
model.fit(x_train, y_train)

Протестируем обученную модель, а затем построим графики прогнозов и r2_score.

Python

from sklearn.metrics import r2_score

test_pred = model.predict(x_test)

accuracy = r2_score(y_test, test_pred)

#showing actual test values and predictions

plt.figure(figsize=(8, 6))  
plt.plot(y_test, label='Actual Values')
plt.plot(test_pred, label='Predicted Values')
plt.xlabel('Index')
plt.ylabel('Values')
plt.title('Actual vs. Predicted Values')
plt.legend(loc="lower center")

# Add R-squared (accuracy) score in a corner
plt.text(0.05, 0.95, f"LightGBM (Accuracy): {accuracy:.4f}", ha='left', va='top', transform=plt.gca().transAxes, fontsize=10, bbox=dict(boxstyle='round', facecolor='white', alpha=0.7))

plt.grid(True)

plt.savefig("LighGBM Test plot")
plt.show()

Результат

График тестирования LightGBM

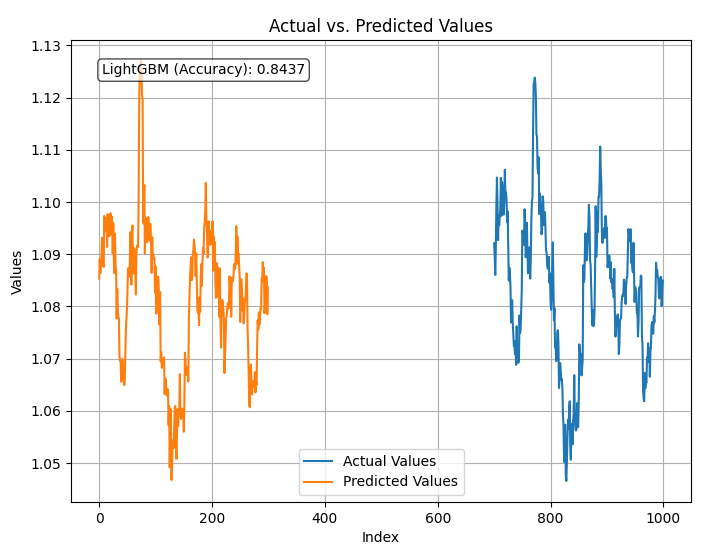
Модель с точностью 84% прогнозирует цены закрытия, используя все предоставленные ей данные. Точность получилась очень хорошей, но нам необходимо изучить все переменные для дальнейшего анализа и улучшения модели.

Используя встроенного метода построения графика LightGBM, мы получили такой график важности признаков.

Python

# Plot feature importance using Gain
lgb.plot_importance(model, importance_type="gain", figsize=(8,6), title="LightGBM Feature Importance (Gain)")

plt.tight_layout()

plt.savefig("LighGBM feature importance(Gain)")
plt.show()

Результат:

Важность признаков в таймсерии по OHLC

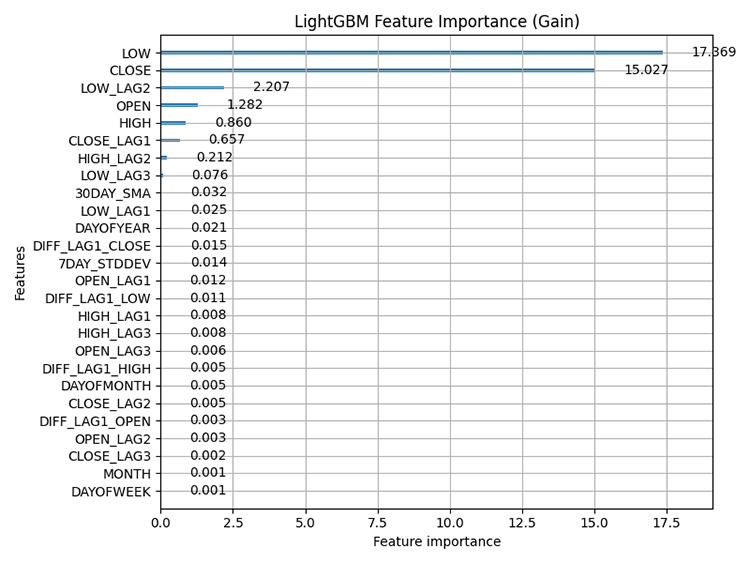
Важность признаков — относится к методам, которые оценивают относительный вклад каждого признака (переменной) в наборе данных в прогнозы, сделанные моделью. Позволяет понять, какие характеристики оказывают наиболее существенное влияние на прогнозы модели.

Важно знать, что методы на основе деревьев, такие как LightGBM и XGBoost, вычисляют важность признаков иначе, чем модели, не основанные на деревьях. Они учитывают, как часто признак используется для принятия решений о разделении в деревьях, и влияние этих разделений на окончательный прогноз.

В качестве альтернативы можно использовать SHAP для проверки важности признаков.

Python:

explainer = shap.TreeExplainer(model)
shap_values = explainer(x_train)  

shap.summary_plot(shap_values, x_train, max_display=len(x_train.columns), show=False)  # Show all features

# Adjust layout and set figure size
plt.subplots_adjust(left=0.12, bottom=0.1, right=0.9, top=0.9)  
plt.gcf().set_size_inches(6, 8) 
plt.tight_layout()

plt.savefig("SHAP_Feature_Importance_Summary_Plot.png")
plt.show()

Результат:

Данные о важности признаков во временных рядах по SHAP

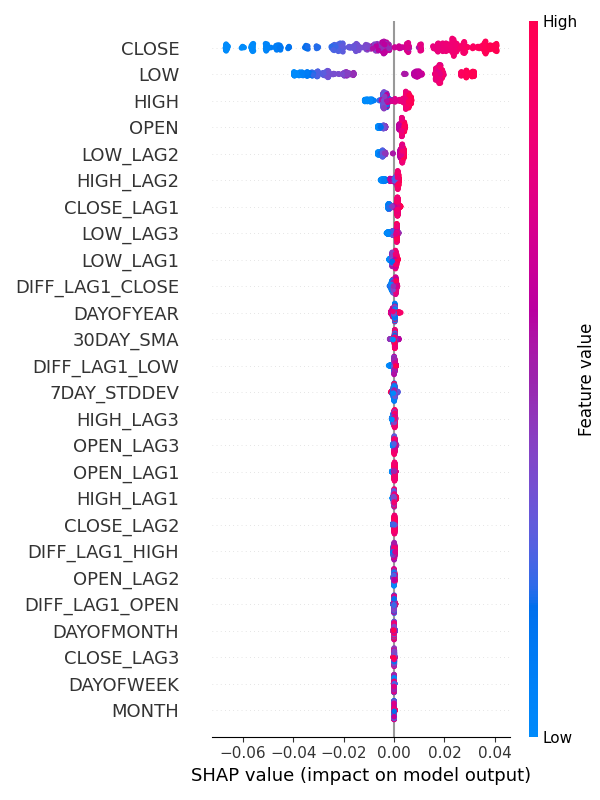
Из графиков важности признаков ясно, что переменные DAYOFWEEK, MONTH, DAYOFMONTH и DAYOFYEAR, отражающие сезонные закономерности, — одни из переменных, вносящих наименьший вклад в прогнозы модели.

Как ни странно, все они стационарны, согласно Расширенному тесту Дики-Фуллера.

Расширенный тест Дики-Фуллера (ADF)

Это статистический тест, используемый для определения того, является ли набор данных временного ряда стационарным или нет. Стационарность является важнейшим свойством многих методов прогнозирования и анализа временных рядов.

Стационарная переменная или стационарный набор данных относится к ряду, статистические свойства которого (среднее значение, дисперсия, автокорреляция) остаются постоянными с течением времени. Например, на фондовом рынке. Среднее значение OHLC может значительно увеличиваться или уменьшаться с течением времени, таким образом эти значения нестационарны в большинстве случаев. Между тем среднее значение или дисперсия разницы между High и Low стационарны во времени.

Я запускал следующий тест на имеющемся у нас наборе данных.

from statsmodels.tsa.stattools import adfuller

def adf_test(series, signif=0.05):
  """
  Performs the ADF test on a pandas Series and interprets the results.

  Args:
      series: The pandas Series containing the time series data.
      signif: Significance level for the test (default: 0.05).

  Returns:
      A dictionary containing the test statistic, p-value, used lags,
      critical values, and interpretation of stationarity.
  """
  dftest = adfuller(series, autolag='AIC')
  adf_stat = dftest[0]  # Access test statistic
  pvalue = dftest[1]  # Access p-value
  usedlag = dftest[2]  # Access used lags
  critical_values = dftest[4]  # Access critical values

  interpretation = 'Stationary' if pvalue < signif else 'Non-Stationary'
  result = {'Statistic': adf_stat, 'p-value': pvalue, 'Used Lags': usedlag,
            'Critical Values': critical_values, 'Interpretation': interpretation}
  return result

for col in df.columns:
  adf_results = adf_test(df[col], signif=0.05)
  print(f"ADF Results for column {col}:\n {adf_results}")

Из 27 переменных только 9 оказались стационарными. Это переменные:

7DAY_STDDEV
DAYOFMONTH
DAYOFWEEK
DAYOFYEAR
MONTH
DIFF_LAG1_OPEN
DIFF_LAG1_HIGH
DIFF_LAG1_LOW
DIFF_LAG1_CLOSE

Определить, являются ли переменные стационарными, можно по графику распределения. Данные, распределенные вокруг среднего значения, являются стационарными.

Стационарные и нестационарные данные

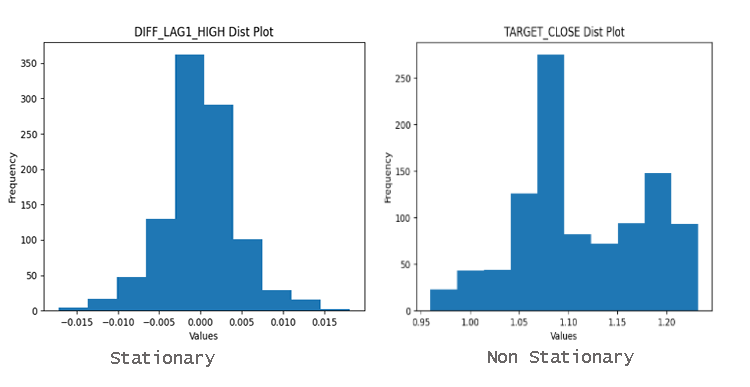
Значение стационарности

Многие статистические методы, используемые при анализе и прогнозировании временных рядов, предполагают стационарность. Если временной ряд нестационарен, эти методы могут давать путающие или неточные результаты.

Давайте подумаем о том, как спрогнозировать будущие цены акций, если они постоянно растут. Модель временного ряда не сможет уловить основную тенденцию.

Классический и даже более современные модели машинного обучения, такие как LightGBM, которые мы использовали, способны обрабатывать нелинейные зависимости между признаками, делая их менее подверженными влиянию стационарности, присутствующей в данных. Важность признаков для этой модели ясно продемонстрировала, что наиболее важными признаками для нашей модели являются нестационарные переменные OHLC.

Однако это не означает, что такие переменные, как день недели, не оказывают влияния на модель. По моему мнению, важность функций — это лишь часть большой истории.

Не нужно исключать эту переменную из-за того, что она имеет более низкий рейтинг, поскольку я уверен, что она влияет на EURUSD.

Прогнозирование стационарной целевой переменной

Наличие стационарной целевой переменной повышает эффективность многих моделей машинного обучения при прогнозировании временных рядов, поскольку стационарные данные имеют постоянную величину (среднее значение, дисперсию, автокорреляцию) во времени. Как вы знаете, предсказать, куда пойдет рынок на следующей свече, сложно, но предсказать количество пипсов или пунктов следующего движения не так уж и сложно.

Если мы можем предсказать количество пунктов, которое сгенерирует следующий бар, мы можем использовать это для установки торговых уровней стоп-лосс и тейк-профит.

Для этого нужно найти разность первого порядка — вычесть предыдущую цену закрытия из следующей цены закрытия.

Python

Y = df["TARGET_CLOSE"] - df["CLOSE"] #first order differencing

Вычисляя разницу между следующими ценами закрытия и предыдущими, мы получаем стационарную переменную.

adf_results = adf_test(Y,signif=0.05)

print(f"ADF Results:\n {adf_results}")

Результат:

ADF Results: {'Statistic': -23.37891429248752, 'p-value': 0.0, 'Used Lags': 1, 'Critical Values': {'1%': -3.4369193380671, '5%': -2.864440383452517, '10%': -2.56831430323573}, 'Interpretation': 'Stationary'}

Мы обучили модель регрессора на новой стационарной целевой переменной и оценили ее эффективности на тестовом наборе данных. Результат получился таким:

Прогнозирование стационарной цели в таймсерии с Lightgbm

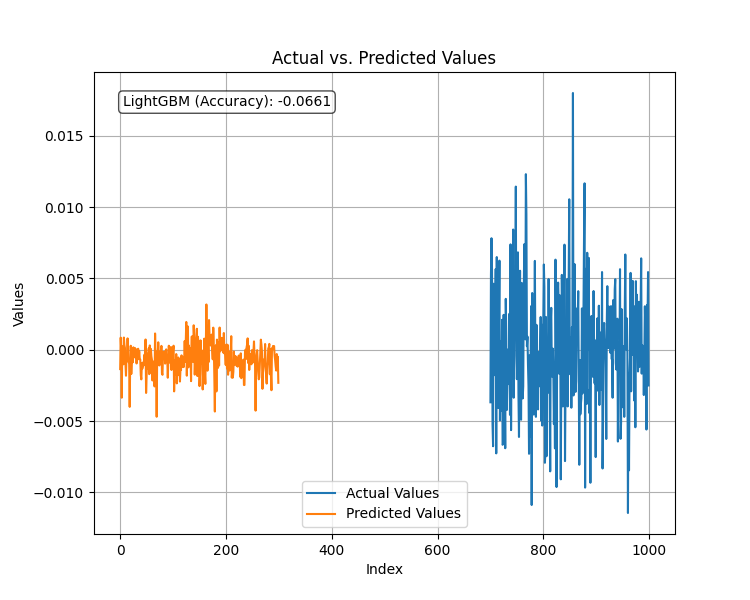
Модель показала ужасные результаты, когда целевая переменная была стационарной. Как всегда в машинном обучении, на это может влиять множество факторов, но на данный момент мы приходим к выводу, что LightGBM не очень хорошо работает для стационарных целевых переменных. Мы будем придерживаться регрессионной модели, созданной для прогнозирования целевых значений цены закрытия.

Наличие этой регрессионной модели, которая предсказывает непрерывные значения цен закрытия, не так полезно, как наличие модели, которая предсказывает торговые сигналы, т.е. покупку или продажу. Для этого нам нужно создать еще одну модель для прогнозирования торговых сигналов.

Построение модели классификатора LightGBM

Чтобы создать модель классификатора, нам необходимо подготовить бинарную целевую переменную, где 1 представляет сигнал на покупку, а 0 — сигнал на продажу.

Python

Y = []
target_open = df["TARGET_OPEN"]
target_close = df["TARGET_CLOSE"]

for i in range(len(target_open)):
    if target_close[i] > target_open[i]: # if the candle closed above where it opened thats a buy signal
        Y.append(1)
    else: #otherwise it is a sell signal
        Y.append(0)

# split Y into irrespective training and testing samples 

y_train = Y[:train_size]
y_test = Y[train_size:]

Я обучил модель LightGBM в Pipeline с использованием алгоритма StandardScaler.

Python

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

params = {
    'boosting_type': 'gbdt',  # Gradient Boosting Decision Tree
    'objective': 'binary',  # For binary classification (use 'regression' for regression tasks)
    'metric': ['auc','binary_logloss'],  # Evaluation metric
    'num_leaves': 25,  # Number of leaves in one tree
    'n_estimators' : 100, # number of trees
    'max_depth': 5,
    'learning_rate': 0.05,  # Learning rate
    'feature_fraction': 0.9  # Fraction of features to be used for each boosting round
}

pipe = Pipeline([
    ("scaler", StandardScaler()),
    ("lgbm", lgb.LGBMClassifier(**params))
])

# Fit the pipeline to the training data
pipe.fit(x_train, y_train)

Результаты тестирования не были поразительными: общая точность составила 53%.

Отчет о классификации:

Classification Report
               precision    recall  f1-score   support

           0       0.49      0.79      0.61       139
           1       0.62      0.30      0.40       161

    accuracy                           0.53       300
   macro avg       0.56      0.54      0.51       300
weighted avg       0.56      0.53      0.50       300

Матрица путаницы

Матрица путаницы lightGBM

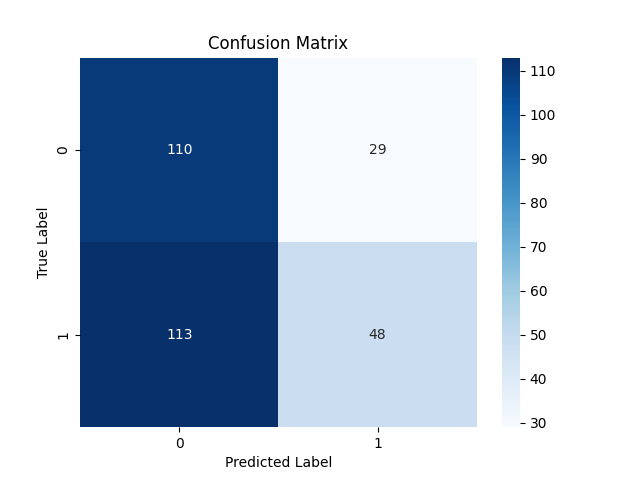
Сохранение модели классификатора LightGBM в ONNX

Процесс сохранения модели LightGBM в формате ONNX очень прост и требует всего нескольких строк кода — его мы уже рассматривали ранее.

import onnxmltools
from onnxmltools.convert import convert_lightgbm
import onnxmltools.convert.common.data_types
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx import convert_sklearn, update_registered_converter

from skl2onnx.common.shape_calculator import (
    calculate_linear_classifier_output_shapes,
)  # noqa

from onnxmltools.convert.lightgbm.operator_converters.LightGbm import (
    convert_lightgbm,
)  # noqa

# registering onnx converter

update_registered_converter(
    lgb.LGBMClassifier,
    "GBMClassifier",
    calculate_linear_classifier_output_shapes,
    convert_lightgbm,
    options={"nocl": [False], "zipmap": [True, False, "columns"]},
)

# Final LightGBM conversion to ONNX

model_onnx = convert_sklearn(
    pipe,
    "pipeline_lightgbm",
    [("input", FloatTensorType([None, x_train.shape[1]]))],
    target_opset={"": 12, "ai.onnx.ml": 2},
)

# And save.
with open("lightgbm.Timeseries Forecasting.D1.onnx", "wb") as f:
    f.write(model_onnx.SerializeToString())

Оборачиваем все в торгового робота

Теперь у нас есть модель машинного обучения, сохраненная в ONNX. И мы можем напрямую подключить его к советнику и использовать классификатор LightGBM для прогнозирования временных рядов в MetaTrader 5.

MQL5

#resource "\\Files\\lightgbm.Timeseries Forecasting.D1.onnx" as uchar lightgbm_onnx[] //load the saved onnx file 
#include <MALE5\LightGBM\LightGBM.mqh>
CLightGBM lgb;

Используя класс LightGBM, который мы построили в предыдущей статье, мне инициализировали модель и использовали ее для составления прогнозов.

int OnInit()
  {
//---
   
   if (!lgb.Init(lightgbm_onnx)) //Initialize the LightGBM model
     return INIT_FAILED;
   
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---
    
   if (NewBar()) //Trade at the opening of a new candle
    {
     vector input_vector = input_data(); 
     long signal = lgb.predict_bin(input_vector);
     
   //---
     
      MqlTick ticks;
      SymbolInfoTick(Symbol(), ticks);
      
      if (signal==1) //if the signal is bullish
       {
          if (!PosExists(POSITION_TYPE_BUY)) //There are no buy positions
           {
             if (!m_trade.Buy(lotsize, Symbol(), ticks.ask, ticks.bid-stoploss*Point(), ticks.ask+takeprofit*Point())) //Open a buy trade
               printf("Failed to open a buy position err=%d",GetLastError());
           }
       }
      else if (signal==0) //Bearish signal
        {
          if (!PosExists(POSITION_TYPE_SELL)) //There are no Sell positions
            if (!m_trade.Sell(lotsize, Symbol(), ticks.bid, ticks.ask+stoploss*Point(), ticks.bid-takeprofit*Point())) //open a sell trade
               printf("Failed to open a sell position err=%d",GetLastError());
        }
      else //There was an error
        return;
    }
  }

Функция input_data() отвечает за данные, а они собираются и сохраняются в CSV-файле с помощью скрипта Feature engineering Timeseries forecasting.mq5.

Тестирование модели в тестере стратегий

Наконец, мы можем протестировать модель в торговой среде. Поскольку данные были собраны на дневном таймфрейме, было бы неплохо протестировать их на более низком таймфрейме, чтобы избежать ошибок market closed, поскольку торговый сигнал проверяется при открытии нового бара. Можно установить тип моделирования по ценам открытия для более быстрого тестирования.

Настройки тестера

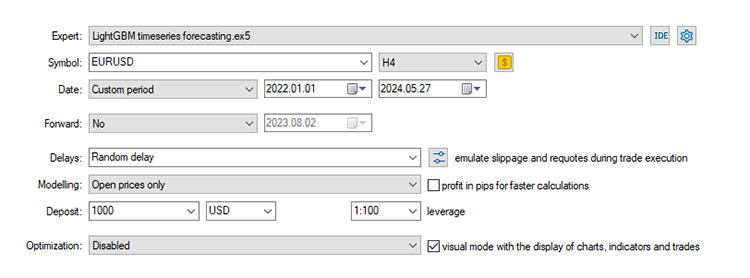
Советник делал верные прогнозы примерно в 51% случаев, учитывая стоп-лосс и тейк-профит в 500 и 700 пунктов соответственно.

Отчет тестера стратегий Metatrader 5

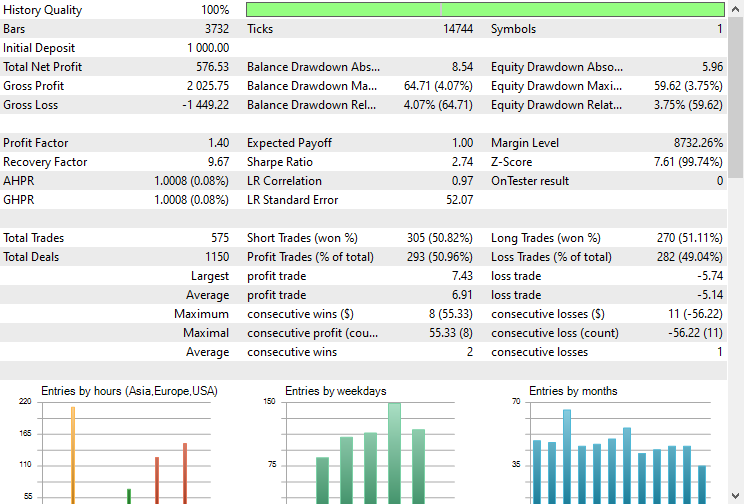
Кривая баланса/капитала получилась впечатляющей.

График тестера Metatrader 5

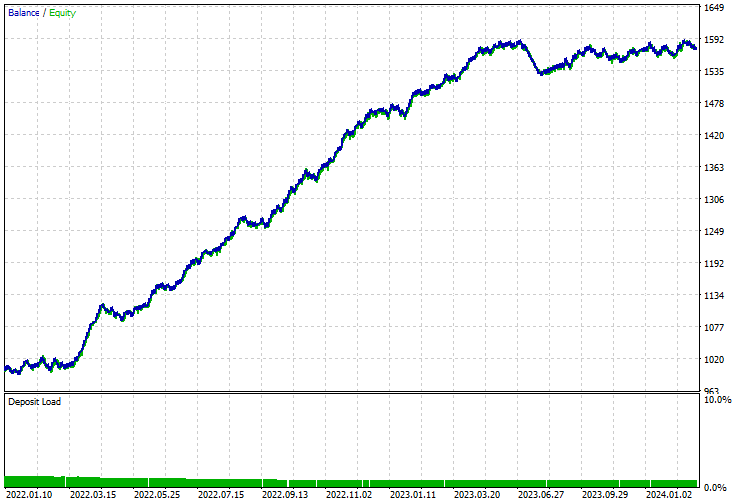
Преимущества использования классических и современных моделей для прогнозирования временных рядов

Использование моделей машинного обучения, не основанных на временных рядах, для прогнозирования временных рядов имеет ряд преимуществ. Ниже приведены некоторые из них:

1. Гибкость в проектировании функций

Классические модели машинного обучения допускают обширную разработку признаков, которую можно использовать для включения различных внешних переменных и производных признаков. Вы можете вручную анализировать и включать те данные, которые посчитаете полезными, включая сложные функции, такие как задержки и скользящая статистика — именно это мы сделали в этой статье.

2. Управление нестационарностью

Вместо того чтобы делать ряд стационарным посредством дифференцирования, можно включить тренд и сезонность непосредственно в качестве признаков, и модель с легкостью изучит закономерности.

3. Нет допущений относительно распределения данных

Многие классические модели временных рядов (например, ARIMA) предполагают, что данные следуют определенному статистическому распределению. С другой стороны, классические и современные модели МО более гибки в отношении распределения данных.

Такие модели, как деревья решений, случайные леса и градиентный бустинг (включая LightGBM), не предполагают какого-либо конкретного распределения данных.

4. Масштабируемость

Классические модели машинного обучения могут более эффективно обрабатывать большие наборы данных и зачастую их легче масштабировать.

5. Сложные взаимодействия

Модели машинного обучения способны улавливать сложные нелинейные связи между признаками и целевой переменной.

6. Устойчивость к отсутствующим данным

Модели машинного обучения часто обладают лучшими механизмами обработки отсутствующих данных по сравнению с традиционными моделями временных рядов.

7. Ансамблевые методы

Можно использовать ансамблевые методы, такие как бэггинг, бустинг и стекирование, для повышения производительности модели путем объединения нескольких моделей с целью улучшения прогностической эффективности и надежности.

8. Простота использования и интеграции

Классические модели машинного обучения зачастую более удобны для пользователя и поставляются с обширными библиотеками и инструментами для реализации, визуализации и оценки.

Такие библиотеки, как Scikit-learn, LightGBM и XGBoost, предоставляют комплексные инструменты для создания, настройки и оценки этих моделей.

Заключение

Классические и современные модели машинного обучения вполне можно использовать для анализа и прогнозирования временных рядов. Более того, они могут превзойти модели временных рядов при наличии правильной информации, настройки и процессов. Я решил использовать LightGBM в качестве примера, однако для таких задач может подойти любая классическая или современная модель машинного обучения, включая SVM, Linear Regression, Naïve Bayes, XGBoost и пр.

Всем добра.

За развитием этой модели машинного обучения и многого другого из этой серии статей можно следить в моем репозиторий на GitHub.

Таблица вложений

Наименование файла	Тип файла	Описание и использование
LightGBM timeseries forecasting.mq5	Expert	Торговый робот для загрузки модели ONNX и тестирования финальной торговой стратегии в MetaTrader 5.
lightgbm.Timeseries Forecasting.D1.onnx	ONNX	Модель LightGBM в формате ONNX.
LightGBM.mqh	Include-файл (библиотека)	Состоит из кода для загрузки модели в формате ONNX и развертывания его на языке MQL5.
Feature engineering Timeseries forecasting.mq5	Скрипт	Это скрипт, в котором все данные собираются и обрабатываются для анализа временных рядов и прогнозирования.
forex-timeseries-forecasting-lightgbm.ipynb	Python-скрипт (Jupyter Notebook)	Этот блокнот содержит весь код Python, обсуждаемый в этой статье.

Источники и ссылки:

Time Series Talk: Stationarity (https://youtu.be/oY-j2Wof51c)
Kishan Manani - Feature Engineering for Time Series Forecasting | PyData London 2022 (https://www.youtube.com/watch?v=9QtL7m3YS9I)
Stock Market Prediction via Deep Learning Techniques: A Survey (https://arxiv.org/abs/2212.12717)
Challenges in Time Series Forecasting (https://www.youtube.com/watch?v=rcdDl8qf0ZA)
Stationarity and differencing (https://otexts.com/fpp2/stationarity.html)
How to perform Target/Mean Encoding for Categorical Attributes | Python (https://www.youtube.com/watch?v=nd7vc4MZQz4)

Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/15013

Прикрепленные файлы |

Загрузить ZIP

Attachments.zip (317.52 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Изучаем индикатор рыночного профиля — Market Profile: Что это и как устроен?

Сегодня познакомимся с "Профилем рынка". Узнаем что лежит за этим названием, попробуем разобраться в принципах работы с Профилем и рассмотрим представленную в терминале его версию под названием MarketProfile.

Циклы и трейдинг

Эта статья посвящена использованию циклов в трейдинге. В ней мы постараемся разобраться, как можно построить торговую стратегию, основываясь на циклических моделях.

Построение модели для ограничения диапазона сигналов по тренду (Часть 5): Система уведомлений (Часть I)

Мы разобьем основной код MQL5 на отдельные фрагменты, чтобы проиллюстрировать интеграцию Telegram и WhatsApp для получения уведомлений о сигналах от индикатора Trend Constraint, который мы создаем в этой серии статей. Статья будет полезна трейдерам, а также начинающим и опытным разработчикам. Сначала мы рассмотрим настройку уведомлений в MetaTrader 5 и пользу их подключения для пользователя. На основе этого разработчики смогут отметить для себя определенные моменты для дальнейшего применения в своих системах.

Нелинейные регрессионные модели на бирже

Нелинейные регрессионные модели на бирже: реально ли прогнозировать финансовые рынки? Попробуем создать моделеь для прогноза цен на евро-доллар, и сделать на ее основе двух роботов - на Python и MQL5.