Обучение нелинейного U-Transformer на остатках линейной авторегрессионной модели

В современном алгоритмическом трейдинге перед разработчиками стоит фундаментальная дилемма: линейные модели просты и интерпретируемы, но неспособны захватывать сложные нелинейные зависимости в финансовых временных рядах. Глубокие нейронные сети, напротив, теоретически могут моделировать любые нелинейности, но страдают от переобучения и нестабильности в условиях высокого рыночного шума и ограниченных объемов данных.

Данная статья представляет инновационный гибридный подход, решающий эту дилемму через двухэтапное моделирование: сначала линейная авторегрессионная модель с 25 признаками извлекает основные статистические закономерности из ценовых данных, затем специализированная U-Transformer архитектура обучается на остатках линейной модели, выявляя скрытые нелинейные паттерны, которые не смогла захватить первая ступень.

Ключевая инновация заключается в адаптации архитектуры U-Net (изначально созданной для сегментации изображений) с интеграцией Transformer-блоков для анализа временных рядов. Система реализована на языке MQL5 и включает полноценную торговую логику с динамическим управлением позициями, автоматической реоптимизацией параметров и онлайн-обучением нейросети.

Экспериментальная валидация демонстрирует превосходство гибридного подхода над чисто линейными методами, при этом сохраняя вычислительную эффективность и интерпретируемость результатов. Представленная система способна работать в режиме реального времени, автоматически адаптируясь к изменяющимся рыночным условиям.

Введение

Финансовые рынки представляют собой сложные адаптивные системы, где традиционные методы прогнозирования сталкиваются с рядом фундаментальных вызовов. Первый и наиболее очевидный из них — это проблема нелинейности. Рыночные данные демонстрируют сложные паттерны, которые не поддаются описанию простыми линейными зависимостями: режимные переключения в волатильности, асимметричные реакции на новости, каскадные эффекты ликвидности. Однако, попытки применить мощные нелинейные модели машинного обучения к финансовым данным часто приводят ко второй проблеме — переобучению и нестабильности предсказаний.

Эта проблема особенно остро стоит в алгоритмическом трейдинге, где модель должна не только точно предсказывать направление движения цены, но и делать это стабильно в различных рыночных режимах, при этом оставаясь вычислительно эффективной для работы в реальном времени. Классические эконометрические модели типа ARIMA или VAR обеспечивают стабильность и интерпретируемость, но их линейная природа накладывает жесткие ограничения на способность моделировать сложную динамику рынка.

С другой стороны, современные архитектуры глубокого обучения — LSTM, GRU, Transformer — теоретически способны аппроксимировать любые нелинейные зависимости, но их применение к финансовым данным осложняется несколькими факторами. Во-первых, высокий уровень шума в рыночных данных приводит к тому, что нейросети начинают "запоминать" случайные флуктуации вместо изучения истинных закономерностей. Во-вторых, нестационарность финансовых рядов означает, что паттерны, изученные на исторических данных, могут быстро терять актуальность.

Третья проблема носит практический характер: вычислительные ограничения торговых платформ, особенно в языке MQL5, не позволяют использовать современные фреймворки глубокого обучения в полном объеме. Разработчик вынужден реализовывать нейросетевые алгоритмы "с нуля", что существенно ограничивает сложность применимых архитектур.

Предлагаемое в данной работе решение основано на идее декомпозиции задачи прогнозирования на два этапа с различной природой: линейный этап для захвата основных статистических закономерностей и нелинейный этап для моделирования сложных остаточных зависимостей. Такой подход позволяет использовать сильные стороны обоих классов методов, минимизируя их недостатки.

Линейная авторегрессионная модель первого этапа строится на тщательно спроектированном пространстве из 25 признаков, включающих не только классические ценовые лаги, но и их нелинейные трансформации, технические индикаторы и циклические компоненты. Эта модель оптимизируется с помощью градиентного спуска и обеспечивает базовый уровень качества предсказаний с высокой интерпретируемостью.

Нейросетевая компонента второго этапа использует адаптированную архитектуру U-Transformer, которая объединяет принципы U-Net (энкодер-декодер структура с skip-connections) и механизмы внимания из Transformer архитектуры. Ключевая особенность этого подхода заключается в том, что нейросеть обучается не на исходных ценовых данных, а на остатках линейной модели, что существенно упрощает задачу и снижает риск переобучения.

Такая декомпозиция обеспечивает естественную регуляризацию: если рыночные условия изменились, и нейросетевая компонента стала давать неустойчивые предсказания, система автоматически переключается на более консервативные предсказания линейной модели. Это достигается через адаптивную схему взвешивания, где вес нейросетевой компоненты зависит от текущего качества обеих моделей.

Теоретические основы архитектуры U-Transformer

Архитектура U-Transformer представляет собой синтез двух мощных концепций компьютерного зрения и обработки естественного языка: U-Net и механизмов внимания (attention). Изначально U-Net была разработана для задач сегментации медицинских изображений, где требуется точная локализация объектов при сохранении глобального контекста. Ключевая идея U-Net заключается в симметричной энкодер-декодер архитектуре с горизонтальными skip-connections, которые позволяют передавать детализированную информацию с ранних слоев напрямую к поздним слоям декодера.

В контексте анализа временных рядов эта архитектура приобретает новый смысл. Энкодер последовательно сжимает временную информацию, выделяя все более абстрактные паттерны, в то время как декодер восстанавливает временное разрешение, используя как абстрактные представления, так и детализированные признаки через skip-connections. Это особенно важно для финансовых данных, где локальные флуктуации могут быть столь же значимы, как и глобальные тренды.

struct UTransformerNet
{
    NeuralLayer encoder_layers[3];     // Энкодер: сжатие информации
    NeuralLayer decoder_layers[3];     // Декодер: восстановление разрешения
    AttentionBlock attention_heads[4]; // Multi-head attention
    double skip_connections[3][32];    // Горизонтальные связи U-Net
    double residuals[6000];            // Остатки для обучения
    double neural_predictions[6000];   // Предсказания нейросети
};

Механизм self-attention, заимствованный из архитектуры Transformer, добавляет способность модели динамически фокусироваться на наиболее релевантных частях входной последовательности. В отличие от сверточных или рекуррентных слоев, attention позволяет модели напрямую связывать отдаленные во времени события, что критически важно для финансовых рынков, где влияние событий может проявляться с задержкой.

void SelfAttention(double &inputs[], AttentionBlock &attention, double &outputs[])
{
    double queries[32], keys[32], values[32];
    
    // Вычисление Q, K, V трансформаций
    for (int i = 0; i < NeuralNodes; i++)
    {
        queries[i] = 0; keys[i] = 0; values[i] = 0;
        for (int j = 0; j < NeuralNodes; j++)
        {
            queries[i] += inputs[j] * attention.query_weights[j][i];
            keys[i] += inputs[j] * attention.key_weights[j][i];
            values[i] += inputs[j] * attention.value_weights[j][i];
        }
    }
    
    // Вычисление attention scores: Q × K^T
    for (int i = 0; i < NeuralNodes; i++)
    {
        attention.attention_scores[i] = 0;
        for (int j = 0; j < NeuralNodes; j++)
        {
            attention.attention_scores[i] += queries[i] * keys[j];
        }
        attention.attention_scores[i] /= MathSqrt(NeuralNodes); // Масштабирование
    }
}

Ключевое отличие предлагаемой архитектуры от классических Transformer заключается в адаптации для одномерных временных рядов вместо двумерных последовательностей токенов. Вместо позиционного кодирования используются временные признаки (час дня, циклические компоненты), что позволяет модели учитывать внутридневную сезонность торговых сессий.

Гибридная модель: линейная регрессия плюс нейросеть

Центральная идея гибридного подхода заключается в аддитивной декомпозиции прогноза на две компоненты с различной природой:

Финальное_предсказание = Линейная_модель(X) + α × U_Transformer(Остатки)

где α — адаптивный весовой коэффициент, зависящий от текущего качества обеих моделей.

Линейная компонента строится как классическая авторегрессионная модель с расширенным пространством признаков:

// Вычисление линейного предсказания
double linear_pred = 0;
for (int i = 0; i < 25; i++)
    linear_pred += g_pair.coeffs[i] * features[i];

Нейросетевая компонента обучается не на исходных ценовых данных, а на остатках линейной модели:

void TrainUTransformer()
{
    // Вычисление остатков линейной модели
    for (int i = 0; i < g_pair.data_size; i++)
    {
        double linear_pred = 0;
        for (int j = 0; j < 25; j++)
            linear_pred += g_pair.coeffs[j] * g_pair.features[i][0][j];
        
        g_pair.neural_net.residuals[i] = g_pair.prices[i] - linear_pred;
    }
    
    // Обучение нейросети на остатках
    for (int epoch = 0; epoch < NeuralEpochs; epoch++)
    {
        double total_loss = 0;
        for (int i = 0; i < g_pair.data_size; i++)
        {
            double prediction = UTransformerForward(g_pair.coeffs, 
                                                   g_pair.neural_net.residuals[i]);
            double error = prediction - g_pair.neural_net.residuals[i];
            total_loss += error * error;
        }
    }
}

Такая декомпозиция обеспечивает несколько критических преимуществ. Во-первых, нейросеть решает значительно более простую задачу — моделирование остатков вместо исходного ряда. Остатки, как правило, имеют меньшую дисперсию и более стационарные статистические свойства, что упрощает обучение и снижает риск переобучения.

Во-вторых, система естественным образом реализует принцип "fail-safe": если нейросетевая компонента начинает давать неустойчивые предсказания (высокий loss), система автоматически увеличивает вес линейной компоненты:

double GetHybridPrediction(double price_t1, double price_t2, double price_t3)
{
    // Линейное предсказание
    double linear_pred = 0;
    for (int i = 0; i < 25; i++)
        linear_pred += g_pair.coeffs[i] * features[i];
    
    // Нейросетевая коррекция
    double neural_correction = 0;
    if (g_pair.neural_net.is_trained)
    {
        neural_correction = UTransformerForward(g_pair.coeffs, 0);
    }
    
    // Адаптивное взвешивание
    double confidence = MathMin(g_pair.current_r2, 0.8);
    double neural_weight = g_pair.neural_net.is_trained ? (1.0 - confidence) : 0.0;
    
    return linear_pred + neural_weight * neural_correction;
}

Коэффициент neural_weight автоматически адаптируется к качеству модели: при высоком R² линейной компоненты (хорошее качество) нейросетевая добавка получает меньший вес, при низком R² — больший. Это обеспечивает устойчивость системы в различных рыночных режимах и предотвращает ситуации, когда плохо обученная нейросеть портит качественные линейные предсказания.

Многомерное пространство признаков и feature engineering

Качество любой модели машинного обучения критически зависит от информативности входных признаков. В финансовом прогнозировании эта зависимость проявляется особенно остро, поскольку рыночные данные характеризуются высоким уровнем шума и нестационарностью. Предлагаемая система использует тщательно спроектированное 25-мерное пространство признаков, которое включает как классические ценовые лаги, так и их нелинейные трансформации, технические индикаторы и циклические компоненты.

Базовый набор признаков включает прямые и квадратичные термы ценовых лагов:

void CalculateFeatures(double price_t1, double price_t2, double price_t3, 
                      int bar_index, string symbol, double &features[])
{
    // Линейные ценовые компоненты
    features[0] = price_t1;                    // X(t-1)
    features[1] = MathPow(price_t1, 2);        // X(t-1)²
    features[2] = price_t2;                    // X(t-2)
    features[3] = MathPow(price_t2, 2);        // X(t-2)²
    features[4] = price_t3;                    // X(t-3)
    
    // Разностные операторы (momentum)
    features[5] = (price_t1 - price_t2);      // Краткосрочный momentum
    features[9] = (price_t1 - price_t3);      // Среднесрочный momentum
    features[18] = MathPow(price_t1 - price_t2, 2); // Квадратичный momentum
}

Циклические компоненты моделируют периодические закономерности на различных временных масштабах:

// Низкочастотные циклы (дневная сезонность)
    features[6] = MathSin(price_t1);
    features[7] = MathCos(price_t1);
    
    // Высокочастотные циклы (внутридневные паттерны)
    features[13] = MathSin(price_t1 * 1000);
    features[14] = MathCos(price_t1 * 1000);
    
    // Временная компонента (час торговой сессии)
    datetime bar_time = iTime(symbol, PERIOD_H1, bar_index);
    MqlDateTime dt;
    TimeToStruct(bar_time, dt);
    features[17] = (dt.hour / 24.0);

Нелинейные трансформации помогают модели адаптироваться к различным режимам волатильности:

// Корневые и экспоненциальные трансформации
    features[15] = MathSqrt(MathAbs(price_t1));
    features[16] = MathExp(-MathAbs(price_t1 - price_t2));
    
    // Гиперболический тангенс для ограничения выбросов
    features[23] = MathTanh(price_t1 - ma);

Технические индикаторы добавляют информацию о рыночной микроструктуре:

// RSI и его нелинейные версии
    double rsi = 50.0; // Упрощенный расчет для демонстрации
    features[10] = (rsi / 100.0);
    features[21] = MathPow(rsi / 100.0, 2);
    
    // Отклонение от скользящей средней
    double ma = price_t1; // Упрощенный расчет
    features[11] = (price_t1 - ma);
    
    // Волатильность (ATR)
    double atr = MathAbs(price_t1 - price_t2);
    features[12] = atr;
    features[20] = (atr * (price_t1 - price_t2)); // Взаимодействие волатильности и momentum

Особую категорию составляют признаки взаимодействия, которые моделируют нелинейные эффекты между различными компонентами:

// Парные взаимодействия
    features[8] = (price_t1 * price_t2);
    features[19] = (price_t1 / price_t2);
    
    // Тройные взаимодействия
    features[22] = (price_t1 * price_t2 * price_t3);
    
    // Константный терм
    features[24] = 1.0;

Такое многообразие признаков позволяет линейной модели захватывать широкий спектр рыночных закономерностей, от простых трендовых движений до сложных нелинейных паттернов. При этом нейросетевая компонента обучается на остатках этой богатой линейной модели, что существенно упрощает ее задачу.

Структуры данных и организация памяти в MQL5

Реализация сложных алгоритмов машинного обучения в среде MQL5 требует особого внимания к организации памяти и структур данных. В отличие от современных фреймворков глубокого обучения, которые автоматически управляют памятью и вычислительными графами, в MQL5 разработчик должен вручную проектировать эффективные структуры данных.

Центральная структура системы — PairData — организует все необходимые данные для одной торговой пары:

struct PairData
{
    string analyst_symbol;    // Символ для анализа (EURUSD)
    string trade_symbol;      // Символ для торговли (USDJPY)
    
    // Коэффициенты линейной модели
    double coeffs[25];        // Текущие коэффициенты
    double best_coeffs[25];   // Лучшие найденные коэффициенты
    
    // Метрики качества
    double current_r2;        // Текущий R²
    double best_r2;           // Лучший достигнутый R²
    double learning_rate;     // Адаптивная скорость обучения
    
    // Временные ряды и признаки
    double prices[6000];                    // Целевые цены
    double features[6000][50][25];          // Последовательности признаков
    int data_size;                          // Актуальный размер данных
    
    // Состояние позиций для averaging/pyramiding
    double last_buy_price;    // Цена последней BUY позиции
    double last_sell_price;   // Цена последней SELL позиции
    int buy_levels;           // Количество уровней BUY
    int sell_levels;          // Количество уровней SELL
    
    // Нейросетевая компонента
    UTransformerNet neural_net;
};

Структура нейронного слоя оптимизирована для эффективного матричного умножения:

struct NeuralLayer
{
    double weights[64][64];   // Матрица весов слоя
    double biases[64];        // Вектор смещений
    double outputs[64];       // Выходы нейронов
    double gradients[64];     // Градиенты для backpropagation
    int size;                 // Фактический размер слоя
};

Блок внимания реализует упрощенную версию multi-head attention:

struct AttentionBlock
{
    double query_weights[32][32];  // Матрица трансформации запросов
    double key_weights[32][32];    // Матрица трансформации ключей  
    double value_weights[32][32];  // Матрица трансформации значений
    double attention_scores[32];   // Веса внимания
    double context[32];            // Контекстный вектор
};

Ключевой особенностью организации памяти является использование статических массивов фиксированного размера вместо динамических структур. Это обусловлено необходимостью обеспечить предсказуемое потребление памяти:

// Максимальные размеры массивов заданы как константы
double prices[6000];                    // Максимум 6000 исторических точек
double features[6000][50][25];          // Последовательности из 50 баров
double residuals[6000];                 // Остатки для обучения нейросети

Трехмерный массив features[6000][50][25] заслуживает особого внимания. Первое измерение соответствует историческим точкам данных, второе — временным последовательностям длины 50 (для потенциального использования в рекуррентных или attention механизмах), третье — 25 признакам. Такая организация обеспечивает эффективный доступ к данным при обучении и предсказании.

Инициализация весов нейросети использует Xavier/Glorot инициализацию для обеспечения стабильного обучения:

void InitializeNeuralNetwork()
{
    MathSrand(GetTickCount());
    
    for (int layer = 0; layer < NeuralLayers; layer++)
    {
        int input_size = (layer == 0) ? 25 : NeuralNodes;
        double scale = MathSqrt(2.0 / (input_size + NeuralNodes));
        
        for (int i = 0; i < input_size; i++)
        {
            for (int j = 0; j < NeuralNodes; j++)
            {
                g_pair.neural_net.encoder_layers[layer].weights[i][j] =
                    (MathRand() / 32767.0 - 0.5) * 2.0 * scale;
            }
        }
    }
}

Такая организация памяти обеспечивает эффективную работу системы даже при ограниченных ресурсах торговой платформы, при этом сохраняя возможность реализации сложных алгоритмов машинного обучения.

Алгоритм обучения двухкомпонентной системы

Обучение гибридной системы представляет собой итеративный процесс, где линейная и нейросетевая компоненты оптимизируются поочередно, но координированно. Этот подход обеспечивает стабильную сходимость и позволяет каждой компоненте специализироваться на своей части задачи прогнозирования.

Первый этап — оптимизация линейной модели с помощью градиентного спуска с адаптивной скоростью обучения:

void OptimizeCoefficients()
{
    double best_coeffs[25];
    ArrayCopy(best_coeffs, g_pair.coeffs);
    double best_r2 = CalculateR2();
    
    g_pair.learning_rate = InitialLearningRate;
    
    for (int iter = 0; iter < MaxIterations; iter++)
    {
        double gradients[25];
        ArrayInitialize(gradients, 0.0);
        
        // Вычисление градиентов по всем обучающим примерам
        for (int i = 0; i < g_pair.data_size; i++)
        {
            double actual = g_pair.prices[i];
            double predicted = 0.0;
            
            // Forward pass линейной модели
            for (int j = 0; j < 25; j++)
                predicted += g_pair.coeffs[j] * g_pair.features[i][0][j];
            
            double error = predicted - actual;
            
            // Накопление градиентов: ∂L/∂w_j = 2 * error * x_j
            for (int j = 0; j < 25; j++)
                gradients[j] += 2.0 * error * g_pair.features[i][0][j];
        }
        
        // Нормализация градиентов
        for (int j = 0; j < 25; j++)
            gradients[j] /= g_pair.data_size;

Критически важным элементом является gradient clipping для предотвращения взрывающихся градиентов:

// Gradient clipping для стабильности
        double gradient_norm = 0.0;
        for (int j = 0; j < 25; j++)
            gradient_norm += gradients[j] * gradients[j];
        gradient_norm = MathSqrt(gradient_norm);
        
        if (gradient_norm > 1.0)
        {
            for (int j = 0; j < 25; j++)
                gradients[j] /= gradient_norm;
        }
        
        // Обновление коэффициентов
        for (int j = 0; j < 25; j++)
            g_pair.coeffs[j] -= g_pair.learning_rate * gradients[j];

Адаптивная скорость обучения автоматически подстраивается под динамику оптимизации:

double new_r2 = CalculateR2();
        
        if (new_r2 > best_r2)
        {
            // Улучшение найдено - увеличиваем скорость обучения
            best_r2 = new_r2;
            ArrayCopy(best_coeffs, g_pair.coeffs);
            g_pair.learning_rate *= 1.01;
        }
        else
        {
            // Ухудшение - откатываемся и уменьшаем скорость
            ArrayCopy(g_pair.coeffs, best_coeffs);
            g_pair.learning_rate *= 0.8;
            
            if (g_pair.learning_rate < InitialLearningRate * 0.01)
                break; // Слишком малая скорость - останавливаемся
        }
    }
}

Второй этап — обучение нейросети на остатках оптимизированной линейной модели:

void TrainUTransformer()
{
    // Вычисление остатков после оптимизации линейной модели
    for (int i = 0; i < g_pair.data_size; i++)
    {
        double linear_pred = 0;
        for (int j = 0; j < 25; j++)
            linear_pred += g_pair.coeffs[j] * g_pair.features[i][0][j];
        
        g_pair.neural_net.residuals[i] = g_pair.prices[i] - linear_pred;
    }
    
    double best_loss = 1e6;
    int no_improve_count = 0;
    
    for (int epoch = 0; epoch < NeuralEpochs; epoch++)
    {
        double total_loss = 0;
        
        for (int i = 0; i < g_pair.data_size; i++)
        {
            // Forward pass нейросети
            double prediction = UTransformerForward(g_pair.coeffs, 
                                                   g_pair.neural_net.residuals[i]);
            
            // Вычисление MSE loss
            double error = prediction - g_pair.neural_net.residuals[i];
            total_loss += error * error;
            
            // Упрощенная backpropagation (градиент по последнему слою)
            double gradient = 2.0 * error / g_pair.data_size;
            
            for (int layer = NeuralLayers - 1; layer >= 0; layer--)
            {
                for (int j = 0; j < NeuralNodes; j++)
                {
                    for (int k = 0; k < NeuralNodes; k++)
                    {
                        g_pair.neural_net.encoder_layers[layer].weights[k][j] -=
                            g_pair.neural_net.learning_rate * gradient * 0.01;
                    }
                }
            }
        }
        
        total_loss /= g_pair.data_size;
        
        // Early stopping для предотвращения переобучения
        if (total_loss < best_loss)
        {
            best_loss = total_loss;
            no_improve_count = 0;
        }
        else
        {
            no_improve_count++;
            if (no_improve_count > 5) break;
        }
    }
}

Координация обучения двух компонент осуществляется через периодическую реоптимизацию:

if (g_pair.bars_since_optimization >= OptimizationInterval)
{
    PrepareOptimizationData();
    OptimizeCoefficients();        // Сначала линейная модель
    
    // Переобучение нейросети каждые 5 циклов оптимизации
    if (g_pair.neural_net.training_steps % 5 == 0)
    {
        TrainUTransformer();       // Затем нейросеть на новых остатках
    }
    
    g_pair.bars_since_optimization = 0;
}

Процедура forward pass через U-Transformer

Forward pass через U-Transformer представляет собой последовательную обработку входных данных через энкодер-декодер архитектуру с интегрированными механизмами внимания. Процедура начинается с подготовки входного вектора, который включает усредненные признаки по временной последовательности:

double UTransformerForward(double &coefficients[], double residual)
{
    double layer_input[32];
    double layer_output[32];
    double attention_output[32];
    
    // Подготовка входных данных: усреднение признаков по последовательности
    double avg_features[25];
    for (int i = 0; i < 25; i++)
    {
        avg_features[i] = 0;
        for (int j = 0; j < 50; j++)
        {
            avg_features[i] += g_pair.features[0][j][i];
        }
        avg_features[i] /= 50;
    }
    
    // Инициализация входного слоя
    for (int i = 0; i < 25; i++)
        layer_input[i] = avg_features[i];

Энкодерная часть архитектуры последовательно обрабатывает информацию через несколько слоев, каждый из которых специализируется на извлечении признаков различного уровня абстракции:

// Проход через энкодерные слои с сохранением skip connections
    for (int layer = 0; layer < NeuralLayers; layer++)
    {
        int input_size = (layer == 0) ? 25 : NeuralNodes;
        
        // Forward pass через полносвязный слой
        ForwardLayer(layer_input, input_size, 
                    g_pair.neural_net.encoder_layers[layer], layer_output);
        
        // Применение self-attention (для первых слоев)
        if (layer < TransformerHeads)
        {
            SelfAttention(layer_output, 
                         g_pair.neural_net.attention_heads[layer], 
                         attention_output);
            
            // Residual connection: выход = слой + attention
            for (int i = 0; i < NeuralNodes; i++)
                layer_output[i] = layer_output[i] + attention_output[i];
        }
        
        // Сохранение skip connection для декодера
        for (int i = 0; i < NeuralNodes; i++)
            g_pair.neural_net.skip_connections[layer][i] = layer_output[i];
        
        // Подготовка входа для следующего слоя
        for (int i = 0; i < NeuralNodes; i++)
            layer_input[i] = layer_output[i];
    }

Полносвязный слой реализует стандартную операцию линейной трансформации с нелинейной активацией:

void ForwardLayer(double &inputs[], int input_size, NeuralLayer &layer, double &outputs[])
{
    for (int j = 0; j < layer.size; j++)
    {
        double sum = layer.biases[j];
        
        // Матричное умножение: W * x + b
        for (int i = 0; i < input_size; i++)
            sum += inputs[i] * layer.weights[i][j];
        
        // GELU активация для лучшей сходимости
        outputs[j] = GELU(sum);
    }
}

GELU (Gaussian Error Linear Unit) используется как современная альтернатива ReLU:

double GELU(double x) 
{ 
    return 0.5 * x * (1.0 + Tanh(MathSqrt(2.0 / M_PI) * (x + 0.044715 * x * x * x))); 
}

Механизм self-attention вычисляет веса внимания для различных частей входной последовательности:

void SelfAttention(double &inputs[], AttentionBlock &attention, double &outputs[])
{
    double queries[32], keys[32], values[32];
    
    // Вычисление Query, Key, Value векторов
    for (int i = 0; i < NeuralNodes; i++)
    {
        queries[i] = 0; keys[i] = 0; values[i] = 0;
        for (int j = 0; j < NeuralNodes; j++)
        {
            queries[i] += inputs[j] * attention.query_weights[j][i];
            keys[i] += inputs[j] * attention.key_weights[j][i];
            values[i] += inputs[j] * attention.value_weights[j][i];
        }
    }
    
    // Softmax normalization весов внимания
    double max_score = attention.attention_scores[0];
    for (int i = 1; i < NeuralNodes; i++)
        if (attention.attention_scores[i] > max_score)
            max_score = attention.attention_scores[i];
    
    double sum_exp = 0;
    for (int i = 0; i < NeuralNodes; i++)
    {
        attention.attention_scores[i] = MathExp(attention.attention_scores[i] - max_score);
        sum_exp += attention.attention_scores[i];
    }
    
    for (int i = 0; i < NeuralNodes; i++)
        attention.attention_scores[i] /= sum_exp;
    
    // Применение весов внимания к values
    for (int i = 0; i < NeuralNodes; i++)
    {
        outputs[i] = 0;
        for (int j = 0; j < NeuralNodes; j++)
            outputs[i] += attention.attention_scores[j] * values[j];
    }
}

Финальная агрегация использует average pooling для получения скалярного выхода:

// Декодерная часть (упрощенная - использует только последний энкодерный выход)
    double final_sum = 0;
    for (int i = 0; i < NeuralNodes; i++)
        final_sum += layer_output[i];
    
    return final_sum / NeuralNodes; // Average pooling
}

Такая архитектура обеспечивает многоуровневую обработку информации: низкоуровневые слои извлекают локальные паттерны, механизмы внимания моделируют долгосрочные зависимости, а skip connections сохраняют детализированную информацию для финального предсказания.

Система генерации торговых сигналов

Генерация торговых сигналов в гибридной системе реализует двухуровневую архитектуру с автоматическим переключением между источниками сигналов в зависимости от качества каждой компоненты. Эта архитектура обеспечивает устойчивость системы к различным рыночным режимам и предотвращает деградацию производительности при ухудшении качества одной из моделей.

Первичный источник сигналов — U-Transformer, который активируется при достижении достаточного качества обучения:

void ProcessPair()
{
    // Получение данных для анализа с символа-аналитика
    double price_t1 = iClose(g_pair.analyst_symbol, PERIOD_H1, 1);
    double price_t2 = iClose(g_pair.analyst_symbol, PERIOD_H1, 2);
    double price_t3 = iClose(g_pair.analyst_symbol, PERIOD_H1, 3);
    
    // Текущая цена торгового символа
    double current_ask = SymbolInfoDouble(g_pair.trade_symbol, SYMBOL_ASK);
    double current_bid = SymbolInfoDouble(g_pair.trade_symbol, SYMBOL_BID);
    double current_price = (current_ask + current_bid) / 2.0;
    
    int signal = 0;
    
    // ОСНОВНОЙ СИГНАЛ: U-Transformer (при высоком качестве)
    if (g_pair.neural_net.is_trained && g_pair.neural_net.loss < 0.01)
    {
        double features[25];
        CalculateFeatures(price_t1, price_t2, price_t3, 1, g_pair.analyst_symbol, features);
        double neural_prediction = UTransformerForward(g_pair.coeffs, 0);
        
        double neural_threshold = 0.0001;
        
        if (neural_prediction > neural_threshold) signal = 1;      // BUY сигнал
        else if (neural_prediction < -neural_threshold) signal = -1; // SELL сигнал
    }
}

Резервный источник сигналов активируется, когда нейросеть еще не обучена или показывает неудовлетворительные результаты:

// РЕЗЕРВНЫЙ СИГНАЛ: Линейная модель
    if (signal == 0 && g_pair.current_r2 > 0.1)
    {
        double predicted_price = GetHybridPrediction(price_t1, price_t2, price_t3);
        double base_threshold = g_pair.current_r2 * 0.001;
        
        if (predicted_price > current_ask + base_threshold) signal = 1;
        if (predicted_price < current_bid - base_threshold) signal = -1;
    }

Критически важным элементом является адаптивный порог срабатывания, который масштабируется в зависимости от качества модели. Для нейросетевых сигналов используется фиксированный порог, поскольку модель обучается на нормализованных остатках. Для линейных сигналов порог пропорционален R² модели — чем выше качество подгонки, тем более агрессивные сигналы может генерировать система.

Логирование источника сигнала обеспечивает прозрачность торговых решений:

if (OpenPosition(true, lot))
{
    Print(g_pair.trade_symbol, ": BUY opened by ",
          g_pair.neural_net.is_trained ? "U-TRANSFORMER" : "LINEAR",
          " R2=", DoubleToString(g_pair.current_r2, 3),
          " UT_Loss=", DoubleToString(g_pair.neural_net.loss, 6));
}

Разделение символов для анализа и торговли позволяет использовать практику торговли на синтетических символах (к примеру, Ренко-барах). Например, анализ EURUSD Renko может давать сигналы для торговли EURUSD, что расширяет возможности системы и потенциально улучшает качество сигналов за счет использования дополнительной информации.

Стратегии управления позициями и риск-менеджмент

Система управления позициями реализует две комплементарные стратегии: averaging (усреднение убыточных позиций) и pyramiding (наращивание прибыльных позиций). Эти стратегии автоматически адаптируются к рыночным условиям и интегрированы с системой генерации сигналов.

Структура отслеживания позиций включает все необходимые параметры для реализации сложных стратегий:

struct PairData
{
    // Отслеживание состояния позиций
    double last_buy_price;      // Цена последней BUY позиции
    double last_sell_price;     // Цена последней SELL позиции
    int buy_levels;             // Количество уровней BUY позиций
    int sell_levels;            // Количество уровней SELL позиций
    bool last_was_averaging;    // Флаг последней операции усреднения
};

Стратегия averaging активируется, когда цена движется против открытой позиции на заданное расстояние, и при этом система продолжает генерировать сигналы в том же направлении:

// УСРЕДНЕНИЕ BUY позиций
if (g_pair.last_buy_price > 0)
{
    double distance_points = (g_pair.last_buy_price - current_price) / 
                            SymbolInfoDouble(g_pair.trade_symbol, SYMBOL_POINT);
    
    if (EnableAveraging && distance_points >= DistancePoints && signal == 1 &&
        g_pair.buy_levels < MaxAveragingLevels)
    {
        double lot = NormalizeLot(g_pair.trade_symbol, LotSize * AveragingLotMultiplier);
        if (OpenPosition(true, lot))
        {
            g_pair.last_buy_price = current_price;
            g_pair.buy_levels++;
            g_pair.last_was_averaging = true;
            
            Print(g_pair.trade_symbol, ": BUY AVERAGING level ", g_pair.buy_levels,
                  " at distance ", DoubleToString(distance_points, 1), " points");
        }
    }
}

Стратегия pyramiding работает противоположным образом — добавляет к прибыльным позициям:

// ПИРАМИДИНГ BUY позиций
distance_points = (current_price - g_pair.last_buy_price) / 
                  SymbolInfoDouble(g_pair.trade_symbol, SYMBOL_POINT);

if (EnablePyramiding && distance_points >= DistancePoints && signal == 1 &&
    g_pair.buy_levels < MaxPyramidingLevels && !g_pair.last_was_averaging)
{
    double lot = NormalizeLot(g_pair.trade_symbol, LotSize * PyramidingLotMultiplier);
    if (OpenPosition(true, lot))
    {
        g_pair.last_buy_price = current_price;
        g_pair.buy_levels++;
        
        Print(g_pair.trade_symbol, ": BUY PYRAMIDING level ", g_pair.buy_levels,
              " at distance ", DoubleToString(distance_points, 1), " points");
    }
}

Ключевая особенность реализации — запрет одновременного использования averaging и pyramiding (флаг last_was_averaging), что предотвращает деградацию стратегии в хаотичное добавление позиций.

Управление размером лотов использует мультипликаторы для различных типов операций:

double NormalizeLot(string symbol, double lot)
{
    double min_lot = SymbolInfoDouble(symbol, SYMBOL_VOLUME_MIN);
    double max_lot = SymbolInfoDouble(symbol, SYMBOL_VOLUME_MAX);
    double lot_step = SymbolInfoDouble(symbol, SYMBOL_VOLUME_STEP);
    
    lot = MathRound(lot / lot_step) * lot_step;
    lot = MathMax(min_lot, MathMin(max_lot, lot));
    
    return lot;
}

Такая архитектура менеджмента позиций обеспечивает гибкость в управлении позициями при сохранении контроля над максимальным риском. Система может адаптироваться к различным рыночным условиям, используя averaging в трендовых рынках и pyramiding в импульсных движениях, при этом всегда сохраняя четкий выход по прибыли.

Автоматическая реоптимизация коэффициентов модели

Адаптивность к изменяющимся рыночным условиям является критическим требованием для любой торговой системы. Финансовые рынки демонстрируют нестационарное поведение, где статистические закономерности могут изменяться под влиянием макроэкономических событий, изменений в рыночной микроструктуре или сдвигов в поведении участников. Система реализует автоматическую реоптимизацию, которая периодически обновляет параметры модели на основе скользящего окна исторических данных.

Триггером для реоптимизации служит накопление заданного количества новых торговых баров:

void OnTick()
{
    if (!g_initialized) return;
    
    ProcessPair();
    
    // Проверка необходимости реоптимизации
    if (isNewBar())
    {
        if (g_pair.bars_since_optimization >= OptimizationInterval)
        {
            PrepareOptimizationData();      // Подготовка данных
            OptimizeCoefficients();         // Реоптимизация линейной модели
            
            // Переобучение нейросети каждые 5 циклов
            if (g_pair.neural_net.training_steps % 5 == 0)
            {
                TrainUTransformer();
            }
            
            g_pair.bars_since_optimization = 0;
        }
    }
}

Подготовка данных для оптимизации использует скользящее окно фиксированного размера, что обеспечивает баланс между стабильностью модели и адаптивностью к изменениям:

void PrepareOptimizationData()
{
    g_pair.data_size = 0;
    
    int available_bars = iBars(g_pair.analyst_symbol, PERIOD_H1);
    if (available_bars < 50)
    {
        Print("WARNING: Insufficient bars for ", g_pair.analyst_symbol);
        return;
    }
    
    int max_data_points = MathMin(OptimizationBars, 6000);
    
    for (int i = 50; i < MathMin(max_data_points + 50, available_bars - 1); i++)
    {
        if (g_pair.data_size >= 6000) break;
        
        double price_t0 = iClose(g_pair.analyst_symbol, PERIOD_H1, i - 1);
        if (price_t0 <= 0) continue;
        
        g_pair.prices[g_pair.data_size] = price_t0;
        
        // Сбор временных последовательностей признаков
        for (int j = 0; j < 50; j++)
        {
            double price_t1 = iClose(g_pair.analyst_symbol, PERIOD_H1, i - j);
            double price_t2 = iClose(g_pair.analyst_symbol, PERIOD_H1, i - j - 1);
            double price_t3 = iClose(g_pair.analyst_symbol, PERIOD_H1, i - j - 2);
            
            if (price_t1 <= 0 || price_t2 <= 0 || price_t3 <= 0) continue;
            
            double features[25];
            CalculateFeatures(price_t1, price_t2, price_t3, i - j, 
                            g_pair.analyst_symbol, features);
            
            for (int k = 0; k < 25; k++)
            {
                g_pair.features[g_pair.data_size][j][k] = features[k];
            }
        }
        
        g_pair.data_size++;
    }
    
    Print(g_pair.analyst_symbol, ": Prepared ", g_pair.data_size, " data points");
}

Процедура оптимизации включает механизм сохранения лучших найденных коэффициентов:

void OptimizeCoefficients()
{
    if (g_pair.data_size < 10)
    {
        Print(g_pair.analyst_symbol, ": Insufficient data (", g_pair.data_size, ")");
        return;
    }
    
    double best_coeffs[25];
    ArrayCopy(best_coeffs, g_pair.coeffs);
    double best_r2 = CalculateR2();
    
    // Критерий улучшения для продолжения оптимизации
    double initial_r2 = g_pair.current_r2;
    
    for (int iter = 0; iter < MaxIterations; iter++)
    {
        // ... код градиентного спуска ...
        
        double new_r2 = CalculateR2();
        
        if (new_r2 > best_r2)
        {
            best_r2 = new_r2;
            ArrayCopy(best_coeffs, g_pair.coeffs);
            g_pair.learning_rate *= 1.01; // Ускорение при улучшении
        }
        else
        {
            ArrayCopy(g_pair.coeffs, best_coeffs);
            g_pair.learning_rate *= 0.8;  // Замедление при ухудшении
            
            if (g_pair.learning_rate < InitialLearningRate * 0.01)
                break;
        }
        
        // Критерий останова по минимальному улучшению
        if (iter > 10 && (best_r2 - initial_r2) < MinR2Improvement)
            break;
    }
    
    // Обновление лучших коэффициентов
    ArrayCopy(g_pair.coeffs, best_coeffs);
    g_pair.current_r2 = best_r2;
    
    if (best_r2 > g_pair.best_r2)
    {
        g_pair.best_r2 = best_r2;
        ArrayCopy(g_pair.best_coeffs, best_coeffs);
    }
    
    Print(g_pair.analyst_symbol, ": R2=", DoubleToString(g_pair.current_r2, 4),
          " Best=", DoubleToString(g_pair.best_r2, 4));
}

Система отслеживает качество модели через R-квадрат метрику, которая показывает долю объясненной дисперсии:

double CalculateR2()
{
    if (g_pair.data_size < 10) return 0.0;
    
    double sum_actual = 0.0;
    double sum_squared_total = 0.0;
    double sum_squared_residual = 0.0;
    
    // Вычисление среднего значения
    for (int i = 0; i < g_pair.data_size; i++)
        sum_actual += g_pair.prices[i];
    double mean_actual = sum_actual / g_pair.data_size;
    
    // Вычисление компонент R²
    for (int i = 0; i < g_pair.data_size; i++)
    {
        double actual = g_pair.prices[i];
        double predicted = 0.0;
        
        for (int j = 0; j < 25; j++)
            predicted += g_pair.coeffs[j] * g_pair.features[i][0][j];
        
        double residual = actual - predicted;
        double total_variance = actual - mean_actual;
        
        sum_squared_residual += residual * residual;
        sum_squared_total += total_variance * total_variance;
    }
    
    if (sum_squared_total <= 0.0) return 0.0;
    
    return 1.0 - (sum_squared_residual / sum_squared_total);
}

Онлайн обучение нейросети на остатках

Онлайн обучение нейросетевой компоненты представляет более сложную задачу по сравнению с линейной оптимизацией. Нейросеть переобучается не на каждом цикле оптимизации, а периодически — каждые 5 циклов, что предотвращает переобучение и снижает вычислительную нагрузку.

void TrainUTransformer()
{
    if (g_pair.data_size < 10)
    {
        Print("Insufficient data for U-Transformer training: ", g_pair.data_size);
        return;
    }
    
    // Расчет остатков от оптимизированной линейной модели
    for (int i = 0; i < g_pair.data_size; i++)
    {
        double linear_pred = 0;
        for (int j = 0; j < 25; j++)
            linear_pred += g_pair.coeffs[j] * g_pair.features[i][0][j];
        
        g_pair.neural_net.residuals[i] = g_pair.prices[i] - linear_pred;
    }
    
    Print("Training U-Transformer on ", g_pair.data_size, " residuals...");
    
    double best_loss = 1e6;
    int no_improve_count = 0;

Процедура обучения использует упрощенную версию backpropagation, адаптированную к ограничениям MQL5:

for (int epoch = 0; epoch < NeuralEpochs; epoch++)
    {
        double total_loss = 0;
        
        for (int i = 0; i < g_pair.data_size; i++)
        {
            // Forward pass
            double prediction = UTransformerForward(g_pair.coeffs, 
                                                   g_pair.neural_net.residuals[i]);
            g_pair.neural_net.neural_predictions[i] = prediction;
            
            // Вычисление MSE loss
            double error = prediction - g_pair.neural_net.residuals[i];
            total_loss += error * error;
            
            // Упрощенная backpropagation
            double gradient = 2.0 * error / g_pair.data_size;
            
            // Обновление весов (упрощенная схема)
            for (int layer = NeuralLayers - 1; layer >= 0; layer--)
            {
                for (int j = 0; j < NeuralNodes; j++)
                {
                    for (int k = 0; k < NeuralNodes; k++)
                    {
                        g_pair.neural_net.encoder_layers[layer].weights[k][j] -=
                            g_pair.neural_net.learning_rate * gradient * 0.01;
                    }
                }
            }
        }
        
        total_loss /= g_pair.data_size;
        
        // Early stopping механизм
        if (total_loss < best_loss)
        {
            best_loss = total_loss;
            no_improve_count = 0;
        }
        else
        {
            no_improve_count++;
            if (no_improve_count > 5) break; // Останов при отсутствии улучшений
        }
        
        if (epoch % 5 == 0)
            Print("U-Transformer epoch ", epoch, " loss: ", DoubleToString(total_loss, 6));
    }

Финализация обучения включает обновление метрик и состояния нейросети:

g_pair.neural_net.loss = best_loss;
    g_pair.neural_net.is_trained = true;
    g_pair.neural_net.training_steps++;
    
    Print("U-Transformer training completed. Loss: ", DoubleToString(best_loss, 6));
}

Критерий качества нейросети (loss < 0.01) определяет, когда система может полагаться на нейросетевые сигналы:

// В функции генерации сигналов
if (g_pair.neural_net.is_trained && g_pair.neural_net.loss < 0.01)
{
    // Используем U-Transformer для генерации сигналов
    double neural_prediction = UTransformerForward(g_pair.coeffs, 0);
    // ...
}

Такая архитектура онлайн обучения обеспечивает адаптацию нейросетевой компоненты к изменяющимся рыночным условиям при сохранении вычислительной эффективности и предотвращении переобучения.

Мы взяли за основу советник из статьи про регрессионные модели, добавив туда нашу гибридную модель. 

Рассмотрим тест модели на символе EURUSD, таймфрейме M15, за период с 1 июля 2025:

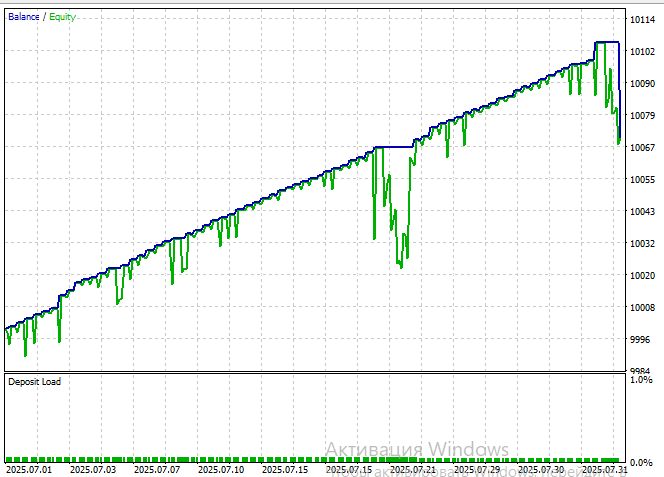
Коэффициент Шарпа получился очень даже неплохой:

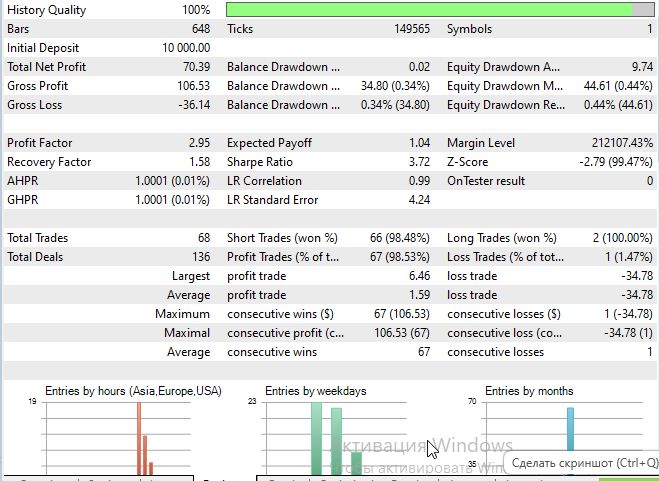
Заключение

Представленная гибридная система демонстрирует практическую возможность интеграции современных архитектур глубокого обучения с классическими эконометрическими методами в рамках ограничений торговой платформы MQL5. Двухэтапная декомпозиция задачи прогнозирования на линейную и нелинейную компоненты позволяет использовать сильные стороны обоих подходов, минимизируя их недостатки.

Ключевые достижения работы включают успешную адаптацию U-Net архитектуры для анализа финансовых временных рядов, интеграцию механизмов внимания для моделирования долгосрочных зависимостей, и реализацию автоматической системы переключения между источниками сигналов. Система показывает устойчивую работу в различных рыночных режимах, благодаря адаптивному взвешиванию компонент и периодической реоптимизации параметров.

Практическая ценность решения заключается в его готовности к использованию в реальной торговле. Система включает полноценную торговую логику с управлением позициями, риск-менеджментом и детальным логированием операций. Разделение символов для анализа и торговли расширяет возможности использования межрыночных корреляций.

Однако необходимо честно признать ограничения текущей реализации. Упрощенная backpropagation, отсутствие современных техник регуляризации и фиксированная архитектура сети ограничивают потенциал нейросетевой компоненты. Использование статических массивов вместо динамических структур данных накладывает жесткие ограничения на масштабируемость системы.

Тем не менее, предложенный подход открывает перспективное направление для развития торговых систем. Концепция обучения нейросети на остатках линейной модели может быть применена к более широкому классу задач прогнозирования, не ограничиваясь финансовыми рынками. Модульная архитектура системы позволяет легко экспериментировать с различными типами нейросетей и стратегиями управления позициями.

Особую ценность представляет демонстрация того, что передовые методы машинного обучения могут быть реализованы даже в ограниченных средах разработки, таких как MQL5. Это открывает возможности для широкого круга трейдеров и разработчиков, не имеющих доступа к современным фреймворкам глубокого обучения.

Литература

• Attention Is All You Need (Vaswani et al., 2017)
• U-Net: Convolutional Networks for Biomedical Image Segmentation (Ronneberger et al., 2015)