Машинное обучение и Data Science (Часть 06): Градиентный спуск
Преждевременная оптимизация — корень всех (или большинства) проблем в программировании.
(Дональд Кнут)
Введение
Согласно Википедии, градиентный спуск — метод нахождения локального минимума функции в направлении градиента с помощью методов одномерной оптимизации. Идея состоит в том, чтобы повторять шаги в направлении, противоположном градиенту (или приблизительному градиенту) функции в текущей точке, потому что это будет направлением наискорейшего спуска. И наоборот, шаг в направлении градиента приведет к локальному максимуму этой функции. Такой процесс называется градиентным восхождением. По сути, градиентный спуск — это алгоритм оптимизации, используемый для поиска минимума функции:
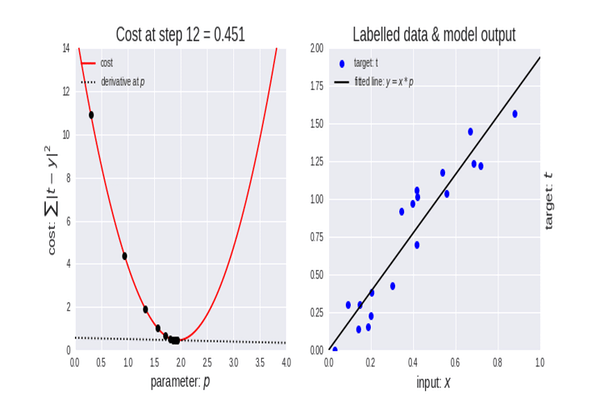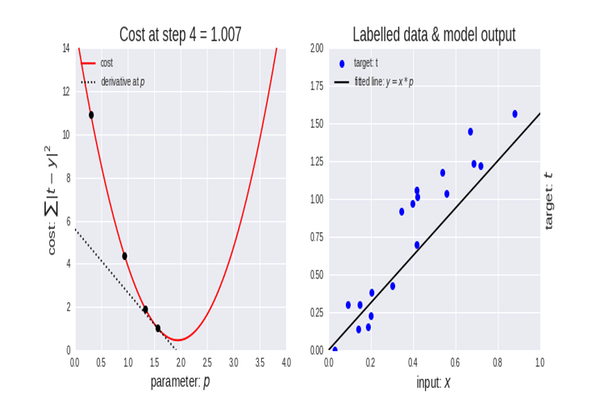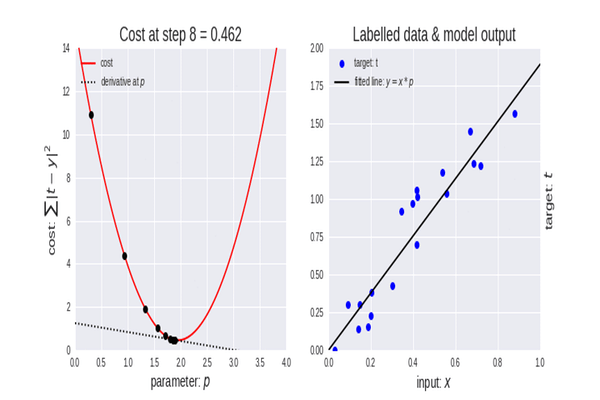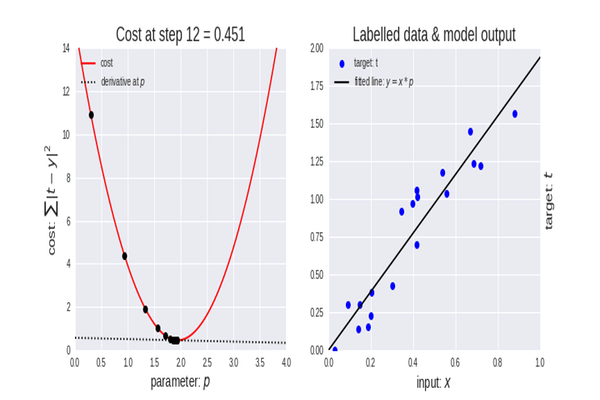
Функция стоимости
Также ее называют функцией потерь, возможно, кому-то то название будет более привычным. Это показатель для расчета того, насколько хорошо или плохо наша модель предсказывает взаимосвязь между значениями x и y.
Существует множество различных показателей, которые можно использовать для определения качества предсказания модели. Но, в отличие от всех остальных, функция стоимости находит среднюю потерю по всему набору данных, и чем больше функция стоимости, тем хуже наша модель находит взаимосвязи в данном наборе данных.
Цель градиентного спуска — минимизация функции стоимости, потому что модель с наименьшей функцией стоимости/потерь является лучшей моделью. Чтобы лучше понять, что я только что объяснил, давайте посмотрим на следующий пример.
Предположим, что наша функция стоимости представляет собой уравнение
![]()
Если мы построим график этой функции с помощью языка Python, он будет выглядеть так:
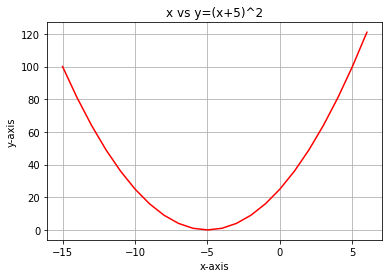
Самый первый шаг, который нужно сделать с нашей функцией стоимости, — это дифференцировать функцию стоимости, используя цепное правило, или Chain rule.
Уравнение y= (x+5)^2 — составная функция (одна функция в другой). Внешняя функция (x+5)^2, а внутренняя —(x+5). Чтобы различать между ними, применим цепное правило. Посмотрите на изображение:

В конце есть ссылка на видео, в котором от руки выполняю математические действия, если так на словах понят трудно. Что ж, теперь эта функция, которую мы только что получили, — это градиент. Процесс нахождения градиента уравнения является наиболее важным шагом из всех. Я бы хотел, чтобы в тот день в школе мой учитель математики сказал мне, что цель дифференцирования функции состоит в том, чтобы получить градиент функции.
Это первый и самый важный шаг. Далее идет второй шаг.
Шаг 2
Двигаемся в отрицательном направлении градиента. Тут возникает вопрос, а как далеко двигаться? Вот тут в игру вступает коэффициент скорости обучения.
Коэффициент скорости обучения
Согласно определению это размер шага на каждой итерации при движении к минимизации функции потерь. Сравним это с человеком, спускающимся с горы: его шаги — это скорость обучения, и чем меньше шаги, тем больше времени им потребуется, чтобы достичь подножия горы и наоборот.Если уменьшить скорость обучения, скажем, до 0,0001, мы тем самым увеличиваем время выполнения программы, поскольку алгоритму может потребоваться больше времени для достижения минимальных значений. И наоборот, использование больших значений коэффициента скорости обучения приведет к тому, что алгоритм будет делать слишком большие шаги и в конечном итоге может пропустить целевое минимальное значение.
Скорость обучения по умолчанию равна 0,01.
Давайте запустим итерации исполнения, чтобы посмотреть, как работает алгоритм.
Итерация первая: берем любую случайную точку в качестве стартовой точки для алгоритма. Я выбрал первое значение для х равным 0, а значения x будем обновлять по такой формуле:

На каждой итерации будем спускаться в направлении минимального значения функции, собственно, отсюда и название "Градиентный спуск". Теперь стало понятнее, не так ли?

Давайте теперь в деталях посмотрим, как это работает. Вручную посчитаем значения на двух итерациях, чтобы получить четкое представление о том, что происходит.
Первая итерация
Формула: x1 = x0 - Learning Rate * ( 2*(x+5) )
x1 = 0 - 0.01 * 0.01 * 2*(0+5)
x1 = -0.01 * 10
x1 = -0.1 (в итоге)
А затем обновляем значения, назначая новые значения старым. Повторяем процесс столько итераций, пока не достигнем минимального значения функции.
x0 = x1
Вторая итерация
x1 = -0.1 - 0.01 * 2*(-0.1+5)
x1 = -0.198
Тогда: x0 = x1
Если повторить этот процесс несколько раз, то для первых десяти итераций вывод будет таким:
RS 0 17:15:16.793 gradient-descent test (EURUSD,M1) Gradient Descent CostFunction CUSTOM QQ 0 17:15:16.793 gradient-descent test (EURUSD,M1) 1 x0 = 0.0000000000 x1 = -0.1000000000 CostFunction = 10.0000000000 ES 0 17:15:16.793 gradient-descent test (EURUSD,M1) 2 x0 = -0.1000000000 x1 = -0.1980000000 CostFunction = 9.8000000000 PR 0 17:15:16.793 gradient-descent test (EURUSD,M1) 3 x0 = -0.1980000000 x1 = -0.2940400000 CostFunction = 9.6040000000 LE 0 17:15:16.793 gradient-descent test (EURUSD,M1) 4 x0 = -0.2940400000 x1 = -0.3881592000 CostFunction = 9.4119200000 JD 0 17:15:16.793 gradient-descent test (EURUSD,M1) 5 x0 = -0.3881592000 x1 = -0.4803960160 CostFunction = 9.2236816000 IG 0 17:15:16.793 gradient-descent test (EURUSD,M1) 6 x0 = -0.4803960160 x1 = -0.5707880957 CostFunction = 9.0392079680 IG 0 17:15:16.793 gradient-descent test (EURUSD,M1) 7 x0 = -0.5707880957 x1 = -0.6593723338 CostFunction = 8.8584238086 JF 0 17:15:16.793 gradient-descent test (EURUSD,M1) 8 x0 = -0.6593723338 x1 = -0.7461848871 CostFunction = 8.6812553325 NI 0 17:15:16.793 gradient-descent test (EURUSD,M1) 9 x0 = -0.7461848871 x1 = -0.8312611893 CostFunction = 8.5076302258 CK 0 17:15:16.793 gradient-descent test (EURUSD,M1) 10 x0 = -0.8312611893 x1 = -0.9146359656 CostFunction = 8.3374776213
Давайте также посмотрим на другие десять значений алгоритма, когда мы очень близки к минимуму функции:
GK 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1052 x0 = -4.9999999970 x1 = -4.9999999971 CostFunction = 0.0000000060 IH 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1053 x0 = -4.9999999971 x1 = -4.9999999971 CostFunction = 0.0000000059 NH 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1054 x0 = -4.9999999971 x1 = -4.9999999972 CostFunction = 0.0000000058 QI 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1055 x0 = -4.9999999972 x1 = -4.9999999972 CostFunction = 0.0000000057 II 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1056 x0 = -4.9999999972 x1 = -4.9999999973 CostFunction = 0.0000000055 RN 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1057 x0 = -4.9999999973 x1 = -4.9999999973 CostFunction = 0.0000000054 KN 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1058 x0 = -4.9999999973 x1 = -4.9999999974 CostFunction = 0.0000000053 JO 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1059 x0 = -4.9999999974 x1 = -4.9999999974 CostFunction = 0.0000000052 JO 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1060 x0 = -4.9999999974 x1 = -4.9999999975 CostFunction = 0.0000000051 QL 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1061 x0 = -4.9999999975 x1 = -4.9999999975 CostFunction = 0.0000000050 QL 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1062 x0 = -4.9999999975 x1 = -4.9999999976 CostFunction = 0.0000000049 HP 0 17:15:16.800 gradient-descent test (EURUSD,M1) Local minimum found =-4.999999997546217
После 1062 (одной тысячи шестидесяти двух) итераций алгоритм смог достичь локального минимума этой функции. Та-дам!
На что обратить внимание в этом алгоритме
Глядя на значения функции стоимости, вы заметите огромное изменение значений в начале, но очень незначительные заметные изменения в последних значениях функции стоимости.
Градиентный спуск делает большие шаги в начале, когда он еще далек от минимума функции, а затем шаги уменьшаются, когда алгоритм приближается к минимуму функции. То же самое мы делаем, когда находимся у подножия горы. Итак, теперь нам понятно, что градиентный спуск довольно умный!
В итоге получаем локальный минимум
HP 0 17:15:16.800 gradient-descent test (EURUSD,M1) Local minimum found =-4.999999997546217
Это очень точное значение, потому что минимумом функции является -5.0.
Внимание, вопрос
Откуда градиент знает, когда остановиться? Ведь алгоритм может продолжать повторяться до бесконечности или, по крайней мере, пока не исчерпаются вычислительные мощности компьютера.
Когда функция стоимости равна нулю, мы знаем, что градиентный спуск выполнил свою работу.
Давайте теперь напишем весь этот процесс на MQL5
while (true) { iterations++; x1 = x0 - m_learning_rate * CustomCostFunction(x0); printf("%d x0 = %.10f x1 = %.10f CostFunction = %.10f",iterations,x0,x1,CustomCostFunction(x0)); if (NormalizeDouble(CustomCostFunction(x0),8) == 0) { Print("Local minimum found =",x0); break; } x0 = x1; }
Приведенный выше блок кода смог дать нам желаемые результаты. Однако он не единственный в классе CGradientDescent. Функция CustomCostFunction — это то, где хранилось и вычислялось наше дифференцированное уравнение. Вот она:
double CGradientDescent::CustomCostFunction(double x) { return(2 * ( x + 5 )); }
В чем цель?
Кто-то может спросить, в чем же смысл всех этих вычислений, ведь можно просто использовать линейную модель по умолчанию, созданную в предыдущих библиотеках, которые мы обсуждали ранее в этой серии статей. Но модель, созданная с использованием значений по умолчанию, не обязательно является лучшей моделью. Поэтому компьютер должен изучить лучшие параметры для модели с небольшим количеством ошибок (лучшая модель).
Мы стали на несколько статей ближе к построению искусственных нейронных сетей. Здесь мы пытаемся подробно и популярно разобрать, как учатся (самообучаются) нейронные сети в процессе обратного распространения ошибки и других методов. Градиентный спуск — самый популярный алгоритм, который сделал все это возможно. Без четкого понимания этого базового процесса невозможно будет понять остальное, ведь дальше все будет становиться только сложнее.
Градиентный спуск для регрессионной модели
На примере набора данных о зарплате давайте построим лучшую модель, используя градиентный спуск.
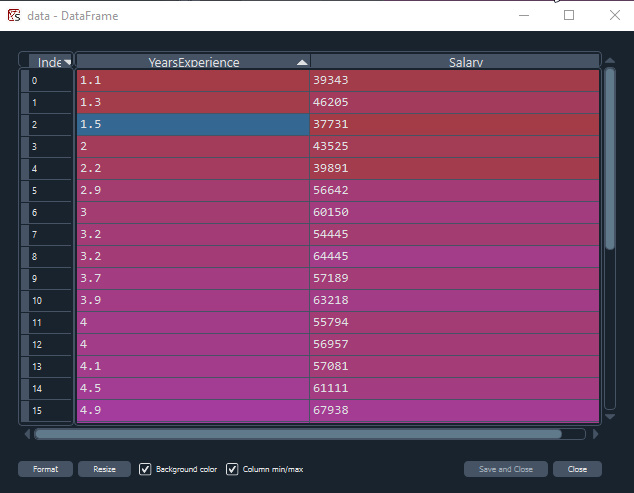
Визуализация данных в Python
import pandas as pd import numpy as np import matplotlib.pyplot as plt data = pd.read_csv(r"C:\Users\Omega Joctan\AppData\Roaming\MetaQuotes\Terminal\892B47EBC091D6EF95E3961284A76097\MQL5\Files\Salary_Data.csv") print(data.head(10)) x = data["YearsExperience"] y = data["Salary"] plt.figure(figsize=(16,9)) plt.title("Experience vs Salary") plt.scatter(x,y,c="green") plt.xlabel(xlabel="Years of Experience") plt.ylabel(ylabel="Salary") plt.show()
Таким будет наш график.
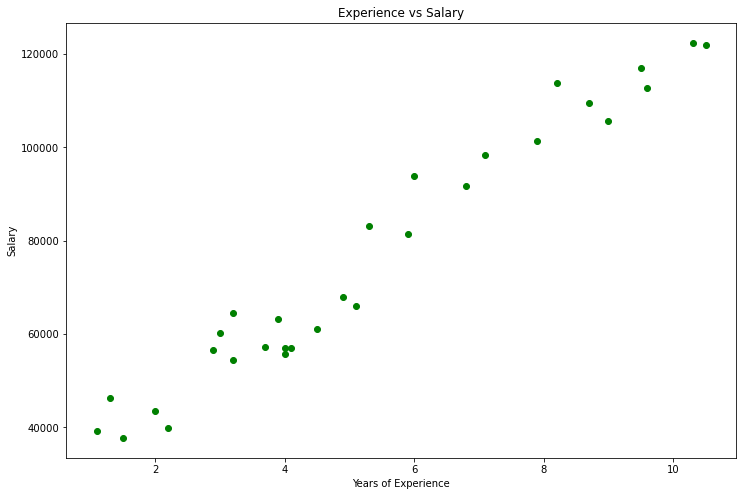
Глядя на наш набор данных, нельзя не заметить, что этот набор предназначен для задач регрессии. Но у нас может быть миллион моделей, которые помогут сделать прогноз или чего-то другого, чего мы пытаемся достичь.
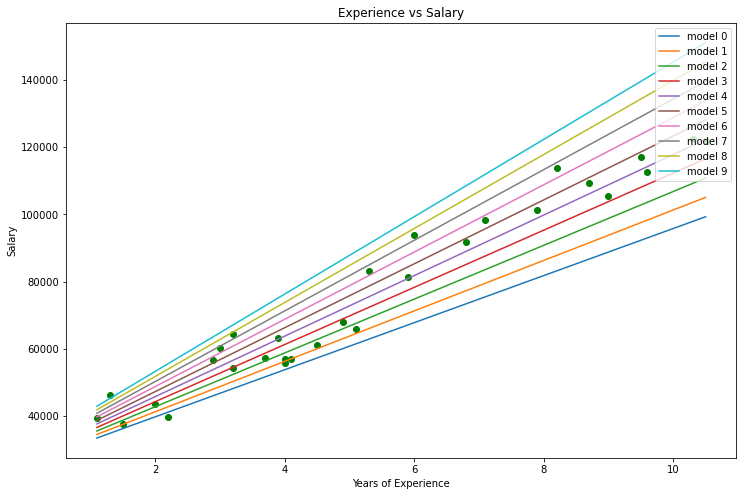
Какую модель лучше использовать для прогнозирования опыта человека и его зарплаты? Это мы и собираемся выяснить. Но сначала давайте выведем функцию стоимости для нашей регрессионной модели.
Теория
Давайте вернемся к линейной регрессии.
Мы точно знаем, что каждая линейная модель имеет свои ошибки. Мы также знаем, что можем создать миллион линий на этом графике, и наилучшей линией всегда будет линия с наименьшим количеством ошибок.
Функция стоимости представляет собой ошибку между фактическими значениями и прогнозируемыми. Можем записать формулу для функции стоимости, которая будет равна:
Стоимость = Y фактическая - Y прогнозируемая. Поскольку мы имеем величину ошибки, которую возводим в квадрат, наша формула теперь становится такой:
![]()
Но мы ищем ошибки во всем нашем наборе данных, поэтому нужно сложить:
![]()
Наконец, делим сумму ошибок на m — количество элементов в наборе данных:
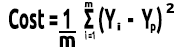
На видео ниже все математические расчеты сделаны вручную.
Мы получили функцию стоимости. Теперь можем написать код для градиентного спуска и найти лучшие параметры для двух значений: коэффициент X (наклон), обозначенный как Bo и Y Intercept, обозначенный как B1
double cost_B0=0, cost_B1=0; if (costFunction == MSE) { int iterations=0; for (int i=0; i<m_iterations; i++, iterations++) { cost_B0 = Mse(b0,b1,Intercept); cost_B1 = Mse(b0,b1,Slope); b0 = b0 - m_learning_rate * cost_B0; b1 = b1 - m_learning_rate * cost_B1; printf("%d b0 = %.8f cost_B0 = %.8f B1 = %.8f cost_B1 = %.8f",iterations,b0,cost_B0,b1,cost_B1); DBL_MAX_MIN(b0); DBL_MAX_MIN(cost_B0); DBL_MAX_MIN(cost_B1); if (NormalizeDouble(cost_B0,8) == 0 && NormalizeDouble(cost_B1,8) == 0) break; } printf("%d Iterations Local Minima are\nB0(Intercept) = %.5f || B1(Coefficient) = %.5f",iterations,b0,b1); }
Обратите внимание на несколько вещей из кода градиентного спуска:
- Процесс остается таким же, как тот, который мы выполняли ранее. Но на этот раз мы находим и обновляем значения дважды, одновременно Bo и B1.
- Ограничим количество итераций. Кто-то однажды сказал, что лучший способ сделать бесконечный цикл — это использовать цикл while, но мы не используем цикл while в этот раз. Все-таки ограничим количество срабатываний алгоритма, в течение которых будем искать коэффициенты для лучшей модели.
- DBL_MAX_MIN — функция, предназначенная для отладки, отвечающая за проверку и вывод предупреждения в случае, если мы достигли пределов математических возможностей компьютера.
Ниже показан результат работы алгоритма при Learning Rate = 0.01 и количестве итераций Iterations = 10000
PD 0 17:29:17.999 gradient-descent test (EURUSD,M1) [20] 91738.0000 98273.0000 101302.0000 113812.0000 109431.0000 105582.0000 116969.0000 112635.0000 122391.0000 121872.0000 JS 0 17:29:17.999 gradient-descent test (EURUSD,M1) Gradient Descent CostFunction MSE RF 0 17:29:17.999 gradient-descent test (EURUSD,M1) 0 b0 = 1520.06000000 cost_B0 = -152006.00000000 B1 = 9547.97400000 cost_B1 = -954797.40000000 OP 0 17:29:17.999 gradient-descent test (EURUSD,M1) 1 b0 = 1995.08742960 cost_B0 = -47502.74296000 B1 = 12056.69235267 cost_B1 = -250871.83526667 LP 0 17:29:17.999 gradient-descent test (EURUSD,M1) 2 b0 = 2194.02117366 cost_B0 = -19893.37440646 B1 = 12707.81767044 cost_B1 = -65112.53177770 QN 0 17:29:17.999 gradient-descent test (EURUSD,M1) 3 b0 = 2319.78332575 cost_B0 = -12576.21520809 B1 = 12868.77569178 cost_B1 = -16095.80213357 LO 0 17:29:17.999 gradient-descent test (EURUSD,M1) 4 b0 = 2425.92576238 cost_B0 = -10614.24366387 B1 = 12900.42596039 cost_B1 = -3165.02686058 GH 0 17:29:17.999 gradient-descent test (EURUSD,M1) 5 b0 = 2526.58198175 cost_B0 = -10065.62193621 B1 = 12897.99808257 cost_B1 = 242.78778134 CJ 0 17:29:17.999 gradient-descent test (EURUSD,M1) 6 b0 = 2625.48307920 cost_B0 = -9890.10974571 B1 = 12886.62268517 cost_B1 = 1137.53974060 DD 0 17:29:17.999 gradient-descent test (EURUSD,M1) 7 b0 = 2723.61498028 cost_B0 = -9813.19010723 B1 = 12872.93147573 cost_B1 = 1369.12094310 HF 0 17:29:17.999 gradient-descent test (EURUSD,M1) 8 b0 = 2821.23916252 cost_B0 = -9762.41822398 B1 = 12858.67435081 cost_B1 = 1425.71249248 <<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< Last Iterations >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> EI 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6672 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 NG 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6673 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 GD 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6674 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 PR 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6675 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 IS 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6676 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 RQ 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6677 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 KN 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6678 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 DL 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6679 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 RM 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6680 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 IK 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6681 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 PH 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6682 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 GF 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6683 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 MG 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6684 b0 = 25792.20019866 cost_B0 = -0.00000000 B1 = 9449.96232146 cost_B1 = 0.00000000 LE 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6684 Iterations Local Minima are OJ 0 17:29:48.247 gradient-descent test (EURUSD,M1) B0(Intercept) = 25792.20020 || B1(Coefficient) = 9449.96232
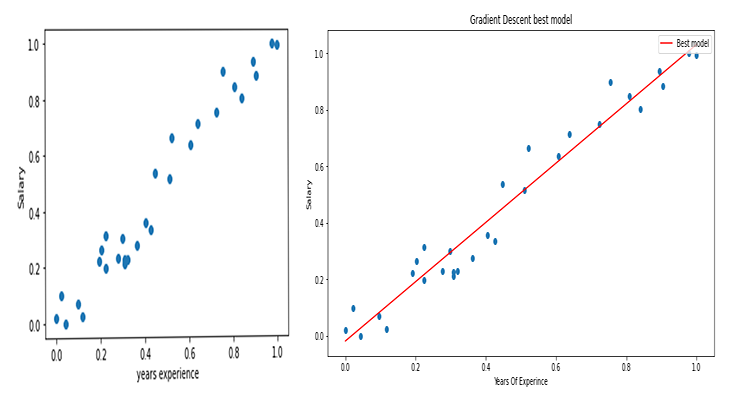
Построим график с помощью matplotlib
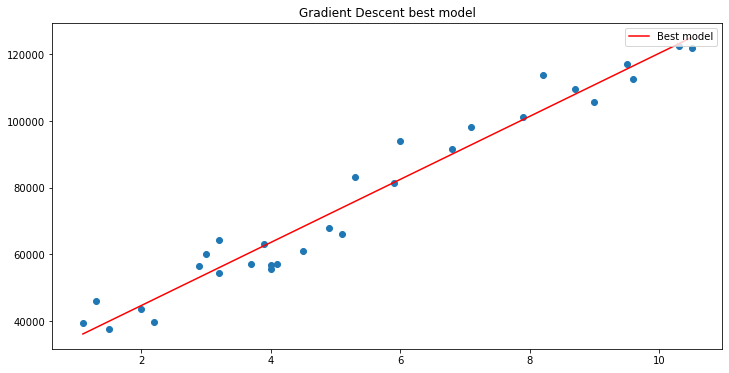
Та-дам! Градиентный спуск смог успешно получить лучшую модель из 10 000 опробованных нами моделей. Отлично, но есть один важный шаг, который мы упускаем. А это может привести к тому, что наша модель будет вести себя странно, и мы получим результаты, которые нам не нужны.
Нормализация данных входных переменных линейной регрессии
Мы знаем, что для разных наборов данных лучшие модели можно найти после разного количества итераций — некоторым может хватить 100 итераций, чтобы достичь лучших моделей, а некоторым может потребоваться и 10 000 или даже миллион, чтобы функция стоимости стала равной нулю. Не говоря уже о том, что, если использовать неправильные значения коэффициента скорости обучения, можно в конечном итоге пропустить локальные минимумы. А если пропустить эту цель, в конечном итоге мы столкнемся с математическими ограничениями компьютера. Давайте взглянем на все это на конкретном примере.
Скорость обучения = 0,1, итераций = 1000
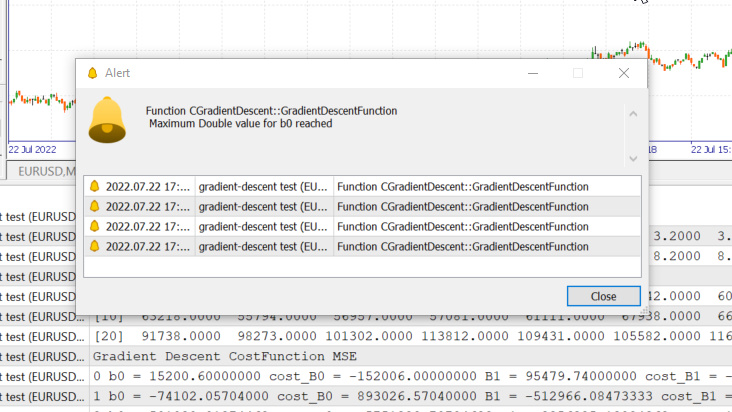
Мы только что достигли максимального значения типа double, разрешенного системой. Вот что у нас в логах.
GM 0 17:28:14.819 gradient-descent test (EURUSD,M1) Gradient Descent CostFunction MSE OP 0 17:28:14.819 gradient-descent test (EURUSD,M1) 0 b0 = 15200.60000000 cost_B0 = -152006.00000000 B1 = 95479.74000000 cost_B1 = -954797.40000000 GR 0 17:28:14.819 gradient-descent test (EURUSD,M1) 1 b0 = -74102.05704000 cost_B0 = 893026.57040000 B1 = -512966.08473333 cost_B1 = 6084458.24733333 NM 0 17:28:14.819 gradient-descent test (EURUSD,M1) 2 b0 = 501030.91374462 cost_B0 = -5751329.70784622 B1 = 3356325.13824362 cost_B1 = -38692912.22976952 LH 0 17:28:14.819 gradient-descent test (EURUSD,M1) 3 b0 = -3150629.51591119 cost_B0 = 36516604.29655810 B1 = -21257352.71857720 cost_B1 = 246136778.56820822 KD 0 17:28:14.819 gradient-descent test (EURUSD,M1) 4 b0 = 20084177.14287909 cost_B0 = -232348066.58790281 B1 = 135309993.40314889 cost_B1 = -1565673461.21726084 OQ 0 17:28:14.819 gradient-descent test (EURUSD,M1) 5 b0 = -127706877.34210962 cost_B0 = 1477910544.84988713 B1 = -860620298.24803317 cost_B1 = 9959302916.51181984 FM 0 17:28:14.819 gradient-descent test (EURUSD,M1) 6 b0 = 812402202.33122230 cost_B0 = -9401090796.73331833 B1 = 5474519904.86084747 cost_B1 = -63351402031.08880615 JJ 0 17:28:14.819 gradient-descent test (EURUSD,M1) 7 b0 = -5167652856.43381691 cost_B0 = 59800550587.65039062 B1 = -34823489070.42410278 cost_B1 = 402980089752.84948730 MP 0 17:28:14.819 gradient-descent test (EURUSD,M1) 8 b0 = 32871653967.62362671 cost_B0 = -380393068240.57440186 B1 = 221513298448.70788574 cost_B1 = -2563367875191.31982422 MM 0 17:28:14.819 gradient-descent test (EURUSD,M1) 9 b0 = -209097460110.12799072 cost_B0 = 2419691140777.51611328 B1 = -1409052343513.33935547 cost_B1 = 16305656419620.47265625 HD 0 17:28:14.819 gradient-descent test (EURUSD,M1) 10 b0 = 1330075004152.67309570 cost_B0 = -15391724642628.00976562 B1 = 8963022367351.18359375 cost_B1 = -103720747108645.23437500 DP 0 17:28:14.819 gradient-descent test (EURUSD,M1) 11 b0 = -8460645083849.12207031 cost_B0 = 97907200880017.93750000 B1 = -57014041694401.67187500 cost_B1 = 659770640617528.50000000
Это означает, что, если мы выбрали неправильный коэффициент скорости обучения, у нас может быть минимальный шанс найти лучшую модель, и высоки шансы, что мы в конечном итоге достигнем математического предела компьютера, как только что мы видели в примере.
Но если попробовать использовать 0,01 для скорости обучения с этим набором данных, проблем не будет, хотя процесс обучения станет намного медленнее. Но если же такую скорость обучения использовать для этого набора данных, в конечном итоге будет достигнут математический предел. Так что теперь вы знаете, что каждый набор данных имеет свою скорость обучения. Но иногда может не быть возможности оптимизировать скорость обучения, потому что бывают сложные наборы данных с несколькими переменными.
Решением будет нормализовать весь набор данных, чтобы он был в одном масштабе. Это улучшит читаемость, когда значения отображаются на одной и той же оси, а также улучшает время обучения, потому что нормализованные значения обычно находятся в диапазоне от 0 до 1. Кроме того, не надо будет беспокоиться о скорости обучения, потому что, когда у нас есть только один параметр скорости обучения, можно использовать его для любого набора данных, с которым мы сталкиваемся. Например, в нашем случае это скорость обучения 0,01. Подробнее о нормализации можно почитать здесь.
И последнее, но не менее важное.
Также мы знаем, что значения данных по зарплате даны в диапазоне от 39 343 до 121 782, а значения опыта равны от 1,1 года до 10,5 лет. Если сохранить данные в таком виде, значения заработной платы будут настолько огромны, что они могут заставить модель думать, что зарплата важнее любых значений. Поэтому они будут иметь огромное влияние по сравнению с годами опыта, а нам нужно, чтобы все независимые переменные оказывали одинаковое влияние наравне с другими. Теперь вы видите, как важно нормализовывать значения.
(Нормализация) Скаляр Min-Max
В этом подходе данные нормализуются так, чтобы они находились в диапазоне от 0 до 1. Формула нормализации такая:
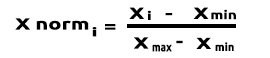
Если перевести эту формулу в строки кода, получим:
void CGradientDescent::MinMaxScaler(double &Array[]) { double mean = Mean(Array); double max,min; double Norm[]; ArrayResize(Norm,ArraySize(Array)); max = Array[ArrayMaximum(Array)]; min = Array[ArrayMinimum(Array)]; for (int i=0; i<ArraySize(Array); i++) Norm[i] = (Array[i] - min) / (max - min); printf("Scaled data Mean = %.5f Std = %.5f",Mean(Norm),std(Norm)); ArrayFree(Array); ArrayCopy(Array,Norm); }
Функция std() нужна только для того, чтобы мы смогли узнать стандартное отклонение после нормализации данных. Вот ее код:
double CGradientDescent::std(double &data[]) { double mean = Mean(data); double sum = 0; for (int i=0; i<ArraySize(data); i++) sum += MathPow(data[i] - mean,2); return(MathSqrt(sum/ArraySize(data))); }
Давайте теперь вызовем все это и выведем результат:
void OnStart() { //--- string filename = "Salary_Data.csv"; double XMatrix[]; double YMatrix[]; grad = new CGradientDescent(1, 0.01,1000); grad.ReadCsvCol(filename,1,XMatrix); grad.ReadCsvCol(filename,2,YMatrix); grad.MinMaxScaler(XMatrix); grad.MinMaxScaler(YMatrix); ArrayPrint("Normalized X",XMatrix); ArrayPrint("Normalized Y",YMatrix); grad.GradientDescentFunction(XMatrix,YMatrix,MSE); delete (grad); }
Результат
OK 0 18:50:53.387 gradient-descent test (EURUSD,M1) Scaled data Mean = 0.44823 Std = 0.29683 MG 0 18:50:53.387 gradient-descent test (EURUSD,M1) Scaled data Mean = 0.45207 Std = 0.31838 MP 0 18:50:53.387 gradient-descent test (EURUSD,M1) Normalized X JG 0 18:50:53.387 gradient-descent test (EURUSD,M1) [ 0] 0.0000 0.0213 0.0426 0.0957 0.1170 0.1915 0.2021 0.2234 0.2234 0.2766 0.2979 0.3085 0.3085 0.3191 0.3617 ER 0 18:50:53.387 gradient-descent test (EURUSD,M1) [15] 0.4043 0.4255 0.4468 0.5106 0.5213 0.6064 0.6383 0.7234 0.7553 0.8085 0.8404 0.8936 0.9043 0.9787 1.0000 NQ 0 18:50:53.387 gradient-descent test (EURUSD,M1) Normalized Y IF 0 18:50:53.387 gradient-descent test (EURUSD,M1) [ 0] 0.0190 0.1001 0.0000 0.0684 0.0255 0.2234 0.2648 0.1974 0.3155 0.2298 0.3011 0.2134 0.2271 0.2286 0.2762 IS 0 18:50:53.387 gradient-descent test (EURUSD,M1) [15] 0.3568 0.3343 0.5358 0.5154 0.6639 0.6379 0.7151 0.7509 0.8987 0.8469 0.8015 0.9360 0.8848 1.0000 0.9939
Теперь графики будут выглядеть так:
Градиентный спуск для логистической регрессии
Мы посмотрели линейную сторону градиентного спуска, теперь давайте посмотрим на логистическую.
Здесь делаем то же самое, что делали только что в части линейной регрессии, потому что задействованы точно такие же процессы, только процесс дифференциации логистической регрессии становится более сложным, чем в линейной модели. Давайте сначала посмотрим на функцию стоимости.
Мы уже обсуждали во второй статье цикла о логистической регрессии. Функция стоимости модели логистической регрессии — это бинарная кросс-энтропия, или логарифмическая функция потерь Log Loss, приведенная ниже.

Давайте сначала исполним сделаем сложную часть — дифференцируем эту функцию, чтобы получить ее градиент.
После находим производные
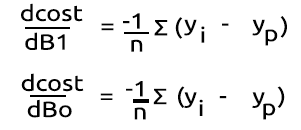
Превратим формулы в MQL5-код внутри функции BCE, что означает Binary Cross Entropy (бинарная кросс-энтропия).
double CGradientDescent::Bce(double Bo,double B1,Beta wrt) { double sum_sqr=0; double m = ArraySize(Y); double x[]; MatrixColumn(m_XMatrix,x,2); if (wrt == Slope) for (int i=0; i<ArraySize(Y); i++) { double Yp = Sigmoid(Bo+B1*x[i]); sum_sqr += (Y[i] - Yp) * x[i]; } if (wrt == Intercept) for (int i=0; i<ArraySize(Y); i++) { double Yp = Sigmoid(Bo+B1*x[i]); sum_sqr += (Y[i] - Yp); } return((-1/m)*sum_sqr); }
Поскольку мы имеем дело с моделью классификации, выберем набор данных по Титанику, с которым мы работали в статье про логистическую регрессию. У нас есть независимая переменная Pclass (пассажирский класс) и зависимая Survived с другой стороны.
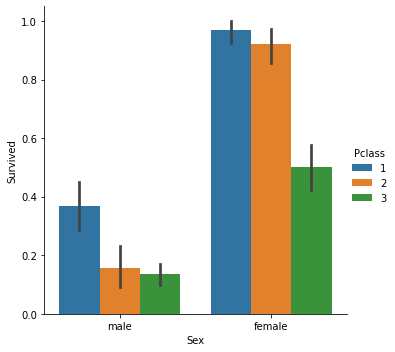
Диаграмма рассеяния
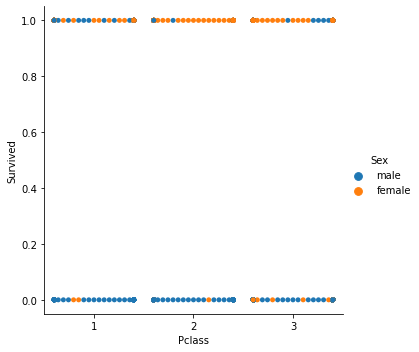
Теперь вызовем класс Gradient Descent, но на этот раз с BCE (бинарная перекрестная энтропия) в виде функции затрат.
filename = "titanic.csv"; ZeroMemory(XMatrix); ZeroMemory(YMatrix); grad.ReadCsvCol(filename,3,XMatrix); grad.ReadCsvCol(filename,2,YMatrix); grad.GradientDescentFunction(XMatrix,YMatrix,BCE); delete (grad);
Посмотрим на результат:
CP 0 07:19:08.906 gradient-descent test (EURUSD,M1) Gradient Descent CostFunction BCE KD 0 07:19:08.906 gradient-descent test (EURUSD,M1) 0 b0 = -0.01161616 cost_B0 = 0.11616162 B1 = -0.04057239 cost_B1 = 0.40572391 FD 0 07:19:08.906 gradient-descent test (EURUSD,M1) 1 b0 = -0.02060337 cost_B0 = 0.08987211 B1 = -0.07436893 cost_B1 = 0.33796541 KE 0 07:19:08.906 gradient-descent test (EURUSD,M1) 2 b0 = -0.02743120 cost_B0 = 0.06827832 B1 = -0.10259883 cost_B1 = 0.28229898 QE 0 07:19:08.906 gradient-descent test (EURUSD,M1) 3 b0 = -0.03248925 cost_B0 = 0.05058047 B1 = -0.12626640 cost_B1 = 0.23667566 EE 0 07:19:08.907 gradient-descent test (EURUSD,M1) 4 b0 = -0.03609603 cost_B0 = 0.03606775 B1 = -0.14619252 cost_B1 = 0.19926123 CF 0 07:19:08.907 gradient-descent test (EURUSD,M1) 5 b0 = -0.03851035 cost_B0 = 0.02414322 B1 = -0.16304363 cost_B1 = 0.16851108 MF 0 07:19:08.907 gradient-descent test (EURUSD,M1) 6 b0 = -0.03994229 cost_B0 = 0.01431946 B1 = -0.17735996 cost_B1 = 0.14316329 JG 0 07:19:08.907 gradient-descent test (EURUSD,M1) 7 b0 = -0.04056266 cost_B0 = 0.00620364 B1 = -0.18958010 cost_B1 = 0.12220146 HE 0 07:19:08.907 gradient-descent test (EURUSD,M1) 8 b0 = -0.04051073 cost_B0 = -0.00051932 B1 = -0.20006123 cost_B1 = 0.10481129 ME 0 07:19:08.907 gradient-descent test (EURUSD,M1) 9 b0 = -0.03990051 cost_B0 = -0.00610216 B1 = -0.20909530 cost_B1 = 0.09034065 JQ 0 07:19:08.907 gradient-descent test (EURUSD,M1) 10 b0 = -0.03882570 cost_B0 = -0.01074812 B1 = -0.21692190 cost_B1 = 0.07826600 <<<<<< Last 10 iterations >>>>>> FN 0 07:19:09.725 gradient-descent test (EURUSD,M1) 6935 b0 = 1.44678930 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 PN 0 07:19:09.725 gradient-descent test (EURUSD,M1) 6936 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 NM 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6937 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 KL 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6938 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 PK 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6939 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 RK 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6940 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 MJ 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6941 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 HI 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6942 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 CH 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6943 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 MH 0 07:19:09.727 gradient-descent test (EURUSD,M1) 6944 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 QG 0 07:19:09.727 gradient-descent test (EURUSD,M1) 6945 b0 = 1.44678931 cost_B0 = -0.00000000 B1 = -0.85010666 cost_B1 = 0.00000000 NG 0 07:19:09.727 gradient-descent test (EURUSD,M1) 6945 Iterations Local Minima are MJ 0 07:19:09.727 gradient-descent test (EURUSD,M1) B0(Intercept) = 1.44679 || B1(Coefficient) = -0.85011
Мы не нормализуем и не масштабируем классифицированные данные для логистической регрессии, как в линейной регрессии.
Вот мы и получили градиентный спуск для двух наиболее важных моделей машинного обучения. Надеюсь, было понятно и полезно. Код на Python, который я использовал в статье, а также набор данных доступны в GitHub-репозитории.
Заключение
Мы рассмотрели градиентный спуск для одной независимой и одной зависимой переменной. Для множества независимых переменных надо использовать векторы/матрицы из уравнения. Думаю, в этот раз читателям уже будет легче самостоятельно все попробовать — ведь как раз недавно в MQL5 была выпущена библиотека матричных функций. Если вам понадобится помощь с матрицами, не стесняйтесь обращаться ко мне — я буду рад помочь.
С наилучшими пожеланиями
Список видео с расчетами:
- https://www.youtube.com/watch?v=5yfh5cf4-0w
- https://www.youtube.com/watch?v=yg_497u6JnA
- https://www.youtube.com/watch?v=HaHsqDjWMLU
Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/11200
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Разработка торговой системы на основе осциллятора Чайкина
Разработка торговой системы на основе осциллятора Чайкина
 Нейросети — это просто (Часть 27): Глубокое Q-обучение (DQN)
Нейросети — это просто (Часть 27): Глубокое Q-обучение (DQN)
 Разработка торговой системы на основе стандартного отклонения
Разработка торговой системы на основе стандартного отклонения
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Первая итерация
Формула: x1 = x0 - Learning Rate * ( 2*(x+5) )
x1 = 0 - 0.01 * 0.01 * 2*(0+5)
x1 = -0.01 * 10
x1 = -0.1 (в итоге)
Два раза написано 0.01.Путаете людей.