Машинное обучение и Data Science (Часть 29): Как отбирать лучшие форекс-данные для обучения ИИ

MetaTrader 5 — Статистика и анализ | 5 марта 2025, 15:07

581

Omega J Msigwa

Разделы

Введение

В трейдинге доступно огромное количество данных и информации: индикаторы (в MetaTrader 5 встроено более 36 индикаторов), торговые символы (более 100), которые могут использоваться в стратегиях корреляции, финансовые новости и другая информация. То есть у трейдеров есть в распоряжении обширный массив данных как для ручной торговли, так и для построения моделей искусственного интеллекта, помогающих принимать более обоснованные торговые решения.

Однако среди всей доступной информации неизбежно присутствуют некачественные или нерелевантные данные. Не все индикаторы, стратегии или данные применимы к конкретному торговому символу, стратегии или рыночной ситуации. Как определить наиболее ценные данные для торговли и построения моделей машинного обучения, чтобы добиться максимальной эффективности и прибыльности? Именно здесь на помощь приходит отбор признаков.

Отбор признаков

Отбор признаков (Feature Selection) — это процесс выявления и выбора подмножества наиболее значимых характеристик из исходного набора данных для построения модели. Этот процесс позволяет определить наиболее полезную информацию, необходимую для машинного обучения, и исключить несущественные или избыточные признаки.

Отбор признаков играет ключевую роль в создании эффективной модели машинного обучения по разным причинам.

Важность подбора признаков для AI-моделей

Снижение размерности

Удаляя нерелевантные или избыточные признаки, мы упрощаем модель и снижаем вычислительные затраты.
Повышение производительности

Сосредотачиваясь на наиболее значимых признаках, можно улучшить точность и предсказательную силу модели.
Улучшение интерпретируемост

Модели с меньшим количеством признаков легче анализировать и объяснять.
Фильтрация шума

Исключая малозначимые данные, можно предотвратить переобучение, которое часто возникает из-за избыточного количества нерелевантных признаков.

Теперь, когда мы понимаем важность отбора признаков, рассмотрим различные методики, которые специалисты по данным и эксперты по машинному обучению используют для поиска наилучших признаков для моделей ИИ.

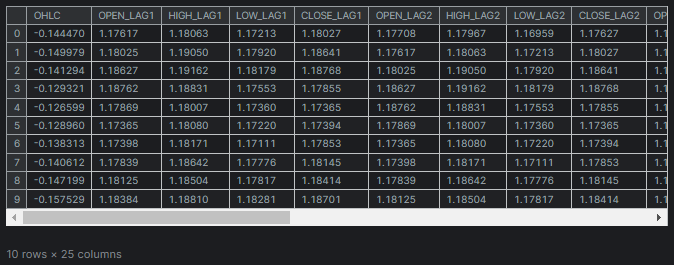
В этой статье мы будем работать с тем же набором данных, что и в этой статье (если вы ее не читали, обязательно прочтите).Этот набор содержит 28 переменных.

Из этих 28 переменных нам необходимо выделить наиболее значимые для столбцов "TARGET_OPEN" (значения цены открытия следующей свечи) и "TARGET_CLOSE" (значения цены закрытия следующей свечи), опустив менее значимые данные.

Методы отбора признаков можно разделить на три основные категории: фильтрационные методы, методы-обертки и встроенные методы. Рассмотрим каждый из них подробнее.

Фильтрационные методы

Фильтрационные методы оценивают признаки независимо от используемой модели машинного обучения. Среди них популярны корреляционная матрица и статистические тесты..

Корреляционная матрица

Корреляционная матрица — это таблица, отображающая коэффициенты корреляции между различными переменными.

Коэффициент корреляции — это статистическая мера, показывающая силу и направление связи между двумя переменными. Он принимает значения от -1 до 1:

Значение 1 означает идеальную положительную корреляцию (увеличение одной переменной сопровождается пропорциональным увеличением другой).

Значение 0 означает отсутствие корреляции (переменные не связаны друг с другом).

Значение -1 означает идеальную отрицательную корреляцию (увеличение одной переменной сопровождается пропорциональным уменьшением другой).

Код ниже показывает, как можно вычислить корреляционную матрицу в Python.

Вычисление корреляционной матрицы

# Compute the correlation matrix
corr_matrix = df.corr()

# We generate a mask for the upper triangle
mask = np.triu(np.ones_like(corr_matrix, dtype=bool))
cmap = sns.diverging_palette(220, 10, as_cmap=True) # Custom colormap


plt.figure(figsize=(28, 28)) # 28 columns to fit better 

# Draw the heatmap with the mask and correct aspect ratio
sns.heatmap(corr_matrix, mask=mask, cmap=cmap, vmax=1.0, center=0, annot=True,
            square=True, linewidths=1, cbar_kws={"shrink": .75})

plt.title('Correlation Matrix')
plt.savefig("correlation matrix.png")
plt.show()

Результаты

Матрица получилась слишком большой, и я не могу показать ее целиком. Ниже привожу самые ее полезные части.

Часть матрицы

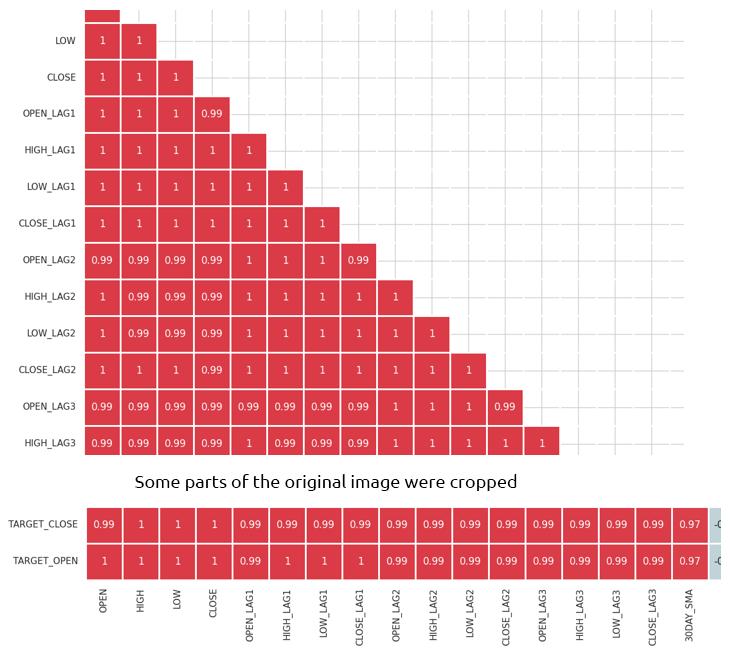
Определение и устранение сильно коррелированных признаков

Высокая мультиколлинеарность возникает, когда две или более переменные имеют сильную корреляцию друг с другом. Это может привести к проблемам в моделях машинного обучения, особенно в линейных моделях, поскольку вызывает нестабильность оценок коэффициентов.

Корреляция между независимыми переменными

Объединяя или удаляя сильно коррелированные признаки, можно упростить модель, не теряя при этом важной информации. Например, в представленной выше корреляционной матрице переменные Open, High и Low имеют 100% корреляцию. Их корреляция составляет 99 с лишним % (округленные значения). В этом случае можно исключить часть этих переменных, оставив лишь одну, либо применить методы снижения размерности, которые мы рассмотрим далее.

Корреляция между независимыми переменными и целевой переменной

Признаки, имеющие сильную корреляцию с целевой переменной, обычно являются более информативными и способны улучшить предсказательную способность модели.

Важно отметить, что матрица неприменима к категориальным переменным, таким как "DAYOFWEEK", "DAYOFYEAR" и "MONTH", так как коэффициенты корреляции оценивают только линейные зависимости между числовыми переменными.

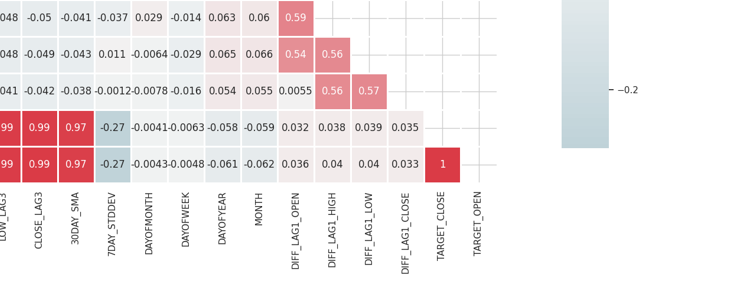
Статистические тесты

Для выбора значимых признаков можно использовать статистические тесты, которые определяют степень связи между переменными и целевой переменной.

Критерий хи-квадрат

Критерий хи-квадрат (Chi-squared test) измеряет соответствие ожидаемых значений наблюдаемым в таблице сопряженности. Этот тест позволяет определить, существует ли статистически значимая взаимосвязь между двумя категориальными переменными.

Таблица сопряженности — это таблица в формате матрицы, отображающая распределение частот между переменными. Она используется для анализа взаимосвязи между двумя категориальными переменными. В критерии хи-квадрат таблица сопряженности помогает сравнить наблюдаемые частоты с ожидаемыми.

Важно отметить, что критерий хи-квадрат применим только к категориальным переменным.

В нашем наборе данных присутствуют несколько категориальных переменных (DAYOFMONTH, DAYOFWEEK, DAYOFYEAR и MONTH). Также необходимо создать целевую переменную, чтобы оценить ее связь с другими признаками.

Код Python

from sklearn.feature_selection import chi2
from sklearn.feature_selection import SelectKBest

target = []

# Loop through each row in the DataFrame to create the target variable

for i in range(len(df)):
    if df.loc[i, 'TARGET_CLOSE'] > df.loc[i, 'TARGET_OPEN']:
        target.append(1)
    else:
        target.append(0)
        

X = pd.DataFrame({
    'DAYOFMONTH': df['DAYOFMONTH'],
    'DAYOFWEEK': df['DAYOFWEEK'],
    'DAYOFYEAR': df['DAYOFYEAR'],
    'MONTH': df['MONTH']
})


chi2_selector = SelectKBest(chi2, k='all')
chi2_selector.fit(X, target)
chi2_scores = chi2_selector.scores_

# Output scores for each feature

feature_scores = pd.DataFrame({'Feature': X.columns, 'Chi2 Score': chi2_scores})
print(feature_scores)

Результаты

      Feature  Chi2 Score
0  DAYOFMONTH    0.622628
1   DAYOFWEEK    0.047481
2   DAYOFYEAR   14.618057
3       MONTH    0.489713

Из результатов выше видно, что DAYOFYEAR имеет наивысший показатель Chi2, что указывает на то, что эта переменная оказывает наибольшее влияние на целевую переменную по сравнению с другими. Это логично, поскольку данные собирались ежедневно, а каждый день однозначно соответствует дню года. Значительное присутствие переменной DAYOFYEAR в наборе данных, вероятно, увеличивает ее частоту и значимость, делая ее ключевым признаком при прогнозировании целевой переменной.

ANOVA (анализ дисперсии)

ANOVA (Analysis of Variance) — это статистический метод, используемый для сравнения средних значений трех или более групп и определения, существует ли между ними статистически значимая разница. Этот метод помогает выявить силу связи между непрерывными признаками и категориальной целевой переменной.

Метод ANOVA анализирует вариацию внутри каждой группы и между группами, а также измеряет изменчивость наблюдений в каждой группе относительно средних значений других групп.

Он вычисляет F-статистику, которая представляет собой отношение межгрупповой дисперсии к внутригрупповой дисперсии. Чем выше значение F-статистики, тем более различаются средние значения групп.

В Python для выполнения ANOVA можно использовать метод f_classif из библиотеки Scikit-learn.

Код Python

from sklearn.feature_selection import f_classif

# We start by dropping the categorical variables in the dataset

X = df.drop(columns=[
    "DAYOFMONTH",
    "DAYOFWEEK",
    "DAYOFYEAR",
    "MONTH",
    "TARGET_CLOSE",
    "TARGET_OPEN"
])


# Perform ANOVA test

selector = SelectKBest(score_func=f_classif, k='all')
selector.fit(X, target)

# Get the F-scores and p-values
anova_scores = selector.scores_
anova_pvalues = selector.pvalues_

# Create a DataFrame to display results
anova_results = pd.DataFrame({'Feature': X.columns, 'F-Score': anova_scores, 'p-Value': anova_pvalues})
print(anova_results)

Результаты

            Feature   F-Score   p-Value
0              OPEN  3.483736  0.062268
1              HIGH  3.627995  0.057103
2               LOW  3.400320  0.065480
3             CLOSE  3.666813  0.055792
4         OPEN_LAG1  3.160177  0.075759
5         HIGH_LAG1  3.363306  0.066962
6          LOW_LAG1  3.309483  0.069181
7        CLOSE_LAG1  3.529789  0.060567
8         OPEN_LAG2  3.015757  0.082767
9         HIGH_LAG2  3.034694  0.081810
10         LOW_LAG2  3.259887  0.071295
11       CLOSE_LAG2  3.206956  0.073629
12        OPEN_LAG3  3.236211  0.072329
13        HIGH_LAG3  3.022234  0.082439
14         LOW_LAG3  3.020219  0.082541
15       CLOSE_LAG3  3.075698  0.079777
16        30DAY_SMA  2.665990  0.102829
17      7DAY_STDDEV  0.639071  0.424238
18   DIFF_LAG1_OPEN  1.237127  0.266293
19   DIFF_LAG1_HIGH  0.991862  0.319529
20    DIFF_LAG1_LOW  0.131002  0.717472
21  DIFF_LAG1_CLOSE  0.198001  0.656435

Высокие значения F-оценки указывают на то, что признак имеет сильную связь с целевой переменной.

Значения P ниже значимого уровня (например, 0,05) считаются статистически значимыми.

Также можно выбрать признаки с самыми высокими F-оценками или самыми низкими P-значениями, которые означают самые важные признаки, и исключить другие. Давайте выберем 10 самых важных признаков.

Код Python

selector = SelectKBest(score_func=f_classif, k=10)
X_selected = selector.fit_transform(X, target)


# print the selected feature names

selected_features = X.columns[selector.get_support()]
print("Selected Features:", selected_features)

Результаты

Selected Features: Index(['OPEN', 'HIGH', 'LOW', 'CLOSE', 'HIGH_LAG1', 'LOW_LAG1', 'CLOSE_LAG1',
       'LOW_LAG2', 'CLOSE_LAG2', 'OPEN_LAG3'],
      dtype='object')

Методы обертки

Эти методы предполагают оценку эффективности модели с использованием различных подмножеств или признаков. В рамках методов обертки мы рассмотрим рекурсивное устранение признаков (RFE) и последовательный отбор признаков (SFS).

Рекурсивное устранение признаков (RFE)

Это метод отбора признаков, целью которого является выбор наиболее релевантных признаков путем рекурсивного рассмотрения все меньших и меньших наборов признаков. Он работает путем обучения модели и удаления наименее важных признаков до тех пор, пока не будет достигнуто желаемое количество признаков.

Как работает метод RFE

Начинаем с обучения любой модели машинного обучения. В этом примере давайте возьмем логистическую регрессию.

Код Python

from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression

# Prepare the target variable, again

y = []

# Loop through each row in the DataFrame to create the target variable
for i in range(len(df)):
    if df.loc[i, 'TARGET_CLOSE'] > df.loc[i, 'TARGET_OPEN']:
        y.append(1)
    else:
        y.append(0)

# Drop future variables from the feature set
X = df.drop(columns=["TARGET_CLOSE", "TARGET_OPEN"])

# Initialize the model
model = LogisticRegression(max_iter=10000)

Затем инициализируем RFE для модели и количества наиболее важных признаков, которые нужно выбрать из данных.

# Initialize RFE with the model and number of features to select
rfe = RFE(estimator=model, n_features_to_select=10)

# Fit RFE
rfe.fit(X, y)
selected_features_mask = rfe.support_

Наконец, определяем наименее важные признаки и исключаем их.

Код Python

# Getting the names of the selected features
feature_names = X.columns
selected_feature_names = feature_names[selected_features_mask]


selected_features = pd.DataFrame({
    "Name": feature_names,
    "Mask": selected_features_mask
})

selected_features.head(-1)

Результаты

        Name    Mask
0       OPEN    True
1       HIGH    True
2       LOW     True
3       CLOSE   True
4       OPEN_LAG1       False
5       HIGH_LAG1       True
6       LOW_LAG1        True
7       CLOSE_LAG1      True
8       OPEN_LAG2       False
9       HIGH_LAG2       False
10      LOW_LAG2        True
11      CLOSE_LAG2      True
12      OPEN_LAG3       True
13      HIGH_LAG3       False
14      LOW_LAG3        False
15      CLOSE_LAG3      False
16      30DAY_SMA       False
17      7DAY_STDDEV     False
18      DAYOFMONTH      False
19      DAYOFWEEK       False
20      DAYOFYEAR       False
21      MONTH   False
22      DIFF_LAG1_OPEN  False
23      DIFF_LAG1_HIGH  False
24      DIFF_LAG1_LOW   False

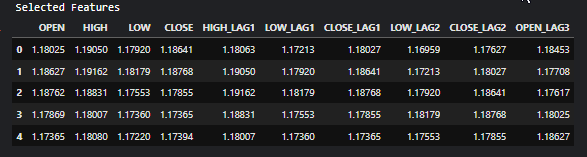
Все признаки, которые получили значение True — наиболее важные переменные. Чтобы получить их, можно извлечь их из оригинальной матрицы Х.

# Filter the dataset to keep only the selected features

X_selected = X.loc[:, selected_features_mask]

#for better readability, we convert this into pandas dataframe

X_selected_df = pd.DataFrame(X_selected, columns=selected_feature_names)

print("Selected Features")
X_selected_df.head()

Результаты

Выбранные признаки

Преимущества метода RFE

RFE может применяться с любой моделью, способной ранжировать признаки по их важности.
Метод исключает нерелевантные признаки и тем самым улучшает производительность модели.
RFE удаляет ненужные признаки и помогает снизить риск переобучения.

Недостатки RFE

При работе с большими наборами данных и сложными моделями RFE может требовать значительных вычислительных ресурсов, поскольку модель переобучается несколько раз.
RFE — это жадный алгоритм, и поэтому он не всегда находит оптимальное подмножество признаков.

Последовательный отбор признаков (SFS)

Это метод-обертка для отбора признаков, который постепенно формирует набор признаков, добавляя или удаляя их на основе вклада в производительность модели. Существует два основных типа последовательного отбора: прямой и обратный.

При прямом отборе признаки добавляются по одному, начиная с пустого набора, пока не соберется желаемое количество признаков или дальнейшее их добавление не будет улучшать качество модели.

Обратный отбор работает наоборот. Он начинается с полного набора признаков, затем они удаляются по одному, начиная с наименее значимого, пока не останется необходимое число признаков.

Прямой отбор

from sklearn.feature_selection import SequentialFeatureSelector

# Create a logistic regression model
model = LogisticRegression(max_iter=10000)

# Create a SequentialFeatureSelector object
sfs = SequentialFeatureSelector(model, n_features_to_select=10, direction='forward')

# Fit the SFS object to the training data
sfs.fit(X, target)

# Get the selected feature indices
selected_features = sfs.get_support(indices=True)
selected_features_names = X.columns[selected_features] # get the feature names

# Print the selected features
print("Selected feature indices:", selected_features)
print("Selected feature names:", selected_feature_names)

Результаты

Selected feature indices: [ 1  7  8 12 17 19 22 23 24 25]
Selected feature names: Index(['OPEN', 'HIGH', 'LOW', 'CLOSE', 'HIGH_LAG1', 'LOW_LAG1', 'CLOSE_LAG1',
       'LOW_LAG2', 'CLOSE_LAG2', 'OPEN_LAG3'],
      dtype='object')

Обратный отбор

# Create a logistic regression model
model = LogisticRegression(max_iter=10000)

# Create a SequentialFeatureSelector object
sfs = SequentialFeatureSelector(model, n_features_to_select=10, direction='backward')

# Fit the SFS object to the training data
sfs.fit(X, target)

# Get the selected feature indices
selected_features = sfs.get_support(indices=True)
selected_features_names = X.columns[selected_features] # get the feature names

# Print the selected features
print("Selected feature indices:", selected_features)
print("Selected feature names:", selected_feature_names)

Результаты

Selected feature indices: [ 2  3  7 10 11 12 13 14 15 16]
Selected feature names: Index(['OPEN', 'HIGH', 'LOW', 'CLOSE', 'HIGH_LAG1', 'LOW_LAG1', 'CLOSE_LAG1',
       'LOW_LAG2', 'CLOSE_LAG2', 'OPEN_LAG3'],
      dtype='object')

Несмотря на разные подходы, оба метода (прямой и обратный) могут закончиться с одинаковым набором признаков. Количество признаков в них может совпадать.

Преимущества последовательного отбора признаков

Простота интерпретации и реализации.
Этот метод можно использовать с любым алгоритмом машинного обучения.
Часто отбор наиболее релевантных признаков приводит к повышению производительности модели.

Недостатки последовательного отбора признаков

Этот метод работает медленно при работе с большими наборами данных или большим количеством признаков.
Может не найти оптимальный набор признаков, поскольку принимает решения на основе локальных улучшений.

Встроенные методы

Эти методы предполагают выполнение отбора признаков в процессе обучения модели. Процесс выбора встроенных функций включает в себя:

Обучение модели
Получение важности признаков
Выбор предикторных переменных с наивысшим рейтингом

Наиболее распространенные встроенные методы включают Lasso-регрессию и методы, основанные на деревьях решений.

Lasso-регрессия

Модели линейной регрессии прогнозируют результат на основе линейной комбинации пространства признаков. Коэффициенты определяются путем минимизации квадрата разницы между реальным и прогнозируемым значением цели. Существует три основных варианта регуляризации: гребнями, Lasso и эластичная сетевая регуляризация, которая объединяет первые две. В Lasso-регрессии коэффициенты уменьшаются на заданную константу с использованием L1-регуляризации. В гребневой регрессии квадрат коэффициентов штрафуется константой с использованием L2-регуляризации. Целью уменьшения коэффициентов является уменьшение дисперсии и предотвращение переобучения. Наилучшую константу (параметр регуляризации) оцениваем с помощью оптимизации гиперпараметров.

Lasso-регуляризация может устанавливать некоторые коэффициенты равными нулю. Это позволяет безопасно удалять эти признаки из данных.

Код Python

from sklearn.model_selection import train_test_split
from sklearn.linear_model import Lasso
from sklearn.metrics import r2_score
from sklearn.preprocessing import MinMaxScaler

y = df["TARGET_CLOSE"]

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# A scaling technique
scaler = MinMaxScaler()

# Initialize and fit the lasso model
lasso = Lasso(alpha=0.001)  # You need tune for the best penalty value

# Train the scaler and transfrom data
X_train = scaler.fit_transform(X_train)

lasso.fit(X_train, y_train)

print(f'Coefficients: {lasso.coef_}') #print coefficients

# Predict on the test set
X_test = scaler.transform(X_test)
y_pred = lasso.predict(X_test)

# Calculate mean squared error
mse = r2_score(y_test, y_pred)
print(f'Lasso regression test accuracy = {mse}')


# select all features with coefficents not equal to zero
selected_features = X.columns[lasso.coef_ != 0]
print(f'Selected Features: {selected_features}')

Результаты

Coefficients: [ 0.          0.02575516  0.05720178  0.1453415   0.          0.
  0.          0.          0.          0.          0.          0.
  0.          0.          0.          0.          0.0228085  -0.
  0.         -0.          0.          0.          0.          0.
  0.          0.        ]
Lasso regression test accuracy = 0.9894539761500866
Selected Features: Index(['HIGH', 'LOW', 'CLOSE', '30DAY_SMA'], dtype='object')

Здесь модель достигла точности 98%, выбрав всего 4 признака.

Преимущества использования Lasso-регрессии для отбора признаков

Lasso автоматически выбирает наиболее важные признаки, упрощая модель и улучшая ее интерпретируемость.
Добавление штрафа (L1-регуляризация) снижает риск переобучения.
Убирая нерелевантные признаки, Lasso упрощает интерпретацию модели.

Недостатки использования Lasso-регрессии для отбора признаков

При высокой корреляции между признаками Lasso может давать нестабильные оценки коэффициентов.
Если число признаков превышает число наблюдений, эффективность Lasso может снижаться.

Методы, основанные на деревьях решений

Алгоритмы деревьев решений прогнозируют результаты, рекурсивно разделяя данные. На каждом узле алгоритм выбирает признак и значение для разделения, стремясь максимизировать снижение нечистоты данных.

Важность признака в деревьях решений определяется суммарным снижением нечистоты, достигаемым данным признаком в дереве. Например, если признак используется для разделения данных на нескольких узлах, его важность рассчитывается как сумма снижения примесей во всех этих узлах.

Случайные леса (Random Forests) строят множество деревьев и усредняют их прогнозы. Окончательный прогноз представляет собой среднее значение (или большинство голосов) прогнозов отдельных деревьев. Важность признака оценивается по средней значимости во всех деревьях.

Градиентный бустинг (XGBoost и другие GBM) строит деревья последовательно, корректируя ошибки предыдущих деревьев. Важность признаков рассчитывается как сумма их важности во всех деревьях.

Анализируя значения важности признаков, полученные с помощью деревьев решений, можно определить и отобрать наиболее значимые признаки для нашей модели.

from sklearn.ensemble import RandomForestClassifier

y = []

# Loop through each row in the DataFrame to create the target variable
for i in range(len(df)):
    if df.loc[i, 'TARGET_CLOSE'] > df.loc[i, 'TARGET_OPEN']:
        y.append(1)
    else:
        y.append(0)

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

model = RandomForestClassifier(n_estimators=50, min_samples_split=10, max_depth=5, min_samples_leaf=5)
model.fit(X_train, y_train)

importances = model.feature_importances_

print(importances)

selected_features = importances > 0.04
selected_feature_names = X.columns[selected_features]

print("selected features\n",selected_feature_names)

Результаты

[0.02691807 0.05334113 0.03780997 0.0563491  0.03162462 0.03486413
 0.02652285 0.0237652  0.03398946 0.02822157 0.01794172 0.02818283
 0.04052433 0.02821834 0.0386661  0.03921218 0.04406372 0.06162133
 0.03103843 0.02206782 0.05104613 0.01700301 0.05191551 0.07251801
 0.0502405  0.05233394]
selected features
 Index(['HIGH', 'CLOSE', 'OPEN_LAG3', '30DAY_SMA', '7DAY_STDDEV', 'DAYOFYEAR',
       'DIFF_LAG1_OPEN', 'DIFF_LAG1_HIGH', 'DIFF_LAG1_LOW', 'DIFF_LAG1_CLOSE'],
      dtype='object')

Прежде чем перейти к непосредственному использованию отобранных признаков, необходимо измерить точность классификатора случайного леса, который выбрал эти признаки. Для получения признаков необходимо использовать модель, которая показала хорошие результаты на тестовых данных.

from sklearn.metrics import accuracy_score

test_pred = model.predict(X_test)

print(f"Random forest test accuracy = ",accuracy_score(y_test, test_pred))

Преимущества случайного леса для отбора признаков

Случайные леса создают ансамбль деревьев, снижая риск переобучения и обеспечивая более надежные оценки значимости признаков. Это делает оценки важности признаков более надежными.
Они могут работать с большими наборами данных без существенного снижения производительности, поэтому они подходят для отбора признаков в многомерных пространствах.
Они могут улавливать сложные нелинейные взаимодействия между признаками, обеспечивая более детальное понимание важности признаков.

Недостатки случайного леса для выбора признаков

Вычислительно затратны при больших объемах данных и большом числе признаков.
Могут присваивать схожие значения важности коррелированным признакам, затрудняя их интерпретацию.
Предпочитают непрерывные признаки перед категориальными, что может искажать значимость признаков.

Методы снижения размерности

Методы снижения размерности также можно использовать в процессе отбора признаков. К таким методам относятся Анализ главных компонент (Principal Component Analysis, PCA), (LDA), Неотрицательная матричная факторизация (NMF), Truncated SVD и пр. Все они направлены на преобразование данных в пространство с меньшей размерностью.

На основе корреляционной матрицы видно, что признаки OPEN, HIGH, LOW и CLOSE сильно коррелируют между собой. Их можно объединить в один новый признак, используя PCA, чтобы упростить модель и сохранить всю важную информацию. Затем можно измерить, насколько точно модель с сокращенным набором признаков предсказывает результаты по сравнению с исходными данными, используя линейную регрессию.

from sklearn.decomposition import PCA
from sklearn.linear_model import LinearRegression

pca = PCA(n_components=1)

ohlc = pd.DataFrame({
    "OPEN": df["OPEN"],
    "HIGH": df["HIGH"],
    "LOW": df["LOW"],
    "CLOSE": df["CLOSE"]
})

y = df["TARGET_CLOSE"]

# let us use the linear regression model 
model = LinearRegression()

# for OHLC original data 

model.fit(ohlc, y)
preds = model.predict(ohlc)

print("ohlc_original data LR accuracy = ",r2_score(y, preds))

# For data reduced in dimension

ohlc_reduced = pca.fit_transform(ohlc)

print(ohlc_reduced[:10]) # print 10 rows of the reduced data 

model.fit(ohlc_reduced, y)
preds = model.predict(ohlc_reduced)

print("ohlc_reduced data LR accuracy = ",r2_score(y, preds))

Результаты

ohlc_original data LR accuracy =  0.9937597843724363
[[-0.14447016]
 [-0.14997874]
 [-0.14129409]
 [-0.1293209 ]
 [-0.12659902]
 [-0.12895961]
 [-0.13831287]
 [-0.14061213]
 [-0.14719862]
 [-0.15752861]]
ohlc_reduced data LR accuracy =  0.9921387699876517

Обе модели дали примерно одинаковое значение точности — около 0,99. В одном из них использовались исходные данные (с 4 признаками), а в другом — данные, уменьшенные в размерности (с 1 признаком).

Наконец, мы можем изменить исходные данные, удалив признаки OPEN, HIGH, LOW и CLOSE и добавив новый признак с именем OHLC, который объединяет предыдущие четыре (4) признака.

new_df = df.drop(columns=["OPEN", "HIGH", "LOW", "CLOSE"]) #
new_df["OHLC"] = ohlc_reduced

# Reorder the columns to make "ohlc" the first column
cols = ["OHLC"] + [col for col in new_df.columns if col != "OHLC"]
new_df = new_df[cols]

new_df.head(10)

Результаты

Преимущества методов снижения размерности при отборе признаков

Уменьшение количества признаков может повысить производительность моделей машинного обучения за счет устранения шума и избыточной информации.
Методы снижения размерности уменьшают пространство признаков и тем самым помогают смягчить переобучение при работе с данными высокой размерности, где вероятность переобучения выше.
Эти методы позволяют отфильтровать шум из набора данных, что приводит к получению более чистых данных, которые могут повысить точность и надежность модели.
Модели с меньшим количеством признаков проще, их легче интерпретировать.

Недостатки методов снижения размерности при отборе признаков

Снижение размерности часто приводит к потере важной информации, что может негативно сказаться на производительности модели.
Такие методы, как PCA, требуют выбора количества сохраняемых компонентов, но это не всегда просто, зачастую происходит методом проб и ошибок или с помощью перекрестной проверки.
Новые признаки, созданные с помощью методов снижения размерности, труднее интерпретировать по сравнению с исходными признаками.
Снижение размерности может привести к чрезмерному упрощению данных, что приведет к созданию моделей, в которых будут упущены тонкие, но важные взаимосвязи между признаками.

Заключительные мысли

Умение извлекать наиболее ценную информацию играет ключевую роль в оптимизации моделей машинного обучения. Эффективный отбор признаков может значительно сократить время обучения и повысить точность модели, что приведет к созданию более эффективных торговых роботов на базе искусственного интеллекта в MetaTrader 5. Тщательно выбирая наиболее релевантные функции, можно значительно повысить эффективность как в реальной торговле, так и во время тестирования стратегий,что в конечном итоге позволит получать лучшие результаты с помощью торговых алгоритмов.

С наилучшими пожеланиями

Таблица вложений

Файл	Описание и использование
feature_selection.ipynb	Этот блокнот Jupiter содержит весь код Python, обсуждаемый в этой статье.
Timeseries OHLC.csv	Набор данных, используемый в этой статье

Источники

A Chi-Square Statistics-Based Feature Selection Method in Text Classification (https://www.researchgate.net/publication/331850396_A_Chi-Square_Statistics_Based_Feature_Selection_Method_in_Text_Classification)
Feature Selection (https://en.wikipedia.org/wiki/Feature_selection)
Embedded Methods (https://www.blog.trainindata.com/feature-selection-with-embedded-methods/)

Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/15482

Прикрепленные файлы |

Загрузить ZIP

feature-selection.ipynb (392.89 KB)

Timeseries_OHLC.csv (219.94 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Последние комментарии | Перейти к обсуждению на форуме трейдеров (1)

linfo2 | 8 авг. 2024 в 00:11

Спасибо за четкую и хорошо написанную статью, Это именно то, что я пытался понять и работал, чтобы проверить корреляции самостоятельно. Спасибо также за файл python, так как он делает простой шаблон для меня, чтобы адаптировать. Надеюсь, после некоторого анализа я скажу спасибо за то, что открыли мне глаза на то, что возможно.

Переосмысливаем классические стратегии (Часть V): Анализ нескольких инструментов в валютной паре USDZAR

В данной серии статей мы вновь рассматриваем классические стратегии, чтобы выяснить, можно ли улучшить стратегию с помощью ИИ. В сегодняшней статье мы рассмотрим популярную стратегию анализа нескольких инструментов с использованием корзины коррелированных ценных бумаг. Сосредоточимся на экзотической валютной паре USDZAR.

Индикатор оценки силы и слабости валютных пар на чистом MQL5

Создаем профессиональный индикатор для анализа силы валют на MQL5. Пошаговое руководство научит вас разрабатывать мощный торговый инструмент с визуальной панелью для MetaTrader 5. Вы узнаете, как рассчитывать силу валютных пар по нескольким таймфреймам (H1, H4, D1), реализовывать динамическое обновление данных и создавать удобный пользовательский интерфейс.

Нейросети в трейдинге: Интеграция теории хаоса в прогнозирование временных рядов (Окончание)

Продолжаем интеграцию методов, предложенных авторами фреймворка Attraos, в торговые модели. Напомню, что данный фреймворк использует концепции теории хаоса для решения задач прогнозирования временных рядов, интерпретируя их как проекции многомерных хаотических динамических систем.

Управление капиталом в трейдинге и программа домашней бухгалтерии трейдера с базой данных

Как трейдеру управлять капиталом? Как трейдеру и инвестору вести учет расходов, доходов, активов и пассивов? Я представлю вам не просто программу для учета, я покажу вам инструмент, который может стать вашим надежным финансовым навигатором в бурном море трейдинга.