Data Science e Machine Learning (Parte 25): Previsão de Séries Temporais de Forex Usando uma Rede Neural Recorrente (RNN)

MetaTrader 5 — Experts | 21 novembro 2024, 09:32

226

Omega J Msigwa

Conteúdo

O que são Redes Neurais Recorrentes (RNNs)

Redes Neurais Recorrentes (RNNs) são redes neurais artificiais projetadas para reconhecer padrões em sequências de dados, como séries temporais, linguagem ou vídeo. Diferente das redes neurais tradicionais, que assumem que as entradas são independentes entre si, as RNNs podem detectar e entender padrões a partir de uma sequência de dados (informação).

Para evitar confusão com as terminologias ao longo deste artigo, quando menciono Rede Neural Recorrente refiro-me ao RNN simples como um modelo, enquanto, quando uso Redes Neurais Recorrentes (RNNs), refiro-me a uma família de modelos de rede neural recorrente, como RNN simples, Long Short Term Memory (LSTM) e Gated Recurrent Unit (GRU).

É necessário um entendimento básico de Python, ONNX em MQL5 e machine learning em Python para compreender totalmente o conteúdo deste artigo.

Compreendendo as RNNs

As RNNs têm algo chamado memória sequencial, que se refere ao conceito de reter e utilizar informações dos passos de tempo anteriores em uma sequência para informar o processamento dos passos subsequentes.

A memória sequencial é semelhante àquela em seu cérebro humano; é o tipo de memória que facilita o reconhecimento de padrões em sequências, como ao articular palavras para falar.

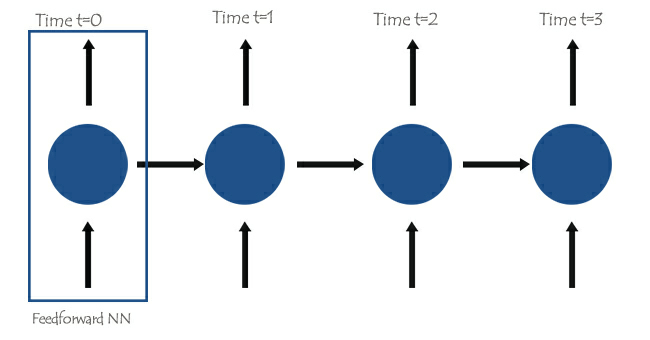
No núcleo das Redes Neurais Recorrentes (RNNs), há redes neurais de alimentação direta interconectadas de tal forma que a próxima rede possui a informação da anterior, dando ao RNN simples a capacidade de aprender e entender a informação atual com base nas anteriores.

Para entender melhor, vejamos um exemplo onde queremos ensinar o modelo de RNN para um chatbot. Queremos que nosso chatbot entenda as palavras e frases de um usuário; suponha que a frase recebida seja: Que horas são?

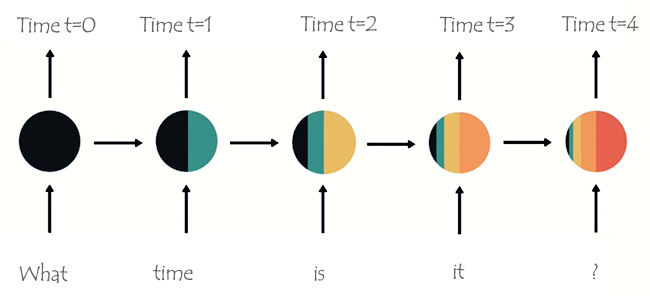
As palavras serão divididas em seus respectivos Timesteps e alimentadas uma após a outra na RNN, como mostrado na imagem abaixo.

Olhando para o último nó na rede, você pode ter notado um arranjo peculiar de cores representando a informação das redes anteriores e da atual. Ao observar as cores, a informação da rede no tempo t=0 e no tempo t=1 é muito pequena (quase inexistente) neste último nó da RNN.

Conforme a RNN processa mais passos, ela tem dificuldade em reter informações dos passos anteriores. Como visto na imagem acima, as palavras que e horas estão quase inexistentes no nó final da rede.

Isso é o que chamamos de memória de curto prazo. É causada por muitos fatores, sendo a retropropagação um dos principais.

As Redes Neurais Recorrentes (RNNs) possuem seu próprio processo de retropropagação, conhecido como retropropagação através do tempo. Durante a retropropagação, os valores de gradiente encolhem exponencialmente à medida que a rede propaga por cada passo de tempo para trás. Gradientes são usados para fazer ajustes nos parâmetros da rede neural (pesos e bias); esse ajuste é o que permite que a rede neural aprenda. Gradientes pequenos significam ajustes menores. Como as camadas iniciais recebem gradientes pequenos, isso faz com que elas não aprendam tão efetivamente quanto deveriam. Isso é conhecido como o problema dos gradientes que desaparecem.

Devido ao problema dos gradientes que desaparecem, o RNN simples não aprende dependências de longo prazo através dos passos de tempo. No exemplo da imagem acima, há uma grande possibilidade de que palavras como que e horas não sejam consideradas quando nosso modelo de chatbot RNN tenta entender uma frase de exemplo de um usuário. A rede tem que fazer sua melhor suposição com meia frase e apenas três palavras; é ?. Isso torna a RNN menos eficaz, pois sua memória é muito curta para entender dados de séries temporais longas, frequentemente encontradas em aplicações do mundo real.,

Para mitigar a memória de curto prazo, foram introduzidas duas Redes Neurais Recorrentes especializadas: Long Short Term Memory (LSTM) e Gated Recurrent Unit (GRU).

Tanto o LSTM quanto o GRU funcionam de maneira semelhante à RNN, mas são capazes de entender dependências de longo prazo usando o mecanismo chamado portas. Discutiremos isso em detalhes no próximo artigo fique atento.

A matemática por trás de uma Rede Neural Recorrente (RNN)

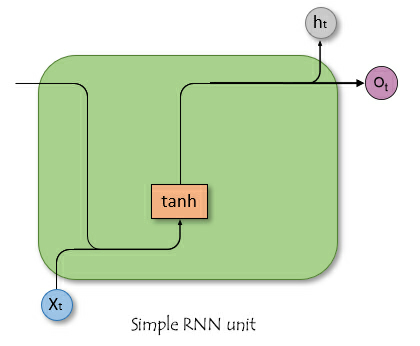
Diferente das redes neurais de alimentação direta, as RNNs têm conexões que formam ciclos, permitindo que a informação persista. A imagem simplista abaixo mostra como uma unidade/célula de RNN se parece quando dissecada.

onde:

é a entrada no tempo t.

é o estado oculto no tempo t.

Estado Oculto

Denotado como , é um vetor que armazena informações dos passos de tempo anteriores. Atua como a memória da rede, permitindo capturar dependências temporais e padrões nos dados de entrada ao longo do tempo.

Funções do estado oculto na rede

O estado oculto serve para várias funções cruciais em uma RNN, como:

Ele retém informações de entradas anteriores, o que permite que a rede aprenda com a sequência inteira.
Ele fornece contexto para a entrada atual, permitindo que a rede faça previsões informadas com base em dados passados.
Ele forma a base para as conexões recorrentes dentro da rede, permitindo que a camada oculta influencie a si mesma em diferentes passos de tempo.

Entender a matemática por trás da RNN não é tão importante quanto saber como, onde e quando usá-las. Sinta-se à vontade para pular para a próxima seção deste artigo, se desejar.

Fórmula Matemática

O estado oculto no passo de tempo é computado usando a entrada no passo de tempo , o estado oculto do passo de tempo anterior e as matrizes de peso e bias correspondentes. A fórmula é a seguinte;

onde:

é a matriz de peso para a entrada no estado oculto.

é a matriz de peso para o estado oculto para o estado oculto.

é o termo de bias para o estado oculto.

σ é a função de ativação (ex.: tanh ou ReLU).

Camada de Saída:

A saída no passo de tempo é computada a partir do estado oculto no passo de tempo .

onde

é a saída no passo de tempo .

é a matriz de peso do estado oculto para a saída.

bias da camada de saída.

Cálculo da Perda

Assumindo uma função de perda (Esta pode ser qualquer função de perda, ex.: Erro Quadrático Médio para regressão ou Entropia Cruzada para classificação).

A perda total ao longo de todos os passos de tempo é;

Retropropagação Através do Tempo (BPTT)

Para atualizar tanto os pesos quanto o bias, é necessário calcular os gradientes da perda em relação a cada peso e bias, respectivamente, e então usar os gradientes obtidos para fazer atualizações. Isso envolve as etapas descritas a seguir.

Etapa	Para pesos	Para Bias
Calculando o gradiente da camada de saída	em relação aos pesos: Onde é o gradiente da perda em relação à saída.	em relação ao bias: Como o bias de saída afeta diretamente as saídas, temos; Portanto.
Calculando os gradientes do estado oculto em relação aos pesos e bias	O gradiente da perda em relação ao estado oculto envolve tanto a contribuição direta do passo de tempo atual quanto a contribuição indireta através dos passos de tempo subsequentes. 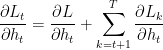Gradiente do estado oculto em relação ao passo de tempo anterior. Gradiente da ativação do estado oculto. Gradiente dos pesos da camada oculta. O gradiente total é a soma dos gradientes ao longo de todos os passos de tempo.	O gradiente da perda em relação ao bias oculto é dado pela soma dos gradientes da perda em relação ao estado oculto ao longo de todos os passos de tempo. Como o bias oculto afeta o estado oculto através da função de ativação, temos; Usando a regra da cadeia e observando que; Onde é a derivada da função de ativação. Portanto: O gradiente total para o bias oculto é a soma dos gradientes ao longo de todos os passos de tempo.
Atualizando pesos e bias. Usando os gradientes calculados acima, podemos atualizar os pesos usando o gradiente descendente ou qualquer uma de suas variantes (ex.: Adam), leia mais.

Apesar de a RNN simples não ter a capacidade de aprender bem dados de séries temporais longas, elas ainda são boas em prever valores futuros usando informações de um passado não muito distante. Podemos construir uma RNN simples para nos ajudar a tomar decisões de trading.

Construindo um Modelo de Rede Neural Recorrente (RNN) em Python

Construir e compilar um modelo de RNN em Python é simples e leva apenas algumas linhas de código usando a biblioteca Keras.

Python

import tensorflow as tf
from tensorflow.keras.models import Sequential #import sequential neural network layer
from sklearn.preprocessing import StandardScaler
from tensorflow.keras.layers import SimpleRNN, Dense, Input
from keras.callbacks import EarlyStopping
from sklearn.preprocessing import MinMaxScaler
from keras.optimizers import Adam

reg_model = Sequential()

reg_model.add(Input(shape=(time_step, x_train.shape[1]))) # input layer
reg_model.add(SimpleRNN(50, activation='sigmoid')) #first hidden layer
reg_model.add(Dense(50, activation='sigmoid')) #second hidden layer
reg_model.add(Dense(units=1, activation='relu'))  # final layer 

adam_optimizer = Adam(learning_rate = 0.001)

reg_model.compile(optimizer=adam_optimizer, loss='mean_squared_error') # Compile the model
reg_model.summary()

O código acima é para uma rede neural recorrente de regressão, por isso temos 1 nó na camada de saída e uma função de ativação Relu na camada final, e há uma razão para isso. Como discutido no artigo Desmistificando Redes Neurais de Feedforward.

Usando os dados que coletamos no artigo anterior Previsão de Séries Temporais de Forex usando modelos de ML regulares(leitura obrigatória), queremos ver como podemos usar modelos de RNN, já que eles são capazes de entender dados de séries temporais para nos ajudar no que eles são bons.

Ao final, avaliaremos o desempenho das RNNs em comparação com o LightGBM construído no artigo anterior, nos mesmos dados. Espero que isso ajude a solidificar seu entendimento sobre previsão de séries temporais em geral.

Criando Dados Sequenciais

Em nosso conjunto de dados temos 28 colunas, todas preparadas para um modelo não-sequencial.

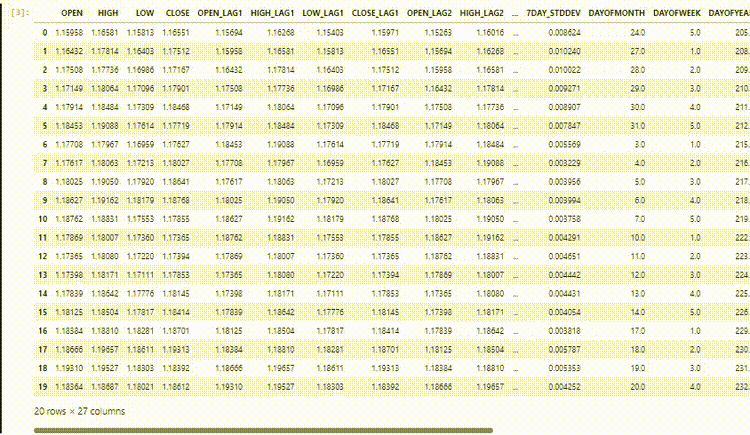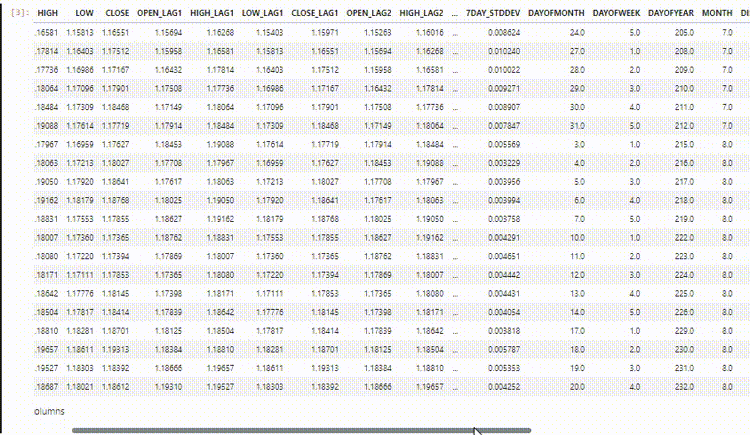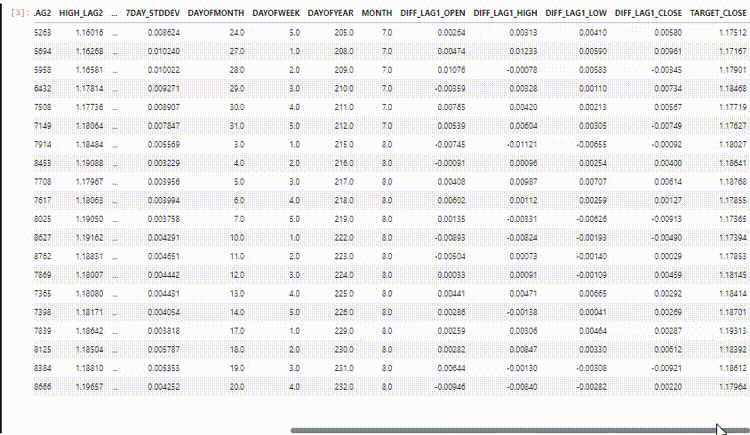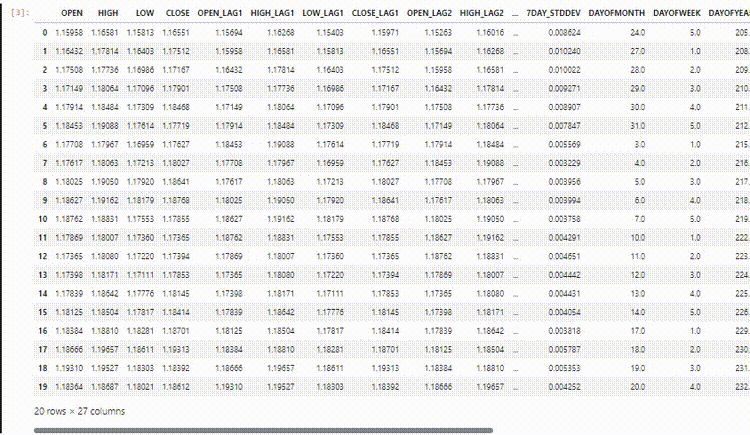
conjunto de dados para previsão de séries temporais

No entanto, esses dados que coletamos e preparamos possuem muitas variáveis defasadas, que foram úteis para o modelo não sequencial detectar padrões dependentes do tempo. Como sabemos, as RNNs podem entender padrões dentro dos intervalos de tempo fornecidos.

Não precisamos desses valores defasados agora, precisamos removê-los.

Python

lagged_columns = [col for col in data.columns if "lag" in col.lower()] #let us obtain all the columns with the name lag

print("lagged columns: ",lagged_columns)

data = data.drop(columns=lagged_columns) #drop them

Saídas:

lagged columns:  ['OPEN_LAG1', 'HIGH_LAG1', 'LOW_LAG1', 'CLOSE_LAG1', 'OPEN_LAG2', 'HIGH_LAG2', 'LOW_LAG2', 'CLOSE_LAG2', 'OPEN_LAG3', 'HIGH_LAG3', 'LOW_LAG3', 'CLOSE_LAG3', 'DIFF_LAG1_OPEN', 'DIFF_LAG1_HIGH', 'DIFF_LAG1_LOW', 'DIFF_LAG1_CL

Os novos dados agora têm 12 colunas.

novo conjunto de dados filtrado

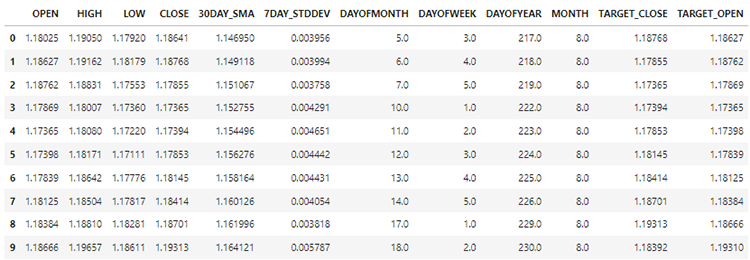
Podemos dividir 70% dos dados para treinamento, enquanto o restante 30% para teste. Se você estiver usando train_test_split do Scikit-Learn, certifique-se de definir shuffle=False. Isso fará com que a função divida o original enquanto preserva a ordem da informação presente.

Lembre-se! Esta é uma previsão de séries temporais.

# Split the data

X = data.drop(columns=["TARGET_CLOSE","TARGET_OPEN"]) #dropping the target variables
Y = data["TARGET_CLOSE"]

test_size = 0.3 #70% of the data should be used for training purpose while the rest 30% should be used for testing

x_train, x_test, y_train, y_test = train_test_split(X, Y, shuffle=False, test_size = test_size) # this is timeseries data so we don't shuffle

print(f"x_train {x_train.shape}\nx_test {x_test.shape}\ny_train{y_train.shape}\ny_test{y_test.shape}")

Depois de também remover as duas variáveis-alvo, nossos dados agora permanecem com 10 características. Precisamos converter essas 10 características em dados sequenciais que as RNNs possam processar.

def create_sequences(X, Y, time_step):
    if len(X) != len(Y):
        raise ValueError("X and y must have the same length")
    
    X = np.array(X)
    Y = np.array(Y)
    
    Xs, Ys = [], []
    
    for i in range(X.shape[0] - time_step):
        Xs.append(X[i:(i + time_step), :])  # Include all features with slicing
        Ys.append(Y[i + time_step])
        
    return np.array(Xs), np.array(Ys)

A função acima gera uma sequência a partir de arrays x e y fornecidos para um passo de tempo especificado. Para entender como essa função funciona, leia o exemplo a seguir:

Suponha que temos um conjunto de dados com 10 amostras e 2 recursos, e queremos criar sequências com um passo de tempo de 3.

X, que é uma matriz de forma (10, 2). Y, que é um vetor de comprimento 10.
A função criará sequências da seguinte forma
Para i=0: Xs obtém [0:3, :] X[0:3, :], e Ys obtém Y[3]. Para i=1: Xs obtém X[1:4, :] X[1:4, :], e Ys obtém Y[4].

E assim por diante, até i=6.

O Xs resultante terá uma forma de (7, 3, 2), e o Ys terá um comprimento de 7.

Após padronizar as variáveis independentes que separamos, podemos então aplicar a função create_sequences para gerar informações sequenciais.

time_step = 7 # we consider the past 7 days

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()

x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)

x_train_seq, y_train_seq = create_sequences(x_train, y_train, time_step)
x_test_seq, y_test_seq = create_sequences(x_test, y_test, time_step)

print(f"Sequential data\n\nx_train {x_train_seq.shape}\nx_test {x_test_seq.shape}\ny_train{y_train_seq.shape}\ny_test{y_test_seq.shape}")

Saídas:

Sequential data

x_train (693, 7, 10)
x_test (293, 7, 10)
y_train(693,)
y_test(293,)

O valor de passo de tempo 7 garante que, em cada instância, a RNN receba informações dos últimos 7 dias, considerando que coletamos todas as informações presentes no conjunto de dados a partir do período diário. Isso é semelhante a obter manualmente atrasos dos últimos 7 dias a partir da barra atual, algo que fizemos no artigo anterior desta série.

Treinando a RNN Simples para um Problema de Regressão

early_stopping = EarlyStopping(monitor='val_loss', patience=5, restore_best_weights=True)

history = reg_model.fit(x_train_seq, y_train_seq, epochs=100, batch_size=64, verbose=1, validation_data=(x_test_seq, y_test_seq), callbacks=[early_stopping])

Saídas:

Epoch 95/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 6.4504e-05 - val_loss: 4.4433e-05
Epoch 96/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 6.4380e-05 - val_loss: 4.4408e-05
Epoch 97/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 6.4259e-05 - val_loss: 4.4386e-05
Epoch 98/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 6.4140e-05 - val_loss: 4.4365e-05
Epoch 99/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 7ms/step - loss: 6.4024e-05 - val_loss: 4.4346e-05
Epoch 100/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 7ms/step - loss: 6.3910e-05 - val_loss: 4.4329e-05

curva de perda do treinamento do regressor RNN

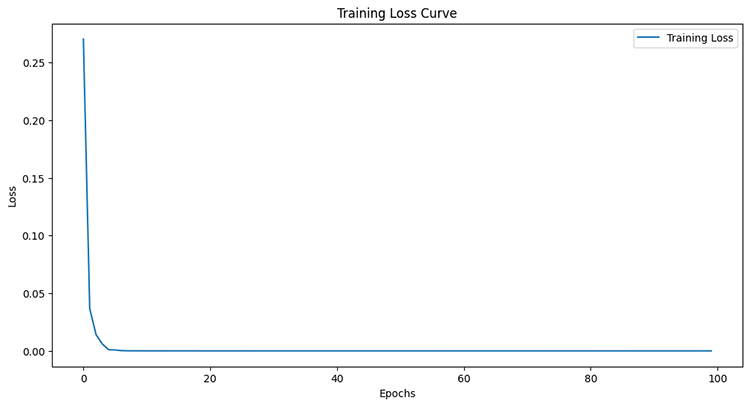
Após medir o desempenho da amostra de teste.

Python

from sklearn.metrics import r2_score

y_pred = reg_model.predict(x_test_seq) # Make predictions on the test set

# Plot the actual vs predicted values
plt.figure(figsize=(12, 6))
plt.plot(y_test_seq, label='Actual Values')
plt.plot(y_pred, label='Predicted Values')
plt.xlabel('Samples')
plt.ylabel('TARGET_CLOSE')
plt.title('Actual vs Predicted Values')
plt.legend()
plt.show()

print("RNN accuracy =",r2_score(y_test_seq, y_pred))

O modelo foi 78% preciso.

regressor RNN real vs previsto

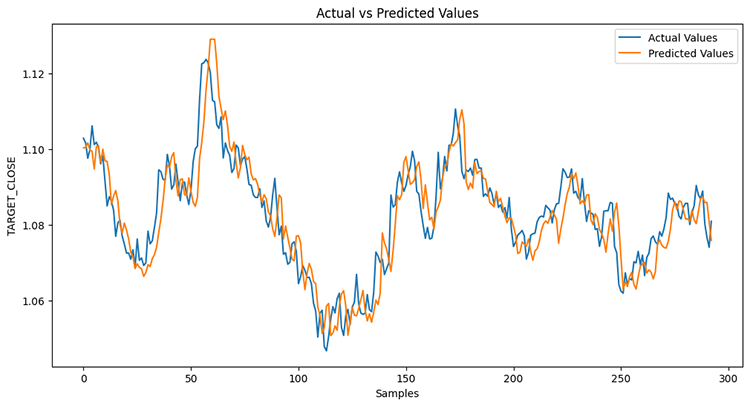
Se você lembra do artigo anterior, o modelo LightGBM teve uma precisão de 86,76% em um problema de regressão; neste ponto, um modelo que não é de séries temporais superou um modelo de séries temporais.

Importância das Variáveis

Eu realizei um teste para verificar como as variáveis afetam o processo de tomada de decisão do modelo RNN usando SHAP.

import shap

# Wrap the model prediction for KernelExplainer
def rnn_predict(data):
    data = data.reshape((data.shape[0], time_step, x_train.shape[1]))
    return reg_model.predict(data).flatten()

# Use SHAP to explain the model
sampled_idx = np.random.choice(len(x_train_seq), size=100, replace=False)
explainer = shap.KernelExplainer(rnn_predict, x_train_seq[sampled_idx].reshape(100, -1))
shap_values = explainer.shap_values(x_test_seq[:100].reshape(100, -1), nsamples=100)

Executei o código para desenhar um gráfico de importância das variáveis.

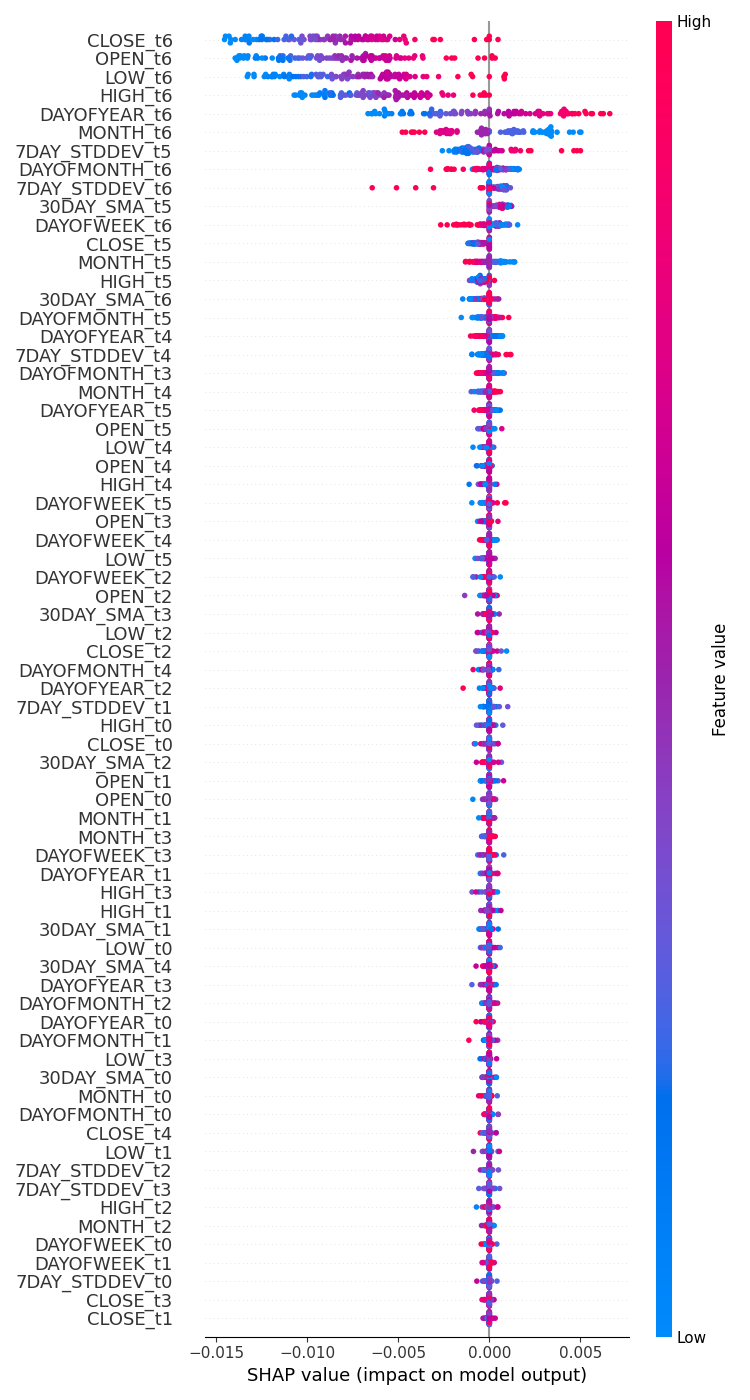
# Update feature names for SHAP
feature_names = [f'{original_feat}_t{t}' for t in range(time_step) for original_feat in X.columns]

# Plot the SHAP values
shap.summary_plot(shap_values, x_test_seq[:100].reshape(100, -1), feature_names=feature_names, max_display=len(feature_names), show=False)

# Adjust layout and set figure size
plt.subplots_adjust(left=0.12, bottom=0.1, right=0.9, top=0.9)  
plt.gcf().set_size_inches(7.5, 14) 
plt.tight_layout()

plt.savefig("regressor-rnn feature-importance.png")
plt.show()

Abaixo está o resultado:

As variáveis mais impactantes são aquelas com informações recentes, enquanto as variáveis menos impactantes são aquelas com informações mais antigas.

É como dizer que a palavra mais recente falada em uma frase carrega o maior significado para toda a frase.

Isso pode ser verdade para um modelo de machine learning, embora não faça muito sentido para nós, seres humanos.

Como mencionado no artigo anterior, não podemos confiar apenas no gráfico de importância das variáveis, considerando que usei KernelExplainer em vez do recomendado DeepExplainer, pois enfrentei muitos erros ao tentar fazer o método funcionar.

Como dito no artigo anterior, ter um modelo de regressão para adivinhar o próximo preço de fechamento ou abertura não é tão prático quanto ter um classificador que nos diga para onde ele acha que o mercado está indo na próxima barra. Vamos criar um modelo de RNN classificador para nos ajudar nessa tarefa.

Treinando a RNN Simples para um Problema de Classificação

Podemos seguir um processo semelhante ao que fizemos ao codificar para um regressor, com algumas alterações; Primeiro, precisamos criar a variável alvo para o problema de classificação.

Python

Y = []
target_open = data["TARGET_OPEN"]
target_close = data["TARGET_CLOSE"]

for i in range(len(target_open)):
    if target_close[i] > target_open[i]: # if the candle closed above where it opened thats a buy signal
        Y.append(1)
    else: #otherwise it is a sell signal
        Y.append(0)
        
Y = np.array(Y) #converting this array to NumPy


classes_in_y = np.unique(Y) # obtaining classes present in the target variable for the sake of setting the number of outputs in the RNN

Em seguida, devemos one-hot-encode a variável alvo logo após a criação da sequência, conforme discutido durante a criação de um modelo de regressão.

from tensorflow.keras.utils import to_categorical

y_train_encoded = to_categorical(y_train_seq)
y_test_encoded = to_categorical(y_test_seq)

print(f"One hot encoded\n\ny_train {y_train_encoded.shape}\ny_test {y_test_encoded.shape}")

Saídas:

One hot encoded

y_train (693, 2)
y_test (293, 2)

Finalmente, podemos construir o modelo RNN classificador e treiná-lo.

cls_model = Sequential()

cls_model.add(Input(shape=(time_step, x_train.shape[1]))) # input layer
cls_model.add(SimpleRNN(50, activation='relu'))
cls_model.add(Dense(50, activation='relu'))
cls_model.add(Dense(units=len(classes_in_y), activation='sigmoid', name='outputs')) 


adam_optimizer = Adam(learning_rate = 0.001)

cls_model.compile(optimizer=adam_optimizer, loss='binary_crossentropy') # Compile the model
cls_model.summary()


early_stopping = EarlyStopping(monitor='val_loss', patience=5, restore_best_weights=True)

history = cls_model.fit(x_train_seq, y_train_encoded, epochs=100, batch_size=64, verbose=1, validation_data=(x_test_seq, y_test_encoded), callbacks=[early_stopping])

Para o modelo RNN classificador, usei sigmoid para a camada final da rede. O número de neurônios (units) na camada final deve corresponder ao número de classes presentes na variável alvo (Y); neste caso, teremos duas unidades.

Model: "sequential_1"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ simple_rnn_1 (SimpleRNN)        │ (None, 50)             │         3,050 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_2 (Dense)                 │ (None, 50)             │         2,550 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ outputs (Dense)                 │ (None, 2)              │           102 │
└─────────────────────────────────┴────────────────────────┴───────────────┘

6 épocas foram suficientes para o modelo de RNN classificador convergir durante o treinamento.

Epoch 1/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 2s 36ms/step - loss: 0.7242 - val_loss: 0.6872
Epoch 2/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - loss: 0.6883 - val_loss: 0.6891
Epoch 3/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.6817 - val_loss: 0.6909
Epoch 4/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.6780 - val_loss: 0.6940
Epoch 5/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.6743 - val_loss: 0.6974
Epoch 6/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.6707 - val_loss: 0.6998

Apesar de ter uma precisão mais baixa na tarefa de regressão em comparação com a precisão fornecida pelo regressor LightGBM, o modelo RNN classificador foi 3% mais preciso do que o classificador LightGBM.

10/10 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
Classification Report
               precision    recall  f1-score   support

           0       0.53      0.27      0.36       137
           1       0.55      0.79      0.65       156

    accuracy                           0.55       293
   macro avg       0.54      0.53      0.50       293
weighted avg       0.54      0.55      0.51       293

Matriz de Confusão - Heatmap

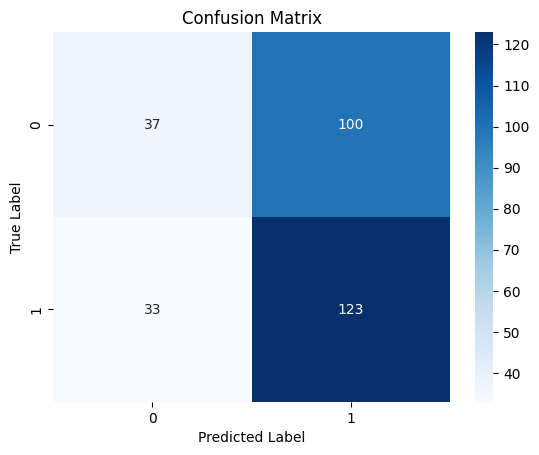
Salvando o Modelo de Rede Neural Recorrente em ONNX

Agora que temos um modelo de RNN classificador, podemos salvá-lo no formato ONNX, que é compreendido pelo MetaTrader 5.

Diferente dos modelos Scikit-learn, salvar modelos de deep learning como RNNs do Keras não é simples. Pipelines também não são uma solução fácil para RNNs.

Como discutido no artigo Superando os desafios do ONNX, podemos escalar os dados em MQL5 logo após coletá-los ou salvar o scaler que temos em Python e carregá-lo no MQL5 usando a biblioteca de pré-processamento para MQL5.

Salvando o Modelo

import tf2onnx

# Convert the Keras model to ONNX
spec = (tf.TensorSpec((None, time_step, x_train.shape[1]), tf.float16, name="input"),)
cls_model.output_names=['output']

onnx_model, _ = tf2onnx.convert.from_keras(cls_model, input_signature=spec, opset=13)

# Save the ONNX model to a file
with open("rnn.EURUSD.D1.onnx", "wb") as f:
    f.write(onnx_model.SerializeToString())

Salvando os parâmetros do Scaler de Padronização

# Save the mean and scale parameters to binary files

scaler.mean_.tofile("standard_scaler_mean.bin")
scaler.scale_.tofile("standard_scaler_scale.bin")

Ao salvar a média e o desvio padrão, que são os principais componentes do Standard scaler, podemos estar confiantes de que salvamos com sucesso o Standard scaler.

Consultor Especializado em Rede Neural Recorrente (RNN)

Dentro do nosso EA, a primeira coisa que devemos fazer é adicionar tanto o modelo RNN no formato ONNX quanto os arquivos binários do Standard Scaler como arquivos de recurso ao nosso EA.

MQL5 | previsão de séries temporais RNN.mq5

#resource "\\Files\\rnn.EURUSD.D1.onnx" as uchar onnx_model[]; //rnn model in onnx format
#resource "\\Files\\standard_scaler_mean.bin" as double standardization_mean[];
#resource "\\Files\\standard_scaler_scale.bin" as double standardization_std[];

Em seguida, podemos carregar as bibliotecas para carregar o modelo RNN no formato ONNX e o Standard Scaler.

MQL5

#include <MALE5\Recurrent Neural Networks(RNNs)\RNN.mqh>
CRNN rnn;

#include <MALE5\preprocessing.mqh>
StandardizationScaler *scaler;

Dentro da função OnInit.

vector classes_in_data_ = {0,1}; //we have to assign the classes manually | it is very important that their order is preserved as they can be seen in python code, HINT: They are usually in ascending order
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
  
//--- Initialize ONNX model
   
   if (!rnn.Init(onnx_model))
     return INIT_FAILED;
   
//--- Initializing the scaler with values loaded from binary files 

   scaler = new StandardizationScaler(standardization_mean, standardization_std);
   
//--- Initializing the CTrade library for executing trades

   m_trade.SetExpertMagicNumber(magic_number);
   m_trade.SetDeviationInPoints(slippage);
   m_trade.SetMarginMode();
   m_trade.SetTypeFillingBySymbol(Symbol());
           
   lotsize = SymbolInfoDouble(Symbol(), SYMBOL_VOLUME_MIN);
   
//--- Initializing the indicators

   ma_handle = iMA(Symbol(),timeframe,30,0,MODE_SMA,PRICE_WEIGHTED); //The Moving averaege for 30 days
   stddev_handle = iStdDev(Symbol(), timeframe, 7,0,MODE_SMA,PRICE_WEIGHTED); //The standard deviation for 7 days
   

   return(INIT_SUCCEEDED);
  }

Antes de podermos implementar o modelo para negociação ao vivo dentro da função OnTick, precisamos coletar dados de forma semelhante a como coletamos os dados de treinamento. Porém, desta vez, temos que evitar as variáveis que foram descartadas durante o treinamento.

Lembre-se! Treinamos o modelo com apenas 10 variáveis independentes.

novo conjunto de dados com variáveis-alvo sombreadas

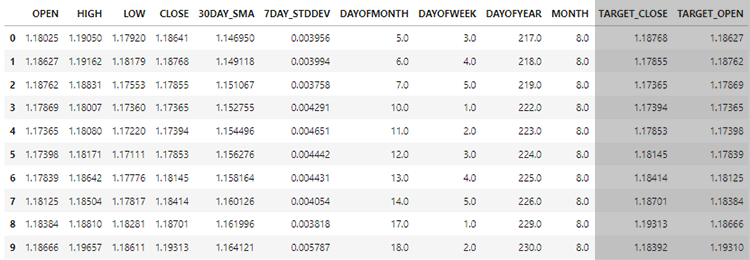
Vamos criar a função GetInputData para coletar apenas essas 10 variáveis independentes.

matrix GetInputData(int bars, int start_bar=1)
 {
   vector open(bars), 
          high(bars),
          low(bars), 
          close(bars), 
          ma(bars), 
          stddev(bars), 
          dayofmonth(bars), 
          dayofweek(bars), 
          dayofyear(bars), 
          month(bars);

//--- Getting OHLC values
   
   open.CopyRates(Symbol(), timeframe, COPY_RATES_OPEN, start_bar, bars);
   high.CopyRates(Symbol(), timeframe, COPY_RATES_HIGH, start_bar, bars);
   low.CopyRates(Symbol(), timeframe, COPY_RATES_LOW, start_bar, bars);
   close.CopyRates(Symbol(), timeframe, COPY_RATES_CLOSE, start_bar, bars);
   
   vector time_vector;
   time_vector.CopyRates(Symbol(), timeframe, COPY_RATES_TIME, start_bar, bars);
   
//---

   
   ma.CopyIndicatorBuffer(ma_handle, 0, start_bar, bars); //getting moving avg values 
   stddev.CopyIndicatorBuffer(stddev_handle, 0, start_bar, bars); //getting standard deviation values
   
   string time = "";
   for (int i=0; i<bars; i++) //Extracting time features 
     {
       time = (string)datetime(time_vector[i]); //converting the data from seconds to date then to string
       TimeToStruct((datetime)StringToTime(time), date_time_struct); //convering the string time to date then assigning them to a structure
       
       dayofmonth[i] = date_time_struct.day;
       dayofweek[i] = date_time_struct.day_of_week;
       dayofyear[i] = date_time_struct.day_of_year;
       month[i] = date_time_struct.mon;
     }
   
   matrix data(bars, 10); //we have 10 inputs from rnn | this value is fixed
   
//--- adding the features into a data matrix
   
   data.Col(open, 0);
   data.Col(high, 1);
   data.Col(low, 2);
   data.Col(close, 3);
   data.Col(ma, 4);
   data.Col(stddev, 5);
   data.Col(dayofmonth, 6);
   data.Col(dayofweek, 7);
   data.Col(dayofyear, 8);
   data.Col(month, 9);
   
   return data;
 }

Finalmente, podemos implementar o modelo RNN para nos fornecer sinais de negociação para nossa estratégia simples.

void OnTick()
  {
//---
   
   if (NewBar()) //Trade at the opening of a new candle
    {
      matrix input_data_matrix = GetInputData(rnn_time_step);
      input_data_matrix = scaler.transform(input_data_matrix); //applying StandardSCaler to the input data
      
      int signal = rnn.predict_bin(input_data_matrix, classes_in_data_); //getting trade signal from the RNN model
     
      Comment("Signal==",signal);
     
   //---
     
      MqlTick ticks;
      SymbolInfoTick(Symbol(), ticks);
      
      if (signal==1) //if the signal is bullish
       {
          if (!PosExists(POSITION_TYPE_BUY)) //There are no buy positions
           {
             if (!m_trade.Buy(lotsize, Symbol(), ticks.ask, ticks.bid-stoploss*Point(), ticks.ask+takeprofit*Point())) //Open a buy trade
               printf("Failed to open a buy position err=%d",GetLastError());
           }
       }
      else if (signal==0) //Bearish signal
        {
          if (!PosExists(POSITION_TYPE_SELL)) //There are no Sell positions
            if (!m_trade.Sell(lotsize, Symbol(), ticks.bid, ticks.ask+stoploss*Point(), ticks.bid-takeprofit*Point())) //open a sell trade
               printf("Failed to open a sell position err=%d",GetLastError());
        }
      else //There was an error
        return;
    }
  }

Testando EA de rede neural recorrente no testador de estratégia

Com uma estratégia de negociação definida, vamos executar testes no testador de estratégias. Estou usando os mesmos valores de Stop loss e Take profit que utilizamos para o modelo LightGBM, incluindo as configurações do testador.

input group "rnn";
input uint rnn_time_step = 7; 
//this value must be the same as the one used during training in a python script

input ENUM_TIMEFRAMES timeframe = PERIOD_D1;
input int magic_number = 1945;
input int slippage = 50;
input int stoploss = 500;
input int takeprofit = 700;

Configurações do testador de estratégia:

configurações do testador modelo RNN

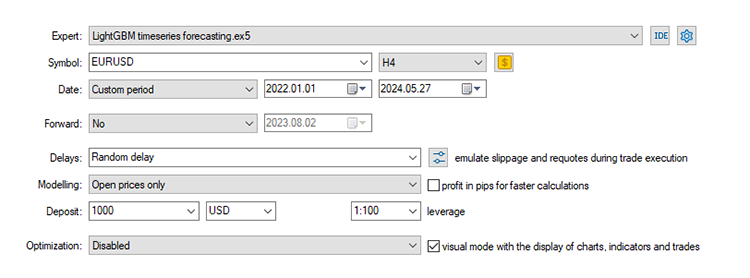
O EA foi lucrativo em 44,56% das 561 negociações realizadas.

relatório do consultor especialista RNN

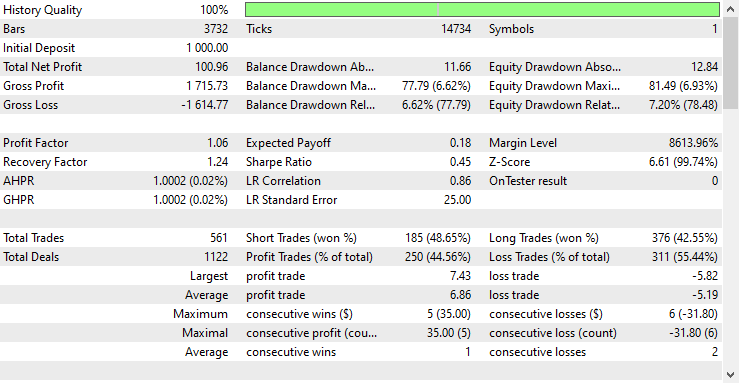
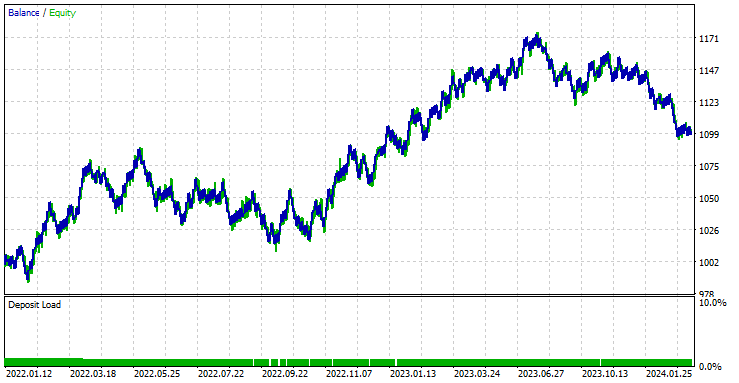
Com os valores atuais de Stop loss e Take profit, é justo dizer que o modelo LightGBM superou um modelo RNN simples para previsão de séries temporais, pois obteve um lucro líquido de $572 em comparação ao RNN, que obteve um lucro líquido de $100. relatório do consultor especialista RNN.

Realizei uma otimização para encontrar os melhores valores de Stop loss e Take profit, e um dos melhores valores foi um Stop Loss de 1000 pontos e um Take profit de 700 pontos.

relatório otimizado do EA RNN

curva de capital/ gráfico otimizado do EA RNN

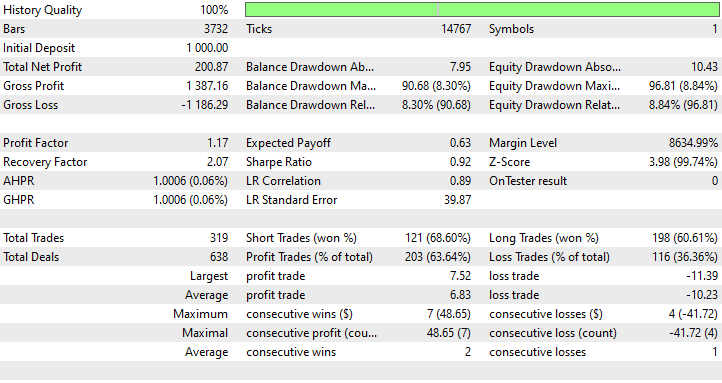
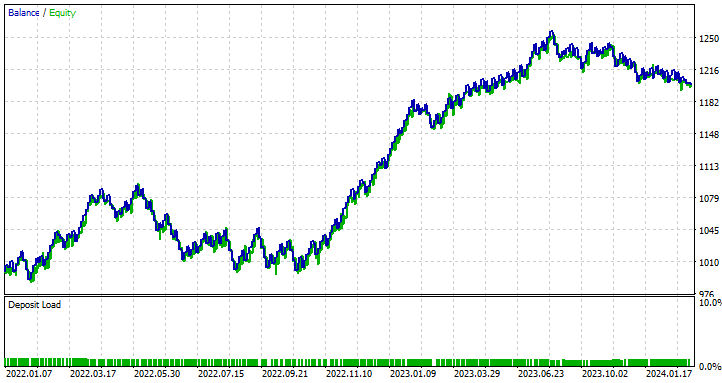
Vantagens do Uso de RNN Simples para Previsão de Séries Temporais

Elas conseguem lidar com dados sequenciais
As RNNs simples são projetadas para lidar com dados sequenciais e são adequadas para tarefas em que a ordem dos pontos de dados importa, como previsão de séries temporais, modelagem de linguagem e reconhecimento de fala.
Elas compartilham parâmetros entre diferentes passos de tempo
Isso ajuda a aprender padrões temporais de maneira eficaz. Esse compartilhamento de parâmetros torna o modelo eficiente em termos de número de parâmetros, especialmente quando comparado a modelos que tratam cada passo de tempo de forma independente.
Elas são capazes de capturar Dependências Temporais
Elas podem capturar dependências ao longo do tempo, o que é essencial para entender o contexto em dados sequenciais. Podem modelar dependências temporais de curto prazo de maneira eficaz.
Flexível em Comprimento de Sequência
As RNNs simples podem lidar com sequências de comprimento variável, tornando-as flexíveis para diferentes tipos de entradas de dados sequenciais.
Simples de usar e implementar
A arquitetura de uma RNN simples é relativamente fácil de implementar. Essa simplicidade pode ser benéfica para entender os conceitos fundamentais de modelagem de sequência.

Considerações Finais

Este artigo proporciona um entendimento profundo de uma Rede Neural Recorrente simples e como ela pode ser implementada na linguagem de programação MQL5. Ao longo do artigo, comparei frequentemente os resultados do modelo RNN com o modelo LightGBM que construímos no artigo anterior desta série, apenas com o intuito de aprimorar seu entendimento sobre previsão de séries temporais usando modelos baseados e não baseados em séries temporais.

A comparação é injusta em muitos aspectos, considerando que esses dois modelos são muito diferentes em estrutura e na forma como fazem previsões. Qualquer conclusão tirada no artigo, por mim ou pelo leitor, deve ser desconsiderada.

Vale mencionar que o modelo RNN não foi alimentado com dados semelhantes ao modelo LightGBM. Neste artigo, removemos alguns lags que eram valores diferenciados entre os preços OHLC (DIFF_LAG1_OPEN, DIFF_LAG1_HIGH, DIFF_LAG1_LOW e DIFF_LAG1_CLOSE).

Poderíamos ter valores não defasados para isso, e a RNN detectaria automaticamente suas defasagens, mas escolhemos não incluí-los, pois eles não estavam presentes no conjunto de dados.

Atenciosamente.

Acompanhe o desenvolvimento de modelos de aprendizado de máquina e muito mais discutido nesta série de artigos neste repositório GitHub.

Tabela de Anexos

Nome do Arquivo	Tipo de Arquivo	Descrição\|Uso
MQL5 \| previsão de séries temporais RNN.mq5	Consultor Especialista	Robô de negociação para carregar o modelo RNN ONNX e testar a estratégia de negociação final no MetaTrader 5.
rnn.EURUSD.D1.onnx	ONNX	Modelo RNN em formato ONNX.
standard_scaler_mean.bin standard_scaler_scale.bin	Arquivos Binários	Arquivos binários para o Scaler de Padronização
preprocessing.mqh	Um arquivo Include	Uma biblioteca que consiste no Scaler de Padronização
RNN.mqh	Um arquivo Include	Uma biblioteca para carregar e implementar o modelo ONNX
rnns-for-forex-forecasting-tutorial.ipynb	Script Python/Notebook Jupyter	Consiste em todo o código Python discutido neste artigo

Fontes e Referências:

Guia Ilustrado para Redes Neurais Recorrentes: Compreendendo a Intuição (https://www.youtube.com/watch?v=LHXXI4-IEns)
Redes Neurais Recorrentes - Ep. 9 (Deep Learning SIMPLIFIED) (https://youtu.be/_aCuOwF1ZjU)
Redes Neurais Recorrentes (https://stanford.edu/~shervine/teaching/cs-230/cheatsheet-recurrent-neural-networks#)

Traduzido do Inglês pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/en/articles/15114

Arquivos anexados |

Baixar como ZIP

Attachments.zip (34.59 KB)

Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.

Outros artigos do autor

Ir para discussão

Construindo um Modelo de Restrição de Tendência com Candlestick (Parte 5): Sistema de Notificação (Parte III)

Esta parte da série de artigos é dedicada à integração do WhatsApp com o MetaTrader 5 para notificações. Incluímos um fluxograma para simplificar o entendimento e discutiremos a importância das medidas de segurança na integração. O principal objetivo dos indicadores é simplificar a análise por meio da automação, e eles devem incluir métodos de notificação para alertar os usuários quando condições específicas forem atendidas. Descubra mais neste artigo.

Redes neurais em trading: Representação linear por partes de séries temporais

Este artigo é um pouco diferente dos trabalhos anteriores desta série. Nele, discutiremos uma representação alternativa de séries temporais. A representação linear por partes de séries temporais é um método de aproximação de séries temporais usando funções lineares em pequenos intervalos.

Reimaginando Estratégias Clássicas em Python: MA Crossovers

Neste artigo, revisitamos a clássica estratégia de cruzamento de médias móveis para avaliar sua eficácia atual. Dado o tempo desde sua criação, exploramos os possíveis aprimoramentos que a IA pode trazer a essa estratégia de negociação tradicional. Ao incorporar técnicas de IA, nosso objetivo é aproveitar as capacidades preditivas avançadas para otimizar pontos de entrada e saída de operações, adaptar-se a condições de mercado variáveis e melhorar o desempenho geral em comparação com abordagens convencionais.

Redes neurais de maneira fácil (Parte 97): Treinamento do modelo usando o MSFformer

Ao estudar diferentes arquiteturas de construção de modelos, temos dado pouca atenção ao processo de treinamento dos modelos. Neste artigo, tentarei preencher essa lacuna.