Aprendizaje automático y Data Science (Parte 25): Predicción de series temporales de divisas mediante una red neuronal recurrente (RNN)

MetaTrader 5 — Asesores Expertos | 4 noviembre 2024, 11:27

243

Omega J Msigwa

Contenido

¿Qué son las redes neuronales recurrentes (RNN)?

Las redes neuronales recurrentes (RNN) son redes neuronales artificiales diseñadas para reconocer patrones en secuencias de datos, como series temporales, lenguaje o vídeo. A diferencia de las redes neuronales tradicionales, que asumen que las entradas son independientes entre sí, las RNN pueden detectar y comprender patrones a partir de una secuencia de datos (información).

Para no confundirnos con la terminología utilizada a lo largo de este artículo, cuando hablo de redes neuronales recurrentes me refiero a una red neuronal simple como modelo, mientras que cuando utilizo redes neuronales recurrentes (RNNs) me refiero a una familia de modelos de redes neuronales recurrentes como la RNN simple, la memoria a largo plazo (LSTM, Long Short Term Memory) y la unidad neuronal recurrente cerrada (GRU, Gated Recurrent Unit).

Se requiere un conocimiento básico de Python, ONNX en MQL5, y aprendizaje automático en Python para entender completamente el contenido de este artículo.

Entender las RNNs

Las RNNs tienen algo llamado memoria secuencial, que se refiere al concepto de retener y utilizar información de los pasos temporales anteriores en una secuencia para informar el procesamiento de los pasos temporales posteriores.

La memoria secuencial es similar a la del cerebro humano. Es el tipo de memoria que le facilita reconocer patrones en secuencias, como cuando articula palabras para hablar.

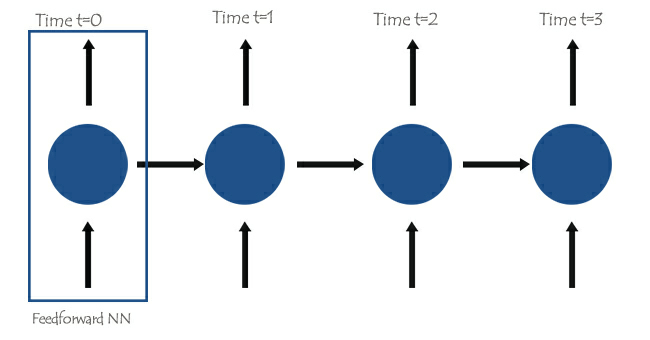
En el núcleo de las redes neuronales recurrentes (RNNs) hay redes neuronales realimentadas (feedforward) interconectadas de tal forma que la red siguiente tiene la información de la anterior, lo que da a la RNN simple la capacidad de aprender y comprender la información actual basándose en las anteriores.

Para entenderlo mejor, veamos un ejemplo en el que queremos enseñar el modelo RNN para un chatbot, queremos que nuestro chatbot entienda las palabras y frases de un usuario, supongamos que la frase recibida es: ¿Qué hora es?.

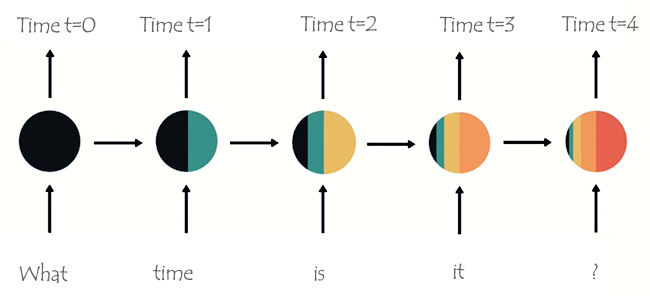
Las palabras se dividirán en sus respectivos pasos temporales y se introducirán en la RNN una tras otra, como se ve en la siguiente imagen.

Si miras el último nodo de la red, habrás notado una extraña disposición de los colores que representan la información de las redes anteriores y la actual. Observando los colores, la información de la red en el tiempo t=0 y en el tiempo t=1 es demasiado pequeña (casi inexistente) en este último nodo de la RNN.

A medida que la RNN procesa más pasos, tiene problemas para retener la información de los pasos anteriores. Como se ve en la imagen anterior, las palabras what y time son casi inexistentes en el nodo final de la red.

Es lo que llamamos memoria a corto plazo. Se debe a muchos factores, uno de los principales es la retropropagación.

Las redes neuronales recurrentes (RNNs) tienen su propio proceso de retropropagación conocido como retropropagación a través del tiempo. Durante la retropropagación, los valores del gradiente se reducen exponencialmente a medida que la red se propaga a través de cada paso de tiempo hacia atrás. Los gradientes se utilizan para realizar ajustes en los parámetros de la red neuronal (pesos y sesgo), este ajuste es lo que permite que la red neuronal aprenda. Los gradientes pequeños implican ajustes más pequeños. Como las primeras capas reciben gradientes pequeños, esto hace que no aprendan tan eficazmente como deberían. Esto se conoce como el problema de gradientes evanescentes.

Debido al problema del gradiente evanescente, la RNN simple no aprende dependencias de largo alcance a través de los pasos de tiempo. En el ejemplo de la imagen anterior, existe una gran posibilidad de que palabras como what y time no se tengan en cuenta en absoluto cuando nuestro modelo RNN del chatbot intenta comprender una frase de ejemplo de un usuario. La red tiene que hacer su mejor suposición con media frase con sólo tres palabras: is it ?. Esto hace que la RNN sea menos eficaz, ya que su memoria es demasiado corta para comprender los datos de series temporales largas que suelen encontrarse en las aplicaciones del mundo real.

Para mitigar la memoria a corto plazo se introdujeron dos redes neuronales recurrentes especializadas, la memoria a largo plazo (LSTM) y la unidad recurrente cerrada (GRU).

Tanto la LSTM como la GRU funcionan de forma similar en muchos aspectos a la RNN, pero son capaces de comprender las dependencias a largo plazo mediante el mecanismo denominado compuertas. Hablaremos de ellos en detalle en el próximo artículo. Estad atentos.

Matemáticas de una red neuronal recurrente (RNN)

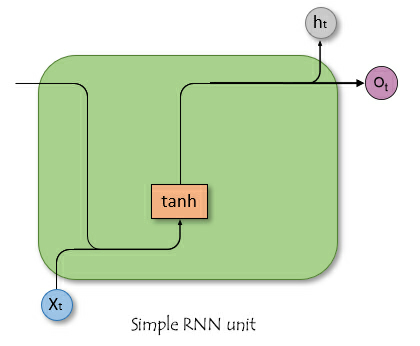
A diferencia de las redes neuronales de propagación hacia adelante, las RNN tienen conexiones que forman ciclos, lo que permite que la información persista. La imagen simplista que aparece a continuación muestra el aspecto de una unidad/célula RNN cuando se disecciona.

Donde:

Es la entrada en el momento t.

Es el estado oculto en el momento t.

Estado oculto.

Denotado como , es un vector que almacena información de los pasos temporales anteriores. Actúa como la memoria de la red permitiéndole capturar dependencias temporales y patrones en los datos de entrada a lo largo del tiempo.

Roles del estado oculto en la red

El estado oculto cumple varias funciones cruciales en una RNN, tales como:

Retiene información de entradas anteriores, lo que permite que la red aprenda de toda la secuencia.
Proporciona contexto para la entrada actual, lo que permite que la red realice predicciones informadas basadas en datos pasados.
Forma la base de las conexiones recurrentes dentro de la red, lo que permite que la capa oculta se influencie a sí misma a lo largo de diferentes pasos de tiempo.

Comprender las matemáticas detrás de las RNN no es tan importante como saber cómo, dónde y cuándo usarlas. Siéntete libre de saltar a la siguiente sección de este artículo si lo deseas.

Fórmula matemática

El estado oculto en el paso de tiempo se calcula utilizando la entrada en el paso de tiempo , el estado oculto del paso de tiempo anterior y las correspondientes matrices de pesos y sesgos. La fórmula es la siguiente:

Donde:

Es la matriz de pesos de la entrada al estado oculto.

Es la matriz de pesos del estado oculto al estado oculto.

Es el término de sesgo para el estado oculto.

σ Es la función de activación (por ejemplo, tanh o ReLU).

Capa de salida

La salida en el paso de tiempo se calcula a partir del estado oculto en el paso de tiempo .

Donde:

Es la salida en el paso de tiempo .

Es la matriz de pesos del estado oculto a la salida.

Sesgo de la capa de salida.

Cálculo de las pérdidas

Suponiendo una función de pérdidas (esta puede ser cualquier función de pérdidas, por ejemplo, el error cuadrático medio para la regresión (MSE, Mean Squared Error) o la entropía cruzada (CE, Cross-Entropy) para la clasificación).

La pérdida total en todos los pasos temporales es:

Propagación hacia atrás a través del tiempo (BPTT, Backpropagation Through Time)

Para actualizar tanto los pesos como el sesgo, necesitamos calcular los gradientes de la pérdida con respecto a cada peso y sesgo respectivamente y luego usar los gradientes obtenidos para realizar actualizaciones. Esto implica los pasos que se describen a continuación.

Paso	Para pesos	Para el sesgo
Cálculo del gradiente de la capa de salida	Con respecto a los pesos: Aquí el gradiente de la pérdida con respecto a la salida.	Con respecto al sesgo: Dado que el sesgo de salida afecta directamente a las salidas tenemos: Por lo tanto:
Cálculo de los gradientes del estado oculto con respecto a los pesos y el sesgo	El gradiente de la pérdida respecto al estado oculto implica tanto la contribución directa del paso temporal actual como la indirecta a través de los pasos temporales posteriores. 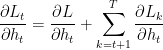Gradiente del estado oculto respecto al paso de tiempo anterior. Gradiente de la activación del estado oculto. Gradiente de los pesos de la capa oculta. El gradiente total es la suma de los gradientes de todos los pasos temporales.	El gradiente de la pérdida con respecto al sesgo oculto viene dado por la suma de los gradientes de la pérdida con respecto al estado oculto sobre todos los pasos de tiempo. Como el sesgo oculto afecta al estado oculto a través de la función de activación, tenemos: Usando la regla de la cadena y observando que: Aquí es la derivada de la función de activación. Por lo tanto: El gradiente total para el sesgo oculto es la suma de los gradientes a lo largo de todos los pasos temporales.
Actualización de pesos y sesgos. Utilizando los gradientes calculados anteriormente, podemos actualizar los pesos utilizando el descenso de gradiente o cualquiera de sus variantes (por ejemplo, Adam). Consulta aquí para más detalles.

A pesar de que las RNN simples no tienen la capacidad de aprender bien series temporales de datos largas, aún son buenas para predecir valores futuros usando información del pasado no muy lejano. Podemos construir una RNN simple para ayudarnos a tomar decisiones comerciales.

Construcción de un modelo de red neuronal recurrente (RNN) en Python

Construir y compilar un modelo RNN en Python es sencillo y requiere unas pocas líneas de código utilizando la biblioteca Keras.

Python

import tensorflow as tf
from tensorflow.keras.models import Sequential #import sequential neural network layer
from sklearn.preprocessing import StandardScaler
from tensorflow.keras.layers import SimpleRNN, Dense, Input
from keras.callbacks import EarlyStopping
from sklearn.preprocessing import MinMaxScaler
from keras.optimizers import Adam

reg_model = Sequential()

reg_model.add(Input(shape=(time_step, x_train.shape[1]))) # input layer
reg_model.add(SimpleRNN(50, activation='sigmoid')) #first hidden layer
reg_model.add(Dense(50, activation='sigmoid')) #second hidden layer
reg_model.add(Dense(units=1, activation='relu'))  # final layer 

adam_optimizer = Adam(learning_rate = 0.001)

reg_model.compile(optimizer=adam_optimizer, loss='mean_squared_error') # Compile the model
reg_model.summary()

El código anterior es para una red neuronal recurrente de regresión por eso tenemos 1 nodo en la capa de salida y una función de activación ReLU en la capa final, hay una razón para esto. Como se comenta en el artículo Aprendizaje automático y Data Science - Redes neuronales (Parte 01): Análisis de redes neuronales con conexión directa.

Utilizando los datos que recopilamos en el artículo anterior: Aprendizaje automático y Data Science (Parte 24): Predicción de series temporales de divisas mediante modelos de IA convencionales (de obligada lectura), queremos ver cómo podemos utilizar los modelos RNN, ya que son capaces de comprender datos de series temporales para ayudarnos en aquello en lo que son buenos.

Al final, evaluaremos el rendimiento de las RNNs en contraste con LightGBM construido en el artículo anterior, sobre los mismos datos. Esperamos que esto le ayude a comprender mejor la predicción de series temporales en general.

Creación de datos secuenciales

En nuestro conjunto de datos tenemos 28 columnas, todas diseñadas para un modelo de series no temporales.

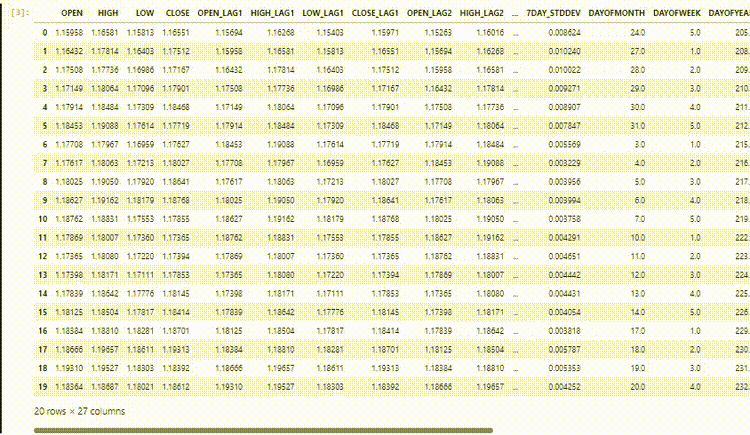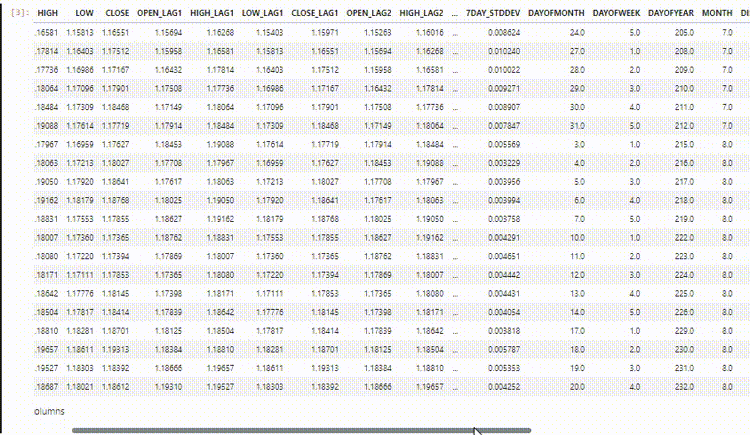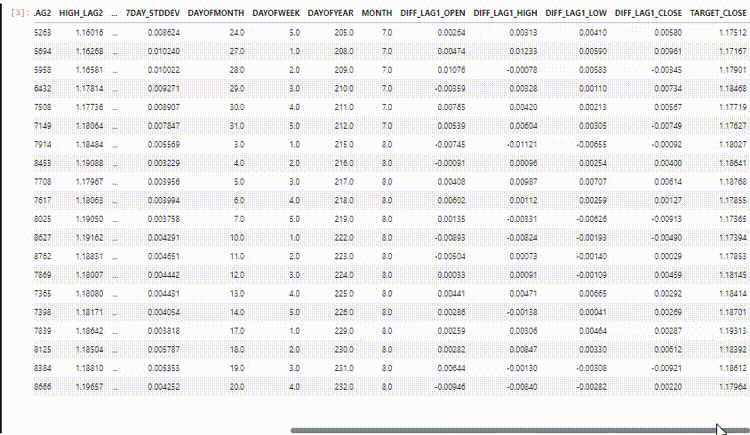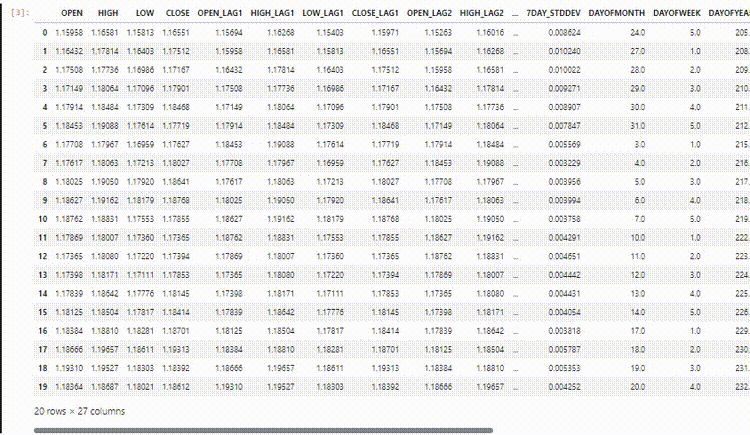
Conjunto de datos de predicción de series temporales

Sin embargo, estos datos que recopilamos y procesamos tienen muchas variables rezagadas, las cuales fueron útiles para que el modelo no basado en series temporales detectara patrones dependientes del tiempo. Como sabemos, las RNN pueden comprender patrones dentro de los pasos de tiempo dados.

No necesitamos estos valores rezagados por ahora, tenemos que eliminarlos.

Python

lagged_columns = [col for col in data.columns if "lag" in col.lower()] #let us obtain all the columns with the name lag

print("lagged columns: ",lagged_columns)

data = data.drop(columns=lagged_columns) #drop them

Salidas:

lagged columns:  ['OPEN_LAG1', 'HIGH_LAG1', 'LOW_LAG1', 'CLOSE_LAG1', 'OPEN_LAG2', 'HIGH_LAG2', 'LOW_LAG2', 'CLOSE_LAG2', 'OPEN_LAG3', 'HIGH_LAG3', 'LOW_LAG3', 'CLOSE_LAG3', 'DIFF_LAG1_OPEN', 'DIFF_LAG1_HIGH', 'DIFF_LAG1_LOW', 'DIFF_LAG1_CL

Los nuevos datos ahora tienen 12 columnas.

Nuevo conjunto de datos filtrado

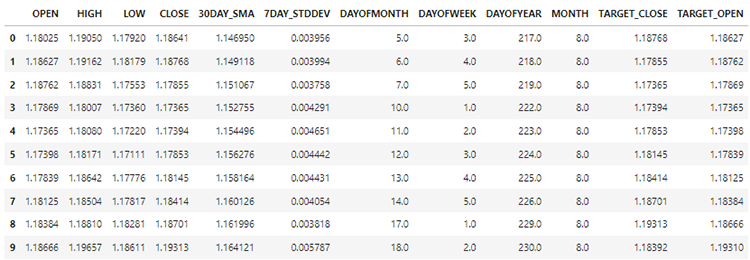
Podemos dividir el 70% de los datos para entrenamiento y el 30% restante para pruebas. Si está utilizando train_test_split de Scikit-Learn asegúrese de establecer shuffle=False. Esto hará que la función divida el original conservando el orden de la información presente.

¡Recuerda! Esto es una predicción de series temporales.

# Split the data

X = data.drop(columns=["TARGET_CLOSE","TARGET_OPEN"]) #dropping the target variables
Y = data["TARGET_CLOSE"]

test_size = 0.3 #70% of the data should be used for training purpose while the rest 30% should be used for testing

x_train, x_test, y_train, y_test = train_test_split(X, Y, shuffle=False, test_size = test_size) # this is timeseries data so we don't shuffle

print(f"x_train {x_train.shape}\nx_test {x_test.shape}\ny_train{y_train.shape}\ny_test{y_test.shape}")

Tras eliminar también las dos variables objetivo, nuestros datos se quedan ahora con 10 características. Tenemos que convertir estas 10 características en datos secuenciales que las RNN puedan digerir.

def create_sequences(X, Y, time_step):
    if len(X) != len(Y):
        raise ValueError("X and y must have the same length")
    
    X = np.array(X)
    Y = np.array(Y)
    
    Xs, Ys = [], []
    
    for i in range(X.shape[0] - time_step):
        Xs.append(X[i:(i + time_step), :])  # Include all features with slicing
        Ys.append(Y[i + time_step])
        
    return np.array(Xs), np.array(Ys)

La función anterior genera una secuencia a partir de las matrices x e y dadas para un paso de tiempo especificado. Para entender cómo funciona esta función, lea el siguiente ejemplo:

Supongamos que tenemos un conjunto de datos con 10 muestras y 2 características, y queremos crear secuencias con un paso de tiempo de 3.

X que es una matriz de forma (10, 2). Y que es un vector de longitud 10.
La función creará secuencias como las siguientes:
Para i=0: Xs obtiene [0:3, :] X[0:3, :], e Ys obtiene Y[3]. Para i=1: Xs obtiene 𝑋[1:4, :] X[1:4, :], e Ys obtiene Y[4].

Y así sucesivamente, hasta i=6.

Las X resultantes tendrán una forma de (7, 3, 2), y las Y tendrán una longitud de 7.

Después de normalizar las variables independientes que hemos dividido, podemos aplicar la función create_sequences para generar información secuencial.

time_step = 7 # we consider the past 7 days

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()

x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)

x_train_seq, y_train_seq = create_sequences(x_train, y_train, time_step)
x_test_seq, y_test_seq = create_sequences(x_test, y_test, time_step)

print(f"Sequential data\n\nx_train {x_train_seq.shape}\nx_test {x_test_seq.shape}\ny_train{y_train_seq.shape}\ny_test{y_test_seq.shape}")

Salidas:

Sequential data

x_train (693, 7, 10)
x_test (293, 7, 10)
y_train(693,)
y_test(293,)

El valor del paso temporal de 7 garantiza que en cada instancia la RNN se conecte con la información de los últimos 7 días, teniendo en cuenta que recopilamos toda la información presente en el conjunto de datos a partir del marco temporal diario. Esto es similar a obtener manualmente los rezagos de los 7 días anteriores a partir de la barra actual, algo que hicimos en el artículo anterior de esta serie.

Entrenamiento de la RNN simple para un problema de regresión

early_stopping = EarlyStopping(monitor='val_loss', patience=5, restore_best_weights=True)

history = reg_model.fit(x_train_seq, y_train_seq, epochs=100, batch_size=64, verbose=1, validation_data=(x_test_seq, y_test_seq), callbacks=[early_stopping])

Salidas:

Epoch 95/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 6.4504e-05 - val_loss: 4.4433e-05
Epoch 96/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 6.4380e-05 - val_loss: 4.4408e-05
Epoch 97/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 6.4259e-05 - val_loss: 4.4386e-05
Epoch 98/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 6.4140e-05 - val_loss: 4.4365e-05
Epoch 99/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 7ms/step - loss: 6.4024e-05 - val_loss: 4.4346e-05
Epoch 100/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 7ms/step - loss: 6.3910e-05 - val_loss: 4.4329e-05

Curva de pérdida de entrenamiento del regresor RNN

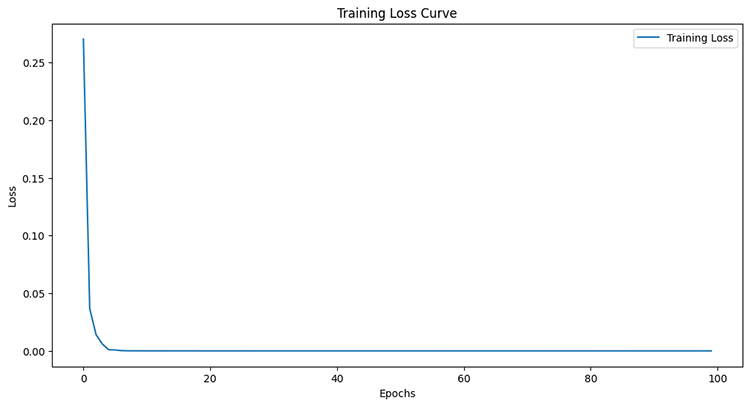
Después de medir el rendimiento de la muestra de prueba.

Python

from sklearn.metrics import r2_score

y_pred = reg_model.predict(x_test_seq) # Make predictions on the test set

# Plot the actual vs predicted values
plt.figure(figsize=(12, 6))
plt.plot(y_test_seq, label='Actual Values')
plt.plot(y_pred, label='Predicted Values')
plt.xlabel('Samples')
plt.ylabel('TARGET_CLOSE')
plt.title('Actual vs Predicted Values')
plt.legend()
plt.show()

print("RNN accuracy =",r2_score(y_test_seq, y_pred))

El modelo tuvo una precisión del 78%.

Regresor RNN real frente a predicción

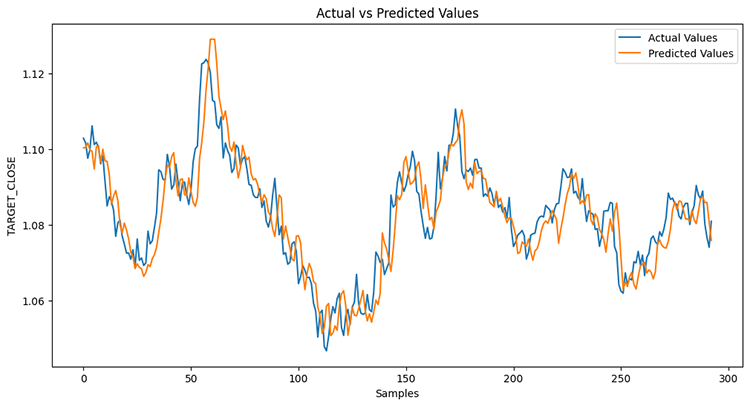
Si recuerdas el artículo anterior, el modelo LightGBM tuvo una precisión del 86,76% en un problema de regresión, en este punto un modelo sin series temporales ha superado a uno con series temporales.

Importancia de las características de RNN

He realizado una prueba para comprobar cómo afectan las variables al proceso de toma de decisiones del modelo RNN utilizando SHAP.

import shap

# Wrap the model prediction for KernelExplainer
def rnn_predict(data):
    data = data.reshape((data.shape[0], time_step, x_train.shape[1]))
    return reg_model.predict(data).flatten()

# Use SHAP to explain the model
sampled_idx = np.random.choice(len(x_train_seq), size=100, replace=False)
explainer = shap.KernelExplainer(rnn_predict, x_train_seq[sampled_idx].reshape(100, -1))
shap_values = explainer.shap_values(x_test_seq[:100].reshape(100, -1), nsamples=100)

He ejecutado un código para dibujar un gráfico de la importancia de las características.

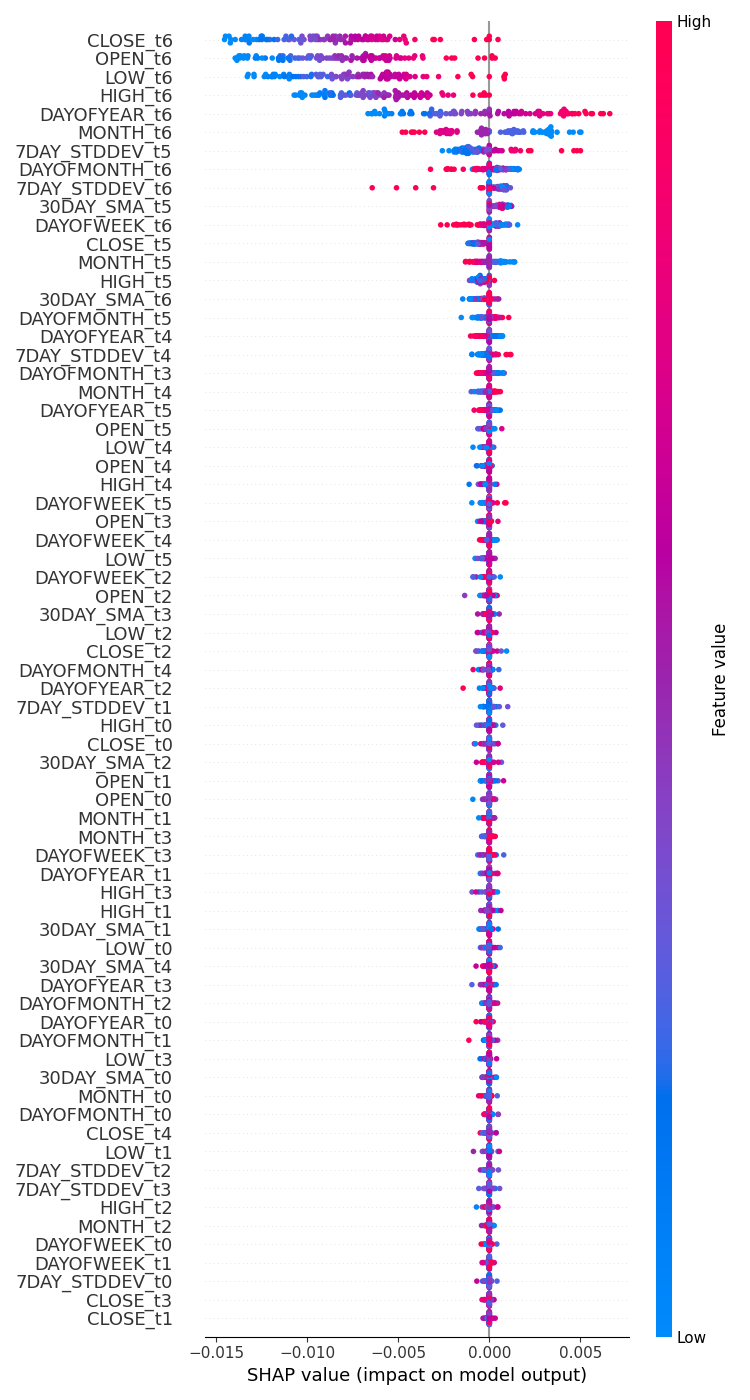
# Update feature names for SHAP
feature_names = [f'{original_feat}_t{t}' for t in range(time_step) for original_feat in X.columns]

# Plot the SHAP values
shap.summary_plot(shap_values, x_test_seq[:100].reshape(100, -1), feature_names=feature_names, max_display=len(feature_names), show=False)

# Adjust layout and set figure size
plt.subplots_adjust(left=0.12, bottom=0.1, right=0.9, top=0.9)  
plt.gcf().set_size_inches(7.5, 14) 
plt.tight_layout()

plt.savefig("regressor-rnn feature-importance.png")
plt.show()

El resultado fue el siguiente.

Las variables más impactantes son las que tienen información reciente, mientras que las menos impactantes son las que tienen información más antigua.

Esto es como decir que la última palabra pronunciada en una oración es la que tiene mayor significado para toda la oración.

Esto puede ser cierto para un modelo de aprendizaje automático a pesar de que no tenga mucho sentido para nosotros, los seres humanos.

Como se dijo en el artículo anterior, no podemos confiar solo en el gráfico de importancia de las características, considerando que he utilizado KernelExplainer, en lugar del recomendado DeepExplainer donde experimenté muchos errores al intentar que el método funcionara.

Como se dijo en el artículo anterior, tener un modelo de regresión para adivinar el próximo precio de cierre o apertura no es tan práctico como tener un clasificador que nos diga hacia dónde cree que se dirige el mercado en la siguiente barra. Hagamos un modelo clasificador RNN para ayudarnos con esa tarea.

Entrenamiento de la RNN simple para un problema de clasificación

Podemos seguir un proceso similar al que hicimos al codificar un regresor con algunos cambios: primero que todo, necesitamos crear la variable objetivo para el problema de clasificación.

Python

Y = []
target_open = data["TARGET_OPEN"]
target_close = data["TARGET_CLOSE"]

for i in range(len(target_open)):
    if target_close[i] > target_open[i]: # if the candle closed above where it opened thats a buy signal
        Y.append(1)
    else: #otherwise it is a sell signal
        Y.append(0)
        
Y = np.array(Y) #converting this array to NumPy


classes_in_y = np.unique(Y) # obtaining classes present in the target variable for the sake of setting the number of outputs in the RNN

Entonces debemos codificar en caliente la variable objetivo poco después de que se cree la secuencia, tal y como se comentó durante la elaboración de un modelo de regresión.

from tensorflow.keras.utils import to_categorical

y_train_encoded = to_categorical(y_train_seq)
y_test_encoded = to_categorical(y_test_seq)

print(f"One hot encoded\n\ny_train {y_train_encoded.shape}\ny_test {y_test_encoded.shape}")

Salidas:

One hot encoded

y_train (693, 2)
y_test (293, 2)

Por último, podemos construir el modelo clasificador RNN y entrenarlo.

cls_model = Sequential()

cls_model.add(Input(shape=(time_step, x_train.shape[1]))) # input layer
cls_model.add(SimpleRNN(50, activation='relu'))
cls_model.add(Dense(50, activation='relu'))
cls_model.add(Dense(units=len(classes_in_y), activation='sigmoid', name='outputs')) 


adam_optimizer = Adam(learning_rate = 0.001)

cls_model.compile(optimizer=adam_optimizer, loss='binary_crossentropy') # Compile the model
cls_model.summary()


early_stopping = EarlyStopping(monitor='val_loss', patience=5, restore_best_weights=True)

history = cls_model.fit(x_train_seq, y_train_encoded, epochs=100, batch_size=64, verbose=1, validation_data=(x_test_seq, y_test_encoded), callbacks=[early_stopping])

Para el modelo RNN clasificador, utilicé sigmoide para la capa final de la red. El número de neuronas (unidades) en la capa final debe coincidir con el número de clases presentes en la variable objetivo (Y), en este caso vamos a tener dos unidades.

Model: "sequential_1"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ simple_rnn_1 (SimpleRNN)        │ (None, 50)             │         3,050 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_2 (Dense)                 │ (None, 50)             │         2,550 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ outputs (Dense)                 │ (None, 2)              │           102 │
└─────────────────────────────────┴────────────────────────┴───────────────┘

6 épocas fueron suficientes para que el modelo clasificador RNN convergiera durante el entrenamiento.

Epoch 1/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 2s 36ms/step - loss: 0.7242 - val_loss: 0.6872
Epoch 2/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - loss: 0.6883 - val_loss: 0.6891
Epoch 3/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.6817 - val_loss: 0.6909
Epoch 4/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.6780 - val_loss: 0.6940
Epoch 5/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.6743 - val_loss: 0.6974
Epoch 6/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.6707 - val_loss: 0.6998

A pesar de tener una menor precisión en la tarea de regresión en comparación con la precisión proporcionada por el regresor LightGBM, el modelo clasificador RNN fue un 3% más preciso que el clasificador LightGBM.

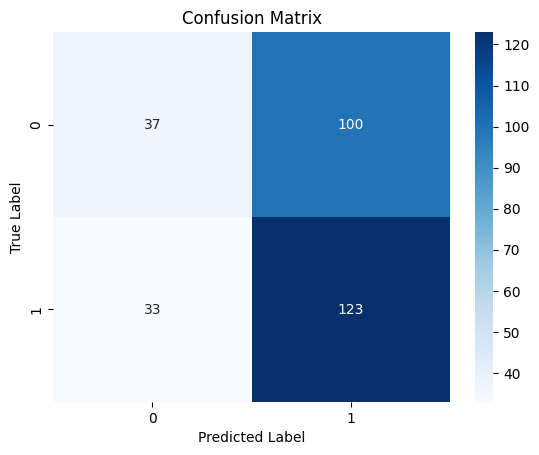
10/10 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
Classification Report
               precision    recall  f1-score   support

           0       0.53      0.27      0.36       137
           1       0.55      0.79      0.65       156

    accuracy                           0.55       293
   macro avg       0.54      0.53      0.50       293
weighted avg       0.54      0.55      0.51       293

Mapa de calor de la matriz de confusión

Cómo guardar el modelo de red neuronal recurrente en ONNX

Ahora que tenemos un modelo clasificador RNN, podemos guardarlo en el formato ONNX que entiende MetaTrader 5.

A diferencia de los modelos de Scikit-learn, guardar modelos de aprendizaje profundo de Keras como RNNs no es sencillo. Los pipelines tampoco son una solución fácil para las RNN.

Como se comenta en el artículo Superar los retos de integración de ONNX, podemos o bien escalar los datos en MQL5 poco después de recopilar o podemos guardar el escalador que tenemos en Python y cargarlo en MQL5 usando la Biblioteca de preprocesamiento para MQL5.

Guardado del modelo

import tf2onnx

# Convert the Keras model to ONNX
spec = (tf.TensorSpec((None, time_step, x_train.shape[1]), tf.float16, name="input"),)
cls_model.output_names=['output']

onnx_model, _ = tf2onnx.convert.from_keras(cls_model, input_signature=spec, opset=13)

# Save the ONNX model to a file
with open("rnn.EURUSD.D1.onnx", "wb") as f:
    f.write(onnx_model.SerializeToString())

Guardar los parámetros del escalador de estandarización

# Save the mean and scale parameters to binary files

scaler.mean_.tofile("standard_scaler_mean.bin")
scaler.scale_.tofile("standard_scaler_scale.bin")

Al guardar la media y la desviación estándar que son los componentes principales del escalador estándar, podemos estar seguros de que hemos guardado con éxito el escalador estándar.

Asesor experto de redes neuronales recurrentes (RNNs)

Dentro de nuestro EA, lo primero que tenemos que hacer es agregar tanto el modelo RNN que está en formato ONNX como los archivos binarios del Standard Scaler como archivos de recursos a nuestro EA.

MQL5 | RNN timeseries forecasting.mq5

#resource "\\Files\\rnn.EURUSD.D1.onnx" as uchar onnx_model[]; //rnn model in onnx format
#resource "\\Files\\standard_scaler_mean.bin" as double standardization_mean[];
#resource "\\Files\\standard_scaler_scale.bin" as double standardization_std[];

Luego podemos cargar las bibliotecas tanto para cargar el modelo RNN en formato ONNX como para el escalador estándar.

MQL5

#include <MALE5\Recurrent Neural Networks(RNNs)\RNN.mqh>
CRNN rnn;

#include <MALE5\preprocessing.mqh>
StandardizationScaler *scaler;

Dentro de la función OnInit.

vector classes_in_data_ = {0,1}; //we have to assign the classes manually | it is very important that their order is preserved as they can be seen in python code, HINT: They are usually in ascending order
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
  
//--- Initialize ONNX model
   
   if (!rnn.Init(onnx_model))
     return INIT_FAILED;
   
//--- Initializing the scaler with values loaded from binary files 

   scaler = new StandardizationScaler(standardization_mean, standardization_std);
   
//--- Initializing the CTrade library for executing trades

   m_trade.SetExpertMagicNumber(magic_number);
   m_trade.SetDeviationInPoints(slippage);
   m_trade.SetMarginMode();
   m_trade.SetTypeFillingBySymbol(Symbol());
           
   lotsize = SymbolInfoDouble(Symbol(), SYMBOL_VOLUME_MIN);
   
//--- Initializing the indicators

   ma_handle = iMA(Symbol(),timeframe,30,0,MODE_SMA,PRICE_WEIGHTED); //The Moving averaege for 30 days
   stddev_handle = iStdDev(Symbol(), timeframe, 7,0,MODE_SMA,PRICE_WEIGHTED); //The standard deviation for 7 days
   

   return(INIT_SUCCEEDED);
  }

Antes de que podamos desplegar el modelo para el comercio en vivo dentro de la función OnTick, tenemos que recoger datos de manera similar a cómo recogimos los datos de entrenamiento, pero esta vez tenemos que evitar las características que dejamos caer durante el entrenamiento.

¡Recuerda! Entrenamos el modelo con 10 características (variables independientes) solamente.

Nuevo conjunto de datos con variables de destino sombreadas

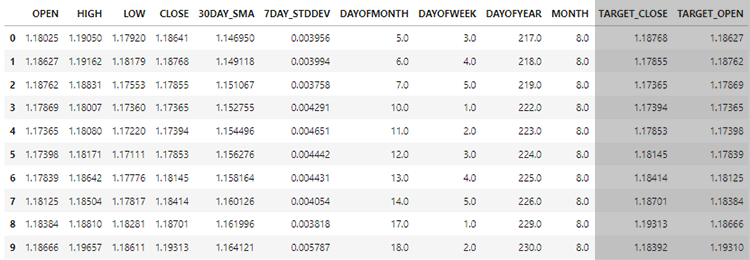
Hagamos la función GetInputData para recopilar únicamente esas 10 variables independientes.

matrix GetInputData(int bars, int start_bar=1)
 {
   vector open(bars), 
          high(bars),
          low(bars), 
          close(bars), 
          ma(bars), 
          stddev(bars), 
          dayofmonth(bars), 
          dayofweek(bars), 
          dayofyear(bars), 
          month(bars);

//--- Getting OHLC values
   
   open.CopyRates(Symbol(), timeframe, COPY_RATES_OPEN, start_bar, bars);
   high.CopyRates(Symbol(), timeframe, COPY_RATES_HIGH, start_bar, bars);
   low.CopyRates(Symbol(), timeframe, COPY_RATES_LOW, start_bar, bars);
   close.CopyRates(Symbol(), timeframe, COPY_RATES_CLOSE, start_bar, bars);
   
   vector time_vector;
   time_vector.CopyRates(Symbol(), timeframe, COPY_RATES_TIME, start_bar, bars);
   
//---

   
   ma.CopyIndicatorBuffer(ma_handle, 0, start_bar, bars); //getting moving avg values 
   stddev.CopyIndicatorBuffer(stddev_handle, 0, start_bar, bars); //getting standard deviation values
   
   string time = "";
   for (int i=0; i<bars; i++) //Extracting time features 
     {
       time = (string)datetime(time_vector[i]); //converting the data from seconds to date then to string
       TimeToStruct((datetime)StringToTime(time), date_time_struct); //convering the string time to date then assigning them to a structure
       
       dayofmonth[i] = date_time_struct.day;
       dayofweek[i] = date_time_struct.day_of_week;
       dayofyear[i] = date_time_struct.day_of_year;
       month[i] = date_time_struct.mon;
     }
   
   matrix data(bars, 10); //we have 10 inputs from rnn | this value is fixed
   
//--- adding the features into a data matrix
   
   data.Col(open, 0);
   data.Col(high, 1);
   data.Col(low, 2);
   data.Col(close, 3);
   data.Col(ma, 4);
   data.Col(stddev, 5);
   data.Col(dayofmonth, 6);
   data.Col(dayofweek, 7);
   data.Col(dayofyear, 8);
   data.Col(month, 9);
   
   return data;
 }

Por último, podemos desplegar el modelo RNN para que nos dé señales de negociación para nuestra estrategia simple.

void OnTick()
  {
//---
   
   if (NewBar()) //Trade at the opening of a new candle
    {
      matrix input_data_matrix = GetInputData(rnn_time_step);
      input_data_matrix = scaler.transform(input_data_matrix); //applying StandardSCaler to the input data
      
      int signal = rnn.predict_bin(input_data_matrix, classes_in_data_); //getting trade signal from the RNN model
     
      Comment("Signal==",signal);
     
   //---
     
      MqlTick ticks;
      SymbolInfoTick(Symbol(), ticks);
      
      if (signal==1) //if the signal is bullish
       {
          if (!PosExists(POSITION_TYPE_BUY)) //There are no buy positions
           {
             if (!m_trade.Buy(lotsize, Symbol(), ticks.ask, ticks.bid-stoploss*Point(), ticks.ask+takeprofit*Point())) //Open a buy trade
               printf("Failed to open a buy position err=%d",GetLastError());
           }
       }
      else if (signal==0) //Bearish signal
        {
          if (!PosExists(POSITION_TYPE_SELL)) //There are no Sell positions
            if (!m_trade.Sell(lotsize, Symbol(), ticks.bid, ticks.ask+stoploss*Point(), ticks.bid-takeprofit*Point())) //open a sell trade
               printf("Failed to open a sell position err=%d",GetLastError());
        }
      else //There was an error
        return;
    }
  }

Prueba del EA de red neuronal recurrente en el Probador de estrategias

Con una estrategia de negociación en su lugar, vamos a ejecutar pruebas en el probador de estrategia. Estoy utilizando los mismos valores de Stop Loss y Take Profit que utilizamos para el modelo LightGBM, incluyendo los ajustes del probador.

input group "rnn";
input uint rnn_time_step = 7; 
//this value must be the same as the one used during training in a python script

input ENUM_TIMEFRAMES timeframe = PERIOD_D1;
input int magic_number = 1945;
input int slippage = 50;
input int stoploss = 500;
input int takeprofit = 700;

Configuración del Probador de estrategias:

Ajustes del probador: Modelo RNN

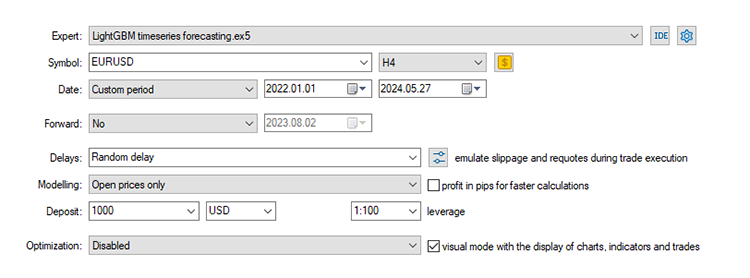
El EA fue rentable en un 44,56% en las 561 operaciones que realizó.

Informe del asesor experto

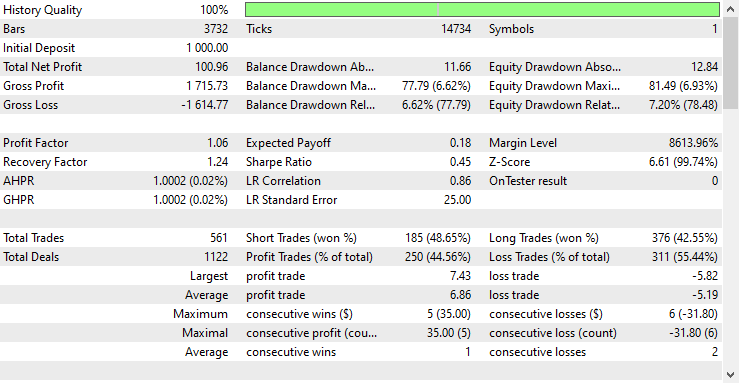
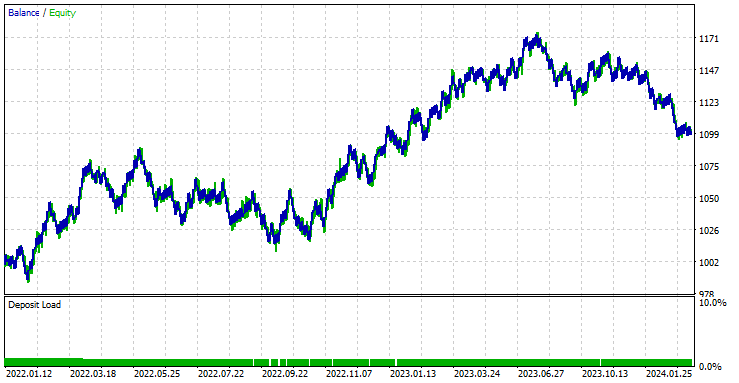
Con los valores actuales de Stop Loss y Take Profit es justo decir que el modelo LightGBM superó a un modelo RNN simple para la predicción de series temporales, ya que obtuvo un beneficio neto de 572 $ en comparación con RNN que obtuvo un beneficio neto de 100 $.

Ejecuté una optimización para encontrar los mejores valores de Stop Loss y Take Profit, y uno de los mejores valores fue un Stop Loss de 1000 puntos y un Take Profit de 700 puntos.

Informe EA optimizado

Curva optimizada

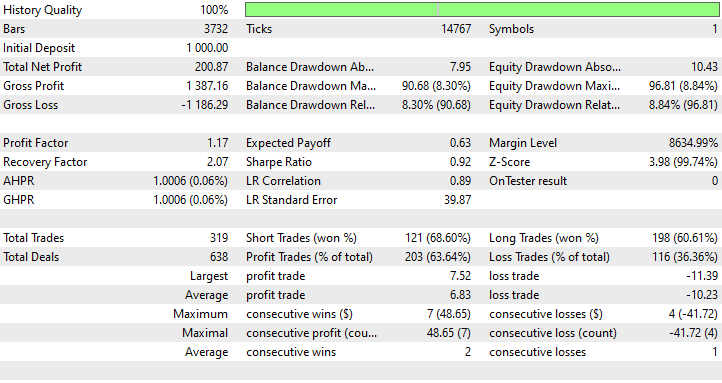
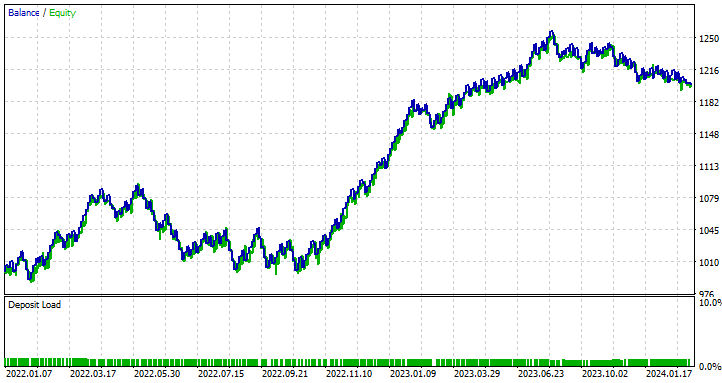
Ventajas del uso de una RNN simple para la predicción de series temporales

Pueden manejar datos secuenciales
Las RNN simples están diseñadas para manejar datos secuenciales y son muy adecuadas para tareas en las que el orden de los puntos de datos es importante, como la predicción de series temporales, el modelado del lenguaje y el reconocimiento del habla.
Comparten parámetros en diferentes pasos temporales
Esto ayuda a aprender patrones temporales de forma eficaz. Este reparto de parámetros hace que el modelo sea eficiente en cuanto al número de parámetros, sobre todo si se compara con los modelos que tratan cada paso temporal de forma independiente.
Son capaces de capturar dependencias temporales
Pueden capturar dependencias a lo largo del tiempo, lo que es esencial para comprender el contexto de los datos secuenciales. Pueden modelar eficazmente dependencias temporales de corto plazo.
Flexible en longitud de secuencia
Las RNN simples pueden manejar secuencias de longitud variable, lo que las hace flexibles para diferentes tipos de entradas de datos secuenciales.
Fácil de usar e implementar
La arquitectura de una RNN simple es relativamente fácil de implementar. Esta simplicidad puede ser beneficiosa para comprender los conceptos fundamentales del modelado de secuencias.

Reflexiones finales

Este artículo le brindará una comprensión profunda de una red neuronal recurrente simple y cómo se puede implementar en el lenguaje de programación MQL5. A lo largo del artículo, he comparado a menudo los resultados del modelo RNN con el modelo LightGBM que construimos en el artículo anterior de esta serie solo con el fin de agudizar su comprensión de la previsión de series temporales utilizando modelos basados en series temporales y no basados en series temporales.

La comparación es injusta en muchos términos considerando que estos dos modelos son muy diferentes en estructura y en cómo hacen predicciones. Cualquier conclusión extraída en el artículo por mí o por la mente de un lector debe ser ignorada.

Vale la pena mencionar que el modelo RNN no fue alimentado con datos similares en comparación con el modelo LightGBM. En este artículo eliminamos algunos rezagos que eran valores diferenciados entre los valores de precios de OHLC (DIFF_LAG1_OPEN, DIFF_LAG1_HIGH, DIFF_LAG1_LOW y DIFF_LAG1_CLOSE).

Podríamos tener valores no rezagados para que RNN auto-detecte sus rezagos, pero optamos por no incluirlos en absoluto, ya que no estaban presentes en el conjunto de datos.

Saludos cordiales.

Siga el desarrollo de modelos de aprendizaje automático y mucho más discutido en esta serie de artículos en este repositorio de GitHub.

Tabla de archivos adjuntos

Nombre del archivo	Tipo de archivo	Descripción y uso
RNN timeseries forecasting.mq5	Asesor experto	Robot comercial para cargar el modelo RNN ONNX y probar la estrategia comercial final en MetaTrader 5.
rnn.EURUSD.D1.onnx	ONNX	Modelo RNN en formato ONNX.
standard_scaler_mean.bin standard_scaler_scale.bin	Archivos binarios	Archivos binarios para el escalador de estandarización.
preprocessing.mqh	Un archivo Include	Una biblioteca que consta del escalador de estandarización.
RNN.mqh	Un archivo Include	Una biblioteca para cargar e implementar el modelo ONNX.
rnns-for-forex-forecasting-tutorial.ipynb	Python Script/Jupyter Notebook	Consiste en todo el código Python analizado en este artículo.

Fuentes y referencias

Guía ilustrada de redes neuronales recurrentes: comprensión de la intuición (https://www.youtube.com/watch?v=LHXXI4-IEns)
Redes neuronales recurrentes - Ep. 9 (Aprendizaje profundo SIMPLIFICADO) (https://youtu.be/_aCuOwF1ZjU)
Redes neuronales recurrentes (https://stanford.edu/~shervine/teaching/cs-230/cheatsheet-recurrent-neural-networks#)

Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/15114

Archivos adjuntos |

Descargar ZIP

Attachments.zip (34.59 KB)

Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores

Redes neuronales: así de sencillo (Parte 88): Codificador de series temporales totalmente conectadas (TiDE)

El deseo de obtener las previsiones más exactas impulsa a los investigadores a aumentar la complejidad de los modelos de previsión. Lo que a su vez conlleva un aumento de los costes de entrenamiento y mantenimiento del modelo. Pero, ¿está esto siempre justificado? En el presente artículo, me propongo presentarles un algoritmo que explota la sencillez y rapidez de los modelos lineales y muestra resultados a la altura de los mejores con arquitecturas más complejas.

Cómo añadir Trailing Stop según el indicador Parabolic SAR

Al crear una estrategia comercial, debemos probar una amplia variedad de stops de protección. Y aquí surge la idea del ajuste dinámico del nivel de Stop Loss siguiendo el precio. El mejor candidato en este punto es el indicador Parabolic SAR, resulta difícil pensar en algo más simple y claro.

Reimaginando estrategias clásicas en Python: Cruce de medias móviles (MAs, Moving Averages)

En este artículo, revisamos la estrategia clásica de cruce de medias móviles para evaluar su eficacia actual. Dado el tiempo transcurrido desde su creación, exploramos las posibles mejoras que la IA puede aportar a esta estrategia de negociación tradicional. Mediante la incorporación de técnicas de IA, pretendemos aprovechar las capacidades predictivas avanzadas para optimizar potencialmente los puntos de entrada y salida de las operaciones, adaptarnos a las condiciones variables del mercado y mejorar el rendimiento global en comparación con los enfoques convencionales.

Características del Wizard MQL5 que debe conocer (Parte 24): Medias móviles

Las medias móviles son un indicador muy común que la mayoría de los operadores utilizan y comprenden. Exploramos posibles casos de uso menos comunes dentro de los Asesores Expertos disponibles en el Asistente de MQL5.