Машинное обучение и Data Science (Часть 14): Применение карт Кохонена на рынках

MetaTrader 5 — Торговые системы | 20 июля 2023, 14:18

892

Omega J Msigwa

Введение

Карты Кохонена, или самоорганизующиеся карты (SOM), или самоорганизующиеся карты характеристик (SOFM) — этот метод машинного обучения без учителя, используемый для создания пространства с низкой размерностью (обычно двумерного) для представления многомерного набора данных с сохранением топологической структуры данных. Например, имеем набор данных из p переменных, измеряемых в n наблюдениях — их можно представить в виде кластеров наблюдений с одинаковыми значениями переменных. Затем эти кластеры можно представить в виде двухмерной карты, при этом наблюдения в близких кластерах будут иметь более схожие значения, чем в отдаленных. Это может упростить визуализацию и анализ многомерных данных.

Карты Кохонена разработал финский математик Теуво Кохонен в 1980-х годах.

Общие сведения

Карта Кохонена состоит из сетки нейронов, которые связаны с соседними нейронами. Во время обучения входные данные представляются в сеть, и каждый нейрон вычисляет свое сходство с входными данными. Нейрон с наибольшим сходством становится победителем, а его веса корректируются для лучшего соответствия входным данным.

Со временем соседние нейроны также корректируют свои веса, чтобы стать более похожими на нейрон-победитель, что приводит к топологическому упорядочению нейронов на карте. Этот процесс самоорганизации позволяет через карты Кохонена представлять сложные отношения между входными данными в пространстве меньших измерений. Такая возможность очень ценна для визуализации и кластеризации данных.

Алгоритм обучения

Цель алгоритма самоорганизующейся карты — заставить разные части сети одинаково реагировать на определенные входные шаблоны. Это частично мотивировано тем, как визуальная, слуховая и другая информация обрабатываются в определенных частях человеческого мозга.

Давайте посмотрим, как работает этот алгоритм применительно к математическим вычислениям и коду MQL5.

Шаги алгоритма

Разработка алгоритма состоит из четырех основных шагов:

Шаг 1 — инициализация весов . Можно использовать случайные значения. На этом этапе также инициализируются другие параметры, такие как скорость обучения и количество кластеров.

CKohonenMaps::CKohonenMaps(matrix &matrix_, bool save_clusters=true, uint clusters=2, double alpha=0.01, uint epochs=100)
 {
   Matrix = matrix_;
   
   n = (uint)matrix_.Cols();
   rows = matrix_.Rows();
   m = clusters;
   
   cluster_tensor = new CTensors(m);
   
   w_matrix =matrix_utils.Random(0.0, 1.0, n, m, RANDOM_STATE); 
 }

Параметры инициализируются в конструкторе класса карт Кохонена.

Карты Кохонена — это метод интеллектуального анализа данных. На это этапе нам нужно получить эти данные. За это отвечает save_clusters=true — здесь мы получаем кластеры, которые для нас собрали карты Кохонена.

Шаг 2 — расчет евклидова расстояния между каждым входом и соответствующими весами.

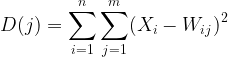
Где:

= Входной вектор

= Вектор весовых коэффициентов

double CKohonenMaps:: Euclidean_distance(const vector &v1, const vector &v2)
  {
   double dist = 0;

   if(v1.Size() != v2.Size())
      Print(__FUNCTION__, " v1 и v2 не совпадают по размеру");
   else
     {
      double c = 0;
      for(ulong i=0; i<v1.Size(); i++)
         c += MathPow(v1[i] - v2[i], 2);

      dist = MathSqrt(c);
     }

   return(dist);
  }

Для проверки работы формулы используем нужен простой набор данных. Будем использовать его при написании кода и тестировании.

   matrix Matrix = {
                     {1.2, 2.3},
                     {0.7, 1.8},
                     {3.6, 4.8},
                     {2.8, 3.9},
                     {5.2, 6.7},
                     {4.8, 5.6}
                   };
   
   maps = new CKohonenMaps(Matrix); // даем данные классов картам Кохонена

Далее вызывается конструктор и генерируются весовые коэффициенты, имеем на выходе:

CS      0       15:52:27.572    Self Organizing map (EURUSD,H1) w Matrix
CS      0       15:52:27.572    Self Organizing map (EURUSD,H1) [[0.005340739158299509,0.01220740379039888]
CS      0       15:52:27.572    Self Organizing map (EURUSD,H1)  [0.5453352458265939,0.9172643208105716]]
CS      0       15:52:27.572    Self Organizing map (EURUSD,H1) Matrix
CS      0       15:52:27.572    Self Organizing map (EURUSD,H1) [[1.2,2.3]
CS      0       15:52:27.572    Self Organizing map (EURUSD,H1)  [0.7,1.8]
CS      0       15:52:27.572    Self Organizing map (EURUSD,H1)  [3.6,4.8]
CS      0       15:52:27.572    Self Organizing map (EURUSD,H1)  [2.8,3.9]
CS      0       15:52:27.572    Self Organizing map (EURUSD,H1)  [5.2,6.7]
CS      0       15:52:27.572    Self Organizing map (EURUSD,H1)  [4.8,5.6]]

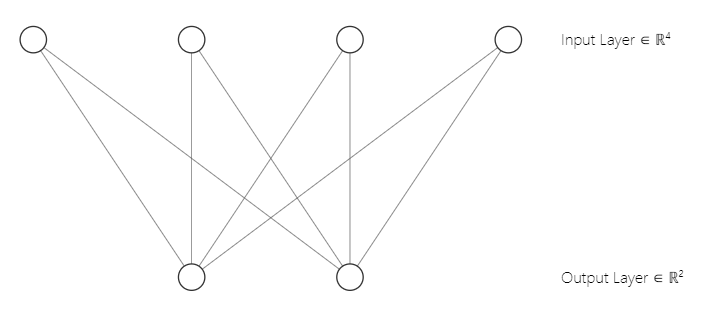
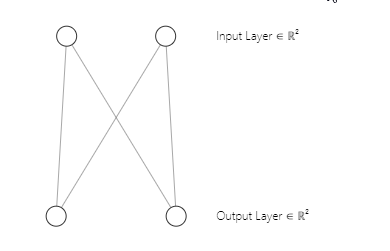
Вы могли заметить, что архитектура нашей нейронной сети представляет собой [2 входа и 2 выхода]. Вот почему у нас получилась матрица весовых коэффициентов 2x2. Матрица сгенерирована с учетом [2 столбцов входной матрицы n и 2 выбранных кластеров m]. Строка кода из первой части:

   w_matrix =matrix_utils.Random(0.0, 1.0, n, m, RANDOM_STATE);

Итак, вот как выглядит архитектура нашей нейронной сети карт Кохонена:

Шаг 3 — поиск победителя с индексом i, при котором D(j) имеет минимальное значение. Проще говоря, находим кластер единиц. Здесь мы подошли к важной теме конкурентного обучения на картах Кохонена.

Конкурентное обучение

Самоорганизующаяся карта — это тип искусственной нейронной сети, которая, в отличие от других типов искусственных нейронных сетей, которые обучаются по ошибкам, например, обратное распространение с градиентным спуском, карты Кохонена используют конкурентное обучение.

При конкурентном обучении нейроны на карте Кохонена соревнуются друг с другом, чтобы стать "победителем". Для этого нейрон должен быть наиболее похожим на входные данные.

На этапе обучения каждая точка входных данных представляется на карте Кохонена. Затем вычисляется сходство между входными данными и весовым вектором каждого нейрона. Нейрон, вектор которого больше всего похож на входные данные, определяется победителем или "лучшей единицей соответствия" (best matching unit, BMU).

BMU выбирается на основе наименьшего евклидова расстояния между входными данными и вектором веса нейрона. Затем нейрон-победитель обновляет свой весовой вектор, делая его более похожим на входные данные. Используемая формула обновления весов — это правило обучения Кохонена, которое перемещает вектор веса победившего нейрона и соседних с ним нейронов ближе к входным данным.

Как выглядит шаг 3 в коде. Он занимает несколько строк кода.

   vector D(m); //Евклидово расстояние между кластерами | Напомню, что m — это количество выбранных кластеров

   for (ulong i=0; i<rows; i++)
       {
         for (ulong j=0; j<m; j++)
           {
             D[j] = Euclidean_distance(Matrix.Row(i),w_matrix.Col(j));
           }
         
         #ifdef DEBUG_MODE  
            Print("Euc distance ",D," Winning cluster ",D.ArgMin());
         #endif

Помним, что нейрон, производящий класс с наименьшим евклидовым расстоянием, является кластером-победителем.

Благодаря конкурентному обучению карта Кохонена учится создавать топологическое представление входных данных в пространстве меньших измерений, сохраняя при этом отношения между входными данными.

Шаг 4 — обновление весовых коэффициентов.

Для обновления весов используем следующую формулу.

Где:

— новый вектор весов

— старый вектор весов

— скорость обучения

— входной вектор

В коде эта формула выглядит так:

//--- обновление весов
   
   ulong min = D.ArgMin(); //кластер-победитель
    
   vector w_new =  w_matrix.Col(min) + (alpha * (Matrix.Row(i) - w_matrix.Col(min)));
   
   w_matrix.Col(w_new, min);

В отличие от других типов искусственных нейронных сетей, в которых задействованы все веса для определенного слоя, карты Кохонена учитывают веса для определенного кластера и используют их для поиска только этого кластера.

Мы закончили с шагами и завершили наш алгоритм. Давайте теперь посмотрим, как это все работает.

Ниже приведен полный код алгоритма по состоянию на данный момент.

CKohonenMaps::CKohonenMaps(matrix &matrix_, bool save_clusters=true, uint clusters=2, double alpha=0.01, uint epochs=100)
 {
   Matrix = matrix_;
   
   n = (uint)matrix_.Cols();
   rows = matrix_.Rows();
   m = clusters;
   
   cluster_tensor = new CTensors(m);
   
   w_matrix =matrix_utils.Random(0.0, 1.0, n, m, RANDOM_STATE); 
      
   vector D(m); //Евклидово расстояние между кластерами
   
   
   for (uint epoch=0; epoch<epochs; epoch++)
    {
      double epoch_start = GetMicrosecondCount()/(double)1e6, epoch_stop=0; 
      
      for (ulong i=0; i<rows; i++)
       {
         for (ulong j=0; j<m; j++)
           {
             D[j] = Euclidean_distance(Matrix.Row(i),w_matrix.Col(j));
           }
         
         #ifdef DEBUG_MODE  
            Print("Euc distance ",D," Winning cluster ",D.ArgMin());
         #endif 
         
   //--- обновление весов
         
         ulong min = D.ArgMin();
          
         vector w_new =  w_matrix.Col(min) + (alpha * (Matrix.Row(i) - w_matrix.Col(min)));
         
         w_matrix.Col(w_new, min);
         
       }
  
      epoch_stop =GetMicrosecondCount()/(double)1e6;    
      
      printf("Epoch [%d/%d] | %sElapsed ",epoch+1,epochs, CalcTimeElapsed(epoch_stop-epoch_start));
      
    }  //end of training

//---

  #ifdef DEBUG_MODE
      Print("\nNew weights\n",w_matrix);
  #endif 
   
 }

Результат

CS      0       04:13:26.617    Self Organizing map (EURUSD,H1) Euc distance [2.122748018266242,1.822857430002081] Winning cluster 1
CS      0       04:13:26.617    Self Organizing map (EURUSD,H1) Euc distance [1.434132188481296,1.100846180984197] Winning cluster 1
CS      0       04:13:26.617    Self Organizing map (EURUSD,H1) Euc distance [5.569896531530945,5.257391342266398] Winning cluster 1
CS      0       04:13:26.617    Self Organizing map (EURUSD,H1) Euc distance [4.36622216533946,4.000958814345993] Winning cluster 1
CS      0       04:13:26.617    Self Organizing map (EURUSD,H1) Euc distance [8.053842751911217,7.646959164093921] Winning cluster 1
CS      0       04:13:26.617    Self Organizing map (EURUSD,H1) Euc distance [6.966950064745546,6.499246789416081] Winning cluster 1
CS      0       04:13:26.617    Self Organizing map (EURUSD,H1) Epoch [1/100] | 0.000 Seconds Elapsed 
....
....
....
CS      0       04:13:26.622    Self Organizing map (EURUSD,H1) Euc distance [0.7271897806071723,4.027137175049654] Winning cluster 0
CS      0       04:13:26.622    Self Organizing map (EURUSD,H1) Euc distance [0.08133608432880858,4.734224801594559] Winning cluster 0
CS      0       04:13:26.622    Self Organizing map (EURUSD,H1) Euc distance [4.18281664576938,0.5635073709012016] Winning cluster 1
CS      0       04:13:26.622    Self Organizing map (EURUSD,H1) Euc distance [2.979092473547668,1.758946102746018] Winning cluster 1
CS      0       04:13:26.622    Self Organizing map (EURUSD,H1) Euc distance [6.664860479474853,1.952054507391296] Winning cluster 1
CS      0       04:13:26.622    Self Organizing map (EURUSD,H1) Euc distance [5.595867985957728,0.8907607121421737] Winning cluster 1
CS      0       04:13:26.622    Self Organizing map (EURUSD,H1) Epoch [100/100] | 0.000 Seconds Elapsed 
CS      0       04:13:26.622    Self Organizing map (EURUSD,H1) 
CS      0       04:13:26.622    Self Organizing map (EURUSD,H1) New weights
CS      0       04:13:26.622    Self Organizing map (EURUSD,H1) [[0.75086979456201,4.028060179594681]
CS      0       04:13:26.622    Self Organizing map (EURUSD,H1)  [1.737580668068743,5.173650598091957]]

Отлично, все работает, наши карты Кохонена смогли сгруппировать нашу первичную матрицу.

   matrix Matrix = {
                     {1.2, 2.3}, //Into cluster 0
                     {0.7, 1.8}, //Into cluster 0
                     {3.6, 4.8}, //Into cluster 1
                     {2.8, 3.9}, //Into cluster 1
                     {5.2, 6.7}, //Into cluster 1
                     {4.8, 5.6}  //Into cluster 1
                   };

Все так, как и ожидалось. Однако представить этот вывод и визуализировать на графике не так просто, как кажется. У нас есть два кластера, один из которых представляет собой матрицу 2x2, а другой — матрицу 4x2. В одном 4 значения, в другом 8. Если вы помните в статье "Кластеризация K-средних" у меня возникли сложности с представлением кластеров из-за этой разницы в размерах.

Тензоры в машинном обучении

Тензор — это обобщение векторов и матриц внутри многомерного массива. Простыми словами, тензор — это массив, содержащий внутри матрицы и векторы. В питоне это выглядит так:

# create tensor
from numpy import array

T = array([
  [[1,2,3],    [4,5,6],    [7,8,9]],
  [[11,12,13], [14,15,16], [17,18,19]],
  [[21,22,23], [24,25,26], [27,28,29]],
  ])

Тензоры — это фундаментальная структура данных, используемая фреймворками машинного обучения, такими как TensorFlow, PyTorch и Keras.

Тензоры используются в алгоритмах машинного обучения для умножения матриц, свертки, объединения и других операций. Тензоры также используются для хранения и управления весами и смещениями нейронных сетей во время обучения и логического вывода. Будучи важной структурой данных в машинном обучении, тензоры позволяют эффективно выполнять вычисления и представлять сложные данные.

Я импортировал библиотеку Tensors.mqh. Более подробно можно почитать у меня в GitHub wiki.

Я добавил тензоры, чтобы собрать наборы кластеров для каждого тензора.

CKohonenMaps::CKohonenMaps(matrix &matrix_, bool save_clusters=true, uint clusters=2, double alpha=0.01, uint epochs=100)
 {
   Matrix = matrix_;
   
   n = (uint)matrix_.Cols();
   rows = matrix_.Rows();
   m = clusters;
   
   cluster_tensor = new CTensors(m);
   
   w_matrix =matrix_utils.Random(0.0, 1.0, n, m, RANDOM_STATE); 
   
   Print("w Matrix\n",w_matrix,"\nMatrix\n",Matrix);
   
   vector D(m); //Евклидово расстояние между кластерами
   
   
   for (uint epoch=0; epoch<epochs; epoch++)
    {
      double epoch_start = GetMicrosecondCount()/(double)1e6, epoch_stop=0; 
      
      for (ulong i=0; i<rows; i++)
       {
         for (ulong j=0; j<m; j++)
           {
             D[j] = Euclidean_distance(Matrix.Row(i),w_matrix.Col(j));
           }
         
         #ifdef DEBUG_MODE  
            Print("Euc distance ",D," Winning cluster ",D.ArgMin());
         #endif 
         
   //--- обновление весов
         
         ulong min = D.ArgMin();
         
         if (epoch == epochs-1) //последняя итерация
            cluster_tensor.TensorAppend(Matrix.Row(i), min);
          
         vector w_new =  w_matrix.Col(min) + (alpha * (Matrix.Row(i) - w_matrix.Col(min)));
         
         w_matrix.Col(w_new, min);
         
         //Print("New w_Matrix\n ",w_matrix);
       }
  
      epoch_stop =GetMicrosecondCount()/(double)1e6;    
      
      printf("Epoch [%d/%d] | %sElapsed ",epoch+1,epochs, CalcTimeElapsed(epoch_stop-epoch_start));
      
    }  //конец обучения

//---

  #ifdef DEBUG_MODE
      Print("\nNew weights\n",w_matrix);
  #endif 
  
//---

   Print("\nclusters");
   cluster_tensor.TensorPrint();
}

Результат

CS      0       04:13:26.624    Self Organizing map (EURUSD,H1) clusters
CS      0       04:13:26.624    Self Organizing map (EURUSD,H1) TENSOR INDEX <<0>>
CS      0       04:13:26.624    Self Organizing map (EURUSD,H1) [[1.2,2.3]
CS      0       04:13:26.624    Self Organizing map (EURUSD,H1)  [0.7,1.8]]
CS      0       04:13:26.624    Self Organizing map (EURUSD,H1) TENSOR INDEX <<1>>
CS      0       04:13:26.624    Self Organizing map (EURUSD,H1) [[3.6,4.8]
CS      0       04:13:26.624    Self Organizing map (EURUSD,H1)  [2.8,3.9]
CS      0       04:13:26.624    Self Organizing map (EURUSD,H1)  [5.2,6.7]
CS      0       04:13:26.624    Self Organizing map (EURUSD,H1)  [4.8,5.6]]

Теперь наши кластеры хранятся в соответствующих тензорах. Пришло время сделать из этого что-то полезное.

Извлечение кластеров

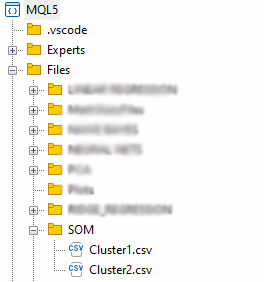
Извлечем кластеры и сохраним их в файлы CSV.

  matrix mat= {};
  
  if (save_clusters)
     for (uint i=0; i<this.cluster_tensor.TENSOR_DIMENSION; i++)
       {
          mat = this.cluster_tensor.Tensor(i); //Получение матрицы, расположенной по индексу I в кластерном тензоре
         
         string header[]; ArrayResize(header, (int)mat.Cols());
         
         for (int k=0; k<ArraySize(header); k++) 
           header[k] = "col"+string(k);
         
         if (this.matrix_utils.WriteCsv("SOM\\Cluster"+string(i+1)+".csv",mat,header))
            Print("CSV файлы кластеров сохранили в папку Files\\SOM");
       }

Файлы будут храниться в каталоге SOM внутри родительского каталога Files.

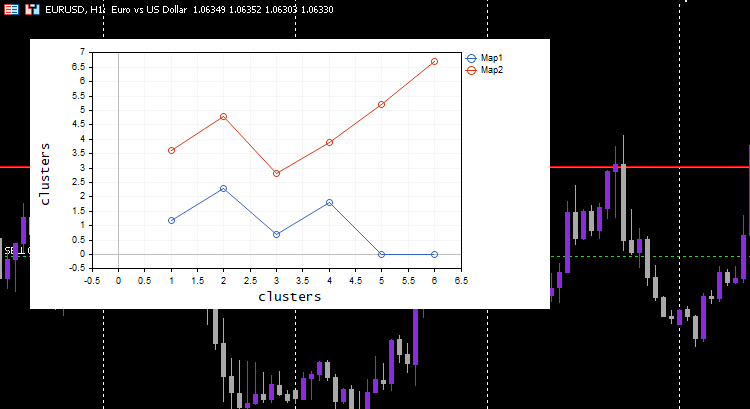
Мы закончили извлечение данных, но важной частью карт Кохонена является визуализация кластеров и построение карт. Библиотеки Python и другие фреймворки обычно используют карты попаданий. Мы будем использовать для этого график кривой.

   vector v;  
   matrix plotmatrix(rows, m); 
   
     for (uint i=0; i<this.cluster_tensor.TENSOR_DIMENSION; i++)
       {
          mat = this.cluster_tensor.Tensor(i);
          
          v  = this.matrix_utils.MatrixToVector(mat);
          
          plotmatrix.Col(v, i);
       }   
    
    this.plt.ScatterCurvePlotsMatrix("kom",plotmatrix,"Map","clusters","clusters");

Результат

Все работает — график отлично визуализирует данные, как и предполагалось. Теперь давайте попробуем алгоритм на чем-нибудь полезном.

Кластеризация показателей индикатора

Соберем 100 баров для пяти разных скользящих средних и попробуем сгруппировать их с помощью карт Кохонена. Все индикаторы будут работать на одном и том же графике, таймфрейме и цене расчета. Отличаться будут только периоды вычисления скользящей.

#include <MALE5\Neural Networks\kohonen maps.mqh> 
#include <MALE5\matrix_utils.mqh>
 

CMatrixutils matrix_utils;
CKohonenMaps *maps;

input int bars = 100;

int handles[5];
int period[5] = {10,20,30,50,100};
matrix Matrix(bars,5);
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   
   vector v;
   
   for (int i=0; i<5; i++)
      {
         handles[i] = iMA(Symbol(),PERIOD_CURRENT,period[i],0,MODE_LWMA,PRICE_CLOSE);
         matrix_utils.CopyBufferVector(handles[i],0,0,bars, v);
         
         Matrix.Col(v, i); //сохраним индикаторы в матрицу
      }
    
   
   maps = new CKohonenMaps(Matrix,true,2,0.01,1000);
      
//---
   return(INIT_SUCCEEDED);
  }

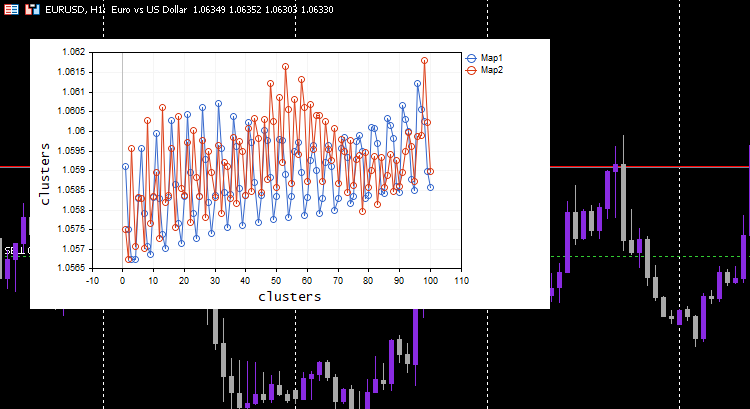
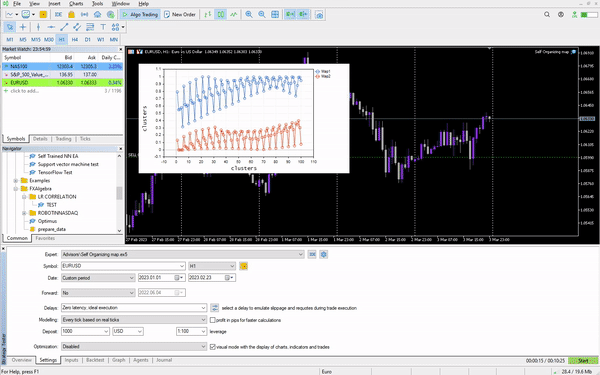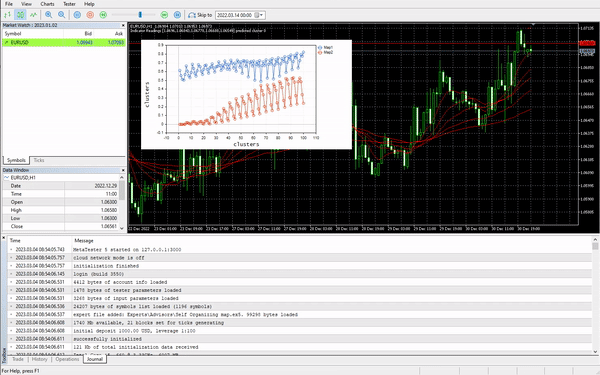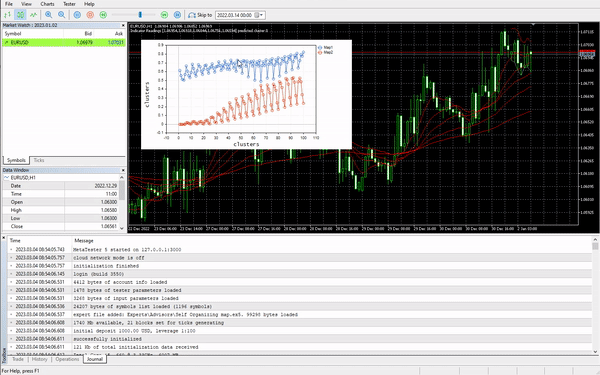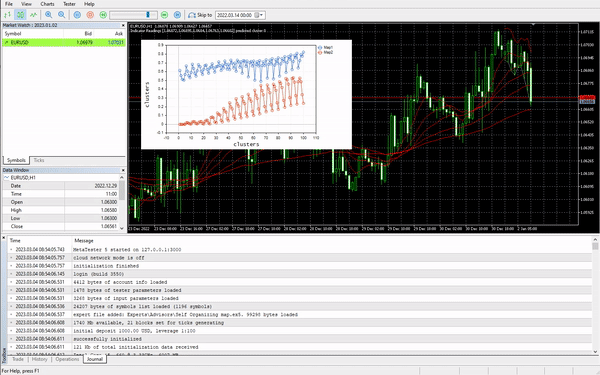
Я установил скорость обучения/альфа = 0,01 и эпохи = 1000. Получились такие карты Кохонена.

Выглядит странно, поэтому я пошел проверять логи, чтобы понять причину. Вот что я нашел:

CS      0       06:19:59.911    Self Organizing map (EURUSD,H1) clusters
CS      0       06:19:59.911    Self Organizing map (EURUSD,H1) TENSOR INDEX <<0>>
CS      0       06:19:59.911    Self Organizing map (EURUSD,H1) [[1.059108363197969,1.057514381244092,1.056754472954214,1.056739184229631,1.058300613902105]
CS      0       06:19:59.911    Self Organizing map (EURUSD,H1)  [1.059578181379783,1.057915286006,1.057066064352063,1.056875795994335,1.05831249905062]
....
....
CS      0       06:19:59.912    Self Organizing map (EURUSD,H1)  [1.063954363197777,1.061619428863266,1.061092386932678,1.060653270504107,1.059293304991227]
CS      0       06:19:59.912    Self Organizing map (EURUSD,H1)  [1.065106545015954,1.062409714577555,1.061610946072463,1.06098919991587,1.059488318852614…]
CS      0       06:19:59.912    Self Organizing map (EURUSD,H1) TENSOR INDEX <<1>>
CS      0       06:19:59.912    Self Organizing map (EURUSD,H1) []
CS      0       06:19:59.912    Self Organizing map (EURUSD,H1) CMatrixutils::MatrixToVector Failed to turn the matrix to a vector rows 0 cols 0

Тензор второго кластера пустой, то есть алгоритм его не предсказал вовсе, а все данные были предсказаны как принадлежащие кластеру 0.

Всегда нормализуйте переменные

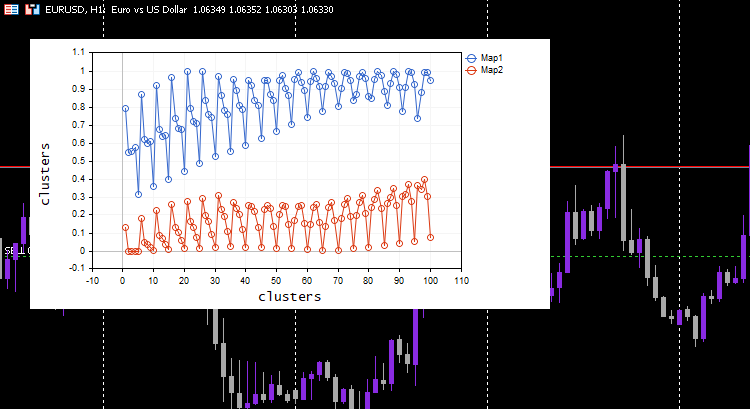
Я уже говорил об этом пару раз и буду говорить снова: нормализация входных данных необходима для всех моделей машинного обучения, с которыми вы сталкиваетесь. И снова мы видим, насколько важна эта нормализация. Давайте посмотрим на результат после нормализации данных.

Для нормализации я использовал методику Min-Max scaler.

#include <MALE5\Neural Networks\kohonen maps.mqh>
#include <MALE5\preprocessing.mqh>
#include <MALE5\matrix_utils.mqh>

CPreprocessing *pre_processing;
CMatrixutils matrix_utils;
CKohonenMaps *maps;

input int bars = 100;

int handles[5];
int period[5] = {10,20,30,50,100};
matrix Matrix(bars,5);
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   
   vector v;
   
   for (int i=0; i<5; i++)
      {
         handles[i] = iMA(Symbol(),PERIOD_CURRENT,period[i],0,MODE_LWMA,PRICE_CLOSE);
         matrix_utils.CopyBufferVector(handles[i],0,0,bars, v);
         
         Matrix.Col(v, i);
      }
   
   pre_processing = new CPreprocessing(Matrix, NORM_MIN_MAX_SCALER);
   
   maps = new CKohonenMaps(Matrix,true,2,0.01,1000);
    
   
//---
   return(INIT_SUCCEEDED);
  }

На этот раз на графике получились красивые карты Кохонена.

Но нормализация данных преобразует данные в меньшие значения. Для тех, кто просто хочет сгруппировать свои данные для понимания шаблонов и использования извлеченных данных в других программах, процесс нормализации нужно интегрировать в ядро алгоритма. Данные нужно нормализовать и разнормализовать, чтобы полученные кластеры были в исходных значениях. Потому что методы кластеризации не изменяют данные, а только группируют их. Для нормализации и разнормализации можно использовать этот класс предобработки.

CKohonenMaps::CKohonenMaps(matrix &matrix_, bool save_clusters=true, uint clusters=2, double alpha=0.01, uint epochs=100, norm_technique NORM_TECHNIQUE=NORM_MIN_MAX_SCALER)
 {
   Matrix = matrix_;
   
   n = (uint)matrix_.Cols();
   rows = matrix_.Rows();
   m = clusters; 
   
   pre_processing = new CPreprocessing(Matrix, NORM_TECHNIQUE);
   cluster_tensor = new CTensors(m);
   
   w_matrix =matrix_utils.Random(0.0, 1.0, n, m, RANDOM_STATE); 
   
   #ifdef DEBUG_MODE
      Print("w Matrix\n",w_matrix,"\nMatrix\n",Matrix);
   #endif 
   
   vector D(m); //Евклидово расстояние между кластерами
   
   
   for (uint epoch=0; epoch<epochs; epoch++)
    {
    
      double epoch_start = GetMicrosecondCount()/(double)1e6, epoch_stop=0; 
      
      for (ulong i=0; i<rows; i++)
       {
         for (ulong j=0; j<m; j++)
           {
             D[j] = Euclidean_distance(Matrix.Row(i),w_matrix.Col(j));
           }
         
         #ifdef DEBUG_MODE  
            Print("Euc distance ",D," Winning cluster ",D.ArgMin());
         #endif 
         
   //--- обновление весов
         
         ulong min = D.ArgMin();
         
         if (epoch == epochs-1) //последняя итерация
            cluster_tensor.TensorAppend(Matrix.Row(i), min); 

          
         vector w_new =  w_matrix.Col(min) + (alpha * (Matrix.Row(i) - w_matrix.Col(min)));
         
         w_matrix.Col(w_new, min);
       }
  
      epoch_stop =GetMicrosecondCount()/(double)1e6;    
      
      printf("Epoch [%d/%d] | %sElapsed ",epoch+1,epochs, CalcTimeElapsed(epoch_stop-epoch_start));
      
    }  //конец обучения

//---

  #ifdef DEBUG_MODE
      Print("\nNew weights\n",w_matrix);
  #endif 

//---
   
   matrix mat= {};

   vector v;  
   matrix plotmatrix(rows, m); 
   
     for (uint i=0; i<this.cluster_tensor.TENSOR_DIMENSION; i++)
       {
          mat = this.cluster_tensor.Tensor(i);
          
          v  = this.matrix_utils.MatrixToVector(mat);
          
          plotmatrix.Col(v, i);
       }   
    
    this.plt.ScatterCurvePlotsMatrix("kom",plotmatrix,"Map","clusters","clusters");       

//---

  
  if (save_clusters)
     for (uint i=0; i<this.cluster_tensor.TENSOR_DIMENSION; i++)
       {
         mat = this.cluster_tensor.Tensor(i);
         pre_processing.ReverseNormalization(mat);
         cluster_tensor.TensorAdd(mat, i);
         
         string header[]; ArrayResize(header, (int)mat.Cols());
         
         for (int k=0; k<ArraySize(header); k++) 
           header[k] = "col"+string(k);
         
         if (this.matrix_utils.WriteCsv("SOM\\Cluster"+string(i+1)+".csv",mat,header))
            Print("CSV файлы кластеров сохранили в папку Files\\SOM");
       }

//---

   Print("\nclusters");
   cluster_tensor.TensorPrint();

 }

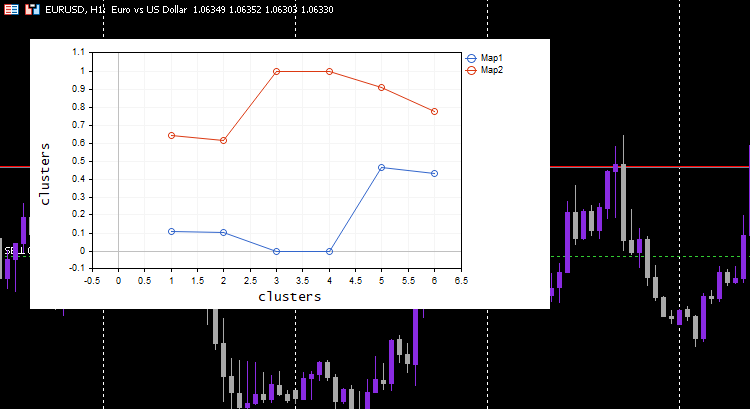
Чтобы показать, как это работает, придется вернуться к простому набору данных, который у нас был в начале.

   matrix Matrix = {
                     {1.2, 2.3},
                     {0.7, 1.8},
                     {3.6, 4.8},
                     {2.8, 3.9},
                     {5.2, 6.7},
                     {4.8, 5.6}
                   };
   
   maps = new CKohonenMaps(Matrix,true,2,0.01,1000);

Результат

CS      0       07:14:44.660    Self Organizing map (EURUSD,H1) w Matrix
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1) [[0.005340739158299509,0.01220740379039888]
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1)  [0.5453352458265939,0.9172643208105716]]
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1) Matrix
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1) [[0.1111111111111111,0.1020408163265306]
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1)  [0,0]
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1)  [0.6444444444444445,0.6122448979591836]
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1)  [0.4666666666666666,0.4285714285714285]
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1)  [1,1]
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1)  [0.911111111111111,0.7755102040816325]]
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1) Epoch [1/1000] | 0.000 Seconds Elapsed 
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1) Epoch [2/1000] | 0.000 Seconds Elapsed 
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1) Epoch [3/1000] | 0.000 Seconds Elapsed 
...
...
...
CS      0       07:14:44.674    Self Organizing map (EURUSD,H1) Epoch [999/1000] | 0.000 Seconds Elapsed 
CS      0       07:14:44.674    Self Organizing map (EURUSD,H1) Epoch [1000/1000] | 0.000 Seconds Elapsed 
CS      0       07:14:44.674    Self Organizing map (EURUSD,H1) 
CS      0       07:14:44.674    Self Organizing map (EURUSD,H1) New weights
CS      0       07:14:44.674    Self Organizing map (EURUSD,H1) [[0.1937869656464888,0.8527427060068337]
CS      0       07:14:44.674    Self Organizing map (EURUSD,H1)  [0.1779676215121214,0.7964618795904062]]
CS      0       07:14:44.725    Self Organizing map (EURUSD,H1) Clusters CSV files saved under the directory Files\SOM
CS      0       07:14:44.726    Self Organizing map (EURUSD,H1) Clusters CSV files saved under the directory Files\SOM
CS      0       07:14:44.726    Self Organizing map (EURUSD,H1) 
CS      0       07:14:44.726    Self Organizing map (EURUSD,H1) clusters
CS      0       07:14:44.726    Self Organizing map (EURUSD,H1) TENSOR INDEX <<0>>
CS      0       07:14:44.726    Self Organizing map (EURUSD,H1) [[1.2,2.3]
CS      0       07:14:44.726    Self Organizing map (EURUSD,H1)  [0.7,1.8]
CS      0       07:14:44.726    Self Organizing map (EURUSD,H1)  [2.8,3.899999999999999]]
CS      0       07:14:44.727    Self Organizing map (EURUSD,H1) TENSOR INDEX <<1>>
CS      0       07:14:44.727    Self Organizing map (EURUSD,H1) [[3.600000000000001,4.8]
CS      0       07:14:44.727    Self Organizing map (EURUSD,H1)  [5.2,6.7]
CS      0       07:14:44.727    Self Organizing map (EURUSD,H1)  [4.8,5.6]]

Работает как по волшебству. Несмотря на то, что модель машинного обучения использует нормализованные данные, модель сможет кластеризовать данные и по-прежнему сможет выдавать ненормализованные/исходные данные. Обратите внимание, что нанесенные кластеры были нормализованными данными. Это важно, потому что трудно представить данные в разных масштабах. На этот раз график для кластеров в простом тестовом наборе данных получился намного лучше:

Расширение карт Кохонена

Хотя первоначальная цель карт Кохонена и других методов анализа данных не является прогнозированием, но поскольку у них есть изученные параметры, а именно веса, можем расширить их и получать кластеры на новых данных.

uint CKohonenMaps::KOMPredCluster(vector &v)
 {
  vector temp_v = v;
  pre_processing.Normalization(v);
  
  if (n != v.Size())
   {
     Print("Невозможно предсказать кластер | размер входного вектора не совпадает с столбцами обученной матрицы");
     return(-1);
   }
   
   vector D(m); //Евклидово расстояние между кластерами
   
   for (ulong j=0; j<m; j++)
       D[j] = Euclidean_distance(v, w_matrix.Col(j));
   
   v.Copy(temp_v);
   return((uint)D.ArgMin());
 }

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+

vector CKohonenMaps::KOMPredCluster(matrix &matrix_)
 {   
   vector v(n);
   
   if (n != matrix_.Cols())
      {
         Print("Невозможно предсказать кластер | столбцы входной матрицы не совпадает с столбцами обученной матрицы");
         return (v);
      }
   
   for (ulong i=0; i<matrix_.Rows(); i++)
      v[i] = KOMPredCluster(matrix_.Row(i));
      
    return(v);
 }

Подадим теперь на вход новые данные. Мы с вами знаем, какой кластер у [0.5, 1.5] и [5.5, 6]. Эти данные относятся к кластерам 0 и 1 соответственно.

   maps = new CKohonenMaps(Matrix,true,2,0.01,1000); //Training
   
   matrix new_data = {
         {0.5,1.5},
         {5.5, 6.0}
      };
   
   Print("new data\n",new_data,"\nprediction clusters\n",maps.KOMPredCluster(new_data)); //используем для предсказаний

Результат

CS      0       07:46:00.857    Self Organizing map (EURUSD,H1) new data
CS      0       07:46:00.857    Self Organizing map (EURUSD,H1) [[0.5,1.5]
CS      0       07:46:00.857    Self Organizing map (EURUSD,H1)  [5.5,6]]
CS      0       07:46:00.857    Self Organizing map (EURUSD,H1) prediction clusters
CS      0       07:46:00.857    Self Organizing map (EURUSD,H1) [0,1]

Карты Кохонена предсказали их правильно!

Карты Кохонена в тестере стратегий

Алгоритм работает отлично. Итак, я заметил, что он предсказывает кластер 0, когда рынок растет, и наоборот с 1. Я не уверен, что вывод правильный, я возможно недостаточно тщательно проанализировал поведение, поэтому оставляю это вам. Если это так, можно даже использовать карты Кохонена в качестве индикатора.

Преимущества карт Кохонена

Карты Кохонена имеют ряд преимуществ:

Они могут фиксировать нелинейные отношения между входными данными и выходной картой, то есть они могут обрабатывать сложные закономерности и структуры данных.
Они могут находить закономерности на неразмеченных данных. То есть использовать их можно, когда размеченных данных недостаточно или их сложно получить.
За счет уменьшения размерности входных данных уменьшается вычислительная сложность последующих задач, таких как регрессия и классификация.
Сохраняются топологические отношения между входными данными и выходной картой: близкие нейроны на карте соответствуют аналогичным областям во входном пространстве, что может помочь в исследовании и визуализации данных.
Устойчивы к шуму и выбросам во входных данных, если шум слишком велик.

Недостатки карт Кохонена

Качество сильно зависит от инициализации вектора весов. Если инициализация плохая, можем получить неоптимальное решение или застрять в локальном минимуме.
Качество карт также зависит от выбора гиперпараметров (скорости обучения, количеству нейронов и т.д.) Настройка этих параметров может занять много времени и потребовать дополнительных работ.
Требует больших вычислительных ресурсов и памяти при работе с большими наборами данных. Размер карт зависит от количества точек входных данных, и чем больше данных, тем больше количество нейронов и тем длительнее обучение.
Если говорить о нейронных сетях, для самообучающихся карт не существует формальных критериев сходимости, поэтому может быть трудно определить, когда нужно остановить обучение.

Заключение

Карты Кохонена или самоорганизующиеся карты — это инновационный подход к торговле, который может помочь трейдерам ориентироваться на рынках. Используя обучение без учителя, карты Кохонена могут выявлять закономерности и структуры в рыночных данных, позволяя трейдерам принимать обоснованные решения. Как мы видели в этой статье, карты Кохонена способны выявлять нелинейные отношения в данных и объединять данные в соответствующие группы. Однако при работе с ними нужно помнить о потенциальных недостатках, таких как чувствительность к инициализации, отсутствие формальных критериев сходимости и др. В целом, карты Кохонена могут стать ценным дополнением к набору инструментов трейдера, но, как и любой инструмент, их следует использовать с осторожностью и вниманием.

Удачи.

Следите за развитием темы в моем репозитории GitHub https://github.com/MegaJoctan/MALE5.

Файл	Содержание и использование
Self Organizing map.mq5	Файл советника для тестирования алгоритма, обсуждаемого в этой статье
kohonen maps.mqh	Библиотека, содержащая алгоритм карт Кохонена
plots.mqh	Библиотека, содержащая функции для рисования графиков на графике в МТ5
preprocessing.mqh	Функции для нормализации и предварительной обработки входных данных
matrix_utils.mqh	Содержит дополнительные функции для матричных операций в MQL5
Tensors.mqh	Библиотека, содержащая классы для создания тензоров

Статьи по теме:

Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/12261

Прикрепленные файлы |

Загрузить ZIP

Kohonen_Maps_Attachments.zip (14.48 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Нейросети — это просто (Часть 50): Soft Actor-Critic (оптимизация модели)

В предыдущей статье мы реализовали алгоритм Soft Actor-Critic, но не смогли обучить прибыльную модель. В данной статье мы проведем оптимизацию ранее созданной модели для получения желаемых результатов её работы.

Теория категорий (Часть 9): Действия моноидов

Статья продолжает серию о реализации теории категорий в MQL5. В статье рассматриваются действия моноидов (monoid actions) как средство преобразования моноидов, описанных в предыдущей статье, для увеличения областей их применения.

Дискретное преобразование Хартли

В этой статье мы познакомимся с одним из методов спектрального анализа и обработки сигналов - дискретным преобразованием Хартли. С его помощью можно фильтровать сигналы, анализировать их спектр и многое другое. Возможности DHT ничуть не меньше, чем у дискретного преобразования Фурье. Однако, в отличие от него, DHT использует только вещественные числа, что делает его более удобным для реализации на практике, а результаты его применения более наглядными.

Модель движения цены и ее основные положения. (Часть 3): Расчет оптимальных параметров биржевой игры

В рамках разработанного автором инженерного подхода, основанного на теории вероятности, находятся условия открытия прибыльной позиции и рассчитываются оптимальные – максимализирующие прибыль - значения тейкпрофита и стоплосса.