
Теория категорий (Часть 9): Действия моноидов
Введение
В предыдущей статье мы представили моноиды и рассмотрели, как их можно использовать в контролируемом обучении для классификации и обоснования торговых решений. В этой статье мы изучим действия моноидов и их применение в неконтролируемом обучении для уменьшения размеров входных данных. На выходе моноидальных операций всегда оказываются члены соответствующего множества, что означает, что такие операции не являются преобразующими. Таким образом, моноидные действия добавляют возможность преобразования, поскольку множество действий не обязательно должен быть подмножеством множества моноидов. Под преобразованием мы подразумеваем возможность получать результаты действий, которые не являются членами множества моноидов.
Формально действие a моноида M (e, *) на множестве S определяется как:
a: M x S - - > S ; (1)
e a s - - > s; (2)
m * (n * s) - - > (m * n) a s (3)
где m, n — элементы моноида M, а s — элемент множества S.
Иллюстрация и методы
Для нас особенно важно понимание относительной важности различных параметров в процессе принятия решений моделью. В нашем случае, согласно предыдущей статье, нашими "параметрами" были:
- Период ретроспективного анализа
- Таймфрейм
- Применимая цена
- Индикатор
- И решение о торговле в диапазоне или по тренду.
Мы рассмотрим несколько методов, которые применимы для взвешивания функций нашей модели и помогут определить наиболее чувствительный к точности нашего прогноза. Мы выберем один метод и, основываясь на его рекомендациях, постараемся добавить преобразование в моноид в этом узле, расширив множество моноидов с помощью моноидных действий, и посмотрим, как это повлияет на нашу способность точно размещать трейлинг-стопы в соответствии с особенностями применения, которые мы рассмотрели в предыдущей статье.
При определении относительной важности каждого столбца данных в обучающем наборе можно использовать несколько инструментов и методов. Эти методы помогают количественно оценить вклад каждой функции (столбца данных) в прогнозы модели и указывают нам, какой столбец данных, возможно, нуждается в разработке, а чему следует уделять меньше внимания. Вот некоторые часто используемые методы:
Рейтинг важности параметра
Этот подход ранжирует параметры по важности, учитывая их влияние на производительность модели. Обычно различные алгоритмы, такие как случайные леса, машины повышения градиента (Gradient Boosting Machines) или дополнительные деревья, предоставляют встроенные меры важности признаков, которые не только помогают в построении деревьев, но и могут быть извлечены после обучения модели.
Чтобы проиллюстрировать это, давайте рассмотрим сценарий, в котором, как и в предыдущей статье, мы хотим прогнозировать изменения ценового диапазона и использовать полученные данные для настройки трейлинг-стопа открытых позиций. Поэтому мы будем рассматривать точки принятия решений, которые у нас были тогда (функции или столбцы данных) как деревья. Если мы используем для этой задачи классификатор случайного леса, используя каждую из наших точек решения в виде дерева, после обучения модели мы можем извлечь ранжирование важности параметров.
Для уточнения, наш набор данных будет содержать следующие деревья:
- Продолжительность периода ретроспективного анализа (целочисленные данные)
- Таймфрейм, выбранный для торговли (данные перечисления: H1, H2, H3 и т.д.)
- Применяемая цена, используемая в анализе (данные перечисления: цена открытия, средняя цена, типичная цена, цена закрытия)
- Выбор индикатора, используемого в анализе (данные перечисления осциллятора RSI или конвертов полос Боллинджера)
После обучения с помощью классификатора случайного леса мы можем извлечь ранжирование важности признаков с помощью весов примесей Джини (Gini impurity weights). Показатели важности параметров указывают на относительную важность (взвешивание) каждого столбца данных в процессе принятия решений в модели.
Предположим, ранжирование важности параметров привело к следующему:
- Выбор индикатора, используемого в анализе: 0,45
- Продолжительность периода ретроспективного анализа: 0.30
- Применяемая цена: 0.20
- Таймфрейм: 0.05
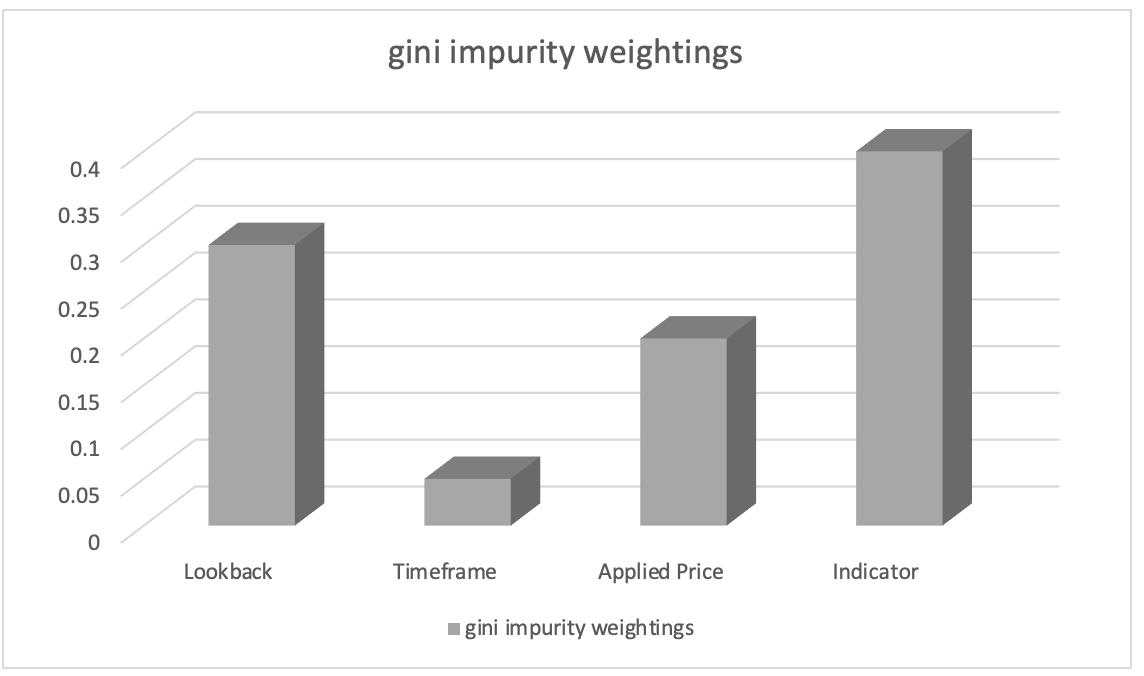
Исходя из этого, мы можем сделать вывод, что параметр "выбор индикатора, используемого в анализе", имеет наибольшее значение, за ним следует параметр "продолжительность периода ретроспективного анализа". "Применяемая цена" занимает третье место, а "таймфрейм" имеет наименьшее значение.
Эта информация может помочь нам понять, какие параметры наиболее важны для прогнозов модели, и с помощью этих знаний мы сосредоточимся на более важных параметрах во время разработки параметров, расставим приоритеты при выборе параметров или изучим дополнительные сведения о предметной области, связанные с этими параметрами. В нашем случае мы могли бы посмотреть на преобразование моноидного множества индикаторов, введя множество(а) моноидного действия других индикаторов, и изучить, как это влияет на наши прогнозы. Таким образом, наши наборы действий добавят альтернативные индикаторы осциллятору RSI и конверту полос Боллинджера. Какой бы индикатор мы ни добавили, как в случае с полосами Боллинджера в предыдущей статье, нам нужно будет упорядочить его выходные данные и убедиться, что он находится в диапазоне от 0 до 100, где 0 указывает на уменьшение диапазона ценового бара, а 100 - на увеличение.
Важность пермутации
Важность пермутации оценивает значимость порядка признаков (или столбцов данных), случайным образом меняя их порядок и измеряя последующее изменение производительности модели при составлении прогнозов. До сих пор порядок был таким: период ретроспективного анализа, таймфрейм, применяемая цена, индикатор и наконец тип торгового решения. Что бы произошло, если бы мы изменили последовательность наших решений? Нам пришлось бы переставлять один столбец данных (параметр) за раз. Более значительное падение точности прогноза для любого из этих столбцов данных будет указывать на более высокую важность. Этот метод не зависит от модели и может применяться к любому алгоритму машинного обучения.
Чтобы проиллюстрировать, давайте рассмотрим сценарий с тем же набором данных из пяти столбцов, что и выше (и в предыдущей статье). Мы хотим прогнозировать изменения диапазона ценового бара. Для этой задачи я решил использовать Классификатор повышения градиента. Мы обучаем нашу модель, чтобы оценить значимость каждого столбца данных с использованием важности пермутации. При обучении Классификатора повышения градиента с использованием функций оператора моноида и настроек идентификации, которые мы использовали в нашей предыдущей статье, наш набор данных будет напоминать таблицу ниже:
Чтобы обучить классификатор повышения градиента с использованием нашего набора данных, мы можем следовать следующему пошаговому руководству:
Данные предварительной обработки :
Этот шаг начинается с преобразования наших дискретных данных (т. е. перечислений, таймфрейма ценового графика, применяемой цены, выбора индикатора, торгового решения) в числовые представления с использованием таких методов, какунитарное кодирование. Затем мы разделяем набор данных на параметры (столбцы данных 1-5) и прогнозы модели плюс фактические значения (столбцы данных 6-7).
Разделение данных: После предварительной обработки нам нужно разделить набор данных на строки для обучающего набора и строки для тестового набора. Это позволяет оценить производительность модели на невидимых данных, используя настройки, которые лучше всего работают на ваших обучающих данных. Обычно используется разделение 80-20, но вы можете настроить соотношение в зависимости от размера и характеристик строк в вашем наборе данных. Для столбцов данных, используемых в этой статье, я бы рекомендовал разделение 60-40.
Создание Классификатора повышения градиента: Затем мы включаем необходимые библиотеки или реализуем необходимые функции для классификации повышения градиента в C/MQL5. Это означает включение в экспертную функцию инициализации созданных экземпляров модели классификатора повышения градиента, где мы также указываем гиперпараметры, такие как количество оценочных функций, скорость обучения и максимальная глубина.
Модель тренировки: Путем повторения обучающих данных и изменения порядка каждого столбца данных в процессе принятия решения обучающий набор используется для обучения классификатора повышения градиента. Затем результаты модели записываются. Для повышения точности прогнозов корректировки диапазонов ценовых баров вы также можете варьировать параметры модели, такие как идентификационный элемент каждого моноида или тип операции (из списка операций, использованных в предыдущей статье).
Оценка системы: Модель будет протестирована на строках тестовых данных (40% отделено при разделении) с использованием лучших настроек из обучения. Это позволяет определить, насколько хорошо обученные настройки модели работают с необученными данными. При этом мы просматриваем все строки данных вне выборки (строки тестовых данных), чтобы оценить способность лучших настроек модели прогнозировать изменения в диапазоне целевых ценовых баров. Затем результаты тестовых прогонов могут быть оценены с использованием таких методов, как F-мера и т.д.
Мы также можем точно настроить модель, если производительность нуждается в улучшении, изменив гиперпараметры классификатора повышения градиента. Чтобы найти лучшие гиперпараметры, вам нужно будет использовать такие методы, как поиск по сетке и перекрестная проверка. После разработки успешной модели вы можете использовать ее, чтобы делать предположения о новых, непредвиденных данных, путем предварительной обработки и кодирования категориальных переменных в новых данных, чтобы убедиться, что они имеют тот же формат, что и обучающие данные. Таким образом, вы сможете прогнозировать изменения диапазона ценовых баров для новых данных, используя обученную модель.
Обратите внимание, что реализация классификации повышения градиента в MQL5 с нуля может быть сложной и трудоемкой. Поэтому настоятельно рекомендую использовать библиотеки машинного обучения, написанные на C, такие как XGBoost или LightGBM, которые предлагают эффективные реализации повышения градиента с API для C.
Давайте для иллюстрации представим, что после перестановки столбцов данных мы получаем следующие результаты:
- При изменении периода ретроспективного анализа эффективность прогнозирования падает на 0,062.
- Таймфрейм для пермутации приводит к снижению производительности на 0,048.
- Применение пермутации к применяемой цене приводит к снижению производительности на 0,027.
- Производительность падает на 0,014 при перетасовке позиции столбцов данных индикатора.
- Потеря производительности после изменения торгового решения приводит к 0,009
Эти результаты приводят нас к выводу, что "период ретроспективного анализа" имеет наибольшее значение в его положении при прогнозировании изменений диапазона ценового бара, поскольку перестановка его значений вызвала наибольшее снижение производительности модели. Вторым наиболее важным параметром является "таймфрейм", за которым следуют "применяемая цена", "индикатор" и, наконец, "торговое решение".
Путем количественной оценки влияния каждого столбца данных на производительность модели этот метод позволяет нам определить их относительную значимость. Оценивая относительную значимость каждого параметра (столбца данных), мы можем лучше выбирать функции, проектировать функции и, возможно, даже выделять области, в которых наша модель прогнозирования нуждается в дополнительных исследованиях и разработках.
Следовательно, мы могли бы предложить моноидные действия для множества моноидов ретроспективного анализа, которые изменяют его, добавляя дополнительные периоды ретроспективного анализа, которых еще нет во множестве моноидов, чтобы дополнительно объяснить улучшение. Таким образом, это позволяет нам исследовать, влияют ли эти дополнительные периоды, если таковые имеются, на то, насколько хорошо наша модель предсказывает изменения в диапазоне ценовых баров. Множество моноидов в настоящее время состоит из значений от 1 до 8, каждое из которых кратно 4. Что, если бы наш множитель был равен 3 или 2? Как бы это повлияло на производительность и повлияло бы вообще? Поскольку теперь мы понимаем место ретроспективного периода в процессе принятия решений и то, что он наиболее чувствителен к общей производительности системы, эти и аналогичные проблемы можно решить.
Значения SHAP
SHAP (SHapley Additive exPlanations, аддитивные объяснения Шепли) - унифицированная структура, которая присваивает значения важности каждому столбцу данных на основе принципов теории игр. Значения SHAP обеспечивают справедливое распределение вклада параметров с учетом всех возможностей. Они предлагают всестороннее понимание важности параметров в сложных моделях, таких как XGBoost, LightGBM или модели глубокого обучения.
Рекурсивное устранение признаков (RFE)
RFE — это метод итеративного отбора признаков, который работает путем рекурсивного исключения менее важных признаков на основе их весов или оценок важности. Процесс продолжается до тех пор, пока не будет достигнуто желаемое количество признаков или не будет достигнут порог производительности. Чтобы проиллюстрировать это, мы можем использовать аналогичный сценарий выше, где у нас есть набор данных из пяти столбцов от периода ретроспективного анализа до типа торгового решения, и мы хотим предсказать изменения диапазона ценового бара на основе каждого из пяти признаков (столбцов данных). Для этой задачи мы используем Классификатор метода опорных векторов (SVM). Вот как будет применяться рекурсивное устранение признаков (RFE):
- Обучите модель с помощью классификатора SVM, используя все столбцы данных в наборе данных. Изначально для обучения используется всё, что есть.
- Далее происходит ранжирование признаков, когда мы получаем веса или оценки важности, присвоенные каждому признаку классификатором SVM. Они указывают на относительную важность каждого из них в задаче классификации.
- Затем выполняется устранение наименее важного признака, когда мы опускаем наименее важный столбец данных на основе весов SVM. Это можно сделать, удалив элемент с наименьшим весом.
- Затем происходит переобучение модели с уменьшенными столбцами данных, где классификатор SVM применяется только к оставшимся признакам.
- Оценка производительности без пропущенного столбца данных выполняется с использованием соответствующей метрики оценки, такой как точность или F-мера.
- Процесс повторяется с шагов 2 по 5 до тех пор, пока не будет достигнуто желаемое количество столбцов, исключая наименее важные признаки (или столбцы данных) в каждой итерации и модели переобучения с сокращенным набором функций.
Например, давайте предположим, что мы начинаем с пяти признаков и применяем RFE, и у нас есть цель - 3 признака. На итерации 1 предположим, что это ранжирование признаков на основе убывающей оценки важности:
- Период ретроспективного анализа
- Таймфрейм
- Применимая цена
- Индикатор
- Торговое решение
Будет выполнено исключение признака с наименьшей оценкой важности - торговое решение. Затем следует переобучение классификатора SVM с оставшимися признаками: ретроспективный анализ, временной интервал, примененная цена и индикатор. Давайте возьмем это за ранжирование на итерации 2:
- Период ретроспективного анализа
- Индикатор
- Таймфрейм
- Применимая цена
Удалите признак с наименьшей оценкой важности. Это будет прикладная цена. Признаков для устранения не осталось. Мы достигли желаемого количества признаков. Итерация останавливается. Итеративный процесс останавливается, когда мы достигаем желаемого количества признаков (или другого предопределенного критерия остановки, такого как пороговое значение F-меры). Таким образом, окончательная модель обучается с использованием выбранных признаков: ретроспективный период, индикатор и таймфрейм. RFE помогает определить наиболее важные функции для задачи классификации, итеративно удаляя менее важные функции. Выбирая подмножество функций, которые больше всего влияют на производительность модели, RFE может повысить эффективность модели, уменьшить подгонку и улучшить интерпретируемость.
L1-регуляризация (Лассо)
L1-регуляризация применяет штрафной член к целевой функции модели, поощряя разреженные веса признаков. В результате менее важные признаки, как правило, имеют нулевой или близкий к нулю вес, что позволяет выбирать признаки на основе величины весов. Рассмотрим сценарий, в котором трейдер хотел бы рассчитать риск своих вложений в недвижимость и инвестиционные фонды недвижимости. У нас есть набор данных о ценах на жилье, который мы хотим использовать для прогнозирования динамики цен на жилые дома на основе различных характеристик, таких как площадь, количество спален, количество ванных комнат, расположение и возраст. Мы можем использовать L1-регуляризацию, в частности алгоритм Лассо, для оценки важности этих признаков. Вот как это работает:
- Мы начинаем с обучения модели линейной регрессии с L1-регуляризацией (Лассо), используя все признаки в наборе данных. Член L1-регуляризации добавляет штраф к целевой функции модели.
- После обучения модели Лассо мы получаем оценочные веса, присвоенные каждому признаку. Эти веса отражают важность каждой характеристики в прогнозировании цен на жилье. L1-регуляризация поощряет разреженные веса признаков, а это означает, что менее важные признаки, как правило, имеют нулевые или почти нулевые веса.
- Ранжирование признаков: Мы можем ранжировать функции на основе величины весов. Признаки с более высокими абсолютными весами считаются более важными, а признаки с весами, близкими к нулю, считаются менее важными.
Предположим, что мы обучаем модель Лассо на наборе данных о ценах на жилье и получаем следующие веса признаков:
- Площадь: 0,23
- Количество спален: 0,56
- Количество ванных комнат: 0,00
- Местоположение: 0.42
- Возраст: 0,09
Основываясь на этих весовых коэффициентах, мы можем ранжировать признаки с точки зрения их важности для прогнозирования цен на жилье:
- Количество спален: 0,56
- Местоположение: 0.42
- Площадь: 0,23
- Возраст: 0,09
- Количество ванных комнат: 0,00
В этом примере количество спален имеет наибольший абсолютный вес, что указывает на его высокую значимость для прогнозирования цен на жилье. Далее идут местоположение и площадь, в то время как возраст имеет относительно меньший вес. Количество ванных комнат в данном случае имеет нулевой вес, что говорит о том, что оно считается неважным и фактически исключено из модели.
Применяя L1-регуляризацию (Лассо), мы можем определить и выбрать наиболее важные функции для прогнозирования цен на жилье. Штраф за регуляризацию способствует разреженности весов признаков, позволяя выбирать признаки на основе величины весов. Этот метод помогает понять, какие признаки больше всего влияют на целевую переменную (тенденцию цен на жилье), и может быть полезен для разработки признаков, интерпретации модели и потенциального улучшения производительности модели за счет уменьшения подгонки.
Principal Component Analysis (PCA)
PCA — это метод уменьшения размерности, который может косвенно оценивать важность признаков путем преобразования исходных признаков в пространство более низкой размерности. PCA определяет направления максимальной дисперсии. Главные компоненты с наибольшей дисперсией можно считать более важными.
Корреляционный анализ
Корреляционный анализ исследует линейную связь между признаками и целевой переменной. Признаки с более высокими значениями абсолютной корреляции часто считаются более важными для прогнозирования целевой переменной. Однако важно отметить, что корреляция не отражает нелинейные отношения.
Взаимная информация
Взаимная информация измеряет статистическую зависимость между переменными. Она количественно определяет, сколько информации об одной переменной можно получить из другой. Более высокие значения взаимной информации указывают на более сильную связь и могут использоваться для оценки относительной важности признаков.
В качестве иллюстрации мы можем рассмотреть сценарий, в котором трейдер/инвестор ищет возможность открыть позицию в растущем стартапе прямых инвестиций на основе набора данных о клиентах с целью прогнозирования оттока клиентов на основе различных доступных признаков (наши столбцы данных), таких как возраст, пол, доход, тип подписки и общее количество покупок. Мы можем использовать взаимную информацию для оценки их важности. Вот как это будет работать:
- Мы начинаем с расчета взаимной информации между каждым признаком и целевой переменной (отток клиентов). Взаимная информация измеряет количество информации, которую одна переменная содержит о другой. В нашем случае она количественно определяет, сколько информации об оттоке клиентов можно получить из каждого признака в наших доступных столбцах данных.
- После того, как мы определили показатели взаимной информации, мы ранжируем их на основе их значений. Более высокие значения взаимной информации указывают на более сильную связь между признаком и оттоком клиентов, что предполагает более высокую важность.
Предположим, что оценки взаимной информации для столбцов данных:
- Возраст: 0,08
- Пол: 0,03
- Доход: 0,12
- Тип подписки: 0,10
- Всего покупок: 0,15
Основываясь на этих данных, мы можем ранжировать признаки с точки зрения их важности для прогнозирования оттока клиентов:
- Всего покупок: 0,15
- Доход: 0,12
- Тип подписки: 0,10
- Возраст: 0,08
- Пол: 0,03
В этом примере общее количество покупок имеет самый высокий показатель взаимной информации, что указывает на то, что этот параметр содержит больше всего информации об оттоке клиентов. Ему на пятки наступаю доход и тип подписки, в то время как возраст и пол получают относительно более низкие взаимные информационные баллы.
Используя взаимную информацию, мы можем взвешивать каждый столбец данных и исследовать, какие столбцы можно исследовать дальше, добавляя моноидные действия. Этот набор данных совершенно новый, в отличие от того, что был в предыдущей статье, поэтому для иллюстрации полезно сначала построить моноиды каждого столбца данных, определив соответствующие наборы. Общее количество покупок с предположительно самым высоким значением взаимной информации представляет собой непрерывные данные, а не дискретные, что означает, что мы не можем так же легко увеличить набор моноидов, вводя перечисления вне области действия в базовом моноиде. Таким образом, для дальнейшего изучения или расширения общего количества покупок в моноиде мы могли бы добавить измерение даты покупки. Это означает, что наше множество действий будет иметь непрерывные данные даты и времени. При сопряжении (через действие) с моноидом по общему количеству покупок для каждой покупки мы могли бы получить ее дату, что позволило бы нам изучить влияние дат и сумм покупок на отток клиентов. Это может повысить точность прогнозов.
Специфичные для модели методы
Некоторые алгоритмы машинного обучения имеют специальные методы для определения важности признаков. Например, алгоритмы на основе дерева решений могут предоставлять оценки важности признаков на основе количества раз, когда признак используется для разделения данных по разным деревьям.
Давайте рассмотрим сценарий, в котором у нас есть набор данных с информацией о клиентах, и мы хотим предсказать, купит ли клиент продукт, основываясь на различных характеристиках, таких как возраст, пол, доход и история просмотров. Для этой задачи мы решили использовать Классификатор случайного леса, который представляет собой алгоритм на основе дерева решений. Вот как мы можем определить важность функции с помощью этого классификатора:
- Мы начинаем с обучения Классификатора случайного леса, используя все признаки в наборе данных. Случайный лес — это ансамблевый алгоритм, который объединяет несколько деревьев решений.
- После обучения модели случайного леса мы можем извлечь оценки важности признаков, характерные для этого алгоритма. Оценки важности признаков указывают на относительную важность каждого признака в задаче классификации.
- Затем мы ранжируем признаки на основе их оценки важности. Признаки с более высокими оценками считаются более важными, поскольку они оказывают большее влияние на производительность модели.
Например, после обучения Классификатора случайного леса мы получаем следующие оценки важности признаков:
- Возраст: 0,28
- Пол: 0,12
- Доход: 0,34
- История просмотров: 0,46
Основываясь на этих оценках важности признаков, мы можем ранжировать признаки с точки зрения их важности для прогнозирования покупок клиентов:
- История просмотров: 0,46
- Доход: 0,34
- Возраст: 0,28
- Пол: 0,12
В этом примере история посещенных страниц имеет наивысшую оценку важности, что указывает на то, что она является наиболее влиятельным признаком при прогнозировании покупок клиентов. Следом идет уровень дохода, в то время как возраст и пол имеют более низкие баллы важности. Используя определенные методы алгоритма случайного леса, мы можем получить оценки важности функций на основе количества раз, когда каждая функция используется для разделения данных по разным деревьям в ансамбле. Эта информация позволяет нам определить ключевые функции, которые вносят наибольший вклад в задачу прогнозирования. В свою очередь это помогает в выборе признаков, понимании основных закономерностей в данных и потенциальном улучшении производительности модели.
Экспертные знания и понимание предметной области
В дополнение к количественным методам, экспертные знания и понимание предметной области имеют решающее значение для оценки важности признаков. Эксперты в предметной области всегда могут оценить актуальность и значимость конкретных признаков, основываясь на своих знаниях и опыте. Также важно отметить, что разные методы могут давать несколько разные результаты, а выбор метода может зависеть от конкретных характеристик используемого набора данных и алгоритма машинного обучения. Часто рекомендуется использовать несколько методов, чтобы получить полное представление о важности параметров.
Реализация
Чтобы реализовать взвешивание наших столбцов данных/параметров, мы будем использовать корреляцию. Поскольку мы придерживаемся тех же параметров, что и в предыдущей статье, мы будем сравнивать корреляцию значений набора моноидов с изменениями диапазона ценовых баров, чтобы получить вес каждого столбца данных. Напомним, что каждый столбец данных представляет собой моноид с множеством, где значения множества являются значениями столбца. Поскольку это тест, в начале мы не знаем, следует ли расширить (преобразовать моноидными действиями) наиболее коррелированный столбец или это должен быть столбец данных с наименьшей корреляцией. С этой целью мы добавим дополнительный параметр, который поможет сделать этот выбор для различных тестовых прогонов. Также мы ввели дополнительные глобальные параметры для обслуживания моноидных действий.
//+------------------------------------------------------------------+ //| TrailingCT.mqh | //| Copyright 2009-2013, MetaQuotes Software Corp. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #include <Math\Stat\Math.mqh> #include <Expert\ExpertTrailing.mqh> #include <ct_9.mqh> // wizard description start //+------------------------------------------------------------------+ //| Description of the class | //| Title=Trailing Stop based on 'Category Theory' monoid-action concepts | //| Type=Trailing | //| Name=CategoryTheory | //| ShortName=CT | //| Class=CTrailingCT | //| Page=trailing_ct | //|.... //| Parameter=IndicatorIdentity,int,0, Indicator Identity | //| Parameter=DecisionOperation,int,0, Decision Operation | //| Parameter=DecisionIdentity,int,0, Decision Identity | //| Parameter=CorrelationInverted,bool,false, Correlation Inverted | //+------------------------------------------------------------------+ // wizard description end //+------------------------------------------------------------------+ //| Class CTrailingCT. | //| Appointment: Class traling stops with 'Category Theory' | //| monoid-action concepts. | //| Derives from class CExpertTrailing. | //+------------------------------------------------------------------+ int __LOOKBACKS[8] = {1,2,3,4,5,6,7,8}; ENUM_TIMEFRAMES __TIMEFRAMES[8] = {PERIOD_H1,PERIOD_H2,PERIOD_H3,PERIOD_H4,PERIOD_H6,PERIOD_H8,PERIOD_H12,PERIOD_D1}; ENUM_APPLIED_PRICE __APPLIEDPRICES[4] = { PRICE_MEDIAN, PRICE_TYPICAL, PRICE_OPEN, PRICE_CLOSE }; string __INDICATORS[2] = { "RSI", "BOLLINGER_BANDS" }; string __DECISIONS[2] = { "TREND", "RANGE" }; #define __CORR 5 int __LOOKBACKS_A[10] = {1,2,3,4,5,6,7,8,9,10}; ENUM_TIMEFRAMES __TIMEFRAMES_A[10] = {PERIOD_H1,PERIOD_H2,PERIOD_H3,PERIOD_H4,PERIOD_H6,PERIOD_H8,PERIOD_H12,PERIOD_D1,PERIOD_W1,PERIOD_MN1}; ENUM_APPLIED_PRICE __APPLIEDPRICES_A[5] = { PRICE_MEDIAN, PRICE_TYPICAL, PRICE_OPEN, PRICE_CLOSE, PRICE_WEIGHTED }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ class CTrailingCT : public CExpertTrailing { protected: //--- adjusted parameters double m_step; // trailing step ... // CMonoidAction<double,double> m_lookback_act; CMonoidAction<double,double> m_timeframe_act; CMonoidAction<double,double> m_appliedprice_act; bool m_correlation_inverted; int m_lookback_identity_act; int m_timeframe_identity_act; int m_appliedprice_identity_act; int m_source_size; // Source Size public: //--- methods of setting adjustable parameters ... void CorrelationInverted(bool value) { m_correlation_inverted=value; } ... };
Кроме того, функции Operate_X были сокращены до одной функции под названием Operate. Кроме того, функции Get для столбцов данных были расширены, чтобы приспособить моноидные действия, и была добавлена перегрузка для каждого из них, чтобы помочь с индексированием соответствующих массивов глобальных переменных.
Наш класс трейлинга выглядит следующим образом.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CTrailingCT::Operate(CMonoid<double> &M,EOperations &O,int &OutputIndex) { OutputIndex=-1; // double _values[]; ArrayResize(_values,M.Cardinality());ArrayInitialize(_values,0.0); // ... // if(O==OP_LEAST) { OutputIndex=0; double _least=_values[0]; for(int i=0;i<M.Cardinality();i++) { if(_least>_values[i]){ _least=_values[i]; OutputIndex=i; } } } else if(O==OP_MOST) { OutputIndex=0; double _most=_values[0]; for(int i=0;i<M.Cardinality();i++) { if(_most<_values[i]){ _most=_values[i]; OutputIndex=i; } } } else if(O==OP_CLOSEST) { double _mean=0.0; for(int i=0;i<M.Cardinality();i++) { _mean+=_values[i]; } _mean/=M.Cardinality(); OutputIndex=0; double _closest=fabs(_values[0]-_mean); for(int i=0;i<M.Cardinality();i++) { if(_closest>fabs(_values[i]-_mean)){ _closest=fabs(_values[i]-_mean); OutputIndex=i; } } } else if(O==OP_FURTHEST) { double _mean=0.0; for(int i=0;i<M.Cardinality();i++) { _mean+=_values[i]; } _mean/=M.Cardinality(); OutputIndex=0; double _furthest=fabs(_values[0]-_mean); for(int i=0;i<M.Cardinality();i++) { if(_furthest<fabs(_values[i]-_mean)){ _furthest=fabs(_values[i]-_mean); OutputIndex=i; } } } } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int CTrailingCT::GetLookback(CMonoid<double> &M,int &L[]) { m_close.Refresh(-1); int _x=StartIndex(); ... int _i_out=-1; // Operate(M,m_lookback_operation,_i_out); if(_i_out==-1){ return(4); } return(4*L[_i_out]); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ ENUM_TIMEFRAMES CTrailingCT::GetTimeframe(CMonoid<double> &M, ENUM_TIMEFRAMES &T[]) { ... int _i_out=-1; // Operate(M,m_timeframe_operation,_i_out); if(_i_out==-1){ return(INVALID_HANDLE); } return(T[_i_out]); }
Если мы запустим тесты, как мы делали в предыдущей статье, для EURUSD на часовом таймфрейме с 2022.05.01 по 2023.05.15, используя встроенный в библиотеку класс сигнала RSI, отчет будет выглядеть так.
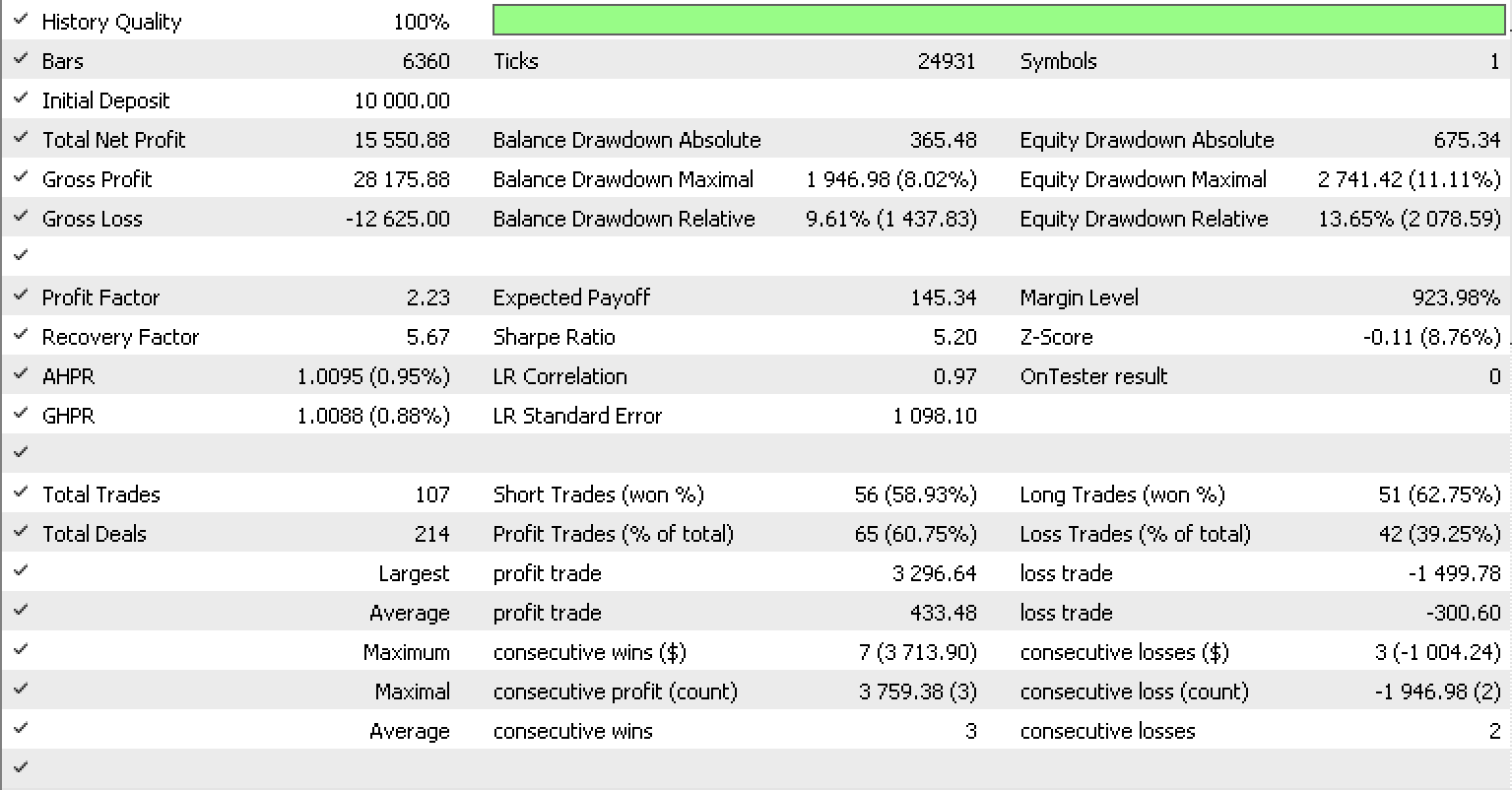
Заключение
Мы рассмотрели, как преобразованные моноиды, также известные как действия моноидов, могут дополнительно улучшить систему трейлинг-стопа, которая делает прогнозы волатильности, чтобы более точно настроить стоп-лосс открытых позиций. Также были рассмотрены различные методы, которые обычно используются для взвешивания функций параметров (столбцы данных в нашем случае), чтобы лучше понять модель, ее чувствительность и какие параметры, если таковые имеются, нуждаются в расширении для повышения точности модели. Спасибо за внимание!
Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/12739
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
