Машинное обучение и Data Science (Часть 8): Кластеризация методом k-средних в MQL5
Данные — как мусор. Нужно понять, что с ними делать, до того, как начнете их собирать.
Обучение без учителя
Это парадигма машинного обучения для задач, имеющих неразмеченные исходные данные. В отличие от методов обучения с учителем, таких как методы регрессии, SVM, деревья решений, нейронные сети и многие другие, обсуждаемые в этой серии статей, где у всегда есть размеченные наборы данных, на которых обучаются наши модели. При обучении без учителя данные никак не размечены, а алгоритм сам должен найти взаимосвязи, закономерности и зависимости, существующие между данными.
Примерами задач обучения без учителя являются кластеризация, уменьшение размерности и оценка плотности.
Кластерный анализ
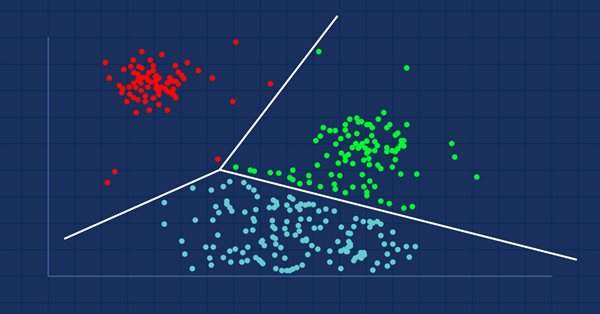
Кластерный анализ — задача упорядочивания множества объектов по группам таким образом, чтобы объекты с одинаковыми атрибутами помещались в одни и те же группы (кластеры).
Например, в магазинах схожие продукты располагаются вместе. Кто-то рассортировал их по группам. Когда данные в наборе не рассортированы по группам, кластерный анализ сделает то же самое — он соберет по группам (кластерам) наиболее схожие значения данных, выделив данные из общего набора.
Кластерный анализ сам по себе не является алгоритмом. Для решения основной задачи можно использовать различные алгоритмы, существенно различающиеся по своему пониманию того, что же представляет собой кластер.
Источник изображения: Википедия
Наиболее широко известны три типа кластеризации:- Исключающая
- Перекрывающая
- Иерархическая
Исключающая кластеризация
Это жесткая кластеризация, в которой точки/элементы данных могут быть отнесены только к одному кластеру, например, кластеризация методом k-средних.
Перекрывающая кластеризация
Это тип мягкой кластеризации, при котором точки/элементы данных могут принадлежать сразу нескольким кластерам. Например, нечеткая кластеризация или метод c-средних.
Иерархическая кластеризация
Этот тип кластеризации стремится построить иерархию кластеров.
Где используются алгоритмы кластеризации?
Например, Amazon и другие онлайн-магазины используют методы кластеризации, чтобы рекомендовать похожие товары, на основе предварительно построенных групп. То же самое делает Netflix, рекомендуя фильмы для просмотра.
По сути, эти алгоритмы используются для идентификации групп схожих объектов или интересов в многомерном наборе данных в разных областях, таких как маркетинг, биомедицина и геопространственная деятельность.
Кластеризация методом k-means
Не путайте этот алгоритм с методом k-ближайших соседей, о котором мы поговорим в следующей статье.
Алгоритм k-средних — это метод векторного квантования, целью которого является разбиение n наблюдений на k кластеров, в которых каждое наблюдение принадлежит кластеру с ближайшим средним/ближайшим центроидом, при этом k < n. Это наиболее широко известный и наиболее часто используемый алгоритм кластеризации. В его основе лежит довольно простая математика. Ниже показаны процессы, задействованные в алгоритме. 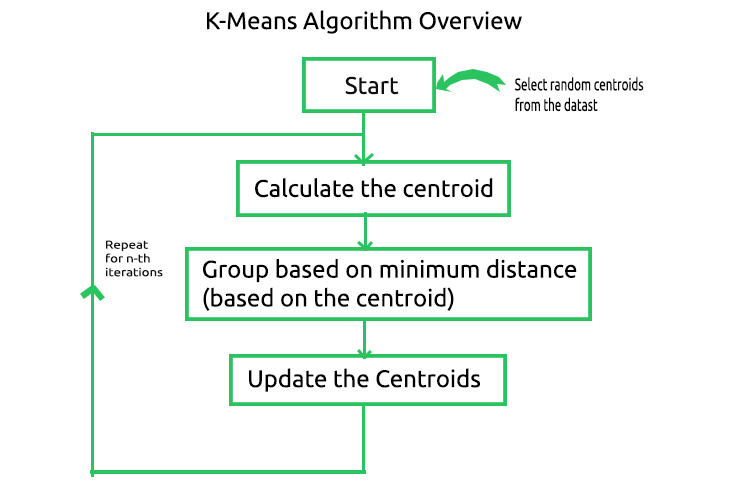
Чтобы понять, как работает этот алгоритм, пройдемся по всем операциям вручную и автоматизируем процесс, написав код в редакторе MetaEditor. Для начала создадим матрицу для хранения центроидов для нашего набора данных в частном разделе библиотеки CKMeans.
class CKMeans { private: ulong n; uint m_clusters; ulong m_cols; matrix InitialCentroids; //Intitial Centroids matrix vector cluster_assign; }
Как всегда, воспользуемся простым набором данных для создания библиотеки, а затем посмотрим, как использовать алгоритм в реальной ситуации на реальном наборе данных.
matrix DMatrix = { {2,10}, {2,5}, {8,4}, {5,8}, {7,5}, {6,4}, {1,2}, {4,9} };
1. Запуск алгоритма и 2. Расчет центроидов
Для запуска алгоритма нам нужны начальные центры для каждого из кластеров, которые будем искать. Поэтому выберем случайные центроиды и сохраним их в матрице InitialCentroid.
m_cols = Matrix.Cols(); n = Matrix.Rows(); //количество элементов | строк матрицы InitialCentroids.Resize(m_clusters,m_cols); vector cluster_comb_v = {}; matrix cluster_comb_m = {}; vector rand_v = {}; for (ulong i=0; i<m_clusters; i++) { rand_v = Matrix.Row(i * m_clusters); InitialCentroids.Row(rand_v,i); } Print("Initial Centroids matrix\n",InitialCentroids);
Получим такие начальные центроиды:
CS 0 06:44:02.152 K-means test (EURUSD,M1) Initial Centroids matrix CS 0 06:44:02.152 K-means test (EURUSD,M1) [[2,10] CS 0 06:44:02.152 K-means test (EURUSD,M1) [5,8] CS 0 06:44:02.152 K-means test (EURUSD,M1) [1,2]]
Мы закончили с начальным, но очень важным этапом. В соответствии с изображением, следующий шаг — вычисление центроидов. Но разве мы только что не нашли центроиды? Да, вначале нам не нужно рассчитывать центроиды, поскольку у нас уже есть начальные значения. Эти центроиды потом обновятся.
3. Группировка по минимальному расстоянию
Теперь будем определять расстояние между каждой точкой в наборе данных от полученных центроидов. Точка данных будет определена к кластеру, к центроиду которого она ближе, чем к другим центроидам.
Чтобы найти расстояние, можно использовать две математические формулы: евклидово расстояние или прямолинейное расстояние.
Евклидово расстояние
Это метод измерения расстояния между двумя точками с помощью Теоремы Пифагора. Формула расчета показана ниже:
Прямолинейное расстояние
Прямолинейное расстояние — это просто сумма разности координат x и y между двумя точками. Формула расчета показана ниже:
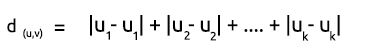
Из-за простоты я предпочитаю использовать прямолинейный метод для нахождения расстояния между центроидами и точками. Построим матрицу в Excel.
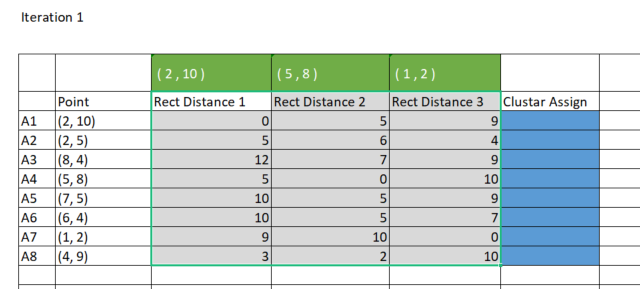
Чтобы сделать это на MQL5, создадим матрицу из 8 рядов по 3 кластера для хранения прямолинейных расстояний, на основе которых будем распределять данные по кластерам. Почему именно три кластера? Я выбрал три кластера при инициализации библиотеки, вы же можете любой количество кластеров в зависимости от целей. Мы подробнее рассмотрим этот момент чуть позже. Ниже показан конструктор библиотеки.
CKMeans::CKMeans(int clusters=3) { m_clusters = clusters; }Далее посмотрим, как создать матрицу для хранения прямолинейных расстояний:
matrix rect_distance = {}; //matrix to store rectilinear distances rect_distance.Reshape(n,m_clusters);
Теперь рассчитаем прямолинейные расстояния и сохраним результаты в матрицу rect_distance, которую только что создали:
vector v_matrix = {}, v_centroid = {}; double output = 0; for (ulong i=0; i<rect_distance.Rows(); i++) for (ulong j=0; j<rect_distance.Cols(); j++) { v_matrix = Matrix.Row(i); v_centroid = InitialCentroids.Row(j); ZeroMemory(output); for (ulong k=0; k<v_matrix.Size(); k++) output += MathAbs(v_matrix[k] - v_centroid[k]); //Прямолинейное расстояние rect_distance[i][j] = output; } Print("Rectilinear distance matrix\n",rect_distance);
Выводимая информация:
CS 0 15:17:52.136 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 15:17:52.136 K-means test (EURUSD,M1) [[0,5,9] CS 0 15:17:52.136 K-means test (EURUSD,M1) [5,6,4] CS 0 15:17:52.136 K-means test (EURUSD,M1) [12,7,9] CS 0 15:17:52.136 K-means test (EURUSD,M1) [5,0,10] CS 0 15:17:52.136 K-means test (EURUSD,M1) [10,5,9] CS 0 15:17:52.136 K-means test (EURUSD,M1) [10,5,7] CS 0 15:17:52.136 K-means test (EURUSD,M1) [9,10,0] CS 0 15:17:52.136 K-means test (EURUSD,M1) [3,2,10]]
Как мы ранее говорили, способ кластеризации k-средних группирует точки данных так, что точка с наименьшим расстоянием от определенного кластера относится к этому кластеру. Каждый столбец в матрице rect_distance представляет кластер, поэтому нужно найти минимальное значение в строке — столбец с минимальным значением назначается этому кластеру. Посмотрите на изображение ниже.
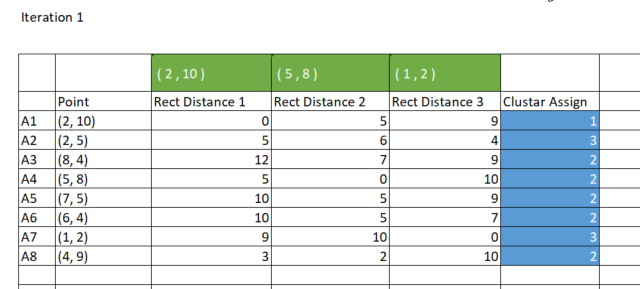
Код, в котором происходит определение нужного кластера:
//--- Определяем принадлежность к кластерам matrix cluster_cent = {}; //центроиды кластеров ulong cluster = 0; for (ulong i=0; i<rect_distance.Rows(); i++) { v_row = rect_distance.Row(i); cluster = v_row.ArgMin(); cluster_assign[i] = (uint)cluster; } Print("Assigned clusters\n",cluster_assign);
Выводимая информация:
CS 0 15:17:52.136 K-means test (EURUSD,M1) Assigned clusters CS 0 15:17:52.136 K-means test (EURUSD,M1) [0,2,1,1,1,1,2,1]
После того, когда мы назначили точки соответствующим кластерам, надо сгруппировать эти точки на основе недавно найденных кластеров. Если выполнить этот процесс в Excel, получатся такие кластеры:
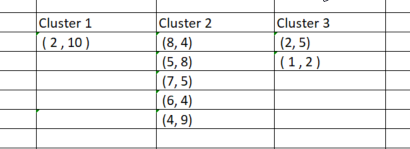
Сгруппировать данные по кластерам вручную довольно просто, однако, когда дело доходит до программирования, все немного сложнее, потому что кластеры всегда будут иметь разные размеры. Поэтому если мы использовать матрицу для хранения кластеров, в столбцах будет разное количество строк. Использовать метод массива неудобно, к тому же их сложно прочитать. CSV-файл для хранения значений не подойдет, потому что нужно динамически записывать столбцы для каждого из кластеров.
У меня появилась идея использовать матрицы кластеров 3 x n для хранения кластеров. Это матрица нулевых значений, размеры которой изначально установлены таким образом, что количество строк равно количеству кластеров, а количество столбцов равно максимальному числу, которое может быть в кластере.
В итоге каждый кластер сохраняется горизонтально в строке матрицы.
Результат будет таким:
CS 0 15:17:52.136 K-means test (EURUSD,M1) clustered Matrix CS 0 15:17:52.136 K-means test (EURUSD,M1) [[2,10,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0] CS 0 15:17:52.136 K-means test (EURUSD,M1) [2,5,1,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0] CS 0 15:17:52.136 K-means test (EURUSD,M1) [8,4,5,8,7,5,6,4,4,9,0,0,0,0,0,0,0,0,0,0,0,0,0,0]]Поскольку эта матрица передается в качестве ссылки в функцию KMeansClustering, где выполняются все операции, ее можно извлечь, а значения можно отфильтровать и убрать нулевые значения после последнего неотрицательного нулевого значения.
void CKMeans::KMeansClustering(const matrix &Matrix, matrix &clustered_matrix)
4. Обновление центроидов
Чтобы определить новые центроиды каждого кластера, нужно найти среднее значение всех отдельных элементов в кластере. Ниже показан код, где этой выполняется:
vector x_y_z = {0,0}; ZeroMemory(rand_v); for (ulong k=0; k<cluster_cent.Cols(); k++) { x_y_z.Resize(cluster_cent.Cols()); rand_v = cluster_cent.Col(k); x_y_z[k] = rand_v.Mean(); } InitialCentroids.Row(x_y_z, i); if (index >= n_each_cluster.Size()) break; } Print("New Centroids\n",InitialCentroids,"\nclustered Matrix\n",clustered_matrix);
Результат будет таким:
CS 0 15:17:52.136 K-means test (EURUSD,M1) New Centroids CS 0 15:17:52.136 K-means test (EURUSD,M1) [[2,10] CS 0 15:17:52.136 K-means test (EURUSD,M1) [1.5,3.5] CS 0 15:17:52.136 K-means test (EURUSD,M1) [6,6]]
Мы рассмотрели процесс одной итерации. Теперь нудно повторять итерации от второго шага до последнего до тех пор, пока данные не будут сгруппированы по соответствующим кластерам. Этого можно сделать двумя способами: кто-то выстраивает логику так, что процесс остановится, когда новые центроиды для кластеров перестанут меняться и оптимальные значения для всех кластеров будут найдены, а кто-то просто устанавливает ограниченное количество итераций в алгоритме. Думаю, проблема с первым способом заключается в том, что нам понадобится бесконечный цикл, который будет контролировать оператор if, и в итоге нам нужно получить break. Думаю, разумнее ограничить алгоритм по количеству итераций.
Ниже приведена полная функция алгоритма кластеризации k-средних с добавлением итераций:
void CKMeans::KMeansClustering(const matrix &Matrix, matrix &clustered_matrix,int iterations = 10) { m_cols = Matrix.Cols(); n = Matrix.Rows(); //количество элементов | строк матрицы InitialCentroids.Resize(m_clusters,m_cols); cluster_assign.Resize(n); clustered_matrix.Resize(m_clusters, m_clusters*n); clustered_matrix.Fill(NULL); vector cluster_comb_v = {}; matrix cluster_comb_m = {}; vector rand_v = {}; for (ulong i=0; i<m_clusters; i++) { rand_v = Matrix.Row(i * m_clusters); InitialCentroids.Row(rand_v,i); } Print("Initial Centroids matrix\n",InitialCentroids); //--- vector v_row; vector n_each_cluster; //Содержимое каждого кластера matrix rect_distance = {}; //matrix to store rectilinear distances rect_distance.Reshape(n,m_clusters); vector v_matrix = {}, v_centroid = {}; double output = 0; //--- for (int iter=0; iter<iterations; iter++) { printf("\n<<<<< %d >>>>>\n",iter ); for (ulong i=0; i<rect_distance.Rows(); i++) for (ulong j=0; j<rect_distance.Cols(); j++) { v_matrix = Matrix.Row(i); v_centroid = InitialCentroids.Row(j); ZeroMemory(output); for (ulong k=0; k<v_matrix.Size(); k++) output += MathAbs(v_matrix[k] - v_centroid[k]); //Прямолинейное расстояние rect_distance[i][j] = output; } Print("Rectilinear distance matrix\n",rect_distance); //--- Определяем принадлежность к кластерам matrix cluster_cent = {}; //центроиды кластеров ulong cluster = 0; for (ulong i=0; i<rect_distance.Rows(); i++) { v_row = rect_distance.Row(i); cluster = v_row.ArgMin(); cluster_assign[i] = (uint)cluster; } Print("Assigned clusters\n",cluster_assign); //--- Объединяем кластеры n_each_cluster.Resize(m_clusters); for (ulong i=0, index =0, sum_count = 0; i<cluster_assign.Size(); i++) { for (ulong j=0, count = 0; j<cluster_assign.Size(); j++) { //printf("cluster_assign[%d] cluster_assign[%d]",i,j); if (cluster_assign[i] == cluster_assign[j]) { count++; n_each_cluster[index] = (uint)count; cluster_comb_m.Resize(count, m_cols); cluster_comb_m.Row(Matrix.Row(j) , count-1); cluster_cent.Resize(count, m_cols); // Новые центроиды cluster_cent.Row(Matrix.Row(j),count-1); sum_count++; } else continue; } //--- MatrixToVector(cluster_comb_m, cluster_comb_v); // расчет для новых кластеров и обновление старых if (iter == iterations-1) clustered_matrix.Row(cluster_comb_v, index); //--- index++; //--- vector x_y_z = {0,0}; ZeroMemory(rand_v); for (ulong k=0; k<cluster_cent.Cols(); k++) { x_y_z.Resize(cluster_cent.Cols()); rand_v = cluster_cent.Col(k); x_y_z[k] = rand_v.Mean(); } InitialCentroids.Row(x_y_z, i); if (index >= n_each_cluster.Size()) break; } Print("New Centroids\n",InitialCentroids);//,"\nclustered Matrix\n",clustered_matrix); } //конец итераций } //+------------------------------------------------------------------+
Вот как выглядит журнал алгоритма после 10 итераций:
CS 0 20:40:05.438 K-means test (EURUSD,M1) <<<<< 0 >>>>> CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 20:40:05.438 K-means test (EURUSD,M1) [[0,5,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5,6,4] CS 0 20:40:05.438 K-means test (EURUSD,M1) [12,7,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5,0,10] CS 0 20:40:05.438 K-means test (EURUSD,M1) [10,5,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [10,5,7] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9,10,0] CS 0 20:40:05.438 K-means test (EURUSD,M1) [3,2,10]] CS 0 20:40:05.438 K-means test (EURUSD,M1) Assigned clusters CS 0 20:40:05.438 K-means test (EURUSD,M1) [0,2,1,1,1,1,2,1] CS 0 20:40:05.438 K-means test (EURUSD,M1) New Centroids CS 0 20:40:05.438 K-means test (EURUSD,M1) [[2,10] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,3.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [6,6]] CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) <<<<< 1 >>>>> CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 20:40:05.438 K-means test (EURUSD,M1) [[0,7,8] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5,2,5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [12,7,4] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5,8,3] CS 0 20:40:05.438 K-means test (EURUSD,M1) [10,7,2] CS 0 20:40:05.438 K-means test (EURUSD,M1) [10,5,2] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9,2,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [3,8,5]] CS 0 20:40:05.438 K-means test (EURUSD,M1) Assigned clusters CS 0 20:40:05.438 K-means test (EURUSD,M1) [0,1,2,2,2,2,1,0] CS 0 20:40:05.438 K-means test (EURUSD,M1) New Centroids CS 0 20:40:05.438 K-means test (EURUSD,M1) [[3,9.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,3.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [6.5,5.25]] CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) <<<<< 2 >>>>> CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 20:40:05.438 K-means test (EURUSD,M1) [[1.5,7,9.25] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5.5,2,4.75] CS 0 20:40:05.438 K-means test (EURUSD,M1) [10.5,7,2.75] CS 0 20:40:05.438 K-means test (EURUSD,M1) [3.5,8,4.25] CS 0 20:40:05.438 K-means test (EURUSD,M1) [8.5,7,0.75] CS 0 20:40:05.438 K-means test (EURUSD,M1) [8.5,5,1.75] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9.5,2,8.75] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,8,6.25]] CS 0 20:40:05.438 K-means test (EURUSD,M1) Assigned clusters CS 0 20:40:05.438 K-means test (EURUSD,M1) [0,1,2,0,2,2,1,0] CS 0 20:40:05.438 K-means test (EURUSD,M1) New Centroids CS 0 20:40:05.438 K-means test (EURUSD,M1) [[3.666666666666667,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,3.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7,4.333333333333333]] CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) <<<<< 3 >>>>> CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 20:40:05.438 K-means test (EURUSD,M1) [[2.666666666666667,7,10.66666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5.666666666666666,2,5.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9.333333333333334,7,1.333333333333333] CS 0 20:40:05.438 K-means test (EURUSD,M1) [2.333333333333333,8,5.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7.333333333333334,7,0.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7.333333333333334,5,1.333333333333333] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9.666666666666666,2,8.333333333333332] CS 0 20:40:05.438 K-means test (EURUSD,M1) [0.3333333333333335,8,7.666666666666667]] CS 0 20:40:05.438 K-means test (EURUSD,M1) Assigned clusters CS 0 20:40:05.438 K-means test (EURUSD,M1) [0,1,2,0,2,2,1,0] CS 0 20:40:05.438 K-means test (EURUSD,M1) New Centroids CS 0 20:40:05.438 K-means test (EURUSD,M1) [[3.666666666666667,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,3.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7,4.333333333333333]] CS 0 20:40:05.438 K-means test (EURUSD,M1) ..... ..... ..... ..... CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) <<<<< 9 >>>>> CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 20:40:05.438 K-means test (EURUSD,M1) [[2.666666666666667,7,10.66666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5.666666666666666,2,5.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9.333333333333334,7,1.333333333333333] CS 0 20:40:05.438 K-means test (EURUSD,M1) [2.333333333333333,8,5.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7.333333333333334,7,0.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7.333333333333334,5,1.333333333333333] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9.666666666666666,2,8.333333333333332] CS 0 20:40:05.438 K-means test (EURUSD,M1) [0.3333333333333335,8,7.666666666666667]] CS 0 20:40:05.438 K-means test (EURUSD,M1) Assigned clusters CS 0 20:40:05.438 K-means test (EURUSD,M1) [0,1,2,0,2,2,1,0] CS 0 20:40:05.438 K-means test (EURUSD,M1) New Centroids CS 0 20:40:05.438 K-means test (EURUSD,M1) [[3.666666666666667,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,3.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7,4.333333333333333]]
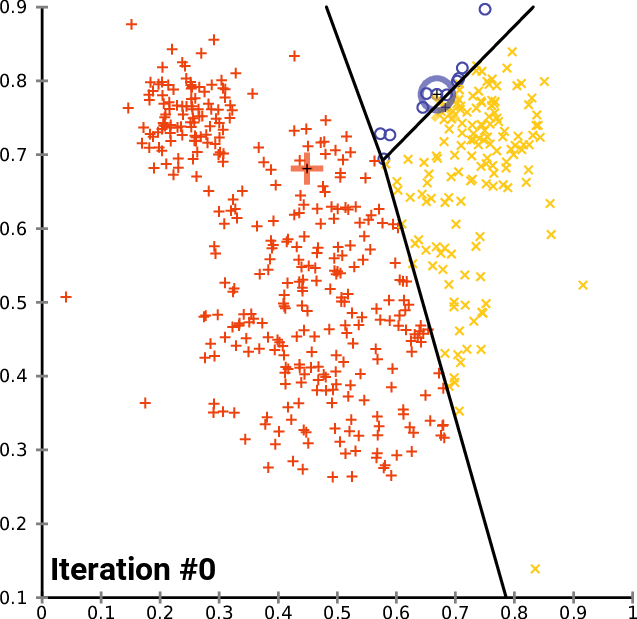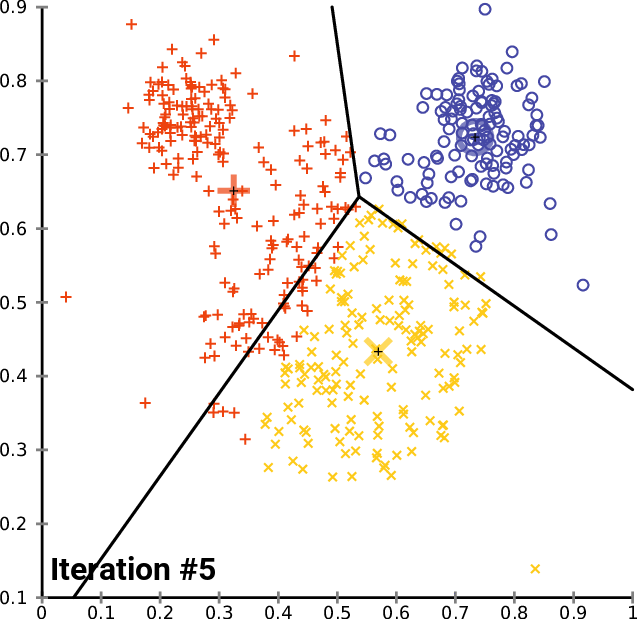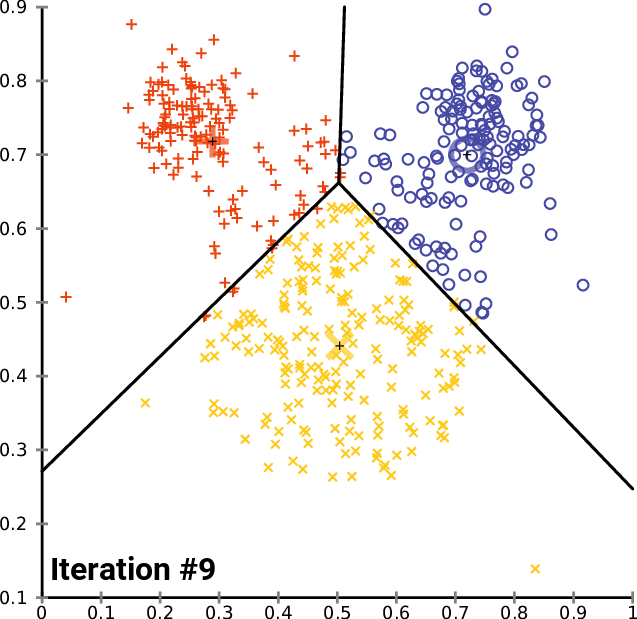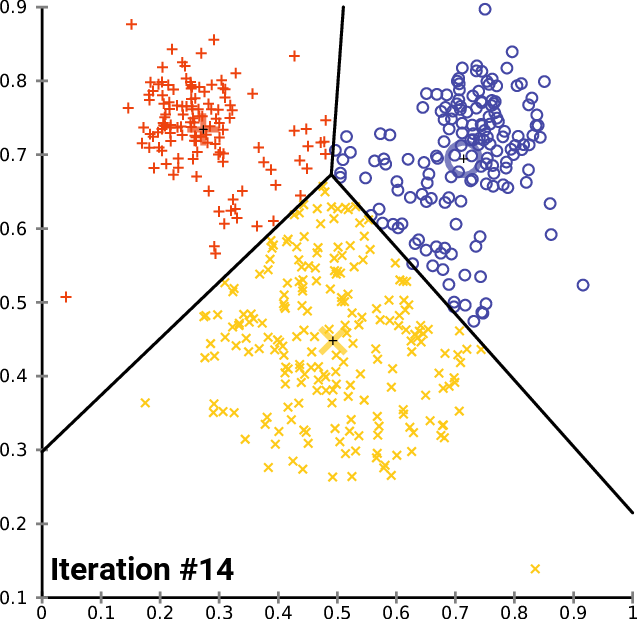
Уже после двух итераций алгоритм сошелся и определил оптимальные значения для центроидов. Это подводит нас к вопросу о том, какое количество итераций является оптимальным для алгоритма такого типа. В отличие от градиентного спуска и других алгоритмов, кластеризация методом k-средних не требует большого количества итераций для достижения оптимальных значений, часто хватает от 5 до 10 итераций для полной кластеризации простого набора данных.
Внутри скрипта K-Means Test
В основной функции тестового скрипта мы инициализируем библиотеку, вызываем функцию k-MeansClustering, наносим кластеры на одну ось и в конце удаляем объект библиотеки. void OnStart() { //--- matrix DMatrix = { {2,10}, {2,5}, {8,4}, {5,8}, {7,5}, {6,4}, {1,2}, {4,9} }; int clusters =3; matrix clusterd_mat; clustering = new CKMeans(clusters); clustering.KMeansClustering(DMatrix,clusterd_mat); ObjectsDeleteAll(0,0); ScatterPlotsMatrix("graph",clusterd_mat,"cluster 1"); delete(clustering); }
Ниже приведена диаграмма кластеров:
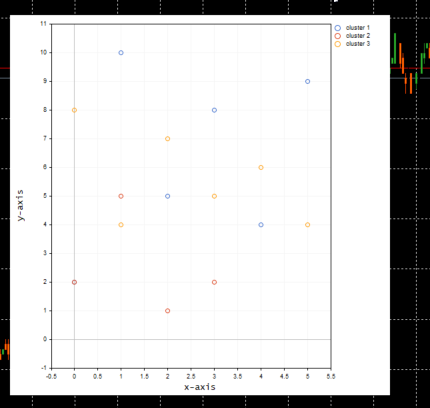
Перед тем как наносить значения на график, внутри функции ScatterPlotsMatrix() была вызвана функция для фильтрации нулевых значений. Все значения, лежащие точно на линии оси x или y на графике, следует игнорировать.
vectortoArray(x,x_arr); FilterZeros(x_arr); graph.CurveAdd(x_arr,CURVE_POINTS," cluster "+string(i+1));
Каково правильное количество k-кластеров?
Мы разобрали, как работает алгоритм, но нельзя же просто вызвать основную функцию кластеризации k-средних и указать количество кластеров. Откуда нам знать, что выбранное количество кластеров является оптимальным, ведь инициализация влияет на весь алгоритм. Чтобы понять это, давайте посмотрим на метод, который называется Методом локтя.
Метод локтя
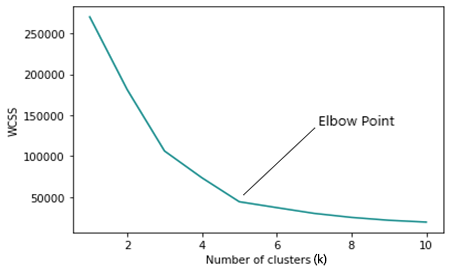
Метод локтя используется для нахождения оптимального количества кластеров при кластеризации методом k-средних. Метод локтя строит график функции стоимости, полученной с помощью различных значений кластеров (k).
По мере увеличения числа k функция стоимости уменьшается, это можно определить как переоснащение.
Если посмотреть на график метода локтя, можно увидеть точку, в которой происходит быстрое изменение направления графика, после чего график начнет двигаться параллельно оси X.
WCSS
Внутрикластерная сумма квадратов остатков (WCSS) представляет собой сумму квадратов расстояний между каждой точкой и центроидом в кластере.
Формула расчета:
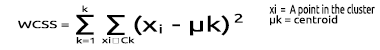
Поскольку метод локтя является методом оптимизации для кластеризации k-средних, каждая его итерация требует вызова функции кластеризации k-средних.
Поэтому, чтобы запустить метод локтя и получить результаты, нужно изменить кое-что в основной функции для кластеризации методом k-средних. Первое, что нам нужно изменить, — это получение центроидов, потому что, когда выбранные кластеры становятся равными количеству строк в матрице или близки к этому значению, метод случайного выбора начального центроида перестает работать.
for (ulong i=0; i<m_clusters; i++) { rand_v = Matrix.Row(i); InitialCentroids.Row(rand_v,i); }
Также нужно изменить логику, чтобы максимальное количество начальных кластеров не превышало количество выборок n, которые находятся в наборе данных. Как мы знаем из определения кластеризации k-средних, k < n.
void CKMeans::ElbowMethod(const int initial_k=1, int total_k=10, bool showPlot = true) { matrix clustered_mat, _centroids = {}; if (total_k > (int)n) total_k = (int)n; //>>k всегда должно быть меньше n
Код Метода локтя целиком показан ниже;
void CKMeans::ElbowMethod(const int initial_k=1, int total_k=10, bool showPlot = true) { matrix clustered_mat, _centroids = {}; if (total_k > (int)n) total_k = (int)n; //k всегда должно быть меньше n vector centroid_v={}, x_y_z={}; vector short_v = {}; //вектор для каждой точки vector minus_v = {}; //вектор для хранения результата операции double wcss = 0; double WCSS[]; ArrayResize(WCSS,total_k); double kArray[]; ArrayResize(kArray,total_k); for (int k=initial_k, count_k=0; k<ArraySize(WCSS)+initial_k; k++, count_k++) { wcss = 0; m_clusters = k; KMeansClustering(clustered_mat,_centroids,1); for (ulong i=0; i<_centroids.Rows(); i++) { centroid_v = _centroids.Row(i); x_y_z = clustered_mat.Row(i); FilterZero(x_y_z); for (ulong j=0; j<x_y_z.Size()/m_cols; j++) { VectorCopy(x_y_z,short_v,uint(j*m_cols),(uint)m_cols); //--- WCSS (within cluster sum of squared residuals) minus_v = (short_v - centroid_v); minus_v = MathPow(minus_v,2); wcss += minus_v.Sum(); } } WCSS[count_k] = wcss; kArray[count_k] = k; } Print("WCSS"); ArrayPrint(WCSS); Print("kArray"); ArrayPrint(kArray); //--- Наносим Метод локтя на график if (showPlot) { ObjectDelete(0,"elbow"); ScatterCurvePlots("elbow",kArray,WCSS,WCSS,"Elbow line","k","WCSS"); } }
Вот что выводит этот блок кода:
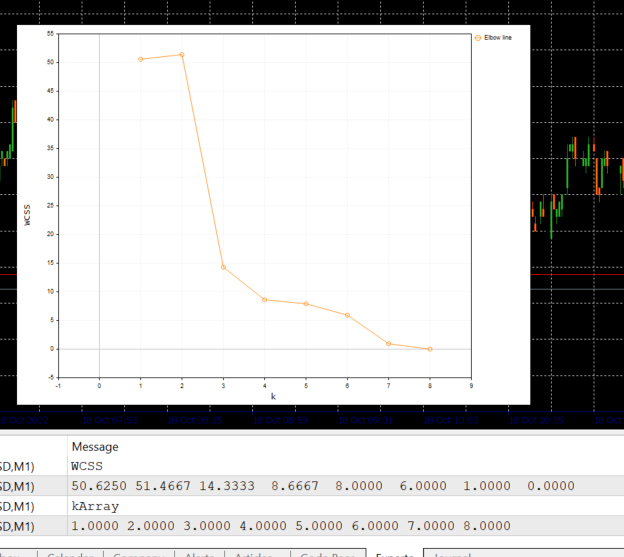
Глядя на график Elbow, становится ясно, что оптимальное количество кластеров равно 3. Значения WCSS резко упали в этот момент — с 51,4667 до 14,333.
Итак, у нас есть все необходимое для реализации алгоритма кластеризации k-средних в MQL5, поэтому давайте посмотрим, как можно реализовать этот алгоритм в сфере трейдинга.
Посмотрим, как можно сгруппировать одни и те же данные рыночных цен по нескольким кластерам:
matrix DMatrix = {}; DMatrix.Resize(bars, 1); //столбцы определяют размер набора данных, 1D не отобразится как надо vector column_v = {}; column_v.CopyRates(symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,1,bars); DMatrix.Col(column_v,0);
Мы только что заменили матрицу матрицей nx1 для значений рыночной цены. На этот раз мы использовали одномерную матрицу. С учетом кода алгоритма мы не получим хорошую визуализацию и кластеризацию одномерных матриц, например, посмотрите на результат всей операции кластеризации для символа NASDAQ на 20 барах на графиках ниже.
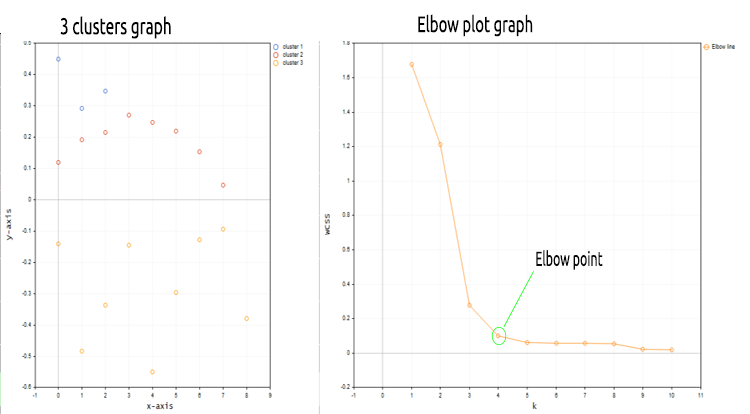
Согласно по методу локтя на графике выше здесь подходит количество кластеров равное четырем. Кластеры выглядят намного лучше, когда нанесены на график.
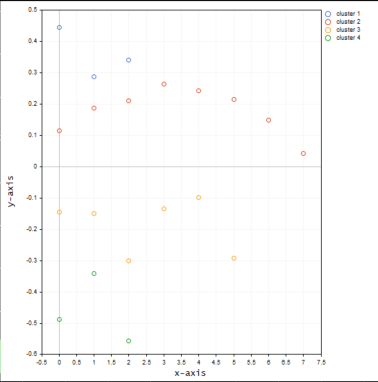
Теперь поместим значения того же символа в трехмерную матрицу и посмотрим, что произойдет с кластерами.
matrix DMatrix = {}; DMatrix.Resize(bars, 3); //столбцы определяют размер набора данных, 1D не отобразится как надо vector column_v = {}; ulong start = 0; for (ulong i=0; i<2; i++) { column_v.CopyRates(symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,start,bars); DMatrix.Col(column_v,i); start += bars; }
Ниже показано, как кластеры будут выглядеть на графике:
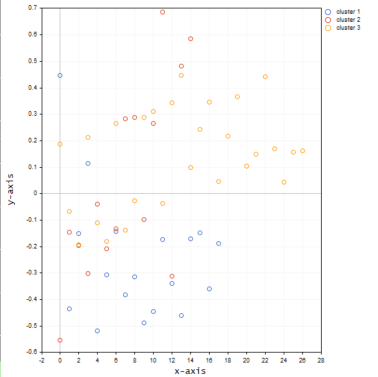
Похоже, что трехмерная матрица при кластеризации на одной оси дает много выбросов в кластерах.
Можно подумать об использовании более чем одномерной матрицы для группировки разных выборок, значения которых лежат, например, на разных уровнях/шкалах. Можно попробовать значения индикатора RSI или скользящей средней, но идеальный вариант — всегда включать эти значения в одномерную матрицу, то есть в один столбец матрицы. Вы можете поэкспериментировать и поделиться результатами в разделе обсуждения.
Прежде чем показывать диаграммы, я забыл упомянуть, что нормализовал значения цен NASDAQ, используя технику Mean-Normalization.
MeanNormalization(DMatrix);
Так данные хорошо распределены по графику. Полный код:
void MeanNormalization(matrix &mat) { vector v = {}; for (ulong i=0; i<mat.Cols(); i++) { v = mat.Col(i); MeanNormalization(v); mat.Col(v,i); } } //+------------------------------------------------------------------+ void MeanNormalization(vector &v) { double mean = v.Mean(), max = v.Max(), min = v.Min(); for (ulong i=0; i<v.Size(); i++) v[i] = (v[i] - mean) / (max - min); }
Заключительные мысли
Кластеризация методом k-средних — очень полезный алгоритм, который должен быть в наборе инструментов каждого трейдера и любого, кто работает с данными. Что надо помнить, так это то, что на алгоритм сильно влияют инициализаторы. Если поискать оптимальный алгоритм с помощью метода локтя, начав с 2 кластеров, можно получить оптимальное количество кластеров, отличное от изначально выбранного количества 4. Кроме того, большое значение имеют начальные центроиды, поэтому мне пришлось добавить входные данные в основную функцию кластеризации. Это позволяет понять, нужно ли выбирать начальные центроиды случайным образом или вместо этого следует выбирать первые три строки матрицы.void CKMeans::KMeansClustering(matrix &clustered_matrix,matrix ¢roids,int iterations = 1,bool rand_cluster =false)
Аргумент функции rand_cluster для случайного выбора центроида установлен в значение false по умолчанию на случай вызова функции кластеризации в функции метода локтя. Это связано с тем, что выбор случайных центроидов при поиске оптимальных кластеров не работает. Он работает, когда известно количество кластеров.
С наилучшими пожеланиями.
MQL5-файлы кодов из статьи прикреплены ниже. В zip-файлах код немного изменен код — некоторые строки удалены для повышения производительности, другие добавлены просто, чтобы легче было понять, что происходит внутри процесса.
Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/11615
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Горная карта, или График "Айсберг"
Горная карта, или График "Айсберг"
 Разработка торговой системы по индикатору фракталов Fractals
Разработка торговой системы по индикатору фракталов Fractals
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
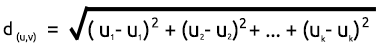
Прежде всего, я хотел бы поблагодарить автора за то, что он поделился этой статьей. Надеюсь, что автор, помимо объяснения теорий, сможет привести примеры использования кластеризации K-mean в реальной торговле, если соответствующих примеров нет, то эта или другие статьи автора практически неотличимы от учебников. Машинное обучение используется во многих областях.
Было бы неплохо, если бы автор смог лучше проиллюстрировать эти теории машинного обучения на примерах торговых механизмов МТ5. Еще раз спасибо, что поделились.
Новая статья Наука о данных и машинное обучение (часть 08): Кластеризация K-Means на простом MQL5 опубликована:
Автор: Omega J Msigwa
Привет Omega J Msigwa, спасибо за вашу очень полезную статью.
Я что-то пропустил или в приведенном выше коде вы имеете в виду DMatrix?
Здравствуйте, Omega J Msigwa, спасибо за вашу очень полезную статью.
Я что-то упустил, или в приведенном выше коде вы имеете в виду DMatrix?
Я имею в виду Matrix, как объясняется в статье, поскольку этот код находится под функцией