MetaTrader 5 / Торговые системы
English 中文 Español Deutsch 日本語 Português
preview
Машинное обучение и Data Science. Нейросети (Часть 02): архитектура нейронных сетей с прямой связью

Машинное обучение и Data Science. Нейросети (Часть 02): архитектура нейронных сетей с прямой связью

MetaTrader 5 — Торговые системы | 4 ноября 2022, 15:32
1 828 4
Omega J Msigwa
Omega J Msigwa

«Я не утверждаю, что нейронные сети — это просто. Нужно быть экспертом, чтобы заставить их работать. Но у этого опыта гораздо более широкое применение. Те усилия, которые раньше уходили на разработку функций, теперь направлены на разработку архитектуры, функции потерь и схемы оптимизации. Ручной труд переходит на более высокий уровень абстракции».

--Стефано Соатто


Введение

В предыдущей статье мы обсуждали основы нейросетей и построили очень простой и статичный многослойный перцептрон (MLP). При этом прекрасно понимаем, что в реальных приложениях навряд ли придется использовать два элементарных входных параметра и два узла скрытых слоев, а именно с этим мы работали в прошлый раз.

Для конкретных задач могут понадобиться сети с 10 узлами во входном слое, 13 узлами/нейронами в скрытом слое и, скажем, четырьмя в выходном слое. В таком случае всю нейронную сеть придется настраивать заново. 

А значит, нужно динамичное решение. Динамический код, параметры которого можно менять и оптимизировать без ущерба для программы. Если для построения нейросетей вы используете библиотеку питон keras, работы по настройке и сборке даже самых сложных архитектур будет меньше. Именно этого я хочу добиться средствами MQL5.

В статье "Линейная регрессия (часть 3)", которую я обязательно рекомендую прочитать, я представил матрично-векторную форму, которая позволяет получить гибкие модели с неограниченным количеством входных данных.

Матрицы в помощь

Если вдруг понадобиться изменить параметры модели со статичным кодом, оптимизация может занять очень много времени — это головная боль, боль в спине и прочие неприятности.

Изображение нейронной сети


Если поближе рассмотреть операции, лежащие в основе нейронной сети, можно заметить, что каждый вход умножается на присвоенный ему весовой коэффициент, а полученный результат добавляется к смещению. С этим хорошо справляются матричные операции.

Умножение матрицы в нейронной сети

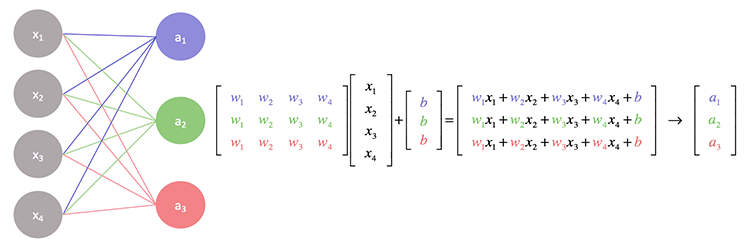
По сути, мы находим скалярное произведение входных данных и матрицы весовых коэффициентов, а затем прибавляем его к смещению.

Чтобы построить гибкую нейронную сеть, попробуем поработать с нечетной архитектурой из двух узлов во входном слое, четырех — в первом скрытом слое, шести — во втором и одного — в третьем слое, и с одним узлом в выходном слое.

Архитектура нейронной сети

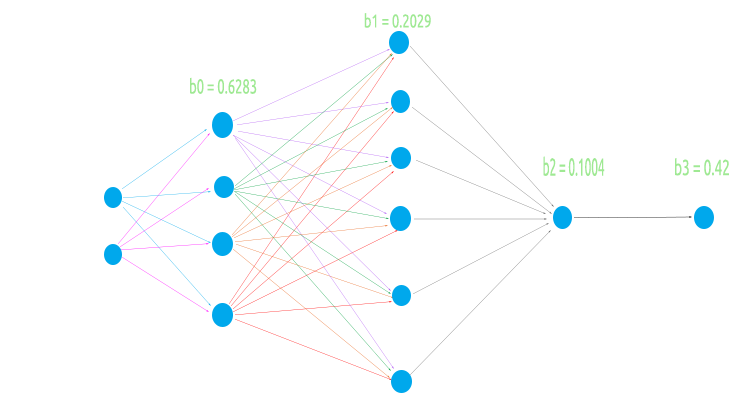
Это позволит проверить, будет ли матричная логика работать во всех нужных сценариях:

  • Когда предыдущий (входной) слой имеет меньше узлов, чем следующий (выходной слой)
  • Когда предыдущий (входной) слой имеет больше узлов, чем следующий
  • Когда имеется равное количество узлов во входном и выходном слое

Прежде чем перейти к написанию кода матричных операций и вычислению значений, выполним необходимые базовые вещи, без которых работа будет невозможна.

Генерация случайных весов и значений смещения

    //Generate random bias
    for(int i=0; i<m_hiddenLayers; i++)         bias[i] = MathRandom(0,1);
    
    //generate weights 
    int sum_weights=0, L_inputs=inputs;
    double L_weights[];
    
    for (int i=0; i<m_hiddenLayers; i++)
      {
         sum_weights += L_inputs * m_hiddenLayerNodes[i];
         ArrayResize(Weights,sum_weights);
         L_inputs = m_hiddenLayerNodes[i];         
      }
    
    for (int j=0; j<sum_weights; j++) Weights[j] = MathRandom(0,1);

С этой операцией мы уже работали в предыдущей части. Следует отметить, что эти значения весовых коэффициентов и смещения нужно сгенерировать один раз и использовать в цикле эпох.


Что такое эпоха?

Эпоха — это полный проход всех данных в нейронной сети. В случае feed-forward — это полный прямой проход всех входных данных, в back propagation — полный прямой и обратный проход. Простыми словами, это когда нейросеть увидела все данные.

В отличие от многослойного перцептрона, о котором мы говорили в предыдущей статье, найдем реализацию, которая учитывает функцию активации в выходном слое. Те, кто использует Keras, наверняка знакомы с эти. Ведь по факту у нас может быть любая функция активации в скрытом слое и приводящая к результату в выходном слое.

CNeuralNets(fx HActivationFx,fx OActivationFx,int &NodesHL[],int outputs=NULL, bool SoftMax=false);

Обратите внимание на входные параметры: HActivationFx — функция активации в скрытых слоях, OActivationFx — функция активации в выходном слое, NodesHL[] — количество узлов в скрытом слое. Если в массиве, скажем, 3 элемента, это означает, что у вас будет 3 скрытых слоя, и количество узлов в этих слоях будет определяться элементами, присутствующими внутри массива. Посмотрим на код ниже.

int hlnodes[3] = {4,6,1};
int outputs = 1;
     
neuralnet = new CNeuralNets(SIGMOID,RELU,hlnodes,outputs);

Это первая архитектура, показанная выше. Параметр outputs необязательный. Если оставить в значении NULL, следующая конфигурация будет применена к выходному слою:

if (m_outputLayers == NULL)
{
  if (A_fx == RELU)     m_outputLayers = 1;
  else                  m_outputLayers = ArraySize(MLPInputs);
}

Если в скрытом слое выбрать функцию активации RELU, в выходном слое будет один узел. В противном случае количество выходов в конечном слое будет равно количеству входов в первом слое. Если в скрытом слое используется функция активации отличная от RELU, скорее всего это классификационная нейронная сеть, поэтому в таком случае выходной слой по умолчанию будет равен количеству столбцов. Вообще-то это не совсем правильно — выходы должны быть по количеству целевых функций из набора данных при работе с задачами классификации. В дальнейших версиях я найду способ изменить это поведение, а пока количество выходных нейронов надо будет выбирать вручную.

Теперь вызовем полную функцию многослойного перцептрона (MLP) и посмотрим результат. Затем я объясню, что для этого было сделано.

LI      0       10:10:29.995    NNTestScript (#NQ100,H1)        CNeural Nets Initialized activation = SIGMOID UseSoftMax = No
IF      0       10:10:29.995    NNTestScript (#NQ100,H1)        biases
EI      0       10:10:29.995    NNTestScript (#NQ100,H1)        0.6283 0.2029 0.1004
IQ      0       10:10:29.995    NNTestScript (#NQ100,H1)        Hidden Layer 1 | Nodes 4 | Bias 0.6283
NS      0       10:10:29.995    NNTestScript (#NQ100,H1)        Inputs 2 Weights 8
JD      0       10:10:29.995    NNTestScript (#NQ100,H1)        4.00000 6.00000
FL      0       10:10:29.995    NNTestScript (#NQ100,H1)        0.954 0.026 0.599 0.952 0.864 0.161 0.818 0.765
EJ      0       10:10:29.995    NNTestScript (#NQ100,H1)        Arr size A 2
EM      0       10:10:29.995    NNTestScript (#NQ100,H1)        AxBMatrix[0] = 3.81519 X A[0] = 4.000 B[0] = 0.954
NI      0       10:10:29.995    NNTestScript (#NQ100,H1)        AxBMatrix[0] = 9.00110 X A[1] = 6.000 B[4] = 0.864
IE      0       10:10:29.995    NNTestScript (#NQ100,H1)        AxBMatrix[1] = 0.10486 X A[0] = 4.000 B[1] = 0.026
DQ      0       10:10:29.995    NNTestScript (#NQ100,H1)        AxBMatrix[1] = 1.06927 X A[1] = 6.000 B[5] = 0.161
MM      0       10:10:29.995    NNTestScript (#NQ100,H1)        AxBMatrix[2] = 2.39417 X A[0] = 4.000 B[2] = 0.599
JI      0       10:10:29.995    NNTestScript (#NQ100,H1)        AxBMatrix[2] = 7.29974 X A[1] = 6.000 B[6] = 0.818
GE      0       10:10:29.995    NNTestScript (#NQ100,H1)        AxBMatrix[3] = 3.80725 X A[0] = 4.000 B[3] = 0.952
KQ      0       10:10:29.995    NNTestScript (#NQ100,H1)        AxBMatrix[3] = 8.39569 X A[1] = 6.000 B[7] = 0.765
DL      0       10:10:29.995    NNTestScript (#NQ100,H1)        before rows 1 cols 4
GI      0       10:10:29.995    NNTestScript (#NQ100,H1)        IxWMatrix
QM      0       10:10:29.995    NNTestScript (#NQ100,H1)        Matrix
CH      0       10:10:29.995    NNTestScript (#NQ100,H1)        [ 
HK      0       10:10:29.995    NNTestScript (#NQ100,H1)        9.00110 1.06927 7.29974 8.39569
OO      0       10:10:29.995    NNTestScript (#NQ100,H1)        ] 
CH      0       10:10:29.995    NNTestScript (#NQ100,H1)        rows = 1 cols = 4

<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< End of the first Hidden Layer >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

NS      0       10:10:29.995    NNTestScript (#NQ100,H1)        Hidden Layer 2 | Nodes 6 | Bias 0.2029
HF      0       10:10:29.995    NNTestScript (#NQ100,H1)        Inputs 4 Weights 24
LR      0       10:10:29.995    NNTestScript (#NQ100,H1)        0.99993 0.84522 0.99964 0.99988
EL      0       10:10:29.996    NNTestScript (#NQ100,H1)        0.002 0.061 0.056 0.600 0.737 0.454 0.113 0.622 0.387 0.456 0.938 0.587 0.379 0.207 0.356 0.784 0.046 0.597 0.511 0.838 0.848 0.748 0.047 0.282
FF      0       10:10:29.996    NNTestScript (#NQ100,H1)        Arr size A 4
EI      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[0] = 0.00168 X A[0] = 1.000 B[0] = 0.002
QE      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[0] = 0.09745 X A[1] = 0.845 B[6] = 0.113
MR      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[0] = 0.47622 X A[2] = 1.000 B[12] = 0.379
NN      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[0] = 0.98699 X A[3] = 1.000 B[18] = 0.511
MI      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[1] = 0.06109 X A[0] = 1.000 B[1] = 0.061
ME      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[1] = 0.58690 X A[1] = 0.845 B[7] = 0.622
PR      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[1] = 0.79347 X A[2] = 1.000 B[13] = 0.207
KN      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[1] = 1.63147 X A[3] = 1.000 B[19] = 0.838
GI      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[2] = 0.05603 X A[0] = 1.000 B[2] = 0.056
GE      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[2] = 0.38353 X A[1] = 0.845 B[8] = 0.387
GS      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[2] = 0.73961 X A[2] = 1.000 B[14] = 0.356
CO      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[2] = 1.58725 X A[3] = 1.000 B[20] = 0.848
KH      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[3] = 0.59988 X A[0] = 1.000 B[3] = 0.600
OD      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[3] = 0.98514 X A[1] = 0.845 B[9] = 0.456
LS      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[3] = 1.76888 X A[2] = 1.000 B[15] = 0.784
KO      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[3] = 2.51696 X A[3] = 1.000 B[21] = 0.748
PH      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[4] = 0.73713 X A[0] = 1.000 B[4] = 0.737
FG      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[4] = 1.53007 X A[1] = 0.845 B[10] = 0.938
RS      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[4] = 1.57626 X A[2] = 1.000 B[16] = 0.046
OO      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[4] = 1.62374 X A[3] = 1.000 B[22] = 0.047
EH      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[5] = 0.45380 X A[0] = 1.000 B[5] = 0.454
DG      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[5] = 0.95008 X A[1] = 0.845 B[11] = 0.587
PS      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[5] = 1.54675 X A[2] = 1.000 B[17] = 0.597
EO      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[5] = 1.82885 X A[3] = 1.000 B[23] = 0.282
KH      0       10:10:29.996    NNTestScript (#NQ100,H1)        before rows 1 cols 6
RL      0       10:10:29.996    NNTestScript (#NQ100,H1)        IxWMatrix
HI      0       10:10:29.996    NNTestScript (#NQ100,H1)        Matrix
NS      0       10:10:29.996    NNTestScript (#NQ100,H1)        [ 
ND      0       10:10:29.996    NNTestScript (#NQ100,H1)        0.98699 1.63147 1.58725 2.51696 1.62374 1.82885
JM      0       10:10:29.996    NNTestScript (#NQ100,H1)        ] 
LG      0       10:10:29.996    NNTestScript (#NQ100,H1)        rows = 1 cols = 6

<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< End of second Hidden Layer >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

ML      0       10:10:29.996    NNTestScript (#NQ100,H1)        Hidden Layer 3 | Nodes 1 | Bias 0.1004
OG      0       10:10:29.996    NNTestScript (#NQ100,H1)        Inputs 6 Weights 6
NQ      0       10:10:29.996    NNTestScript (#NQ100,H1)        0.76671 0.86228 0.85694 0.93819 0.86135 0.88409
QM      0       10:10:29.996    NNTestScript (#NQ100,H1)        0.278 0.401 0.574 0.301 0.256 0.870
RD      0       10:10:29.996    NNTestScript (#NQ100,H1)        Arr size A 6
NO      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[0] = 0.21285 X A[0] = 0.767 B[0] = 0.278
QK      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[0] = 0.55894 X A[1] = 0.862 B[1] = 0.401
CG      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[0] = 1.05080 X A[2] = 0.857 B[2] = 0.574
DS      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[0] = 1.33314 X A[3] = 0.938 B[3] = 0.301
HO      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[0] = 1.55394 X A[4] = 0.861 B[4] = 0.256
CJ      0       10:10:29.996    NNTestScript (#NQ100,H1)        AxBMatrix[0] = 2.32266 X A[5] = 0.884 B[5] = 0.870
HF      0       10:10:29.996    NNTestScript (#NQ100,H1)        before rows 1 cols 1
LR      0       10:10:29.996    NNTestScript (#NQ100,H1)        IxWMatrix
NS      0       10:10:29.996    NNTestScript (#NQ100,H1)        Matrix
DF      0       10:10:29.996    NNTestScript (#NQ100,H1)        [ 
NN      0       10:10:29.996    NNTestScript (#NQ100,H1)        2.32266
DJ      0       10:10:29.996    NNTestScript (#NQ100,H1)        ] 
GM      0       10:10:29.996    NNTestScript (#NQ100,H1)        rows = 1 cols = 1

Изображение ниже — визуализация сети. На нем видно, что мы сделали только на первом слое, остальное — просто повторение той же самой процедуры.

Работа однослойной нейронной сети

Матричное умножение здесь помножает весовые коэффициенты первого слоя на входные данные, как и ожидалось. Однако программирование логики оказалось не таким простым. Здесь можно запутаться, посмотрите на код ниже. Обратите внимание на функцию MatrixMultiply, остальной код можно пока игнорировать.

void   CNeuralNets::FeedForwardMLP(
                    double &MLPInputs[],
                    double &MLPOutput[])
 {    
//---

    m_hiddenLayers = m_hiddenLayers+1;
    
    ArrayResize(m_hiddenLayerNodes,m_hiddenLayers);    
    m_hiddenLayerNodes[m_hiddenLayers-1] = m_outputLayers;
         
    int HLnodes = ArraySize(MLPInputs); 
    int weight_start = 0;
    
    double Weights[], bias[];
    ArrayResize(bias,m_hiddenLayers);
    
//---
    
    int inputs=ArraySize(MLPInputs);
    int w_size = 0; //size of weights

    int cols = inputs, rows=1;
    
    double IxWMatrix[]; //dot product matrix 
    
    //Generate random bias
    for(int i=0; i<m_hiddenLayers; i++)         bias[i] = MathRandom(0,1);
         
    //generate weights 
    int sum_weights=0, L_inputs=inputs;
    double L_weights[];
    
    for (int i=0; i<m_hiddenLayers; i++)
      {
         sum_weights += L_inputs * m_hiddenLayerNodes[i];
         ArrayResize(Weights,sum_weights);
         L_inputs = m_hiddenLayerNodes[i];         
      }
    
    for (int j=0; j<sum_weights; j++) Weights[j] = MathRandom(0,1);
                        
    for (int i=0; i<m_hiddenLayers; i++)
      {          
          w_size = (inputs*m_hiddenLayerNodes[i]);
          ArrayResize(L_weights,w_size);
                     
            ArrayCopy(L_weights,Weights,0,0,w_size);
            ArrayRemove(Weights,0,w_size); 
             
              MatrixMultiply(MLPInputs,L_weights,IxWMatrix,cols,cols,rows,cols);
               
              
              ArrayFree(MLPInputs); ArrayResize(MLPInputs,m_hiddenLayerNodes[i]);
              inputs = ArraySize(MLPInputs); 
              
              for(int k=0; k<ArraySize(IxWMatrix); k++) MLPInputs[k] = ActivationFx(IxWMatrix[k]+bias[i]); 
               
      } 
 }

Первый вход в сеть на входном слое — матрица 1xn означает, что в ней одна строка и неизвестное количество столбцов (n). Инициализируем эту логику перед циклом for в строке

  int cols = inputs, rows=1;

чтобы получить общее количество весовых коэффициентов, необходимых для завершения процесса умножения. Умножаем количество узлов входного/предыдущего слоя на количество в выходном/следующем слое. В данном случае имеем 2 входа и 4 узла в первом скрытом слое, поэтому нам нужно 2x4 = 8 значений весов. Самая важная фишка всего этого показана далее:

 MatrixMultiply(MLPInputs,L_weights,IxWMatrix,cols,cols,rows,cols);

Чтобы лучше понять, посмотрим, что делает матричное умножение:

void MatrixMultiply(double &A[],double &B[],double &AxBMatrix[], int colsA,int rowsB,int &new_rows,int &new_cols)

Последние параметры new_rows и new_cols — обновленные значения количества строк и столбцов в новой матрице. Далее значения повторно используются как количество строк и столбцов для следующей матрицы. Помните, что входом для следующего слоя служат выходные значения предыдущего слоя?

Это еще более важно для матрицы, потому что

  • В первом слое входная матрица это матрица весов 1x2 = 2x4, а выходная матрица = 1x4.
  • Во втором слое входная матрица это матрица весов 1x4 = 4x6, а выходная матрица1x6
  • Соответственно, в третий слой входит 1x6 матрица весов 6x1, а ан выходе матрица 1x1

Мы знаем, что для умножения матриц количество столбцов в первой матрице должно быть равно количеству строк во второй. Полученная матрица будет иметь размерность по количеству строк из первой матрицы и количеству столбцов из второй.

На основе вышеперечисленных операций

Самые первые входные параметры — это те, размеры которых известны. Но в матрице весовых коэффициентов 8 элементов, которые были получены путем умножения входных данных и количества узлов в скрытом слое, поэтому мы можем окончательно заключить, что в ней есть строки, равные количеству столбцов в предыдущем слое/на входе, и это практически все. Такая логика становится возможной благодаря процессу изменения значений новых строк и новых столбцов на старые (внутри функции умножения матриц)

 new_rows = rowsA;  new_cols = colsB;

Подробнее о матрицах можно узнать в стандартной библиотеке. Если же вас интересует что-то большее, не входящее в библиотеку, вы найдете ссылку в конце статьи.

Итак, у нас есть гибкая архитектура. Теперь давайте посмотрим, как может выглядеть обучение сети и тестирование в случае многослойного перцептрона MLP с прямой связью.

Задействованные процессы

  1. Обучаем сеть на х эпох, находим модель с наименьшим количеством ошибок.
  2. Сохраняем параметры модели в бинарном файле, который можно открыть в других программах, например, внутри советника.

Подождите секунду, я только что сказал, что мы находим модель с наименьшим количеством ошибок? На самом деле нет, это просто прямой подход.

Некоторые участникb MQL5.community любят оптимизировать советники с этими параметрами на вход. Это работает, но в этом случае веса и смещения генерируются только один раз, а затем используются для остальных эпох, так же как в обратном проходе, вот только эти значения затем не обновляются.

Используем количество эпох по умолчанию, равное 1.

void CNeuralNets::train_feedforwardMLP(double &XMatrix[],int epochs=1)

Можно попробовать изменить код, чтобы передавать весовые коэффициенты на вход в скрипт, оттуда же можно установить любое значение количества эпох. Есть и много других способов.


Тестирование или использование модели на новых данных

Чтобы иметь возможность использовать модель, которую мы обучили, нам нужно иметь возможность делиться ее параметрами с другими программами. Это можно сделать через файлы. Поскольку параметры нашей модели представляют собой значения double из массивов, нам нужны binary- файлы. Читаем файлы, в которых сохранены весовые коэффициенты и смещение, и сохраняем их в соответствующих массивах для использования.

Вот эта функция отвечает за обучение нейронной сети.

void CNeuralNets::train_feedforwardMLP(double &XMatrix[],int epochs=1)
   {         
      double MLPInputs[]; ArrayResize(MLPInputs,m_inputs);
      double MLPOutputs[]; ArrayResize(MLPOutputs,m_outputLayers);
      
      double Weights[], bias[];
      
      setmodelParams(Weights,bias); //Generating random weights and bias
      
      for (int i=0; i<epochs; i++)
         {
           int start = 0;
           int rows = ArraySize(XMatrix)/m_inputs;
           
               {
                 if (m_debug) printf("<<<< %d >>>",j+1);
                 ArrayCopy(MLPInputs,XMatrix,0,start,m_inputs);
             
                 FeedForwardMLP(MLPInputs,MLPOutputs,Weights,bias);
             
                 start+=m_inputs;
               }
         }
       
       WriteBin(Weights,bias);
   }

Функция setmodelParams() генерирует случайные значения весовых коэффициентов и смещения. После обучения модели получаем значения весов и смещения, сохраняем их в binary-файл.

WriteBin(Weights,bias);

Чтобы посмотреть, как все работает в MLP, будем использовать набор данных из реального примера отсюда.

Параметр XMatrix[] представляет собой матрицу всех входных значений, которым будем хотим обучать нашу модель. В нашем случае нужно импортировать файл CSV в матрицу.

nasdaq dataset


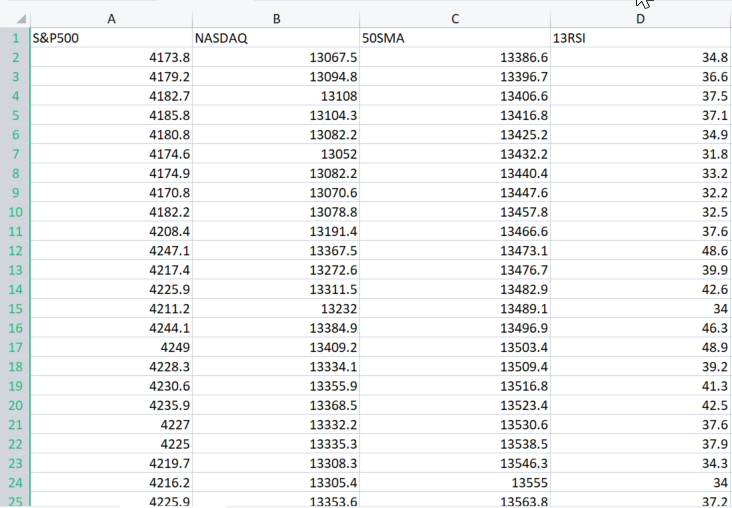
Импортируем набор данных

     double XMatrix[]; int rows,cols;
     
     CSVToMatrix(XMatrix,rows,cols,"NASDAQ_DATA.csv");
     MatrixPrint(XMatrix,cols,3);

Вывод того кода будет таким:

MN      0       12:02:13.339    NNTestScript (#NQ100,H1)        Matrix
MI      0       12:02:13.340    NNTestScript (#NQ100,H1)        [ 
MJ      0       12:02:13.340    NNTestScript (#NQ100,H1)         4173.800 13067.500 13386.600    34.800
RD      0       12:02:13.340    NNTestScript (#NQ100,H1)         4179.200 13094.800 13396.700    36.600
JQ      0       12:02:13.340    NNTestScript (#NQ100,H1)         4182.700 13108.000 13406.600    37.500
FK      0       12:02:13.340    NNTestScript (#NQ100,H1)         4185.800 13104.300 13416.800    37.100
.....
.....
.....
DK      0       12:02:13.353    NNTestScript (#NQ100,H1)         4332.700 14090.200 14224.600    43.700
GD      0       12:02:13.353    NNTestScript (#NQ100,H1)         4352.500 14162.000 14225.000    47.300
IN      0       12:02:13.353    NNTestScript (#NQ100,H1)         4401.900 14310.300 14226.200    56.100
DK      0       12:02:13.353    NNTestScript (#NQ100,H1)         4405.200 14312.700 14224.500    56.200
EE      0       12:02:13.353    NNTestScript (#NQ100,H1)         4415.800 14370.400 14223.200    60.000
OS      0       12:02:13.353    NNTestScript (#NQ100,H1)        ] 
IE      0       12:02:13.353    NNTestScript (#NQ100,H1)        rows = 744 cols = 4

Теперь весь файл CSV хранится внутри XMatrix[]. Ура!

Преимущество этой полученной матрицы заключается в том, что больше не нужно беспокоиться о входных данных нейронной сети, поскольку переменная cols получает количество столбцов из CSV-файла. Это будут входы нейронной сети. И вот как выглядит весь скрипт целиком:

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+

#include "NeuralNets.mqh";
CNeuralNets *neuralnet; 

//+------------------------------------------------------------------+
void OnStart()
  {
     
     int hlnodes[3] = {4,6,1};
     int outputs = 1;
     int inputs_=2;
     
     double XMatrix[]; int rows,cols;
     
     CSVToMatrix(XMatrix,rows,cols,"NASDAQ_DATA.csv");
     MatrixPrint(XMatrix,cols,3);
     
     neuralnet = new CNeuralNets(SIGMOID,RELU,cols,hlnodes,outputs);     
     
     neuralnet.train_feedforwardMLP(XMatrix);
     
     delete(neuralnet);
    
  }

Просто, не так ли? Однако нужно исправить несколько строк кода. В train_feedforwardMLP добавлены итерации всего набора данных в одну итерацию эпохи.

       for (int i=0; i<epochs; i++)
         {
           int start = 0;
           int rows = ArraySize(XMatrix)/m_inputs;
           
             for (int j=0; j<rows; j++) //iterate the entire dataset in a single epoch
               {
                 if (m_debug) printf("<<<< %d >>>",j+1);
                 ArrayCopy(MLPInputs,XMatrix,0,start,m_inputs);
             
                 FeedForwardMLP(MLPInputs,MLPOutputs,Weights,bias);
             
                 start+=m_inputs;
               }
         }

Проверим логи при запуске программы в режиме отладки.

bool m_debug = true;

Режим отладки занимает много места на диске. Поэтому при любом другом использовании (не в режиме отладки) установите значение false. После одного запуска программы у меня логи были размером в 21Мб.

Краткий обзор двух итераций:

MR      0       12:23:16.485    NNTestScript (#NQ100,H1)        <<<< 1 >>>
DE      0       12:23:16.485    NNTestScript (#NQ100,H1)        Hidden layer nodes plus the output
FS      0       12:23:16.485    NNTestScript (#NQ100,H1)        4 6 1 1
KK      0       12:23:16.485    NNTestScript (#NQ100,H1)        Hidden Layer 1 | Nodes 4 | Bias 0.3903
IN      0       12:23:16.485    NNTestScript (#NQ100,H1)        Inputs 4 Weights 16
MJ      0       12:23:16.485    NNTestScript (#NQ100,H1)         4173.80000 13067.50000 13386.60000    34.80000
DF      0       12:23:16.485    NNTestScript (#NQ100,H1)        0.060 0.549 0.797 0.670 0.420 0.914 0.146 0.968 0.464 0.031 0.855 0.240 0.717 0.288 0.372 0.805
....
PD      0       12:23:16.485    NNTestScript (#NQ100,H1)        MLP Final Output
LM      0       12:23:16.485    NNTestScript (#NQ100,H1)        1.333
HP      0       12:23:16.485    NNTestScript (#NQ100,H1)        <<<< 2 >>>
PG      0       12:23:16.485    NNTestScript (#NQ100,H1)        Hidden layer nodes plus the output
JR      0       12:23:16.485    NNTestScript (#NQ100,H1)        4 6 1 1
OH      0       12:23:16.485    NNTestScript (#NQ100,H1)        Hidden Layer 1 | Nodes 4 | Bias 0.3903
EI      0       12:23:16.485    NNTestScript (#NQ100,H1)        Inputs 4 Weights 16
FM      0       12:23:16.485    NNTestScript (#NQ100,H1)         4179.20000 13094.80000 13396.70000    36.60000
II      0       12:23:16.486    NNTestScript (#NQ100,H1)        0.060 0.549 0.797 0.670 0.420 0.914 0.146 0.968 0.464 0.031 0.855 0.240 0.717 0.288 0.372 0.805
GJ      0       12:23:16.486    NNTestScript (#NQ100,H1)        

Все настроено и работает хорошо, как и ожидалось. Теперь сохраним параметры модели в файл binary.

Сохранение параметров модели в файле

bool CNeuralNets::WriteBin(double &w[], double &b[])
 {
      string file_name_w = NULL, file_name_b=  NULL;
      int handle_w, handle_b;
      
      file_name_w = MQLInfoString(MQL_PROGRAM_NAME)+"\\"+"model_w.bin";
      file_name_b =  MQLInfoString(MQL_PROGRAM_NAME)+"\\"+"model_b.bin"; 
      
      FileDelete(file_name_w); FileDelete(file_name_b);
      
       handle_w = FileOpen(file_name_w,FILE_WRITE|FILE_BIN);       
       if (handle_w == INVALID_HANDLE)   {  printf("Invalid %s Handle err %d",file_name_w,GetLastError());  }
       else                                 FileWriteArray(handle_w,w);
      
       FileClose(handle_w);    
       
       handle_b = FileOpen(file_name_b,FILE_WRITE|FILE_BIN);
       if (handle_b == INVALID_HANDLE)   {  printf("Invalid %s Handle err %d",file_name_b,GetLastError());  }
       else                                 FileWriteArray(handle_b,b);
     
       FileClose(handle_b);
     
     return(true);
 }


Этот шаг крайне важен. Как уже говорили, это помогает совместно использовать параметры модели с другими программами, использующими одну и ту же библиотеку. Файлы будут храниться в подпапке, название которой совпадает с названием файла скрипта:

Файлы модели нейронной сети mql5

Пример того, как получить доступ к параметрам модели в других программах:

     double weights[], bias[];
     
     int handlew = FileOpen("NNTestScript\\model_w.bin",FILE_READ|FILE_BIN);
     FileReadArray(handlew,weights);
     FileClose(handlew);
     
     int handleb = FileOpen("NNTestScript\\model_b.bin",FILE_READ|FILE_BIN);
     FileReadArray(handleb,bias);
     FileClose(handleb);
     
     Print("bias"); ArrayPrint(bias,4);
     Print("Weights"); ArrayPrint(weights,4);

Результат

HR      0       14:14:02.380    NNTestScript (#NQ100,H1)        bias
DG      0       14:14:02.385    NNTestScript (#NQ100,H1)        0.0063 0.2737 0.9216 0.4435
OQ      0       14:14:02.385    NNTestScript (#NQ100,H1)        Weights
GG      0       14:14:02.385    NNTestScript (#NQ100,H1)        [ 0] 0.5338 0.6378 0.6710 0.6256 0.8313 0.8093 0.1779 0.4027 0.5229 0.9181 0.5449 0.4888 0.9003 0.2870 0.7107 0.8477
NJ      0       14:14:02.385    NNTestScript (#NQ100,H1)        [16] 0.2328 0.1257 0.4917 0.1930 0.3924 0.2824 0.4536 0.9975 0.9484 0.5822 0.0198 0.7951 0.3904 0.7858 0.7213 0.0529
EN      0       14:14:02.385    NNTestScript (#NQ100,H1)        [32] 0.6332 0.6975 0.9969 0.3987 0.4623 0.4558 0.4474 0.4821 0.0742 0.5364 0.9512 0.2517 0.3690 0.4989 0.5482
Доступ к файлам можно получить из любого места, для этого нужно только знать название и расположение.

Использование модели

Это была легкая часть. Функция прямого прохода MLP изменилась — мы добавили новые входные веса и смещения, это поможет запустить модель, например, для работы на последних ценовых данных или чем-то еще.

void   CNeuralNets::FeedForwardMLP(double &MLPInputs[],double &MLPOutput[],double &Weights[], double &bias[])

В завершении кода извлекаем веса и смещение и используем модель на практике. Сначала читаем параметры, затем задаем входные значения, не входную матрицу, потому что в этот раз используем обученную модель для прогнозирования результатов входных значений. MLPOutput[] дает выходной массив:

     double weights[], bias[];
     
     int handlew = FileOpen("NNTestScript\\model_w.bin",FILE_READ|FILE_BIN);
     FileReadArray(handlew,weights);
     FileClose(handlew);
     
     int handleb = FileOpen("NNTestScript\\model_b.bin",FILE_READ|FILE_BIN);
     FileReadArray(handleb,bias);
     FileClose(handleb);
     
     double Inputs[]; ArrayCopy(Inputs,XMatrix,0,0,cols); //copy the four first columns from this matrix
     double Output[];
     
     neuralnet = new CNeuralNets(SIGMOID,RELU,cols,hlnodes,outputs);     
     
     neuralnet.FeedForwardMLP(Inputs,Output,weights,bias);
     
     Print("Outputs");
     ArrayPrint(Output);
     
     delete(neuralnet);

Все это работает.

Теперь можно изучать различные виды архитектуры и различные варианты, чтобы понять, что лучше всего подходит именно для вас.

Нейронная сеть с прямой связью была первым и самым простым типом разработанной искусственной нейронной сети. В этой сети информация движется только в одном направлении — вперед — от входных узлов, через скрытые узлы (если они есть) и к выходным узлам. В сети нет циклов

Модель, которую мы только что написали, является базовой и может не давать желаемых результатов без должной оптимизации (уверен на 100%). Надеюсь, вы проявите творческий подход и поработаете над этим.

Заключительные мысли

Важно понимать теорию и все, что находится за закрытыми дверями различных техник машинного обучения. У нас нет пакетов data science в MQL5, но есть как минимум фреймворки Python. Однако, бывают случаи, когда работу нужно организовать в MetaTrader. Не имея четкого понимания теории, стоящей за такого рода вещами, человеку будет трудно разобраться и извлечь максимальную пользу из машинного обучения. По мере продвижения важность теории и изученных ранее в этой серии вещей возрастает.

Всем удачи!

Репозиторий GitHub: https://github.com/MegaJoctan/NeuralNetworks-MQL5

Познакомьтесь с моей библиотекой для работы с матрицами и векторами


Дополнительная литература

Статьи:

Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/11334

Прикрепленные файлы |
Загрузить ZIP
NeuralNets_Lib.zip (24.33 KB)
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Последние комментарии | Перейти к обсуждению на форуме трейдеров (4)
Denis Kirichenko
Denis Kirichenko | 7 нояб. 2022 в 19:33

Имхо, в этом цикле материал гораздо лучше представлен, чем например в цикле "Нейросети - это просто"...

Вопрос скорее к админам. А разве можно вставлять в коде ссылки на платные биб-ки? 

//+------------------------------------------------------------------+
//|                                                   NeuralNets.mqh |
//|                                    Copyright 2022, Omega Joctan. |
//|                        https://www.mql5.com/en/users/omegajoctan |
//+------------------------------------------------------------------+
#property copyright "Copyright 2022, Omega Joctan."
#property link      "https://www.mql5.com/en/users/omegajoctan"
//+------------------------------------------------------------------+

#import "The_Matrix.ex5" //source code here >>> https://www.mql5.com/en/market/product/81533
   void MatrixMultiply(double &A[],double &B[],double &AxBMatrix[], int colsA,int rowsB,int &new_rows,int &new_cols);
   void CSVToMatrix(double &Matrix[],int &mat_rows,int &mat_cols,string csv_file,string sep=",");
   void MatrixPrint(double &Matrix[],int cols,int digits=5);
#import

bool m_debug = true;
Omega J Msigwa
Omega J Msigwa | 8 нояб. 2022 в 09:42
Denis Kirichenko #:

Имхо, в этом цикле материал гораздо лучше представлен, чем например в цикле "Нейросети - это просто"...

Вопрос скорее к админам. А разве можно вставлять в коде ссылки на платные биб-ки? 

нет, не возможно я забыл удалить ссылку

Denis Kirichenko
Denis Kirichenko | 9 нояб. 2022 в 09:47

В статье есть такое:

Ok so here is the function responsible for training the neural network. 

void CNeuralNets::train_feedforwardMLP(double &XMatrix[],int epochs=1)

Специально привожу выдержку на языке, на котором автор написал статью.

Стесняюсь спросить, а в каком месте происходит обучение? Имхо, имеет место прямое распространение...

Забавно:

CNeuralNets::CNeuralNets(fx HActivationFx, fx OActivationFx, int inputs, int &NodesHL[], int outputs=NULL, bool SoftMax=false)
   {
   e = 2.718281828;
    ...
   }

А что если так?  ))

CNeuralNets::CNeuralNets(fx HActivationFx, fx OActivationFx, int inputs, int &NodesHL[], int outputs=NULL, bool SoftMax=false)
   {
    e = M_E;
   ...
   }
Denis Kirichenko
Denis Kirichenko | 9 нояб. 2022 в 09:52

Когда увидел, что есть в статье раздел:

Матрицы в помощь

Если вдруг понадобиться изменить параметры модели со статичным кодом, оптимизация может занять очень много времени — это головная боль, боль в спине и прочие неприятности.

то подумал, что ну вот, наконец-то кто-то опишет МО в терминах нативных матриц (matrix). Но головная боль от самопальных матриц в виде одномерного массива а-ля XMatrix[] только усилилась... 

Магия временных торговых интервалов с инструментом Frames Analyzer Магия временных торговых интервалов с инструментом Frames Analyzer
Что такое Frames Analyzer? Это подключаемый модуль к любому торговому эксперту для анализа фреймов оптимизации во время оптимизации параметров в тестере стратегий, а также вне тестера посредством чтения MQD-файла или базы данных, которая создаётся сразу после оптимизации параметров. Вы сможете делиться этими результатами оптимизации с другими пользователями, у которых есть инструмент Frames Analyzer, чтобы обсудить полученные результаты оптимизации вместе.
DoEasy. Элементы управления (Часть 25): WinForms-объект "Tooltip" DoEasy. Элементы управления (Часть 25): WinForms-объект "Tooltip"
В статье начнём разработку элемента управления Tooltip ("всплывающая подсказка") и начнём создание новых графических примитивов для библиотеки. Естественно, не у каждого элемента есть всплывающая подсказка, но возможность её задать для него есть у каждого графического объекта.
Нейросети — это просто (Часть 32): Распределенное Q-обучение Нейросети — это просто (Часть 32): Распределенное Q-обучение
В одной из статей данной серии мы с вами уже познакомились с методом Q-обучения. Данный метод усредняет вознаграждения за каждое действие. В 2017 году были представлены сразу 2 работы, в которых большего успеха добиваются при изучении функции распределения вознаграждения. Давайте рассмотрим возможность использования подобной технологии для решения наших задач.
Адаптивные индикаторы Адаптивные индикаторы
В этой статье мы рассмотрим несколько возможных подходов к созданию адаптивных индикаторов. Адаптивные индикаторы отличаются наличием обратной связи между значениями входных и выходного сигналов. Эта связь позволяет индикатору самостоятельно подстраиваться на оптимальную обработку значений финансового временного ряда.