Дискретное преобразование Хартли
Введение
В 1942 году Ральф Хартли в своей статье «A More Symmetrical Fourier Analysis Applied to Transmission Problems» предложил преобразование, которое является аналогом преобразования Фурье.
Так же, как и преобразование Фурье (FT), преобразование Хартли (HT) трансформирует исходный сигнал в сумму тригонометрических функций. Но между ними есть одно существенное отличие. FT преобразует вещественные значения в комплексные числа, а HT дает только вещественный результат. Из-за этого различия преобразование Хартли не стало популярным – научные и технические работники не увидели в нем каких-либо преимуществ и продолжили пользоваться привычным преобразованием Фурье. Только в 1983 году Рональд Брейсуэлл представил дискретный вариант преобразования Хартли.
Немного теории
Дискретное преобразование Хартли (DHT) можно применять при анализе и обработке дискретных временных рядов. С его помощью можно фильтровать сигналы, анализировать их спектр и многое другое. Возможности DHT ничуть не меньше, чем у дискретного преобразования Фурье. Однако, в отличие от него, DHT использует только вещественные числа, что делает его более удобным для реализации на практике, а результаты его применения более наглядными.
Пусть у нас имеется N вещественных чисел h[0] … h[N-1]. С помощью дискретного преобразования Хартли мы получим из них N вещественных чисел H[0]…H[N-1].
Это преобразование позволяет перевести сигнал из временной области в область частоты. С его помощью мы можем оценить, насколько велико влияние той или иной гармоники в исходном сигнале. Число H[0] содержит основную информацию о сигнале. А числа H[1]…H[N-1] – дополнительную, уточняющую информацию. Эти числа показывают, насколько сильна та или иная гармоника в исходном сигнале. А индекс этих чисел показывает сколько циклов этой гармоники уместится в исходном сигнале. То есть, чем больше индекс, тем выше частота гармоники.
Для перехода из частотной области в область времени применяется обратное преобразование Хартли. Его формула выглядит так.
В обеих формулах функция cas (cos and sin) – сумма тригонометрических функций.
Хотя, ее можно заменить и на разность. Суть преобразования от этого не изменится. Теперь, давайте посмотрим, как можно использовать DHT на практике.
Знакомство с дискретным преобразованием Хартли
Итак, DHT переводит сигнал из временной области в частотную. Но можно ли из этого получить какую-то практическую пользу?
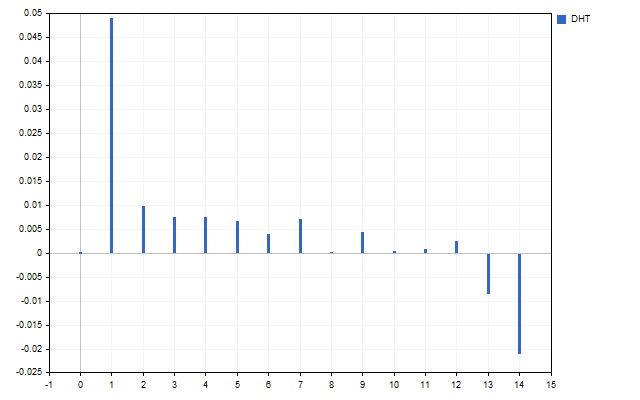
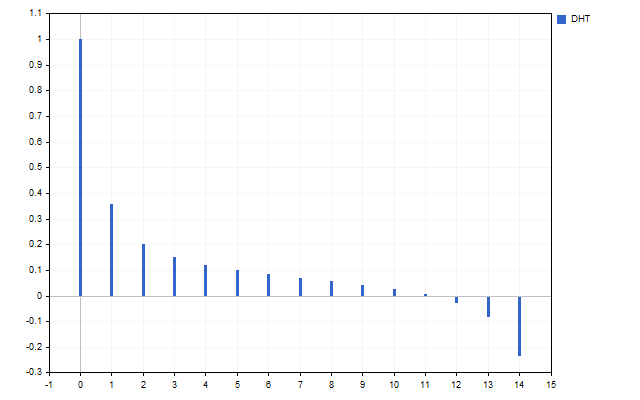
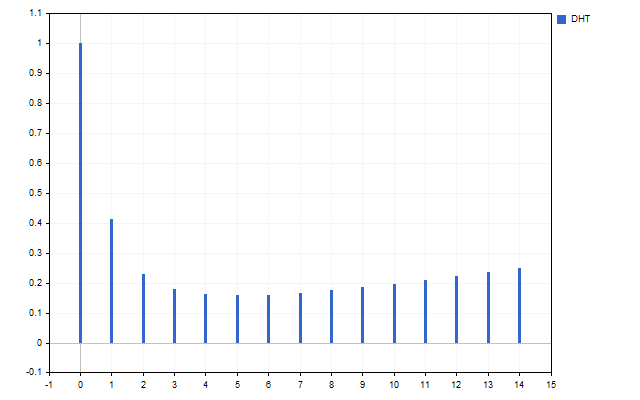
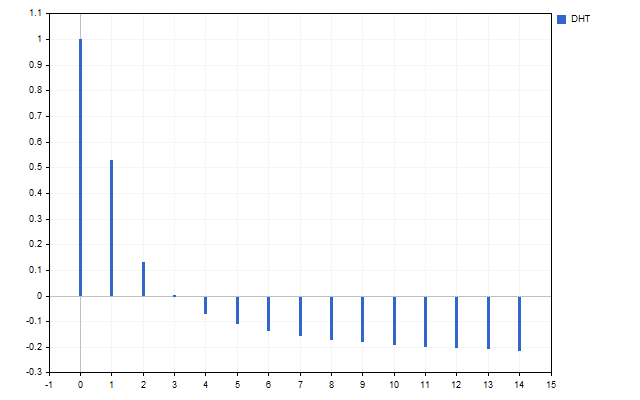
В качестве сигнала я взял 15 цен Open. Вот так выглядит спектр этого временного ряда (значение H[0] не показано из-за разницы масштабов).
На рисунке хорошо видно, что разные гармоники имеют неодинаковую силу. Но, что можно сделать с этим спектром?
Давайте, в качестве примера, возьмем индикатор простой скользящей средней. Его формула очень проста.
А что будет с индикатором, если мы одну из цен приравняем нулю? Вряд ли мы получим что-то хорошее. А вот в частотной области такое возможно – мы можем обнулить любое количество гармоник.
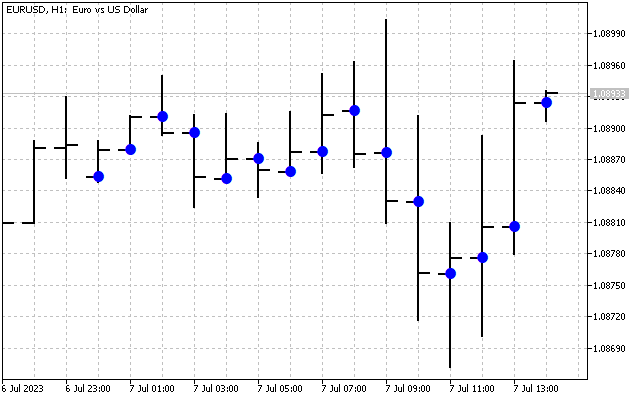
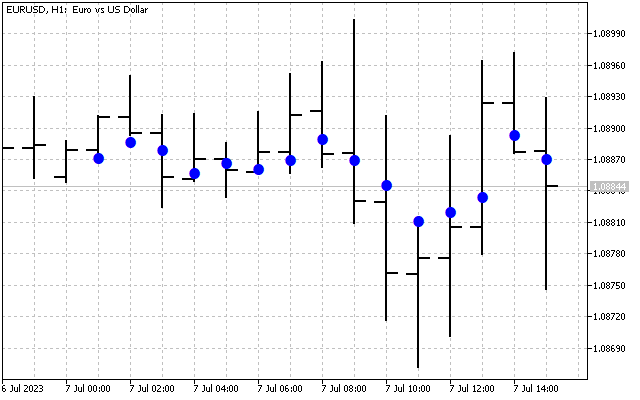
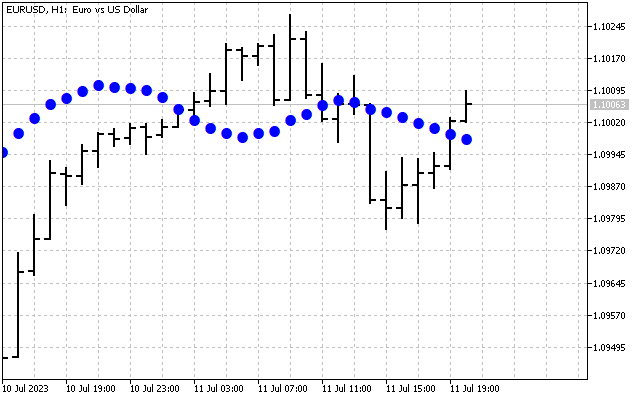
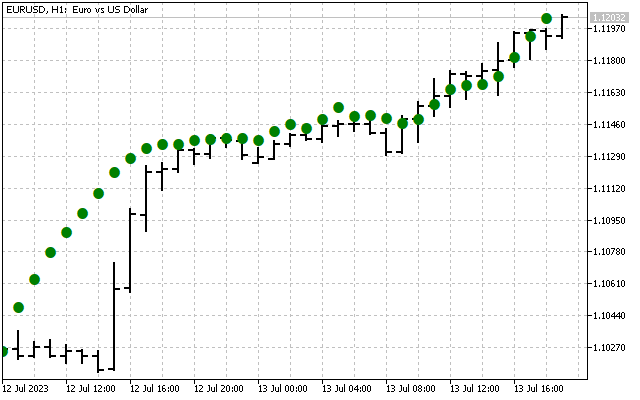
Вот так выглядит исходный сигнал.
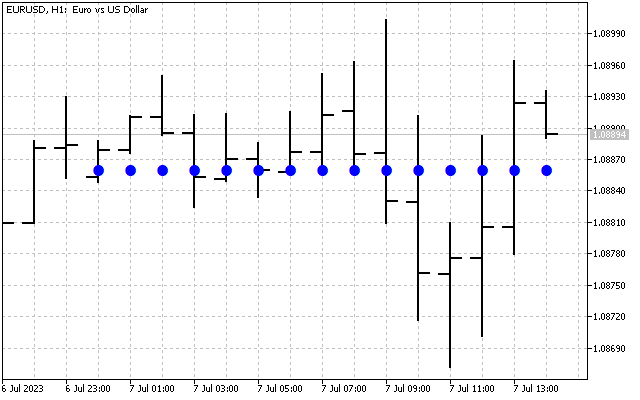
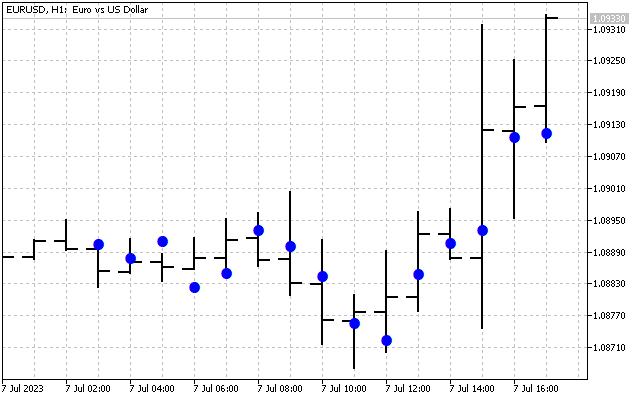
А теперь давайте все гармоники H[1] – H[14] приравняем нулю. Теперь у нас останется только основная информация об исходном сигнале. Применим к этому спектру обратное преобразование Хартли.
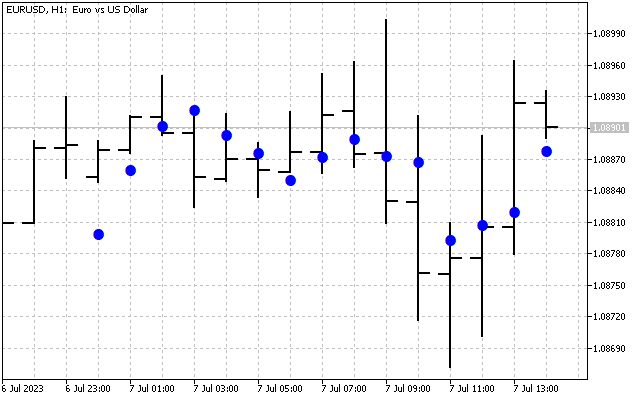
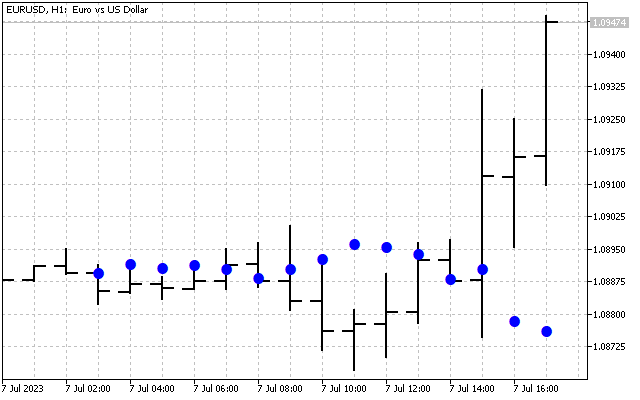
Теперь давайте удалим гармоники с самыми высокими частотами H[10] – H[14]. Преобразование Хартли выдаст нам такой результат.
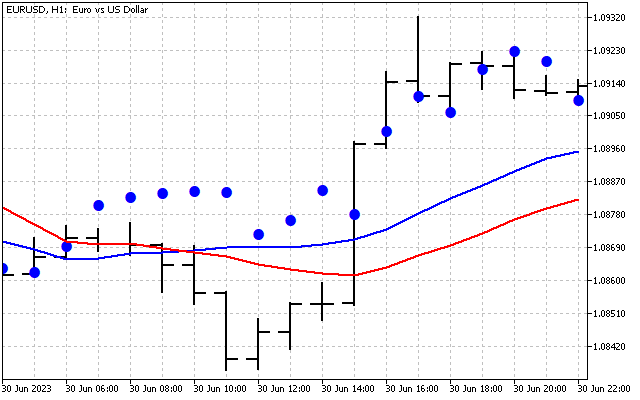
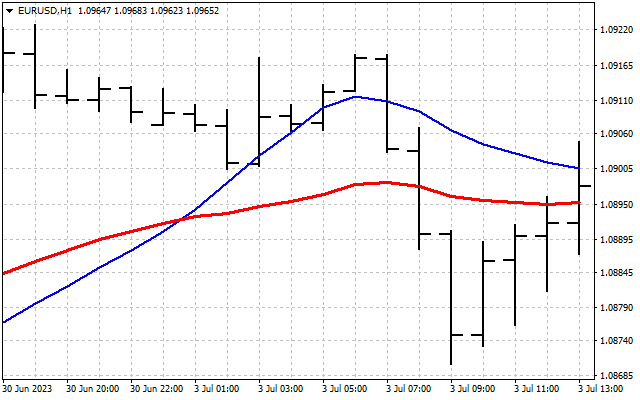
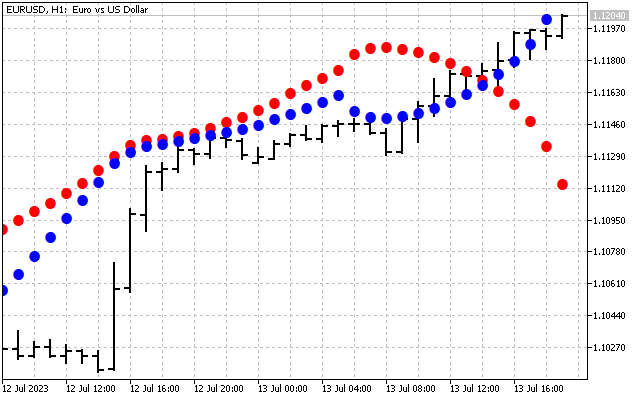
То есть, мы сгладили исходный сигнал. Вот и первый способ применения преобразования Хартли на практике. Сначала мы можем сгладить временной ряд в области частот. После чего полученные значения передаются на вход привычных индикаторов. Давайте для примера возьмем две скользящих средних. Одну из них применим к ценам как обычно (красная линия). А вторую мы применим к значениям DHT (синяя линия).
Обнуление некоторых гармоник не единственный способ обработки спектра сигнала. Мы можем ослабить все гармоники сразу. Например, поделив их на какое-то заданное число.
Или ослабить каждую гармонику в соответствии с ее частотой – чем выше частота, тем сильнее ослабление.
В любом случае, у нас получится сглаженный временной ряд. Вот так выглядит сигнал с гармониками, ослабленными в 2 раза.
Еще один способ обработки спектра – оставить только самые сильные гармоники. Для этого нам придется найти среднее всех гармоник.
И оставить только те из них, которые превосходят это среднее по своему абсолютному значению.
Тогда у нас останутся только основной сигнал плюс наиболее сильные гармоники.
Еще один вариант обработки сигнала – мы можем изменить значения гармоник на противоположное. Тогда восстановленный сигнал будет находиться в противоположной фазе.
В этом случае мы получим зеркальное отражение сигнала – восходящий тренд заменяется нисходящим и наоборот. Такой подход может оказаться полезным при расчете уровней поддержки и сопротивления.
Все варианты обработки спектра исходного сигнала могут применяться как по отдельности, так и в сочетании друг с другом. Например, вы можете сначала оставить только самые сильные гармоники, а потом поменять их знак на противоположный. В этом случае результат будет показывать возможный контртрендовый импульс.
Индикатор с оптимальным спектром
Любой линейный индикатор представляет собой набор коэффициентов. Если к этим коэффициентам применить преобразование Хартли, то мы получим спектральную характеристику индикатора.
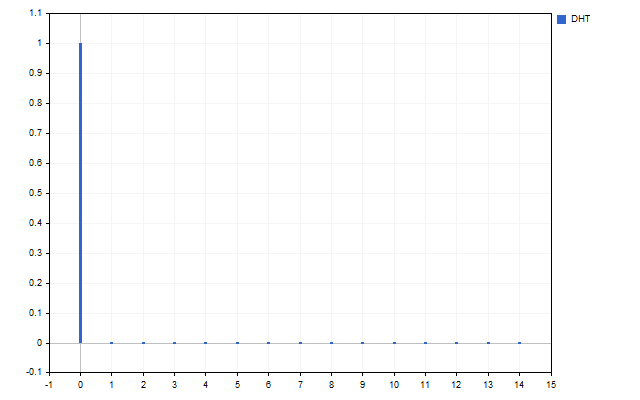
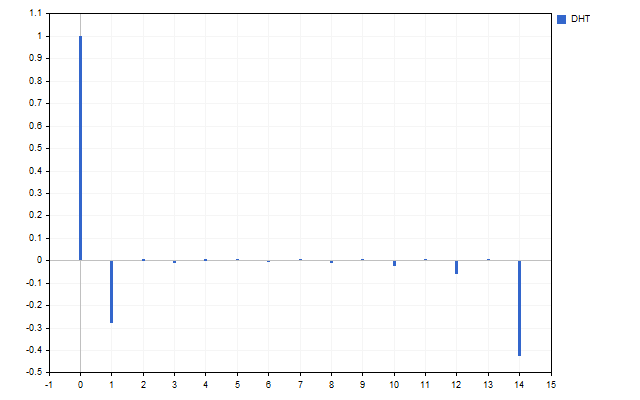
Все мы слышали, что SMA является фильтром нижних частот. Давайте проверим это утверждение. Все коэффициенты этого индикатора равны 1/N. Преобразование Хартли дает нам такой спектр этого индикатора.
Как мы видим – SMA пропускает только основной сигнал H[0], а вот все остальные гармоники полностью подавляются.
Спектры, то есть частотные характеристики, индикаторов могут очень сильно отличаться друг от друга. Например, LWMA пропускает все гармоники входного сигнала.
А SMMA пропускает только некоторые гармоники, а остальные подавляет.
У каждого индикатора свой уникальный спектр. И его можно использовать для обработки ценового ряда. Для этого нам нужно сначала найти спектр исходного сигнала H[]. Потом почленно умножаем его на спектр индикатора I[].
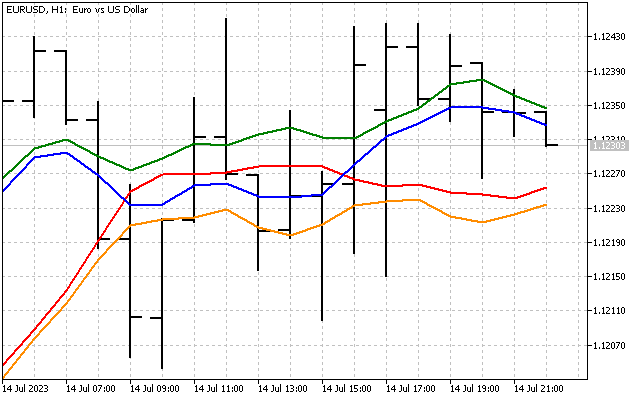
К полученному результату применяем обратное преобразование Хартли. В итоге мы получаем фильтрацию сигнала в частотной области. Так выглядит работа частотного фильтра, построенного на индикаторе LWMA.
Но мы можем пойти и другим путем – сначала задать спектр индикатора, а потом получить его коэффициенты. Давайте попробуем сделать индикатор, спектральная характеристика которого будет соответствовать спектру сигнала.
Алгоритм наших действий будет следующим. Сначала с помощью DHT получим спектр сигнала. Потом нам нужно нормализовать его. Для этого нужно поделить все значения гармоник на D = H[0].
Обратите внимание, что после нормализации значение H[0] = 1 – это обязательное условие при построении индикатора.
После чего нам нужно применить обратное преобразование, которое даст нам весовые коэффициенты индикатора.
Эти коэффициенты не очень сильно отличаются от SMA. Но такой индикатор будет иметь меньшее запаздывание по сравнению со скользящей средней, что даст возможность точнее отслеживать динамику рынка.
Шум и цвет
При обработке финансовых временных рядов под термином шум чаще всего подразумевается нежелательное искажение сигнала. Для борьбы с такими шумами могут использоваться самые различные фильтры – SMA и многие другие индикаторы.
Но шумом может считаться и случайный или непредсказуемый сигнал. А что будет, если мы представим движение цен на рынке в виде суммы шумов? Для этого нам нужно обратиться к концепции цветных шумов. Цветные шумы – это шумы, которые имеют различную энергию в разных частотных диапазонах. Они получили свое название по аналогии с различными цветами видимого света: красный шум – низкочастотный, а фиолетовый – шум с высокой частотой.
Представление движения цены в виде суммы цветных шумов может дать интересный результат при анализе финансовых временных рядов. Такой подход позволяет учесть различные частотные составляющие движения цены.
Каждый цветной шум имеет свою уникальную характеристику, которая отражает распределение энергии в спектре в зависимости от частоты f.
Всего существуют пять основных цветов шума.
| параметр p | цвет шума |
|---|---|
| -2 | красный |
| -1 | розовый |
| 0 | белый |
| +1 | синий |
| +2 | фиолетовый |
Каждый шум связан с определенным движением цены. Например, красный шум может указывать на наличие долгосрочных трендов или циклов в движении цен. Белый шум указывает на то, что рынок находится в состоянии флета. А фиолетовый шум может указывать на случайное и непредсказуемое поведение цены. Применение цветных шумов при анализе финансовых временных рядов может помочь в выявлении скрытых закономерностей и паттернов, которые не всегда видны при обычном анализе.
А теперь давайте посмотрим, как ведут себя разные шумы на рынке. Для этого нам нужно сделать несколько несложных шагов.
Сначала нам нужно найти спектр сигнала, с помощью которого мы сможем оценить энергию каждой гармоники. Для этого нам нужно возвести в квадрат значение каждой гармоники.
Теперь, мы можем оценить значение масштабирующего коэффициента для шума с параметром p. При использовании этого коэффициента полные энергии сигнала и шума будут равны.
Зная этот коэффициент, мы можем построить энергетический спектр шума EN[].
Теперь мы можем найти спектр шума HN[]. Для этого нам нужно извлечь квадратный корень из энергетического спектра.
Осталось совсем немного – гармоникам спектра шума присвоить знаки +/- как и у гармоник исходного сигнала. В этом случае, шум и исходный сигнал будут находиться в одной фазе.
После этого нам нужно выполнить обратное преобразование Хартли, чтобы получить значения шума на ценовом графике. Так выглядит красный шум на рынке.
Но, мы можем взять и противоположные знаки гармоник. В этом случае шум будет находиться в противоположной фазе по отношению к исходному сигналу. Кроме того, можно взять и строго положительные или отрицательные значения гармоник – в частотной области мы можем себе это позволить. Тогда мы сможем увидеть границы шумовых движений на рынке.
Концепцию цветных шумов можно применять не только для описания рыночной динамики, но и для разработки индикаторов.
Для этого нам нужно сначала задать мощность индикатора E > 0. От этого параметра зависит насколько чувствителен будет индикатор. После этого мы выполняем уже знакомые процедуры. Сначала находим масштабирующий коэффициент.
После этого находим спектр индикатора HI[], при этом не забываем, что HI[0] должен быть равен 1.
Нам осталось присвоить знаки +/- гармоникам спектра индикатора, если в этом есть необходимость. После чего нужно применить обратное преобразование Хартли и получить коэффициенты индикатора. Так выглядит индикатор красного шума с разными вариантами знаков гармоник.
При разработке индикаторов можно использовать не только чистые шумы, но и их различные комбинации. Например, так выглядит спектр суммы красного и фиолетового шумов.
А вот так выглядит разность между спектрами красного и белого шумов.
После получения коэффициентов индикатора coefficient[], необходима их нормализация. Для этого нужно сначала найти сумму всех коэффициентов.
После этого нужно каждый коэффициент разделить на полученную сумму.
Кроме перечисленных основных шумов существуют и другие. Например, одно из определений черного шума – это шум с параметром p < -2. Давайте попробуем другой подход. Предположим, что параметр шума p может принимать дробные значения, и посмотрим, как он меняется со временем.
Для вычисления параметра шума нам нужно сначала найти энергетический спектр сигнала E[]. После этого нужно вычислить четыре коэффициента.
Во всех формулах k = 1…N-1. Наиболее подходящий параметр шума можно рассчитать по формуле.
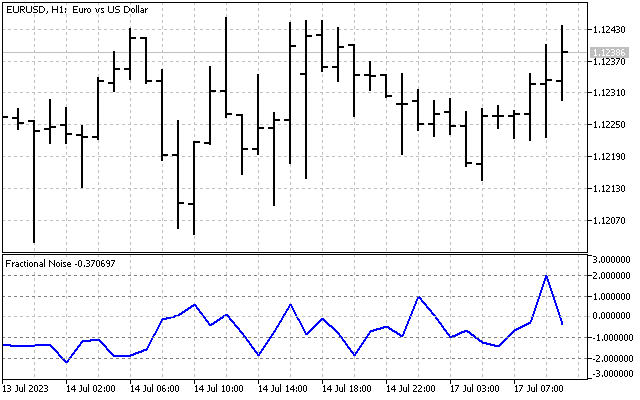
А вот так изменяется этот параметр в условиях рынка.
Как мы могли убедиться, использование цветных шумов в анализе финансовых временных рядов может быть полезным инструментом для исследования и понимания рыночной динамики. Этот подход может помочь выявить скрытые закономерности и улучшить прогнозирование ценовых движений.
Заключение
Для дискретного преобразования Хартли есть свои алгоритмы быстрого преобразования. Но, если под значения cas заранее выделить массив, то можно значительно ускорить скорость обработки данных. Размер этого массива должен быть равен (N-1)^2+1, где N - период индикатора. Тогда значения этого массива устанавливаются следующим образом:
При написании статьи я использовал именно такой подход.
К статье приложены следующие индикаторы.
| Наименование | Описание |
|---|---|
| DHT | Индикатор демонстрирует возможности по обработке гармоник сигнала.
|
| DHT LWMA | Индикатор показывает обработку цены индикатором LWMA в спектральной области |
| Spectrum | Индикатор коэффициенты которого дают спектральную характеристику как у исходного сигнала |
| Noise Levels | Индикатор показывает уровни цветных шумов. Noise - цвет шума Type - изменение фазы исходного сигнала |
| Noise Indicator | Индикатор подбирает коэффициенты, соответствующие выбранному цвету шума. E - мощность шума. |
| Fractional Noise | Индикатор, отображающий дробный параметр шума. |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
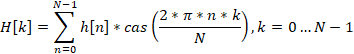
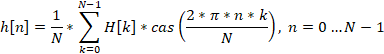
Спасибо за статью!
Буквально вчера думал о методах выявления стадий рынка за счёт статистических показателей в подвыборке, и тут в статье увидел схожие идеи.
Проводили ли какие либо более глубокие исследования в данном направлении? Интересно, как быстро (с каким запаздыванием) и с какой ошибкой удавалось классифицировать тренды\флэты?
Спасибо за статью!
Буквально вчера думал о методах выявления стадий рынка за счёт статистических показателей в подвыборке, и тут в статье увидел схожие идеи.
Проводили ли какие либо более глубокие исследования в данном направлении? Интересно, как быстро (с каким запаздыванием) и с какой ошибкой удавалось классифицировать тренды\флэты?
Выявление стадий рынка, наверное самая простая задача. Берем спектр цены (без основного сигнала) и пропускаем через кластерный анализ (карты Кохонена) - вот и получим стадии рынка. А вот с трендами все очень непросто - признак изменения/зарождения нового тренда - относительная слабость низкочастотной составляющей, и относительное усиление высокочастотных гармоник. Но, к сожалению, по направлению тренда - тут можно и серьезно промахнуться.