
Redes Neurais de Maneira Fácil(Parte 4): Redes Recorrentes
Conteúdo
- Introdução
- 1. Características distintas das redes neurais recorrentes
- 2. Princípios de treinamento das redes recorrentes
- 3. Construindo uma rede neural recorrente
- 3.1. Método de inicialização da classe
- 3.2. Feed-forward
- 3.3. Cálculo do gradiente do erro
- 3.4. Atualizando os pesos
- 4. Teste
- Conclusão
- Links
- Programas utilizados no artigo
Introdução
Nós continuamos os estudos das redes neurais. Nós já discutimos anteriormente o perceptron multicamadas e as redes neurais convolucionais. Todos eles trabalham com os dados estáticos no âmbito dos processos de Markov, segundo os quais o estado do sistema subsequente depende apenas de seu estado atual e não depende do estado do sistema no passado. Agora, eu sugiro considerar as Redes Neurais Recorrentes. Este é um tipo especial de redes neurais projetadas para trabalhar com séries temporais, sendo considerado o líder nesta esfera.
1. Características distintas das redes neurais recorrentes
Todos os tipos de redes neurais discutidos anteriormente funcionam com uma quantidade predeterminada de dados. No entanto, em nosso caso, é difícil determinar a quantidade ideal de dados analisados para o gráfico de preços. Diferentes padrões podem aparecer em diferentes intervalos de tempo. Mesmo os intervalos em si nem sempre são estáticos e podem variar dependendo da situação atual. Alguns eventos podem ser raros no mercado, mas eles funcionam com um alto grau de probabilidade. É bom quando o evento está dentro da janela de dados analisados. Se ele ficar além da série analisada, a rede neural irá ignorá-lo, mesmo que o mercado esteja trabalhando em uma reação a este evento naquele exato momento. Um aumento na janela analisada levará a um aumento no consumo de recursos computacionais e exigirá mais tempo para a tomada de decisão.
Os neurônios recorrentes nas redes neurais têm sido propostos para resolver esse problema ao trabalhar com as séries temporais. Esta é uma tentativa de implementar a memória de curto prazo nas redes neurais, quando o estado atual do sistema é alimentado em um neurônio junto com o estado anterior do mesmo neurônio. Este procedimento é baseado na suposição de que o valor na saída do neurônio leva em consideração a influência de todos os fatores (incluindo seu estado anterior) e na próxima etapa ele irá transferir "todo o seu conhecimento" para o seu estado futuro. Isso é semelhante a nós, quando nós agimos com base em nossa experiência passada e nas ações realizadas anteriormente. A duração da memória e sua influência no estado atual do neurônio dependerão dos pesos.
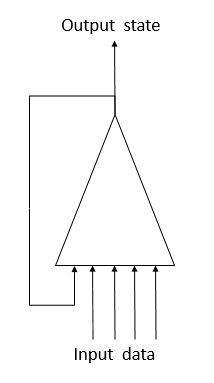
Infelizmente, uma solução tão simples tem suas desvantagens. Esta abordagem permite salvar a "memória" por um curto intervalo de tempo. A multiplicação cíclica do sinal por um fator menor que 1 e a aplicação da função de ativação do neurônio levam a uma atenuação gradual do sinal à medida que o número de ciclos aumenta. Para resolver este problema, Sepp Hochreiter e Jürgen Schmidhuber propuseram em 1997 o uso da arquitetura Long Short-Term Memory (LSTM). O algoritmo LTSM é considerado uma das melhores soluções para os problemas de classificação e previsão de séries temporais, em que eventos significativos são separados no tempo e estendidos em intervalos de tempo.
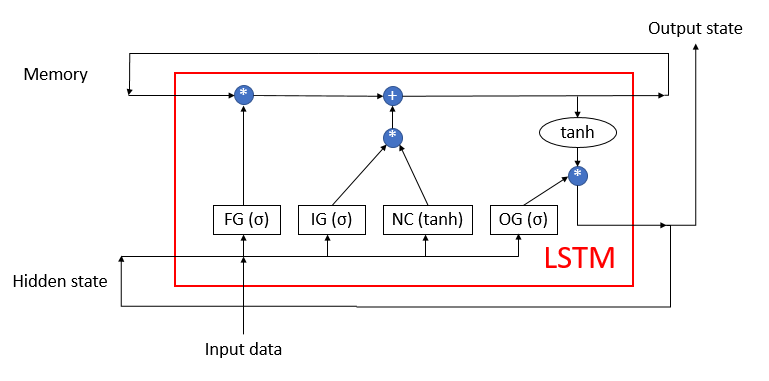
O LSTM dificilmente pode ser chamado de neurônio. Ele já é uma rede neural com 3 canais de entrada e 3 canais de saída. Destes canais, apenas dois são utilizados para a troca de dados com o mundo externo (um para entrada e outro para saída). Os quatro canais restantes são fechados em pares para a troca de informações cíclicas (Memory - memória e Hidden state - estado oculto)
O bloco LSTM contém dois fluxos de dados principais que são interconectados por 4 camadas neurais totalmente conectadas. Todas as camadas neurais contêm o mesmo número de neurônios, que é igual ao tamanho do fluxo de saída e do fluxo de memória. Vamos considerar o algoritmo com mais detalhes.
O fluxo de dados da memória é usado para armazenar e transmitir as informações importantes ao longo do tempo. Ela é inicializada com valores iguais a zero e, em seguida, preenchida durante a operação da rede neural. Isso pode ser comparado a um ser humano que nasce sem conhecimento e aprende ao longo da vida.
O fluxo do Hidden state (estado oculto) destina-se a transmitir ao longo do tempo o estado de saída do sistema. O tamanho do canal de dados é igual ao canal de dados da "memória".
Os canais Input data (dados de entrada) e Output state (estado de saída) são destinados à troca de informações com o mundo exterior.
Três fluxos de dados são alimentados no algoritmo:
- Input data>: descreve o estado atual do sistema.
- Memory e Hidden state são obtidos do estado anterior.
No início do algoritmo, as informações de Input data e Hidden state são combinadas em uma única matriz de dados, que é então alimentada para todas as 4 camadas neurais ocultas da LSTM.
A primeira camada neural, "Forget gate", determina quais dados recebidos na memória podem ser esquecidos e quais devem ser lembrados. Ela é implementada como uma camada neural totalmente conectada com uma função de ativação sigmoide. O número de neurônios na camada corresponde ao número de células de memória no fluxo Memory (memória). Cada neurônio da camada recebe na entrada a matriz total dos fluxos Input data e Hidden state, e emite um número no intervalo de 0 (esquecer completamente) a 1 (salvar na memória). O produto elemento a elemento dos dados de saída da camada neural com o fluxo de memória retorna a memória corrigida.
Na próxima etapa, o algoritmo determina quais dos dados obtidos nesta etapa devem ser armazenados na memória. As duas camadas neurais a seguir são usadas para esta finalidade:
- New Content — uma camada neural totalmente conectada com uma tangente hiperbólica como função de ativação. Ela normaliza as informações recebidas no intervalo de -1 a 1.
- Input gate — uma camada neural totalmente conectada com um sigmoide como função de ativação. Ela é semelhante ao Forget gate e determina quais novos dados devem ser lembrados.
O produto elemento a elemento de New Content e Input gate é adicionado aos valores da célula de memória. Como resultado dessas operações, nós obtemos um estado de memória atualizado, que é então inserido no próximo ciclo de iteração.
Após atualizar a memória, os valores do fluxo de saída devem ser gerados. Aqui, da mesma forma que Forget gate e Input gate, nós calculamos o Output gate e normalizamos o valor da memória atual usando a tangente hiperbólica. O produto elemento a elemento dos dois conjuntos de dados recebidos produz a matriz do sinal de saída, que é enviada da LSTM para o mundo externo. A mesma matriz de dados é passada para o próximo ciclo de iteração como um fluxo de estado oculto.
2. Princípios de treinamento das redes recorrentes
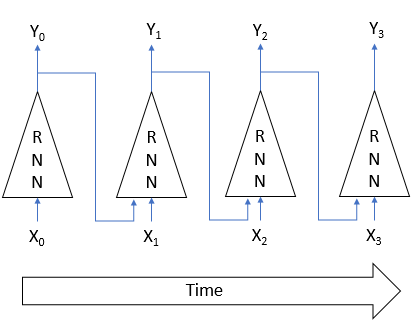
As redes neurais recorrentes são treinadas pelo já conhecido método backpropagation - retropropagação. Similarmente ao treinamento das redes neurais convolucionais, a natureza cíclica do processo no tempo é decomposta em um perceptron multicamadas. Cada intervalo de tempo em tal perceptron atua como uma camada oculta. No entanto, é usada uma matriz de pesos para todas as camadas de tal perceptron. Portanto, para ajustar os pesos, obtemos a soma dos gradientes para todas as camadas e calculamos o delta dos pesos uma vez para o gradiente total de todas as camadas.
3. Construindo uma rede neural recorrente
Nós usaremos o bloco LSTM para construir nossa rede neural recorrente. Vamos começar com a criação da classe CNeuronLSTM. Para preservar a estrutura de herança da classe criada no artigo anterior, nós vamos criar a nova classe como herdeira da classe CNeuronProof.
class CNeuronLSTM : public CNeuronProof { protected: CLayer *ForgetGate; CLayer *InputGate; CLayer *OutputGate; CLayer *NewContent; CArrayDouble *Memory; CArrayDouble *Input; CArrayDouble *InputGradient; //--- virtual bool feedForward(CLayer *prevLayer); virtual bool calcHiddenGradients(CLayer *&nextLayer); virtual bool updateInputWeights(CLayer *&prevLayer); virtual bool updateInputWeights(CLayer *gate, CArrayDouble *input_data); virtual bool InitLayer(CLayer *layer, int numOutputs, int numOutputs); virtual CArrayDouble *CalculateGate(CLayer *gate, CArrayDouble *sequence); public: CNeuronLSTM(void); ~CNeuronLSTM(void); virtual bool Init(uint numOutputs,uint myIndex,int window, int step, int units_count); //--- virtual CLayer *getOutputLayer(void) { return OutputLayer; } virtual bool calcInputGradients(CLayer *prevLayer) ; virtual bool calcInputGradients(CNeuronBase *prevNeuron, uint index) ; //--- methods for working with files virtual bool Save( int const file_handle); virtual bool Load( int const file_handle); virtual int Type(void) const { return defNeuronLSTM; } };
A classe pai contém uma camada de neurônios de saída OutputLayer. Vamos adicionar 4 camadas neurais necessárias para a operação do algoritmo: ForgetGate, InputGate, OutputGate e NewContent. Adicionamos também 3 arrays para armazenar os dados da "memória", para combinar com Input data e Hidden state, bem como o gradiente de erro dos dados de entrada. O nome e a funcionalidade dos métodos de classe correspondem aos considerados anteriormente. No entanto, seus códigos têm algumas diferenças, que são necessárias para a operação do algoritmo. Vamos considerar os métodos principais com mais detalhes.
3.1. Método de inicialização da classe.
O método de inicialização da classe recebe nos parâmetros as informações básicas sobre o bloco que está sendo criado. Os nomes dos parâmetros do método foram herdados da classe base, mas alguns deles possuem agora um significado diferente:
- numOutputs — o número de conexões de saída. Eles são usados quando uma camada totalmente conectada segue a camada de bloco LSTM.
- myIndex — índice de um neurônio na camada. Ele é usado para a identificação do bloco.
- window — Tamanho do canal de dados de entrada.
- step — não é usado.
- units_count — a largura do canal de saída e o número de neurônios nas camadas ocultas do bloco. Todas as camadas neurais de um bloco contêm o mesmo número de neurônios.
bool CNeuronLSTM::Init(uint numOutputs,uint myIndex,int window,int step,int units_count) { if(units_count<=0) return false; //--- Init Layers if(!CNeuronProof::Init(numOutputs,myIndex,window,step,units_count)) return false; if(!InitLayer(ForgetGate,units_count,window+units_count)) return false; if(!InitLayer(InputGate,units_count,window+units_count)) return false; if(!InitLayer(OutputGate,units_count,window+units_count)) return false; if(!InitLayer(NewContent,units_count,window+units_count)) return false; if(!Memory.Reserve(units_count)) return false; for(int i=0; i<units_count; i++) if(!Memory.Add(0)) return false; //--- return true; }
Dentro do método, nós verificamos primeiro se pelo menos um neurônio foi criado em cada camada neural do bloco. Em seguida, nós chamamos o método correspondente da classe base. Após a conclusão bem-sucedida do método, inicializamos as camadas ocultas do bloco, enquanto as operações que se repetem para cada camada serão fornecidas em um método separado InitLayer. Assim que a inicialização das camadas neurais estiver concluída, a matriz de memória é inicializada com valores iguais a zero.
O método de inicialização da camada neural InitLayer recebe em parâmetros um ponteiro para o objeto da camada neural inicializada, o número de neurônios na camada e o número de conexões de saída. No início do método, verificamos a validade do ponteiro recebido. Se o ponteiro for inválido, criamos uma nova instância de classe da camada neural. Se o ponteiro for válido, limpamos a camada de neurônios.
bool CNeuronLSTM::InitLayer(CLayer *layer,int numUnits, int numOutputs) { if(CheckPointer(layer)==POINTER_INVALID) { layer=new CLayer(numOutputs); if(CheckPointer(layer)==POINTER_INVALID) return false; } else layer.Clear();
Preenchemos a camada com o número necessário de neurônios. Se ocorrer um erro em qualquer um dos estágios do método, saímos da função com o resultado false.
if(!layer.Reserve(numUnits)) return false; //--- CNeuron *temp; for(int i=0; i<numUnits; i++) { temp=new CNeuron(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.Init(numOutputs+1,i)) return false; if(!layer.Add(temp)) return false; } //--- return true; }
Após a conclusão bem-sucedida de todas as iterações, saímos do método com o resultado true.
3.2. Feed-forward.
O método feed forward (propagação direta) é implementado no método feedForward. O método recebe nos parâmetros um ponteiro para a camada neural anterior. No início do método, verificamos a validade do ponteiro recebido e a disponibilidade dos neurônios na camada anterior. Verificamos também a validade da matriz usada para os dados de entrada. Se o objeto não foi criado, criamos uma nova instância de classe. Se um objeto já existe, limpamos a matriz.
bool CNeuronLSTM::feedForward(CLayer *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID || prevLayer.Total()<=0) return false; CNeuronBase *temp; CConnection *temp_con; if(CheckPointer(Input)==POINTER_INVALID) { Input=new CArrayDouble(); if(CheckPointer(Input)==POINTER_INVALID) return false; } else Input.Clear();
Em seguida, combinamos os dados sobre o estado atual do sistema e os dados sobre o estado no intervalo de tempo anterior em uma única matriz de dados de entrada Input.
int total=prevLayer.Total(); if(!Input.Reserve(total+OutputLayer.Total())) return false; for(int i=0; i<total; i++) { temp=prevLayer.At(i); if(CheckPointer(temp)==POINTER_INVALID || !Input.Add(temp.getOutputVal())) return false; } total=OutputLayer.Total(); for(int i=0; i<total; i++) { temp=OutputLayer.At(i); if(CheckPointer(temp)==POINTER_INVALID || !Input.Add(temp.getOutputVal())) return false; } int total_data=Input.Total();
Calculamos o valor das portas. Da mesma forma que a inicialização, movemos as operações repetidas para cada porta em um método CalculateGate separado. Chamamos aqui este método, inserindo nele os ponteiros para a porta processada e a matriz de dados inicial.
//--- Calculated forget gate CArrayDouble *forget_gate=CalculateGate(ForgetGate,Input); if(CheckPointer(forget_gate)==POINTER_INVALID) return false; //--- Calculated input gate CArrayDouble *input_gate=CalculateGate(InputGate,Input); if(CheckPointer(input_gate)==POINTER_INVALID) return false; //--- Calculated output gate CArrayDouble *output_gate=CalculateGate(OutputGate,Input); if(CheckPointer(output_gate)==POINTER_INVALID) return false;
Calculamos e normalizamos os dados de entrada na matriz new_content.
//--- Calculated new content CArrayDouble *new_content=new CArrayDouble(); if(CheckPointer(new_content)==POINTER_INVALID) return false; total=NewContent.Total(); for(int i=0; i<total; i++) { temp=NewContent.At(i); if(CheckPointer(temp)==POINTER_INVALID) return false; double val=0; for(int c=0; c<total_data; c++) { temp_con=temp.Connections.At(c); if(CheckPointer(temp_con)==POINTER_INVALID) return false; val+=temp_con.weight*Input.At(c); } val=TanhFunction(val); temp.setOutputVal(val); if(!new_content.Add(val)) return false; }
Finalmente, depois de todos os cálculos intermediários, calculamos a matriz de "memória" e determinamos os dados de saída.
//--- Calculated output sequences for(int i=0; i<total; i++) { double value=Memory.At(i)*forget_gate.At(i)+new_content.At(i)*input_gate.At(i); if(!Memory.Update(i,value)) return false; temp=OutputLayer.At(i); value=TanhFunction(value)*output_gate.At(i); temp.setOutputVal(value); }
Em seguida, removemos as matrizes de dados intermediárias e saímos do método com true.
delete forget_gate; delete input_gate; delete new_content; delete output_gate; //--- return true; }
No método CalculateGate acima, a matriz de pesos é multiplicada pelo vetor de dados inicial, seguido pela normalização dos dados através da função de ativação sigmoide. Este método recebe nos parâmetros 2 ponteiros para os objetos da camada neural e a sequência de dados original. Primeiro, verificamos a validade dos ponteiros recebidos.
CArrayDouble *CNeuronLSTM::CalculateGate(CLayer *gate,CArrayDouble *sequence)
{
CNeuronBase *temp;
CConnection *temp_con;
CArrayDouble *result=new CArrayDouble();
if(CheckPointer(gate)==POINTER_INVALID)
return NULL;
Em seguida, implementamos um loop por todos os neurônios.
int total=gate.Total(); int total_data=sequence.Total(); for(int i=0; i<total; i++) { temp=gate.At(i); if(CheckPointer(temp)==POINTER_INVALID) { delete result; return NULL; }
Depois de verificar a validade do ponteiro para o objeto neuron, implementamos um loop aninhado por todos os pesos do neurônio, enquanto calculamos a soma dos produtos dos pesos pelo elemento correspondente na matriz de dados inicial.
double val=0; for(int c=0; c<total_data; c++) { temp_con=temp.Connections.At(c); if(CheckPointer(temp_con)==POINTER_INVALID) { delete result; return NULL; } val+=temp_con.weight*(sequence.At(c)==DBL_MAX ? 1 : sequence.At(c)); }
A soma de produtos resultante é passada pela função de ativação. O resultado é gravado na saída do neurônio e adicionado ao array. Depois de iterar com sucesso todos os neurônios da camada, saímos do método retornando uma matriz de resultados. Se ocorrer um erro em qualquer estágio de cálculo, o método retornará um valor vazio.
val=SigmoidFunction(val); temp.setOutputVal(val); if(!result.Add(val)) { delete result; return NULL; } } //--- return result; }
3.3. Cálculo do gradiente do erro.
Os gradientes de erro são calculados no método calcHiddenGradients, que recebe um ponteiro para a próxima camada de neurônios nos parâmetros. No início do método, verificamos a relevância do objeto criado anteriormente usado para armazenar a sequência de gradientes de erro para os dados originais. Se o objeto ainda não foi criado, criamos uma nova instância. Se um objeto já existe, limpamos a matriz. Além disso, declaramos as variáveis internas e as instâncias de classe.
bool CNeuronLSTM::calcHiddenGradients(CLayer *&nextLayer) { if(CheckPointer(InputGradient)==POINTER_INVALID) { InputGradient=new CArrayDouble(); if(CheckPointer(InputGradient)==POINTER_INVALID) return false; } else InputGradient.Clear(); //--- int total=OutputLayer.Total(); CNeuron *temp; CArrayDouble *MemoryGradient=new CArrayDouble(); CNeuron *gate; CConnection *con;
Em seguida, calculamos o gradiente de erro para a camada de saída dos neurônios, que veio da próxima camada neural.
for(int i=0; i<total; i++) { temp=OutputLayer.At(i); if(CheckPointer(temp)==POINTER_INVALID) return false; temp.setGradient(temp.sumDOW(nextLayer)); }
Estendemos o gradiente resultante para todas as camadas neurais internas da LSTM.
if(CheckPointer(MemoryGradient)==POINTER_INVALID) return false; if(!MemoryGradient.Reserve(total)) return false; for(int i=0; i<total; i++) { temp=OutputLayer.At(i); gate=OutputGate.At(i); if(CheckPointer(gate)==POINTER_INVALID) return false; double value=temp.getGradient()*gate.getOutputVal(); value=TanhFunctionDerivative(Memory.At(i))*value; if(i>=MemoryGradient.Total()) { if(!MemoryGradient.Add(value)) return false; } else { value=MemoryGradient.At(i)+value; if(!MemoryGradient.Update(i,value)) return false; } gate.setGradient(gate.getOutputVal()!=0 && temp.getGradient()!=0 ? temp.getGradient()*temp.getOutputVal()*SigmoidFunctionDerivative(gate.getOutputVal())/gate.getOutputVal() : 0); //--- Calcculated gates and new content gradients gate=ForgetGate.At(i); if(CheckPointer(gate)==POINTER_INVALID) return false; gate.setGradient(gate.getOutputVal()!=0 && value!=0? value*SigmoidFunctionDerivative(gate.getOutputVal()) : 0); gate=InputGate.At(i); temp=NewContent.At(i); if(CheckPointer(gate)==POINTER_INVALID) return false; gate.setGradient(gate.getOutputVal()!=0 && value!=0 ? value*temp.getOutputVal()*SigmoidFunctionDerivative(gate.getOutputVal()) : 0); temp.setGradient(temp.getOutputVal()!=0 && value!=0 ? value*gate.getOutputVal()*TanhFunctionDerivative(temp.getOutputVal()) : 0); }
Depois de calcular os gradientes nas camadas neurais internas, calculamos o gradiente de erro para a sequência de dados iniciais.
//--- Calculated input gradients int total_inp=temp.getConnections().Total(); for(int n=0; n<total_inp; n++) { double value=0; for(int i=0; i<total; i++) { temp=ForgetGate.At(i); con=temp.getConnections().At(n); value+=temp.getGradient()*con.weight; //--- temp=InputGate.At(i); con=temp.getConnections().At(n); value+=temp.getGradient()*con.weight; //--- temp=OutputGate.At(i); con=temp.getConnections().At(n); value+=temp.getGradient()*con.weight; //--- temp=NewContent.At(i); con=temp.getConnections().At(n); value+=temp.getGradient()*con.weight; } if(InputGradient.Total()>=n) { if(!InputGradient.Add(value)) return false; } else if(!InputGradient.Update(n,value)) return false; }
Depois de calcular todos os gradientes, excluímos os objetos desnecessários e saímos do método com true.
delete MemoryGradient; //--- return true; }
Preste atenção no seguinte ponto: na parte teórica, eu mencionei a necessidade de desenrolar a sequência no tempo e calcular os gradientes de erro em cada etapa do tempo. Isso não foi feito aqui, uma vez que o coeficiente de treinamento usado é muito menor que 1, e a influência do gradiente de erro nos intervalos de tempo anteriores será tão pequena que ela pode ser ignorada para melhorar o desempenho geral do algoritmo.
3.4. Atualizando os pesos.
Naturalmente, após obter os gradientes de erro, nós precisamos corrigir os pesos de todas as camadas neurais da LSTM. Esta tarefa é implementada no método updateInputWeights, que recebeu um ponteiro para a camada neural anterior nos parâmetros. Observe que a inserção de um ponteiro para a camada anterior só é implementada para preservar a estrutura de herança.
No início do método, verificamos a validade do ponteiro recebido e a disponibilidade da matriz de dados inicial. Após a validação bem-sucedida dos ponteiros, continuamos ajustando os pesos das camadas neurais internas. Novamente, as ações repetidas são movidas para um método updateInputWeights separado, cujo parâmetros nós passamos os ponteiros para uma camada neural específica e uma matriz de dados inicial. Aqui, o método auxiliar é chamado sucessivamente para cada camada neural.
bool CNeuronLSTM::updateInputWeights(CLayer *&prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID || CheckPointer(Input)==POINTER_INVALID) return false; //--- if(!updateInputWeights(ForgetGate,Input) || !updateInputWeights(InputGate,Input) || !updateInputWeights(OutputGate,Input) || !updateInputWeights(NewContent,Input)) { return false; } //--- return true; }
Vamos considerar as operações realizadas no método updateInputWeights(CLayer *gate, CArrayDouble *input_data). No início do método, verificamos a validade dos ponteiros recebidos nos parâmetros e declaramos as variáveis internas.
bool CNeuronLSTM::updateInputWeights(CLayer *gate,CArrayDouble *input_data) { if(CheckPointer(gate)==POINTER_INVALID || CheckPointer(input_data)==POINTER_INVALID) return false; CNeuronBase *neuron; CConnection *con; int total_n=gate.Total(); int total_data=input_data.Total();
Organizamos os loops aninhados para iterar sobre todos os neurônios da camada e os pesos nos neurônios, com a correção da matriz de peso. A fórmula de ajuste de peso é a mesma que foi considerada anteriormente para CNeuron::updateInputWeights(CArrayObj *&prevLayer). No entanto, nós não podemos usar aqui o método criado anteriormente porque daquela vez nós usamos as conexões de neurônios para se conectar com a próxima camada, enquanto agora eles são usados para se conectar com a camada anterior.
for(int n=0; n<total_n; n++) { neuron=gate.At(n); if(CheckPointer(neuron)==POINTER_INVALID) return false; for(int i=0; i<total_data; i++) { con=neuron.getConnections().At(i); if(CheckPointer(con)==POINTER_INVALID) return false; double data=input_data.At(i); con.weight+=con.deltaWeight=(neuron.getGradient()!=0 && data!=0 ? eta*neuron.getGradient()*(data!=DBL_MAX ? data : 1) : 0)+alpha*con.deltaWeight; } } //--- return true; }
Depois de atualizar a matriz de peso, saímos do método com true.
Depois de criar a classe, vamos fazer pequenos ajustes nos despachantes da classe base CNeuronBase para que eles possam manipular corretamente as instâncias da nova classe. O código completo de todos os métodos e funções está disponível no anexo.
4. Teste
O bloco LSTM recém-criado foi testado nas mesmas condições que usamos para testar as redes convolucionais no artigo anterior. O Expert Advisor Fractal_LSTM foi criado para testes. Essencialmente, este é o mesmo Fractal_conv do artigo anterior. Mas na função OnInit, no bloco de especificação da estrutura de rede, as camadas convolucionais e de subamostragem foram substituídas por uma camada de 4 blocos LSTM (por analogia com 4 filtros da rede convolucional).
//--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=4; desc.type=defNeuronLSTM; desc.window=(int)HistoryBars*12; desc.step=(int)HistoryBars/2; if(!Topology.Add(desc)) return INIT_FAILED;
Nenhuma outra alteração foi feita no código do EA. Todo o código e as classes do EA estão em anexo.
Obviamente, o uso de 4 camadas neurais internas em cada bloco LSTM e a complexidade do algoritmo em si afetaram o desempenho e, portanto, a velocidade dessa rede neural é um pouco menor do que a rede convolucional, que foi considerada anteriormente. No entanto, a raiz do erro quadrático médio da rede recorrente é muito menor.
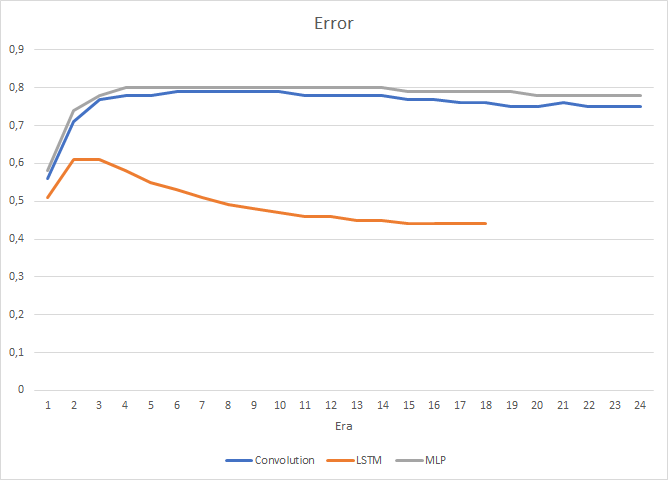
No processo de treinamento recorrente da rede neural, o gráfico de precisão de acerto do alvo tem uma tendência ascendente, quase que em linha reta.
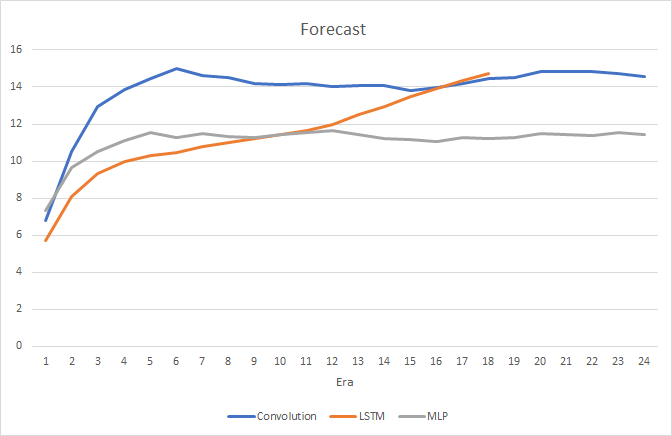
No gráfico de preços, são visíveis apenas alguns pontos dos fractais previstos. Nos testes anteriores, o gráfico de preços estava cheio de rótulos de previsão.
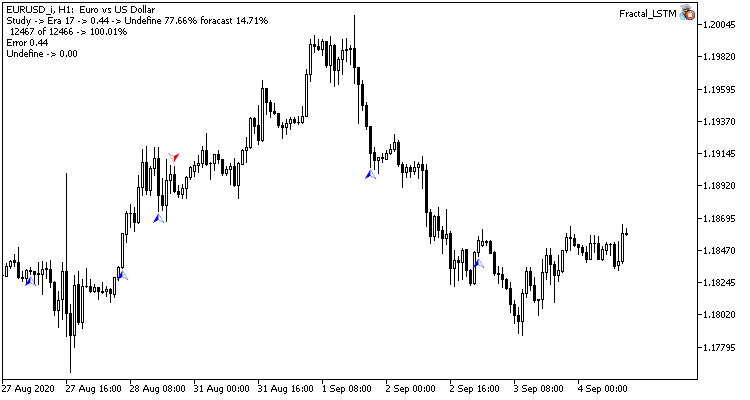
Conclusão
Neste artigo, nós examinamos o algoritmo de redes neurais recorrentes, construímos um bloco LSTM e testamos a operação da rede neural criada usando dados reais. Em comparação com os tipos de redes neurais considerados anteriormente, as redes recorrentes são mais intensivas em recursos e esforços, tanto durante uma passagem da propagação direta quanto no processo de aprendizagem. No entanto, elas apresentam melhores resultados, o que foi confirmado pelos testes realizados.
Links
- Redes Neurais de Maneira Fácil
- Redes neurais de maneira fácil (Parte 2): Treinamento e teste da rede
- Redes Neurais de Maneira Fácil (Parte 3): Redes Convolucionais
- Entendendo as redes LSTM
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Fractal.mq5 | Expert Advisor | Um Expert Advisor com a rede neural de regressão (1 neurônio na camada de saída) |
| 2 | Fractal_2.mq5 | Expert Advisor | Um Expert Advisor com a rede neural de classificação (3 neurônios na camada de saída) |
| 3 | NeuroNet.mqh | Biblioteca de classe | Uma biblioteca de classes para a criação de uma rede neural (um perceptron) |
| 4 | ractal_conv.mq5 | Expert Advisor | Um Expert Advisor com a rede neural convolucional (3 neurônios na camada de saída) |
| 5 | Fractal_LSTM.mq5 | Expert Advisor | Um Expert Advisor com a rede neural recorrente (3 neurônios na camada de saída) |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/8385
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Como ganhar US$ 1 000 000 por meio do trading algorítmico? Nos serviços MQL5.com!
Como ganhar US$ 1 000 000 por meio do trading algorítmico? Nos serviços MQL5.com!
 Grade e martingale: o que são e como usá-los?
Grade e martingale: o que são e como usá-los?
 Redes Neurais de Maneira Fácil (Parte 5): Cálculos em Paralelo com o OpenCL
Redes Neurais de Maneira Fácil (Parte 5): Cálculos em Paralelo com o OpenCL
 Redes Neurais de Maneira Fácil (Parte 3): Redes Convolucionais
Redes Neurais de Maneira Fácil (Parte 3): Redes Convolucionais
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Boa discussão sobre NN! Espero encontrar algo sobre como carregar no MQL5 um NN treinado externamente no MT5.
No meu caso, tenho um mxnet, que gostaria que pudesse ser carregado no mql5. Verifiquei a base de código, mas não encontrei nenhum exemplo sobre quais bibliotecas usar. Alguma ajuda?
Pesquisa e análise de detalhes fascinantes. O profissionalismo do autor é inquestionável - a implementação dos blocos de software confirma isso. A questão que se coloca é a seguinte: Se o Python e, consequentemente, o Keras, o TensorFlow e o PyTorch puderem ser usados em programas MQL5, seria mais fácil e mais promissor implementar redes neurais com essas ferramentas usando o rico kit de ferramentas?
Pesquisa e análise de detalhes fascinantes. O profissionalismo do autor é inquestionável - a implementação dos blocos de software confirma isso. A questão que se coloca é a seguinte: Se o Python e, consequentemente, o Keras, o TensorFlow e o PyTorch puderem ser usados em programas MQL5, seria mais fácil e mais promissor implementar redes neurais com essas ferramentas usando o rico kit de ferramentas?
Há vários motivos.
1. Este artigo permite que você veja os princípios do algoritmo. Se não estiver interessado, você sempre poderá usar bibliotecas prontas do Python e de outras linguagens de programação.
2. A primeira integração do Python foi adicionada em 12 de junho de 2019, versão 2085, na qual você só podia obter cotações. Desde então, os recursos de integração têm sido continuamente expandidos. Mas, mesmo agora, eles não estão completos. As possibilidades da MQL5 são mais amplas.
3. Muitas pessoas aqui não são programadores profissionais. E para elas, aprender a integração e outra linguagem de programação pode ser difícil. Talvez alguém ache o artigo difícil de entender, mas sempre poderá usar o código pronto anexado para seus desenvolvimentos.
Dê uma olhada no Python. As bibliotecas que você mencionou também foram criadas uma vez e usam integração com outras linguagens de programação, o que o usuário talvez nem perceba. E a criação de tais bibliotecas em MQL5 apenas expande seus recursos.