Perceptron Multicamadas e o Algoritmo Backpropagation

Introdução:

• Recentemente, ao aumentar a popularidade desses métodos, tantas bibliotecas foram desenvolvidas em Matlab, R, Python, C++, e etc, que recebem o conjunto de treinamento como entrada e constroem automaticamente uma Rede Neural apropriada para o suposto problema.

• Mas usando essas bibliotecas, às vezes não entendemos exatamente o que aconteceu e como chegamos à rede otimizada. Conhecer o fundamental de uma solução é muito importante no desenvolvimento dos métodos passados. Então, neste artigo, faremos uma estrutura muito simples do algoritmo da Rede Neural

• Vamos entender como funciona um tipo básico de Rede Neural, (Perceptron de um único neurônio e Perceptron Multicamadas), e um fascinante algoritmo responsável pelo aprendizado da rede, (Gradiente descendente e o Backpropagation). Tais modelos de rede serviram de base para os modelos mais complexos existentes hoje.

Uma breve passagem pela história:

• A primeira rede neural foi concebida por Warren McCulloch e Walter Pitts em 1943. Eles escreveram um artigo seminal sobre como os neurônios devem funcionar e, então, modelaram suas ideias criando uma rede neural simples com circuitos elétricos.

• As Pesquisas em IA aceleraram rapidamente, com Kunihiko Fukushima a primeira rede neural multicamada de verdade em 1975.

• O objetivo original de uma rede neural era criar um sistema computacional capaz de resolver problemas como um cérebro humano. No entanto, com o passar do tempo, os pesquisadores mudaram o foco e passaram a usar redes neurais para resolver tarefas específicas. Desde então, as redes neurais têm oferecido suporte às mais diversas tarefas, incluindo visão computacional, reconhecimento de fala, tradução de máquina, filtragem de redes sociais, jogos de tabuleiro ou videogame, diagnósticos médicos, previsão meteorológica, previsão de séries temporais, reconhecimento de (imagem, texto, voz) etc.

Perceptron de um neurônio:

O Perceptron é inspirado no processamento de informações de uma única célula neural chamada neurônio. Um neurônio aceita sinais de entrada através de seus dendritos, que passam o sinal elétrico para o corpo celular. Da mesma forma, o Perceptron recebe sinais de entrada de exemplos de dados de treinamento que ponderamos e combinados em uma equação linear chamada ativação.

• z = sum(weight_i * x_i) + bias

Onde weight  é um peso de rede, X é uma entrada, i é o índice de um peso ou uma entrada e bias é um peso especial que não tem entrada para multiplicar (ou você pode pensar na entrada como sempre sendo 1.0).

A ativação é então transformada em um valor de saída (previsão) usando uma função de transferência (Função de Ativação).

• y = 1.0 se z >= 0.0 senão 0.0

Desta forma, o Perceptron é um algoritmo de classificação para problemas com duas classes, (classificador binário) onde uma equação linear pode ser usada para separar as duas classes.

Está intimamente relacionada à regressão linear e à regressão logística que fazem previsões de forma semelhante (por exemplo, uma soma ponderada de insumos).

O algoritmo Perceptron é o tipo mais simples de rede neural artificial. É um modelo de um único neurônio que pode ser usado para problemas de classificação de duas classes e fornece a base para o desenvolvimento posterior de redes muito maiores.

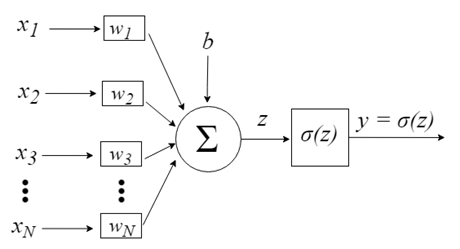
Modelo computacional de um neurônio - (Perceptron)

As entradas nos neurônios são representadas pelo vetor x = [x1, x2, x3, …, xN], podendo corresponder a uma serie de preço de cotação de um ativo, valores de indicadores técnicos, uma sequência numérica, pixels de uma imagem, por exemplo. Ao chegarem ao neurônio, são multiplicados pelos respectivos pesos sinápticos, que são os elementos do vetor w = [w1, w2, w3, …, wN], gerando o valor z, comumente denominado potencial de ativação, de acordo com a expressão:

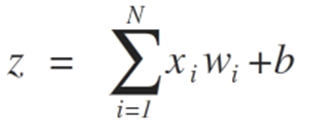
b provê um grau de liberdade maior, e não é afetado pela entrada nessa expressão, correspondendo tipicamente ao “bias” (viés). O valor z passa então por uma função de ativação σ, responsável por limitar tal valor a um certo intervalo,(0 - 1 por exemplo), produzindo o valor final de saída y do neurônio. Algumas funções de ativação usadas são a degrau, sigmoide, tangente hiperbólica, softmax e ReLU (Rectified Linear Unit).

A fim de ilustrar o processo visando o alcance da fronteira da separabilidade entre classes apresentamos abaixo duas situações que mostram sua convergência rumo a estabilização considerando apenas duas entradas {x1 e x2}

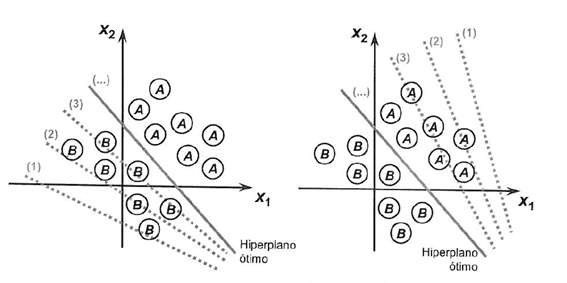
Os pesos do algoritmo Perceptron devem ser estimados a partir de seus dados de treinamento usando descida de gradiente estocástico.

Gradiente Estocástico:

Descida de gradiente é o processo de minimizar uma função seguindo os gradientes da função de custo.

Isso envolve conhecer a forma do custo, bem como o derivado para que a partir de um determinado ponto você conheça o gradiente e possa se mover nessa direção, por exemplo, ladeira abaixo em direção ao valor mínimo.

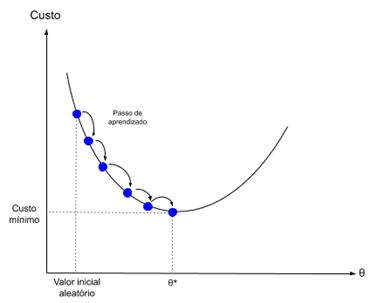
No aprendizado de máquina, podemos usar uma técnica que avalia e atualiza os pesos de cada iteração chamada descida de gradiente estocástico para minimizar o erro de um modelo em nossos dados de treinamento.

A maneira como este algoritmo de otimização funciona é que cada instância de treinamento é mostrada ao modelo um de cada vez. O modelo faz uma previsão para uma instância de treinamento, o erro é calculado e o modelo é atualizado a fim de reduzir o erro para a próxima previsão.

Este procedimento pode ser usado para encontrar o conjunto de pesos em um modelo que resulte no menor erro para o modelo nos dados de treinamento.

Para o algoritmo Perceptron, cada iteração os pesos w são atualizados usando a equação:

• w = w + learning_rate * (expected - predicted) * x

Onde  w está sendo otimizado,  learning_rate é uma taxa de aprendizado que você deve configurar (por exemplo, 0,1),  (esperado – previsto) é o erro de previsão para o modelo sobre os dados de treinamento atribuídos ao peso e  X é o valor de entrada.

A descida de gradiente estocástico requer dois parâmetros:

• Taxa de Aprendizagem: Usado para limitar a quantidade cada peso é corrigido cada vez que é atualizado.
• Épocas: O número de vezes para executar através dos dados de treinamento enquanto atualiza o peso.

Estes, juntamente com os dados de treinamento serão os argumentos para a função.

Há 3 loops que precisamos executar na função:

1. Loop para cada época.

2. Loop para cada linha nos dados de treinamento para uma época.

3. Loop para cada peso atualizando-o para uma linha em uma época.

Os pesos são atualizados com base no erro que o modelo cometeu. O erro é calculado como a diferença entre o valor real e a previsão feita com os pesos.

Há um peso para cada atributo de entrada, e estes são atualizados de forma consistente, por exemplo:

• w(t+1)= w(t) + learning_rate * (expected(t) - predicted(t)) * x(t)

O viés é atualizado de forma semelhante, exceto sem uma entrada, pois não está associado a um valor de entrada específico:

• bias(t+1) = bias(t) + learning_rate * (expected(t) - predicted(t)).

Aplicação do modelo de um neurônio:

Agora, vamos passar à aplicação prática.

Este tutorial é dividido em 2 partes:

1. Fazendo previsões.

2. Otimização dos Pesos da Rede

Estas etapas lhe darão a base para poder implementar e aplicar o algoritmo Perceptron a outros problemas de classificação.

Precisamos definir o número de colunas de nosso conjunto X, para isso definimos a constante

#define nINPUT 3

---

Em MQL5 um array multidimensional pode ser estático ou dinâmico apenas para a primeira dimensão, sendo que todas as outras dimensões serão estáticas, por esse motivo somos obrigados a definir o tamanho na declaração do array.

 

1. Fazendo previsões

O primeiro passo é desenvolver uma função que possa fazer previsões.

Isso será necessário tanto na avaliação dos valores de pesos dos candidatos na descida do gradiente estocástico, quanto após a finalização do modelo e queremos começar a fazer previsões sobre dados de teste ou novos dados.

Abaixo está uma função nomeada  predict que prevê um valor de saída para uma linha dado um conjunto de pesos.

O primeiro peso é sempre o viés, pois é autônomo e não é responsável por um valor de entrada específico.

// Make a prediction with weights
template <typename Array>
double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0)
  {
   double z = weights[0];
   for(int i=0; i<ArrayRange(X, 1)-1; i++)
     {
      z+=weights[i+1]*X[row][i];
     }
   return activation(z);
  }

Transferência de neurônios:

Uma vez que um neurônio é ativado, precisamos transferir a ativação para ver o que a saída do neurônio realmente é.

//+------------------------------------------------------------------+
//|                Transfer neuron activation                        |
//+------------------------------------------------------------------+
double activation(const double activation) //#
  {
   return activation>=0.0?1.0:0.0;
  }

Recebemos como argumento na função predict o conjunto de entrada X, o array com os pesos (W) e a linha a qual está sendo feita a previsão do conjunto de entrada X.

Podemos inventar um pequeno conjunto de dados para testar nossa função de previsão.

Também podemos usar pesos previamente preparados para fazer previsões para este conjunto de dados.

double weights[] = {-0.1, 0.20653640140000007, -0.23418117710000003};

Juntando tudo isso podemos testar nossa função de previsão abaixo.

#define nINPUT 3
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   random.seed(42);
   double dataset[][nINPUT] = {     //X1     //X2   //Y  
                               {2.7810836,2.550537003,0},
                               {1.465489372,2.362125076,0},
                               {3.396561688,4.400293529,0},
                               {1.38807019,1.850220317,0},
                               {3.06407232,3.005305973,0},
                               {7.627531214,2.759262235,1},
                               {5.332441248,2.088626775,1},
                               {6.922596716,1.77106367,1},
                               {8.675418651,-0.242068655,1},
                               {7.673756466,3.508563011,1}
                              };
   double weights[] = {-0.1, 0.20653640140000007, -0.23418117710000003};
   for(int row=0; row<ArrayRange(dataset, 0); row++)
     {
      double predict = predict(dataset, weights, row);
      printf("Expected=%.1f, Predicted=%.1f", dataset[row][nINPUT-1], predict);
     }
  }
//+------------------------------------------------------------------+
// Make a prediction with weights
template <typename Array>
double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0)
  {
   double z = weights[0];
   for(int i=0; i<ArrayRange(X, 1)-1; i++)
     {
      z+=weights[i+1]*X[row][i];
     }
   return activation(z);
  }
//+------------------------------------------------------------------+
//|                Transfer neuron activation                        |
//+------------------------------------------------------------------+
double activation(const double activation) //#
  {
   return activation>=0.0?1.0:0.0;
  }

Existem dois valores de entradas ( X1 e  X2) e três valores de peso (viés,  w1 e  w2). A equação de ativação que modelamos para este problema é:

activation = (w1 * X1) + (w2 * X2) + b

Ou, com os valores de peso específicos, escolhemos à mão como:

activation = (0.206 * X1) + (-0.234 * X2) + -0.1

Executando esta função temos previsões que correspondem aos valores de saída esperados y .

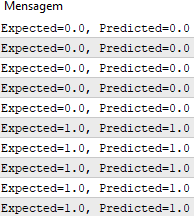
Agora podemos implementar a descida de gradiente estocástico para otimizar os valores dos pesos.

2. Otimização dos pesos da rede

Podemos estimar os valores de peso para nossos dados de treinamento usando descida de gradiente estocástico, como dito anteriormente.

Abaixo está uma função chamada train_weights() que calcula os valores de peso para um conjunto de dados de treinamento usando descida de gradiente estocástico.

Em MQL5 não podemos ter um retorno desse array com os dados dos pesos treinados, pois, ao contrário das variáveis, os arrays apenas podem ser passados para uma função por referência. Isso significa que a função não cria a sua própria instância do array e, ao invés disso, trabalha diretamente com o array passado para ela. Assim, todas as mudanças realizadas nesse array dentro da função fazem com que o array original seja afetado.

//+------------------------------------------------------------------+
//|  Estimate Perceptron weights using stochastic gradient descent   |
//+------------------------------------------------------------------+
template <typename Array>
void train_weights(Array &weights[], const Array &X[][nINPUT], double l_rate=0.1, int n_epoch=5)
  {
   ArrayResize(weights, ArrayRange(X, 1));
   for(int i=0; i<ArrayRange(X, 1); i++)
     {
      weights[i]=random.random();
     }
     
   for(int epoch=0; epoch<n_epoch; epoch++)
     {
      double sum_error = 0.0;
      for(int row=0; row<ArrayRange(X, 0); row++)
        {
         double y = predict(X, weights, row);
         double error = X[row][nINPUT-1] - y;
         sum_error += pow(error, 2);
         weights[0] = weights[0] + l_rate * error;

         for(int i=0; i<ArrayRange(X, 1)-1; i++)
           {
            weights[i+1] = weights[i+1] + l_rate * error * X[row][i];
           }
        }
      printf(">epoch=%d, lrate=%.3f, error=%.3f",epoch, l_rate, sum_error);
     }
  }

Você pode ver que acompanhamos a soma do erro quadrado (um valor positivo) em cada época para acompanhar a diminuição do erro, assim podemos ver em qual época o algoritmo conseguiu minimizar o erro.

Podemos então testar nossa função com o mesmo conjunto de dados apresentado acima.

#define nINPUT 3
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   random.seed(42);
   double dataset[][nINPUT] = {     //X1     //X2   //Y  
                               {2.7810836,2.550537003,0},
                               {1.465489372,2.362125076,0},
                               {3.396561688,4.400293529,0},
                               {1.38807019,1.850220317,0},
                               {3.06407232,3.005305973,0},
                               {7.627531214,2.759262235,1},
                               {5.332441248,2.088626775,1},
                               {6.922596716,1.77106367,1},
                               {8.675418651,-0.242068655,1},
                               {7.673756466,3.508563011,1}
                              };
   double weights[];
   train_weights(weights, dataset);
   ArrayPrint(weights, 20);
   for(int row=0; row<ArrayRange(dataset, 0); row++)
     {
      double predict = predict(dataset, weights, row);
      printf("Expected=%.1f, Predicted=%.1f", dataset[row][nINPUT-1], predict);
     }
  }
//+------------------------------------------------------------------+
// Make a prediction with weights
template <typename Array>
double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0)
  {
   double z = weights[0];
   for(int i=0; i<ArrayRange(X, 1)-1; i++)
     {
      z+=weights[i+1]*X[row][i];
     }
   return activation(z);
  }
//+------------------------------------------------------------------+
//|                Transfer neuron activation                        |
//+------------------------------------------------------------------+
double activation(const double activation) //#
  {
   return activation>=0.0?1.0:0.0;
  }
//+------------------------------------------------------------------+
//|  Estimate Perceptron weights using stochastic gradient descent   |
//+------------------------------------------------------------------+
template <typename Array>
void train_weights(Array &weights[], const Array &X[][nINPUT], double l_rate=0.1, int n_epoch=5)
  {
   ArrayResize(weights, ArrayRange(X, 1));
   ArrayInitialize(weights, 0);
     
   for(int epoch=0; epoch<n_epoch; epoch++)
     {
      double sum_error = 0.0;
      for(int row=0; row<ArrayRange(X, 0); row++)
        {
         double y = predict(X, weights, row);
         double error = X[row][nINPUT-1] - y;
         sum_error += pow(error, 2);
         weights[0] = weights[0] + l_rate * error;

         for(int i=0; i<ArrayRange(X, 1)-1; i++)
           {
            weights[i+1] = weights[i+1] + l_rate * error * X[row][i];
           }
        }
      printf(">epoch=%d, lrate=%.3f, error=%.3f",epoch, l_rate, sum_error);
     }
  }

Usamos uma taxa de aprendizagem de 0,1 e treinamos o modelo para apenas 5 épocas, ou 5 exposições dos pesos para todo o conjunto de dados de treinamento.

Executar o exemplo imprime uma mensagem em cada época com a soma do erro ao quadrado para aquela época e o conjunto final de pesos.

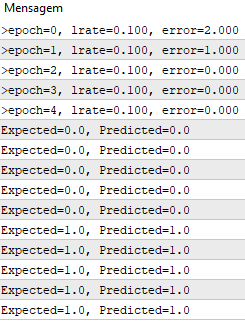
Você pode ver como o problema é aprendido muito rapidamente pelo algoritmo.

Esse teste pode ser encontrado no arquivo PerceptronScript.mq5.

Perceptron Multicamadas:

• Combinando neurônios em camadas

o   Com apenas um neurônio não se pode fazer muita coisa, mas podemos combiná-los em uma estrutura em camadas, cada uma com número diferente de neurônios, formando uma rede neural denominada Perceptron Multicamadas (“Multi Layer Perceptron — MLP”). O vetor de valores de entrada X passa pela camada inicial, cujos valores de saída são ligados às entradas da camada seguinte, e assim por diante, até a rede fornecer como resultado os valores de saída da última camada. Pode-se arranjar a rede em várias camadas, tornando-a profunda e capaz de aprender relações cada vez mais complexas.

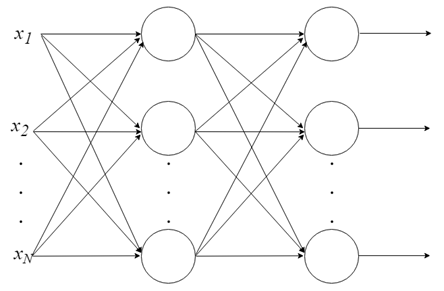
Treinamento de um MLP:

o   Para que uma rede dessas funcione, é preciso treiná-la. É como ensinar a uma criança o beabá. O treinamento de uma rede MLP insere-se no contexto de aprendizado de máquina supervisionado, mas como isso funciona?

Aprendizagem supervisionada:

• Nos é dado um conjunto de dados rotulados que já sabemos qual é a nossa saída correta e que deve ser semelhante ao conjunto, tendo a ideia de que existe uma relação entre a entrada e a saída.
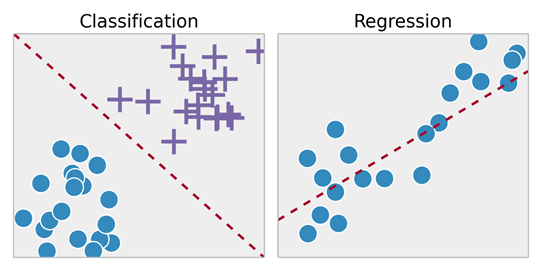
• Problemas de aprendizagem supervisionados são classificados em problemas de “regressão” e “classificação”. Em um problema de regressão, estamos tentando prever os resultados em uma saída contínua, o que significa que estamos a tentando mapear variáveis ​​de entrada para alguma função contínua. Em um problema de classificação, estamos tentando prever os resultados em uma saída discreta. Em outras palavras, estamos tentando mapear variáveis ​​de entrada em categorias distintas.

Exemplo 1:

• Dado um conjunto de dados sobre o tamanho de casas no mercado imobiliário, tentar prever o seu preço. Preço em função do tamanho é uma saída contínua, de modo que este é um problema de regressão.
• Poderíamos também transformar esse exemplo em um problema de classificação, e em vez de fazer a nossa produção sobre se a casa “é vendida por mais ou menos do que o preço pedido.” Aqui estamos classificando as casas com base no preço em duas categorias distintas.

Backpropagation:

O backpropagation é indiscutivelmente o algoritmo mais importante na história das redes neurais – sem backpropagation (eficiente), seria impossível treinar redes de aprendizagem profunda da forma que vemos hoje. O backpropagation pode ser considerado a pedra angular das redes neurais modernas e aprendizagem profunda

“Não é errando que se aprende?”

A ideia do algoritmo backpropagation é, com base no cálculo do erro ocorrido na camada de saída da rede neural, recalcular o valor dos pesos do vetor W da camada última camada de neurônios e assim proceder para as camadas anteriores, de trás para a frente, ou seja, atualizar todos os pesos w das camadas a partir da última até atingir a camada de entrada da rede, para isso realizando a retropropagação do erro obtido pela rede. Em outras palavras, calcula-se o erro entre o que a rede previu e o que de fato era (real 1 previsto 0 — temos aí um erro!), então recalculamos o valor de todos os pesos, começando da última camada e indo até a primeira, sempre tendo em vista diminuir esse erro. 

O algoritmo de backpropagation consiste em duas fases:

1. O passo para frente (forward pass), onde nossas entradas são passadas através da rede e as previsões de saída obtidas (essa etapa também é conhecida como fase de propagação).

2. O passo para trás (backward pass), onde calculamos o gradiente da função de perda na camada final (ou seja, camada de previsão) da rede e usamos esse gradiente para aplicar recursivamente a regra da cadeia (chain rule) para atualizar os pesos em nossa rede (etapa também conhecida como fase de atualização de pesos ou retro-propagação).

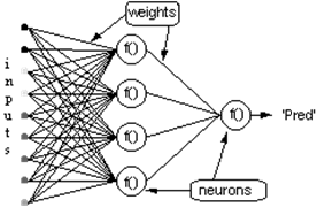
Considere a rede acima, com uma camada de neurônios ocultos e um neurônio de saída. Quando um vetor de entrada é propagado pela rede, para o conjunto atual de pesos há uma saída Pred(y). O objetivo do treinamento supervisionado é ajustar os pesos de forma que a diferença entre a saída Pred(Ŷ)da rede e a saída necessária Req(Y) seja reduzida. Isso requer um algoritmo que reduza o erro absoluto, que é o mesmo que reduzir o erro quadrado, onde:

(1)

Erro de rede = Pred - Req

      = E

 

O algoritmo deve ajustar os pesos de forma que E² seja minimizado. A retropropagação é um algoritmo que executa uma minimização de gradiente descendente de E². Para minimizar E², deve-se calcular sua sensibilidade a cada um dos pesos. Em outras palavras, precisamos saber qual efeito a alteração de cada um dos pesos terá em E². Se isso for conhecido, os pesos podem ser ajustados na direção que reduz o erro absoluto. A notação para a seguinte descrição da regra de propagação reversa é baseada no diagrama abaixo.

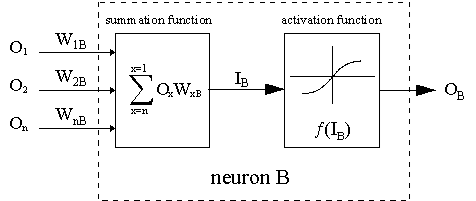
A linha tracejada representa um neurônio B, que pode ser um neurônio oculto ou de saída. As saídas de n neurônios (O 1 ... O n) na camada anterior fornecem as entradas para o neurônio B. Se o neurônio B está na camada oculta, então este é simplesmente o vetor de entrada. Essas saídas são multiplicadas pelos respectivos pesos (W1B ... WnB), onde WnB é o peso que conecta o neurônio n ao neurônio B. A função de soma adiciona todos esses produtos para fornecer a entrada, IB, que é processada pela função de ativação f (.) do neurônio B. f (IB) é a saída, OB, do neurônio B. Para o propósito desta ilustração, deixe o neurônio 1 ser chamado de neurônio A e então considere o peso WAB conectando os dois neurônios. A aproximação usada para a mudança de peso é dada pela regra delta:

(2)

onde  é o parâmetro da taxa de aprendizagem, que determina a taxa de aprendizagem, e

é a sensibilidade do erro, E², ao peso WAB e determina a direção de busca no espaço de peso para o novo peso WAB (novo) conforme ilustrado na figura abaixo.

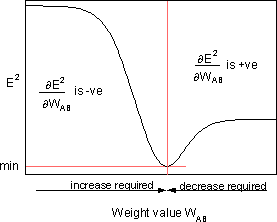
A fim de minimizar E², a regra delta fornece a direção da mudança de peso necessária

O conceito-chave da equação anterior é o cálculo da expressão ∂E² /∂WAB, consistindo em computar as derivadas parciais da função do erro E² em relação a cada peso do vetor W.

Regra de cadeia:

(3)

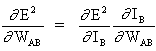
E

(4)

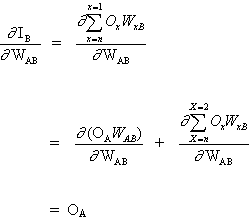
uma vez que o resto das entradas para o neurônio B não dependem do peso WAB. Assim, a partir de equações (3) e (4), equação. (2) torna-se,

(5)

e a mudança de peso de WAB depende da sensibilidade do erro quadrático, E², à entrada, IB, da unidade B e do sinal de entrada OA.

Existem duas situações possíveis:

1. B é o neurônio de saída;

2. B é um neurônio oculto.

Considerando o primeiro caso:

Visto que B é o neurônio de saída, a mudança no erro quadrático devido a um ajuste de WAB é simplesmente a mudança no erro quadrático da saída de B.

(6)

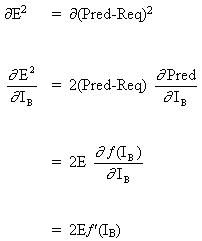
combinando equação (5) com (6) obtemos:

(7)

a regra para modificar os pesos quando o neurônio B é um neurônio de saída, se a função de ativação de saída, f (.), É a função logística:

(8)

Diferenciando equação (8) por seu argumento x:

(9)

Mas,

(10)

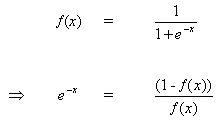
inserir (10) em (9) dá:

(11)

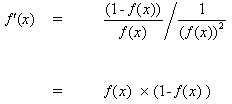
da mesma forma para a função tanh,

ou para a função linear (identidade),

Isto dá:

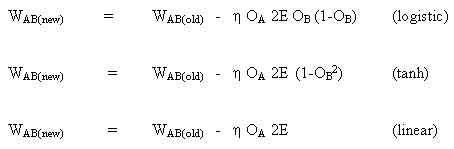
Considerando o segundo caso:

B é um neurônio oculto.

(12)

onde O, representa o neurônio de saída.

(13)

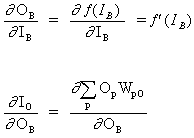
onde p é um índice que abrange todos os neurônios, incluindo o neurônio B, que fornece sinais de entrada para o neurônio de saída. Expandindo o lado direito da equação (13),

(14)

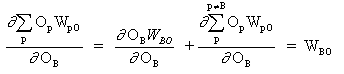
uma vez que os pesos dos outros neurônios, WpO (p! = B) não têm dependência de OB.

Inserindo (13) e (13) em (12):

(15)

Portanto  agora é expresso como uma função de   calculado como descrito na equação (6).

A regra completa para modificar o peso WAB entre um neurônio A enviando um sinal para um neurônio B é,

(16)

onde,

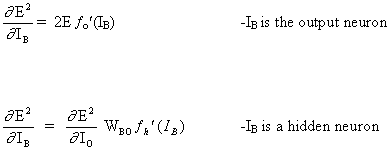
onde fo (.) e fh (.) são as funções de saída e ativação oculta, respectivamente.

Exemplo:

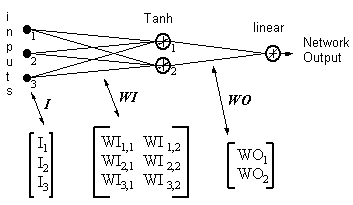
Saída da rede = [tanh(I ^T .WI)] . WO

HID = [Tanh(I ^T.WI)] ^T- as saídas dos neurônios ocultos

ERROR = (saída de rede - saída necessária)

LR = taxa de aprendizagem

As atualizações de peso se tornam,

 

neurônio de saída linear:

(17)

WO = WO - ( LR x ERROR x HID )

neurônio oculto tanh,

(18)

WI = WI - { LR x [ERROR x WO x (1- HID ²)] . I ^T } ^T

 

As Equações 17 e 18 mostram que a mudança de peso é um sinal de entrada multiplicado por um gradiente local. Isso fornece uma direção que também tem magnitude dependente da magnitude do erro. Se a direção for tomada sem magnitude, todas as mudanças serão do mesmo tamanho, o que dependerá da taxa de aprendizagem. O algoritmo acima é uma versão simplificada, pois há apenas um neurônio de saída. No algoritmo original, mais de uma saída é permitida e a descida do gradiente minimiza o erro quadrático total de todas as saídas. Existem muitos algoritmos que evoluíram do algoritmo original com o objetivo de aumentar a velocidade de aprendizagem. Eles estão resumidos em:

 

" Back Propagation family album" - Technical report C/TR96-05, Department of Computing, Macquarie University, NSW, Australia.”

 

O backpropagation é um algoritmo elegante e engenhoso. Os atuais modelos deep learning como Redes Neurais Convolucionais, embora mais refinados que o MLP, têm se mostrado muito superiores em tarefas como classificação de imagens e utilizam como método de aprendizado o backpropagation, assim como as chamadas Redes Neurais Recorrentes, em processamento de linguagem natural, também fazem uso desse algoritmo. O mais incrível é que tais modelos conseguem encontrar padrões inobserváveis e obscuros para nós, humanos, o que é fascinante e permite considerar que em breve contaremos com a ajuda do deep learning para resolver muitos dos principais problemas que afligem a humanidade.

Aplicação do modelo MLP:

Este tutorial é dividido em 5 partes:

1.       Inicialização da rede

2.       Propagação (FeedForward).

3.       Backpropagation.

4.       Treinamento da rede.

5.       Prever.

 

Para o nosso desenvolvimento faremos a implementação em MQL puro. É sabido que há bibliotecas em outras linguagens que já estão muito mais sofisticadas e é fortemente recomendado usá-las, por questões práticas e de performance, mas, como dito no início é importante entender o funcionamento interno de tais bibliotecas a fim de ter maior controle de todo o processo. Também não usamos OOP em nosso teste, pois como é apenas um algoritmo para ilustrar as equações acima não se faz necessário, porém, em casos do mundo real é muito mais pratico usar OOP, visto que traz uma escalabilidade para o projeto.

1. Inicialização da Rede

Cada neurônio tem um conjunto de pesos que precisam ser mantidos. Um peso para cada conexão de entrada e um peso adicional para o viés.

É uma boa prática inicializar os pesos da rede para pequenos números aleatórios. Neste caso, usaremos números aleatórios na faixa de 0 a 1. Para isso criamos uma função para a geração de números aleatórios.

double random(void)
  {
   return ((double)rand())/(double)SHORT_MAX;
  }

Abaixo está uma função chamada initialize_network() que cria os pesos da nossa rede neural.

// Forward propagate input to a network output
void forward_propagate(void)
  {
//calculate the outputs of the hidden neurons
//the hidden neurons are tanh
   int i = 0;
   for(i = 0; i<numHidden; i++)
     {
      hiddenVal[i] = 0.0;
      for(int j = 0; j<numInputs; j++)
        {
         hiddenVal[i] += (X[patNum][j] * weightsIH[j][i]);
        }
      hiddenVal[i] = tanh(hiddenVal[i]);
     }
//calculate the output of the network
//the output neuron is linear
   outPred = 0.0;
   for(i = 0; i<numHidden; i++)
     {
      outPred += hiddenVal[i] * weightsHO[i];
     }
//calculate the error
   errThisPat = outPred - y[patNum];
  }

3. Backpropagation

O algoritmo de retropagação é nomeado pela forma como os pesos são treinados.

O erro é calculado entre as saídas esperadas e as saídas para a frente propagadas da rede. Esses erros são então propagados para trás através da rede da camada de saída para a camada oculta, atribuindo a culpa pelo erro e atualizando pesos à medida que eles vão.

A matemática para erro de retropagação foi explicada acima.

//+------------------------------------------------------------------+
//|        Backpropagate error and change network weights            |
//+------------------------------------------------------------------+
void backward_propagate_error(void)
  {
//adjust the weights hidden-output
   for(int k = 0; k<numHidden; k++)
     {
      double weightChange = LR_HO * errThisPat * hiddenVal[k];
      weightsHO[k] -= weightChange;
      //regularisation on the output weights
      regularisationWeights(weightsHO[k]);
     }
// adjust the weights input-hidden
   for(int i = 0; i<numHidden; i++)
     {
      for(int k = 0; k<numInputs; k++)
        {
         double x = 1 - pow(hiddenVal[i],2);
         x = x * weightsHO[i] * errThisPat * LR_IH;
         x = x * X[patNum][k];
         double weightChange = x;
         weightsIH[k][i] -= weightChange;
        }
     }
  }

o método regularisationWeights foi criado apenas para regularizar os pesos numa faixa de -5 a 5.

//regularisation on the output weights
void regularisationWeights(double &weight)
  {
   weight<-5?weight=-5:weight>5?weight=5:weight=weight;
  }

4. Treinamento da rede

A rede é treinada usando descida de gradiente estocástico.

Isso envolve várias iterações de expor um conjunto de dados de treinamento à rede e para cada linha de dados para a frente propagando as entradas, retropagando o erro e atualizando os pesos da rede.

//# Train a network for a fixed number of epochs
void train(void)
  {
   for(int j = 0; j <= numEpochs; j++)
     {
      for(int i = 0; i<numPatterns; i++)
        {
         //select a pattern at random
         patNum = rand()%numPatterns;
         //calculate the current network output
         //and error for this pattern
         forward_propagate();
         backward_propagate_error();
        }
      //display the overall network error
      //after each epoch
      calcOverallError();
      printf("epoch = %d RMS Error = %f",j,RMSerror);
     }
  }

5. Prever

Fazer previsões com uma rede neural treinada é bastante fácil.

Já vimos como propagar um padrão de entrada para obter uma saída. Isso é tudo que precisamos fazer para fazer uma previsão. Podemos usar os valores de saída diretamente como a probabilidade de um padrão pertencente a cada classe de saída.

// # Make a prediction with a network
void predict(void)
  {
   for(int i = 0; i<numPatterns; i++)
     {
      patNum = i;
      forward_propagate();
      printf("real = %d predict = %f",y[patNum],outPred);
     }
  }

O Exemplo completo pode ser encontrado no arquivo MLP_Script.mq5

Conclusão:

Abordamos os cálculos envolvidos no processo de desenvolvimento de um neurônio perceptron e também de uma rede de neurônios perceptrons denominada Multi Layer Perceptron — MLP, nesse processo entendemos como é feito o treinamento desse tipo de rede, usando retropropagação e descida de gradiente.