
Redes Neurais de Maneira Fácil
Índice
- Introdução
- 1. Princípios de criação das redes de IA
- 2. A estrutura de um neurônio artificial
- 3. Treinamento da rede
- 4. Construindo a nossa própria rede neural usando a MQL
- Conclusão
- Referências
- Programas utilizados no artigo
Introdução
A Inteligência Artificial está cada vez mais cobrindo vários aspectos da nossa vida. Muitas publicações novas aparecem, afirmando que "a rede neural foi treinada para..." no entanto, a inteligência artificial ainda está associada a algo fantástico. A ideia parece ser muito complicada, sobrenatural e inexplicável. Portanto, esse milagre de última geração só pode ser criado por um grupo de cientistas. Parece que um programa semelhante não pode ser desenvolvido usando nosso computador doméstico. Mas acredite, não é tão difícil. Vamos tentar entender o que são as redes neurais e como elas podem ser aplicadas na negociação.
1. Princípios de criação das redes de IA
Na Wikipedia é fornecida a seguinte definição de rede neural:
As redes neurais artificiais (RNA) são sistemas computacionais vagamente inspirados nas redes neurais biológicas que constituem os cérebros de animais. Uma RNA é baseada em uma coleção de unidades ou nós conectados chamados neurônios artificiais, que modelam livremente os neurônios em um cérebro biológico.
Ou seja, uma rede neural é uma entidade composta por neurônios artificiais, entre os quais existe um relacionamento organizado. Essas relações são semelhantes a um cérebro biológico.
A figura abaixo mostra um diagrama de rede neural simples. Aqui, os círculos indicam os neurônios e as linhas visualizam as conexões entre os neurônios. Os neurônios estão localizados em camadas que são divididas em três grupos. Em azul indica a camada de neurônios de entrada, que significa a entrada de informações da fonte. Em verde e azul são os neurônios de saída, que emitem o resultado da operação da rede neural. Entre eles, os neurônios cinzentos formam uma camada oculta.
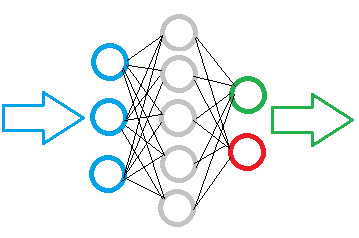
Apesar das camadas, toda a rede é construída dos mesmos neurônios, com vários elementos para os sinais de entrada e apenas um elemento para o resultado. Os dados de entrada são processados dentro do neurônio e, em seguida, um resultado lógico simples é gerado. Por exemplo, isso pode ser sim ou não. Quando aplicado à negociação, o resultado pode ser emitido como um sinal de negociação ou como uma direção de negociação.
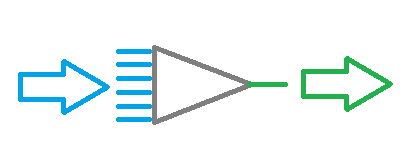
A informação inicial é inserida na camada de neurônios de entrada, depois ela é processada e o resultado do processamento serve como fonte de informação para os neurônios da próxima camada. As operações são repetidas de uma camada para outra até que se atinja a camada de neurônios de saída. Assim, os dados iniciais são processados e filtrados de uma camada para outra e, depois disso, um resultado é gerado.
Dependendo da complexidade da tarefa e dos modelos criados, o número de neurônios em cada camada pode variar. Algumas variações de rede podem incluir várias camadas ocultas. Uma rede neural mais avançada pode resolver problemas mais complexos. No entanto, isso exigiria mais recursos computacionais.
Portanto, ao criar um modelo de rede neural, é necessário definir o volume de dados a serem processados e o resultado desejado. Isso influencia o número de neurônios necessários nas camadas do modelo.
Se nós precisarmos inserir uma matriz de 10 elementos em uma rede neural, a camada da rede de entrada deverá conter 10 neurônios. Isso permitirá a aceitação de todos os 10 elementos do array de dados. Neurônios extras de entrada serão excessivos.
A qualidade dos neurônios de saída é determinada pelo resultado esperado. Para obter um resultado lógico inequívoco, basta um neurônio de saída. Se você deseja receber respostas para várias perguntas, crie um neurônio para cada uma das perguntas.
Camadas ocultas servem como um centro analítico que processa e analisa as informações recebidas. Portanto, o número de neurônios na camada depende da variabilidade dos dados da camada anterior, ou seja, cada neurônio sugere uma certa hipótese de eventos.
O número de camadas ocultas é determinado por um relacionamento causal entre os dados de origem e o resultado esperado. Por exemplo, se desejamos criar um modelo para a técnica "5 why", uma solução lógica é usar 4 camadas ocultas, que, juntamente com a camada de saída, possibilitarão colocar 5 perguntas aos dados de origem.
Resumo:
- uma rede neural é construída com os mesmos neurônios; portanto, uma classe de neurônios é suficiente para construir um modelo;
- os neurônios no modelo são organizados em camadas;
- o fluxo de dados na rede neural é implementado como uma transmissão serial de dados através de todas as camadas do modelo, dos neurônios de entrada aos neurônios de saída;
- o número de neurônios de entrada depende da quantidade de dados analisados por passagem, enquanto o número de neurônios de saída depende da quantidade de dados resultante;
- como um resultado lógico é formado na saída, as perguntas dadas à rede neural devem fornecer a possibilidade de dar uma resposta inequívoca.
2. A estrutura de um neurônio artificial
Agora que nós consideramos a estrutura da rede neural, vamos para a criação de um modelo de neurônio artificial. Todos os cálculos matemáticos e tomada de decisão são realizados dentro desse neurônio. Surge uma pergunta aqui: Como podemos implementar muitas soluções diferentes com base nos mesmos dados de origem e usando a mesma fórmula? A solução está em mudar as conexões entre os neurônios. Um coeficiente de peso é determinado para cada conexão. Esse peso define quanta influência o valor de entrada terá no resultado.
O modelo matemático de um neurônio consiste em duas funções. Os produtos dos dados de entrada por seus coeficientes de peso são sintetizados primeiro.
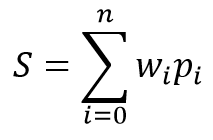
Com base no valor recebido, o resultado é calculado na chamada da função de ativação. Na prática, diferentes variantes da função de ativação são usadas. Os mais usados são os seguintes:
- Função sigmoide — o intervalo de valores de retorno é de "0" a "1"
- Tangente hiperbólica — o intervalo de valores de retorno é de "-1" a "1"
A escolha da função de ativação depende dos problemas que estão sendo resolvidos. Por exemplo, se nós esperamos uma resposta lógica como resultado do processamento de dados de origem, uma função sigmoide é preferida. Para fins de negociação, eu prefiro usar a tangente hiperbólica. O valor "-1" corresponde ao sinal de venda, "1" corresponde ao sinal de compra. Um resultado médio indica incerteza.
3. Treinamento da rede
Como mencionado acima, a variabilidade do resultado de cada neurônio e de toda a rede neural depende dos pesos selecionados para as conexões entre os neurônios. O problema de seleção do peso é chamado aprendizado da rede neural.
Uma rede pode ser treinada seguindo vários algoritmos e métodos:
- Aprendizado supervisionado;
- Aprendizagem não supervisionado;
- Aprendizagem por reforço.
O método de aprendizado depende dos dados de origem e das tarefas definidas para a rede neural.
O aprendizado supervisionado é usado quando há um conjunto suficiente de dados iniciais com as respostas corretas correspondentes às perguntas colocadas. Durante o processo de aprendizado, os dados iniciais são inseridos na rede e a saída é verificada com a resposta correta conhecida. Depois disso, os pesos são ajustados para reduzir o erro.
O aprendizado não supervisionado é usado quando há um conjunto de dados iniciais sem as respostas corretas correspondentes. Nesse método, a rede neural procura conjuntos de dados semelhantes e permite dividir os dados de origem em grupos semelhantes.
O aprendizado por reforço é usado quando não há respostas corretas, mas nós entendemos o resultado desejado. Durante o processo de aprendizado, os dados de origem são inseridos na rede, que tenta resolver o problema. Depois de verificar o resultado, um "feedback" é enviado como uma certa recompensa. Durante o aprendizado, a rede tenta receber a recompensa máxima.
Neste artigo, nós usaremos o aprendizado supervisionado. Como exemplo, eu uso o algoritmo de backpropagation. Essa abordagem permite o treinamento contínuo da rede neural em tempo real.
O método baseia-se no uso do erro de saída da rede neural para a correção de seus pesos. O algoritmo de aprendizado consiste em dois estágios. Primeiramente, com base nos dados de entrada, a rede calcula o valor resultante, que é verificado com o valor de referência e um erro é calculado. Em seguida, é realizado uma passagem reversa, com a propagação do erro da saída da rede para suas entradas, com o ajuste de todos os fatores de ponderação. Essa é uma abordagem interativa e a rede é treinada passo a passo. Depois de aprender a usar os dados históricos, a rede pode ser treinada ainda mais no modo online.
O método de backpropagation usa o gradiente descendente estocástico, o que permite atingir um erro aceitável mínimo. A possibilidade de treinar ainda mais a rede no modo online permite manter esse nível mínimo por um longo intervalo de tempo.
4. Construindo a nossa própria rede neural usando a MQL
Agora, vamos à parte prática do artigo. Para uma melhor visualização da operação da rede neural (RNA), nós criaremos um exemplo usando apenas a linguagem MQL5, sem bibliotecas de terceiros. Vamos começar com a criação das classes que armazenam os dados sobre as conexões elementares entre os neurônios.
4.1. Conexões
Primeiro, criamos a classe СConnection para armazenar o coeficiente de peso de uma conexão. Ela é criada como o filho da classe CObject. A classe conterá duas variáveis do tipo double: weight para armazenar o peso e deltaWeight, na qual armazenaremos o valor da última alteração do peso (usada no aprendizado). Para evitar a necessidade de usar métodos adicionais para trabalhar com as variáveis, nós vamos torná-las públicas. Os valores iniciais para as variáveis são definidos no construtor da classe.
class СConnection : public CObject { public: double weight; double deltaWeight; СConnection(double w) { weight=w; deltaWeight=0; } ~СConnection(){}; //--- methods for working with files virtual bool Save(const int file_handle); virtual bool Load(const int file_handle); };
Para habilitar o armazenamento de mais informações sobre as conexões, nós vamos criar um método para salvar os dados em um arquivo (Save) e ler esses dados (Load). Os métodos são baseados em um esquema clássico: o identificador do arquivo é recebido nos parâmetros do método, depois ele é verificado e, em seguida, os dados são escritos (ou lidos no método Load).
bool СConnection::Save(const int file_handle) { if(file_handle==INVALID_HANDLE) return false; //--- if(FileWriteDouble(file_handle,weight)<=0) return false; if(FileWriteDouble(file_handle,deltaWeight)<=0) return false; //--- return true; }
A próxima etapa é criar uma matriz para armazenar os pesos: CArrayCon com base na CArrayObj. Aqui, nós substituímos os dois métodos virtuais, CreateElement e Type. O primeiro será usado para criar um novo elemento e o segundo identificará a nossa classe.
class CArrayCon : public CArrayObj { public: CArrayCon(void){}; ~CArrayCon(void){}; //--- virtual bool CreateElement(const int index); virtual int Type(void) const { return(0x7781); } };
Nos parâmetros do método CreateElement, que cria um novo elemento, nós passaremos o índice desse novo elemento. Verificamos a validade do método, o tamanho da matriz de armazenamento de dados e redimensionamos-o se necessário. Em seguida, criamos uma nova instância da classe СConnection, atribuindo um peso aleatório inicial.
bool CArrayCon::CreateElement(const int index) { if(index<0) return false; //--- if(m_data_max<index+1) { if(ArrayResize(m_data,index+10)<=0) return false; m_data_max=ArraySize(m_data)-1; } //--- m_data[index]=new СConnection(MathRand()/32767.0); if(!CheckPointer(m_data[index])!=POINTER_INVALID) return false; m_data_total=MathMax(m_data_total,index); //--- return (true); }
4.2. Um neurônio
O próximo passo é criar o neurônio artificial. Como mencionado anteriormente, eu uso a tangente hiperbólica como função de ativação do meu neurônio. O intervalo de valores resultantes está entre "-1" e "1". "-1" indica um sinal de venda e "1" significa um sinal de compra.
Da mesma forma que o elemento CConnection anterior, a classe de neurônios artificiais CNeuron é herdada da classe CObject. No entanto, sua estrutura é um pouco mais complicada.
class CNeuron : public CObject { public: CNeuron(uint numOutputs,uint myIndex); ~CNeuron() {}; void setOutputVal(double val) { outputVal=val; } double getOutputVal() const { return outputVal; } void feedForward(const CArrayObj *&prevLayer); void calcOutputGradients(double targetVals); void calcHiddenGradients(const CArrayObj *&nextLayer); void updateInputWeights(CArrayObj *&prevLayer); //--- methods for working with files virtual bool Save(const int file_handle) { return(outputWeights.Save(file_handle)); } virtual bool Load(const int file_handle) { return(outputWeights.Load(file_handle)); } private: double eta; double alpha; static double activationFunction(double x); static double activationFunctionDerivative(double x); double sumDOW(const CArrayObj *&nextLayer) const; double outputVal; CArrayCon outputWeights; uint m_myIndex; double gradient; };
Nos parâmetros do construtor da classe, passamos o número de conexões dos neurônios de saída e o número ordinal do neurônio na camada (será usado para identificação subsequente do neurônio). No corpo do método, definimos as constantes, salvamos os dados recebidos e criamos uma matriz de conexões de saída.
CNeuron::CNeuron(uint numOutputs, uint myIndex) : eta(0.15), // net learning rate alpha(0.5) // momentum { for(uint c=0; c<numOutputs; c++) { outputWeights.CreateElement(c); } m_myIndex=myIndex; }
Os métodos setOutputVal e getOutputVal são usados para acessar o valor resultante do neurônio. Esse valor resultante do neurônio é calculado no método feedForward. A camada anterior de neurônios é inserida como os parâmetros para esse método.
void CNeuron::feedForward(const CArrayObj *&prevLayer) { double sum=0.0; int total=prevLayer.Total(); for(int n=0; n<total && !IsStopped(); n++) { CNeuron *temp=prevLayer.At(n); double val=temp.getOutputVal(); if(val!=0) { СConnection *con=temp.outputWeights.At(m_myIndex); sum+=val * con.weight; } } outputVal=activationFunction(sum); }
O corpo do método contém um loop através de todos os neurônios da camada anterior. Os produtos dos valores e pesos resultantes dos neurônios também são somados no corpo do método. Após o cálculo da soma, o valor resultante do neurônio é calculado no método activationFunction (a função de ativação do neurônio é implementada como em um método separado).
double CNeuron::activationFunction(double x) { //output range [-1.0..1.0] return tanh(x); }
O próximo bloco de métodos é usado no aprendizado da RNA. Criamos um método para calcular a derivada para a função de ativação, activationFunctionDerivative. Isso permite determinar uma alteração necessária na função de soma para compensar o erro do valor resultante do neurônio.
double CNeuron::activationFunctionDerivative(double x) { return 1/MathPow(cosh(x),2); }
Em seguida, criamos dois métodos de cálculo do gradiente para o ajuste do peso. Nós precisamos criar 2 métodos, porque o erro do valor resultante é calculado de maneiras diferentes para os neurônios da camada de saída e os das camadas ocultas. Para a camada de saída, o erro é calculado como a diferença entre o valor resultante e o valor de referência. Para os neurônios da camada oculta, o erro é calculado como a soma dos gradientes de todos os neurônios da camada subsequente ponderados com base nos pesos das conexões entre os neurônios. Este cálculo é implementado como um método sumDOW separado.
void CNeuron::calcHiddenGradients(const CArrayObj *&nextLayer) { double dow=sumDOW(nextLayer); gradient=dow*CNeuron::activationFunctionDerivative(outputVal); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CNeuron::calcOutputGradients(double targetVals) { double delta=targetVals-outputVal; gradient=delta*CNeuron::activationFunctionDerivative(outputVal); }
O gradiente é então determinado multiplicando o erro pela derivada da função de ativação.
Vamos considerar com mais detalhes o método sumDOW que determina o erro do neurônio para a camada oculta. O método recebe um ponteiro para a próxima camada de neurônios como parâmetro. No corpo do método, nós definimos primeiro o valor resultante da 'soma' como zero e, em seguida, implementamos um loop através de todos os neurônios da próxima camada e somamos o produto dos gradientes dos neurônios e o peso de sua conexão.
double CNeuron::sumDOW(const CArrayObj *&nextLayer) const { double sum=0.0; int total=nextLayer.Total()-1; for(int n=0; n<total; n++) { СConnection *con=outputWeights.At(n); CNeuron *neuron=nextLayer.At(n); sum+=con.weight*neuron.gradient; } return sum; }
Depois que o trabalho preparatório acima estiver concluído, nós precisamos apenas criar o método updateInputWeights que recalculará os pesos. No meu modelo, um neurônio armazena os pesos de saída, de modo que o método de atualização de peso recebe a camada anterior de neurônios nos parâmetros.
void CNeuron::updateInputWeights(CArrayObj *&prevLayer) { int total=prevLayer.Total(); for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron= prevLayer.At(n); СConnection *con=neuron.outputWeights.At(m_myIndex); con.weight+=con.deltaWeight=eta*neuron.getOutputVal()*gradient + alpha*con.deltaWeight; } }
O corpo do método contém um loop através de todos os neurônios da camada anterior, com o ajuste de pesos indicando a influência no neurônio atual.
Observe que o ajuste do peso é realizado usando dois coeficientes: eta (para reduzir a reação ao desvio atual) e alfa (coeficiente de inércia). Essa abordagem permite uma certa média da influência de várias iterações de aprendizado subsequentes e filtra os dados de ruído.
4.3. Rede neural
Depois de criar o neurônio artificial, nós precisamos combinar os objetos criados em uma única entidade, a rede neural. Os objetos resultantes devem ser flexíveis e devem permitir a criação das redes neurais de diferentes configurações. Isso nos permitirá usar a solução resultante para várias tarefas.
Como já mencionado acima, uma rede neural consiste de camadas de neurônios. Portanto, o primeiro passo é combinar os neurônios em uma camada. Vamos criar a classe CLayer. Seus métodos básicos são herdados da CArrayObj.
class CLayer: public CArrayObj { private: uint iOutputs; public: CLayer(const int outputs=0) { iOutputs=outpus; }; ~CLayer(void){}; //--- virtual bool CreateElement(const int index); virtual int Type(void) const { return(0x7779); } };
Nos parâmetros do método de inicialização da classe CLayer, nós definimos o número de elementos da próxima camada. Além disso, vamos reescrever dois métodos virtuais: CreateElement (criação de um novo neurônio da camada) e Type (método de identificação do objeto).
Ao criar um novo neurônio, nós especificamos o seu índice nos parâmetros do método. A validade do índice recebido é verificada no corpo do método. Em seguida, nós verificamos o tamanho da matriz para armazenar os ponteiros para as instâncias de objetos de neurônios e aumentamos o tamanho da matriz, se necessário. Depois disso, nós criamos o neurônio. Se a nova instância do neurônio for criada com sucesso, nós definimos o seu valor inicial e alteramos o número de objetos na matriz. Então saímos do método com 'true'.
bool CLayer::CreateElement(const uint index) { if(index<0) return false; //--- if(m_data_max<index+1) { if(ArrayResize(m_data,index+10)<=0) return false; m_data_max=ArraySize(m_data)-1; } //--- CNeuron *neuron=new CNeuron(iOutputs,index); if(!CheckPointer(neuron)!=POINTER_INVALID) return false; neuron.setOutputVal((neuronNum%3)-1) //--- m_data[index]=neuron; m_data_total=MathMax(m_data_total,index); //--- return (true); }
Usando uma abordagem semelhante, nós criamos a classe CArrayLayer para armazenar os ponteiros em nossas camadas de rede.
class CArrayLayer : public CArrayObj { public: CArrayLayer(void){}; ~CArrayLayer(void){}; //--- virtual bool CreateElement(const uint neurons, const uint outputs); virtual int Type(void) const { return(0x7780); } };
A diferença da classe anterior aparece no método CreateElement, que cria um novo elemento da matriz. Nos parâmetros deste método, nós especificamos o número de neurônios nas camadas atual e posterior a serem criadas. No corpo do método, nós verificamos o número de neurônios na camada. Se não houver neurônios na camada criada, saímos com 'false'. Em seguida, nós verificamos se é necessário redimensionar os ponteiros de armazenamento da matriz. Depois disso, o objeto pode ser criado: criamos uma nova camada e implementamos um loop para criar os neurônios. Verificamos o objeto criado em cada etapa. Em caso de erro, saímos com o valor 'false'. Depois de criar todos os elementos, salvamos o ponteiro na camada criada da matriz e saímos com 'true'.
bool CArrayLayer::CreateElement(const uint neurons, const uint outputs) { if(neurons<=0) return false; //--- if(m_data_max<=m_data_total) { if(ArrayResize(m_data,m_data_total+10)<=0) return false; m_data_max=ArraySize(m_data)-1; } //--- CLayer *layer=new CLayer(outputs); if(!CheckPointer(layer)!=POINTER_INVALID) return false; for(uint i=0; i<neurons; i++) if(!layer.CreatElement(i)) return false; //--- m_data[m_data_total]=layer; m_data_total++; //--- return (true); }
A criação das classes separadas para a camada e a matriz de camadas permite a criação de várias redes neurais com configurações diferentes, sem a necessidade de alterar as classes. Esta é uma entidade flexível que permite inserir o número desejado de camadas e neurônios por camada.
Agora vamos considerar a classe CNet, que cria uma rede neural.
class CNet { public: CNet(const CArrayInt *topology); ~CNet(){}; void feedForward(const CArrayDouble *inputVals); void backProp(const CArrayDouble *targetVals); void getResults(CArrayDouble *&resultVals); double getRecentAverageError() const { return recentAverageError; } bool Save(const string file_name, double error, double undefine, double forecast, datetime time, bool common=true); bool Load(const string file_name, double &error, double &undefine, double &forecast, datetime &time, bool common=true); //--- static double recentAverageSmoothingFactor; private: CArrayLayer layers; double recentAverageError; };
Nós já implementamos muito do que é necessário nas classes acima e, portanto, a própria classe de rede neural contém um mínimo de variáveis e métodos. O código da classe contém apenas duas variáveis estatísticas para calcular e armazenar o erro médio (recentAverageSmoothingFactor e recentAverageError), além de um ponteiro para a matriz 'layers' que contém as camadas da rede.
Vamos considerar os métodos dessa classe com mais detalhes. Um ponteiro para a matriz de dados do tipo int é passada nos parâmetros do construtor da classe. O número de elementos na matriz indica o número de camadas, enquanto cada elemento da matriz contém o número de neurônios na camada apropriada. Assim, essa classe universal pode ser usada para criar uma rede neural de qualquer nível de complexidade.
CNet::CNet(const CArrayInt *topology) { if(CheckPointer(topology)==POINTER_INVALID) return; //--- int numLayers=topology.Total(); for(int layerNum=0; layerNum<numLayers; layerNum++) { uint numOutputs=(layerNum==numLayers-1 ? 0 : topology.At(layerNum+1)); if(!layers.CreateElement(topology.At(layerNum), numOutputs)) return; } }
No corpo do método, nós verificamos a validade do ponteiro transmitido e implementamos um loop para criar as camadas na rede neural. Um valor igual a zero de conexões de saída é especificado para o nível de saída.
O método feedForward é usado para calcular o valor da rede neural. Nos parâmetros, o método recebe uma matriz de valores de entrada, com base nos quais os valores resultantes da rede neural serão calculados.
void CNet::feedForward(const CArrayDouble *inputVals) { if(CheckPointer(inputVals)==POINTER_INVALID) return; //--- CLayer *Layer=layers.At(0); if(CheckPointer(Layer)==POINTER_INVALID) { return; } int total=inputVals.Total(); if(total!=Layer.Total()-1) return; //--- for(int i=0; i<total && !IsStopped(); i++) { CNeuron *neuron=Layer.At(i); neuron.setOutputVal(inputVals.At(i)); } //--- total=layers.Total(); for(int layerNum=1; layerNum<total && !IsStopped(); layerNum++) { CArrayObj *prevLayer = layers.At(layerNum - 1); CArrayObj *currLayer = layers.At(layerNum); int t=currLayer.Total()-1; for(int n=0; n<t && !IsStopped(); n++) { CNeuron *neuron=currLayer.At(n); neuron.feedForward(prevLayer); } } }
No corpo do método, nós verificamos a validade do ponteiro de recebimento e da camada zero de nossa rede. Em seguida, definimos os valores iniciais recebidos como os valores resultantes dos neurônios da camada zero e implementamos um loop duplo com um recálculo em fases dos valores resultantes dos neurônios em toda a rede neural, da primeira camada oculta aos neurônios de saída.
O resultado é obtido usando o método getResults, que contém um loop coletando os valores resultantes dos neurônios da camada de saída.
void CNet::getResults(CArrayDouble *&resultVals) { if(CheckPointer(resultVals)==POINTER_INVALID) { resultVals=new CArrayDouble(); } resultVals.Clear(); CArrayObj *Layer=layers.At(layers.Total()-1); if(CheckPointer(Layer)==POINTER_INVALID) { return; } int total=Layer.Total()-1; for(int n=0; n<total; n++) { CNeuron *neuron=Layer.At(n); resultVals.Add(neuron.getOutputVal()); } }
O processo de aprendizado da rede neural é implementado no método backProp. O método recebe uma matriz de valores de referência de parâmetros. No corpo do método, nós verificamos a validade da matriz recebida e calculamos o erro quadrático médio da camada resultante. Então, no loop, recalculamos os gradientes dos neurônios em todas as camadas. Depois disso, na última camada do método, nós atualizamos os pesos das conexões entre os neurônios com base nos gradientes calculados anteriormente.
void CNet::backProp(const CArrayDouble *targetVals) { if(CheckPointer(targetVals)==POINTER_INVALID) return; CArrayObj *outputLayer=layers.At(layers.Total()-1); if(CheckPointer(outputLayer)==POINTER_INVALID) return; //--- double error=0.0; int total=outputLayer.Total()-1; for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron=outputLayer.At(n); double delta=targetVals[n]-neuron.getOutputVal(); error+=delta*delta; } error/= total; error = sqrt(error); recentAverageError+=(error-recentAverageError)/recentAverageSmoothingFactor; //--- for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron=outputLayer.At(n); neuron.calcOutputGradients(targetVals.At(n)); } //--- for(int layerNum=layers.Total()-2; layerNum>0; layerNum--) { CArrayObj *hiddenLayer=layers.At(layerNum); CArrayObj *nextLayer=layers.At(layerNum+1); total=hiddenLayer.Total(); for(int n=0; n<total && !IsStopped();++n) { CNeuron *neuron=hiddenLayer.At(n); neuron.calcHiddenGradients(nextLayer); } } //--- for(int layerNum=layers.Total()-1; layerNum>0; layerNum--) { CArrayObj *layer=layers.At(layerNum); CArrayObj *prevLayer=layers.At(layerNum-1); total=layer.Total()-1; for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron=layer.At(n); neuron.updateInputWeights(prevLayer); } } }
Para evitar a necessidade de treinar novamente o sistema em caso de reinicialização do programa, vamos criar o método 'Save' para salvar os dados em um arquivo local e o método 'Load' para carregar os dados salvos no arquivo.
O código completo de todos os métodos de classe está disponível em anexo.
Conclusão
O objetivo deste artigo foi mostrar como uma rede neural pode ser criada em casa. Claro, isso é apenas a ponta do iceberg. O artigo considera apenas uma das versões possíveis, ou seja, o perceptron, introduzido por Frank Rosenblatt em 1957. Mais de 60 anos se passaram desde a introdução do modelo, e vários outros modelos apareceram. No entanto, o modelo perceptron ainda é viável e gera bons resultados - você pode testar o modelo por conta própria. Aqueles que desejam aprofundar a ideia da inteligência artificial devem ler materiais relevantes, porque é impossível cobrir tudo, mesmo em uma série de artigos.
Referências
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | NeuroNet.mqh | Biblioteca da classe | Uma biblioteca de classes para a criação de uma rede neural (um perceptron) |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/7447
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Tradução automática aplicada pelo moderador
É muito frustrante quando se começa a ler um artigo com aproximadamente 50 partes e logo de cara dá um erro na compilação.
Por favor professor, poderia resolver este problema?
Alguém pode resolver?
Remova o "const" destas declarações e compilará normalmente