ニューラルネットワークが簡単に(第7回): 適応的最適化法

MetaTrader 5 — トレーディングシステム | 25 1月 2021, 08:51

918

Dmitriy Gizlyk

イントロダクション

以前の記事では、異なる種類のニューロンを使用していましたが、ニューラルネットワークのトレーニングには必ずストキャスティクススロープ降下法を使用していました。この方法はおそらく基本的なものと呼ぶことができ、そのバリエーションは実際にはよく使われています。しかし、ニューラルネットワークのトレーニングメソッドは他にもたくさんあります。今回は適応学習法の検討を提案します。この手法は、ニューラルネットワークの学習中にニューロンの学習速度を変化させることを可能にします。

1. 適応的最適化手法の特徴

ニューラルネットワークにインプットされたすべての特徴が最終的な結果に同じ影響を与えるわけではないことを知っています。パラメータは、多くのノイズを含む可能性があり、振幅の異なる他のパラメータよりも多くの頻度で変化することができます。他のパラメータのサンプルは、固定の学習率でニューラルネットワークをトレーニングする際に気づかれないようなレアな値を含んでいる場合があります。以前に検討されたストキャスティクススロープ降下法の欠点の一つは、このようなサンプルでは最適化機構が利用できないことです。その結果、学習のプロセスがローカルの最小値で止まってしまうことがあります。この問題は、ニューラルネットワークをトレーニングするための適応的手法を用いて解決することができます。これらの方法では、ニューラルネットワークの学習プロセスにおける学習率を動的に変化させることができます。このような方法とそのバリエーションはいくつかあります。その中でも人気の高いものを考えてみましょう。

1.1. 適応的スロープ法 (AdaGrad)

適応スロープ法は2011年に提案されました。ストキャスティクススロープ降下法のバリエーションです。メソッドの数式を比較することで、1つ差に気づくことができます：AdaGradの学習率は、以前のすべての学習繰り返しのスロープの２乗和の平方根で除算されます。このアプローチにより、頻繁に更新されるパラメータの学習率を低減することができます。

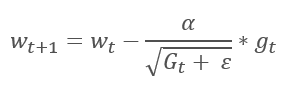
この方法の主な欠点は、その式にあります：スロープの２乗の和が大きくなるだけなので、学習率は0になるトレンドがあります。では、最終的にはトレーニングがストップしてしまいます。

この方法を利用するには、各ニューロンのスロープの２乗の和を格納するための追加の計算と追加のメモリの割り当てが必要です。

1.2. RMSPropメソッド

AdaGradメソッドの論理的な続きは、RMSPropメソッドです。学習率が0に落ちないように、過去のスロープの2乗和を、加重の更新に用いる式の分母の2乗スロープの指数平均に置き換えています。この方法では、分母の値が一定で無限に伸びることはありません。さらに、モデルの現在の状態を特徴づけるスロープの最新値にも注目します。

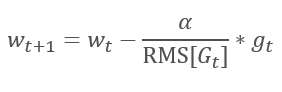
1.3. アダデルタ法

アダデルタ適応法は、RMSPropとほぼ同時に提案されました。このメソッドも同様で、加重の更新に使用する式の分母に２乗スロープの和の指数平均を使用します。しかし、RMSPropとは異なり、この方法は更新式の学習率を完全に拒否し、分析パラメータの過去の変化の２乗和の指数平均に置き換えます。

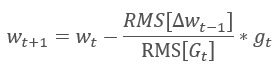
このアプローチにより、加重を更新する際に使用する式から学習率を削除し、適応性の高い学習アルゴリズムを作成することができます。しかし、このメソッドでは、各ニューロンに追加の値を格納するための計算の追加の繰り返しとメモリの割り当てが必要となります。

1.4. 適応モーメント推定法（アダム)

2014年には、Diederik P. KingmaとJimmy Lei Baが適応モーメント推定法(Adaptive Moment Estimation Method)（Adam)を提案しました。この著者らによると、このメソッドはAdaGrad法とRMSProp法の利点を組み合わせたもので、オンライントレーニングに適しているとのことです。このメソッドは、さまざまなサンプルで一貫して良好な結果を示します。様々なパッケージでデフォルトで使用することを推奨されることが多いです。

スロープの指数平均値mと２乗スロープの指数平均値vを算出する方法であって、前記方法は、前記スロープの指数平均値mと前記２乗スロープの指数平均値vを算出する方法です。各指数平均は、平均化期間を決定する独自のハイパーパラメータßがあります。

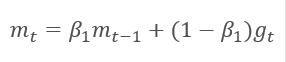
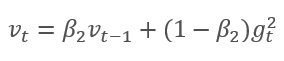
著者らは、ß1を0.9で、ß2を0.999でデフォルト使用することを提案します。この場合、m0とv0はゼロ値を取る。パラメータでは、上記のような式は、学習開始時に０に近い値を返すため、学習開始時の学習率が低くなります。学習のスピードを上げるために、得られたモーメントを修正することを提案します。

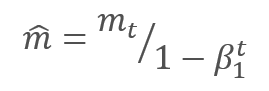
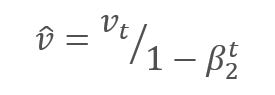
補正されたスロープモーメントmと２乗スロープの補正されたモーメントvの平方根との比を調整することで、パラメータを更新します。 0で割らないように、0に近いƐ定数を分母に加えます。結果として得られる比率は、学習係数αによって調整され、この場合、学習ステップの上限です。著者らは、デフォルトでαを0.001で使用することを提案しています。

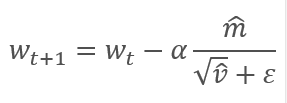
2. 実装

理論的に検討した後、実用化に進むことができます。著者が提供するデフォルトのハイパーパラメータを用いて Adam メソッドを実装することを提案します。さらに、ハイパーパラメータの他のバリエーションを試すことができます。

先に構築されたニューラルネットワークでは、学習にストキャスティクススロープ降下を使用していましたが、ついてはすでに逆伝播アルゴリズムを実装します。既存のバックプロパゲーション関数を使用してアダム法を実装することができます。加重更新アルゴリズムを実装するだけです。この関数は、ニューロンの各クラスに実装されているupdateInputWeightsメソッドによって実行されます。もちろん、先に作成したストキャスティクススロープ降下アルゴリズムは削除しません。トレーニング方法の選択が可能な代替アルゴリズムを作成してみましょう。

2.1. OpenCL カーネルの構築

CNeuronBaseOCL クラスの Adam メソッドの実装を考えてみましょう。まず、OpenCLでメソッドを実装するUpdateWeightsAdamカーネルを作成します。以下の行列へのポインタは、パラメータとしてカーネルに渡されます。

加重の行列 - matrix_w.
誤差スロープの行列 - matrix_g.
インプットデータ行列 - matrix_i.
スロープの指数平均の行列 - matrix_m.
２乗スロープの指数平均の行列 - matrix_v.

__kernel void UpdateWeightsAdam(__global double *matrix_w,
                                __global double *matrix_g,
                                __global double *matrix_i,
                                __global double *matrix_m,
                                __global double *matrix_v,
                                int inputs, double l, double b1, double b2)

さらに，カーネルパラメータでは，インプットデータ配列のサイズとアダムアルゴリズムのハイパーパラメータを渡します．

カーネルの開始時に、現在の層と前の層のニューロンの数をそれぞれ示す2次元のストリームのシリアル番号を取得します。受信した番号を使用して、バッファ内の処理された要素の初期番号を決定します。第2次元の結果として得られるストリーム番号に「4」が掛けられていることに注意してください。これは、ストリーム数の削減とプログラムの総実行時間を短縮するために、4要素のベクトル計算を使用するためです。

  {
   int i=get_global_id(0);
   int j=get_global_id(1);
   int wi=i*(inputs+1)+j*4;

データバッファ内の処理済み要素のポジションを決定した後、ベクトル変数を宣言し、対応する値で埋めます。前に説明したメソッドを使い、欠けているデータをゼロでベクトルに埋めます。

   double4 m, v, weight, inp;
   switch(inputs-j*4)
     {
      case 0:
        inp=(double4)(1,0,0,0);
        weight=(double4)(matrix_w[wi],0,0,0);
        m=(double4)(matrix_m[wi],0,0,0);
        v=(double4)(matrix_v[wi],0,0,0);
        break;
      case 1:
        inp=(double4)(matrix_i[j],1,0,0);
        weight=(double4)(matrix_w[wi],matrix_w[wi+1],0,0);
        m=(double4)(matrix_m[wi],matrix_m[wi+1],0,0);
        v=(double4)(matrix_v[wi],matrix_v[wi+1],0,0);
        break;
      case 2:
        inp=(double4)(matrix_i[j],matrix_i[j+1],1,0);
        weight=(double4)(matrix_w[wi],matrix_w[wi+1],matrix_w[wi+2],0);
        m=(double4)(matrix_m[wi],matrix_m[wi+1],matrix_m[wi+2],0);
        v=(double4)(matrix_v[wi],matrix_v[wi+1],matrix_v[wi+2],0);
        break;
      case 3:
        inp=(double4)(matrix_i[j],matrix_i[j+1],matrix_i[j+2],1);
        weight=(double4)(matrix_w[wi],matrix_w[wi+1],matrix_w[wi+2],matrix_w[wi+3]);
        m=(double4)(matrix_m[wi],matrix_m[wi+1],matrix_m[wi+2],matrix_m[wi+3]);
        v=(double4)(matrix_v[wi],matrix_v[wi+1],matrix_v[wi+2],matrix_v[wi+3]);
        break;
      default:
        inp=(double4)(matrix_i[j],matrix_i[j+1],matrix_i[j+2],matrix_i[j+3]);
        weight=(double4)(matrix_w[wi],matrix_w[wi+1],matrix_w[wi+2],matrix_w[wi+3]);
        m=(double4)(matrix_m[wi],matrix_m[wi+1],matrix_m[wi+2],matrix_m[wi+3]);
        v=(double4)(matrix_v[wi],matrix_v[wi+1],matrix_v[wi+2],matrix_v[wi+3]);
        break;
     }

スロープベクトルは、現在のニューロンのスロープにインプットデータベクトルを乗算して得られます。

   double4 g=matrix_g[i]*inp;

次に、スロープと２乗スロープの指数平均を計算します。

   double4 mt=b1*m+(1-b1)*g;
   double4 vt=b2*v+(1-b2)*pow(g,2)+0.00000001;

パラメータ変更デルタを計算します。

   double4 delta=l*mt/sqrt(vt);

カーネルの受信モーメントを調整していないことに注意してください。このステップは、ここでは意図的に省略します。 ß1 とß2はすべてのニューロンで同じであり、ここでニューロン・パラメータ更新の繰り返し回数であるtもすべてのニューロンで同じであるので、補正係数もすべてのニューロンで同じになります。そのため、ニューロンごとに係数を再計算するのではなく、メインプログラムのコードで一度計算し、この値で調整した学習係数をカーネルに渡します。

デルタを計算した後は、加重係数を調整し、バッファ内の計算されたモーメントを更新するだけです。そしてカーネルを終了します。

   switch(inputs-j*4)
     {
      case 2:
        matrix_w[wi+2]+=delta.s2;
        matrix_m[wi+2]=mt.s2;
        matrix_v[wi+2]=vt.s2;
      case 1:
        matrix_w[wi+1]+=delta.s1;
        matrix_m[wi+1]=mt.s1;
        matrix_v[wi+1]=vt.s1;
      case 0:
        matrix_w[wi]+=delta.s0;
        matrix_m[wi]=mt.s0;
        matrix_v[wi]=vt.s0;
        break;
      default:
        matrix_w[wi]+=delta.s0;
        matrix_m[wi]=mt.s0;
        matrix_v[wi]=vt.s0;
        matrix_w[wi+1]+=delta.s1;
        matrix_m[wi+1]=mt.s1;
        matrix_v[wi+1]=vt.s1;
        matrix_w[wi+2]+=delta.s2;
        matrix_m[wi+2]=mt.s2;
        matrix_v[wi+2]=vt.s2;
        matrix_w[wi+3]+=delta.s3;
        matrix_m[wi+3]=mt.s3;
        matrix_v[wi+3]=vt.s3;
        break;
     }
  };

このコードにはもう一つの仕掛けがあります。 switch演算子のcaseケースの逆順に注意してください。また、break演算子は、case 0とdefaultのケースの後にのみ使用します。このアプローチにより、すべての亜種で同じコードの重複を避けることができます。

2.2. メイン・プログラムのニューロン・クラスのコードの変更

カーネルを構築した後、メインプログラムのコードを変更する必要があります。まず、カーネルを操作するための 'define' ブロックに定数を追加します。

#define def_k_UpdateWeightsAdam   4
#define def_k_uwa_matrix_w        0
#define def_k_uwa_matrix_g        1
#define def_k_uwa_matrix_i        2
#define def_k_uwa_matrix_m        3
#define def_k_uwa_matrix_v        4
#define def_k_uwa_inputs          5
#define def_k_uwa_l               6
#define def_k_uwa_b1              7
#define def_k_uwa_b2              8

トレーニング方法を示す列挙を作成し、列挙にモーメントバッファを追加します。

enum ENUM_OPTIMIZATION
  {
   SGD,
   ADAM
  };
//---
enum ENUM_BUFFERS
  {
   WEIGHTS,
   DELTA_WEIGHTS,
   OUTPUT,
   GRADIENT,
   FIRST_MOMENTUM,
   SECOND_MOMENTUM
  };

次に、CNeuronBaseOCL クラス・ボディに、モーメントを格納するバッファ、指数平均定数、トレーニング繰り返し回数カウンタ、トレーニング方法を格納する変数を追加します。

class CNeuronBaseOCL    :  public CObject
  {
protected:
   .........
   .........
   ..........
   CBufferDouble     *FirstMomentum;
   CBufferDouble     *SecondMomentum;
//---
   .........
   .........
   const double      b1;
   const double      b2;
   int               t;
//---
   .........
   .........
   ENUM_OPTIMIZATION optimization;

クラスのコンストラクタでは、定数の値を設定し、バッファを初期化します。

CNeuronBaseOCL::CNeuronBaseOCL(void)   :  alpha(momentum),
                                          activation(TANH),
                                          optimization(SGD),
                                          b1(0.9),
                                          b2(0.999),
                                          t(1)
  {
   OpenCL=NULL;
   Output=new CBufferDouble();
   PrevOutput=new CBufferDouble();
   Weights=new CBufferDouble();
   DeltaWeights=new CBufferDouble();
   Gradient=new CBufferDouble();   
   FirstMomentum=new CBufferDouble();   
   SecondMomentum=new CBufferDouble();   
  }

クラスデストラクタにバッファオブジェクトの削除を追加することを忘れないでください。

CNeuronBaseOCL::~CNeuronBaseOCL(void)
  {
   if(CheckPointer(Output)!=POINTER_INVALID)
      delete Output;
   if(CheckPointer(PrevOutput)!=POINTER_INVALID)
      delete PrevOutput;
   if(CheckPointer(Weights)!=POINTER_INVALID)
      delete Weights;
   if(CheckPointer(DeltaWeights)!=POINTER_INVALID)
      delete DeltaWeights;
   if(CheckPointer(Gradient)!=POINTER_INVALID)
      delete Gradient;
   if(CheckPointer(FirstMomentum)!=POINTER_INVALID)
      delete FirstMomentum;
   if(CheckPointer(SecondMomentum)!=POINTER_INVALID)
      delete SecondMomentum;
   OpenCL=NULL;
  }

クラス初期化関数のパラメータには、トレーニングメソッドを追加し、指定されたトレーニングメソッドに応じてバッファを初期化します。学習にストキャスティクススロープ降下を使用する場合は、デルタのバッファを初期化し、モーメントのバッファーを削除します。アダムメソッドを使用している場合は、モーメントバッファを初期化し、デルタのバッファを削除します。

bool CNeuronBaseOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint numNeurons, ENUM_OPTIMIZATION optimization_type)
  {
   if(CheckPointer(open_cl)==POINTER_INVALID || numNeurons<=0)
      return false;
   OpenCL=open_cl;
   optimization=optimization_type;
//---
   ....................
   ....................
   ....................
   ....................
//---
   if(numOutputs>0)
     {
      if(CheckPointer(Weights)==POINTER_INVALID)
        {
         Weights=new CBufferDouble();
         if(CheckPointer(Weights)==POINTER_INVALID)
            return false;
        }
      int count=(int)((numNeurons+1)*numOutputs);
      if(!Weights.Reserve(count))
         return false;
      for(int i=0;i<count;i++)
        {
         double weigh=(MathRand()+1)/32768.0-0.5;
         if(weigh==0)
            weigh=0.001;
         if(!Weights.Add(weigh))
            return false;
        }
      if(!Weights.BufferCreate(OpenCL))
         return false;
   //---
      if(optimization==SGD)
        {
         if(CheckPointer(DeltaWeights)==POINTER_INVALID)
           {
            DeltaWeights=new CBufferDouble();
            if(CheckPointer(DeltaWeights)==POINTER_INVALID)
               return false;
           }
         if(!DeltaWeights.BufferInit(count,0))
            return false;
         if(!DeltaWeights.BufferCreate(OpenCL))
            return false;
         if(CheckPointer(FirstMomentum)==POINTER_INVALID)
            delete FirstMomentum;
         if(CheckPointer(SecondMomentum)==POINTER_INVALID)
            delete SecondMomentum;
        }
      else
        {
         if(CheckPointer(DeltaWeights)==POINTER_INVALID)
            delete DeltaWeights;
//---
         if(CheckPointer(FirstMomentum)==POINTER_INVALID)
           {
            FirstMomentum=new CBufferDouble();
            if(CheckPointer(FirstMomentum)==POINTER_INVALID)
               return false;
           }
         if(!FirstMomentum.BufferInit(count,0))
            return false;
         if(!FirstMomentum.BufferCreate(OpenCL))
            return false;
//---
         if(CheckPointer(SecondMomentum)==POINTER_INVALID)
           {
            SecondMomentum=new CBufferDouble();
            if(CheckPointer(SecondMomentum)==POINTER_INVALID)
               return false;
           }
         if(!SecondMomentum.BufferInit(count,0))
            return false;
         if(!SecondMomentum.BufferCreate(OpenCL))
            return false;
        }
     }
   else
     {
      if(CheckPointer(Weights)!=POINTER_INVALID)
         delete Weights;
      if(CheckPointer(DeltaWeights)!=POINTER_INVALID)
         delete DeltaWeights;
     }
//---
   return true;
  }

また、ウェイトの更新方法updateInputWeightsにも変更を加えます。まず、トレーニング方法に応じて分岐アルゴリズムを作成します。

bool CNeuronBaseOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID)
      return false;
   uint global_work_offset[2]={0,0};
   uint global_work_size[2];
   global_work_size[0]=Neurons();
   global_work_size[1]=NeuronOCL.Neurons();
   if(optimization==SGD)
     {

ストキャスティクススロープ降下については、コード全体をそのまま使用してください。

      OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_w,NeuronOCL.getWeightsIndex());
      OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_g,getGradientIndex());
      OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_i,NeuronOCL.getOutputIndex());
      OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_dw,NeuronOCL.getDeltaWeightsIndex());
      OpenCL.SetArgument(def_k_UpdateWeightsMomentum,def_k_uwm_inputs,NeuronOCL.Neurons());
      OpenCL.SetArgument(def_k_UpdateWeightsMomentum,def_k_uwm_learning_rates,eta);
      OpenCL.SetArgument(def_k_UpdateWeightsMomentum,def_k_uwm_momentum,alpha);
      ResetLastError();
      if(!OpenCL.Execute(def_k_UpdateWeightsMomentum,2,global_work_offset,global_work_size))
        {
         printf("Error of execution kernel UpdateWeightsMomentum: %d",GetLastError());
         return false;
        }
     }

アダムメソッドブランチでは、適切なカーネルのデータ交換バッファを設定します。

   else
     {
      if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_w,NeuronOCL.getWeightsIndex()))
         return false;
      if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_g,getGradientIndex()))
         return false;
      if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_i,NeuronOCL.getOutputIndex()))
         return false;
      if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_m,NeuronOCL.getFirstMomentumIndex()))
         return false;
      if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_v,NeuronOCL.getSecondMomentumIndex()))
         return false;

そして、現在の学習繰り返しの学習率を調整します。

      double lt=eta*sqrt(1-pow(b2,t))/(1-pow(b1,t));

トレーニングハイパーパラメータを設定します。

      if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_inputs,NeuronOCL.Neurons()))
         return false;
      if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_l,lt))
         return false;
      if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_b1,b1))
         return false;
      if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_b2,b2))
         return false;

カーネル内の計算にベクトル値を使用していたので、2次元のスレッド数を4倍に減らします。

      uint rest=global_work_size[1]%4;
      global_work_size[1]=(global_work_size[1]-rest)/4 + (rest>0 ? 1 : 0);

準備タスクが終わったら、カーネルを呼び出して学習繰り返しカウンタを増やします。

      ResetLastError();
      if(!OpenCL.Execute(def_k_UpdateWeightsAdam,2,global_work_offset,global_work_size))
        {
         printf("Error of execution kernel UpdateWeightsAdam: %d",GetLastError());
         return false;
        }
      t++;
     }

分岐後は、トレーニング方法に関わらず、再計算したウェイトを読み込みます。前回の記事でも説明しましたが、この操作はデータを読み込むだけでなく、カーネルの実行を開始するため、隠しレイヤーについてもバッファを読み込む必要があります。

//---
   return NeuronOCL.Weights.BufferRead();
  }

また、トレーニング方法の計算アルゴリズムの追加に加えて、前回のニューロントレーニング結果に関する情報の格納・読み込み方法を調整する必要があります。 Saveメソッドでは、トレーニングメソッドの保存を実装し、トレーニング繰り返し回数カウンタを追加します。

bool CNeuronBaseOCL::Save(const int file_handle)
  {
   if(file_handle==INVALID_HANDLE)
      return false;
   if(FileWriteInteger(file_handle,Type())<INT_VALUE)
      return false;
//---
   if(FileWriteInteger(file_handle,(int)activation,INT_VALUE)<INT_VALUE)
      return false;
   if(FileWriteInteger(file_handle,(int)optimization,INT_VALUE)<INT_VALUE)
      return false;
   if(FileWriteInteger(file_handle,(int)t,INT_VALUE)<INT_VALUE)
      return false;

どちらのトレーニング方法にも共通するバッファの保存は変更していません。

   if(CheckPointer(Output)==POINTER_INVALID || !Output.BufferRead() || !Output.Save(file_handle))
      return false;
   if(CheckPointer(PrevOutput)==POINTER_INVALID || !PrevOutput.BufferRead() || !PrevOutput.Save(file_handle))
      return false;
   if(CheckPointer(Gradient)==POINTER_INVALID || !Gradient.BufferRead() || !Gradient.Save(file_handle))
      return false;
//---
   if(CheckPointer(Weights)==POINTER_INVALID)
     {
      FileWriteInteger(file_handle,0);
      return true;
     }
   else
      FileWriteInteger(file_handle,1);
//---
   if(CheckPointer(Weights)==POINTER_INVALID || !Weights.BufferRead() || !Weights.Save(file_handle))
      return false;

その後、特定のバッファを保存しながら、各学習方法の分岐アルゴリズムを作成します。

   if(optimization==SGD)
     {
      if(CheckPointer(DeltaWeights)==POINTER_INVALID || !DeltaWeights.BufferRead() || !DeltaWeights.Save(file_handle))
         return false;
     }
   else
     {
      if(CheckPointer(FirstMomentum)==POINTER_INVALID || !FirstMomentum.BufferRead() || !FirstMomentum.Save(file_handle))
         return false;
      if(CheckPointer(SecondMomentum)==POINTER_INVALID || !SecondMomentum.BufferRead() || !SecondMomentum.Save(file_handle))
         return false;
     }
//---
   return true;
  }

Loadメソッドでも同じようなオーダーで同様の変更を行います。

すべてのメソッドと関数のフルコードは添付ファイルにあります。

2.3. OpenCLを使用していないクラスのコードの変更

すべてのクラスで同じ動作条件を維持するために、OpenCLを使用せずに純粋なMQL5で動作するクラスにも同様の変更が行われています。

まず、CConnectionクラスにモーメントデータを格納するための変数を追加し、クラスのコンストラクタで初期値を設定します。

class CConnection : public CObject
  {
public:
   double            weight;
   double            deltaWeight;
   double            mt;
   double            vt;

                     CConnection(double w) { weight=w; deltaWeight=0; mt=0; vt=0; }

また、接続データを保存したりロードしたりするメソッドに、新しい変数の処理を追加する必要があります。

bool CConnection::Save(int file_handle)
  {
   ...........
   ...........
   ...........
   if(FileWriteDouble(file_handle,mt)<=0)
      return false;
   if(FileWriteDouble(file_handle,vt)<=0)
      return false;
//---
   return true;
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CConnection::Load(int file_handle)
  {
   ............
   ............
   ............
   mt=FileReadDouble(file_handle);
   vt=FileReadDouble(file_handle);
//---
   return true;
  }

次に、CNeuronBaseニューロン・クラスに最適化の方法と計量更新の繰り返しのカウンタを格納するための変数を追加します。

class CNeuronBase    :  public CObject
  {
protected:
   .........
   .........
   .........
   ENUM_OPTIMIZATION optimization;

   const double      b1;
   const double      b2;
   int               t;

そうすると、ニューロンの初期化方法も変更する必要があります。メソッドパラメータに最適化方法を示す変数を追加し、上記で定義した変数に保存を実装します。

bool CNeuronBase::Init(uint numOutputs,uint myIndex, ENUM_OPTIMIZATION optimization_type)
  {
   optimization=optimization_type;

その後、最適化手法に応じて分岐するアルゴリズムをupdateInputWeightsメソッドに作成してみましょう。接続を介してループする前に、調整された学習率を再計算し、ループ内では、加重を計算するための2つのブランチを作成します。

bool CNeuron::updateInputWeights(CLayer *&prevLayer)
  {
   if(CheckPointer(prevLayer)==POINTER_INVALID)
      return false;
//---
   double lt=eta*sqrt(1-pow(b2,t))/(1-pow(b1,t));
   int total=prevLayer.Total();
   for(int n=0; n<total && !IsStopped(); n++)
     {
      CNeuron *neuron= prevLayer.At(n);
      CConnection *con=neuron.Connections.At(m_myIndex);
      if(CheckPointer(con)==POINTER_INVALID)
         continue;
      if(optimization==SGD)
         con.weight+=con.deltaWeight=(gradient!=0 ? eta*neuron.getOutputVal()*gradient : 0)+(con.deltaWeight!=0 ? alpha*con.deltaWeight : 0);
      else
        {
         con.mt=b1*con.mt+(1-b1)*gradient;
         con.vt=b2*con.vt+(1-b2)*pow(gradient,2)+0.00000001;
         con.weight+=con.deltaWeight=lt*con.mt/sqrt(con.vt);
         t++;
        }
     }
//---
   return true;
  }

保存・読み込みメソッドに新しい変数の処理を追加しました。

すべてのメソッドのフルコードは、以下の添付ファイルで提供されています。

2.4. メインプログラムのニューラルネットワーククラスのコードの変更

ニューロン・クラスの変更に加えて、コード内の他のオブジェクトの変更も必要です。まず、メインプログラムからニューロンにトレーニング方法の情報を渡す必要があります。メインプログラムからのデータは CLayerDescription クラスを介してニューラルネットワーククラスに渡されます。このクラスには、トレーニング方法に関する情報を渡すための適切なメソッドを追加する必要があります。

class CLayerDescription    :  public CObject
  {
public:
                     CLayerDescription(void);
                    ~CLayerDescription(void) {};
   //---
   int               type;
   int               count;
   int               window;
   int               step;
   ENUM_ACTIVATION   activation;
   ENUM_OPTIMIZATION optimization;
  };

さて，CNetニューラルネットワーククラスのコンストラクタに直近の追加を行います．ネットワークニューロンを初期化する際の最適化方法の表示をここに追加し、使用するOpenCLカーネルの数を増やし、新しい最適化カーネルを宣言します - アダム。以下は強調表示を変更したコンストラクタのコードです。

CNet::CNet(CArrayObj *Description)
  {
   if(CheckPointer(Description)==POINTER_INVALID)
      return;
//---
   int total=Description.Total();
   if(total<=0)
      return;
//---
   layers=new CArrayLayer();
   if(CheckPointer(layers)==POINTER_INVALID)
      return;
//---
   CLayer *temp;
   CLayerDescription *desc=NULL, *next=NULL, *prev=NULL;
   CNeuronBase *neuron=NULL;
   CNeuronProof *neuron_p=NULL;
   int output_count=0;
   int temp_count=0;
//---
   next=Description.At(1);
   if(next.type==defNeuron || next.type==defNeuronBaseOCL)
     {
      opencl=new COpenCLMy();
      if(CheckPointer(opencl)!=POINTER_INVALID && !opencl.Initialize(cl_program,true))
         delete opencl;
     }
   else
     {
      if(CheckPointer(opencl)!=POINTER_INVALID)
         delete opencl;
     }
//---
   for(int i=0; i<total; i++)
     {
      prev=desc;
      desc=Description.At(i);
      if((i+1)<total)
        {
         next=Description.At(i+1);
         if(CheckPointer(next)==POINTER_INVALID)
            return;
        }
      else
         next=NULL;
      int outputs=(next==NULL || (next.type!=defNeuron && next.type!=defNeuronBaseOCL) ? 0 : next.count);
      temp=new CLayer(outputs);
      int neurons=(desc.count+(desc.type==defNeuron || desc.type==defNeuronBaseOCL ? 1 : 0));
      if(CheckPointer(opencl)!=POINTER_INVALID)
        {
         CNeuronBaseOCL *neuron_ocl=NULL;
         switch(desc.type)
           {
            case defNeuron:
            case defNeuronBaseOCL:
              neuron_ocl=new CNeuronBaseOCL();
              if(CheckPointer(neuron_ocl)==POINTER_INVALID)
                {
                 delete temp;
                 return;
                }
              if(!neuron_ocl.Init(outputs,0,opencl,desc.count,desc.optimization))
                {
                 delete temp;
                 return;
                }
              neuron_ocl.SetActivationFunction(desc.activation);
              if(!temp.Add(neuron_ocl))
                {
                 delete neuron_ocl;
                 delete temp;
                 return;
                }
              neuron_ocl=NULL;
              break;
            default:
              return;
              break;
           }
        }
      else
      for(int n=0; n<neurons; n++)
        {
         switch(desc.type)
           {
            case defNeuron:
               neuron=new CNeuron();
               if(CheckPointer(neuron)==POINTER_INVALID)
                 {
                  delete temp;
                  delete layers;
                  return;
                 }
               neuron.Init(outputs,n,desc.optimization);
               neuron.SetActivationFunction(desc.activation);
               break;
            case defNeuronConv:
               neuron_p=new CNeuronConv();
               if(CheckPointer(neuron_p)==POINTER_INVALID)
                 {
                  delete temp;
                  delete layers;
                  return;
                 }
               if(CheckPointer(prev)!=POINTER_INVALID)
                 {
                  if(prev.type==defNeuron)
                    {
                     temp_count=(int)((prev.count-desc.window)%desc.step);
                     output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
                    }
                  else
                     if(n==0)
                       {
                        temp_count=(int)((output_count-desc.window)%desc.step);
                        output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
                       }
                 }
               if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count,desc.optimization))
                  neuron=neuron_p;
               break;
            case defNeuronProof:
               neuron_p=new CNeuronProof();
               if(CheckPointer(neuron_p)==POINTER_INVALID)
                 {
                  delete temp;
                  delete layers;
                  return;
                 }
               if(CheckPointer(prev)!=POINTER_INVALID)
                 {
                  if(prev.type==defNeuron)
                    {
                     temp_count=(int)((prev.count-desc.window)%desc.step);
                     output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
                    }
                  else
                     if(n==0)
                       {
                        temp_count=(int)((output_count-desc.window)%desc.step);
                        output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
                       }
                 }
               if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count,desc.optimization))
                  neuron=neuron_p;
               break;
            case defNeuronLSTM:
               neuron_p=new CNeuronLSTM();
               if(CheckPointer(neuron_p)==POINTER_INVALID)
                 {
                  delete temp;
                  delete layers;
                  return;
                 }
               output_count=(next!=NULL ? next.window : desc.step);
               if(neuron_p.Init(outputs,n,desc.window,1,output_count,desc.optimization))
                  neuron=neuron_p;
               break;
           }
         if(!temp.Add(neuron))
           {
            delete temp;
            delete layers;
            return;
           }
         neuron=NULL;
        }
      if(!layers.Add(temp))
        {
         delete temp;
         delete layers;
         return;
        }
     }
//---
   if(CheckPointer(opencl)==POINTER_INVALID)
      return;
//--- create kernels
   opencl.SetKernelsCount(5);
   opencl.KernelCreate(def_k_FeedForward,"FeedForward");
   opencl.KernelCreate(def_k_CaclOutputGradient,"CaclOutputGradient");
   opencl.KernelCreate(def_k_CaclHiddenGradient,"CaclHiddenGradient");
   opencl.KernelCreate(def_k_UpdateWeightsMomentum,"UpdateWeightsMomentum");
   opencl.KernelCreate(def_k_UpdateWeightsAdam,"UpdateWeightsAdam");
//---
   return;
  }

すべてのクラスとそのメソッドのフルコードは添付ファイルにあります。

3. テスト

アダム法による最適化のテストは、以前のテストで使用されたのと同じ条件で行われました：シンボルEURUSD、タイムフレームH1、20個の連続したローソク足のデータがネットワークに供給され、トレーニングは過去2年間のヒストリーを使用して実行されます。テスト用にFractal_OCL_Adam Expert Advisorを作成しました。このExpert Advisorは、Fractal_OCLEAをベースに、メインプログラムのOnInit関数でニューラルネットワークを記述する際にAdam最適化手法を指定して作成しました。

      desc.count=(int)HistoryBars*12;
      desc.type=defNeuron;
      desc.optimization=ADAM;

ニューロン層やニューロンの数は変わっていません。

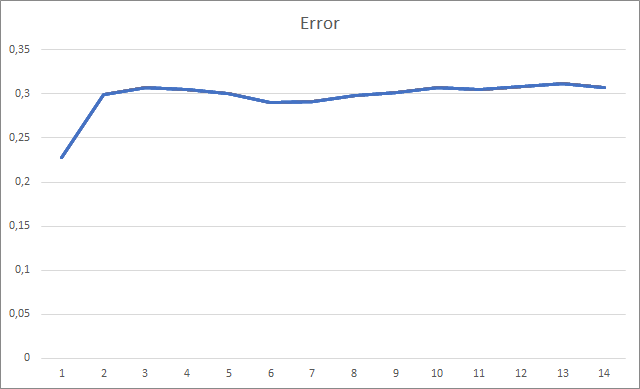
このEAは、ゼロ値を除いて-1から1までのランダムな加重で初期化されました。テスト中、2回目のトレーニングエポック後には、ニューラルネットワークの誤差は30%程度に安定していました。ご記憶の通り、ストキャスティクススロープ降下法で学習した場合、5回目の学習エポックを経て、誤差は42%程度に安定しました。

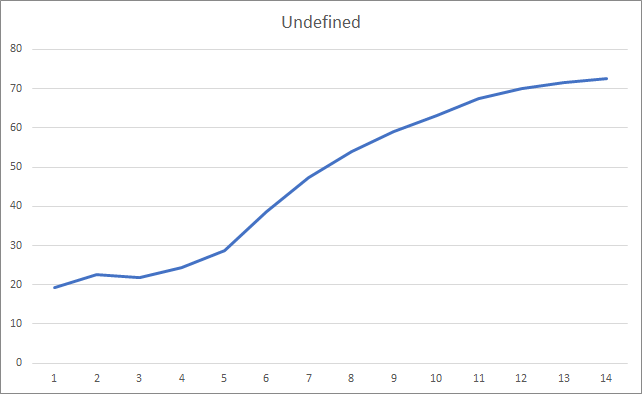
ミスフラクタルのチャートを見ると、トレーニング全体を通して徐々に値が上がっていることがわかります。しかし、12回のトレーニングエポックを経て、徐々に値の成長率が低下していきます。エポック１４回目以降は72.5%でした。ストキャスティックスロープ降下法を用いて同様のニューラルネットワークを学習したところ、10エポック後のフラクタルの欠落率は学習率の差で97～100%でありました。

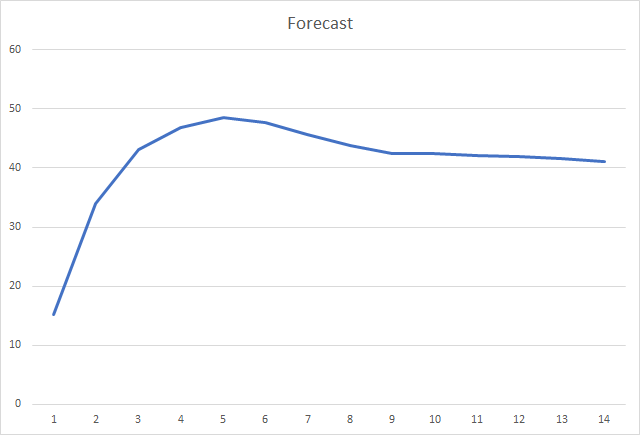
そして、おそらく、最も重要なインジケータは、正しく定義されたフラクタルの割合です。第5回学習エポック後は48.6％に達し、その後は徐々に減少して41.1％となりました。ストキャスティクススロープ降下法を用いた場合、90エポック後も10%を超えませんでした。

結論

この論文では、ニューラルネットワークのパラメータを最適化するための適応的な手法を検討しました。先に作成したニューラルネットワークモデルにアダム最適化法を追加しました。テストの間、ニューラルネットワークはアダム法を用いてトレーニングされました。ストキャスティクススロープ降下法を用いて同様のニューラルネットワークをトレーニングすると、以前に受けた結果を上回る結果が得られました。

行われたタスクは、今回の目標に向かっての進捗状況も示しています。

レファレンス

記事内で使用しているプログラム

#	名前	タイプ	詳細
1	Fractal_OCL_Adam.mq5	EA	OpenCLとAdam学習法を用いた分類ニューラルネットワーク（出力層に3つのニューロン）を用いたEA
2	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
3	NeuroNet.cl	コードベース	OpenCL プログラムコードライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/8598

添付されたファイル |

ZIPをダウンロード

MQL5.zip (430.54 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

MetaTrader5のWebSocket

MQL5 APIが更新されてネットワーク機能が導入される前は、MetaTraderプログラムでは、WebSocketベースのサービスに接続してインターフェイスする機能が制限されていました。しかしもちろん、これはすべて変わっています。本稿では、純粋なMQL5でのWebSocketライブラリの実装について説明します。WebSocketプロトコルの簡単な説明とともに結果のライブラリの使用方法に関する手順のガイドが提示されます。

アルゴリズム取引から100万ドルを稼ぐ方法？MQL5.comサービスを使用してください

トレーダーは皆、最初の百万ドルを稼ぐことを目標に市場を訪れます。過度のリスクと初期予算なしでこれを行う方法は何でしょうか。MQL5サービスは、世界中の開発者やトレーダーにそのような機会を提供します。

トランスダクション・アクティブ機械学習におけるスロープブースト

本記事では、実データを活用したアクティブな機械学習手法について考察するとともに、その長所と短所について考察していきます. おそらく、いくつかの方法が有用であるとわかるでしょうし、機械学習モデルのアーセナルにインクルードするでしょう. トランスダクションは、サポートベクターマシン（SVM）の共同発明者であるVladimir Vapnik氏が紹介しています.

取引システムの開発と分析への最適なアプローチ

本稿では、資金を投資するためのシステムまたはシグナルを選択する際に使用する基準を示すとともに、取引システムの開発への最適なアプローチを説明し、外国為替取引におけるこの問題の重要性を強調します。

目次