Redes Neurais de Maneira Fácil (Parte 3): Redes Convolucionais
1 197
0
Conteúdo
- Introdução
- 1. Características distintas das redes neurais convolucionais
- 2. Princípios de treinamento dos neurônios nas camadas convolucionais
- 3. Construindo uma rede neural convolucional
- 3.1. Classe base dos neurônios
- 3.2. Elemento da camada de subamostragem
- 3.3. Elemento da camada convolucional
- 3.4. Criação de uma classe da rede neural convolucional
- 4. Teste
- Conclusão
- Lista de referências
- Programas utilizados no artigo
Introdução
Como uma continuação do tópico das redes neurais, eu proponho ao leitor a análise das redes neurais convolucionais. Essas redes neurais são geralmente aplicadas em problemas relacionados ao processamento de imagens em fotos e vídeos. Acredita-se que as redes neurais convolucionais sejam resistentes ao zoom, alteração de ângulos e outras distorções espaciais de imagem. Sua arquitetura permite reconhecer objetos com igual sucesso em qualquer lugar da cena. Quando aplicado à negociação, eu quero usar as redes neurais convolucionais para melhorar o reconhecimento dos padrões de negociação em um gráfico de preços.
1. Características distintas das redes neurais convolucionais
As redes convolucionais, em comparação com um perceptron totalmente conectado, têm dois novos tipos de camada: a convolucional (filtro) e a de subamostragem. Essas camadas se alternam com o objetivo de selecionar os componentes principais e eliminar os ruídos nos dados de origem, enquanto reduz a dimensão dos dados (volume). Esses dados são então inseridos em um perceptron totalmente conectado para a tomada de decisão. A estrutura de uma rede neural convolucional é mostrada graficamente na figura abaixo. Dependendo das tarefas, nós podemos usar sequencialmente vários grupos de camadas convolucionais e de subamostragem alternadas.
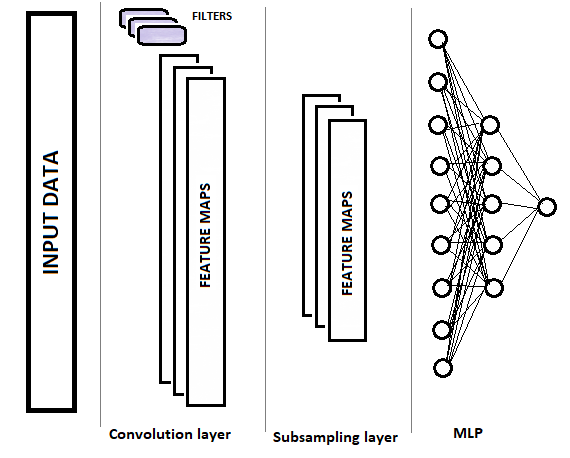
1.1. Camada convolucional
A camada convolucional é responsável por reconhecer os objetos na matriz de dados de origem. Essa camada realiza operações sequenciais de convolução matemática dos dados originais, com um pequeno padrão (filtro) atuando como um kernel de convolução.
A convolução é uma operação de análise funcional em duas funções (f e g) que produz uma terceira função correspondente à função de correlação cruzada f(x) e g(-x). A operação de convolução pode ser interpretada como a "similaridade" de uma função com uma cópia invertida e deslocada de outra (Wikipedia)
Em outras palavras, a camada convolucional procura um elemento padrão em toda a amostra original. A cada iteração, o modelo é deslocado ao longo da matriz de dados inicial com um determinado passo, cujo tamanho pode ser de "1" até o tamanho do padrão. Se o tamanho do passo de deslocamento for menor que o tamanho do padrão, tal convolução é chamada de sobreposição.
A operação de convolução produz uma matriz de características mostrando a "similaridade" dos dados originais com o padrão requerido em cada iteração. As funções de ativação são usadas para normalizar os dados. O tamanho da matriz resultante será menor do que a matriz de dados original. O número dessas matrizes é igual ao número de filtros.
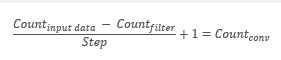
Um ponto importante é que os padrões não são especificados ao projetar uma rede neural, mas são selecionados no processo de aprendizagem.
1.2. Camadas de subamostragem
A próxima camada de subamostragem é usada para reduzir a dimensão da matriz de características e para filtrar o ruído. O uso dessa iteração decorre da suposição de que a presença de similaridade entre os dados originais e o padrão é primária, enquanto as coordenadas exatas da característica na matriz de dados original não são tão importantes. Isso fornece uma solução para o problema de dimensionamento, pois permite alguma variabilidade na distância entre os objetos desejados.
Nesta fase, os dados são compactados mantendo o valor máximo ou médio dentro de uma determinada "janela". Assim, apenas um valor é salvo para cada "janela" de dados. As operações são realizadas iterativamente, e a janela é deslocada por um determinado passo a cada nova iteração. A compactação dos dados é realizada separadamente para cada matriz de características.
As camadas de subamostragem com uma janela e um passo igual a 2 são frequentemente usadas - isso permite reduzir pela metade a dimensão da matriz de características. No entanto, as janelas maiores podem ser usadas, enquanto as iterações de compactação podem ser executadas com sobreposição (quando o tamanho do passo é menor que o tamanho da janela) ou sem ela.
A camada de subamostragem produz a matriz de características de uma dimensão menor.
Dependendo da complexidade dos problemas, é possível usar um ou mais grupos da camada convolucional e de subamostragem após a camada de subamostragem. Seus princípios de construção e funcionalidade correspondem à camada descrita acima. No caso geral, após um ou vários grupos de convolução + compactação, as matrizes de características obtidas para todos os filtros são coletadas em um único vetor e alimentadas em um perceptron multicamadas para que a rede neural tome uma decisão (a construção do perceptron multicamadas é descrito em detalhes na primeira parte desta série de artigos).
2. Princípios de treinamento dos neurônios nas camadas convolucionais
As redes neurais convolucionais são treinadas pelo método retro-propagação (backpropagation) que foi discutido nos artigos anteriores. Este é um dos métodos de aprendizagem supervisionada. Ele consiste na retro-propagação do erro da camada de saída dos neurônios, passando pelas camadas ocultas, até a camada de entrada dos neurônios, com correção de peso em direção ao antigradiente.
O treinamento do perceptron multicamadas foi explicado no primeiro artigo, portanto, eu não vou fornecer uma explicação aqui. Vamos considerar o treinamento dos neurônios da camada convolucional e de subamostragem.
Na camada de subamostragem, o gradiente do erro é calculado para cada elemento da matriz de características, de forma semelhante aos gradientes dos neurônios em um perceptron totalmente conectado. O algoritmo para transferir o gradiente para a camada anterior depende da operação de compactação aplicada. Se apenas o valor máximo for usado, todo o gradiente é alimentado para o neurônio com o valor máximo (um gradiente de valor zero é definido para todos os outros elementos dentro da janela de compactação). Se a operação de cálculo da média na janela for usada, o gradiente será distribuído uniformemente para todos os elementos da janela.
A operação de compactação não utiliza pesos, por isso nada é ajustado no processo de aprendizagem.
Os cálculos são um pouco mais complexos durante o treinamento dos neurônios da camada convolucional. O gradiente do erro é calculado para cada elemento da matriz de características e é alimentado para os neurônios correspondentes da camada anterior. O processo de treinamento da camada convolucional é baseado nas operações de convolução e convolução inversa.
Para passar o gradiente do erro da camada de subamostragem para a convolucional, as bordas da matriz do gradiente do erro obtidas a partir da camada de subamostragem são primeiro suplementadas com zero elementos e, em seguida, a matriz resultante é convolvida com o núcleo de convolução rotacionado em 180°. A saída é uma matriz do gradiente do erro com a dimensão igual à matriz de dados de entrada, na qual os índices do gradiente correspondem ao índice do neurônio correspondente que precede a camada convolucional.
O delta de pesos é obtido pela convolução da matriz de valores de entrada com a matriz do gradiente do erro desta camada rotacionada em 180°. Isso gera uma matriz de deltas com um tamanho igual ao kernel da convolução. Os deltas resultantes precisam ser ajustados para a derivada da função de ativação da camada convolucional e o fator de aprendizagem. Depois disso, os pesos do kernel da convolução são alterados pelo valor dos deltas ajustados.
Isso pode parecer muito difícil de entender. Eu vou tentar esclarecer alguns momentos na análise detalhada do código abaixo.
3. Construindo uma rede neural convolucional
A rede neural convolucional consistirá em três tipos de camadas neurais (convolucional, subamostragem e totalmente conectada) com classes distintas de neurônios e funções diferentes para a propagação direta (feedforward) e retro-propagação (backpropagation). Ao mesmo tempo, nós precisamos combinar todos os neurônios em uma única rede e organizar a chamada do método de processamento de dados que corresponde ao neurônio processado. Acho que a maneira mais fácil de organizar esse processo é usar a herança de classe e virtualização da função.
Primeiro, vamos construir a estrutura da herança de classe.
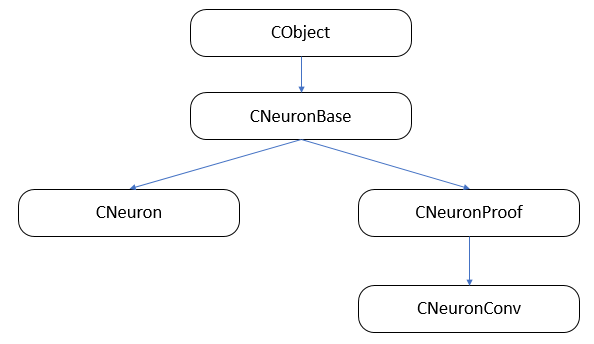
3.1. Classe base de neurônios.
No primeiro artigo, nós criamos a classe da camada CLayer como descendente da CArrayObj, que é uma classe de array dinâmico para armazenar ponteiros para os objetos da classe CObject. Portanto, todos os neurônios devem ser herdados dessa classe. Criado a classe CNeuronBase com base na classe CObject. No corpo da classe, nós declaramos as variáveis que são comuns a todos os tipos de neurônios e criamos modelos para os métodos principais. Todos os métodos da classe são declarados de maneira virtual para permitir as redefinições adicionais.
class CNeuronBase : public CObject { protected: double eta; double alpha; double outputVal; uint m_myIndex; double gradient; CArrayCon *Connections; //--- virtual bool feedForward(CLayer *prevLayer) { return false; } virtual bool calcHiddenGradients( CLayer *&nextLayer) { return false; } virtual bool updateInputWeights(CLayer *&prevLayer) { return false; } virtual double activationFunction(double x) { return 1.0; } virtual double activationFunctionDerivative(double x) { return 1.0; } virtual CLayer *getOutputLayer(void) { return NULL; } public: CNeuronBase(void); ~CNeuronBase(void); virtual bool Init(uint numOutputs, uint myIndex); //--- virtual void setOutputVal(double val) { outputVal=val; } virtual double getOutputVal() { return outputVal; } virtual void setGradient(double val) { gradient=val; } virtual double getGradient() { return gradient; } //--- virtual bool feedForward(CObject *&SourceObject); virtual bool calcHiddenGradients( CObject *&TargetObject); virtual bool updateInputWeights(CObject *&SourceObject); //--- virtual bool Save( int const file_handle); virtual bool Load( int const file_handle) { return(Connections.Load(file_handle)); } //--- virtual int Type(void) const { return defNeuronBase; } };
Os nomes das variáveis e métodos são os mesmos descritos anteriormente. Vamos considerar os métodos feedForward(CObject *&SourceObject), сalcHiddenGradients(CObject *&TargetObject) e updateInputWeights(CObject *&SourceObject), no qual são executados os despachos para trabalhar com as camadas totalmente conectadas e convolucionais.
3.1.1. Feed-forward.
O método feedForward(CObject *&SourceObject) é chamado durante uma passagem para frente, para calcular o valor do neurônio resultante. Durante uma passagem para frente, cada neurônio em camadas totalmente conectadas obtém os valores de todos os neurônios da camada anterior e deve receber toda a camada anterior como entrada. Nas camadas convolucionais e de subamostragem, apenas uma parte dos dados relacionados a esse filtro é enviada ao neurônio. No método considerado, o algoritmo é selecionado com base no tipo da classe obtida nos parâmetros.
Primeiro, verificamos a validade do ponteiro do objeto obtido nos parâmetros do método.
bool CNeuronBase::feedForward(CObject *&SourceObject) { bool result=false; //--- if(CheckPointer(SourceObject)==POINTER_INVALID) return result;
Como as instâncias da classe não podem ser declaradas dentro do operador de seleção, nós precisamos preparar os modelos com antecedência.
CLayer *temp_l; CNeuronProof *temp_n;
A seguir, no operador de seleção, verificamos o tipo de objeto recebido nos parâmetros. Se um ponteiro para uma camada de neurônios for recebido, a camada anterior está totalmente conectada e, portanto, nós precisamos chamar um método para trabalhar com as camadas totalmente conectadas (descrito em detalhes no primeiro artigo) Se for um neurônio de uma camada convolucional ou de subamostragem, então, primeiro nós obtemos uma camada de neurônios de saída desse filtro e, em seguida, usamos um método de processamento de uma camada totalmente conectada, à qual nós devemos inserir uma camada de neurônios do filtro atual, e o resultado do processamento deve ser salvo na variável result (mais detalhes sobre a estrutura dos neurônios nas camadas convolucional e de subamostragem serão fornecidos abaixo). Após a operação, saímos do método e passamos o resultado da operação.
switch(SourceObject.Type()) { case defLayer: temp_l=SourceObject; result=feedForward(temp_l); break; case defNeuronConv: case defNeuronProof: temp_n=SourceObject; result=feedForward(temp_n.getOutputLayer()); break; } //--- return result; }
3.1.2. Cálculo do gradiente do erro.
Da mesma forma que um passo para frente, um despachante foi criado para chamar a função que calcula o gradiente do erro nas camadas ocultas da rede neural - сalcHiddenGradients(CObject *&TargetObject). A lógica e a estrutura do método são semelhantes às descritas acima. Primeiro, verificamos a validade do ponteiro recebido. Em seguida, declaramos as variáveis para armazenar os ponteiros para os objetos correspondentes. Em seguida, selecionamos o método adequado na função de seleção, de acordo com o tipo do objeto recebido. As diferenças ocorrem se um ponteiro para um elemento de uma camada convolucional ou de subamostragem for passado nos parâmetros. O cálculo do gradiente do erro por meio de tais neurônios é diferente e não se aplica a todos os neurônios da camada anterior, mas apenas aos neurônios dentro da janela de amostragem. É por isso que o cálculo do gradiente foi transferido para esses neurônios no método calcInputGradients. Além disso, existem diferenças nos métodos de cálculo por camada ou para um neurônio específico. Portanto, o método necessário é chamado dependendo do tipo de objeto do qual é chamado.
bool CNeuronBase::calcHiddenGradients(CObject *&TargetObject) { bool result=false; //--- if(CheckPointer(TargetObject)==POINTER_INVALID) return result; //--- CLayer *temp_l; CNeuronProof *temp_n; switch(TargetObject.Type()) { case defLayer: temp_l=TargetObject; result=calcHiddenGradients(temp_l); break; case defNeuronConv: case defNeuronProof: switch(Type()) { case defNeuron: temp_n=TargetObject; result=temp_n.calcInputGradients(GetPointer(this),m_myIndex); break; default: temp_n=GetPointer(this); temp_l=temp_n.getOutputLayer(); temp_n=TargetObject; result=temp_n.calcInputGradients(temp_l); break; } break; } //--- return result; }
O despachante updateInputWeights (CObject *&SourceObject) atualizando todo o peso é baseado nos princípios acima. O código completo está disponível em anexo.
3.2. Elemento da camada de subamostragem.
O principal bloco de construção da camada de subamostragem é a classe CNeuronProof, que herda da classe base CNeuronBase, que foi descrita anteriormente. Uma instância desta classe será criada para cada filtro na camada de subamostragem. Portanto, as variáveis adicionais (iWindow e iStep) são introduzidas para armazenar o tamanho da janela de compactação e a etapa de deslocamento. Nós também adicionamos uma camada interna de neurônios para armazenar as matrizes de características, gradiente do erro e, se necessário, os pesos para realizar a propagação para um perceptron totalmente conectado. Além disso, nós adicionamos um método para receber um ponteiro para a camada interna de neurônios sob demanda.
class CNeuronProof : public CNeuronBase { protected: CLayer *OutputLayer; int iWindow; int iStep; virtual bool feedForward(CLayer *prevLayer); virtual bool calcHiddenGradients( CLayer *&nextLayer); public: CNeuronProof(void){}; ~CNeuronProof(void); virtual bool Init(uint numOutputs,uint myIndex,int window, int step, int output_count); //--- virtual CLayer *getOutputLayer(void) { return OutputLayer; } virtual bool calcInputGradients( CLayer *prevLayer) ; virtual bool calcInputGradients( CNeuronBase *prevNeuron, uint index) ; //--- methods for working with files virtual bool Save( int const file_handle) { return(CNeuronBase::Save(file_handle) && OutputLayer.Save(file_handle)); } virtual bool Load( int const file_handle) { return(CNeuronBase::Load(file_handle) && OutputLayer.Load(file_handle)); } virtual int Type(void) const { return defNeuronProof; } };
Não se esqueça de redefinir a lógica das funções virtuais declaradas na classe base.
3.2.1. Feed-forward.
O método feedForward ou propagação direta é aplicado para filtrar o ruído e reduzir a dimensão da matriz de características. Na solução descrita, a função da média aritmética é usada para compactar os dados. Vamos considerar o código do método com mais detalhes. No início do método, verificamos a relevância do ponteiro obtido para a camada anterior de neurônios.
bool CNeuronProof::feedForward(CLayer *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false;
Em seguida, iteramos em um loop por todos os neurônios da camada obtida nos parâmetros, com um determinado passo.
int total=prevLayer.Total()-iWindow+1; CNeuron *temp; for(int i=0;(i<=total && result);i+=iStep) {
No corpo do loop, criamos um loop aninhado para calcular a soma dos valores de saída dos neurônios da camada anterior dentro da janela de compactação especificada.
double sum=0; for(int j=0;j<iWindow;j++) { temp=prevLayer.At(i+j); if(CheckPointer(temp)==POINTER_INVALID) continue; sum+=temp.getOutputVal(); }
Depois de calcular a soma, usamos o neurônio correspondente da camada interna armazenando os dados resultantes e escrevemos a razão da soma obtida para o tamanho da janela em seu valor resultante. Essa proporção será a média aritmética para a janela de compactação atual.
temp=OutputLayer.At(i/iStep); if(CheckPointer(temp)==POINTER_INVALID) return false; temp.setOutputVal(sum/iWindow); } //--- return true; }
Depois de passar por todos os neurônios, o método é concluído.
3.2.2. Cálculo do gradiente do erro.
Dois métodos são criados nesta classe para calcular o gradiente do erro: calcHiddenGradients e calcInputGradients. A primeira classe coleta os dados sobre o gradiente do erro da camada subsequente e calcula o gradiente para os elementos da camada atual. A segunda classe usa os dados obtidos no primeiro método e distribui o erro entre os elementos da camada anterior.
Novamente, verificamos a validade do ponteiro obtido no início do método calcHiddenGradients. Além disso, nós verificamos o estado da camada interna dos neurônios.
bool CNeuronProof::calcHiddenGradients( CLayer *&nextLayer) { if(CheckPointer(nextLayer)==POINTER_INVALID || CheckPointer(OutputLayer)==POINTER_INVALID || OutputLayer.Total()<=0) return false;
Em seguida, iteramos em um loop por todos os neurônios da camada interna e chamamos um método para calcular o gradiente do erro.
gradient=0; int total=OutputLayer.Total(); CNeuron *temp; for(int i=0;i<total;i++) { temp=OutputLayer.At(i); if(CheckPointer(temp)==POINTER_INVALID) return false; temp.setGradient(temp.sumDOW(nextLayer)); } //--- return true; }
Observe que este método funciona corretamente se for seguido por uma camada de neurônios totalmente conectada. Se for seguido por uma camada convolucional ou de subamostragem, usamos o método calcInputGradients do neurônio da próxima camada.
O método calcInputGradients recebe um ponteiro para a camada anterior nos parâmetros. Não se esqueça de verificar a validade do ponteiro no início do método.
bool CNeuronProof::calcInputGradients(CLayer *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID || CheckPointer(OutputLayer)==POINTER_INVALID) return false;
Em seguida, verificamos o tipo do primeiro elemento obtido nos parâmetros da camada. Se a referência resultante apontar para uma subamostragem ou camada convolucional, solicitamos uma referência à camada interna de neurônios correspondentes ao filtro.
if(prevLayer.At(0).Type()!=defNeuron) { CNeuronProof *temp=prevLayer.At(m_myIndex); if(CheckPointer(temp)==POINTER_INVALID) return false; prevLayer=temp.getOutputLayer(); if(CheckPointer(prevLayer)==POINTER_INVALID) return false; }
Em seguida, iteramos em um loop por todos os neurônios da camada anterior, verificando a validade da referência ao neurônio processado.
CNeuronBase *prevNeuron, *outputNeuron; int total=prevLayer.Total(); for(int i=0;i<total;i++) { prevNeuron=prevLayer.At(i); if(CheckPointer(prevNeuron)==POINTER_INVALID) continue;
Determinamos quais neurônios da camada interna são afetados pelo neurônio processado.
double prev_gradient=0; int start=i-iWindow+iStep; start=(start-start%iStep)/iStep; double stop=(i-i%iStep)/iStep+1;
Em um loop, calculamos o gradiente do erro para o neurônio processado e salvamos o resultado. O método termina após o processamento de todos os neurônios da camada anterior.
for(int out=(int)fmax(0,start);out<(int)fmin(OutputLayer.Total(),stop);out++) { outputNeuron=OutputLayer.At(out); if(CheckPointer(outputNeuron)==POINTER_INVALID) continue; prev_gradient+=outputNeuron.getGradient()/iWindow; } prevNeuron.setGradient(prev_gradient); } //--- return true; }
O método com o mesmo nome que calcula um gradiente de neurônio separado tem uma estrutura semelhante. A diferença é que os neurônios iterativos do ciclo externo são excluídos. Em vez disso, um neurônio é chamado por um índice.
Visto que os pesos não são usados na camada de subamostragem, o método de atualização de peso pode ser omitido. Se você deseja preservar a estrutura das classes de neurônios, você pode criar um método vazio que irá criar true quando chamado.
O código completo de todos os métodos e funções está disponível em anexo.
3.3. Elemento da camada convolucional.
A camada convolucional será construída usando os objetos de classe CNeuronConv que herdarão da classe CNeuronProof. Eu escolhi o ReLU paramétrico como a função de ativação para estes tipos de neurônios. Esta função é mais fácil de calcular do que a tangente hiperbólica que é usada nos neurônios perceptron totalmente conectados. Vamos introduzir uma variável adicional param, para calcular a função.
class CNeuronConv : public CNeuronProof { protected: double param; //PReLU param virtual bool feedForward(CLayer *prevLayer); virtual bool calcHiddenGradients(CLayer *&nextLayer); virtual double activationFunction(double x); virtual bool updateInputWeights(CLayer *&prevLayer); public: CNeuronConv() : param(0.01) { }; ~CNeuronConv(void) { }; //--- virtual bool calcInputGradients(CLayer *prevLayer) ; virtual bool calcInputGradients(CNeuronBase *prevNeuron, uint index) ; virtual double activationFunctionDerivative(double x); virtual int Type(void) const { return defNeuronConv; } };
Os métodos backpropagation e feedforwad são baseados nos algoritmos semelhantes à classe CNeuron Proof. A diferença está no uso da função de ativação e os coeficientes de peso. Portanto, eu não os descreverei em detalhes. Vamos considerar o método de ajuste do peso updateInputWeights.
O método receberá um ponteiro para a camada anterior de neurônios. Novamente, nós verificamos a validade do ponteiro e o estado da camada interna no início do método.
bool CNeuronConv::updateInputWeights(CLayer *&prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID || CheckPointer(OutputLayer)==POINTER_INVALID) return false;
Em seguida, iteramos em um loop por todos os pesos. Não se esqueça de verificar a validade do ponteiro do objeto recebido.
CConnection *con; for(int n=0; n<iWindow && !IsStopped(); n++) { con=Connections.At(n); if(CheckPointer(con)==POINTER_INVALID) continue;
Depois disso, calculamos a convolução da matriz de dados de entrada com a matriz de gradiente do erro da camada interna rotacionada em 180°. Isso é feito em um loop por todos os elementos da camada interna, multiplicado pelos elementos da matriz de dados de entrada de acordo com o seguinte esquema:
- o primeiro elemento da matriz de dados de entrada (com uma mudança pelo número de passos igual ao número ordinal do peso) multiplicado pelo último elemento da matriz do gradiente do erro,
- o segundo elemento da matriz de dados de entrada (com uma mudança pelo número de passos igual ao número ordinal do peso) multiplicado pelo penúltimo elemento da matriz do gradiente do erro,
- e assim por diante, até que o elemento com o índice igual ao número de elementos na matriz da camada interna com um deslocamento pelo número de passos igual ao número ordinal do peso, seja multiplicado pelo primeiro elemento da matriz do gradiente do erro.
Em seguida, encontramos a soma dos produtos resultantes.
double delta=0; int total_i=OutputLayer.Total(); CNeuron *prev, *out; for(int i=0;i<total_i;i++) { prev=prevLayer.At(n*iStep+i); out=OutputLayer.At(total_i-i-1); if(CheckPointer(prev)==POINTER_INVALID || CheckPointer(out)==POINTER_INVALID) continue; delta+=prev.getOutputVal()*out.getGradient(); }
A soma calculada dos produtos serve de base para o ajuste dos pesos. O ajuste dos pesos levando em consideração a velocidade de treinamento definida.
con.weight+=con.deltaWeight=(delta!=0 ? eta*delta : 0)+(con.deltaWeight!=0 ? alpha*con.deltaWeight : 0); } //--- return true; }
Após ajustar todos os pesos, saímos do método.
A classe CNeuron é descrita em detalhes no primeiro artigo. Ele não mudou muito, então eu não irei fornecer sua descrição aqui.
3.4. Criação de uma classe de rede neural convolucional.
Agora que todos os tijolos foram criados, nós podemos começar a construir uma casa. Nós criaremos uma classe de rede neural convolucional que combinará todos os tipos de neurônios em uma estrutura clara e organizará o trabalho de nossa rede neural. A primeira questão que surge ao criar esta classe é como definir a estrutura da rede necessária. No caso de um perceptron totalmente conectado, nós passamos uma série de elementos com informações sobre o número de neurônios em cada camada. Agora nós precisamos de mais informações para gerar a camada de rede desejada. Vamos criar uma pequena classe CLayerDescription para descrever a construção da camada. Esta classe não contém nenhum método (exceto para o construtor e destrutor), e ele só inclui as variáveis para especificar o tipo de neurônios na camada, o número de tais neurônios, o tamanho da janela e o passo para os neurônios nas camadas convolucionais e de subamostragem. Será passado um ponteiro para um array de classes com a descrição das camadas nos parâmetros do construtor de classes da rede convolucional.
class CLayerDescription : public CObject { public: CLayerDescription(void); ~CLayerDescription(void){}; //--- int type; int count; int window; int step; }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ CLayerDescription::CLayerDescription(void) : type(defNeuron), count(0), window(1), step(1) {}
Vamos considerar a estrutura da classe da rede neural convolucional CNetConvolution. A classe contém:
- layers — uma matriz de camadas;
- recentAverageError — erro de rede atual;
- recentAverageSmoothingFactor — fator do erro médio;
- CNetConvolution — construtor da classe;
- ~CNetConvolution — destrutor da classe;
- feedForward — método da propagação direta;
- backProp — método da retro-propagação;
- getResults — método para obter os resultados da última propagação direta (feedforward);
- getRecentAverageError — método para obter o erro da rede atual;
- Save e Load — métodos para salvar e carregar o método previamente criado e treinado.
class CNetConvolution { public: CNetConvolution(CArrayObj *Description); ~CNetConvolution(void) { delete layers; } bool feedForward( CArrayDouble *inputVals); void backProp( CArrayDouble *targetVals); void getResults(CArrayDouble *&resultVals) ; double getRecentAverageError() { return recentAverageError; } bool Save( string file_name, double error, double undefine, double forecast, datetime time, bool common=true); bool Load( string file_name, double &error, double &undefine, double &forecast, datetime &time, bool common=true); //--- static double recentAverageSmoothingFactor; virtual int Type(void) const { return defNetConv; } private: CArrayLayer *layers; double recentAverageError; };
Os nomes dos métodos e algoritmos de construção são semelhantes aos de um perceptron totalmente conectado, que foram descritos no primeiro artigo. Vamos detalhar apenas nos métodos principais da classe.
3.4.1. Construtor de classe da rede neural convolucional.
Considere o construtor da classe. O construtor recebe nos parâmetros um ponteiro para uma série de descrições da camada para construir uma rede. Portanto, nós precisamos verificar a validade do ponteiro recebido, para determinar o número de camadas e para criar uma nova instância da matriz de camadas.
CNetConvolution::CNetConvolution(CArrayObj *Description)
{
if(CheckPointer(Description)==POINTER_INVALID)
return;
//---
int total=Description.Total();
if(total<=0)
return;
//---
layers=new CArrayLayer();
if(CheckPointer(layers)==POINTER_INVALID)
return;
Em seguida, declaramos as variáveis internas.
CLayer *temp; CLayerDescription *desc=NULL, *next=NULL, *prev=NULL; CNeuronBase *neuron=NULL; CNeuronProof *neuron_p=NULL; int output_count=0; int temp_count=0;
Isso conclui o trabalho preparatório. Vamos prosseguir diretamente para a geração cíclica das camadas da rede neural. No início do ciclo, lemos as informações sobre a camada atual e a próxima.
for(int i=0;i<total;i++) { prev=desc; desc=Description.At(i); if((i+1)<total) { next=Description.At(i+1); if(CheckPointer(next)==POINTER_INVALID) return; } else next=NULL;
Contamos o número de conexões de saída para a camada e criamos uma nova instância de classe da camada neural. Observamos que o número de conexões na saída da camada deve ser indicado apenas antes da camada totalmente conectada, caso contrário, especificamos o valor zero. Isso ocorre porque os neurônios convolucionais armazenam os próprios pesos de entrada, enquanto a camada de subamostragem não os usam de forma alguma.
int outputs=(next==NULL || next.type!=defNeuron ? 0 : next.count); temp=new CLayer(outputs);
Em seguida, os neurônios são gerados, com o algoritmo de divisão de acordo com o tipo de neurônios da camada. Para as camadas totalmente conectadas, uma nova instância do neurônio é criada e inicializada. Observe que, para as camadas totalmente conectadas, mais um neurônio é criado, além do número indicado na descrição. Este neurônio será usado como um viés bayesiano.
for(int n=0;n<(desc.count+(i>0 && desc.type==defNeuron ? 1 : 0));n++) { switch(desc.type) { case defNeuron: neuron=new CNeuron(); if(CheckPointer(neuron)==POINTER_INVALID) { delete temp; delete layers; return; } neuron.Init(outputs,n); break;
Criamos uma nova instância de neurônio para a camada de convolução. Contamos o número de elementos de saída com base nas informações sobre a camada anterior e inicializamos o neurônio recém-criado.
case defNeuronConv: neuron_p=new CNeuronConv(); if(CheckPointer(neuron_p)==POINTER_INVALID) { delete temp; delete layers; return; } if(CheckPointer(prev)!=POINTER_INVALID) { if(prev.type==defNeuron) { temp_count=(int)((prev.count-desc.window)%desc.step); output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2)); } else if(n==0) { temp_count=(int)((output_count-desc.window)%desc.step); output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2)); } } if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count)) neuron=neuron_p; break;
Um algoritmo semelhante é aplicado aos neurônios na camada de subamostragem.
case defNeuronProof: neuron_p=new CNeuronProof(); if(CheckPointer(neuron_p)==POINTER_INVALID) { delete temp; delete layers; return; } if(CheckPointer(prev)!=POINTER_INVALID) { if(prev.type==defNeuron) { temp_count=(int)((prev.count-desc.window)%desc.step); output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2)); } else if(n==0) { temp_count=(int)((output_count-desc.window)%desc.step); output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2)); } } if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count)) neuron=neuron_p; break; }
Depois de declarar e inicializar o neurônio, adicionamos ele à camada neural.
if(!temp.Add(neuron)) { delete temp; delete layers; return; } neuron=NULL; }
Depois que o ciclo de geração de neurônios para a próxima camada for concluído, adicionamos a camada ao armazenamento. Saímos do método após a geração de todas as camadas.
if(!layers.Add(temp)) { delete temp; delete layers; return; } } //--- return; }
3.4.2. Método feedforward das redes neurais convolucionais.
Todo o funcionamento da rede neural é organizado no método feedForward (propagação direta). Este método recebe nos parâmetros os dados originais para análise (no nosso caso, esses dados são as informações do gráfico de preços e dos indicadores). Em primeiro lugar, nós verificamos a validade da referência recebida para a matriz de dados e o estado de inicialização da rede neural.
bool CNetConvolution::feedForward(CArrayDouble *inputVals) { if(CheckPointer(layers)==POINTER_INVALID || CheckPointer(inputVals)==POINTER_INVALID || layers.Total()<=1) return false;
Em seguida, declaramos as variáveis auxiliares e transferimos os dados externos recebidos para a camada de entrada da rede neural.
CLayer *previous=NULL; CLayer *current=layers.At(0); int total=MathMin(current.Total(),inputVals.Total()); CNeuronBase *neuron=NULL; for(int i=0;i<total;i++) { neuron=current.At(i); if(CheckPointer(neuron)==POINTER_INVALID) return false; neuron.setOutputVal(inputVals.At(i)); }
Depois de carregar os dados de origem na rede neural, executamos um loop por todas as camadas neurais, desde a entrada da rede até sua saída.
CObject *temp=NULL; for(int l=1;l<layers.Total();l++) { previous=current; current=layers.At(l); if(CheckPointer(current)==POINTER_INVALID) return false;
Dentro do loop lançado, executamos um loop aninhado para cada camada, para iterar sobre todos os neurônios na camada e recalcular os seus valores. Observe que, para as camadas neurais totalmente conectadas, o valor do último neurônio não é recalculado. Como mencionado acima, esse neurônio é usado como um viés Bayesiano e, portanto, apenas o seu peso será usado.
total=current.Total(); if(current.At(0).Type()==defNeuron) total--; //--- for(int n=0;n<total;n++) { neuron=current.At(n); if(CheckPointer(neuron)==POINTER_INVALID) return false;
Além disso, a escolha do método depende do tipo de neurônios na camada anterior. Para as camadas totalmente conectadas, chamamos o método de propagação direta ou feedforward, especificando uma referência à camada anterior em seus parâmetros.
if(previous.At(0).Type()==defNeuron) { temp=previous; if(!neuron.feedForward(temp)) return false; continue; }
Se anteriormente havia uma camada convolucional ou de subamostragem, verificamos o tipo do neurônio recalculado. Para um neurônio de uma camada totalmente conectada, reunimos as camadas internas de todos os neurônios da camada anterior em uma única camada e então chamamos o método de propagação direta do neurônio atual, com uma referência à camada total de neurônios especificada nos parâmetros.
if(neuron.Type()==defNeuron) { if(n==0) { CLayer *temp_l=new CLayer(total); if(CheckPointer(temp_l)==POINTER_INVALID) return false; CNeuronProof *proof=NULL; for(int p=0;p<previous.Total();p++) { proof=previous.At(p); if(CheckPointer(proof)==POINTER_INVALID) return false; temp_l.AddArray(proof.getOutputLayer()); } temp=temp_l; } if(!neuron.feedForward(temp)) return false; if(n==total-1) { CLayer *temp_l=temp; temp_l.FreeMode(false); temp_l.Shutdown(); delete temp_l; } continue; }
Uma vez que o loop por todos os neurônios desta camada for concluído, excluímos o objeto da camada total. Aqui, é necessário excluir o objeto de camada sem excluir os objetos dos neurônios contidos nesta camada, pois os mesmos objetos continuarão a ser usados em nossas camadas convolucionais e de subamostragem. Isso deve ser feito definindo a flag m_free_mode para o estado false, em seguida, excluindo o objeto.
Se este for um elemento de uma camada convolucional ou de subamostragem, então o método de propagação direta, passa um ponteiro para o elemento anterior do filtro apropriado como parâmetro.
temp=previous.At(n); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!neuron.feedForward(temp)) return false; } } //--- return true; }
Depois de iterar todos os neurônios e camadas, saímos do método.
3.4.3. Método backpropagation da rede neural convolucional.
A rede neural é treinada usando o método backProp de retro-propagação. Ele implementa o método de propagação do erro reverso da camada de saída da rede neural para suas entradas. Portanto, o método recebe os dados reais nos parâmetros.
No início do método, verificamos a validade do ponteiro para a referência do valor do objeto.
void CNetConvolution::backProp(CArrayDouble *targetVals) { if(CheckPointer(targetVals)==POINTER_INVALID) return;
Em seguida, calcule a raiz quadrada do erro médio na saída da propagação direta da rede neural em comparação com os dados reais e calculamos o gradiente do erro dos neurônios da camada de saída.
CLayer *outputLayer=layers.At(layers.Total()-1); if(CheckPointer(outputLayer)==POINTER_INVALID) return; //--- double error=0.0; int total=outputLayer.Total()-1; for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron=outputLayer.At(n); double target=targetVals.At(n); double delta=(target>1 ? 1 : target<-1 ? -1 : target)-neuron.getOutputVal(); error+=delta*delta; neuron.calcOutputGradients(targetVals.At(n)); } error/= total; error = sqrt(error); recentAverageError+=(error-recentAverageError)/recentAverageSmoothingFactor;
O próximo passo é organizar um loop reverso em todas as camadas da rede neural. Aqui, nós executamos um loop aninhado por todos os neurônios da camada correspondente para recalcular o gradiente do erro dos neurônios das camadas ocultas.
CNeuronBase *neuron=NULL; CObject *temp=NULL; for(int layerNum=layers.Total()-2; layerNum>0; layerNum--) { CLayer *hiddenLayer=layers.At(layerNum); CLayer *nextLayer=layers.At(layerNum+1); total=hiddenLayer.Total(); for(int n=0; n<total && !IsStopped(); ++n) {
Similarmente ao método de propagação direta, o método necessário para atualizar o gradiente de erro é selecionado com base nos tipos do neurônio atual e dos neurônios da próxima camada. Se uma camada totalmente conectada de neurônios vier em seguida, chamamos o método calcHiddenGradients do neurônio analisado, passando o ponteiro para o objeto da próxima camada da rede neural nos parâmetros.
neuron=hiddenLayer.At(n); if(nextLayer.At(0).Type()==defNeuron) { temp=nextLayer; neuron.calcHiddenGradients(temp); continue; }
Se isso for seguido por uma camada convolucional ou de subamostragem, verificamos o tipo do neurônio atual. Para um neurônio totalmente conectado, iteramos em um loop por todos os filtros da próxima camada, enquanto iniciamos o recálculo do gradiente de erro para cada filtro de um determinado neurônio. Em seguida, somamos os gradientes resultantes. Se a camada atual também for convolucional ou de subamostragem, determinamos o gradiente do erro usando o filtro correspondente.
if(neuron.Type()==defNeuron) { double g=0; for(int i=0;i<nextLayer.Total();i++) { temp=nextLayer.At(i); neuron.calcHiddenGradients(temp); g+=neuron.getGradient(); } neuron.setGradient(g); continue; } temp=nextLayer.At(n); neuron.calcHiddenGradients(temp); } }
Depois de atualizar todos os gradientes, executamos loops semelhantes com a mesma lógica de ramificação para atualizar os pesos dos neurônios. Saímos do método após a atualização dos pesos.
for(int layerNum=layers.Total()-1; layerNum>0; layerNum--) { CLayer *layer=layers.At(layerNum); CLayer *prevLayer=layers.At(layerNum-1); total=layer.Total()-(layer.At(0).Type()==defNeuron ? 1 : 0); int n_conv=0; for(int n=0; n<total && !IsStopped(); n++) { neuron=layer.At(n); if(CheckPointer(neuron)==POINTER_INVALID) return; if(neuron.Type()==defNeuronProof) continue; switch(prevLayer.At(0).Type()) { case defNeuron: temp=prevLayer; neuron.updateInputWeights(temp); break; case defNeuronConv: case defNeuronProof: if(neuron.Type()==defNeuron) { for(n_conv=0;n_conv<prevLayer.Total();n_conv++) { temp=prevLayer.At(n_conv); neuron.updateInputWeights(temp); } } else { temp=prevLayer.At(n); neuron.updateInputWeights(temp); } break; default: temp=NULL; break; } } } }
O código completo de todos os métodos e classes está disponível em anexo abaixo.
4. Teste
Vamos usar o Expert Advisor de classificação do segundo artigo dentro desta série, a fim de testar o funcionamento da rede neural convolucional. O objetivo da rede neural é aprender a prever um fractal no candle atual. Para este propósito, alimentamos a rede neural com as informações sobre a formação das últimas N velas e dados de 4 osciladores para o mesmo período.
Na camada convolucional da rede neural, criamos 4 filtros que procurarão padrões nos dados de formação total das velas e fará leituras do oscilador na vela analisada. A janela e o passo do filtro corresponderão à quantidade de dados pela descrição da vela. Em outras palavras, isso irá comparar todas as informações sobre cada vela com um determinado padrão e retornará o valor de convergência. Essa abordagem permite complementar os dados iniciais com novas informações sobre as velas (como adicionar mais indicadores para a análise e assim por diante) sem perda significativa de desempenho.
O tamanho da matriz de características é reduzido na camada de subamostragem, bem como os resultados são suavizados pela média.
O próprio EA exigiu o mínimo de alterações. A mudança aplica-se à classe da rede neural, nomeadamente a declaração de variáveis e a criação de uma instância.
CNetConvolution *Net;
Outras mudanças dizem respeito à parte que define a estrutura da rede neural na função OnInit. O teste foi realizado usando uma rede com uma camada convolucional e uma subamostragem, cada uma com 4 filtros. A estrutura das camadas totalmente conectadas não mudou (foi feito intencionalmente para avaliar o impacto das camadas convolucionais na operação de toda a rede).
Net=new CNetConvolution(NULL); ResetLastError(); if(CheckPointer(Net)==POINTER_INVALID || !Net.Load(FileName+".nnw",dError,dUndefine,dForecast,dtStudied,false)) { printf("%s - %d -> Error of read %s prev Net %d",__FUNCTION__,__LINE__,FileName+".nnw",GetLastError()); CArrayObj *Topology=new CArrayObj(); if(CheckPointer(Topology)==POINTER_INVALID) return INIT_FAILED; //--- CLayerDescription *desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuron; if(!Topology.Add(desc)) return INIT_FAILED; //--- int filters=4; desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=filters; desc.type=defNeuronConv; desc.window=12; desc.step=12; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=filters; desc.type=defNeuronProof; desc.window=3; desc.step=2; if(!Topology.Add(desc)) return INIT_FAILED; //--- int n=1000; bool result=true; for(int i=0;(i<4 && result);i++) { desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=n; desc.type=defNeuron; result=(Topology.Add(desc) && result); n=(int)MathMax(n*0.3,20); } if(!result) { delete Topology; return INIT_FAILED; } //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=3; desc.type=defNeuron; if(!Topology.Add(desc)) return INIT_FAILED; delete Net; Net=new CNetConvolution(Topology); delete Topology; if(CheckPointer(Net)==POINTER_INVALID) return INIT_FAILED; dError=-1; dUndefine=0; dForecast=0; dtStudied=0; }
O resto do código do Expert Advisor permaneceu inalterado.
O teste foi realizado usando o par EURUSD com o período gráfico H1. Dois Expert Advisors, um com a rede neural convolucional e outro com a rede totalmente conectada, foram lançados simultaneamente em diferentes gráficos do mesmo símbolo, na mesma plataforma. Os parâmetros das camadas totalmente conectadas da rede neural convolucional correspondem aos parâmetros da rede totalmente conectada do segundo Expert Advisor, ou seja, nós simplesmente adicionamos as camadas convolucionais e de subamostragem a uma rede criada anteriormente.
Os testes mostraram um pequeno ganho de desempenho na rede neural convolucional. Apesar da adição de duas camadas, o tempo médio de treinamento para uma época (com base nos resultados de 24 épocas) de uma rede neural convolucional foi de 2 horas e 4 minutos, e para uma rede totalmente conectada foi de 2 horas e 10 minutos.
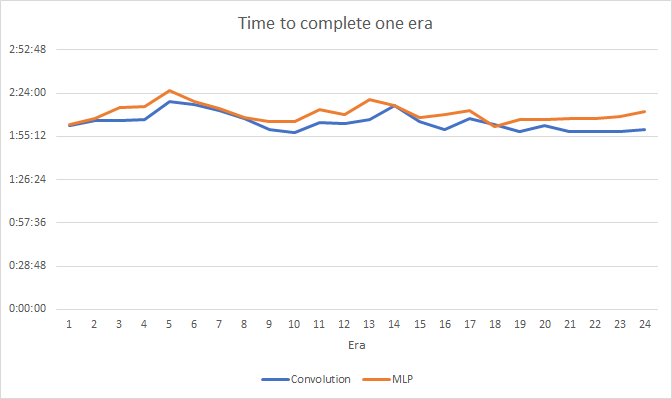
A rede neural convolucional mostra resultados ligeiramente melhores em termos de erro de previsão e "acerto no alvo".
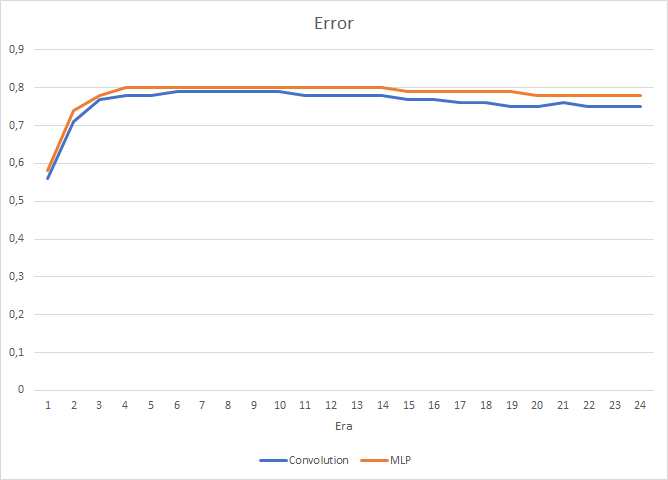
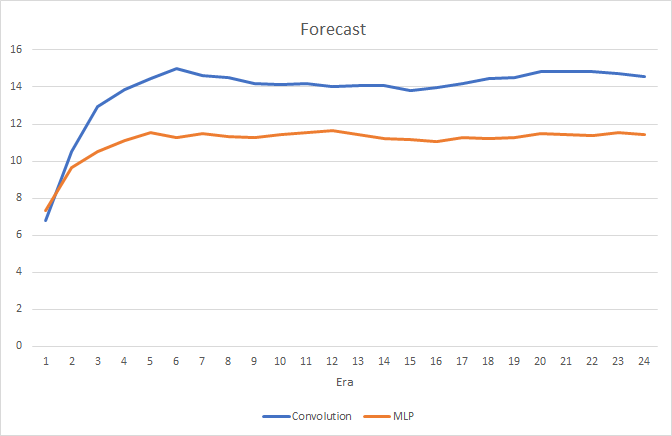
Visualmente, você pode ver que os sinais aparecem com menos frequência no gráfico da rede neural convolucional, mas eles estão mais próximos do alvo.
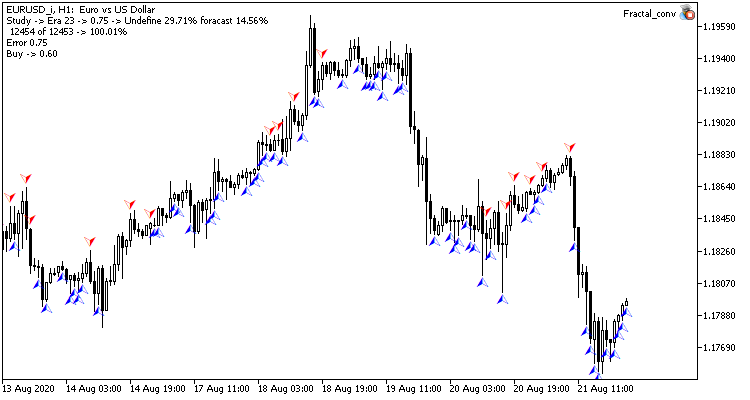
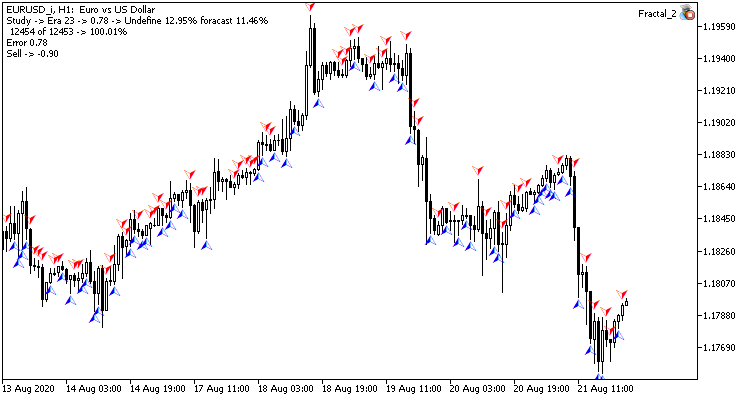
Conclusão
Neste artigo, nós examinamos a possibilidade de usar as redes neurais convolucionais nos mercados financeiros. Os testes mostraram que, ao usá-los, nós podemos melhorar os resultados de uma rede neural totalmente conectada. Isso pode ser conectado com o pré-processamento dos dados que alimentamos no perceptron totalmente conectado. Os dados originais são filtrados nas camadas convolucionais e de subamostragem para remover o ruído, o que melhora a qualidade dos dados de origem e a qualidade da rede neural. Além disso, a dimensionalidade reduzida ajuda a reduzir o número de conexões do perceptron com os dados originais, o que proporciona um aumento no desempenho.
Lista de referências
- Redes Neurais de Maneira Fácil
- Redes neurais de maneira fácil (Parte 2): Treinamento e teste da rede
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Fractal.mq5 | Expert Advisor | Um Expert Advisor com a rede neural de regressão (1 neurônio na camada de saída) |
| 2 | Fractal_2.mq5 | Expert Advisor | Um Expert Advisor com a rede neural de classificação (3 neurônios na camada de saída) |
| 3 | NeuroNet.mqh | Biblioteca de classe | Uma biblioteca de classes para a criação de uma rede neural (um perceptron) |
| 4 | Fractal_conv.mq5 | Expert Advisor | Um Expert Advisor com a rede neural convolucional (3 neurônios na camada de saída) |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/8234
Grade e martingale: o que são e como usá-los?
Trabalhando com séries temporais na biblioteca DoEasy (Parte 55): classe-coleção de indicadores
Redes Neurais de Maneira Fácil(Parte 4): Redes Recorrentes
Trabalhando com séries temporais na biblioteca DoEasy (Parte 54): classes herdeiras do indicador base abstrato
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso