
Redes neurais de maneira fácil (Parte 2): Treinamento e teste da rede
Conteúdo
- Introdução
- 1. Definição do problema
- 2. Projetando o modelo da rede neural
- 2.1. Determinando o número de neurônios na camada de entrada
- 2.2. Projetando as camadas ocultas
- 2.3. Determinando o número de neurônios na camada de saída
- 3. Programação
- 3.1. Preparação do trabalho
- 3.2. Inicialização das classes
- 3.3. Treinamento da rede neural
- 3.4. Melhorando o método de cálculo do gradiente
- 4. Teste
- Conclusão
- Programas utilizados no artigo
Introdução
No artigo anterior intitulado de Redes neurais de maneira fácil, nós consideramos os princípios de construção da CNet para trabalhar com as redes neurais totalmente conectadas usando a MQL5. Neste artigo, eu vou demonstrar um exemplo de como usar esta classe em um Expert Advisor e avaliar a classe em condições reais.
1. Definição do problema
Antes de começarmos a criar nosso Expert Advisor, é necessário definir as metas e objetivos que definiremos para nossa nova rede neural. Obviamente, o objetivo comum de qualquer Expert Advisor no mercado financeiro é a obtenção de lucro. No entanto, esse propósito é muito geral. Nós precisamos definir as tarefas mais específicas para a rede neural. Além disso, nós precisamos entender como avaliar os resultados futuros da rede neural.
Outro momento importante é que a classe CNet criada anteriormente utilizava princípios de aprendizagem supervisionada e, portanto, ela requer dados rotulados para o conjunto de treinamento.
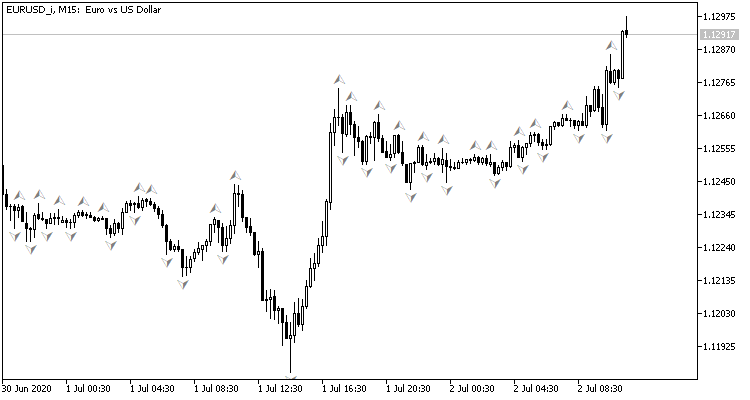
Se você olhar o gráfico de preços, o desejo natural seria executar operações de negociação em picos de preços, que podem ser mostrados pelo indicador padrão Fractal de Bill Williams. O problema com o indicador é que ele determina picos em 3 velas e sempre produz um sinal atrasado em 1 vela, que pode então ter um sinal oposto. E se nós definirmos a rede neural para determinar os pontos de pivô antes da formação do terceiro candle? Esta abordagem daria pelo menos um candle prévio de movimento na direção da negociação.
Isso se refere ao conjunto de treinamento:
- Na passagem direta, nós inseriremos a situação atual do mercado na rede neural e ela produzirá uma estimativa da probabilidade de formação de picos no último candle fechado.
- Para a passagem reversa, após a formação do próximo candle, nós verificaremos se houve fractal no candle anterior e inseriremos o resultado para ajustar os pesos.
Para avaliar o resultado das operações da rede, nós podemos usar o erro quadrático médio, a porcentagem de predições de fractais corretas e a porcentagem de fractais não reconhecidos.
Agora nós precisamos determinar quais dados devem ser inseridos em nossa rede neural. Você se lembra do que faz quando tenta avaliar a situação do mercado com base no gráfico?
Em primeiro lugar, um trader novato é aconselhado a avaliar visualmente a direção da tendência no gráfico. Portanto, nós devemos digitalizar as informações sobre os movimentos de preços e inseri-las na rede neural. Eu proponho inserir os dados sobre preços de abertura, fechamento, máxima, mínima, volumes e tempo de formação.
Outro método popular para determinar a tendência é usar os indicadores de oscilação. O uso de tais indicadores é conveniente porque os indicadores geram os dados normalizados. Eu decidi usar para o experimento quatro indicadores padrão: RSI, CCI, ATR e MACD, todos com seus parâmetros padrão. Eu não realizei nenhuma análise adicional para selecionar os indicadores e seus parâmetros.
Alguém pode dizer que o uso de indicadores não faz sentido, uma vez que seus dados são construídos a partir do recálculo dos dados de preços de velas, que nós já inserimos na rede neural. Mas isso não é totalmente verdade. Os valores do indicador são determinados por meio do cálculo dos dados de várias velas, o que permite uma certa expansão da amostra analisada. O processo de treinamento da rede neural determinará como eles afetarão o resultado.
Para poder avaliar a dinâmica do mercado, nós inseriremos todas as informações de um determinado período do histórico na rede neural.
2. Projetando o modelo da rede neural
2.1. Determinando o número de neurônios na camada de entrada
Aqui, nós precisamos entender o número de neurônios na camada de entrada. Para fazer isso, nós avaliamos as informações iniciais de cada vela e multiplicamos elas pela profundidade do histórico analisado.
Não há necessidade de pré-processar os dados do indicador, pois eles são normalizados e o número relevante de buffers do indicador é conhecido (no total, os 4 indicadores acima possuem 5 valores). Portanto, para receber esses indicadores na camada de entrada, nós precisamos criar 5 neurônios para cada vela analisada.
A situação é um pouco diferente com os dados de preço das velas. Ao determinar a direção e a força da tendência visualmente em um gráfico, nós analisamos primeiro a direção e o tamanho da vela. Só depois disso, quando nós chegamos a determinar a direção da tendência e os prováveis pontos de pivô, nós prestamos atenção ao nível de preço do símbolo analisado. Portanto, é necessário normalizar esses dados antes de inseri-los na rede neural. Eu, pessoalmente, insiro a diferença entre os preços de fechamento, máxima e mínima em relação ao preço de abertura da vela descrita. Nessa abordagem, basta descrever três neurônios, onde o sinal do primeiro neurônio determina a direção da vela.
Existem muitos materiais diferentes que descrevem a influência de vários fatores temporais na volatilidade da moeda. Por exemplo, a temporada, as diferenças na dinâmica por semanas e dias, bem como os pregões europeus, americanos e asiáticos afetam as taxas de câmbio de maneiras diferentes. Para analisar esses fatores, insira o mês, a hora e o dia da semana de formação da vela na rede neural. Eu divido deliberadamente a hora e a data de formação da vela em componentes, pois isso permite que a rede neural generalize e encontre dependências.
Além disso, vamos incluir informações sobre o volume. Se sua corretora fornecer dados sobre volume real, indique esse volume; caso contrário, especifique o volume de tick.
Portanto, nós precisamos de 12 neurônios para descrever cada vela. Multiplicando esse número pela profundidade do histórico analisado, você receberá o tamanho da camada de entrada da rede neural.
2.2. Projetando as camadas ocultas
A próxima etapa é preparar as camadas ocultas de nossa rede neural. A seleção de uma estrutura de rede (número de camadas e neurônios) é uma das tarefas mais difíceis. O perceptron de camada única é bom para a separação linear das classes. Redes de duas camadas podem seguir limites não lineares. As redes de três camadas permitem a descrição de áreas complexas com várias conexões. Quando nós aumentamos o número de camadas, a classe de funções é expandida, mas isso leva a pior convergência e aumento do custo de treinamento. O número de neurônios em cada camada deve satisfazer a variabilidade de funções esperada. De fato, redes muito simples não são capazes de simular o comportamento com a precisão necessária em condições reais, enquanto redes muito complexas são treinadas para repetir não apenas a função objetivo, mas também o ruído.
No primeiro artigo, eu mencionei o método "5-why". Agora, eu proponho continuar esta experiência e criar uma rede com 4 camadas ocultas. Eu defino o número de neurônios na primeira camada oculta igual a 1000. No entanto, ele também pode ser possível estabelecer alguma dependência da profundidade do período analisado. Usando a regra de Pareto, nós reduziremos o número de neurônios em cada camada subsequente em 70%. Além disso, a seguinte limitação será usada: o número de neurônios na camada oculta não deve ser inferior a 20.
2.3. Determinando o número de neurônios na camada de saída
O número de neurônios na camada de saída depende da tarefa e da abordagem para sua solução. Para resolver problemas de regressão, basta ter um neurônio que produzirá o valor esperado. Para resolver problemas de classificação, nós precisamos de um número de neurônios igual ao número esperado de classes - cada um dos neurônios produzirá a probabilidade de atribuir o objeto original a cada classe. Na prática, a classe de um objeto é determinada pela probabilidade máxima.
Para nosso caso, eu proponho criar 2 variantes da rede neural e avaliar sua aplicabilidade para o nosso problema na prática. No primeiro caso, a camada de saída terá um neurônio. Valores na faixa de 0.5 ... 1.0 corresponderão a um fractal de compra, -0.5 ... -1.0 corresponderá a um sinal de venda e valores na faixa de -0.5 ... 0.5 significarão que não há sinal. Nesta solução, a tangente hiperbólica é usada como a função de ativação - ela pode ter valores de saída na faixa de -1.0 a +1.0.
No segundo caso, 3 neurônios serão criados na camada de saída (compra, venda, sem sinal). Nesta variante, nós treinaremos a rede neural para obter um resultado no intervalo de 0.0 ... 1.0. Aqui, o resultado é a probabilidade do surgimento de um fractal. O sinal será determinado de acordo com a probabilidade máxima, e sua direção será determinada de acordo com o índice do neurônio com maior probabilidade.
3. Programação
3.1. Preparação do trabalho
Agora é hora de programar. Primeiro, adicionamos as bibliotecas necessárias:
- NeuroNet.mqh — uma biblioteca para a criação de uma rede neural do artigo anterior
- SymbolInfo.mqh — biblioteca padrão para receber os dados dos símbolos
- TimeSeries.mqh — biblioteca padrão para trabalhar com as séries temporais
- Volumes.mqh — biblioteca padrão para receber os dados de volume
- Oscilators.mqh — biblioteca padrão com as classes de osciladores
#include "NeuroNet.mqh" #include <Trade\SymbolInfo.mqh> #include <Indicators\TimeSeries.mqh> #include <Indicators\Volumes.mqh> #include <Indicators\Oscilators.mqh>
A próxima etapa é escrever os parâmetros do programa, com os quais a rede neural e os parâmetros do indicador serão definidos.
//+------------------------------------------------------------------+ //| input parameters | //+------------------------------------------------------------------+ input int StudyPeriod = 10; //Study period, years input uint HistoryBars = 20; //Depth of history ENUM_TIMEFRAMES TimeFrame = PERIOD_CURRENT; //--- input group "---- RSI ----" input int RSIPeriod = 14; //Period input ENUM_APPLIED_PRICE RSIPrice = PRICE_CLOSE; //Applied price //--- input group "---- CCI ----" input int CCIPeriod = 14; //Period input ENUM_APPLIED_PRICE CCIPrice = PRICE_TYPICAL; //Applied price //--- input group "---- ATR ----" input int ATRPeriod = 14; //Period //--- input group "---- MACD ----" input int FastPeriod = 12; //Fast input int SlowPeriod = 26; //Slow input int SignalPeriod= 9; //Signal input ENUM_APPLIED_PRICE MACDPrice = PRICE_CLOSE; //Applied price
Em seguida, declaramos as variáveis globais - seu uso será explicado mais tarde.
CSymbolInfo *Symb; CiOpen *Open; CiClose *Close; CiHigh *High; CiLow *Low; CiVolumes *Volumes; CiTime *Time; CNet *Net; CArrayDouble *TempData; CiRSI *RSI; CiCCI *CCI; CiATR *ATR; CiMACD *MACD; //--- double dError; double dUndefine; double dForecast; double dPrevSignal; datetime dtStudied; bool bEventStudy;
Isso conclui o trabalho preparatório. Agora, nós prosseguimos para a inicialização das classes.
3.2 Inicialização das classes
A inicialização das classes será realizada na função OnInit. Primeiro, vamos criar uma instância da classe CSymbolInfo para trabalhar com os símbolos e atualizar os dados sobre o símbolo do gráfico.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Symb=new CSymbolInfo(); if(CheckPointer(Symb)==POINTER_INVALID || !Symb.Name(_Symbol)) return INIT_FAILED; Symb.Refresh();
Em seguida, criamos as instâncias da série temporal. Cada vez que você criar uma instância de classe, verifique se ela foi criada com sucesso e inicialize-a. Em caso de erro, saia da função com o resultado INIT_FAILED.
Open=new CiOpen(); if(CheckPointer(Open)==POINTER_INVALID || !Open.Create(Symb.Name(),TimeFrame)) return INIT_FAILED; //--- Close=new CiClose(); if(CheckPointer(Close)==POINTER_INVALID || !Close.Create(Symb.Name(),TimeFrame)) return INIT_FAILED; //--- High=new CiHigh(); if(CheckPointer(High)==POINTER_INVALID || !High.Create(Symb.Name(),TimeFrame)) return INIT_FAILED; //--- Low=new CiLow(); if(CheckPointer(Low)==POINTER_INVALID || !Low.Create(Symb.Name(),TimeFrame)) return INIT_FAILED; //--- Volumes=new CiVolumes(); if(CheckPointer(Volumes)==POINTER_INVALID || !Volumes.Create(Symb.Name(),TimeFrame,VOLUME_TICK)) return INIT_FAILED; //--- Time=new CiTime(); if(CheckPointer(Time)==POINTER_INVALID || !Time.Create(Symb.Name(),TimeFrame)) return INIT_FAILED;
O volume de ticks é usado neste exemplo. Se você quiser usar o volume real, substitua "VOLUME_TICK" por "VOLUME_REAL" ao chamar o método Volumes.Create.
Após declarar a série temporal, criamos as instâncias de classes para trabalhar com os indicadores de maneira semelhante.
RSI=new CiRSI(); if(CheckPointer(RSI)==POINTER_INVALID || !RSI.Create(Symb.Name(),TimeFrame,RSIPeriod,RSIPrice)) return INIT_FAILED; //--- CCI=new CiCCI(); if(CheckPointer(CCI)==POINTER_INVALID || !CCI.Create(Symb.Name(),TimeFrame,CCIPeriod,CCIPrice)) return INIT_FAILED; //--- ATR=new CiATR(); if(CheckPointer(ATR)==POINTER_INVALID || !ATR.Create(Symb.Name(),TimeFrame,ATRPeriod)) return INIT_FAILED; //--- MACD=new CiMACD(); if(CheckPointer(MACD)==POINTER_INVALID || !MACD.Create(Symb.Name(),TimeFrame,FastPeriod,SlowPeriod,SignalPeriod,MACDPrice)) return INIT_FAILED;
Agora nós podemos prosseguir para trabalhar diretamente com a classe da rede neural. Primeiro, criamos uma instância da classe. Durante a inicialização da classe CNet, os parâmetros do construtor passam uma referência a um array com a especificação da estrutura da rede. Observe que o processo de treinamento da rede consome recursos computacionais e leva muito tempo. Portanto, seria incorreto treinar a rede após cada reinício. Aqui está o que eu faço: primeiro eu declaro a instância de rede sem especificar a estrutura e tento carregar uma rede previamente treinada de um armazenamento local (o nome do arquivo é fornecido em #define).
#define FileName Symb.Name()+"_"+EnumToString((ENUM_TIMEFRAMES)Period())+"_"+IntegerToString(HistoryBars,3)+"fr_ea" ... ... ... ... Net=new CNet(NULL); ResetLastError(); if(CheckPointer(Net)==POINTER_INVALID || !Net.Load(FileName+".nnw",dError,dUndefine,dForecast,dtStudied,false)) { printf("%s - %d -> Error of read %s prev Net %d",__FUNCTION__,__LINE__,FileName+".nnw",GetLastError());
Se os dados treinados anteriormente não puderam ser carregados, uma mensagem é impressa no log, indicando o código de erro, e a criação de uma nova rede não treinada é iniciada. Primeiro, declaramos uma instância da classe CArrayInt e especificamos lá a estrutura da rede neural. O número de elementos indica o número de camadas da rede neural e o valor dos elementos indica o número de neurônios na camada correspondente.
CArrayInt *Topology=new CArrayInt(); if(CheckPointer(Topology)==POINTER_INVALID) return INIT_FAILED;
Como já mencionado mais cedo, nós precisamos de 12 neurônios na camada de entrada para descrever cada vela. Portanto, devemos escrever o produto de 12 pela profundidade do histórico analisado no primeiro elemento do array.
if(!Topology.Add(HistoryBars*12)) return INIT_FAILED;
Em seguida, descrevemos as camadas ocultas. Nós determinamos que haverá 4 camadas ocultas com 1000 neurônios na primeira camada oculta. Então, o número de neurônios diminuirá 70% em cada camada subsequente, mas cada camada terá pelo menos 20 neurônios. Os dados serão adicionados a uma matriz em um loop.
int n=1000; bool result=true; for(int i=0;(i<4 && result);i++) { result=(Topology.Add(n) && result); n=(int)MathMax(n*0.3,20); } if(!result) { delete Topology; return INIT_FAILED; }
Indique 1 na camada de saída para construir um modelo de regressão.
if(!Topology.Add(1)) return INIT_FAILED;
Se usarmos um modelo de classificação, nós precisaremos especificar o valor 3 para o neurônio de saída.
Em seguida, removemos a instância da classe CNet criada anteriormente e criamos uma nova, na qual seja indicada a estrutura da rede neural a ser criada. Depois de criar uma nova instância da rede neural, excluímos a classe da estrutura de rede, porque ela não será mais usada.
delete Net; Net=new CNet(Topology); delete Topology; if(CheckPointer(Net)==POINTER_INVALID) return INIT_FAILED;
Definimos os valores iniciais das variáveis para coletar os dados estatísticos:
- dError - desvio padrão (erro)
- dUndefine - percentual de fractais indefinidos
- dForecast - percentual de fractais previstos corretamente
- dtStudied - a data da última vela de treinamento.
dError=-1; dUndefine=0; dForecast=0; dtStudied=0; }
Não se esqueça de que nós precisamos definir a estrutura da rede neural, para criar uma nova instância de classe da rede neural e inicializar as variáveis estatísticas apenas se não houver uma rede neural previamente treinada para carregarmos do armazenamento local.
No final da função OnInit, criamos uma instância da classe CArrayDouble(), que será usada para trocar dados com a rede neural e iniciar o processo de treinamento da rede neural.
Eu gostaria de compartilhar mais uma solução aqui. A MQL5 não possui chamadas de funções assíncronas. Se chamarmos explicitamente a função de aprendizagem da função OnInit, o terminal irá considerar o processo de inicialização do programa inacabado até que o treinamento seja concluído. É por isso que, em vez de chamar diretamente a função, nós criamos um evento personalizado, enquanto a função de treinamento é chamada a partir da função OnChartEvent. Ao criar um evento, especifique o dia de início do treinamento no parâmetro lparam. Essa abordagem nos permite fazer uma chamada de função e completar a função OnInit.
TempData=new CArrayDouble(); if(CheckPointer(TempData)==POINTER_INVALID) return INIT_FAILED; //--- bEventStudy=EventChartCustom(ChartID(),1,(long)MathMax(0,MathMin(iTime(Symb.Name(),PERIOD_CURRENT,(int)(100*Net.recentAverageSmoothingFactor*(dForecast>=70 ? 1 : 10))),dtStudied)),0,"Init"); //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| ChartEvent function | //+------------------------------------------------------------------+ void OnChartEvent(const int id, const long &lparam, const double &dparam, const string &sparam) { //--- if(id==1001) { Train(lparam); bEventStudy=false; OnTick(); } }
Não se esqueça de limpar a memória na função OnDeinit.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- if(CheckPointer(Symb)!=POINTER_INVALID) delete Symb; //--- if(CheckPointer(Open)!=POINTER_INVALID) delete Open; //--- if(CheckPointer(Close)!=POINTER_INVALID) delete Close; //--- if(CheckPointer(High)!=POINTER_INVALID) delete High; //--- if(CheckPointer(Low)!=POINTER_INVALID) delete Low; //--- if(CheckPointer(Time)!=POINTER_INVALID) delete Time; //--- if(CheckPointer(Volumes)!=POINTER_INVALID) delete Volumes; //--- if(CheckPointer(RSI)!=POINTER_INVALID) delete RSI; //--- if(CheckPointer(CCI)!=POINTER_INVALID) delete CCI; //--- if(CheckPointer(ATR)!=POINTER_INVALID) delete ATR; //--- if(CheckPointer(MACD)!=POINTER_INVALID) delete MACD; //--- if(CheckPointer(Net)!=POINTER_INVALID) delete Net; if(CheckPointer(TempData)!=POINTER_INVALID) delete TempData; }
3.3. Treinamento da rede neural
Para treinar a rede neural, criamos a função Train. A data de início do período de treinamento será passada para os parâmetros da função.
void Train(datetime StartTrainBar=0)
Declaramos as seguintes variáveis locais no início da função:
- count - contagem de épocas de aprendizagem
- prev_un - percentual de fractais não reconhecidos na época anterior
- prev_for - percentual de fractais "previstos" corretamente na época anterior
- prev_er - erro da época anterior
- bar_time - data da barra de recálculo
- stop - flag para rastrear a chamada de encerramento forçado do programa.
int count=0; double prev_up=-1; double prev_for=-1; double prev_er=-1; datetime bar_time=0; bool stop=IsStopped(); MqlDateTime sTime;
Em seguida, verificamos se a data obtida nos parâmetros da função não está além do período de treinamento, que foi especificado inicialmente.
MqlDateTime start_time; TimeCurrent(start_time); start_time.year-=StudyPeriod; if(start_time.year<=0) start_time.year=1900; datetime st_time=StructToTime(start_time); dtStudied=MathMax(StartTrainBar,st_time);
O treinamento da rede neural será implementado no loop do-while. No início do loop, recalculamos o número de barras do histórico para treinar a rede neural e salvar as estatísticas do passe anterior.
do { int bars=(int)MathMin(Bars(Symb.Name(),TimeFrame,dtStudied,TimeCurrent())+HistoryBars,Bars(Symb.Name(),TimeFrame)); prev_un=dUndefine; prev_for=dForecast; prev_er=dError; ENUM_SIGNAL bar=Undefine;
Em seguida, ajustamos o tamanho dos buffers e carregamos os dados históricos necessários.
if(!Open.BufferResize(bars) || !Close.BufferResize(bars) || !High.BufferResize(bars) || !Low.BufferResize(bars) || !Time.BufferResize(bars) || !RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars) || !Volumes.BufferResize(bars)) break; Open.Refresh(OBJ_ALL_PERIODS); Close.Refresh(OBJ_ALL_PERIODS); High.Refresh(OBJ_ALL_PERIODS); Low.Refresh(OBJ_ALL_PERIODS); Volumes.Refresh(OBJ_ALL_PERIODS); Time.Refresh(OBJ_ALL_PERIODS); RSI.Refresh(OBJ_ALL_PERIODS); CCI.Refresh(OBJ_ALL_PERIODS); ATR.Refresh(OBJ_ALL_PERIODS); MACD.Refresh(OBJ_ALL_PERIODS);
Atualizamos a flag para rastrear o encerramento forçado do programa e declaramos uma nova flag indicando que a época de aprendizado passou (add_loop).
stop=IsStopped(); bool add_loop=false;
Organizamos um ciclo de treinamento aninhado por meio de todos os dados do histórico. No início do ciclo, verificamos se foi alcançado o fim dos dados históricos. Se necessário, alteramos a flag add_loop. Além disso, exibimos o estado atual do treinamento da rede neural no gráfico usando comentários. Isso ajudará a monitorar o processo de treinamento.
for(int i=(int)(bars-MathMax(HistoryBars,0)-1); i>=0 && !stop; i--) { if(i==0) add_loop=true; string s=StringFormat("Study -> Era %d -> %.2f -> Undefine %.2f%% foracast %.2f%%\n %d of %d -> %.2f%% \nError %.2f\n%s -> %.2f",count,dError,dUndefine,dForecast,bars-i+1,bars,(double)(bars-i+1.0)/bars*100,Net.getRecentAverageError(),EnumToString(DoubleToSignal(dPrevSignal)),dPrevSignal); Comment(s);
Em seguida, verificamos se o estado do sistema previsto foi calculado na etapa anterior do ciclo. Se sim, ajustamos os pesos na direção do valor correto. Para fazer isso, limpamos o conteúdo do array TempData, verificamos se o fractal foi formado na vela anterior e adicionamos um valor correto ao array TempData (abaixo está o código para uma rede neural de regressão com um neurônio na camada de saída). Depois disso, chamamos o método backProp da rede neural, passando uma referência ao array TempData como parâmetro. Atualizamos os dados estatísticos no dForecast (percentual de fractais previstos corretamente) e dUndefine (percentual de fractais não reconhecidos).
if(i<(int)(bars-MathMax(HistoryBars,0)-1) && i>1 && Time.GetData(i)>dtStudied && dPrevSignal!=-2) { TempData.Clear(); bool sell=(High.GetData(i+2)<High.GetData(i+1) && High.GetData(i)<High.GetData(i+1)); bool buy=(Low.GetData(i+2)<Low.GetData(i+1) && Low.GetData(i)<Low.GetData(i+1)); TempData.Add(buy && !sell ? 1 : !buy && sell ? -1 : 0); Net.backProp(TempData); if(DoubleToSignal(dPrevSignal)!=Undefine) { if(DoubleToSignal(dPrevSignal)==DoubleToSignal(TempData.At(0))) dForecast+=(100-dForecast)/Net.recentAverageSmoothingFactor; else dForecast-=dForecast/Net.recentAverageSmoothingFactor; dUndefine-=dUndefine/Net.recentAverageSmoothingFactor; } else { if(sell || buy) dUndefine+=(100-dUndefine)/Net.recentAverageSmoothingFactor; } }
Depois de ajustar os coeficientes de peso da rede neural, calculamos a probabilidade de surgimento de um fractal na barra atual do histórico (se i for igual a 0, a probabilidade de formação de um fractal na barra atual é calculada). Para fazer isso, limpamos o array TempData e adicionamos a ele os dados atuais da camada de entrada da rede neural. Se a adição de dados falhar ou não houver dados suficientes, saímos do loop.
TempData.Clear(); int r=i+(int)HistoryBars; if(r>bars) continue; //--- for(int b=0; b<(int)HistoryBars; b++) { int bar_t=r+b; double open=Open.GetData(bar_t); TimeToStruct(Time.GetData(bar_t),sTime); if(open==EMPTY_VALUE || !TempData.Add(Close.GetData(bar_t)-open) || !TempData.Add(High.GetData(bar_t)-open) || !TempData.Add(Low.GetData(bar_t)-open) || !TempData.Add(Volumes.Main(bar_t)/1000) || !TempData.Add(sTime.mon) || !TempData.Add(sTime.hour) || !TempData.Add(sTime.day_of_week) || !TempData.Add(RSI.Main(bar_t)) || !TempData.Add(CCI.Main(bar_t)) || !TempData.Add(ATR.Main(bar_t)) || !TempData.Add(MACD.Main(bar_t)) || !TempData.Add(MACD.Signal(bar_t))) break; } if(TempData.Total()<(int)HistoryBars*12) break;
Após a preparação dos dados iniciais, executamos o método feedForward e gravamos os resultados da rede neural na variável dPrevSignal. Abaixo está o código para uma rede neural de regressão com um neurônio na camada de saída. O código para uma rede neural de classificação com três neurônios na camada de saída está anexado abaixo.
Net.feedForward(TempData);
Net.getResults(TempData);
dPrevSignal=TempData[0];
Para visualizar a operação da rede neural em um gráfico, exibimos o rótulo dos fractais previstos para as últimas 200 velas.
bar_time=Time.GetData(i); if(i<200) { if(DoubleToSignal(dPrevSignal)==Undefine) DeleteObject(bar_time); else DrawObject(bar_time,dPrevSignal,High.GetData(i),Low.GetData(i)); }
No final do ciclo de dados históricos, atualizamos a flag de encerramento forçado do programa.
stop=IsStopped();
}
Depois que a rede neural tiver sido treinada em todos os dados históricos disponíveis, aumentamos o contador de períodos de treinamento e salvamos o estado atual da rede neural em um arquivo local. Nós poderemos usar isso quando iniciarmos a rede neural dos dados da próxima vez.
if(add_loop) count++; if(!stop) { dError=Net.getRecentAverageError(); if(add_loop) { Net.Save(FileName+".nnw",dError,dUndefine,dForecast,dtStudied,false); printf("Era %d -> error %.2f %% forecast %.2f",count,dError,dForecast); } }
Ao final, especificamos as condições de saída do ciclo de treinamento. As condições podem ser as seguintes: um sinal com a probabilidade de atingir a meta acima de um nível pré-determinado é recebido; o parâmetro de erro de destino é alcançado; ou quando, após uma época de treinamento, os dados estatísticos não mudam ou mudam de forma insignificante (o treinamento parou no mínimo local). Você pode definir suas próprias condições para sair do processo de treinamento.
} while((!(DoubleToSignal(dPrevSignal)!=Undefine || dForecast>70) || !(dError<0.1 && MathAbs(dError-prev_er)<0.01 && MathAbs(dUndefine-prev_up)<0.1 && MathAbs(dForecast-prev_for)<0.1)) && !stop);
Salve o tempo do última vela de treinamento antes de sair da função de treinamento.
if(count>0) { dtStudied=bar_time; } }
3.4. Melhorando o método de cálculo do gradiente
Eu gostaria de chamar sua atenção para o seguinte aspecto que encontrei durante o processo de teste. Ao treinar uma rede neural, em alguns casos, houve um aumento descontrolado nos coeficientes de peso dos neurônios da camada oculta, devido ao qual os valores máximos permitidos das variáveis foram excedidos e, como consequência, toda a rede neural foi paralisada. Isso aconteceu quando o erro de camada subsequente exigiu que os neurônios produzissem valores além da faixa de valores possíveis da função de ativação. A solução que encontrei foi normalizar os valores-alvo dos neurônios. O código corrigido do método de cálculo de gradiente é mostrado abaixo.
void CNeuron::calcOutputGradients(double targetVals) { double delta=(targetVals>1 ? 1 : targetVals<-1 ? -1 : targetVals)-outputVal; gradient=(delta!=0 ? delta*CNeuron::activationFunctionDerivative(targetVals) : 0); }
O código completo de todos os métodos e funções está disponível no anexo.
4. Teste
O treinamento de teste da rede neural foi realizado no par EURUSD, no intervalo de tempo H1. Os dados de 20 velas foram inseridos na rede neural. O treinamento foi realizado nos últimos 2 anos. Para verificar os resultados, eu lancei dois Expert Advisors em dois gráficos do mesmo terminal: um EA com a rede neural de regressão (Fractal - com 1 neurônio na camada de saída) e a rede neural de classificação (Fractal_2 - com 3 neurônios na camada de saída)
A primeira época de treinamento em 12432 barras durou 2 horas e 20 minutos. Ambos os EAs tiveram um desempenho semelhante, com uma taxa de acerto de pouco mais de 6%.
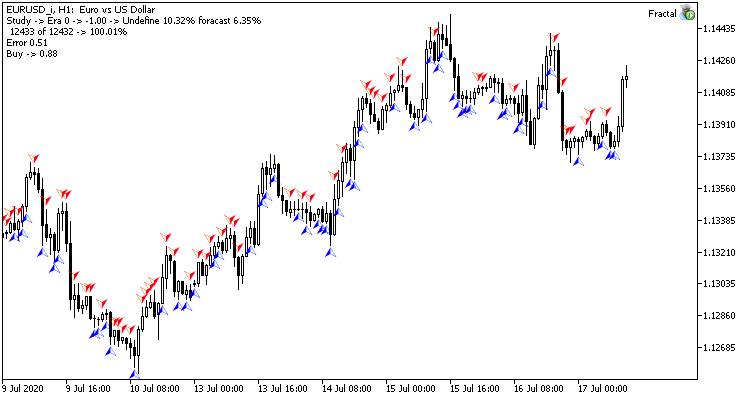
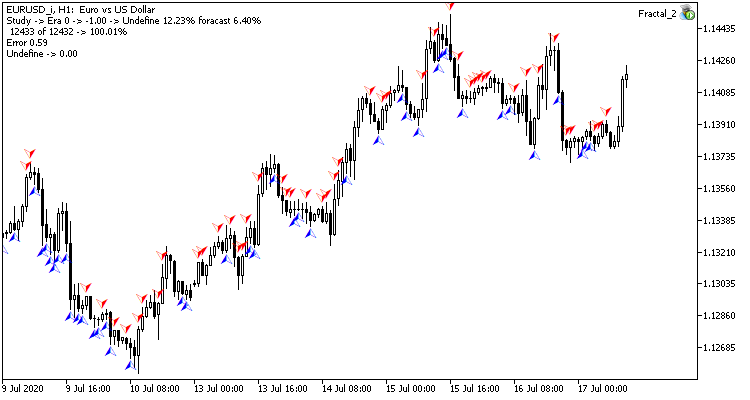
A primeira época é fortemente dependente dos pesos da rede neural que foram selecionados aleatoriamente no estágio inicial.
Após 35 épocas de treinamento, a diferença nas estatísticas aumentou ligeiramente - o modelo de rede neural de regressão obteve um melhor desempenho:
| Valor | Rede neural de regressão | Rede neural de classificação |
|---|---|---|
| Raiz do erro quadrático médio | 0.68 | 0.78 |
| Percentual de acerto | 12.68% | 11.22% |
| Fractais não reconhecidos | 20.22% | 24.65% |
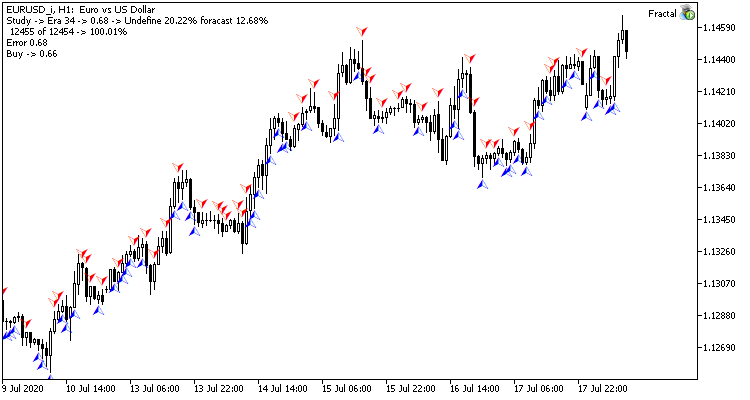
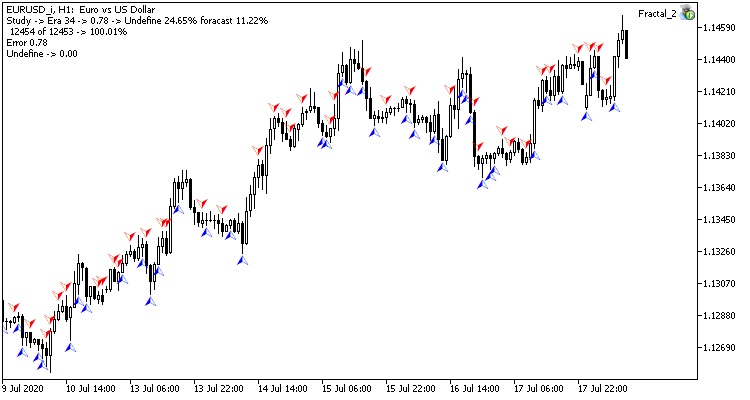
Os resultados dos testes mostram que ambas as variantes da organização da rede neural geram resultados semelhantes em termos de tempo de treinamento e precisão de previsão. Ao mesmo tempo, os resultados obtidos mostram que a rede neural necessita de tempo e recursos adicionais para o treinamento. Se você deseja analisar a dinâmica de aprendizagem da rede neural, verifique as capturas de tela de cada época de aprendizagem no anexo.
Conclusão
Neste artigo, nós consideramos o processo de criação, treinamento e teste da rede neural. Os resultados obtidos mostram que existe potencial para o uso desta tecnologia. No entanto, o processo de treinamento da rede neural consome muitos recursos computacionais e leva muito tempo.
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| Experts\NeuroNet_DNG\ | |||
| 1 | Fractal.mq5 | Expert Advisor | Um Expert Advisor com a rede neural de regressão (1 neurônio na camada de saída) |
| 2 | Fractal_2.mq5 | Expert Advisor | Um Expert Advisor com a rede neural de classificação (3 neurônios na camada de saída) |
| 3 | NeuroNet.mqh | Biblioteca de classe | Uma biblioteca de classes para a criação de uma rede neural (um perceptron) |
| Files\ | |||
| 4 | Fractal | Diretório | Contém capturas de tela mostrando o teste da rede neural de regressão |
| 5 | Fractal_2 | Diretório | Contém capturas de tela mostrando o teste da rede neural de classificação |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/8119
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 O que é uma tendência e qual estrutura o mercado se baseia: Tendência ou Lateral?
O que é uma tendência e qual estrutura o mercado se baseia: Tendência ou Lateral?
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Obrigado, Dmitriy.
Que artigo fantástico (e o artigo anterior)! Eu estava procurando algo para começar, algum código que eu pudesse adaptar, e isso é perfeito. Sou novo em MQL5, mas já estou aprendendo com a leitura do código. Ao compilar, tive os mesmos dois erros de outro autor, mas graças à resposta de Dmitriy, consegui editar o NeuroNet.mqh e obter uma compilação bem-sucedida.
Alguém escreveu o código para fazer pedidos? Gostaria de compartilhar?
Como poderíamos incorporar também a previsão de quais parâmetros de abertura de posição funcionariam melhor, como volume, sl e tp?
Gosto muito do fato de haver apenas cerca de 500 linhas de código no exemplo e na biblioteca. É um tamanho gerenciável para aprendizado e adaptação.
Acho que encontrei o problema com os rótulos dos fractais previstos que não estão sendo exibidos para a rede neural de regressão (Fractal).
O artigo diz o seguinte:
A variável i percorre as velas. Esse código está correto na rede neural de classificação (Fractal_2), embora lá o teste seja i<300.
Entretanto, na rede neural de regressão (Fractal), a contagem é usada como variável de teste, e o teste é ">".
A contagem parece ser o número Era. Isso significaria que os rótulos seriam colocados em todas as velas relevantes, não apenas naquelas das últimas 200, e somente após 200 Eras. Presumo que isso seja um erro.
Isso parece correto?
Uma ótima experiência de aprendizado.
Bom dia
Muito obrigado por este artigo, mas encontrei um erro no compilador ao compilar o Fractal_2.mq5 e o Fractal.mq5. O problema era "void feedForward(const CArrayObj *&prevLayer);" e eu o alterei para "void feedForward(const CArrayObj *prevLayer);". Essa alteração está correta?
Atenciosamente
Atenciosamente
Olá, sim, você pode usá-la.