
Redes Neurais de Maneira Fácil (Parte 5): Cálculos em Paralelo com o OpenCL
Conteúdo
- Introdução
- 1. Como a computação multithread é organizada na MQL5
- 2. A computação multithread nas redes neurais
- 3. Implementando a computação multithread com o OpenCL
- 3.1. Kernel Feed-forward
- 3.2. Kernels Backpropagation
- 3.3. Atualizando os pesos
- 3.4. Criação das classes do programa principal
- 3.5. Criação de uma classe base do neurônio para trabalhar com o OpenCL
- 3.6. Adições na classe CNet
- 4. Teste
- Conclusão
- Links
- Programas utilizados no artigo
Introdução
Nos artigos anteriores, nós discutimos alguns tipos de implementações da rede neural. Como você pode ver, as redes neurais são construídas com um grande número de neurônios do mesmo tipo, nos quais as mesmas operações são realizadas. No entanto, quanto mais neurônios uma rede possui, mais recursos de computação ela consome. Como resultado, o tempo necessário para treinar uma rede neural aumenta exponencialmente, já que a adição de um neurônio à camada oculta exige o aprendizado das conexões com todos os neurônios nas camadas anteriores e na próxima. Existe uma maneira de reduzir o tempo de treinamento da rede neural. Os recursos de multithreading dos computadores modernos permitem o cálculo de vários neurônios simultaneamente. O tempo será reduzido consideravelmente devido ao aumento no número de threads.
1. Como a computação multithread é organizada na MQL5
A plataforma MetaTrader 5 possui uma arquitetura multithread. A distribuição de threads na plataforma é estritamente regulamentada. De acordo com a Documentação, scripts e Expert Advisors são executados em threads individuais. Quanto aos indicadores, são fornecidos threads separadas para cada símbolo. O processamento de ticks e a sincronização do histórico são executados na thread com os indicadores. Isso significa que a plataforma aloca apenas uma thread por Expert Advisor. Alguns cálculos podem ser executados em um indicador, o que fornecerá uma thread adicional. No entanto, os cálculos excessivos em um indicador podem desacelerar a operação da plataforma em relação ao processamento de dados de tick, o que pode levar à uma perda do controle sobre a situação do mercado. Esta situação pode ter um efeito negativo no desempenho do EA.
No entanto, existe uma solução. Os desenvolvedores da MetaTrader 5 forneceram a capacidade de usar DLLs de terceiros. A criação de bibliotecas dinâmicas em uma arquitetura multithread fornece automaticamente as operações multithreading implementadas na biblioteca. Aqui, a operação do EA junto com a troca de dados com a biblioteca permanecem na thread principal do Expert Advisor.
A segunda opção é usar a tecnologia OpenCL. Nesse caso, nós podemos usar os meios padrão para organizar a computação multithread tanto no processador suportado pela tecnologia quanto nas placas de vídeo. Para esta opção, o código do programa não depende do dispositivo utilizado. Existem várias publicações relacionadas à tecnologia OpenCL neste site. Em particular, o tópico é bem abordado nos artigos [5] e [6]
Então, eu decidi usar o OpenCL. Em primeiro lugar, ao usar essa tecnologia, os usuários não precisam realizar configurações adicionais na plataforma e definir uma permissão para o uso de DLLs de terceiros. Em segundo lugar, esse Expert Advisor pode ser transferido entre as plataformas com um arquivo EX5. Isso permite a transferência de parte do cálculo para uma placa de vídeo, cujos recursos costumam ficar ociosos durante a operação da plataforma.
2. A computação multithread nas redes neurais
Nós selecionamos a tecnologia. Agora, nós precisamos decidir sobre o processo de divisão dos cálculos nas threads. Você se lembra do algoritmo perceptron totalmente conectado durante uma passagem da propagação direta (feed-forward)? O sinal se move sequencialmente da camada de entrada para as camadas ocultas e, em seguida, para a camada de saída. Não adianta alocar uma thread para cada camada, pois os cálculos devem ser executados sequencialmente. O cálculo da camada não pode começar até que seja obtido o resultado da camada anterior. O cálculo de um neurônio individual em uma camada não depende dos resultados do cálculo de outros neurônios nessa camada. Isso significa que nós podemos alocar as threads separadas para cada neurônio e enviar todos os neurônios de uma camada para computar de forma paralela.
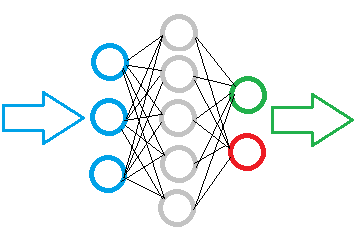
Descendo ao nível de operações de um neurônio, nós poderíamos considerar a possibilidade de paralelizar o cálculo do produto dos valores de entrada pelos seus coeficientes de peso. No entanto, a soma adicional dos valores resultantes e o cálculo do valor da função de ativação são combinados em uma única thread. Eu decidi implementar essas operações em um único kernel OpenCL usando as funções vetoriais.
Uma abordagem semelhante é usada para dividir as threads para a retropropagação (backpropagation). A implementação é exibida abaixo.
3. Implementando a computação multithread com o OpenCL
Tendo escolhido as abordagens básicas, nós podemos prosseguir com a implementação. Vamos começar com a criação dos kernels (funções executáveis do OpenCL). De acordo com a lógica acima, nós iremos criar 4 kernels.
3.1. Kernel feed-forward.
Semelhante aos métodos discutidos nos artigos anteriores, vamos criar um kernel feed-forward chamado FeedForward.
Não se esqueça de que o kernel é uma função executada em cada thread. O número de threads é definido ao chamar o kernel. As operações dentro do kernel são operações aninhadas dentro de um certo loop; o número de iterações do loop é igual ao número de threads chamadas. Portanto, no kernel feed-forward, nós podemos especificar as operações para calcular um estado do neurônio separado, e o número de neurônios pode ser especificado ao chamar o kernel do programa principal.
O kernel recebe nos parâmetros as referências para a matriz de pesos, uma matriz de dados de entrada e uma matriz de dados de saída, bem como o número de elementos da matriz de entrada e o tipo da função de ativação. Preste atenção que todos os arrays em OpenCL são unidimensionais. Portanto, se uma matriz bidimensional é usada para os coeficientes de peso em MQL5, nós precisamos calcular os deslocamentos da posição inicial para ler os dados do segundo neurônio e os subsequentes.
__kernel void FeedForward(__global double *matrix_w, __global double *matrix_i, __global double *matrix_o, int inputs, int activation)
No início do kernel, nós obtemos o número da sequência da thread que determina o número da sequência do neurônio calculado. Declaramos as variáveis privadas (internas), incluindo as variáveis vetoriais inp e weight. Definimos também o deslocamento para os pesos do nosso neurônio.
{
int i=get_global_id(0);
double sum=0.0;
double4 inp, weight;
int shift=(inputs+1)*i;
A seguir, organizamos um ciclo para obter a soma dos produtos dos valores recebidos com os seus pesos. Como mencionado acima, nós usamos os vetores de 4 elementos inp e weight para calcular a soma dos produtos. No entanto, nem todos os arrays recebidos pelo kernel serão múltiplos de 4, então os elementos ausentes devem ser substituídos por valores iguais a zero. Preste atenção para o "1" no vetor de dados de entrada - ele corresponderá a um peso do viés Bayesiana.
for(int k=0; k<=inputs; k=k+4) { switch(inputs-k) { case 0: inp=(double4)(1,0,0,0); weight=(double4)(matrix_w[shift+k],0,0,0); break; case 1: inp=(double4)(matrix_i[k],1,0,0); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],0,0); break; case 2: inp=(double4)(matrix_i[k],matrix_i[k+1],1,0); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],0); break; case 3: inp=(double4)(matrix_i[k],matrix_i[k+1],matrix_i[k+2],1); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],matrix_w[shift+k+3]); break; default: inp=(double4)(matrix_i[k],matrix_i[k+1],matrix_i[k+2],matrix_i[k+3]); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],matrix_w[shift+k+3]); break; } sum+=dot(inp,weight); }
Depois de obter a soma dos produtos, calculamos a função de ativação e escrevemos o resultado na matriz de dados de saída.
switch(activation) { case 0: sum=tanh(sum); break; case 1: sum=pow((1+exp(-sum)),-1); break; } matrix_o[i]=sum; }
3.2. Kernels de Backpropagation.
Criamos dois kernels para propagar o gradiente de erro. Calculamos o erro da camada de saída no primeiro CaclOutputGradient. Sua lógica é simples. Os valores de referência obtidos são normalizados dentro dos valores da função de ativação. Em seguida, a diferença entre os valores de referência e reais é multiplicada pela derivada da função de ativação. Escrevemos o valor resultante na célula correspondente da matriz do gradiente.
__kernel void CaclOutputGradient(__global double *matrix_t, __global double *matrix_o, __global double *matrix_ig, int activation) { int i=get_global_id(0); double temp=0; double out=matrix_o[i]; switch(activation) { case 0: temp=clamp(matrix_t[i],-1.0,1.0)-out; temp=temp*(1+out)*(1-(out==1 ? 0.99 : out)); break; case 1: temp=clamp(matrix_t[i],0.0,1.0)-out; temp=temp*(out==0 ? 0.01 : out)*(1-(out==1 ? 0.99 : out)); break; } matrix_ig[i]=temp; }
No segundo kernel, calculamos o gradiente de erro do neurônio da camada oculta CaclHiddenGradient. A construção do kernel é semelhante ao kernel feed-forward descrito acima. Ele também usa as operações vetoriais. As diferenças estão no uso do vetor de gradiente da próxima camada em vez dos valores de saída da camada anterior, como acontece no feed-forward, e no uso de uma matriz de peso diferente. Além disso, em vez de calcular a função de ativação, a soma resultante é multiplicada pela derivada da função de ativação. O código do kernel é fornecido abaixo.
__kernel void CaclHiddenGradient(__global double *matrix_w, __global double *matrix_g, __global double *matrix_o, __global double *matrix_ig, int outputs, int activation) { int i=get_global_id(0); double sum=0; double out=matrix_o[i]; double4 grad, weight; int shift=(outputs+1)*i; for(int k=0;k<outputs;k+=4) { switch(outputs-k) { case 0: grad=(double4)(1,0,0,0); weight=(double4)(matrix_w[shift+k],0,0,0); break; case 1: grad=(double4)(matrix_g[k],1,0,0); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],0,0); break; case 2: grad=(double4)(matrix_g[k],matrix_g[k+1],1,0); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],0); break; case 3: grad=(double4)(matrix_g[k],matrix_g[k+1],matrix_g[k+2],1); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],matrix_w[shift+k+3]); break; default: grad=(double4)(matrix_g[k],matrix_g[k+1],matrix_g[k+2],matrix_g[k+3]); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],matrix_w[shift+k+3]); break; } sum+=dot(grad,weight); } switch(activation) { case 0: sum=clamp(sum+out,-1.0,1.0); sum=(sum-out)*(1+out)*(1-(out==1 ? 0.99 : out)); break; case 1: sum=clamp(sum+out,0.0,1.0); sum=(sum-out)*(out==0 ? 0.01 : out)*(1-(out==1 ? 0.99 : out)); break; } matrix_ig[i]=sum; }
3.3. Atualizando os pesos.
Vamos criar outro kernel para atualizar os pesos -UpdateWeights. O procedimento para atualizar cada peso individual não depende de outros pesos dentro de um neurônio e de outros neurônios. Isso permite o envio de tarefas para a computar paralelamente todos os pesos de todos os neurônios em uma camada ao mesmo tempo. Nesse caso, nós executamos um kernel em um espaço bidimensional de threads: uma dimensão indica o número de série do neurônio e a segunda dimensão significa o número de conexões dentro do neurônio. Isso é mostrado nas primeiras 2 linhas do código do kernel, onde ele recebe os IDs da thread em duas dimensões.
__kernel void UpdateWeights(__global double *matrix_w, __global double *matrix_g, __global double *matrix_i, __global double *matrix_dw, int inputs, double learning_rates, double momentum) { int i=get_global_id(0); int j=get_global_id(1); int wi=i*(inputs+1)+j; double delta=learning_rates*matrix_g[i]*(j<inputs ? matrix_i[j] : 1) + momentum*matrix_dw[wi]; matrix_dw[wi]=delta; matrix_w[wi]+=delta; };
Em seguida, determinamos o deslocamento para o peso atualizado na matriz de pesos, calculamos o delta (ajuste) e, em seguida, adicionamos o valor resultante na matriz de deltas e adicionamos ele ao peso atual.
Todos os kernels são colocados em um arquivo separado NeuroNet.cl, que será conectado como um recurso ao programa principal.
#resource "NeuroNet.cl" as string cl_program
3.4. Criação das classes do programa principal.
Depois de criar os kernels, vamos voltar ao MQL5 e começar a trabalhar com o código do programa principal. A troca dos dados entre o programa principal e os kernels acontece através dos buffers das matrizes unidimensionais (isto é explicado no artigo [5]). Para organizar esses buffers no lado do programa principal, vamos criar a classe CBufferDouble. Esta classe contém uma referência ao objeto da classe para trabalhar com o OpenCL e o índice do buffer que ele recebe ao ser criado no OpenCL.
class CBufferDouble : public CArrayDouble { protected: COpenCLMy *OpenCL; int m_myIndex; public: CBufferDouble(void); ~CBufferDouble(void); //--- virtual bool BufferInit(uint count, double value); virtual bool BufferCreate(COpenCLMy *opencl); virtual bool BufferFree(void); virtual bool BufferRead(void); virtual bool BufferWrite(void); virtual int GetData(double &values[]); virtual int GetData(CArrayDouble *values); virtual int GetIndex(void) { return m_myIndex; } //--- virtual int Type(void) const { return defBufferDouble; } };
Preste atenção que na criação do buffer OpenCL, o seu identificador é retornado. Este identificador é armazenado na matriz m_buffers da classe COpenCL. Na variável m_myIndex, apenas o índice da matriz especificada é armazenado. Isso ocorre porque todo a operação da classe COpenCL usa a especificação de tal índice e não o kernel ou o identificador do buffer. Observe também que o algoritmo de operação da classe COpenCL, pronta para uso, requer a especificação inicial do número de buffers usados e a criação posterior dos buffers com um índice específico. Em nosso caso, nós adicionaremos os buffers dinamicamente ao criar as camadas neurais. É por isso que a classe COpenCLMy é derivada da COpenCL. Esta classe contém apenas um método adicional. Você pode encontrar o seu código em anexo.
Os seguintes métodos foram criados na classe CBufferDouble para trabalhar com o buffer:
- BufferInit — inicialização do buffer da matriz com o valor especificado
- BufferCreate — cria um buffer em OpenCL
- BufferFree — exclui um buffer no OpenCL
- BufferRead — lê os dados do buffer em OpenCL para um array
- BufferWrite — escreve os dados do array no buffer OpenCL
- GetData — obtém os dados do array solicitado. Ele é implementado em duas variantes para retornar os dados para um array e para a classe CArrayDouble
- GetIndex — retorna o índice do buffer
A arquitetura de todos os métodos é bastante simples e seu código ocupa 1-2 linhas. O código completo de todos os métodos é fornecido no anexo abaixo.
3.5. Criação de uma classe base do neurônio para trabalhar com o OpenCL.
Vamos prosseguir e considerar a classe CNeuronBaseOCL que inclui as adições principais e o algoritmo de operação. É difícil nomear o objeto criado como neurônio, pois ele contém o trabalho de toda a camada neural totalmente conectada. O mesmo se aplica às camadas convolucionais e os blocos LSTM considerados anteriormente. Mas essa abordagem permite preservar a arquitetura da rede neural construída anteriormente.
A classe CNeuronBaseOCL contém um ponteiro para o objeto de classe COpenCLMy e quatro buffers: os valores de saída, uma matriz de coeficientes de peso, os últimos deltas de peso e o gradiente de erro.
class CNeuronBaseOCL : public CObject { protected: COpenCLMy *OpenCL; CBufferDouble *Output; CBufferDouble *Weights; CBufferDouble *DeltaWeights; CBufferDouble *Gradient;
Além disso, declaramos o coeficiente de aprendizado e momentum, o número ordinal do neurônio na camada e o tipo de função de ativação.
const double eta; const double alpha; //--- int m_myIndex; ENUM_ACTIVATION activation;
Adicionamos mais três métodos ao bloco protegido: feed-forward, cálculo do gradiente oculto e a atualização da matriz de peso.
virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool calcHiddenGradients(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL);
No bloco público, declaramos o construtor e o destrutor da classe, o método de inicialização do neurônio e um método para especificar a função de ativação.
public: CNeuronBaseOCL(void); ~CNeuronBaseOCL(void); virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons); virtual void SetActivationFunction(ENUM_ACTIVATION value) { activation=value; }
Para o acesso externo aos dados dos neurônios, declaramos os métodos para a obtenção dos índices do buffer (eles serão usados ao chamar os kernels) e os métodos para receber as informações atuais dos buffers na forma de matrizes. Além disso, adicionamos os métodos para buscar o número de neurônios e as funções de ativação.
virtual int getOutputIndex(void) { return Output.GetIndex(); } virtual int getGradientIndex(void) { return Gradient.GetIndex(); } virtual int getWeightsIndex(void) { return Weights.GetIndex(); } virtual int getDeltaWeightsIndex(void) { return DeltaWeights.GetIndex(); } //--- virtual int getOutputVal(double &values[]) { return Output.GetData(values); } virtual int getOutputVal(CArrayDouble *values) { return Output.GetData(values); } virtual int getGradient(double &values[]) { return Gradient.GetData(values); } virtual int getWeights(double &values[]) { return Weights.GetData(values); } virtual int Neurons(void) { return Output.Total(); } virtual ENUM_ACTIVATION Activation(void) { return activation; }
E, é claro, criamos os métodos de despacho para o feed-forward, o cálculo do gradiente de erro e a atualização da matriz de peso. Não se esqueça de reescrever as funções virtuais para salvar e ler os dados.
virtual bool feedForward(CObject *SourceObject); virtual bool calcHiddenGradients(CObject *TargetObject); virtual bool calcOutputGradients(CArrayDouble *Target); virtual bool updateInputWeights(CObject *SourceObject); //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual int Type(void) const { return defNeuronBaseOCL; } };
Vamos considerar os algoritmos para a construção dos métodos. O construtor e o destrutor de classes são bem simples. Seu código está disponível em anexo. Dê uma olhada na função de inicialização da classe. O método recebe nos parâmetros o número de neurônios da próxima camada, o número ordinal do neurônio, um ponteiro para o objeto da classe COpenCLMy e o número de neurônios a serem criados.
Observe que o método recebe nos parâmetros um ponteiro para o objeto da classe COpenCLMy e não instancia um objeto dentro da classe. Isso garante que apenas uma instância do objeto COpenCLMy seja usada durante a operação do EA. Todos os kernels e buffers de dados serão criados em um objeto, portanto, nós não precisaremos perder tempo passando os dados entre as camadas da rede neural. Eles terão acesso direto aos mesmos buffers de dados.
No início do método, verificamos a validade do ponteiro para o objeto da classe COpenCLMy e certificamos de que pelo menos um neurônio deve ser criado. Em seguida, criamos as instâncias de objetos do buffer, inicializamos as matrizes com seus valores iniciais e criamos os buffers em OpenCL. O tamanho do buffer 'Output' é igual ao número de neurônios a serem criados e o tamanho do buffer de gradientes é 1 elemento maior que o de saída. Os tamanhos da matriz de peso e seus buffers delta são iguais ao produto do tamanho do buffer de gradientes pelo número de neurônios na próxima camada. Uma vez que este produto será "0" para a camada de saída, os buffers não são criados para esta camada.
bool CNeuronBaseOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint numNeurons) { if(CheckPointer(open_cl)==POINTER_INVALID || numNeurons<=0) return false; OpenCL=open_cl; //--- if(CheckPointer(Output)==POINTER_INVALID) { Output=new CBufferDouble(); if(CheckPointer(Output)==POINTER_INVALID) return false; } if(!Output.BufferInit(numNeurons,1.0)) return false; if(!Output.BufferCreate(OpenCL)) return false; //--- if(CheckPointer(Gradient)==POINTER_INVALID) { Gradient=new CBufferDouble(); if(CheckPointer(Gradient)==POINTER_INVALID) return false; } if(!Gradient.BufferInit(numNeurons+1,0.0)) return false; if(!Gradient.BufferCreate(OpenCL)) return false; //--- if(numOutputs>0) { if(CheckPointer(Weights)==POINTER_INVALID) { Weights=new CBufferDouble(); if(CheckPointer(Weights)==POINTER_INVALID) return false; } int count=(int)((numNeurons+1)*numOutputs); if(!Weights.Reserve(count)) return false; for(int i=0;i<count;i++) { double weigh=(MathRand()+1)/32768.0-0.5; if(weigh==0) weigh=0.001; if(!Weights.Add(weigh)) return false; } if(!Weights.BufferCreate(OpenCL)) return false; //--- if(CheckPointer(DeltaWeights)==POINTER_INVALID) { DeltaWeights=new CBufferDouble(); if(CheckPointer(DeltaWeights)==POINTER_INVALID) return false; } if(!DeltaWeights.BufferInit(count,0)) return false; if(!DeltaWeights.BufferCreate(OpenCL)) return false; } //--- return true; }
O método despachante do feedForward é semelhante ao método com o mesmo nome da classe CNeuronBase. Agora, apenas um tipo de neurônio é especificado aqui, mas mais tipos podem ser adicionados posteriormente.
bool CNeuronBaseOCL::feedForward(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: temp=SourceObject; return feedForward(temp); break; } //--- return false; }
O kernel OpenCL é chamado diretamente no método feedForward (CNeuronBaseOCL *NeuronOCL). No início do método, verificamos a validade do ponteiro para o objeto da classe COpenCLMy e do ponteiro recebido para a camada anterior da rede neural.
bool CNeuronBaseOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false;
Indicamos a unidimensionalidade do espaço das threads e definimos o número de threads necessárias igual ao número de neurônios.
uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=Output.Total();
Em seguida, definimos os ponteiros para os buffers de dados usados e os argumentos para a operação do kernel.
OpenCL.SetArgumentBuffer(def_k_FeedForward,def_k_ff_matrix_w,NeuronOCL.getWeightsIndex());
OpenCL.SetArgumentBuffer(def_k_FeedForward,def_k_ff_matrix_i,NeuronOCL.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_FeedForward,def_k_ff_matrix_o,Output.GetIndex());
OpenCL.SetArgument(def_k_FeedForward,def_k_ff_inputs,NeuronOCL.Neurons());
OpenCL.SetArgument(def_k_FeedForward,def_k_ff_activation,(int)activation);
Depois disso, chamamos o kernel.
if(!OpenCL.Execute(def_k_FeedForward,1,global_work_offset,global_work_size)) return false;
Eu queria terminar aqui, mas eu tive um problema durante o teste: o método COpenCL::Execute não inicia o kernel, mas apenas o enfileira. A própria execução ocorre na tentativa de ler os resultados do kernel. É por isso que os resultados do processamento devem ser carregados em uma matriz antes de sair do método.
Output.BufferRead(); //--- return true; }
Os métodos para lançar outros kernels são semelhantes ao algoritmo acima. O código completo de todos os métodos e classes está disponível em anexo.
3.6. Adições na classe CNet.
Depois que todas as classes necessárias foram criadas, vamos fazer alguns ajustes na classe CNet da rede neural principal.
No construtor da classe, nós precisamos adicionar a criação e inicialização de uma instância da classe COpenCLMy. Não se esqueça de excluir o objeto da classe no destrutor.
opencl=new COpenCLMy(); if(CheckPointer(opencl)!=POINTER_INVALID && !opencl.Initialize(cl_program,true)) delete opencl;
Além disso, no construtor e no bloco de adição dos neurônios nas camadas, nós adicionamos um código criando e inicializando os objetos da classe CNeuronBaseOCL criada anteriormente.
if(CheckPointer(opencl)!=POINTER_INVALID) { CNeuronBaseOCL *neuron_ocl=NULL; switch(desc.type) { case defNeuron: case defNeuronBaseOCL: neuron_ocl=new CNeuronBaseOCL(); if(CheckPointer(neuron_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_ocl.Init(outputs,0,opencl,desc.count)) { delete temp; return; } neuron_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_ocl)) { delete neuron_ocl; delete temp; return; } neuron_ocl=NULL; break; default: return; break; } }
Além disso, adicionamos a criação dos kernels em OpenCL no construtor.
if(CheckPointer(opencl)==POINTER_INVALID) return; //--- create kernels opencl.SetKernelsCount(4); opencl.KernelCreate(def_k_FeedForward,"FeedForward"); opencl.KernelCreate(def_k_CaclOutputGradient,"CaclOutputGradient"); opencl.KernelCreate(def_k_CaclHiddenGradient,"CaclHiddenGradient"); opencl.KernelCreate(def_k_UpdateWeights,"UpdateWeights");
Adicionamos a escrita dos dados de origem para o buffer no método CNet::feedForward
{
CNeuronBaseOCL *neuron_ocl=current.At(0);
double array[];
int total_data=inputVals.Total();
if(ArrayResize(array,total_data)<0)
return false;
for(int d=0;d<total_data;d++)
array[d]=inputVals.At(d);
if(!opencl.BufferWrite(neuron_ocl.getOutputIndex(),array,0,0,total_data))
return false;
}
Adicionamos também a chamada de método apropriada da classe recém-criada CNeuronBaseOCL.
for(int l=1; l<layers.Total(); l++) { previous=current; current=layers.At(l); if(CheckPointer(current)==POINTER_INVALID) return false; //--- if(CheckPointer(opencl)!=POINTER_INVALID) { CNeuronBaseOCL *current_ocl=current.At(0); if(!current_ocl.feedForward(previous.At(0))) return false; continue; }
Para o processo de retropropagação, vamos criar o métodoCNet::backPropOCL. Seu algoritmo é semelhante ao método principal CNet::backProp, que foi descrito no primeiro artigo.
void CNet::backPropOCL(CArrayDouble *targetVals) { if(CheckPointer(targetVals)==POINTER_INVALID || CheckPointer(layers)==POINTER_INVALID || CheckPointer(opencl)==POINTER_INVALID) return; CLayer *currentLayer=layers.At(layers.Total()-1); if(CheckPointer(currentLayer)==POINTER_INVALID) return; //--- double error=0.0; int total=targetVals.Total(); double result[]; CNeuronBaseOCL *neuron=currentLayer.At(0); if(neuron.getOutputVal(result)<total) return; for(int n=0; n<total && !IsStopped(); n++) { double target=targetVals.At(n); double delta=(target>1 ? 1 : target<-1 ? -1 : target)-result[n]; error+=delta*delta; } error/= total; error = sqrt(error); recentAverageError+=(error-recentAverageError)/recentAverageSmoothingFactor; if(!neuron.calcOutputGradients(targetVals)) return;; //--- Calc Hidden Gradients CObject *temp=NULL; total=layers.Total(); for(int layerNum=total-2; layerNum>0; layerNum--) { CLayer *nextLayer=currentLayer; currentLayer=layers.At(layerNum); neuron=currentLayer.At(0); neuron.calcHiddenGradients(nextLayer.At(0)); } //--- CLayer *prevLayer=layers.At(total-1); for(int layerNum=total-1; layerNum>0; layerNum--) { currentLayer=prevLayer; prevLayer=layers.At(layerNum-1); neuron=currentLayer.At(0); neuron.updateInputWeights(prevLayer.At(0)); } }
Algumas pequenas alterações foram feitas no método getResult.
if(CheckPointer(opencl)!=POINTER_INVALID && output.At(0).Type()==defNeuronBaseOCL) { CNeuronBaseOCL *temp=output.At(0); temp.getOutputVal(resultVals); return; }
O código completo de todos os métodos e funções está disponível no anexo.
4. Teste
A operação da classe criada foi testada nas mesmas condições que nós usamos nos testes anteriores. O EA Fractal_OCL foi criado para teste, que é um análogo completo do Fractal_2 criado anteriormente. O treinamento de teste da rede neural foi realizado no par EURUSD, no tempo gráfico H1. Os dados de 20 velas foram inseridos na rede neural. O treinamento foi realizado usando os dados dos últimos 2 anos. O experimento foi realizado em um dispositivo CPU 'Intel (R) Core (TM) 2 Duo CPU T5750 @ 2.00GHz' com suporte a OpenCL.
Durante 5 horas e 27 minutos de teste, o EA usando a tecnologia OpenCL executou 75 épocas de treinamento. Isso deu em média 4 minutos e 22 segundos para uma época de 12.405 velas. O mesmo Expert Advisor sem tecnologia OpenCL, no mesmo laptop com a mesma arquitetura da rede neural gasta em média 40 minutos e 48 segundos por época. Portanto, o processo de aprendizado é 9.35 vezes mais rápido com o OpenCL.
Conclusão
Este artigo demonstrou a possibilidade de usar a tecnologia OpenCL para organizar as computações multithread (paralelismo em nível de threads) nas redes neurais. Os testes mostraram um aumento de quase 10 vezes no desempenho na mesma CPU. Espera-se que o uso de uma GPU possa melhorar ainda mais o desempenho do algoritmo - neste caso, a transferência de cálculos para uma GPU compatível não requer mudanças no código do Expert Advisor.
De maneira geral, os resultados comprovam que o aprofundamento nessa direção tem boas perspectivas.
Links
- Redes Neurais de Maneira Fácil
- Redes neurais de maneira fácil (Parte 2): Treinamento e teste da rede
- Redes Neurais de Maneira Fácil (Parte 3): Redes Convolucionais
- Redes Neurais de Maneira Fácil(Parte 4): Redes Recorrentes
- OpenCL: A ponte para os mundos paralelos
- OpenCL: Da programação ingênua até a mais perceptível
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Fractal_OCL.mq5 | Expert Advisor | Um Expert Advisor com a rede neural de classificação (3 neurônios na camada de saída) usando a tecnologia OpenCL |
| 2 | NeuroNet.mqh | Biblioteca de classe | Uma biblioteca de classes para a criação de uma rede neural |
| 3 | NeuroNet.cl | Código Base | Biblioteca do código do programa OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/8435
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Conjunto de ferramentas para marcação manual de gráficos e negociação (Parte II). Fazendo a marcação
Conjunto de ferramentas para marcação manual de gráficos e negociação (Parte II). Fazendo a marcação
 Como ganhar US$ 1 000 000 por meio do trading algorítmico? Nos serviços MQL5.com!
Como ganhar US$ 1 000 000 por meio do trading algorítmico? Nos serviços MQL5.com!
 Redes neurais de Maneira Fácil (Parte 6): Experimentos com a taxa de aprendizado da rede neural
Redes neurais de Maneira Fácil (Parte 6): Experimentos com a taxa de aprendizado da rede neural
 Redes Neurais de Maneira Fácil(Parte 4): Redes Recorrentes
Redes Neurais de Maneira Fácil(Parte 4): Redes Recorrentes
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Você poderia me dizer que recentAverageSmoothingFactor = 10000 é baseado em 2 anos?
365 dias * 2 anos * 24 horas = 17.520 velas de hora (duração da amostra).
Estou usando uma amostra de 1 ano, então preciso reduzir para 8.760 (365 * 24 = 8.760)?
Nos testes, tenho dForecast saltando de 0 a 23, e o erro é 0,32 e permanece constante, é normal ou é porque recentAverageSmoothingFactor está errado? 😀
Oi Dimitri,
Adoro seus artigos e estou começando a trabalhar neles.
Onde está a classe CBuffer? Não consigo encontrá-la.
Com os melhores cumprimentos,
Benjamin
Olá, Dimitri,
Adoro seus artigos e estou começando a trabalhar neles.
Onde está a classe CBuffer? Não consigo encontrá-la.
Com os melhores cumprimentos,
Benjamin
Não importa, encontrei a solução para alterá-lo para CBufferFloat, conforme descrito por você em outros artigos :)