
Redes neurais em trading: Método abrangente de previsão de trajetórias (Traj-LLM)
Introdução
Prever o próximo movimento dos preços nos mercados financeiros desempenha um papel crítico na tomada de decisões do trader. Previsões de qualidade permitem tomar decisões mais embasadas e minimizar riscos. No entanto, a previsão das trajetórias futuras dos preços enfrenta muitos desafios devido ao caráter caótico e estocástico dos mercados. Mesmo os modelos preditivos mais avançados frequentemente não conseguem levar em conta adequadamente todos os fatores que influenciam a dinâmica do mercado, como mudanças repentinas no comportamento dos participantes ou eventos externos inesperados.
Nos últimos anos, o avanço da inteligência artificial, especialmente no campo dos grandes modelos de linguagem (LLM), abriu novas oportunidades para a realização de diversas tarefas. Os LLM demonstraram capacidades surpreendentes no processamento de informações complexas e na modelagem de cenários semelhantes ao pensamento humano. Esses modelos têm sido aplicados com sucesso em diversas áreas, desde o processamento de linguagem natural até a previsão de séries temporais, tornando-se ferramentas promissoras para análise e previsão de movimentos de mercado.
Apresento a você o algoritmo Traj-LLM, descrito no artigo "Traj-LLM: A New Exploration for Empowering Trajectory Prediction with Pre-trained Large Language Models". O modelo Traj-LLM foi desenvolvido para resolver problemas na área de controle autônomo de veículos. Os autores do método propõem utilizar as capacidades dos LLM para melhorar a precisão e a adaptabilidade da previsão de trajetórias futuras dos participantes do movimento.
Além disso, o Traj-LLM combina o poder dos grandes modelos de linguagem com novas abordagens para modelagem de dependências temporais e interações entre objetos, permitindo prever trajetórias com maior precisão, mesmo em condições complexas e dinâmicas. Esse modelo não apenas melhora a precisão das previsões, mas também oferece novas perspectivas para a análise e compreensão dos possíveis cenários de desenvolvimento. Esperamos que a aplicação do método proposto pelos autores seja eficaz na resolução de nossos desafios e nos permita aumentar a qualidade das previsões de movimentos futuros de preços.
1. Algoritmo Traj-LLM
A arquitetura do Traj-LLM contém quatro componentes essenciais:
- codificação conjunta de contexto esparso,
- modelagem de interação de alto nível,
- aprendizado probabilístico considerando a faixa de rodagem,
- decodificador multimodal de Laplace.
Os autores do método Traj-LLM propõem utilizar as capacidades dos LLM para resolver o problema da previsão de trajetórias, eliminando a necessidade de um projeto operacional explícito. Inicialmente, a codificação conjunta com contexto esparso envolve a análise das características dos agentes e do cenário de maneira compreensível para os LLM. Posteriormente, as representações obtidas são introduzidas nos LLM pré-treinados para resolver tarefas de interação em alto nível. Para imitar uma função cognitiva semelhante à humana e aprimorar ainda mais a compreensão do cenário no Traj-LLM, é introduzido o aprendizado probabilístico considerando a faixa de rodagem, com base no módulo Mamba. Além disso, o decodificador multimodal de Laplace é utilizado para gerar previsões mais robustas.
O primeiro passo do Traj-LLM é a codificação dos dados brutos espaço-temporais do cenário, como os estados do agente e das faixas de rodagem. Para cada um deles, utilizamos um modelo de incorporação composto por uma camada recorrente e MLP para extrair características multidimensionais. Após essa etapa, os tensores resultantes hi e fl são direcionados ao submódulo Fusion, facilitando a troca complexa de informações entre os estados dos agentes e das faixas de rodagem em áreas localizadas. Esse processo é realizado com base no princípio de incorporação de tokens, garantindo compatibilidade com a arquitetura dos LLM.
Em particular, o processo de fusão envolve a utilização do mecanismo de Self-Attention multicausal para integrar as características entre os agentes. Além disso, a fusão das características Agente-Faixa e Faixa-Agente inclui a atualização das representações do Agente e da Faixa por meio do mecanismo de atenção cruzada multicausal com conexões residuais. Formalmente, esse processo pode ser representado da seguinte maneira:

Em seguida, combinamos hi e fl para criar codificações conjuntas de contexto esparso gi, que intuitivamente transferem as dependências relativas aos campos receptivos locais das entidades vetorizadas. A codificação conjunta com contexto esparso foi projetada para permitir que os LLM compreendam os dados sobre trajetórias, ampliando assim suas capacidades LLM.
As transições de trajetória seguem padrões governados por restrições de alto nível, originadas por diversos elementos do cenário. Para explorar essas interações de alto nível, os autores do método investigam a capacidade dos LLM de modelar uma série de dependências inerentes às tarefas de previsão de trajetória. Apesar das semelhanças entre os dados de trajetória e os textos em linguagem natural, o uso direto dos LLM para processar codificações conjuntas de contexto esparso não é considerado viável, pois os LLM pré-treinados foram desenvolvidos principalmente para lidar com dados textuais. Uma alternativa seria o re-treinamento completo de todos os LLM. Um processo que exige recursos computacionais significativos, tornando-o inviável em certa medida. Uma solução mais eficiente é aplicar o método Parameter-Efficient Fine-Tuning (PEFT) para ajustar os LLM pré-treinados.
No Traj-LLM, os autores utilizam parâmetros de arquiteturas Transformer NLP pré-treinadas, com foco especial no modelo GPT-2, para modelagem de interações em alto nível. Eles propõem congelar todos os parâmetros previamente treinados e introduzir novos parâmetros treináveis por meio da técnica de adaptação de baixa classificação (LoRA). LoRA é aplicada às entidades Query e Key do mecanismo de atenção LLM.
Dessa forma, as codificações conjuntas de contexto esparso gi são passadas para os LLM, que contêm uma série de blocos Transformer pré-treinados equipados com LoRA. Esse processo resulta na geração das representações de alto nível de interação zi.
![]()
Os resultados da LLM pré-treinada são transformados por meio de MLP para se ajustarem às dimensões de gi, obtendo assim os estados finais de interação de alto nível si.
A grande maioria dos motoristas experientes presta atenção apenas a alguns segmentos específicos da faixa de rodagem que influenciam significativamente seus movimentos futuros. Para imitar essa função cognitiva semelhante à humana e aprimorar ainda mais a compreensão do cenário no Traj-LLM, os autores do método aplicam aprendizado probabilístico considerando a faixa de rodagem para avaliar continuamente a probabilidade de alinhamento dos estados de movimento com os segmentos da pista. Mais precisamente, eles sincronizam o movimento do agente-alvo com as informações da faixa de rodagem em cada instante de tempo t∈{1,…,tf}, introduzindo a camada Mamba. Atuando como um modelo estruturado seletivo do espaço de estados (SSM), Mamba permite refinar e generalizar informações relevantes. Isso é análogo ao complexo processo de tomada de decisão dos motoristas humanos, que ponderam cuidadosamente sinais informacionais essenciais, como faixas de rodagem potenciais, para fazer sua escolha.
Na arquitetura proposta, a camada Mamba é composta por um bloco Mamba, uma normalização de três camadas e uma rede de propagação para frente baseada em posições. Especificamente, o bloco Mamba inicialmente amplia a dimensionalidade original por meio de projeções lineares, gerando diferentes representações para dois fluxos de informação paralelos. Em seguida, um dos fluxos é processado por meio de convolução e ativação SiLU para capturar dependências considerando a faixa de rodagem. O núcleo do bloco Mamba inclui um modelo seletivo do espaço de estados com parâmetros discretizados com base nos dados brutos. Para aumentar a robustez, os autores do método incorporam, adicionalmente, normalização por instâncias e conexões residuais para gerar estados implícitos.
Após essa etapa, a rede FeedForward baseada em posições é utilizada para aprimorar a modelagem da avaliação, considerando a faixa de rodagem na dimensão latente. Mais uma vez, são aplicadas a normalização por instâncias e a conexão residual para obter vetores de aprendizado que levem em conta as faixas de rodagem, que são então encaminhados para a camada MLP.
Como mencionado anteriormente, motoristas experientes prestam atenção especial a alguns segmentos específicos da faixa de rodagem, o que contribui para uma tomada de decisão mais eficiente. Para esse fim, são cuidadosamente selecionados os segmentos mais relevantes como candidatos a faixas de movimento, que são posteriormente combinados na forma ℳ.
O aprendizado probabilístico considerando a faixa de rodagem é modelado como um problema de classificação, no qual a entropia cruzada binária ℒlane é aplicada para otimizar a estimativa de probabilidade.
A visualização do método Traj-LLM pelos autores está apresentada abaixo.
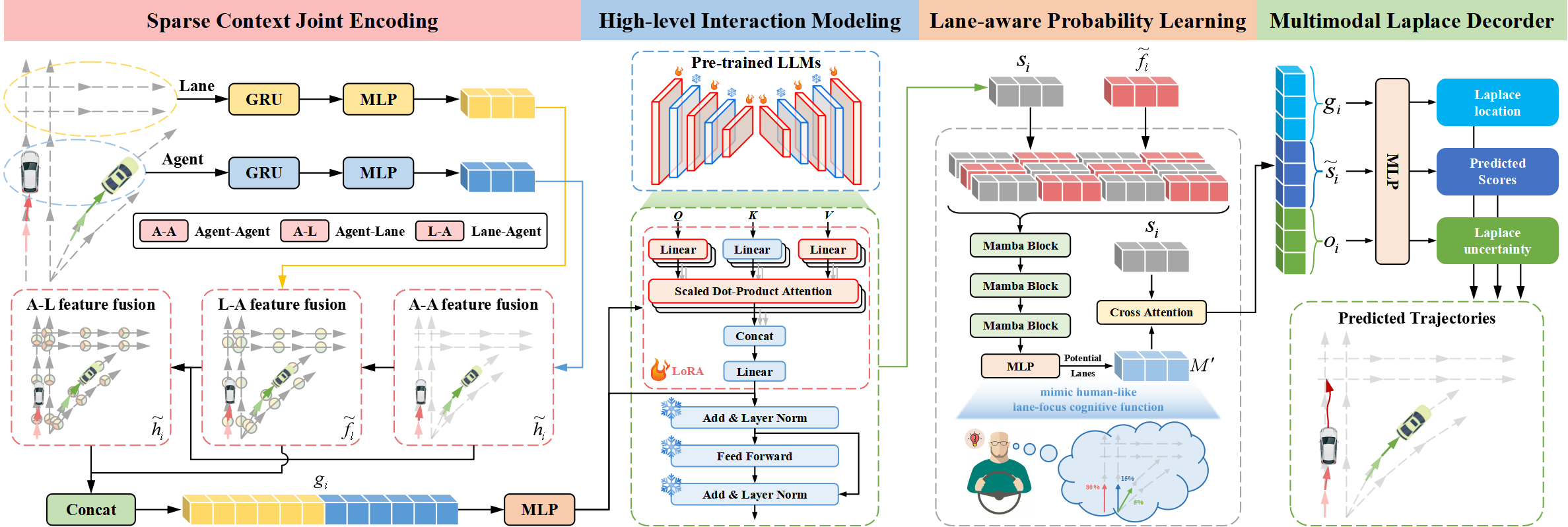

2. Implementação em MQL5
Após analisar a descrição teórica do método Traj-LLM, passamos à parte prática do artigo, na qual implementamos nossa interpretação dos conceitos propostos utilizando MQL5. O algoritmo Traj-LLM é uma estrutura complexa que combina blocos de diferentes soluções arquitetônicas, muitas das quais já exploramos anteriormente. Portanto, ao construí-lo, podemos utilizar alguns componentes já desenvolvidos. No entanto, algumas adaptações específicas serão necessárias.
2.1 Ajuste do algoritmo do bloco LSTM
Vamos analisar a visualização do método Traj-LLM apresentada acima. Os dados brutos são inicialmente direcionados para o bloco de codificação conjunta de contexto esparso, que consiste em uma camada recorrente e um MLP. Nossa biblioteca já contém uma implementação de camada recorrente chamada CNeuronLSTMOCL. No entanto, essa implementação utiliza um array de dados brutos como uma representação integral do estado do ambiente. Neste caso, os autores do método propõem realizar a codificação independentemente do estado de cada agente e da faixa de rodagem. Em outras palavras, precisamos codificar de forma independente em canais de dados separados. Claro, poderíamos criar um objeto CNeuronLSTMOCL separado para cada canal de informação analisado. No entanto, essa abordagem levaria a um aumento descontrolado do número de objetos internos e ao seu processamento sequencial, impactando negativamente o desempenho do modelo.
A segunda opção de solução envolve a modificação do algoritmo da classe existente CNeuronLSTMOCL. Iniciamos fazendo alterações no lado do programa OpenCL. O algoritmo de propagação para frente da nossa camada recorrente é implementado no kernel LSTM_FeedForward. Para permitir o funcionamento dentro de sequências independentes, não alteraremos os parâmetros externos do kernel. Em vez disso, para processar de maneira paralela os dados de sequências individuais, adicionaremos uma nova dimensão ao espaço de tarefas.
__kernel void LSTM_FeedForward(__global const float *inputs, int inputs_size, __global const float *weights, __global float *concatenated, __global float *memory, __global float *output) { uint id = (uint)get_global_id(0); uint total = (uint)get_global_size(0); uint id2 = (uint)get_local_id(1); uint idv = (uint)get_global_id(2); uint total_v = (uint)get_global_size(2);
Lembrando que o funcionamento do bloco LSTM é baseado em quatro entidades, cujos valores são calculados pelas camadas internas:
- Forget Gate – Porta de esquecimento;
- Input Gate – Porta de entrada;
- Output Gate – Porta de saída;
- New Content – Novo conteúdo.
O algoritmo de cálculo dessas entidades é o mesmo da camada totalmente conectada. A única diferença está na função de ativação. Portanto, em nossa implementação, estruturamos o processo de cálculo dos valores dessas entidades em fluxos paralelos dentro do grupo de trabalho. Para a troca de dados entre os fluxos, utilizamos um array criado na memória local.
__local float Temp[4];
Em seguida, definimos as constantes de deslocamento nos buffers globais de dados.
float sum = 0; uint shift_in = idv * inputs_size; uint shift_out = idv * total; uint shift = (inputs_size + total + 1) * (id2 + id);
Aqui, vale destacar um ponto importante. Estamos estruturando o funcionamento do bloco recorrente por meio de canais independentes. No entanto, segundo a lógica do algoritmo Traj-LLM, todos os canais independentes contêm dados comparáveis, seja sobre o estado de diferentes agentes ou sobre as faixas de rodagem existentes. Portanto, faz sentido utilizar uma única matriz de pesos para codificar as informações de diferentes canais de dados, o que permitirá obter incorporações comparáveis na saída.
Dessa forma, o identificador do canal influencia o deslocamento nos buffers de dados brutos e nos resultados, mas não afeta o deslocamento na matriz de pesos.
Agora, iniciamos o ciclo de cálculo da soma ponderada do estado oculto.
for(uint i = 0; i < total; i += 4) { if(total - i > 4) sum += dot((float4)(output[shift_out + i], output[shift_out + i + 1], output[shift_out + i + 2], output[shift_out + i + 3]), (float4)(weights[shift + i], weights[shift + i + 1], weights[shift + i + 2], weights[shift + i + 3])); else for(uint k = i; k < total; k++) sum += output[shift_out + k] * weights[shift + k]; }
E adicionamos a influência dos dados brutos.
shift += total; for(uint i = 0; i < inputs_size; i += 4) { if(total - i > 4) sum += dot((float4)(inputs[shift_in + i], inputs[shift_in + i + 1], inputs[shift_in + i + 2], inputs[shift_in + i + 3]), (float4)(weights[shift + i], weights[shift + i + 1], weights[shift + i + 2], weights[shift + i + 3])); else for(uint k = i; k < total; k++) sum += inputs[shift_in + k] * weights[shift + k]; } sum += weights[shift + inputs_size];
Aplicamos a função de ativação correspondente ao valor obtido.
if(isnan(sum) || isinf(sum)) sum = 0; if(id2 < 3) sum = Activation(sum, 1); else sum = Activation(sum, 0);
Depois, armazenamos o resultado das operações e sincronizamos os fluxos do grupo de trabalho.
Temp[id2] = sum; concatenated[4 * shift_out + id2 * total + id] = sum; //--- barrier(CLK_LOCAL_MEM_FENCE);
Por fim, resta apenas calcular o resultado do bloco LSTM, que ao mesmo tempo representa o estado oculto da célula.
if(id2 == 0) { float mem = memory[shift_out + id + total_v * total] = memory[shift_out + id]; float fg = Temp[0]; float ig = Temp[1]; float og = Temp[2]; float nc = Temp[3]; //--- memory[shift_out + id] = mem = mem * fg + ig * nc; output[shift_out + id] = og * Activation(mem, 0); } }
Os resultados das operações são armazenados nos elementos correspondentes dos buffers globais de dados.
Fizemos modificações semelhantes nos kernels da propagação reversa. As alterações mais significativas ocorreram no kernel LSTM_HiddenGradient. Assim como no kernel da propagação para frente, não alteramos os parâmetros externos, apenas ajustamos o espaço de tarefas.
__kernel void LSTM_HiddenGradient(__global float *concatenated_gradient, __global float *inputs_gradient, __global float *weights_gradient, __global float *hidden_state, __global float *inputs, __global float *weights, __global float *output, const int hidden_size, const int inputs_size) { uint id = get_global_id(0); uint total = get_global_size(0); uint idv = (uint)get_global_id(1); uint total_v = (uint)get_global_size(1);
Aqui, é importante lembrar que todos os canais independentes utilizam a mesma matriz de pesos. Portanto, para os coeficientes de peso, precisamos reunir os gradientes de erro de todos os canais independentes. Cada canal de dados opera em seu próprio fluxo, que agrupamos em grupos de trabalho. Para a troca de informações entre os fluxos, utilizamos um array na memória local.
__local float Temp[LOCAL_ARRAY_SIZE]; uint ls = min(total_v, (uint)LOCAL_ARRAY_SIZE);
Em seguida, definimos os deslocamentos nos buffers de dados.
uint shift_in = idv * inputs_size; uint shift_out = idv * total; uint weights_step = hidden_size + inputs_size + 1;
Iniciamos o ciclo de iteração sobre o buffer concatenado de dados brutos. Primeiro, simplesmente atualizamos o estado oculto.
for(int i = id; i < (hidden_size + inputs_size); i += total) { float inp = 0; if(i < hidden_size) { inp = hidden_state[shift_out + i]; hidden_state[shift_out + i] = output[shift_out + i]; }
Depois, calculamos o gradiente de erro no nível dos dados brutos.
else { inp = inputs[shift_in + i - hidden_size]; float grad = 0; for(uint g = 0; g < 3 * hidden_size; g++) { float temp = concatenated_gradient[4 * shift_out + g]; grad += temp * (1 - temp) * weights[i + g * weights_step]; } for(uint g = 3 * hidden_size; g < 4 * hidden_size; g++) { float temp = concatenated_gradient[4 * shift_out + g]; grad += temp * (1 - pow(temp, 2.0f)) * weights[i + g * weights_step]; } inputs_gradient[shift_in + i - hidden_size] = grad; }
Nesse ponto, também determinamos o gradiente de erro no nível dos coeficientes de peso. Primeiro, zeramos os valores do array local.
for(uint g = 0; g < 3 * hidden_size; g++) { float temp = concatenated_gradient[4 * shift_out + g]; if(idv < ls) Temp[idv % ls] = 0; barrier(CLK_LOCAL_MEM_FENCE);
Durante esse processo, garantimos a sincronização obrigatória dos fluxos do grupo de trabalho.
Em seguida, reunimos o gradiente total de erro de todos os canais de dados. Na primeira etapa, armazenamos valores individuais no array local.
for(uint v = 0; v < total_v; v += ls) { if(idv >= v && idv < v + ls) Temp[idv % ls] += temp * (1 - temp) * inp; barrier(CLK_LOCAL_MEM_FENCE); }
Partimos do pressuposto de que os dados analisados terão um número relativamente pequeno de canais independentes. Assim, somamos os valores do array em um único fluxo e, em seguida, armazenamos o valor final no buffer global de dados.
if(idv == 0) { temp = Temp[0]; for(int v = 1; v < ls; v++) temp += Temp[v]; weights_gradient[i + g * weights_step] = temp; } barrier(CLK_LOCAL_MEM_FENCE); }
De maneira semelhante, coletamos o gradiente de erro dos coeficientes de peso do New Content.
for(uint g = 3 * hidden_size; g < 4 * hidden_size; g++) { float temp = concatenated_gradient[4 * shift_out + g]; if(idv < ls) Temp[idv % ls] = 0; barrier(CLK_LOCAL_MEM_FENCE); for(uint v = 0; v < total_v; v += ls) { if(idv >= v && idv < v + ls) Temp[idv % ls] += temp * (1 - pow(temp, 2.0f)) * inp; barrier(CLK_LOCAL_MEM_FENCE); } if(idv == 0) { temp = Temp[0]; for(int v = 1; v < ls; v++) temp += Temp[v]; weights_gradient[i + g * weights_step] = temp; } barrier(CLK_LOCAL_MEM_FENCE); } }
Vale ressaltar que, ao longo da execução das operações do ciclo principal, deixamos de lado os coeficientes de peso do viés bayesiano. Para calcular os gradientes de erro correspondentes, realizamos operações adicionais seguindo o mesmo esquema descrito anteriormente.
for(int i = id; i < 4 * hidden_size; i += total) { if(idv < ls) Temp[idv % ls] = 0; barrier(CLK_LOCAL_MEM_FENCE); float temp = concatenated_gradient[4 * shift_out + (i + 1) * hidden_size]; if(i < 3 * hidden_size) { for(uint v = 0; v < total_v; v += ls) { if(idv >= v && idv < v + ls) Temp[idv % ls] += temp * (1 - temp); barrier(CLK_LOCAL_MEM_FENCE); } } else { for(uint v = 0; v < total_v; v += ls) { if(idv >= v && idv < v + ls) Temp[idv % ls] += 1 - pow(temp, 2.0f); barrier(CLK_LOCAL_MEM_FENCE); } } if(idv == 0) { temp = Temp[0]; for(int v = 1; v < ls; v++) temp += Temp[v]; weights_gradient[(i + 1) * weights_step] = temp; } barrier(CLK_LOCAL_MEM_FENCE); } }
Nesse caso, é essencial prestar atenção aos pontos de sincronização dos fluxos. O número de sincronizações deve ser suficiente para garantir o funcionamento correto do algoritmo. A quantidade excessiva de pontos de sincronização reduz a velocidade de execução das operações. Além disso, se houver pontos de sincronização nos quais nem todos os fluxos convergem, a execução do programa pode ser interrompida.
Com isso, concluímos a revisão das modificações feitas no programa OpenCL para viabilizar a operação do bloco LSTM com canais independentes. Quanto às alterações específicas no código da aplicação principal, recomendo que você as analise por conta própria. O código completo da classe CNeuronLSTMOCL, atualizado e com todos os seus métodos, está disponível no anexo.
2.2 Construção do bloco Mamba
O próximo passo em nossa preparação é a construção do bloco Mamba. O nome do bloco não é coincidência, pois está em sintonia com o método analisado em nosso artigo anterior. Os autores do Traj-LLM expandem o uso de modelos de espaço de estados e propõem uma arquitetura de bloco, que pode ser comparada a um Codificador Transformer, mas com a substituição do mecanismo Self-Attention pela arquitetura Mamba.
Para implementar o algoritmo proposto, criaremos uma nova classe chamada CNeuronMambaBlockOCL, cuja estrutura está apresentada abaixo.
class CNeuronMambaBlockOCL : public CNeuronBaseOCL { protected: uint iWindow; CNeuronMambaOCL cMamba; CNeuronBaseOCL cMambaResidual; CNeuronConvOCL cFF[2]; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- public: CNeuronMambaBlockOCL(void) {}; ~CNeuronMambaBlockOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronMambaBlockOCL; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
O conjunto básico de funcionalidades será herdado da classe da camada totalmente conectada CNeuronBaseOCL. No entanto, redefiniremos a lista usual de métodos virtuais.
Na estrutura da nova classe, podemos identificar objetos internos, cuja funcionalidade será analisada durante a implementação dos métodos. Todos os objetos são declarados estaticamente, o que nos permite manter os construtores e destrutores vazios. A inicialização de todos os objetos internos e variáveis ocorre dentro do método Init.
Como mencionado anteriormente, a arquitetura do bloco Mamba lembra a de um Codificador Transformer. Isso também se reflete nos parâmetros do método de inicialização, que fornecem uma visão clara da estrutura do bloco em questão.
bool CNeuronMambaBlockOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
No corpo do método, chamamos um método homônimo da classe pai, que já inclui um bloco mínimo de controle dos parâmetros recebidos e a inicialização de todos os objetos herdados.
Após a execução bem-sucedida do método de inicialização da classe pai, armazenamos localmente o tamanho da janela de análise de dados.
iWindow = window;
Em seguida, inicializamos os objetos internos declarados. O primeiro a ser inicializado é a camada de espaço de estados Mamba.
if(!cMamba.Init(0, 0, OpenCL, window, window_key, units_count, optimization, iBatch)) return false;
Logo após, inicializamos a camada totalmente conectada, cujo buffer armazenará os valores normalizados dos resultados da análise seletiva do espaço de estados com conexão residual.
if(!cMambaResidual.Init(0, 1, OpenCL, window * units_count, optimization, iBatch)) return false; cMambaResidual.SetActivationFunction(None);
Em seguida, adicionamos o bloco FeedForward.
if(!cFF[0].Init(0, 2, OpenCL, window, window, 4 * window, units_count, 1, optimization, iBatch)) return false; cFF[0].SetActivationFunction(LReLU); if(!cFF[1].Init(0, 2, OpenCL, 4 * window, 4 * window, window, units_count, 1, optimization, iBatch)) return false; cFF[1].SetActivationFunction(None);
Substituímos os ponteiros para os buffers de dados para evitar operações de cópia desnecessárias.
SetActivationFunction(None); SetGradient(cFF[1].getGradient(), true); //--- return true; }
Vale ressaltar que somente o ponteiro para o buffer de gradientes de erro é substituído. Isso ocorre porque, durante a propagação para frente, antes de enviar os resultados para a saída da camada, será adicionada uma conexão residual e uma normalização dos valores obtidos.
Devemos sempre controlar o resultado das operações em cada etapa. Ao final do método, retornamos um resultado lógico para a aplicação que o chamou.
Após a inicialização do objeto da classe, passamos para a construção do algoritmo de propagação para frente, implementado no método feedForward. Aqui, tudo é descrito de maneira concisa e direta.
bool CNeuronMambaBlockOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cMamba.FeedForward(NeuronOCL)) return false;
Nos parâmetros do método, como de costume, recebemos um ponteiro para o objeto da camada anterior, que nos fornece os dados brutos. No corpo do método, passamos imediatamente esse ponteiro para o modelo seletivo do espaço de estados.
Após a execução bem-sucedida das operações do método de propagação para frente da camada interna, somamos os resultados obtidos com os dados brutos e normalizamos os valores.
if(!SumAndNormilize(cMamba.getOutput(), NeuronOCL.getOutput(), cMambaResidual.getOutput(), iWindow, true)) return false;
Em seguida, ocorre a propagação para frente do bloco FeedForward.
if(!cFF[0].FeedForward(cMambaResidual.AsObject())) return false; if(!cFF[1].FeedForward(cFF[0].AsObject())) return false;
Depois, fazemos a conexão residual e normalizamos os dados.
if(!SumAndNormilize(cMambaResidual.getOutput(), cFF[1].getOutput(), getOutput(), iWindow, true)) return false; //--- return true; }
Os métodos de propagação reversa também não apresentam grande complexidade algorítmica, e recomendo que os analisem por conta própria. Lembro que o código completo dessa classe e de todos os seus métodos está disponível no anexo.
Com isso, finalizamos a parte preparatória e passamos para a construção do algoritmo geral do método Traj-LLM.
Montando os blocos individuais no algoritmo completo
Acima, realizamos a preparação necessária e complementamos nossa biblioteca com os "blocos essenciais" que utilizaremos para construir o algoritmo Traj-LLM dentro da classe CNeuronTrajLLMOCL. Abaixo, apresentamos a estrutura da nova classe.
class CNeuronTrajLLMOCL : public CNeuronBaseOCL { protected: //--- State Encoder CNeuronLSTMOCL cStateRNN; CNeuronConvOCL cStateMLP[2]; //--- Variables Encoder CNeuronTransposeOCL cTranspose; CNeuronLSTMOCL cVariablesRNN; CNeuronConvOCL cVariablesMLP[2]; //--- Context Encoder CNeuronLearnabledPE cStatePE; CNeuronLearnabledPE cVariablesPE; CNeuronMLMHAttentionMLKV cStateToState; CNeuronMLCrossAttentionMLKV cVariableToState; CNeuronMLCrossAttentionMLKV cStateToVariable; CNeuronBaseOCL cContext; CNeuronConvOCL cContextMLP[2]; //--- CNeuronMLMHAttentionMLKV cHighLevelInteraction; CNeuronMambaBlockOCL caMamba[3]; CNeuronMLCrossAttentionMLKV cLaneAware; CNeuronConvOCL caForecastMLP[2]; CNeuronTransposeOCL cTransposeOut; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- public: CNeuronTrajLLMOCL(void) {}; ~CNeuronTrajLLMOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint forecast, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronTrajLLMOCL; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
Como pode ser observado, redefinimos os mesmos métodos virtuais na estrutura da classe. No entanto, essa classe se destaca pelo grande número de objetos internos, algo esperado para uma arquitetura tão complexa. A funcionalidade dos objetos declarados será explorada durante a implementação dos métodos da classe.
Todos os objetos internos da classe foram declarados estaticamente. Como consequência, os construtores e destrutores permanecem vazios. A inicialização de todos os objetos declarados ocorre no método Init.
Nos parâmetros do método, recebemos constantes principais que serão usadas para inicializar os objetos aninhados. Aqui, encontramos os nomes de parâmetros já conhecidos. No entanto, vale ressaltar que algumas dessas constantes podem ter funções distintas para diferentes objetos internos.
bool CNeuronTrajLLMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint forecast, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * forecast, optimization_type, batch)) return false;
Seguindo a tradição já estabelecida, no corpo do método, chamamos primeiro o método homônimo da classe pai. Como sabemos, esse método já contém verificações de parâmetros e a inicialização de todos os objetos herdados. Após a execução bem-sucedida do método da classe pai, passamos à inicialização dos objetos internos declarados.
Com base na experiência com modelos anteriores, assumimos que a entrada do modelo é uma matriz que descreve a situação atual do mercado. Cada linha dessa matriz contém um conjunto de parâmetros que descrevem um candle do mercado, juntamente com os valores correspondentes dos indicadores analisados.
De acordo com o algoritmo Traj-LLM, os dados brutos recebidos são inicialmente encaminhados para o bloco codificador de contexto esparso, que inclui um codificador de agentes e um codificador de faixas de rodagem. No nosso caso, esses codificadores correspondem a um codificador de estados do ambiente (dados individuais das barras) e a um codificador de trajetórias históricas dos parâmetros analisados (indicadores).
O codificador de estados será construído a partir de um bloco recorrente para análise de barras individuais e duas camadas convolucionais subsequentes, que gerenciam a operação do MLP em canais independentes de informação.
//--- State Encoder if(!cStateRNN.Init(0, 0, OpenCL, window_key, units_count, optimization, iBatch) || !cStateRNN.SetInputs(window)) return false; if(!cStateMLP[0].Init(0, 1, OpenCL, window_key, window_key, 4 * window_key, units_count, optimization, iBatch)) return false; cStateMLP[0].SetActivationFunction(LReLU); if(!cStateMLP[1].Init(0, 2, OpenCL, 4 * window_key, 4 * window_key, window_key, units_count, optimization, iBatch)) return false;
O codificador de trajetórias históricas dos indicadores analisados segue a mesma arquitetura. No entanto, ele recebe na entrada um tensor transposto dos dados brutos, o que afeta o tamanho da janela de análise e o número de canais independentes.
//--- Variables Encoder if(!cTranspose.Init(0, 3, OpenCL, units_count, window, optimization, iBatch)) return false; if(!cVariablesRNN.Init(0, 4, OpenCL, window_key, window, optimization, iBatch) || !cVariablesRNN.SetInputs(units_count)) return false; if(!cVariablesMLP[0].Init(0, 5, OpenCL, window_key, window_key, 4 * window_key, window, optimization, iBatch)) return false; cVariablesMLP[0].SetActivationFunction(LReLU); if(!cVariablesMLP[1].Init(0, 6, OpenCL, 4 * window_key, 4 * window_key, window_key, window, optimization, iBatch)) return false;
Vale destacar que o algoritmo Traj-LLM prevê a análise conjunta de agentes e faixas de rodagem. Por isso, na saída dos codificadores, obtemos vetores de descrição de um único elemento da sequência (seja um estado do ambiente ou uma trajetória histórica do indicador analisado) com o mesmo tamanho. No entanto, as sequências podem ter tamanhos diferentes, já que o número de estados do ambiente analisados nem sempre coincide com o número de parâmetros que os descrevem.
Seguindo o algoritmo Traj-LLM, os resultados dos codificadores são então enviados para o bloco Fusion, onde ocorre uma análise abrangente das interdependências entre os elementos individuais das sequências, utilizando os algoritmos Self-Attention e Cross-Attention. No entanto, sabemos que, para melhorar a eficiência dos blocos de atenção, é necessário adicionar rótulos de codificação posicional aos elementos da sequência. Para implementar essa funcionalidade, adicionamos duas camadas de codificação posicional que podem ser treinadas.
//--- Position Encoder if(!cStatePE.Init(0, 7, OpenCL, cStateMLP[1].Neurons(), optimization, iBatch)) return false; if(!cVariablesPE.Init(0, 8, OpenCL, cVariablesMLP[1].Neurons(), optimization, iBatch)) return false;
Somente depois disso realizamos a análise das dependências entre estados individuais no bloco Self-Attention.
//--- Context if(!cStateToState.Init(0, 9, OpenCL, window_key, window_key, heads, heads / 2, units_count, 2, 1, optimization, iBatch)) return false;
Em seguida, analisamos as dependências cruzadas nos dois blocos subsequentes de Cross-Attention.
if(!cStateToVariable.Init(0, 10, OpenCL, window_key, window_key, heads, window_key, heads / 2, units_count, window, 2, 1, optimization, iBatch)) return false; if(!cVariableToState.Init(0, 11, OpenCL, window_key, window_key, heads, window_key, heads / 2, window, units_count, 2, 1, optimization, iBatch)) return false;
As representações enriquecidas dos estados e trajetórias são concatenadas em um único tensor.
if(!cContext.Init(0, 12, OpenCL, window_key * (units_count + window), optimization, iBatch)) return false;
Após essa etapa, os dados passam por mais um MLP.
if(!cContextMLP[0].Init(0, 13, OpenCL, window_key, window_key, 4 * window_key, window + units_count, optimization, iBatch)) return false; cContextMLP[0].SetActivationFunction(LReLU); if(!cContextMLP[1].Init(0, 14, OpenCL, 4 * window_key, 4 * window_key, window_key, window + units_count, optimization, iBatch)) return false;
Em seguida, temos o bloco de modelagem de interações de alto nível. Aqui, os autores do método Traj-LLM utilizam um modelo de linguagem pré-treinado, que substituímos por um bloco Transformer.
if(!cHighLevelInteraction.Init(0, 15, OpenCL, window_key, window_key, heads, heads / 2, window + units_count, 4, 2, optimization, iBatch)) return false;
O próximo passo é o bloco cognitivo de aprendizado probabilístico do movimento futuro considerando as faixas de rodagem existentes. Para isso, utilizamos três blocos Mamba sequenciais, todos com a mesma arquitetura.
for(int i = 0; i < int(caMamba.Size()); i++) { if(!caMamba[i].Init(0, 16 + i, OpenCL, window_key, 2 * window_key, window + units_count, optimization, iBatch)) return false; }
Os valores obtidos são comparados com as trajetórias históricas no bloco de Cross-Attention.
if(!cLaneAware.Init(0, 19, OpenCL, window_key, window_key, heads, window_key, heads / 2, window, window + units_count, 2, 1, optimization, iBatch)) return false;
Por fim, utilizamos um MLP para prever as trajetórias futuras dos canais independentes de dados.
if(!caForecastMLP[0].Init(0, 20, OpenCL, window_key, window_key, 4 * forecast, window, optimization, iBatch)) return false; caForecastMLP[0].SetActivationFunction(LReLU); if(!caForecastMLP[1].Init(0, 21, OpenCL, 4 * forecast, 4 * forecast, forecast, window, optimization, iBatch)) return false; caForecastMLP[1].SetActivationFunction(TANH); if(!cTransposeOut.Init(0, 22, OpenCL, window, forecast, optimization, iBatch)) return false;
Vale destacar que o tensor das trajetórias previstas é transposto para adequar as informações ao formato dos dados brutos.
SetOutput(cTransposeOut.getOutput(), true); SetGradient(cTransposeOut.getGradient(), true); SetActivationFunction((ENUM_ACTIVATION)caForecastMLP[1].Activation()); //--- return true; }
Também substituímos os ponteiros dos buffers de dados para evitar operações de cópia desnecessárias. Em seguida, retornamos à aplicação chamadora um resultado lógico indicando a conclusão bem-sucedida das operações do método.
Após finalizar o método de inicialização da classe, passamos para a construção do algoritmo de propagação para frente, implementado no método feedForward.
bool CNeuronTrajLLMOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- State Encoder if(!cStateRNN.FeedForward(NeuronOCL)) return false; if(!cStateMLP[0].FeedForward(cStateRNN.AsObject())) return false; if(!cStateMLP[1].FeedForward(cStateMLP[0].AsObject())) return false;
Nos parâmetros do método, recebemos um ponteiro para o objeto contendo os dados brutos, que imediatamente processamos por meio do bloco de codificação de estados.
Em seguida, transpomos os dados brutos e codificamos as trajetórias históricas dos parâmetros analisados que descrevem o estado do ambiente.
//--- Variables Encoder if(!cTranspose.FeedForward(NeuronOCL)) return false; if(!cVariablesRNN.FeedForward(cTranspose.AsObject())) return false; if(!cVariablesMLP[0].FeedForward(cVariablesRNN.AsObject())) return false; if(!cVariablesMLP[1].FeedForward(cVariablesMLP[0].AsObject())) return false;
Adicionamos codificação posicional aos dados processados.
//--- Position Encoder if(!cStatePE.FeedForward(cStateMLP[1].AsObject())) return false; if(!cVariablesPE.FeedForward(cVariablesMLP[1].AsObject())) return false;
Depois, enriquecemos os dados com o contexto das interdependências.
//--- Context if(!cStateToState.FeedForward(cStatePE.AsObject())) return false; if(!cStateToVariable.FeedForward(cStateToState.AsObject(), cVariablesPE.getOutput())) return false; if(!cVariableToState.FeedForward(cVariablesPE.AsObject(), cStateToVariable.getOutput())) return false;
Os dados enriquecidos são concatenados em um único tensor.
if(!Concat(cStateToVariable.getOutput(), cVariableToState.getOutput(), cContext.getOutput(), cStateToVariable.Neurons(), cVariableToState.Neurons(), 1)) return false;
Esse tensor é então processado por um MLP.
if(!cContextMLP[0].FeedForward(cContext.AsObject())) return false; if(!cContextMLP[1].FeedForward(cContextMLP[0].AsObject())) return false;
Em seguida, passamos para o bloco de análise das dependências de alto nível.
//--- Lane aware if(!cHighLevelInteraction.FeedForward(cContextMLP[1].AsObject())) return false;
Depois, os dados seguem para o modelo de espaço de estados.
if(!caMamba[0].FeedForward(cHighLevelInteraction.AsObject())) return false; for(int i = 1; i < int(caMamba.Size()); i++) { if(!caMamba[i].FeedForward(caMamba[i - 1].AsObject())) return false; }
As trajetórias históricas são então correlacionadas com os resultados da análise.
if(!cLaneAware.FeedForward(cVariablesPE.AsObject(), caMamba[caMamba.Size() - 1].getOutput())) return false;
Com base nos dados obtidos, fazemos uma previsão da alteração mais provável dos parâmetros analisados.
//--- Forecast if(!caForecastMLP[0].FeedForward(cLaneAware.AsObject())) return false; if(!caForecastMLP[1].FeedForward(caForecastMLP[0].AsObject())) return false;
Posteriormente, convertamos os valores previstos para o formato dos dados brutos.
if(!cTransposeOut.FeedForward(caForecastMLP[1].AsObject())) return false; //--- return true; }
E finalmente, retornamos à aplicação chamadora um resultado lógico indicando a conclusão do método.
O próximo passo é construir os algoritmos de propagação reversa. Primeiramente, é necessário implementar a distribuição dos gradientes de erro para todos os objetos, de acordo com sua influência no resultado final, e então ajustar os parâmetros treináveis para minimizar o erro.
A atualização dos parâmetros, por si só, não é complexa, pois os parâmetros treináveis estão contidos apenas nos objetos aninhados. Assim, o processo é realizado chamando sequencialmente os métodos de ajuste desses objetos. No entanto, a distribuição dos gradientes de erro representa um desafio mais intrincado.
A distribuição dos gradientes de erro ocorre exatamente no sentido oposto à propagação para frente. No entanto, é importante notar que a propagação para frente não é um fluxo linear único. Peço desculpas pela redundância, mas esse ponto é importante. No algoritmo de propagação para frente, identificamos múltiplos fluxos paralelos de informação, e nossa tarefa agora é coletar os gradientes de erro de todos esses fluxos.
O algoritmo de distribuição dos gradientes de erro será implementado no método calcInputGradients. Nos parâmetros do método, recebemos um ponteiro para o objeto da camada anterior, para o qual devemos transmitir o gradiente de erro de acordo com a influência dos dados brutos no resultado final do modelo. No corpo do método, verificamos imediatamente a validade do ponteiro recebido, pois, sem um ponteiro correto, todo o processo subsequente é inválido.
bool CNeuronTrajLLMOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
É importante lembrar que, no momento da chamada desse método, o gradiente de erro da camada atual já está armazenado em seu buffer. Ele foi gravado durante a execução do método equivalente da camada seguinte do nosso modelo. Além disso, devido à substituição de ponteiros para buffers de dados que realizamos anteriormente, esse mesmo gradiente de erro também está contido no buffer da nossa camada interna de transposição dos resultados da previsão. Assim, iniciamos a distribuição do gradiente de erro passando-o pelo MLP de previsão do movimento futuro.
//--- Forecast if(!caForecastMLP[1].calcHiddenGradients(cTransposeOut.AsObject())) return false; if(!caForecastMLP[0].calcHiddenGradients(caForecastMLP[1].AsObject())) return false;
Depois disso, encaminhamos o gradiente de erro para a camada de correspondência entre as trajetórias históricas dos parâmetros analisados e os resultados da análise cognitiva.
//--- Lane aware if(!cLaneAware.calcHiddenGradients(caForecastMLP[0].AsObject())) return false;
Vale notar que o bloco Cross-Attention compara dados de dois fluxos de informação. Portanto, precisamos dividir o gradiente de erro entre esses dois fluxos, considerando proporcionalmente sua influência no resultado final.
if(!cVariablesPE.calcHiddenGradients(cLaneAware.AsObject(), caMamba[caMamba.Size() - 1].getOutput(), caMamba[caMamba.Size() - 1].getGradient(), (ENUM_ACTIVATION)caMamba[caMamba.Size() - 1].Activation())) return false;
Em seguida, transmitimos o gradiente de erro através do modelo de espaço de estados.
for(int i = int(caMamba.Size()) - 2; i >= 0; i--) if(!caMamba[i].calcHiddenGradients(caMamba[i + 1].AsObject())) return false;
Depois, passamos pelo bloco de análise das dependências de alto nível.
if(!cHighLevelInteraction.calcHiddenGradients(caMamba[0].AsObject())) return false;
O gradiente de erro então passa pelo MLP de contexto, descendo um nível. até o buffer de dados concatenados das trajetórias e estados.
if(!cContextMLP[1].calcHiddenGradients(cHighLevelInteraction.AsObject())) return false; if(!cContextMLP[0].calcHiddenGradients(cContextMLP[1].AsObject())) return false; if(!cContext.calcHiddenGradients(cContextMLP[0].AsObject())) return false;
E agora começa a parte mais interessante, portanto é essencial prestar atenção extra para não deixar escapar nenhum detalhe.
Precisamos separar o gradiente do buffer concatenado em dois fluxos. Isso não é complexo por si só; basta executar um método de desconcatenização, especificando os buffers de dados correspondentes. Nesse caso, os dois fluxos a serem separados pertencem aos dois blocos de Cross-Attention: Trajetórias dos parâmetros analisados em relação aos estados do ambiente e vice-versa. No entanto, há um detalhe importante: o próximo passo envolve a transmissão do gradiente de erro através do bloco Cross-Attention das trajetórias para os estados, que, por sua vez, transmitirá o gradiente para a camada Cross-Attention de estados para trajetórias. Portanto, para evitar perda de informações na próxima etapa, devemos armazenar temporariamente o gradiente de erro em um buffer auxiliar. No entanto, já temos um número considerável de objetos criados dentro dessa classe, e muitos desses objetos ainda estão ociosos. Aproveitaremos esses objetos para armazenamento temporário de informações. Assim, o gradiente de erro no nível do bloco Cross-Attention de estados para trajetórias será armazenado na camada correspondente de codificação posicional.
if(!DeConcat(cStatePE.getGradient(), cVariableToState.getGradient(), cContext.getGradient(), cStateToVariable.Neurons(), cVariableToState.Neurons(), 1)) return false;
Além disso, devemos lembrar que o buffer de gradientes da camada de codificação posicional das trajetórias já contém uma parte dos gradientes de erro úteis. Para evitar a perda dessa informação, a transferimos temporariamente para o buffer MLP do codificador correspondente.
if(!SumAndNormilize(cVariablesPE.getGradient(), cVariablesPE.getGradient(), cVariablesMLP[1].getGradient(), 1, false)) return false;
Agora que garantimos a preservação de todas as informações necessárias, podemos prosseguir com a distribuição do gradiente de erro através do bloco Cross-Attention das trajetórias para os estados.
if(!cVariablesPE.calcHiddenGradients(cVariableToState.AsObject(), cStateToVariable.getOutput(), cStateToVariable.getGradient(), (ENUM_ACTIVATION)cStateToVariable.Activation())) return false;
Em seguida, somamos os gradientes de erro na camada do bloco Cross-Attention dos estados para as trajetórias, combinando os dois fluxos de dados.
if(!SumAndNormilize(cStateToVariable.getGradient(), cStatePE.getGradient(), cStateToVariable.getGradient(), 1, false, 0, 0, 0, 1)) return false;
No entanto, no próximo passo, precisaremos novamente transmitir o gradiente de erro para a camada de codificação posicional das trajetórias, agora pela terceira vez. Por isso, antes de prosseguir, primeiro somamos os gradientes de erro já acumulados a partir dos dois fluxos de dados.
if(!SumAndNormilize(cVariablesPE.getGradient(), cVariablesMLP[1].getGradient(), cVariablesMLP[1].getGradient(), 1, false, 0, 0, 0, 1)) return false;
Somente depois chamamos o método de distribuição do gradiente de erro através do bloco Cross-Attention dos estados para as trajetórias.
if(!cStateToState.calcHiddenGradients(cStateToVariable.AsObject(), cVariablesPE.getOutput(), cVariablesPE.getGradient(), (ENUM_ACTIVATION)cVariablesPE.Activation())) return false;
Agora podemos somar os gradientes de erro na camada de codificação posicional das trajetórias, consolidando as informações de três fluxos de dados.
if(!SumAndNormilize(cVariablesPE.getGradient(), cVariablesMLP[1].getGradient(), cVariablesPE.getGradient(), 1, false, 0, 0, 0, 1)) return false;
Em seguida, descemos o gradiente de erro para a camada de codificação posicional dos estados.
if(!cStatePE.calcHiddenGradients(cStateToState.AsObject())) return false;
É importante destacar que as camadas de codificação posicional são utilizadas em dois fluxos independentes e paralelos de informação. Por isso, o gradiente de erro é repassado aos codificadores correspondentes.
//--- Position Encoder if(!cStateMLP[1].calcHiddenGradients(cStatePE.AsObject())) return false; if(!cVariablesMLP[1].calcHiddenGradients(cVariablesPE.AsObject())) return false;
No próximo estágio, precisamos propagar o gradiente de erro através dos dois codificadores paralelos, que utilizam um tensor compartilhado de dados brutos. Novamente, encontramos a necessidade de registrar os gradientes de erro de dois fluxos de informação em um único buffer. Mais uma vez, precisaríamos de um buffer auxiliar de dados, que ainda não foi criado. Além disso, no momento de gravar os dados no buffer da camada anterior, todos os nossos objetos internos já estarão preenchidos com informações úteis, que não podemos perder.
Mas há um detalhe importante. A camada de transposição de dados, utilizada para alterar a ordem dos dados brutos antes do codificador de trajetórias, não possui parâmetros que possam ser treinados. Além disso, o buffer de gradientes de erro dessa camada só é utilizado durante a propagação dos dados para a camada anterior. Mais do que isso: o tamanho desse buffer é ideal para armazenar os mesmos dados, mas em uma ordem diferente. Perfeito! Podemos propagar o gradiente de erro através do bloco de codificação de trajetórias.
//--- Variables Encoder if(!cVariablesMLP[0].calcHiddenGradients(cVariablesMLP[1].AsObject())) return false; if(!cVariablesRNN.calcHiddenGradients(cVariablesMLP[0].AsObject())) return false; if(!cTranspose.calcHiddenGradients(cVariablesRNN.AsObject())) return false; if(!NeuronOCL.FeedForward(cTranspose.AsObject())) return false;
E, por fim, transferimos o gradiente de erro resultante para o buffer da camada de transposição de dados.
if(!SumAndNormilize(NeuronOCL.getGradient(), NeuronOCL.getGradient(), cTranspose.getGradient(), 1, false)) return false;
De maneira semelhante, propagamos o gradiente de erro através do bloco de codificação de estados.
//--- State Encoder if(!cStateMLP[0].calcHiddenGradients(cStateMLP[1].AsObject())) return false; if(!cStateRNN.calcHiddenGradients(cStateMLP[0].AsObject())) return false; if(!NeuronOCL.calcHiddenGradients(cStateRNN.AsObject())) return false;
Em seguida, somamos os gradientes de erro dos dois fluxos de informação.
if(!SumAndNormilize(cTranspose.getGradient(), NeuronOCL.getGradient(), NeuronOCL.getGradient(), 1, false, 0, 0, 0, 1)) return false; //--- return true; }
Por fim, basta retornar um resultado lógico para a aplicação chamadora, indicando a conclusão bem-sucedida das operações do método.
Com isso, finalizamos a análise dos algoritmos que estruturam o funcionamento da classe CNeuronTrajLLMOCL. O código completo dessa classe e de todos os seus métodos está disponível no anexo para consulta.
2.4 Arquitetura dos modelos
Após a implementação dos algoritmos do novo bloco, precisamos integrá-lo à nossa arquitetura de modelo para analisar a eficácia dos métodos propostos em dados históricos reais. O Traj-LLM foi desenvolvido para previsão de trajetórias futuras, e métodos semelhantes já são utilizados no codificador do estado do ambiente.
Vale ressaltar que nossa abordagem prática foi implementada dentro de um único bloco integrado, o que permite manter a arquitetura externa do modelo o mais simples possível, sem comprometer sua funcionalidade.
Como de costume, a entrada do modelo consiste em dados brutos que descrevem a situação atual do mercado.
bool CreateEncoderDescriptions(CArrayObj *&encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } //--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
A pré-processamento inicial dos dados ocorre na camada de normalização em lote.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Em seguida, os dados são diretamente enviados para o novo bloco Traj-LLM. Dado o nível de complexidade desse componente arquitetônico, não podemos classificá-lo como apenas uma camada neural convencional.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTrajLLMOCL; descr.window = BarDescr; //window descr.window_out = EmbeddingSize; //Inside Dimension descr.count = HistoryBars; //Units prev_count = descr.layers = NForecast; //Forecast descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Na saída do bloco, já temos os valores previstos, aos quais adicionamos parâmetros estatísticos dos valores originais.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; }
Por fim, ajustamos os resultados na frequência.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
A arquitetura das demais partes do modelo permaneceu inalterada, assim como o código de todas as rotinas utilizadas. Esses arquivos estão disponíveis no anexo para consulta. Agora, partimos para a etapa final do nosso trabalho.
3. Testes
Realizamos um extenso trabalho de implementação do método Traj-LLM em MQL5. Agora é o momento de analisar os resultados práticos dessa abordagem. Vamos treinar os modelos com dados históricos reais e verificar sua eficácia em dados fora do conjunto de treinamento.
Conforme mencionado anteriormente, as mudanças na arquitetura do modelo não alteraram a estrutura dos dados brutos nem dos resultados. Isso nos permite reutilizar os conjuntos de dados de treinamento previamente coletados para o pré-treinamento.
No primeiro estágio, treinamos o Codificador do Estado do Ambiente para prever a movimentação futura dos preços. O treinamento prossegue até que o erro de previsão se estabilize em um nível determinado. Durante essa fase, não realizamos atualizações na base de treinamento. Na presente etapa, obtivemos resultados bastante bons. Os resultados preliminares foram bastante satisfatórios. O modelo identificou corretamente as tendências de movimento futuro dos preços.
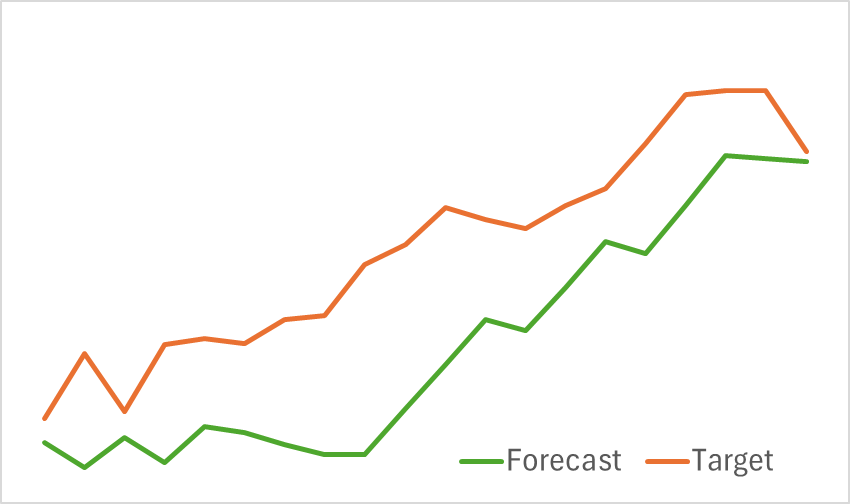
Na segunda etapa, realizamos o treinamento iterativo da política de comportamento do Ator e da função de recompensa do Crítico. O treinamento do modelo Crítico tem caráter auxiliar, sendo utilizado apenas para ajustar as ações do Ator. Nosso objetivo principal é treinar uma política lucrativa para o Ator. No entanto, para avaliar corretamente suas ações durante o treinamento, atualizamos o conjunto de treinamento periodicamente. Após algumas iterações, conseguimos desenvolver uma política capaz de gerar lucro no conjunto de teste.
Lembrando que o treinamento dos modelos foi realizado com dados históricos do EURUSD de 2023, no timeframe H1. O teste foi conduzido com dados de janeiro de 2024, mantendo todos os outros parâmetros inalterados.
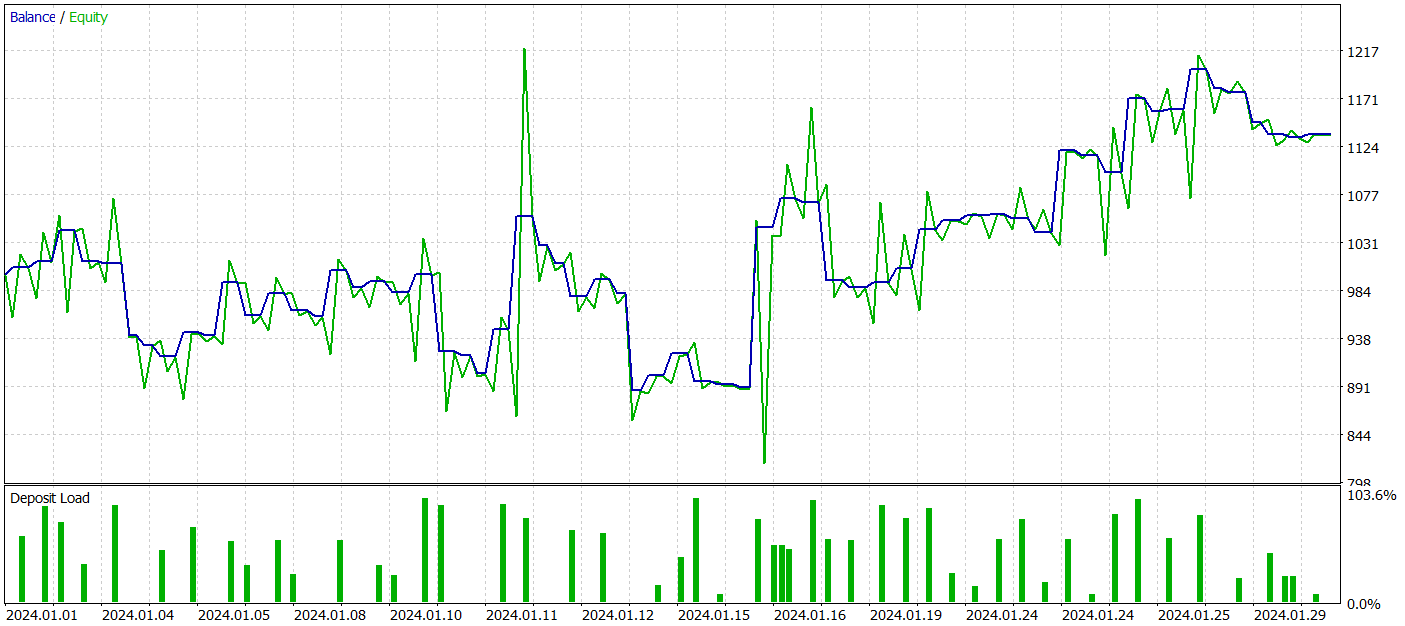
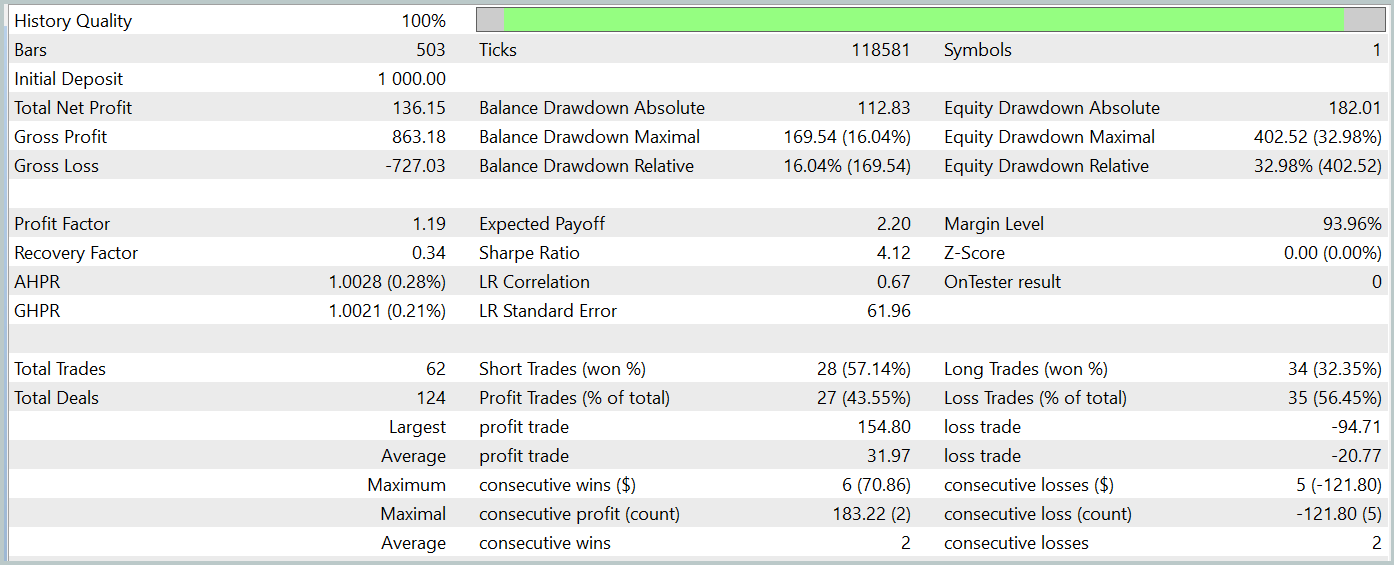
Durante o período de testes, nosso modelo executou 62 operações, das quais 27 (43,55%) foram encerradas com lucro. Entretanto, como o lucro máximo e o lucro médio das operações vencedoras foram mais de 50% superiores às perdas médias das operações perdedoras, o resultado final do teste foi um lucro de 13,6%. O profit factor foi registrado em 1,19. Apesar dos bons resultados, um ponto preocupante foi o drawdown da equidade, que atingiu quase 33%. Obviamente, nessa forma atual, o modelo não pode ser utilizado para trading real e requer aprimoramentos.
Considerações finais
Neste artigo, exploramos o método Traj-LLM, no qual os autores propõem uma nova abordagem para o uso de grandes modelos de linguagem (LLM). O método demonstra como as capacidades desses modelos podem ser adaptadas para prever valores futuros de diferentes séries temporais, permitindo uma previsão mais precisa e adaptável em ambientes de incerteza e volatilidade.
Na parte prática do artigo, implementamos nossa versão dos métodos propostos e os testamos em dados históricos reais. Os resultados obtidos não são perfeitos, mas mostram um potencial promissor.
Referências
- Traj-LLM: A New Exploration for Empowering Trajectory Prediction with Pre-trained Large Language Models
- Outras publicações da série
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA para coleta de exemplos |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA para coleta de exemplos usando o método Real-ORL |
| 3 | Study.mq5 | Expert Advisor | EA para treinamento de modelos |
| 4 | StudyEncoder.mq5 | Expert Advisor | EA para treinamento do Codificador |
| 5 | Test.mq5 | Expert Advisor | EA para testar o modelo |
| 6 | Trajectory.mqh | Biblioteca de classe | Estrutura para descrição do estado do sistema |
| 7 | NeuroNet.mqh | Biblioteca de classe | Biblioteca de classes para criação de redes neurais |
| 8 | NeuroNet.cl | Biblioteca | Código da biblioteca OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/15595
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Algoritmo de algas artificiais (AAA)
Algoritmo de algas artificiais (AAA)
 Introdução ao MQL5 (Parte 8): Guia do Iniciante para Construção de Expert Advisors (II)
Introdução ao MQL5 (Parte 8): Guia do Iniciante para Construção de Expert Advisors (II)
 Simulação de mercado (Parte 06): Transferindo informações do MetraTrader 5 para o Excel
Simulação de mercado (Parte 06): Transferindo informações do MetraTrader 5 para o Excel
 Métodos de William Gann (Parte II): Criando um Indicador do Quadrado de Gann
Métodos de William Gann (Parte II): Criando um Indicador do Quadrado de Gann
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso