
Data Science e Machine Learning (Parte 21): Desvendando Redes Neurais, Algoritmos de Otimização Desmistificados
Não estou sugerindo que redes neurais são fáceis. Você precisa ser um especialista para fazer essas coisas funcionarem. Mas essa expertise serve a um espectro mais amplo de aplicações. De certo modo, todo o esforço que anteriormente era dedicado ao design de características agora se dirige ao design da arquitetura, design da função de perda e design do esquema de otimização. O trabalho manual foi elevado a um nível superior de abstração.
Stefano Soatto
Introdução
Parece que hoje em dia todo mundo está interessado em Inteligência Artificial, está em toda parte, e os gigantes da indústria de tecnologia, como Google e Microsoft por trás da openAI, estão impulsionando a adaptação da IA em diferentes aspectos e indústrias, como entretenimento, saúde, artes, criatividade, etc.
Vejo essa tendência também na comunidade MQL5 por que não, com a introdução de matrizes e vetores e ONNX ao MetaTrader5. Agora é possível criar modelos de negociação com Inteligência Artificial de qualquer complexidade. Você nem precisa ser um especialista em álgebra linear ou nerd o suficiente para entender tudo o que está envolvido no sistema.
Apesar de tudo isso, os fundamentos do aprendizado de máquina estão agora mais difíceis de encontrar do que nunca, e ainda assim são tão importantes quanto saber para solidificar sua compreensão de IA. Eles permitem que você saiba por que faz o que faz, o que te torna flexível e te dá opções. Há muitas coisas que ainda precisamos discutir sobre aprendizado de máquina. Hoje, veremos quais são os algoritmos de otimização, como eles se comparam entre si, quando e qual algoritmo de otimização você deve escolher para melhor desempenho e precisão em suas Redes Neurais.
O conteúdo discutido neste artigo ajudará você a entender os algoritmos de otimização em geral, o que significa que esse conhecimento será útil mesmo ao trabalhar com modelos do Scikit-Learn, Tensorflow ou Pytorch em Python, pois esses otimizadores são universais para todas as redes neurais, independentemente da linguagem de programação que você use.
O que são os Otimizadores de Redes Neurais?
Por definição, otimizadores são algoritmos que ajustam os parâmetros das redes neurais durante o treinamento. Seu objetivo é minimizar a função de perda, levando, em última análise, a um desempenho aprimorado.
Simplificando, os otimizadores de redes neurais fazem:
- Estes são os principais parâmetros que influenciam a rede neural. Os otimizadores determinam como modificar cada parâmetro em cada iteração de treinamento.
- Os otimizadores avaliam a discrepância entre os valores reais e as previsões da rede neural. Eles se esforçam para reduzir esse erro progressivamente.
Recomendo a leitura de um artigo anterior Redes Neurais Desmistificadas se você ainda não o fez. Neste artigo, estaremos aprimorando o modelo de rede neural que construímos do zero neste artigo, adicionando otimizadores a ele.
Antes de vermos quais são os diferentes tipos de otimizadores, precisamos entender os algoritmos de retropropagação. Existem geralmente três algoritmos;
- Descida do Gradiente Estocástica (SGD)
- Descida do Gradiente em Lote (BGD)
- Descida de gradiente em minilote
01: Algoritmo de Descida do Gradiente Estocástica (SGD)
A Descida do Gradiente Estocástica (SGD) é um algoritmo de otimização fundamental usado para treinar redes neurais. Ele atualiza iterativamente os pesos e os vieses da rede de forma a minimizar a função de perda. A função de perda mede a discrepância entre as previsões da rede e os rótulos reais (valores-alvo) nos dados de treinamento.
Os principais processos envolvidos nesses algoritmos de otimização são os mesmos, eles incluem:
- iteração
- retropropagação
- atualização de pesos e vieses
Esses algoritmos diferem na forma como as iterações são tratadas e na frequência com que os pesos e os vieses são atualizados. O algoritmo SGD atualiza os parâmetros da rede neural (pesos e vieses) um exemplo de treinamento (ponto de dados) por vez.
void CRegressorNets::backpropagation(const matrix& x, const vector &y) { for (ulong epoch=0; epoch<epochs && !IsStopped(); epoch++) { for (ulong iter=0; iter<rows; iter++) //iterate through all data points { for (int layer=(int)mlp.hidden_layers-1; layer>=0 && !IsStopped(); layer--) //Loop through the network backward from last to first layer { // find partial derivatives of each layer WRT the loss function dW and dB //--- Weights updates optimizer_weights.update(W, dW); optimizer_bias.update(B, dB); this.W_tensor.Add(W, layer); this.B_tensor.Add(B, layer); } } } }
Suas Vantagens:
- Computacionalmente eficiente para grandes conjuntos de dados.
- Pode, às vezes, convergir mais rápido do que a Descida do Gradiente em Lote (BGD) e a Descida do Gradiente em Mini-batch, especialmente para funções de perda não convexas, pois usa uma amostra de treinamento por vez.
- Bom para evitar mínimos locais: Devido às atualizações ruidosas no SGD, ele tem a capacidade de escapar dos mínimos locais e convergir para mínimos globais.
Desvantagens:
- As atualizações podem ser ruidosas, levando a um comportamento de "ziguezague" durante o treinamento.
- Pode não convergir sempre para o mínimo global.
- Convergência lenta, pode exigir mais épocas para convergir, pois atualiza os parâmetros para cada exemplo de treinamento um por vez.
- Sensível à taxa de aprendizado: A escolha da taxa de aprendizado pode ser crítica para esse algoritmo; uma taxa de aprendizado mais alta pode fazer o algoritmo ultrapassar o mínimo global, enquanto uma taxa de aprendizado mais baixa desacelera o processo de convergência.
02: Algoritmo de Descida do Gradiente em Lote (BGD):
Ao contrário do SGD, a Descida do Gradiente em Lote (BGD) calcula os gradientes usando todo o conjunto de dados em cada iteração.
Vantagens:
Em teoria, converge para um mínimo se a função de perda for suave e convexa.
Desvantagens:
Pode ser computacionalmente caro para grandes conjuntos de dados, pois requer o processamento repetido de todo o conjunto de dados.
Não vou implementá-lo na rede neural que temos no momento, mas pode ser implementado facilmente, assim como a Descida do Gradiente em Mini-batch abaixo, você pode implementá-lo se desejar.
03: Descida do Gradiente em Mini-batch:
Este algoritmo é um compromisso entre SGD e BGD; ele atualiza os parâmetros da rede usando um pequeno subconjunto (mini-batch) dos dados de treinamento em cada iteração.
Vantagens:
- Oferece um bom equilíbrio entre eficiência computacional e estabilidade de atualização em comparação com SGD e BGD.
- Pode lidar com conjuntos de dados maiores de forma mais eficaz do que o BGD.
Desvantagens:
- Pode exigir mais ajustes no tamanho do mini-batch em comparação com o SGD.
- Computacionalmente caro em comparação com o SGD, consome muita memória para armazenamento e processamento de batches.
- Pode levar muito tempo para treinar com muitos batches grandes.
Abaixo está o pseudocódigo de como o algoritmo de descida do gradiente em mini-batch se parece:
void CRegressorNets::backpropagation(const matrix& x, const vector &y, OptimizerSGD *sgd, const uint epochs, uint batch_size=0, bool show_batch_progress=false) { //.... for (ulong epoch=0; epoch<epochs && !IsStopped(); epoch++) { for (uint batch=0, batch_start=0, batch_end=batch_size; batch<num_batches; batch++, batch_start+=batch_size, batch_end=(batch_start+batch_size-1)) { matrix batch_x = MatrixExtend::Get(x, batch_start, batch_end-1); vector batch_y = MatrixExtend::Get(y, batch_start, batch_end-1); rows = batch_x.Rows(); for (ulong iter=0; iter<rows ; iter++) //replace to rows { pred_v[0] = predict(batch_x.Row(iter)); actual_v[0] = y[iter]; // Find derivatives WRT weights dW and bias dB //.... //--- Updating the weights using a given optimizer optimizer_weights.update(W, dW); optimizer_bias.update(B, dB); this.Weights_tensor.Add(W, layer); this.Bias_tensor.Add(B, layer); } } } }
No coração desses dois algoritmos, por padrão, eles têm uma simples regra de atualização de gradiente, que muitas vezes é referida como otimizador SGD ou Mini-BGD.
class OptimizerSGD { protected: double m_learning_rate; public: OptimizerSGD(double learning_rate=0.01); ~OptimizerSGD(void); virtual void update(matrix ¶meters, matrix &gradients); }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ OptimizerSGD::OptimizerSGD(double learning_rate=0.01): m_learning_rate(learning_rate) { } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ OptimizerSGD::~OptimizerSGD(void) { } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void OptimizerSGD::update(matrix ¶meters, matrix &gradients) { parameters -= this.m_learning_rate * gradients; //Simple gradient descent update rule } //+------------------------------------------------------------------+ //| Batch Gradient Descent (BGD): This optimizer computes the | //| gradients of the loss function on the entire training dataset | //| and updates the parameters accordingly. It can be slow and | //| memory-intensive for large datasets but tends to provide a | //| stable convergence. | //+------------------------------------------------------------------+ class OptimizerMinBGD: public OptimizerSGD { public: OptimizerMinBGD(double learning_rate=0.01); ~OptimizerMinBGD(void); }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ OptimizerMinBGD::OptimizerMinBGD(double learning_rate=0.010000): OptimizerSGD(learning_rate) { } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ OptimizerMinBGD::~OptimizerMinBGD(void) { }
Agora vamos treinar um modelo usando esses dois otimizadores e observar o resultado para entendê-los melhor:
#include <MALE5\MatrixExtend.mqh> #include <MALE5\preprocessing.mqh> #include <MALE5\metrics.mqh> #include <MALE5\Neural Networks\Regressor Nets.mqh> CRegressorNets *nn; StandardizationScaler scaler; vector open_, high_, low_; vector hidden_layers = {5}; input uint nn_epochs = 100; input double nn_learning_rate = 0.0001; input uint nn_batch_size =32; input bool show_batch = false; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- string headers; matrix dataset = MatrixExtend::ReadCsv("airfoil_noise_data.csv", headers); matrix x_train, x_test; vector y_train, y_test; MatrixExtend::TrainTestSplitMatrices(dataset, x_train, y_train, x_test, y_test, 0.7); nn = new CRegressorNets(hidden_layers, AF_RELU_, LOSS_MSE_); x_train = scaler.fit_transform(x_train); nn.fit(x_train, y_train, new OptimizerMinBGD(nn_learning_rate), nn_epochs, nn_batch_size, show_batch); delete nn; }
Quando o parâmetro nn_batch_size for atribuído um valor maior que zero, o gradiente descendente em Mini-Batch será ativado independentemente de qual Otimizador for aplicado na função de ajuste/retropropagação.
backprop CRegressorNets::backpropagation(const matrix& x, const vector &y, OptimizerSGD *optimizer, const uint epochs, uint batch_size=0, bool show_batch_progress=false) { //... //... //--- Optimizer use selected optimizer when batch_size ==0 otherwise use the batch gradient descent OptimizerSGD optimizer_weights = optimizer; OptimizerSGD optimizer_bias = optimizer; if (batch_size>0) { OptimizerMinBGD optimizer_weights; OptimizerMinBGD optimizer_bias; } //--- Cross validation CCrossValidation cross_validation; CTensors *cv_tensor; matrix validation_data = MatrixExtend::concatenate(x, y); matrix validation_x; vector validation_y; cv_tensor = cross_validation.KFoldCV(validation_data, 10); //k-fold cross validation | 10 folds selected //--- matrix DELTA = {}; double actual=0, pred=0; matrix temp_inputs ={}; matrix dB = {}; //Bias Derivatives matrix dW = {}; //Weight Derivatives for (ulong epoch=0; epoch<epochs && !IsStopped(); epoch++) { double epoch_start = GetTickCount(); uint num_batches = (uint)MathFloor(x.Rows()/(batch_size+DBL_EPSILON)); vector batch_loss(num_batches), batch_accuracy(num_batches); vector actual_v(1), pred_v(1), LossGradient = {}; if (batch_size==0) //Stochastic Gradient Descent { for (ulong iter=0; iter<rows; iter++) //iterate through all data points { pred = predict(x.Row(iter)); actual = y[iter]; pred_v[0] = pred; actual_v[0] = actual; //--- DELTA.Resize(mlp.outputs,1); for (int layer=(int)mlp.hidden_layers-1; layer>=0 && !IsStopped(); layer--) //Loop through the network backward from last to first layer { //..... backpropagation and finding derivatives code //-- Observation | DeLTA matrix is same size as the bias matrix W = this.Weights_tensor.Get(layer); B = this.Bias_tensor.Get(layer); //--- Derivatives wrt weights and bias dB = DELTA; dW = DELTA.MatMul(temp_inputs.Transpose()); //--- Weights updates optimizer_weights.update(W, dW); optimizer_bias.update(B, dB); this.Weights_tensor.Add(W, layer); this.Bias_tensor.Add(B, layer); } } } else //Batch Gradient Descent { for (uint batch=0, batch_start=0, batch_end=batch_size; batch<num_batches; batch++, batch_start+=batch_size, batch_end=(batch_start+batch_size-1)) { matrix batch_x = MatrixExtend::Get(x, batch_start, batch_end-1); vector batch_y = MatrixExtend::Get(y, batch_start, batch_end-1); rows = batch_x.Rows(); for (ulong iter=0; iter<rows ; iter++) //iterate through all data points { pred_v[0] = predict(batch_x.Row(iter)); actual_v[0] = y[iter]; //--- DELTA.Resize(mlp.outputs,1); for (int layer=(int)mlp.hidden_layers-1; layer>=0 && !IsStopped(); layer--) //Loop through the network backward from last to first layer { //..... backpropagation and finding derivatives code } //-- Observation | DeLTA matrix is same size as the bias matrix W = this.Weights_tensor.Get(layer); B = this.Bias_tensor.Get(layer); //--- Derivatives wrt weights and bias dB = DELTA; dW = DELTA.MatMul(temp_inputs.Transpose()); //--- Weights updates optimizer_weights.update(W, dW); optimizer_bias.update(B, dB); this.Weights_tensor.Add(W, layer); this.Bias_tensor.Add(B, layer); } } pred_v = predict(batch_x); batch_loss[batch] = pred_v.Loss(batch_y, ENUM_LOSS_FUNCTION(m_loss_function)); batch_loss[batch] = MathIsValidNumber(batch_loss[batch]) ? (batch_loss[batch]>1e6 ? 1e6 : batch_loss[batch]) : 1e6; //Check for nan and return some large value if it is nan batch_accuracy[batch] = Metrics::r_squared(batch_y, pred_v); if (show_batch_progress) printf("----> batch[%d/%d] batch-loss %.5f accuracy %.3f",batch+1,num_batches,batch_loss[batch], batch_accuracy[batch]); } } //--- End of an epoch vector validation_loss(cv_tensor.SIZE); vector validation_acc(cv_tensor.SIZE); for (ulong i=0; i<cv_tensor.SIZE; i++) { validation_data = cv_tensor.Get(i); MatrixExtend::XandYSplitMatrices(validation_data, validation_x, validation_y); vector val_preds = this.predict(validation_x);; validation_loss[i] = val_preds.Loss(validation_y, ENUM_LOSS_FUNCTION(m_loss_function)); validation_acc[i] = Metrics::r_squared(validation_y, val_preds); } pred_v = this.predict(x); if (batch_size==0) { backprop_struct.training_loss[epoch] = pred_v.Loss(y, ENUM_LOSS_FUNCTION(m_loss_function)); backprop_struct.training_loss[epoch] = MathIsValidNumber(backprop_struct.training_loss[epoch]) ? (backprop_struct.training_loss[epoch]>1e6 ? 1e6 : backprop_struct.training_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan backprop_struct.validation_loss[epoch] = validation_loss.Mean(); backprop_struct.validation_loss[epoch] = MathIsValidNumber(backprop_struct.validation_loss[epoch]) ? (backprop_struct.validation_loss[epoch]>1e6 ? 1e6 : backprop_struct.validation_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan } else { backprop_struct.training_loss[epoch] = batch_loss.Mean(); backprop_struct.training_loss[epoch] = MathIsValidNumber(backprop_struct.training_loss[epoch]) ? (backprop_struct.training_loss[epoch]>1e6 ? 1e6 : backprop_struct.training_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan backprop_struct.validation_loss[epoch] = validation_loss.Mean(); backprop_struct.validation_loss[epoch] = MathIsValidNumber(backprop_struct.validation_loss[epoch]) ? (backprop_struct.validation_loss[epoch]>1e6 ? 1e6 : backprop_struct.validation_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan } double epoch_stop = GetTickCount(); printf("--> Epoch [%d/%d] training -> loss %.8f accuracy %.3f validation -> loss %.5f accuracy %.3f | Elapsed %s ",epoch+1,epochs,backprop_struct.training_loss[epoch],Metrics::r_squared(y, pred_v),backprop_struct.validation_loss[epoch],validation_acc.Mean(),this.ConvertTime((epoch_stop-epoch_start)/1000.0)); } isBackProp = false; if (CheckPointer(optimizer)!=POINTER_INVALID) delete optimizer; return backprop_struct; }
Resultados:
Descida de Gradiente Estocástico (SGD): taxa de aprendizado = 0,0001
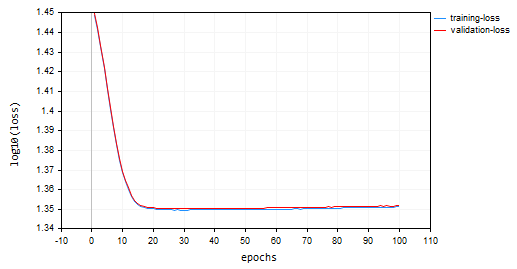
Descida de Gradiente em Lote (BGD): taxa de aprendizado = 0,0001, tamanho do lote = 16
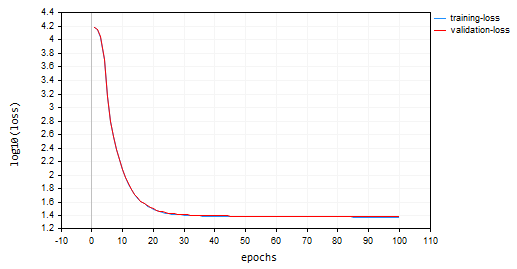
SGD convergiu mais rápido, ficando próximo do mínimo local por volta da 10ª época, enquanto o BGD estava por volta da 20ª época. O SGD convergiu para aproximadamente 60% de acurácia tanto no treinamento quanto na validação, enquanto a acurácia do BGD foi de 15% durante a amostra de treinamento e 13% na amostra de validação. Não podemos concluir ainda, pois não temos certeza de que o BGD possui a melhor taxa de aprendizado e o tamanho de lote adequado para este conjunto de dados. Diferentes otimizadores funcionam melhor em diferentes taxas de aprendizado. Isso pode ser uma das causas para o SGD não ter tido um bom desempenho. No entanto, ele convergiu bem sem oscilações ao redor do mínimo local, algo que não pode ser visto no SGD. O gráfico do BGD é suave, indicando um processo de treinamento estável. Isso ocorre porque, no BGD, a perda geral é a média das perdas em lotes individuais.
backprop_struct.training_loss[epoch] = batch_loss.Mean(); backprop_struct.training_loss[epoch] = MathIsValidNumber(backprop_struct.training_loss[epoch]) ? (backprop_struct.training_loss[epoch]>1e6 ? 1e6 : backprop_struct.training_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan backprop_struct.validation_loss[epoch] = validation_loss.Mean(); backprop_struct.validation_loss[epoch] = MathIsValidNumber(backprop_struct.validation_loss[epoch]) ? (backprop_struct.validation_loss[epoch]>1e6 ? 1e6 : backprop_struct.validation_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan
Você deve ter notado nos gráficos que o log10 foi aplicado aos valores de perda para o gráfico. Essa normalização garante que os valores de perda sejam bem plotados, pois, nas primeiras épocas, os valores de perda podem ser, às vezes, maiores. Isso visa penalizar os valores maiores para que pareçam melhores em um gráfico. Os valores reais da perda podem ser vistos na aba de especialistas e não no gráfico.
void CRegressorNets::fit(const matrix &x, const vector &y, OptimizerSGD *optimizer, const uint epochs, uint batch_size=0, bool show_batch_progress=false) { trained = true; //The fit method has been called vector epochs_vector(epochs); for (uint i=0; i<epochs; i++) epochs_vector[i] = i+1; backprop backprop_struct; backprop_struct = this.backpropagation(x, y, optimizer, epochs, batch_size, show_batch_progress); //Run backpropagation CPlots plt; backprop_struct.training_loss = log10(backprop_struct.training_loss); //Logarithmic scalling plt.Plot("Loss vs Epochs",epochs_vector,backprop_struct.training_loss,"epochs","log10(loss)","training-loss",CURVE_LINES); backprop_struct.validation_loss = log10(backprop_struct.validation_loss); plt.AddPlot(backprop_struct.validation_loss,"validation-loss",clrRed); while (MessageBox("Close or Cancel Loss Vs Epoch plot to proceed","Training progress",MB_OK)<0) Sleep(1); isBackProp = false; }
O otimizador SGD é uma ferramenta geral para minimizar funções de perda, enquanto o algoritmo SGD para retropropagação é uma técnica específica dentro do SGD, voltada para o cálculo de gradientes em redes neurais.
Pense no otimizador SGD como o carpinteiro e os algoritmos SGD ou Min-BGD para retropropagação como uma ferramenta especializada em sua caixa de ferramentas.
Tipos de Otimizadores de Redes Neurais
Além dos otimizadores SGD que acabamos de discutir. Existem outros otimizadores de redes neurais, cada um empregando estratégias distintas para alcançar valores ótimos de parâmetros. Abaixo estão alguns dos otimizadores de redes neurais mais comumente usados:
- Propagação do Quadrado da Média das Raízes (RMSProp)
- Descida de Gradiente Adaptativa (AdaGrad)
- Estimativa de Momento Adaptativa (Adam)
- Adadelta
- Estimativa de Momento Adaptativa Acelerada por Nesterov (Nadam)
01: Propagação do Quadrado da Média das Raízes (RMSProp)
Este algoritmo de otimização visa resolver as limitações da Descida de Gradiente Estocástica (SGD) adaptando a taxa de aprendizado para cada parâmetro de peso e viés com base em seus gradientes históricos.
Problema com o SGD:
O SGD atualiza pesos e vieses usando o gradiente atual e uma taxa de aprendizado fixa. No entanto, em funções complexas como redes neurais, a magnitude dos gradientes pode variar significativamente para diferentes parâmetros. Isso pode levar a uma convergência lenta, pois parâmetros com gradientes pequenos podem ser atualizados muito lentamente, dificultando o aprendizado geral. Além disso, o SGD pode causar grandes oscilações, pois parâmetros com grandes gradientes podem experimentar variações excessivas durante as atualizações, tornando o processo de aprendizado instável.Teoria:
Aqui está a ideia central por trás do RMSprop:
- Manter uma Média Móvel Exponencial (EMA) dos gradientes quadrados. Para cada parâmetro, o RMSprop acompanha uma média decrescente exponencialmente dos gradientes quadrados. Essa média reflete o histórico recente de quanto o parâmetro deve ser atualizado.
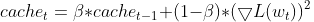
- Normalizar o Gradiente. O gradiente atual para cada parâmetro é dividido pela raiz quadrada da EMA dos gradientes quadrados, juntamente com um pequeno termo de suavização (geralmente denotado por ε) para evitar divisão por zero.
- Atualizar o Parâmetro. O gradiente normalizado é multiplicado pela taxa de aprendizado para determinar a atualização do parâmetro.
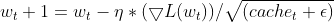
onde:
![]() EMA dos gradientes quadrados no passo de tempo t
EMA dos gradientes quadrados no passo de tempo t
![]() Taxa de decaimento (hiperparâmetro, tipicamente entre 0,9 e 0,999) - controla a influência dos gradientes passados
Taxa de decaimento (hiperparâmetro, tipicamente entre 0,9 e 0,999) - controla a influência dos gradientes passados
![]() Gradiente da função de perda em relação ao parâmetro w no passo de tempo t
Gradiente da função de perda em relação ao parâmetro w no passo de tempo t
![]() Valor do parâmetro no passo de tempo t
Valor do parâmetro no passo de tempo t
![]() Valor atualizado do parâmetro no passo de tempo t+1
Valor atualizado do parâmetro no passo de tempo t+1
η: Taxa de aprendizado (hiperparâmetro)
ε: Termo de suavização (geralmente um valor pequeno como 1e-8)
class OptimizerRMSprop { protected: double m_learning_rate; double m_decay_rate; double m_epsilon; matrix<double> cache; //Dividing double/matrix causes compilation error | this is the fix to the issue matrix divide(const double numerator, const matrix &denominator) { matrix res = denominator; for (ulong i=0; i<denominator.Rows(); i++) res.Row(numerator / denominator.Row(i), i); return res; } public: OptimizerRMSprop(double learning_rate=0.01, double decay_rate=0.9, double epsilon=1e-8); ~OptimizerRMSprop(void); virtual void update(matrix& parameters, matrix& gradients); }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ OptimizerRMSprop::OptimizerRMSprop(double learning_rate=0.01, double decay_rate=0.9, double epsilon=1e-8): m_learning_rate(learning_rate), m_decay_rate(decay_rate), m_epsilon(epsilon) { } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ OptimizerRMSprop::~OptimizerRMSprop(void) { } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void OptimizerRMSprop::update(matrix ¶meters,matrix &gradients) { if (cache.Rows()!=parameters.Rows() || cache.Cols()!=parameters.Cols()) { cache.Init(parameters.Rows(), parameters.Cols()); cache.Fill(0.0); } //--- cache += m_decay_rate * cache + (1 - m_decay_rate) * MathPow(gradients, 2); parameters -= divide(m_learning_rate, cache + m_epsilon) * gradients; }
Utilizando 100 épocas e uma taxa de aprendizado de 0,0001, os mesmos valores padrão usados para os otimizadores anteriores. A rede neural não conseguiu convergir após 100 épocas, apresentando aproximadamente -319 e -324 de acurácia nas amostras de treinamento e validação, respectivamente. Parece que pode ser necessário mais de 1000 épocas nesse ritmo, assumindo que não ultrapassamos o mínimo local por esse grande número de épocas.
HK 0 15:10:15.632 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [90/100] training -> loss 15164.85487215 accuracy -320.064 validation -> loss 15164.99272 accuracy -325.349 | Elapsed 0.031 Seconds HQ 0 15:10:15.663 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [91/100] training -> loss 15161.78717397 accuracy -319.999 validation -> loss 15161.92323 accuracy -325.283 | Elapsed 0.031 Seconds DO 0 15:10:15.694 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [92/100] training -> loss 15158.07142844 accuracy -319.921 validation -> loss 15158.20512 accuracy -325.203 | Elapsed 0.031 Seconds GE 0 15:10:15.727 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [93/100] training -> loss 15154.92004326 accuracy -319.854 validation -> loss 15155.05184 accuracy -325.135 | Elapsed 0.032 Seconds GS 0 15:10:15.760 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [94/100] training -> loss 15151.84229952 accuracy -319.789 validation -> loss 15151.97226 accuracy -325.069 | Elapsed 0.031 Seconds DH 0 15:10:15.796 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [95/100] training -> loss 15148.77653633 accuracy -319.724 validation -> loss 15148.90466 accuracy -325.003 | Elapsed 0.031 Seconds MF 0 15:10:15.831 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [96/100] training -> loss 15145.56414236 accuracy -319.656 validation -> loss 15145.69033 accuracy -324.934 | Elapsed 0.047 Seconds IL 0 15:10:15.869 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [97/100] training -> loss 15141.85430749 accuracy -319.577 validation -> loss 15141.97859 accuracy -324.854 | Elapsed 0.031 Seconds KJ 0 15:10:15.906 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [98/100] training -> loss 15138.40751503 accuracy -319.504 validation -> loss 15138.52969 accuracy -324.780 | Elapsed 0.032 Seconds PP 0 15:10:15.942 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [99/100] training -> loss 15135.31136641 accuracy -319.439 validation -> loss 15135.43169 accuracy -324.713 | Elapsed 0.046 Seconds NM 0 15:10:15.975 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [100/100] training -> loss 15131.73032246 accuracy -319.363 validation -> loss 15131.84854 accuracy -324.636 | Elapsed 0.032 Seconds
Gráfico de Perda vs Época: 100 épocas, taxa de aprendizado de 0,0001.
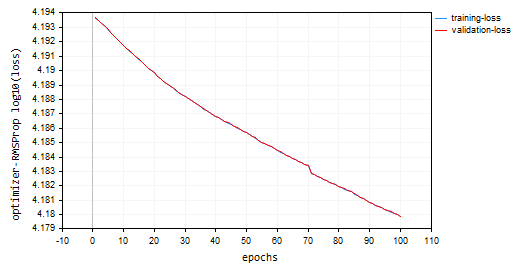
Onde usar RMSProp?
Bom para objetivos não estacionários, gradientes esparsos, mais simples que Adam.
02: Adagrad (Algoritmo de Gradiente Adaptativo)
Adagrad é um otimizador para redes neurais que utiliza uma taxa de aprendizado adaptativa, similar ao RMSprop. No entanto, Adagrad e RMSprop têm algumas diferenças chave em suas abordagens.
Matemática por trás:
- Acumula Gradientes Passados. O Adagrad mantém o controle da soma dos gradientes quadrados para cada parâmetro durante todo o processo de treinamento. Esse valor acumulado reflete o quanto um parâmetro foi atualizado no passado.
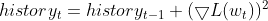
cache += MathPow(gradients, 2);
- Normaliza o Gradiente. O gradiente atual para cada parâmetro é dividido pela raiz quadrada da soma acumulada dos gradientes quadrados, juntamente com um pequeno termo de suavização (geralmente denotado por ε) para evitar divisão por zero.
- Atualiza o Parâmetro. O gradiente normalizado é multiplicado pela taxa de aprendizado para determinar a atualização do parâmetro.
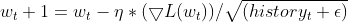
parameters -= divide(this.m_learning_rate, MathSqrt(cache + this.m_epsilon)) * gradients;
nn_learning_rate = 0.0001, epochs = 100
nn.fit(x_train, y_train, new OptimizerAdaGrad(nn_learning_rate), nn_epochs, nn_batch_size, show_batch); Gráfico de Perda vs Época:
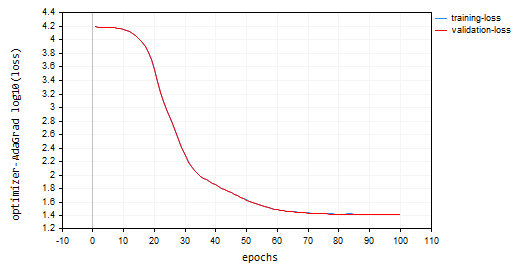
O Adagrad teve uma curva de aprendizado mais acentuada e foi muito estável durante as atualizações, mas precisou de mais de 100 épocas para convergir, terminando com aproximadamente 44% de acurácia nas amostras de treinamento e validação, respectivamente.
RK 0 15:15:52.202 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [90/100] training -> loss 26.22261537 accuracy 0.445 validation -> loss 26.13118 accuracy 0.440 | Elapsed 0.031 Seconds ER 0 15:15:52.239 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [91/100] training -> loss 26.12443561 accuracy 0.447 validation -> loss 26.03635 accuracy 0.442 | Elapsed 0.047 Seconds NJ 0 15:15:52.277 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [92/100] training -> loss 26.11449352 accuracy 0.447 validation -> loss 26.02561 accuracy 0.442 | Elapsed 0.032 Seconds IQ 0 15:15:52.316 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [93/100] training -> loss 26.09263184 accuracy 0.448 validation -> loss 26.00461 accuracy 0.443 | Elapsed 0.046 Seconds NH 0 15:15:52.354 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [94/100] training -> loss 26.14277865 accuracy 0.447 validation -> loss 26.05529 accuracy 0.442 | Elapsed 0.032 Seconds HP 0 15:15:52.393 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [95/100] training -> loss 26.09559950 accuracy 0.448 validation -> loss 26.00845 accuracy 0.443 | Elapsed 0.047 Seconds PO 0 15:15:52.442 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [96/100] training -> loss 26.05409769 accuracy 0.448 validation -> loss 25.96754 accuracy 0.443 | Elapsed 0.046 Seconds PG 0 15:15:52.479 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [97/100] training -> loss 25.98822082 accuracy 0.450 validation -> loss 25.90384 accuracy 0.445 | Elapsed 0.032 Seconds PN 0 15:15:52.519 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [98/100] training -> loss 25.98781231 accuracy 0.450 validation -> loss 25.90438 accuracy 0.445 | Elapsed 0.047 Seconds EE 0 15:15:52.559 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [99/100] training -> loss 25.91146212 accuracy 0.451 validation -> loss 25.83083 accuracy 0.446 | Elapsed 0.031 Seconds CN 0 15:15:52.595 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [100/100] training -> loss 25.87412572 accuracy 0.452 validation -> loss 25.79453 accuracy 0.447 | Elapsed 0.047 Seconds
Vantagens do Adagrad:
Ele converge mais rápido para características esparsas. Em situações onde muitos parâmetros têm atualizações infrequentes devido a características esparsas nos dados, o Adagrad pode reduzir efetivamente suas taxas de aprendizado, permitindo uma convergência mais rápida para esses parâmetros.
Limitações do Adagrad:
Com o tempo, a soma acumulada dos gradientes quadrados no Adagrad continua crescendo, causando uma diminuição contínua das taxas de aprendizado para todos os parâmetros. Isso pode eventualmente interromper o progresso do treinamento.
Quando Usar o Adagrad:
Em conjuntos de dados com características esparsas: Ao lidar com conjuntos de dados onde muitas características têm atualizações infrequentes, o Adagrad pode ser eficaz em acelerar a convergência para esses parâmetros.
Durante os estágios iniciais do treinamento: Em alguns cenários, os ajustes iniciais da taxa de aprendizado pelo Adagrad podem ser úteis antes de mudar para outro otimizador posteriormente no treinamento.
03: Estimativa de Momento Adaptativa (Adam)
Um algoritmo de otimização altamente eficaz amplamente utilizado no treinamento de redes neurais. Ele combina as forças do AdaGrad e do RMSprop para resolver suas limitações e proporcionar um aprendizado eficiente e estável.
Teoria:
Adam possui duas características principais:
- Média Móvel Exponencial (EMA) dos Gradientes: Semelhante ao RMSprop, o Adam mantém uma EMA dos gradientes quadrados (cache) para capturar o histórico recente das atualizações necessárias para cada parâmetro.
- Média Móvel Exponencial dos Momentos: O Adam introduz outra EMA (momento), que acompanha a média móvel dos próprios gradientes. Isso ajuda a mitigar o problema de gradientes que podem desaparecer, o que pode ocorrer em algumas arquiteturas de redes.
Normalização e Atualização:
- Atualização do Momento: O gradiente atual é utilizado para atualizar a EMA dos momentos (m_t).
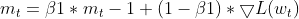
this.moment = this.m_beta1 * this.moment + (1 - this.m_beta1) * gradients;
- Atualização dos Gradientes Quadrados: O gradiente quadrado atual é utilizado para atualizar a EMA dos gradientes quadrados (cache_t).
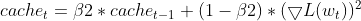
this.cache = this.m_beta2 * this.cache + (1 - this.m_beta2) * MathPow(gradients, 2);
- Correção de Viés: Ambas as EMAs (moment_t e cache_t) são corrigidas para viés usando fatores de decaimento exponencial (β1 e β2) para garantir que sejam estimativas não enviesadas dos verdadeiros momentos.
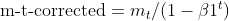
matrix moment_hat = this.moment / (1 - MathPow(this.m_beta1, this.time_step));
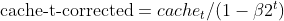
matrix cache_hat = this.cache / (1 - MathPow(this.m_beta2, this.time_step));
- Normalização: Semelhante ao RMSprop, o gradiente atual é normalizado usando as EMAs corrigidas e um pequeno termo de suavização (ε).
- Atualizações de Parâmetros: O gradiente normalizado é multiplicado pela taxa de aprendizado (η) para determinar a atualização do parâmetro.
parameters -= (this.m_learning_rate * moment_hat) / (MathPow(cache_hat, 0.5) + this.m_epsilon);
Assim é como o construtor para o otimizador Adam se parece:
OptimizerAdam(double learning_rate=0.01, double beta1=0.9, double beta2=0.999, double epsilon=1e-8);
Eu o chamei com a taxa de aprendizado:
nn.fit(x_train, y_train, new OptimizerAdam(nn_learning_rate), nn_epochs, nn_batch_size, show_batch); O gráfico de Perda vs Época resultante:
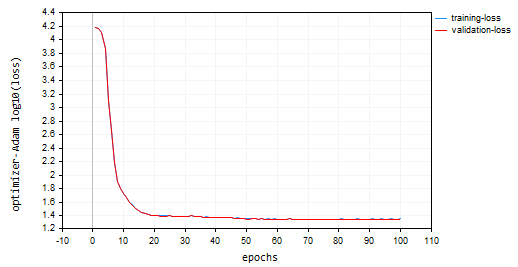
O Adam teve um desempenho melhor do que os otimizadores anteriores, exceto pelo SGD, proporcionando aproximadamente 53% e 52% de acurácia nas amostras de treinamento e validação, respectivamente.
MD 0 15:23:37.651 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [90/100] training -> loss 22.05051037 accuracy 0.533 validation -> loss 21.92528 accuracy 0.529 | Elapsed 0.047 Seconds DS 0 15:23:37.703 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [91/100] training -> loss 22.38393234 accuracy 0.526 validation -> loss 22.25178 accuracy 0.522 | Elapsed 0.046 Seconds OK 0 15:23:37.756 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [92/100] training -> loss 22.12091827 accuracy 0.532 validation -> loss 21.99456 accuracy 0.528 | Elapsed 0.063 Seconds OR 0 15:23:37.808 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [93/100] training -> loss 21.94438889 accuracy 0.535 validation -> loss 21.81944 accuracy 0.532 | Elapsed 0.047 Seconds NI 0 15:23:37.862 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [94/100] training -> loss 22.41965082 accuracy 0.525 validation -> loss 22.28371 accuracy 0.522 | Elapsed 0.062 Seconds LQ 0 15:23:37.915 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [95/100] training -> loss 22.27254037 accuracy 0.528 validation -> loss 22.13931 accuracy 0.525 | Elapsed 0.047 Seconds FH 0 15:23:37.969 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [96/100] training -> loss 21.93193893 accuracy 0.536 validation -> loss 21.80427 accuracy 0.532 | Elapsed 0.047 Seconds LG 0 15:23:38.024 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [97/100] training -> loss 22.41523220 accuracy 0.525 validation -> loss 22.27900 accuracy 0.522 | Elapsed 0.063 Seconds MO 0 15:23:38.077 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [98/100] training -> loss 22.23551304 accuracy 0.529 validation -> loss 22.10466 accuracy 0.526 | Elapsed 0.046 Seconds QF 0 15:23:38.129 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [99/100] training -> loss 21.96662717 accuracy 0.535 validation -> loss 21.84087 accuracy 0.531 | Elapsed 0.063 Seconds GM 0 15:23:38.191 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [100/100] training -> loss 22.29715377 accuracy 0.528 validation -> loss 22.16686 accuracy 0.524 | Elapsed 0.062 Seconds
Vantagens do Adam:
- Ele converge mais rápido: O Adam geralmente converge mais rápido do que o SGD e pode ser mais eficiente do que o RMSprop em vários cenários.
- Menos Sensível à Taxa de Aprendizado: Comparado ao SGD, o Adam é menos sensível à escolha da taxa de aprendizado, tornando-o mais robusto.
- Adequado para Funções de Perda Não Convexas: Ele pode lidar de maneira eficaz com funções de perda não convexas comuns em tarefas de aprendizado profundo.
- Ampla Aplicabilidade: A combinação de características do Adam o torna um otimizador amplamente aplicável para várias arquiteturas de rede e conjuntos de dados.
Desvantagens:
- Afinamento de Hiperparâmetros: Embora geralmente seja menos sensível, o Adam ainda requer ajuste de hiperparâmetros como a taxa de aprendizado e taxas de decaimento para um desempenho ideal.
- Uso de Memória: Manter as EMAs pode levar a um consumo de memória ligeiramente maior em comparação com o SGD.
Onde usar o Adam?
Use o Adam (Estimativa de Momento Adaptativa) para o treinamento de sua rede neural quando você quiser:
Convergência mais rápida. Você quer que sua rede seja menos sensível à taxa de aprendizado e, quando quiser uma taxa de aprendizado adaptativa com momentum.
04: Adadelta (Aprendizado Adaptativo com delta)
Este é outro algoritmo de otimização usado em redes neurais, que compartilha algumas semelhanças com o SGD e RMSProp, oferecendo uma taxa de aprendizado adaptativa com um termo de momentum específico.
O Adadelta visa resolver o problema da taxa de aprendizado fixa do SGD, que leva à convergência lenta e oscilações. Ele emprega uma taxa de aprendizado adaptativa que se ajusta com base em gradientes quadrados passados, semelhante ao RMSProp.
Matemática por trás:
- Manter uma Média Móvel Exponencial (EMA) das deltas quadradas, o Adadelta calcula uma EMA das diferenças quadradas entre atualizações consecutivas de parâmetros (deltas) para cada parâmetro. Isso reflete o histórico recente de quanto o parâmetro mudou.
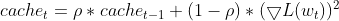
this.cache = m_decay_rate * this.cache + (1 - m_decay_rate) * MathPow(gradients, 2);
- Taxa de Aprendizado Adaptativa: O gradiente quadrado atual para um parâmetro é dividido pela EMA das deltas quadradas (com um termo de suavização). Isso efetivamente serve como uma taxa de aprendizado adaptativa, controlando o tamanho da atualização para cada parâmetro.
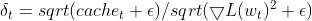
matrix delta = lr * sqrt(this.cache + m_epsilon) / sqrt(pow(gradients, 2) + m_epsilon);
-
Momentum: O Adadelta incorpora um termo de momentum que considera a atualização anterior para o parâmetro, semelhante ao momentum no SGD. Isso ajuda a acumular gradientes e potencialmente escapar de mínimos locais.
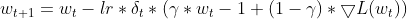
matrix momentum_term = this.m_gamma * parameters + (1 - this.m_gamma) * gradients; parameters -= delta * momentum_term;
onde:
![]() : EMA das deltas quadradas no passo de tempo t
: EMA das deltas quadradas no passo de tempo t
![]() : Taxa de decaimento (hiperparâmetro, tipicamente entre 0,9 e 0,999)
: Taxa de decaimento (hiperparâmetro, tipicamente entre 0,9 e 0,999)
![]() : Gradiente da função de perda em relação ao parâmetro w no passo de tempo t
: Gradiente da função de perda em relação ao parâmetro w no passo de tempo t
![]() : Valor do parâmetro no passo de tempo t
: Valor do parâmetro no passo de tempo t
![]() : Valor atualizado do parâmetro no passo de tempo t+1
: Valor atualizado do parâmetro no passo de tempo t+1
ε: Termo de suavização (geralmente um valor pequeno como 1e-8)
γ: Coeficiente de Momentum (hiperparâmetro, tipicamente entre 0 e 1)
Vantagens do Adadelta:
- Converge Mais Rápido: Comparado ao SGD com uma taxa de aprendizado fixa, o Adadelta pode frequentemente convergir mais rápido, especialmente para problemas com gradientes não estacionários.
- Usa Momentum para Escapar de Mínimos Locais: O termo de momentum ajuda a acumular gradientes e potencialmente escapar de mínimos locais na função de perda.
- Menos Sensível à Taxa de Aprendizado: Semelhante ao RMSprop, o Adadelta é menos sensível à taxa de aprendizado específica escolhida do que o SGD.
Desvantagens do Adadelta:
- Requer ajuste de hiperparâmetros como a taxa de decaimento (ρ) e o coeficiente de momentum (γ) para um desempenho ideal.
OptimizerAdaDelta(double learning_rate=0.01, double decay_rate=0.95, double gamma=0.9, double epsilon=1e-8);
- Computacionalmente caro: Manter a EMA e incorporar o momentum aumenta ligeiramente o custo computacional em comparação com o SGD.
Onde usar o Adadelta:
O Adadelta pode ser uma alternativa valiosa em certos cenários:
- Gradientes não estacionários. Se o seu problema exibir gradientes não estacionários, a taxa de aprendizado adaptativa com momentum do Adadelta pode ser benéfica.
- Em situações onde escapar de mínimos locais é crucial, o termo de momentum do Adadelta pode ser vantajoso.
Treinei o modelo usando o Adadelta, por 100 épocas, com uma taxa de aprendizado de 0,0001. Tudo foi o mesmo que foi usado em outros otimizadores:
nn.fit(x_train, y_train, new OptimizerAdaDelta(nn_learning_rate), nn_epochs, nn_batch_size, show_batch); Gráfico de Perda vs Época:
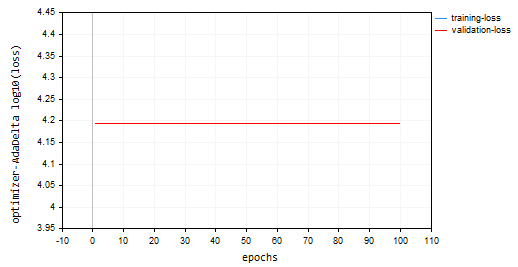
O otimizador Adadelta não conseguiu aprender nada, pois forneceu o mesmo valor de perda de 15625 e uma acurácia de aproximadamente -335 nas amostras de treinamento e validação. Parece que o mesmo aconteceu com o RMSProp.
NP 0 15:32:30.664 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [90/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.062 Seconds ON 0 15:32:30.724 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [91/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds IK 0 15:32:30.788 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [92/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.062 Seconds JQ 0 15:32:30.848 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [93/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds RO 0 15:32:30.914 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [94/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.062 Seconds PE 0 15:32:30.972 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [95/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds CS 0 15:32:31.029 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [96/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.047 Seconds DI 0 15:32:31.086 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [97/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.062 Seconds DG 0 15:32:31.143 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [98/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds FM 0 15:32:31.202 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [99/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.046 Seconds GI 0 15:32:31.258 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [100/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds
05: Nadam: Estimativa de Momento Adaptativa Acelerada por Nesterov
Este algoritmo de otimização combina as forças de dois otimizadores populares: Adam (Estimativa de Momento Adaptativa) e o Momentum de Nesterov. Ele visa alcançar uma convergência mais rápida e potencialmente um desempenho melhor em comparação com o Adam, especialmente em situações com gradientes ruidosos.
Abordagem do Nadam:
Ele herda as funcionalidades principais do Adam:
class OptimizerNadam: protected OptimizerAdam { protected: double m_gamma; public: OptimizerNadam(double learning_rate=0.01, double beta1=0.9, double beta2=0.999, double gamma=0.9, double epsilon=1e-8); ~OptimizerNadam(void); virtual void update(matrix ¶meters, matrix &gradients); }; //+------------------------------------------------------------------+ //| Initializes the Adam optimizer with hyperparameters. | //| | //| learning_rate: Step size for parameter updates | //| beta1: Decay rate for the first moment estimate | //| (moving average of gradients). | //| beta2: Decay rate for the second moment estimate | //| (moving average of squared gradients). | //| epsilon: Small value for numerical stability. | //+------------------------------------------------------------------+ OptimizerNadam::OptimizerNadam(double learning_rate=0.010000, double beta1=0.9, double beta2=0.999, double gamma=0.9, double epsilon=1e-8) :OptimizerAdam(learning_rate, beta1, beta2, epsilon), m_gamma(gamma) { }
Incluindo:
-
Manter EMAs (Médias Móveis Exponenciais): Ele acompanha a EMA dos gradientes quadrados (cache_t) e a EMA dos momentos (m_t), semelhante ao Adam.
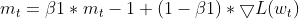
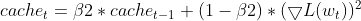
- Cálculos de taxa de aprendizado adaptativa: Com base nessas EMAs, ele calcula uma taxa de aprendizado adaptativa que se ajusta para cada parâmetro.
- Ele incorpora o Momentum de Nesterov: O Nadam adota o conceito de Momentum de Nesterov do SGD com Momentum de Nesterov. Isso envolve:
- Gradiente "Peek": Antes de atualizar o parâmetro com base no gradiente atual, o Nadam estima um gradiente "peek" usando o gradiente atual e o termo de momentum.
- Atualização com Gradiente "Peek": A atualização do parâmetro é então realizada usando esse gradiente "peek", potencialmente levando a uma convergência mais rápida e melhor manejo de gradientes ruidosos.
Matemática por trás do Nadam:
- Atualizando a EMA dos momentos (igual ao Adam)
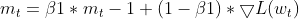
- Atualizando a EMA dos gradientes quadrados (igual ao Adam)
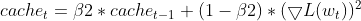
- Correção de viés para momentos (igual ao Adam)
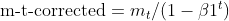
- Correção de viés para gradientes quadrados (igual ao Adam)
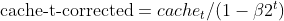
- Momentum de Nesterov (usando a estimativa do gradiente anterior)
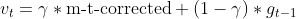
- Atualizar estimativa do gradiente anterior
- Atualizar parâmetro com o Momentum de Nesterov
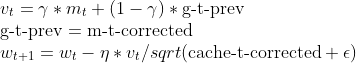
matrix nesterov_moment = m_gamma * moment_hat + (1 - m_gamma) * gradients; // Nesterov accelerated gradient parameters -= m_learning_rate * nesterov_moment / sqrt(cache_hat + m_epsilon); // Update parameters
Vantagens do Nadam:
- É mais rápido: Comparado ao Adam, o Nadam pode potencialmente alcançar uma convergência mais rápida, especialmente para problemas com gradientes ruidosos.
- É melhor em lidar com gradientes ruidosos: O termo de momentum de Nesterov no Nadam pode ajudar a suavizar gradientes ruidosos e levar a um desempenho melhor.
- Ele tem as vantagens do Adam: Mantém os benefícios do Adam, como adaptabilidade e menor sensibilidade à seleção da taxa de aprendizado.
Desvantagens:
- Requer ajuste de hiperparâmetros como taxa de aprendizado, taxas de decaimento e coeficiente de momentum para um desempenho ideal.
- Embora o Nadam mostre potencial, ele pode não superar o Adam em todos os cenários. Mais pesquisas e experimentações são necessárias.
Onde Usar o Nadam?
Pode ser uma ótima alternativa ao Adam em problemas onde há gradientes ruidosos.
Eu chamei o Nadam com parâmetros padrão e a mesma taxa de aprendizado que usamos para todos os otimizadores discutidos anteriormente. Ele ficou em segundo lugar após o Adam, proporcionando aproximadamente 47% de acurácia nos conjuntos de treinamento e validação. O Nadam fez muitas oscilações ao redor do mínimo local em comparação com os outros métodos discutidos neste artigo.
IL 0 15:37:56.549 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [90/100] training -> loss 25.23632476 accuracy 0.466 validation -> loss 25.06902 accuracy 0.462 | Elapsed 0.062 Seconds LK 0 15:37:56.619 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [91/100] training -> loss 24.60851222 accuracy 0.479 validation -> loss 24.44829 accuracy 0.475 | Elapsed 0.078 Seconds RS 0 15:37:56.690 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [92/100] training -> loss 24.68657614 accuracy 0.477 validation -> loss 24.53442 accuracy 0.473 | Elapsed 0.078 Seconds IJ 0 15:37:56.761 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [93/100] training -> loss 24.89495551 accuracy 0.473 validation -> loss 24.73423 accuracy 0.469 | Elapsed 0.063 Seconds GQ 0 15:37:56.832 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [94/100] training -> loss 25.25899364 accuracy 0.465 validation -> loss 25.09940 accuracy 0.461 | Elapsed 0.078 Seconds QI 0 15:37:56.901 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [95/100] training -> loss 25.17698272 accuracy 0.467 validation -> loss 25.01065 accuracy 0.463 | Elapsed 0.063 Seconds FP 0 15:37:56.976 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [96/100] training -> loss 25.36663261 accuracy 0.463 validation -> loss 25.20273 accuracy 0.459 | Elapsed 0.078 Seconds FO 0 15:37:57.056 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [97/100] training -> loss 23.34069092 accuracy 0.506 validation -> loss 23.19590 accuracy 0.502 | Elapsed 0.078 Seconds OG 0 15:37:57.128 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [98/100] training -> loss 23.48894694 accuracy 0.503 validation -> loss 23.33753 accuracy 0.499 | Elapsed 0.078 Seconds ON 0 15:37:57.203 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [99/100] training -> loss 23.03205165 accuracy 0.512 validation -> loss 22.88233 accuracy 0.509 | Elapsed 0.062 Seconds ME 0 15:37:57.275 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [100/100] training -> loss 24.98193438 accuracy 0.471 validation -> loss 24.82652 accuracy 0.467 | Elapsed 0.079 Seconds
Abaixo estava o gráfico de perda vs época:
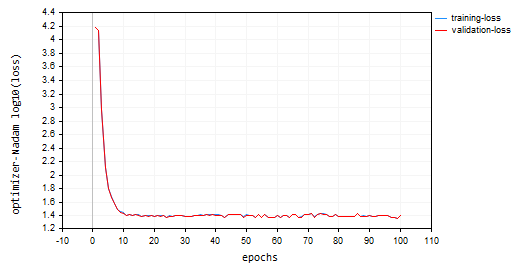
Considerações Finais
A melhor escolha de otimizador depende do seu problema específico, conjunto de dados, arquitetura de rede e parâmetros. A experimentação é fundamental para encontrar o otimizador mais eficaz para sua tarefa de treinamento de rede neural. O Adam prova ser o melhor otimizador para muitas redes neurais devido à sua capacidade de convergir mais rapidamente, ser menos sensível à taxa de aprendizado e adaptar sua taxa de aprendizado com momentum. É uma boa escolha para tentar primeiro, especialmente para problemas complexos ou quando você não tem certeza de qual otimizador usar inicialmente.
Melhores desejos.
Acompanhe o desenvolvimento de modelos de aprendizado de máquina e muito mais discutido nesta série de artigos neste repositório GitHub.
Anexos:
| Arquivo | Descrição/Utilização |
|---|---|
| MatrixExtend.mqh | Contém funções adicionais para manipulação de matrizes. |
| metrics.mqh | Contém funções e código para medir o desempenho de modelos de aprendizado de máquina. |
| preprocessing.mqh | Biblioteca para pré-processamento de dados de entrada brutos para torná-los adequados para uso em modelos de aprendizado de máquina. |
| plots.mqh | Biblioteca para plotar vetores e matrizes |
| optimizers.mqh | Um arquivo Include contendo todos os otimizadores de redes neurais discutidos neste artigo |
| cross_validation.mqh | Uma biblioteca contendo técnicas de validação cruzada |
| Tensors.mqh | Uma biblioteca contendo Tensores, objetos de matrizes algébricas 3D programados em linguagem MQL5 pura |
| Regressor Nets.mqh | Contém redes neurais para resolver um problema de regressão |
| Optimization Algorithms testScript.mq5 | Um script para rodar o código de todos os arquivos Include e o conjunto de dados/Este é o arquivo principal |
| airfoil_noise_data.csv | Dados do problema de regressão Airfoil |
Traduzido do Inglês pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/en/articles/14435
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Desenvolvendo um sistema de Replay (Parte 62): Dando play no serviço (III)
Desenvolvendo um sistema de Replay (Parte 62): Dando play no serviço (III)
 Algoritmos de otimização populacionais: enxame de pássaros (Bird Swarm Algorithm, BSA)
Algoritmos de otimização populacionais: enxame de pássaros (Bird Swarm Algorithm, BSA)
 Processos não estacionários e regressão espúria
Processos não estacionários e regressão espúria
 Desenvolvendo um EA multimoeda (Parte 6): Automatizando a seleção de um grupo de instâncias
Desenvolvendo um EA multimoeda (Parte 6): Automatizando a seleção de um grupo de instâncias
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
O script do artigo apresenta um erro:
2024.11.21 15:09:16.213 Optimisation Algorithms testScript(EURUSD,M1) Zero divide, verifique se o divisor é zero para evitar esse erro em 'D:\Market\MT5\MQL5\Scripts\Optimization Algorithms testScript.ex5'
O problema acabou sendo que o script não encontrou o arquivo com os dados de treinamento. Mas, de qualquer forma, o programa deve lidar com esse caso se o arquivo de dados não for encontrado.
Mas agora existe esse problema:
2024.11.21 17:27:37.038 Optimisation Algorithms testScript (EURUSD,M1) 50 undeleted dynamic objects found:
2024.11.21 17:27:37.038 Algoritmos de otimização testScript (EURUSD,M1) 10 objetos da classe 'CTensors'
2024.11.21 17:21 17:27:37.038 Algoritmos de otimização testScript (EURUSD,M1) 40 objetos da classe 'CMatrix'
2024.11.21 17:27:37.038 Algoritmos de otimização testScript (EURUSD,M1) 14816 bytes de memória vazada encontrados
O problema acabou sendo que o script não encontrou o arquivo de dados para treinamento. Mas, de qualquer forma, o programa deve lidar com esse caso, se o arquivo de dados não for encontrado.
Mas agora existe esse problema:
2024.11.21 17:27:37.038 Optimisation Algorithms testScript (EURUSD,M1) 50 undeleted dynamic objects found:
2024.11.21 17:27:37.038 Algoritmos de otimização testScript (EURUSD,M1) 10 objetos da classe 'CTensors'
2024.11.21 17:21 17:27:37.038 Algoritmos de otimização testScript (EURUSD,M1) 40 objetos da classe 'CMatrix'
2024.11.21 17:27:37.038 Algoritmos de otimização testScript (EURUSD,M1) 14816 bytes de memória vazada encontrados
Isso ocorre porque apenas uma função "fit" deve ser chamada para uma instância de uma classe. Eu chamei várias funções de ajuste, o que resulta na criação de vários tensores na memória, para fins educacionais.
Deveria ser assim;