
Aprendizaje automático y Data Science (Parte 21): Desbloqueando las redes neuronales: desmitificando los algoritmos de optimización
No estoy sugiriendo que las redes neuronales sean fáciles. Hay que ser un experto para que estas cosas funcionen. Pero esa experiencia le sirve para un espectro más amplio de aplicaciones. En cierto sentido, todos los esfuerzos que antes se dedicaban al diseño de características ahora se dedican al diseño de la arquitectura, el diseño de la función de pérdida y el diseño del esquema de optimización. El trabajo manual se ha elevado a un nivel superior de abstracción.
Stefano Soatto
Introducción
Parece que hoy en día todo el mundo está interesado en la Inteligencia Artificial, está en todas partes, y los grandes de la industria tecnológica como Google y Microsoft detrás de OpenAI están impulsando la adaptación de la IA en diferentes aspectos e industrias como el entretenimiento, la industria de la salud, las artes, la creatividad, etc.
Veo esta tendencia también en la comunidad MQL5, ¿por qué no?, con la introducción de matrices y vectores y ONNX en MetaTrader 5. Ahora es posible realizar modelos de negociación con inteligencia artificial de cualquier complejidad. Ni siquiera hace falta ser un experto en álgebra lineal o lo bastante empollón para entender todo lo que entra en el sistema.
A pesar de todo ello, los fundamentos del aprendizaje automático son ahora más difíciles de encontrar que nunca, y sin embargo son tan importantes conociendo para solidificar su comprensión de la IA. Te permiten saber por qué haces lo que haces, lo que te hace flexible y te permite ejercer tus opciones. Hay muchas cosas que aún tenemos que debatir sobre el aprendizaje automático. Hoy veremos cuáles son los algoritmos de optimización, cómo se comportan entre sí, cuándo y qué algoritmo de optimización debe elegir para un mejor rendimiento y precisión de sus redes neuronales.
El contenido tratado en este artículo te ayudará a entender los algoritmos de optimización en general, lo que significa que este conocimiento te servirá incluso cuando trabajes con modelos Scikit-Learn, Tensorflow, o Pytorch desde Python, ya que estos optimizadores son universales para todas las redes neuronales independientemente del lenguaje de programación que utilices.
¿Qué son los optimizadores de redes neuronales?
Por definición, los optimizadores son algoritmos que ajustan los parámetros de las redes neuronales durante el entrenamiento. Su objetivo es minimizar la función de pérdida y, en última instancia, mejorar el rendimiento.
En pocas palabras, los optimizadores de redes neuronales hacen lo siguiente:
- Estos son los parámetros clave que influyen en la red neuronal. Los optimizadores determinan cómo modificar cada parámetro en cada iteración de entrenamiento.
- Los optimizadores miden la discrepancia entre los valores reales y las predicciones de la red neuronal. Se esfuerzan por reducir progresivamente este error.
Te recomiendo leer un artículo anterior, Análisis de redes neuronales con conexión directa, si aún no lo has hecho. En este artículo vamos a mejorar el modelo de red neuronal que construimos desde cero en este artículo, añadiéndole los optimizadores.
Antes de ver cuáles son los diferentes tipos de optimizadores, tenemos que entender los algoritmos de retropropagación. Por lo general, existen tres algoritmos:
- Descenso Gradiente Estocástico (SGD, Stochastic Gradient Descent)
- Descenso Gradual por Lotes (BGD, Batch Gradient Descent)
- Mini-lote de Descenso Gradual
01: Descenso Gradiente Estocástico (SGD, Stochastic Gradient Descent)
El Descenso Gradiente Estocástico (SGD), es un algoritmo de optimización fundamental utilizado para entrenar redes neuronales. Actualiza iterativamente los pesos y sesgos de la red de forma que se minimice la función de pérdida. La función de pérdida mide la discrepancia entre las predicciones de la red y las etiquetas reales (valores objetivo) en los datos de entrenamiento.
Los principales procesos que intervienen en estos algoritmos de optimización son los mismos, e incluyen:
- Iteración
- Retropropagación
- Actualización de pesos y sesgos
Estos algoritmos difieren en cómo se gestionan las iteraciones y con qué frecuencia se actualizan las ponderaciones y los sesgos. El algoritmo SGD (Stochastic Gradient Descent) actualiza los parámetros de la red neuronal (pesos y sesgos) de un ejemplo de entrenamiento (punto de datos) a la vez.
void CRegressorNets::backpropagation(const matrix& x, const vector &y) { for (ulong epoch=0; epoch<epochs && !IsStopped(); epoch++) { for (ulong iter=0; iter<rows; iter++) //iterate through all data points { for (int layer=(int)mlp.hidden_layers-1; layer>=0 && !IsStopped(); layer--) //Loop through the network backward from last to first layer { // find partial derivatives of each layer WRT the loss function dW and dB //--- Weights updates optimizer_weights.update(W, dW); optimizer_bias.update(B, dB); this.W_tensor.Add(W, layer); this.B_tensor.Add(B, layer); } } } }
Ventajas:
- Eficacia informática para grandes conjuntos de datos.
- A veces puede converger más rápido que BGD y el Mini-lote de Descenso Gradual, especialmente para funciones de pérdida no convexas, ya que utiliza una muestra de entrenamiento cada vez.
- Bueno para evitar los mínimos locales: Debido a las actualizaciones ruidosas en SGD, tiene la capacidad de escapar de los mínimos locales y converger a los mínimos globales.
Desventajas:
- Las actualizaciones pueden ser ruidosas, lo que provoca un comportamiento zigzagueante durante el entrenamiento.
- Puede que no siempre converja al mínimo global.
- Convergencia lenta, puede requerir más épocas para converger ya que actualiza los parámetros para cada ejemplo de entrenamiento de uno en uno.
- Sensible a la cotización de aprendizaje: La elección de la tasa de aprendizaje puede ser crítica para este algoritmo, una tasa de aprendizaje más alta puede hacer que el algoritmo sobrepase los mínimos globales, mientras que una tasa de aprendizaje más baja ralentiza el proceso de convergencia.
02: Descenso Gradual por Lotes (BGD, Batch Gradient Descent)
A diferencia del SGD, el Descenso Gradual por Lotes (BGD, Batch Gradient Descent) calcula los gradientes utilizando todo el conjunto de datos en cada iteración.
Ventajas:
En teoría, converge a un mínimo si la función de pérdida es suave y convexa.
Desventajas:
Puede ser costoso desde el punto de vista informático para grandes conjuntos de datos, ya que requiere procesar todo el conjunto de datos repetidamente.
No lo implementaré en la red neuronal que tenemos en este momento, pero se puede implementar fácilmente al igual que el Mini-lote de Descenso Gradual a continuación, puede implementarlo si lo desea.
03: Mini-lote de Descenso Gradual
Este algoritmo es un compromiso entre SGD (Stochastic Gradient Descent) y BGD (Batch Gradient Descent); actualiza los parámetros de la red utilizando un pequeño subconjunto (Mini-lote) de los datos de entrenamiento en cada iteración.
Ventajas:
- Proporciona un buen equilibrio entre eficiencia computacional y estabilidad de actualización en comparación con SGD y BGD.
- Puede manejar conjuntos de datos más grandes con más eficacia que BGD.
Desventajas:
- Puede requerir un mayor ajuste del tamaño del Mini-lote en comparación con SGD.
- Computacionalmente caro en comparación con SGD, consume mucha memoria para el almacenamiento y procesamiento por lotes.
- Puede llevar mucho tiempo entrenar muchos lotes grandes.
A continuación se muestra el pseudocódigo de cómo es el algoritmo:
void CRegressorNets::backpropagation(const matrix& x, const vector &y, OptimizerSGD *sgd, const uint epochs, uint batch_size=0, bool show_batch_progress=false) { //.... for (ulong epoch=0; epoch<epochs && !IsStopped(); epoch++) { for (uint batch=0, batch_start=0, batch_end=batch_size; batch<num_batches; batch++, batch_start+=batch_size, batch_end=(batch_start+batch_size-1)) { matrix batch_x = MatrixExtend::Get(x, batch_start, batch_end-1); vector batch_y = MatrixExtend::Get(y, batch_start, batch_end-1); rows = batch_x.Rows(); for (ulong iter=0; iter<rows ; iter++) //replace to rows { pred_v[0] = predict(batch_x.Row(iter)); actual_v[0] = y[iter]; // Find derivatives WRT weights dW and bias dB //.... //--- Updating the weights using a given optimizer optimizer_weights.update(W, dW); optimizer_bias.update(B, dB); this.Weights_tensor.Add(W, layer); this.Bias_tensor.Add(B, layer); } } } }
En el corazón de estos dos algoritmos por defecto, tienen una regla de actualización de descenso de gradiente simple, que a menudo se conoce como Optimizador SGD o Mini-BGD.
class OptimizerSGD { protected: double m_learning_rate; public: OptimizerSGD(double learning_rate=0.01); ~OptimizerSGD(void); virtual void update(matrix ¶meters, matrix &gradients); }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ OptimizerSGD::OptimizerSGD(double learning_rate=0.01): m_learning_rate(learning_rate) { } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ OptimizerSGD::~OptimizerSGD(void) { } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void OptimizerSGD::update(matrix ¶meters, matrix &gradients) { parameters -= this.m_learning_rate * gradients; //Simple gradient descent update rule } //+------------------------------------------------------------------+ //| Batch Gradient Descent (BGD): This optimizer computes the | //| gradients of the loss function on the entire training dataset | //| and updates the parameters accordingly. It can be slow and | //| memory-intensive for large datasets but tends to provide a | //| stable convergence. | //+------------------------------------------------------------------+ class OptimizerMinBGD: public OptimizerSGD { public: OptimizerMinBGD(double learning_rate=0.01); ~OptimizerMinBGD(void); }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ OptimizerMinBGD::OptimizerMinBGD(double learning_rate=0.010000): OptimizerSGD(learning_rate) { } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ OptimizerMinBGD::~OptimizerMinBGD(void) { }
Ahora vamos a entrenar un modelo utilizando estos dos optimizadores y a observar el resultado para entenderlos mejor:
#include <MALE5\MatrixExtend.mqh> #include <MALE5\preprocessing.mqh> #include <MALE5\metrics.mqh> #include <MALE5\Neural Networks\Regressor Nets.mqh> CRegressorNets *nn; StandardizationScaler scaler; vector open_, high_, low_; vector hidden_layers = {5}; input uint nn_epochs = 100; input double nn_learning_rate = 0.0001; input uint nn_batch_size =32; input bool show_batch = false; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- string headers; matrix dataset = MatrixExtend::ReadCsv("airfoil_noise_data.csv", headers); matrix x_train, x_test; vector y_train, y_test; MatrixExtend::TrainTestSplitMatrices(dataset, x_train, y_train, x_test, y_test, 0.7); nn = new CRegressorNets(hidden_layers, AF_RELU_, LOSS_MSE_); x_train = scaler.fit_transform(x_train); nn.fit(x_train, y_train, new OptimizerMinBGD(nn_learning_rate), nn_epochs, nn_batch_size, show_batch); delete nn; }
Cuando a la entrada nn_batch_size se le asigna un valor mayor que cero, se activará el Mini-lote de Descenso Gradual independientemente del optimizador que se aplique a la función de ajuste/retropropagación.
backprop CRegressorNets::backpropagation(const matrix& x, const vector &y, OptimizerSGD *optimizer, const uint epochs, uint batch_size=0, bool show_batch_progress=false) { //... //... //--- Optimizer use selected optimizer when batch_size ==0 otherwise use the batch gradient descent OptimizerSGD optimizer_weights = optimizer; OptimizerSGD optimizer_bias = optimizer; if (batch_size>0) { OptimizerMinBGD optimizer_weights; OptimizerMinBGD optimizer_bias; } //--- Cross validation CCrossValidation cross_validation; CTensors *cv_tensor; matrix validation_data = MatrixExtend::concatenate(x, y); matrix validation_x; vector validation_y; cv_tensor = cross_validation.KFoldCV(validation_data, 10); //k-fold cross validation | 10 folds selected //--- matrix DELTA = {}; double actual=0, pred=0; matrix temp_inputs ={}; matrix dB = {}; //Bias Derivatives matrix dW = {}; //Weight Derivatives for (ulong epoch=0; epoch<epochs && !IsStopped(); epoch++) { double epoch_start = GetTickCount(); uint num_batches = (uint)MathFloor(x.Rows()/(batch_size+DBL_EPSILON)); vector batch_loss(num_batches), batch_accuracy(num_batches); vector actual_v(1), pred_v(1), LossGradient = {}; if (batch_size==0) //Stochastic Gradient Descent { for (ulong iter=0; iter<rows; iter++) //iterate through all data points { pred = predict(x.Row(iter)); actual = y[iter]; pred_v[0] = pred; actual_v[0] = actual; //--- DELTA.Resize(mlp.outputs,1); for (int layer=(int)mlp.hidden_layers-1; layer>=0 && !IsStopped(); layer--) //Loop through the network backward from last to first layer { //..... backpropagation and finding derivatives code //-- Observation | DeLTA matrix is same size as the bias matrix W = this.Weights_tensor.Get(layer); B = this.Bias_tensor.Get(layer); //--- Derivatives wrt weights and bias dB = DELTA; dW = DELTA.MatMul(temp_inputs.Transpose()); //--- Weights updates optimizer_weights.update(W, dW); optimizer_bias.update(B, dB); this.Weights_tensor.Add(W, layer); this.Bias_tensor.Add(B, layer); } } } else //Batch Gradient Descent { for (uint batch=0, batch_start=0, batch_end=batch_size; batch<num_batches; batch++, batch_start+=batch_size, batch_end=(batch_start+batch_size-1)) { matrix batch_x = MatrixExtend::Get(x, batch_start, batch_end-1); vector batch_y = MatrixExtend::Get(y, batch_start, batch_end-1); rows = batch_x.Rows(); for (ulong iter=0; iter<rows ; iter++) //iterate through all data points { pred_v[0] = predict(batch_x.Row(iter)); actual_v[0] = y[iter]; //--- DELTA.Resize(mlp.outputs,1); for (int layer=(int)mlp.hidden_layers-1; layer>=0 && !IsStopped(); layer--) //Loop through the network backward from last to first layer { //..... backpropagation and finding derivatives code } //-- Observation | DeLTA matrix is same size as the bias matrix W = this.Weights_tensor.Get(layer); B = this.Bias_tensor.Get(layer); //--- Derivatives wrt weights and bias dB = DELTA; dW = DELTA.MatMul(temp_inputs.Transpose()); //--- Weights updates optimizer_weights.update(W, dW); optimizer_bias.update(B, dB); this.Weights_tensor.Add(W, layer); this.Bias_tensor.Add(B, layer); } } pred_v = predict(batch_x); batch_loss[batch] = pred_v.Loss(batch_y, ENUM_LOSS_FUNCTION(m_loss_function)); batch_loss[batch] = MathIsValidNumber(batch_loss[batch]) ? (batch_loss[batch]>1e6 ? 1e6 : batch_loss[batch]) : 1e6; //Check for nan and return some large value if it is nan batch_accuracy[batch] = Metrics::r_squared(batch_y, pred_v); if (show_batch_progress) printf("----> batch[%d/%d] batch-loss %.5f accuracy %.3f",batch+1,num_batches,batch_loss[batch], batch_accuracy[batch]); } } //--- End of an epoch vector validation_loss(cv_tensor.SIZE); vector validation_acc(cv_tensor.SIZE); for (ulong i=0; i<cv_tensor.SIZE; i++) { validation_data = cv_tensor.Get(i); MatrixExtend::XandYSplitMatrices(validation_data, validation_x, validation_y); vector val_preds = this.predict(validation_x);; validation_loss[i] = val_preds.Loss(validation_y, ENUM_LOSS_FUNCTION(m_loss_function)); validation_acc[i] = Metrics::r_squared(validation_y, val_preds); } pred_v = this.predict(x); if (batch_size==0) { backprop_struct.training_loss[epoch] = pred_v.Loss(y, ENUM_LOSS_FUNCTION(m_loss_function)); backprop_struct.training_loss[epoch] = MathIsValidNumber(backprop_struct.training_loss[epoch]) ? (backprop_struct.training_loss[epoch]>1e6 ? 1e6 : backprop_struct.training_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan backprop_struct.validation_loss[epoch] = validation_loss.Mean(); backprop_struct.validation_loss[epoch] = MathIsValidNumber(backprop_struct.validation_loss[epoch]) ? (backprop_struct.validation_loss[epoch]>1e6 ? 1e6 : backprop_struct.validation_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan } else { backprop_struct.training_loss[epoch] = batch_loss.Mean(); backprop_struct.training_loss[epoch] = MathIsValidNumber(backprop_struct.training_loss[epoch]) ? (backprop_struct.training_loss[epoch]>1e6 ? 1e6 : backprop_struct.training_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan backprop_struct.validation_loss[epoch] = validation_loss.Mean(); backprop_struct.validation_loss[epoch] = MathIsValidNumber(backprop_struct.validation_loss[epoch]) ? (backprop_struct.validation_loss[epoch]>1e6 ? 1e6 : backprop_struct.validation_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan } double epoch_stop = GetTickCount(); printf("--> Epoch [%d/%d] training -> loss %.8f accuracy %.3f validation -> loss %.5f accuracy %.3f | Elapsed %s ",epoch+1,epochs,backprop_struct.training_loss[epoch],Metrics::r_squared(y, pred_v),backprop_struct.validation_loss[epoch],validation_acc.Mean(),this.ConvertTime((epoch_stop-epoch_start)/1000.0)); } isBackProp = false; if (CheckPointer(optimizer)!=POINTER_INVALID) delete optimizer; return backprop_struct; }
Resultados:
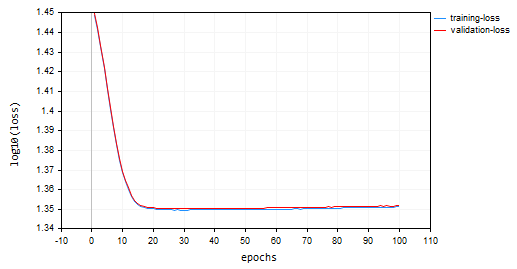
Descenso de Gradiente Estocástico (SGD): Tasa de aprendizaje = 0.0001
Descenso de Gradiente por Lotes (BGD): Tasa de aprendizaje = 0.0001, Tamaño del lote = 16
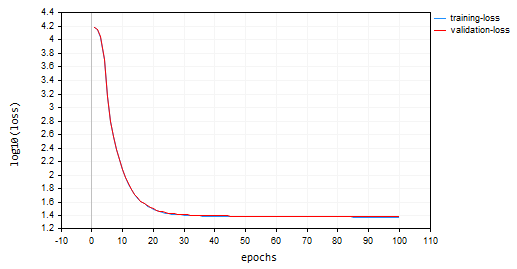
SGD convergió más rápido, acercándose a un mínimo local alrededor de la décima época, mientras que BGD lo hizo alrededor de la vigésima época. SGD alcanzó aproximadamente un 60% de precisión tanto en el entrenamiento como en la validación, mientras que BGD obtuvo una precisión del 15% en la muestra de entrenamiento y del 13% en la muestra de validación. Todavía no podemos llegar a una conclusión, ya que no estamos seguros de que el BGD tenga la mejor cotización de aprendizaje y el tamaño de lote adecuado para este conjunto de datos. Diferentes optimizadores funcionan mejor con diferentes tasas de aprendizaje. Esta puede ser una de las causas de que SGD no rinda. Sin embargo, convergió bien sin oscilar en torno a los mínimos locales, algo que no puede observarse en SGD, el gráfico de BGD es suave lo que indica un proceso de entrenamiento estable esto se debe a que en BGD la pérdida global es el promedio de las pérdidas en lotes individuales.
backprop_struct.training_loss[epoch] = batch_loss.Mean(); backprop_struct.training_loss[epoch] = MathIsValidNumber(backprop_struct.training_loss[epoch]) ? (backprop_struct.training_loss[epoch]>1e6 ? 1e6 : backprop_struct.training_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan backprop_struct.validation_loss[epoch] = validation_loss.Mean(); backprop_struct.validation_loss[epoch] = MathIsValidNumber(backprop_struct.validation_loss[epoch]) ? (backprop_struct.validation_loss[epoch]>1e6 ? 1e6 : backprop_struct.validation_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan
Es posible que hayas notado en los gráficos que se ha aplicado la función log10 a los valores de la pérdida para el gráfico. Esta normalización garantiza que los valores de pérdida estén bien representados, ya que en las primeras épocas los valores de pérdida pueden ser a veces mayores. El objetivo es penalizar los valores más grandes para que queden bien en un gráfico. Los valores reales de la pérdida se pueden ver en la pestaña de expertos y no en el gráfico.
void CRegressorNets::fit(const matrix &x, const vector &y, OptimizerSGD *optimizer, const uint epochs, uint batch_size=0, bool show_batch_progress=false) { trained = true; //The fit method has been called vector epochs_vector(epochs); for (uint i=0; i<epochs; i++) epochs_vector[i] = i+1; backprop backprop_struct; backprop_struct = this.backpropagation(x, y, optimizer, epochs, batch_size, show_batch_progress); //Run backpropagation CPlots plt; backprop_struct.training_loss = log10(backprop_struct.training_loss); //Logarithmic scalling plt.Plot("Loss vs Epochs",epochs_vector,backprop_struct.training_loss,"epochs","log10(loss)","training-loss",CURVE_LINES); backprop_struct.validation_loss = log10(backprop_struct.validation_loss); plt.AddPlot(backprop_struct.validation_loss,"validation-loss",clrRed); while (MessageBox("Close or Cancel Loss Vs Epoch plot to proceed","Training progress",MB_OK)<0) Sleep(1); isBackProp = false; }
El optimizador SGD es una herramienta general para minimizar funciones de pérdida, mientras que el algoritmo SGD para retropropagación es una técnica específica dentro de SGD adaptada para calcular gradientes en redes neuronales.
Piense en el optimizador SGD como el carpintero y en los algoritmos SGD o Mini-BGD para la retropropagación como una herramienta especializada de su caja de herramientas.
Tipos de optimizadores de redes neuronales
Aparte de los optimizadores SGD que acabamos de comentar. Existen otros optimizadores de redes neuronales, cada uno de los cuales emplea distintas estrategias para alcanzar los valores óptimos de los parámetros. A continuación se indican algunos de los optimizadores de redes neuronales más utilizados:
- Propagación Media Cuadrática (RMSProp, Root Mean Square Propagation)
- Descenso Gradual Adaptativo (AdaGrad, Adaptive Gradient Descent)
- Estimación Adaptativa del Momento (Adam, Adaptive Moment Estimation)
- Adadelta (Aprendizaje Adaptativo con Delta)
- Estimación Adaptativa del Momento Acelerada de Nesterov (Nadam, Nesterov-Accelerated Adaptive Moment Estimation)
01: Propagación Media Cuadrática (RMSProp, Root Mean Square Propagation)
Este algoritmo de optimización pretende abordar las limitaciones del Descenso Gradiente Estocástico (SGD) adaptando la cotización de aprendizaje para cada parámetro de peso y sesgo basándose en sus gradientes históricos.
Problemas con SGD:
SGD actualiza los pesos y los sesgos utilizando el gradiente actual y una cotización fija de aprendizaje. Sin embargo, en funciones complejas como las redes neuronales, la magnitud de los gradientes puede variar significativamente para distintos parámetros. Esto puede llevar a una convergencia lenta ya que los parámetros con gradientes pequeños podrían actualizarse muy lentamente, dificultando el aprendizaje general. Además, SGD puede causar grandes oscilaciones ya que los parámetros con gradientes grandes podrían experimentar fluctuaciones excesivas durante las actualizaciones, haciendo que el proceso de aprendizaje sea inestable.Teoría:
Esta es la idea central de RMSprop:
- Mantener una media móvil exponencial (EMA) de gradientes al cuadrado. Para cada parámetro, RMSprop rastrea una media exponencialmente decreciente de los gradientes al cuadrado. Esta media refleja el historial reciente de cuánto debe actualizarse el parámetro.
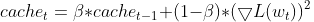
- Normalizar el gradiente. El gradiente actual de cada parámetro se divide por la raíz cuadrada de la EMA de gradientes al cuadrado, junto con un pequeño término de suavizado (normalmente denotado por ε) para evitar la división por cero.
- Actualiza el parámetro. El gradiente normalizado se multiplica por la cotización de aprendizaje para determinar la actualización del parámetro.
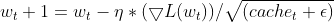
Donde:
![]() EMA de los gradientes al cuadrado en el paso de tiempo 't'
EMA de los gradientes al cuadrado en el paso de tiempo 't'
![]() Cotización (Hiperparámetro. Normalmente entre 0.9 y 0.999.): Controla la influencia de los gradientes anteriores.
Cotización (Hiperparámetro. Normalmente entre 0.9 y 0.999.): Controla la influencia de los gradientes anteriores.
![]() Gradiente de la función de pérdida con respecto al parámetro 'w' en el paso de tiempo 't'
Gradiente de la función de pérdida con respecto al parámetro 'w' en el paso de tiempo 't'
![]() Valor del parámetro en el paso temporal 't'
Valor del parámetro en el paso temporal 't'
![]() Valor actualizado del parámetro en el paso temporal 't+1'
Valor actualizado del parámetro en el paso temporal 't+1'
η: Cotización de aprendizaje (hiperparámetro)
ε: Término de suavizado (normalmente un valor pequeño como 1e-8)
class OptimizerRMSprop { protected: double m_learning_rate; double m_decay_rate; double m_epsilon; matrix<double> cache; //Dividing double/matrix causes compilation error | this is the fix to the issue matrix divide(const double numerator, const matrix &denominator) { matrix res = denominator; for (ulong i=0; i<denominator.Rows(); i++) res.Row(numerator / denominator.Row(i), i); return res; } public: OptimizerRMSprop(double learning_rate=0.01, double decay_rate=0.9, double epsilon=1e-8); ~OptimizerRMSprop(void); virtual void update(matrix& parameters, matrix& gradients); }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ OptimizerRMSprop::OptimizerRMSprop(double learning_rate=0.01, double decay_rate=0.9, double epsilon=1e-8): m_learning_rate(learning_rate), m_decay_rate(decay_rate), m_epsilon(epsilon) { } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ OptimizerRMSprop::~OptimizerRMSprop(void) { } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void OptimizerRMSprop::update(matrix ¶meters,matrix &gradients) { if (cache.Rows()!=parameters.Rows() || cache.Cols()!=parameters.Cols()) { cache.Init(parameters.Rows(), parameters.Cols()); cache.Fill(0.0); } //--- cache += m_decay_rate * cache + (1 - m_decay_rate) * MathPow(gradients, 2); parameters -= divide(m_learning_rate, cache + m_epsilon) * gradients; }
Optando por 100 épocas y 0.0001, los mismos valores predeterminados utilizados para los optimizadores anteriores. La red neuronal no logró converger en 100 épocas, ya que proporcionó una precisión de aproximadamente -319 en las muestras de entrenamiento y -324 en las muestras de validación, respectivamente. Parece que podría necesitar más de 1000 épocas a su ritmo, suponiendo que no sobrepasemos el mínimo local con ese gran número de épocas.
HK 0 15:10:15.632 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [90/100] training -> loss 15164.85487215 accuracy -320.064 validation -> loss 15164.99272 accuracy -325.349 | Elapsed 0.031 Seconds HQ 0 15:10:15.663 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [91/100] training -> loss 15161.78717397 accuracy -319.999 validation -> loss 15161.92323 accuracy -325.283 | Elapsed 0.031 Seconds DO 0 15:10:15.694 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [92/100] training -> loss 15158.07142844 accuracy -319.921 validation -> loss 15158.20512 accuracy -325.203 | Elapsed 0.031 Seconds GE 0 15:10:15.727 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [93/100] training -> loss 15154.92004326 accuracy -319.854 validation -> loss 15155.05184 accuracy -325.135 | Elapsed 0.032 Seconds GS 0 15:10:15.760 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [94/100] training -> loss 15151.84229952 accuracy -319.789 validation -> loss 15151.97226 accuracy -325.069 | Elapsed 0.031 Seconds DH 0 15:10:15.796 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [95/100] training -> loss 15148.77653633 accuracy -319.724 validation -> loss 15148.90466 accuracy -325.003 | Elapsed 0.031 Seconds MF 0 15:10:15.831 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [96/100] training -> loss 15145.56414236 accuracy -319.656 validation -> loss 15145.69033 accuracy -324.934 | Elapsed 0.047 Seconds IL 0 15:10:15.869 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [97/100] training -> loss 15141.85430749 accuracy -319.577 validation -> loss 15141.97859 accuracy -324.854 | Elapsed 0.031 Seconds KJ 0 15:10:15.906 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [98/100] training -> loss 15138.40751503 accuracy -319.504 validation -> loss 15138.52969 accuracy -324.780 | Elapsed 0.032 Seconds PP 0 15:10:15.942 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [99/100] training -> loss 15135.31136641 accuracy -319.439 validation -> loss 15135.43169 accuracy -324.713 | Elapsed 0.046 Seconds NM 0 15:10:15.975 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [100/100] training -> loss 15131.73032246 accuracy -319.363 validation -> loss 15131.84854 accuracy -324.636 | Elapsed 0.032 Seconds
Gráfico de pérdidas frente a épocas: 100 Épocas, 0.0001 de cotización de aprendizaje.
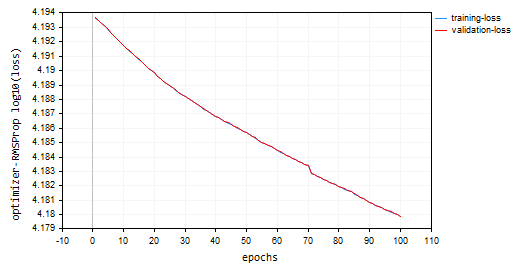
¿Dónde utilizar RMSProp?
Bueno para objetivos no estacionarios, gradientes dispersos, más simple que Adam.
02: Descenso Gradual Adaptativo (AdaGrad, Adaptive Gradient Descent)
AdaGrad es un optimizador para redes neuronales que utiliza una cotización de aprendizaje adaptativa similar a RMSProp. Sin embargo, AdaGrad y RMSProp tienen algunas diferencias clave en su enfoque.
Matemáticas por detrás:
- Acumula Gradientes Pasados. AdaGrad realiza un seguimiento de la suma de gradientes al cuadrado para cada parámetro a lo largo del proceso de entrenamiento. Este valor acumulado refleja cuánto se ha actualizado un parámetro en el pasado.
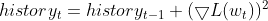
cache += MathPow(gradients, 2);
- Normaliza el gradiente. El gradiente actual de cada parámetro se divide por la raíz cuadrada de la suma acumulada de gradientes al cuadrado, junto con un pequeño término de suavizado (normalmente denotado por ε) para evitar la división por cero.
- Actualizar el parámetro. El gradiente normalizado se multiplica por la cotización de aprendizaje para determinar la actualización del parámetro.
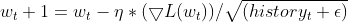
parameters -= divide(this.m_learning_rate, MathSqrt(cache + this.m_epsilon)) * gradients;
nn_learning_rate = 0.0001, épocas = 100
nn.fit(x_train, y_train, new OptimizerAdaGrad(nn_learning_rate), nn_epochs, nn_batch_size, show_batch); Gráfico de pérdidas frente a épocas:
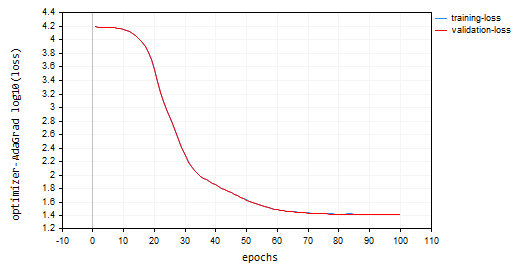
AdaGrad tuvo una curva de aprendizaje más pronunciada y fue muy estable durante las actualizaciones, pero necesitó más de 100 épocas para converger, ya que terminó con una precisión aproximada del 44% tanto en las muestras de entrenamiento como en las de validación, respectivamente.
RK 0 15:15:52.202 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [90/100] training -> loss 26.22261537 accuracy 0.445 validation -> loss 26.13118 accuracy 0.440 | Elapsed 0.031 Seconds ER 0 15:15:52.239 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [91/100] training -> loss 26.12443561 accuracy 0.447 validation -> loss 26.03635 accuracy 0.442 | Elapsed 0.047 Seconds NJ 0 15:15:52.277 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [92/100] training -> loss 26.11449352 accuracy 0.447 validation -> loss 26.02561 accuracy 0.442 | Elapsed 0.032 Seconds IQ 0 15:15:52.316 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [93/100] training -> loss 26.09263184 accuracy 0.448 validation -> loss 26.00461 accuracy 0.443 | Elapsed 0.046 Seconds NH 0 15:15:52.354 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [94/100] training -> loss 26.14277865 accuracy 0.447 validation -> loss 26.05529 accuracy 0.442 | Elapsed 0.032 Seconds HP 0 15:15:52.393 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [95/100] training -> loss 26.09559950 accuracy 0.448 validation -> loss 26.00845 accuracy 0.443 | Elapsed 0.047 Seconds PO 0 15:15:52.442 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [96/100] training -> loss 26.05409769 accuracy 0.448 validation -> loss 25.96754 accuracy 0.443 | Elapsed 0.046 Seconds PG 0 15:15:52.479 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [97/100] training -> loss 25.98822082 accuracy 0.450 validation -> loss 25.90384 accuracy 0.445 | Elapsed 0.032 Seconds PN 0 15:15:52.519 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [98/100] training -> loss 25.98781231 accuracy 0.450 validation -> loss 25.90438 accuracy 0.445 | Elapsed 0.047 Seconds EE 0 15:15:52.559 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [99/100] training -> loss 25.91146212 accuracy 0.451 validation -> loss 25.83083 accuracy 0.446 | Elapsed 0.031 Seconds CN 0 15:15:52.595 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [100/100] training -> loss 25.87412572 accuracy 0.452 validation -> loss 25.79453 accuracy 0.447 | Elapsed 0.047 Seconds
Ventajas de AdaGrad:
Converge más rápido para características dispersas. En situaciones en las que muchos parámetros se actualizan con poca frecuencia debido a las características dispersas de los datos, AdaGrad puede reducir eficazmente sus cotizaciones de aprendizaje, lo que permite una convergencia más rápida para esos parámetros.
Limitaciones de AdaGrad:
Con el tiempo, la suma acumulada de gradientes al cuadrado en AdaGrad sigue creciendo, lo que provoca una disminución continua de las cotizaciones de aprendizaje de todos los parámetros. Esto puede llegar a paralizar el progreso del entrenamiento.
Cuándo utilizar AdaGrad:
En conjuntos de datos de características dispersas: Cuando se trata de conjuntos de datos en los que muchas características tienen actualizaciones poco frecuentes, AdaGrad puede ser eficaz para acelerar la convergencia de esos parámetros.
Durante las primeras fases del entrenamiento: En algunos escenarios, los ajustes iniciales de la cotización de aprendizaje por AdaGrad pueden ser útiles antes de cambiar a otro optimizador más adelante en el entrenamiento.
03: Estimación Adaptativa del Momento (Adam, Adaptive Moment Estimation)
Un algoritmo de optimización muy eficaz y ampliamente utilizado en el entrenamiento de redes neuronales. Combina los puntos fuertes de AdaGrad y RMSProp para hacer frente a sus limitaciones y ofrece un aprendizaje eficaz y estable.
Teoría:
Adam tiene dos características clave:
- Media móvil exponencial (EMA) de gradientes: De forma similar a RMSProp, Adam mantiene una EMA de los gradientes al cuadrado (caché) para capturar el historial reciente de actualizaciones necesarias para cada parámetro.
- Media móvil exponencial de momentos: Adam introduce otra EMA (momento), que sigue la media móvil de los propios gradientes. Esto ayuda a mitigar el problema de la desaparición de gradientes que puede producirse en algunas arquitecturas de red.
Normalización y actualización:
- Actualización de momentos: El gradiente actual se utiliza para actualizar el EMA de momentos (m_t).
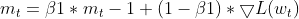
this.moment = this.m_beta1 * this.moment + (1 - this.m_beta1) * gradients;
- Actualización del gradiente al cuadrado: El gradiente al cuadrado actual se utiliza para actualizar el EMA de gradientes al cuadrado (cache_t).
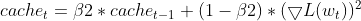
this.cache = this.m_beta2 * this.cache + (1 - this.m_beta2) * MathPow(gradients, 2);
- Corrección del sesgo: Ambas EMAs (moment_t y cache_t) se corrigen de sesgo utilizando factores de decaimiento exponencial (β1 y β2) para asegurar que son estimaciones insesgadas de los momentos verdaderos.
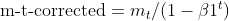
matrix moment_hat = this.moment / (1 - MathPow(this.m_beta1, this.time_step));
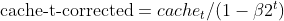
matrix cache_hat = this.cache / (1 - MathPow(this.m_beta2, this.time_step));
- Normalización: De forma similar a RMSProp, el gradiente actual se normaliza utilizando las EMA corregidas y un pequeño término de suavizado (ε).
- Actualización de parámetros: El gradiente normalizado se multiplica por la cotización de aprendizaje (η) para determinar la actualización del parámetro.
parameters -= (this.m_learning_rate * moment_hat) / (MathPow(cache_hat, 0.5) + this.m_epsilon);
Este es el aspecto del constructor del optimizador Adam:
OptimizerAdam(double learning_rate=0.01, double beta1=0.9, double beta2=0.999, double epsilon=1e-8);
Lo llamé con la cotización de aprendizaje:
nn.fit(x_train, y_train, new OptimizerAdam(nn_learning_rate), nn_epochs, nn_batch_size, show_batch); El gráfico resultante de Pérdidas frente a Épocas:
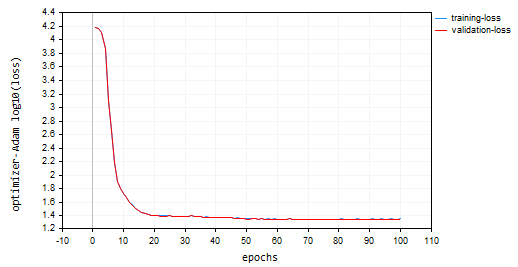
Adam obtuvo mejores resultados que los optimizadores anteriores, aparte de SGD, proporcionando una precisión aproximada del 53% y el 52% en las muestras de entrenamiento y validación, respectivamente.
MD 0 15:23:37.651 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [90/100] training -> loss 22.05051037 accuracy 0.533 validation -> loss 21.92528 accuracy 0.529 | Elapsed 0.047 Seconds DS 0 15:23:37.703 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [91/100] training -> loss 22.38393234 accuracy 0.526 validation -> loss 22.25178 accuracy 0.522 | Elapsed 0.046 Seconds OK 0 15:23:37.756 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [92/100] training -> loss 22.12091827 accuracy 0.532 validation -> loss 21.99456 accuracy 0.528 | Elapsed 0.063 Seconds OR 0 15:23:37.808 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [93/100] training -> loss 21.94438889 accuracy 0.535 validation -> loss 21.81944 accuracy 0.532 | Elapsed 0.047 Seconds NI 0 15:23:37.862 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [94/100] training -> loss 22.41965082 accuracy 0.525 validation -> loss 22.28371 accuracy 0.522 | Elapsed 0.062 Seconds LQ 0 15:23:37.915 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [95/100] training -> loss 22.27254037 accuracy 0.528 validation -> loss 22.13931 accuracy 0.525 | Elapsed 0.047 Seconds FH 0 15:23:37.969 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [96/100] training -> loss 21.93193893 accuracy 0.536 validation -> loss 21.80427 accuracy 0.532 | Elapsed 0.047 Seconds LG 0 15:23:38.024 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [97/100] training -> loss 22.41523220 accuracy 0.525 validation -> loss 22.27900 accuracy 0.522 | Elapsed 0.063 Seconds MO 0 15:23:38.077 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [98/100] training -> loss 22.23551304 accuracy 0.529 validation -> loss 22.10466 accuracy 0.526 | Elapsed 0.046 Seconds QF 0 15:23:38.129 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [99/100] training -> loss 21.96662717 accuracy 0.535 validation -> loss 21.84087 accuracy 0.531 | Elapsed 0.063 Seconds GM 0 15:23:38.191 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [100/100] training -> loss 22.29715377 accuracy 0.528 validation -> loss 22.16686 accuracy 0.524 | Elapsed 0.062 Seconds
Ventajas de Adam:
- Converge más rápido: Adam suele converger más rápido que SGD y puede ser más eficiente que RMSProp en varios escenarios.
- Menos sensible a la cotización: En comparación con SGD, Adam es menos sensible a la elección de la cotización de aprendizaje, por lo que es más robusto.
- Adecuado para funciones de pérdida no convexas: Puede manejar eficazmente funciones de pérdida no convexas comunes en tareas de aprendizaje profundo.
- Amplia aplicabilidad: La combinación de características de Adam lo convierte en un optimizador ampliamente aplicable a diversas arquitecturas de red y conjuntos de datos.
Desventajas:
- Ajuste de hiperparámetros: Aunque por lo general es menos sensible, Adam aún requiere el ajuste de hiperparámetros como la cotización de aprendizaje y las tasas de decaimiento para un rendimiento óptimo.
- Consumo de memoria: El mantenimiento de las EMA puede suponer un consumo de memoria ligeramente superior en comparación con SGD.
¿Dónde utilizar Adam?
Utiliza Adam (Estimación de Momento Adaptativo) para el entrenamiento de tu red neuronal cuando desees:
Una convergencia más rápida. Quieres que tu red sea menos sensible a la tasa de aprendizaje y que tenga una tasa de aprendizaje adaptativa con impulso.
04: Adadelta (Aprendizaje Adaptativo con Delta)
Este es otro algoritmo de optimización utilizado en redes neuronales, comparte algunas similitudes con SGD y RMSProp ofreciendo una cotización de aprendizaje adaptable con un término de impulso específico.
Adadelta pretende hacer frente a la cotización fija del SGD, que provoca una convergencia lenta y oscilaciones. Emplea una cotización de aprendizaje adaptable que se ajusta en función de los gradientes al cuadrado pasados, similar a RMSProp.
Matemáticas detrás:
- Mantener una media móvil exponencial (EMA) de los deltas al cuadrado, Adadelta calcula una EMA de las diferencias al cuadrado entre las actualizaciones consecutivas de los parámetros (deltas) para cada parámetro. Esto refleja la historia reciente de lo mucho que ha cambiado el parámetro.
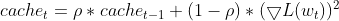
this.cache = m_decay_rate * this.cache + (1 - m_decay_rate) * MathPow(gradients, 2);
- Cotización de aprendizaje adaptativo: El gradiente actual al cuadrado de un parámetro se divide por el EMA de deltas al cuadrado (con un término de suavizado). Se trata de una cotización adaptativa que controla el tamaño de la actualización de cada parámetro.
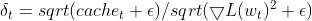
matrix delta = lr * sqrt(this.cache + m_epsilon) / sqrt(pow(gradients, 2) + m_epsilon);
-
Momento: Adadelta incorpora un término de momento que considera la actualización anterior del parámetro, similar al SGD con momento. Esto ayuda a acumular gradientes y a escapar potencialmente de los mínimos locales.
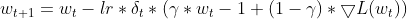
matrix momentum_term = this.m_gamma * parameters + (1 - this.m_gamma) * gradients; parameters -= delta * momentum_term;
Donde:
![]() : EMA de los deltas al cuadrado en el paso temporal 't'
: EMA de los deltas al cuadrado en el paso temporal 't'
![]() : Cotización (Hiperparámetro, normalmente entre 0.9 y 0.999)
: Cotización (Hiperparámetro, normalmente entre 0.9 y 0.999)
![]() : Gradiente de la función de pérdida con respecto al parámetro 'w' en el paso de tiempo 't'
: Gradiente de la función de pérdida con respecto al parámetro 'w' en el paso de tiempo 't'
![]() : Valor del parámetro en el paso de tiempo 't'
: Valor del parámetro en el paso de tiempo 't'
![]() : Valor actualizado del parámetro en el paso temporal 't+1'
: Valor actualizado del parámetro en el paso temporal 't+1'
ε: Término de suavizado (normalmente un valor pequeño como 1e-8)
γ: Coeficiente de momento (Hiperparámetro, normalmente entre 0 y 1)
Ventajas de Adadelta:
- Converge más rápido: En comparación con SGD con una cotización fija de aprendizaje, Adadelta a menudo puede converger más rápido, especialmente para problemas con gradientes no estacionarios.
- Utiliza el impulso para escapar de los mínimos locales: El término impulso ayuda a acumular gradientes y a escapar potencialmente de los mínimos locales en la función de pérdida.
- Menos sensible a la cotización: Al igual que RMSProp, Adadelta es menos sensible a la cotización de aprendizaje elegida que SGD.
Desventajas de Adadelta:
- Requiere el ajuste de hiperparámetros como la cotización de decaimiento (ρ) y el coeficiente de impulso (γ) para un rendimiento óptimo.
OptimizerAdaDelta(double learning_rate=0.01, double decay_rate=0.95, double gamma=0.9, double epsilon=1e-8);
- Costes computacionales elevados: Mantener el EMA e incorporar el impulso aumenta ligeramente el coste computacional en comparación con SGD.
Dónde utilizar Adadelta:
Adadelta puede ser una alternativa valiosa en determinados escenarios:
- Gradientes no estacionarios. Si su problema presenta gradientes no estacionarios, la cotización de aprendizaje adaptativo con impulso de Adadelta puede ser beneficiosa.
- En situaciones en las que escapar de los mínimos locales es crucial, el término de impulso de Adadelta puede resultar ventajoso.
He entrenado el modelo usando Adadelta, para 100 épocas, 0.0001 de cotización de aprendizaje. Todo era igual que en otros optimizadores:
nn.fit(x_train, y_train, new OptimizerAdaDelta(nn_learning_rate), nn_epochs, nn_batch_size, show_batch); Gráfico de pérdidas frente a épocas:
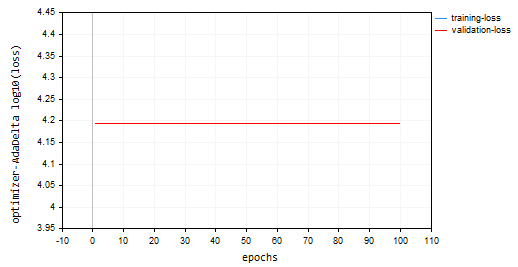
El optimizador Adadelta no logró aprender nada, ya que proporcionó el mismo valor de pérdida de 15625 y una precisión de aproximadamente -335 en las muestras de entrenamiento y validación. Parece similar a lo que ocurrió con RMSProp.
NP 0 15:32:30.664 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [90/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.062 Seconds ON 0 15:32:30.724 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [91/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds IK 0 15:32:30.788 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [92/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.062 Seconds JQ 0 15:32:30.848 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [93/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds RO 0 15:32:30.914 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [94/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.062 Seconds PE 0 15:32:30.972 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [95/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds CS 0 15:32:31.029 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [96/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.047 Seconds DI 0 15:32:31.086 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [97/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.062 Seconds DG 0 15:32:31.143 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [98/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds FM 0 15:32:31.202 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [99/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.046 Seconds GI 0 15:32:31.258 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [100/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds
05: Estimación Adaptativa del Momento Acelerada de Nesterov (Nadam, Nesterov-Accelerated Adaptive Moment Estimation)
Este algoritmo de optimización combina los puntos fuertes de dos populares optimizadores: Adam (Adaptive Moment Estimation) y Nesterov Momentum. Su objetivo es lograr una convergencia más rápida y un rendimiento potencialmente mejor en comparación con Adam, especialmente en situaciones con gradientes ruidosos.
Enfoque de Nadam:
Hereda las funciones básicas de Adam:
class OptimizerNadam: protected OptimizerAdam { protected: double m_gamma; public: OptimizerNadam(double learning_rate=0.01, double beta1=0.9, double beta2=0.999, double gamma=0.9, double epsilon=1e-8); ~OptimizerNadam(void); virtual void update(matrix ¶meters, matrix &gradients); }; //+------------------------------------------------------------------+ //| Initializes the Adam optimizer with hyperparameters. | //| | //| learning_rate: Step size for parameter updates | //| beta1: Decay rate for the first moment estimate | //| (moving average of gradients). | //| beta2: Decay rate for the second moment estimate | //| (moving average of squared gradients). | //| epsilon: Small value for numerical stability. | //+------------------------------------------------------------------+ OptimizerNadam::OptimizerNadam(double learning_rate=0.010000, double beta1=0.9, double beta2=0.999, double gamma=0.9, double epsilon=1e-8) :OptimizerAdam(learning_rate, beta1, beta2, epsilon), m_gamma(gamma) { }
Incluyendo:
-
Seguimiento de las EMA (medias móviles exponenciales): Realiza el seguimiento de la EMA de gradientes al cuadrado (cache_t) y la EMA de momentos (m_t), de forma similar a Adam.
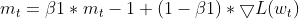
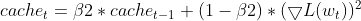
- Cálculos de la cotización de aprendizaje adaptativo: A partir de estas EMA, calcula una cotización de aprendizaje adaptativa que se ajusta para cada parámetro.
- Incorpora el 'Nesterov Momentum': Nadam toma el concepto del Momento de Nesterov del SGD con Momento de Nesterov. Esto implica:
- Gradiente de "vistazo": Antes de actualizar el parámetro basándose en el gradiente actual, Nadam estima un gradiente de "vistazo" utilizando el gradiente actual y el término de momento.
- Actualización con el gradiente de "vistazo": Luego, la actualización del parámetro se realiza utilizando este gradiente de "vistazo", lo que puede llevar a una convergencia más rápida y a una mejor gestión de los gradientes ruidosos.
Matemáticas detrás de Nadam:
- Actualización de EMA de momentos (igual que Adam)
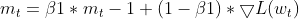
- Actualización de EMA de gradientes al cuadrado (igual que Adam)
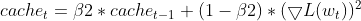
- Corrección del sesgo de los momentos (igual que Adam)
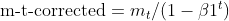
- Corrección del sesgo de los gradientes al cuadrado (igual que Adam)
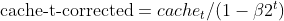
- Nesterov Momentum (utilizando la estimación del gradiente anterior)
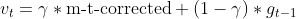
- Actualizar la estimación anterior del gradiente
- Parámetro de actualización con Nesterov Momentum
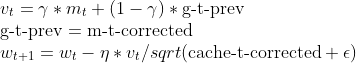
matrix nesterov_moment = m_gamma * moment_hat + (1 - m_gamma) * gradients; // Nesterov accelerated gradient parameters -= m_learning_rate * nesterov_moment / sqrt(cache_hat + m_epsilon); // Update parameters
Ventajas de Nadam:
- Es más rápido: Comparado con Adam, Nadam puede lograr potencialmente una convergencia más rápida, especialmente para problemas con gradientes ruidosos.
- Maneja mejor los gradientes ruidosos: El término de Nesterov Momentum de Nadam puede ayudar a suavizar gradientes ruidosos y mejorar el rendimiento.
- Tiene las ventajas de Adam: Conserva las ventajas de Adam, como la adaptabilidad y una menor sensibilidad a la selección de la cotización de aprendizaje.
Desventajas:
- Requiere el ajuste de hiperparámetros como la cotización de aprendizaje, las tasas de decaimiento y el coeficiente de impulso para un rendimiento óptimo.
- Aunque Nadam es prometedor, puede que no siempre supere a Adam en todos los escenarios. Es necesario seguir investigando y experimentando.
¿Dónde utilizar Nadam?
Puede ser una gran alternativa a Adam en problemas donde hay gradientes ruidosos.
Llamé a Nadam con los parámetros por defecto y la misma cotización de aprendizaje que usamos para todos los optimizadores discutidos anteriormente. Acabé en segundo lugar por detrás de Adam, con una precisión aproximada del 47% en los conjuntos de entrenamiento y validación. Nadam hizo muchas oscilaciones alrededor de los mínimos locales que otros métodos discutidos en este artículo.
IL 0 15:37:56.549 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [90/100] training -> loss 25.23632476 accuracy 0.466 validation -> loss 25.06902 accuracy 0.462 | Elapsed 0.062 Seconds LK 0 15:37:56.619 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [91/100] training -> loss 24.60851222 accuracy 0.479 validation -> loss 24.44829 accuracy 0.475 | Elapsed 0.078 Seconds RS 0 15:37:56.690 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [92/100] training -> loss 24.68657614 accuracy 0.477 validation -> loss 24.53442 accuracy 0.473 | Elapsed 0.078 Seconds IJ 0 15:37:56.761 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [93/100] training -> loss 24.89495551 accuracy 0.473 validation -> loss 24.73423 accuracy 0.469 | Elapsed 0.063 Seconds GQ 0 15:37:56.832 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [94/100] training -> loss 25.25899364 accuracy 0.465 validation -> loss 25.09940 accuracy 0.461 | Elapsed 0.078 Seconds QI 0 15:37:56.901 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [95/100] training -> loss 25.17698272 accuracy 0.467 validation -> loss 25.01065 accuracy 0.463 | Elapsed 0.063 Seconds FP 0 15:37:56.976 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [96/100] training -> loss 25.36663261 accuracy 0.463 validation -> loss 25.20273 accuracy 0.459 | Elapsed 0.078 Seconds FO 0 15:37:57.056 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [97/100] training -> loss 23.34069092 accuracy 0.506 validation -> loss 23.19590 accuracy 0.502 | Elapsed 0.078 Seconds OG 0 15:37:57.128 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [98/100] training -> loss 23.48894694 accuracy 0.503 validation -> loss 23.33753 accuracy 0.499 | Elapsed 0.078 Seconds ON 0 15:37:57.203 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [99/100] training -> loss 23.03205165 accuracy 0.512 validation -> loss 22.88233 accuracy 0.509 | Elapsed 0.062 Seconds ME 0 15:37:57.275 Optimization Algorithms testScript (EURUSD,H1) --> Epoch [100/100] training -> loss 24.98193438 accuracy 0.471 validation -> loss 24.82652 accuracy 0.467 | Elapsed 0.079 Seconds
A continuación se muestra el gráfico de pérdidas frente a épocas:
Reflexiones finales
La elección del mejor optimizador depende del problema específico, el conjunto de datos, la arquitectura de red y los parámetros. La experimentación es clave para encontrar el optimizador más eficaz para su tarea de entrenamiento de redes neuronales. Adam resulta ser el mejor optimizador para muchas redes neuronales debido a su capacidad para converger más rápidamente, es menos sensible a la cotización de aprendizaje y adapta su cotización de aprendizaje con el momentum. Es una buena opción para probar primero, especialmente para problemas complejos o cuando no se está seguro de qué optimizador utilizar inicialmente.
Mis mejores deseos.
Sigue el desarrollo de modelos de aprendizaje automático y mucho más discutido en esta serie de artículos en este repositorio de GitHub.
Archivos adjuntos:
| Archivo | Descripción/Uso |
|---|---|
| MatrixExtend.mqh | Dispone de funciones adicionales para la manipulación de matrices. |
| metrics.mqh | Contiene funciones y código para medir el rendimiento de los modelos ML. |
| preprocessing.mqh | La librería para el preprocesamiento de datos de entrada sin procesar para hacerlos aptos para el uso de modelos de aprendizaje automático. |
| plots.mqh | Librería para el trazado de vectores y matrices. |
| optimizers.mqh | Un archivo 'Include' que contiene todos los optimizadores de redes neuronales analizados en este artículo. |
| cross_validation.mqh | Una librería con técnicas de validación cruzada. |
| Tensors.mqh | Una librería que contiene tensores y objetos de matrices algebraicas 3D programados en lenguaje MQL5 puro. |
| Regressor Nets.mqh | Contiene redes neuronales para resolver un problema de regresión. |
| Optimization Algorithms testScript.mq5 | Un script para ejecutar el código de todos los archivos de inclusión y el conjunto de datos (Este es el archivo principal). |
| airfoil_noise_data.csv | Datos del problema de regresión de perfiles aerodinámicos. |
Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/14435
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Modelo de aprendizaje profundo GRU en Python usando ONNX en asesores expertos, GRU vs LSTM
Modelo de aprendizaje profundo GRU en Python usando ONNX en asesores expertos, GRU vs LSTM
 Hibridación de algoritmos basados en poblaciones. Esquema secuencial y paralelo
Hibridación de algoritmos basados en poblaciones. Esquema secuencial y paralelo
 Gestor de riesgos para el trading manual
Gestor de riesgos para el trading manual
 Características del Wizard MQL5 que debe conocer (Parte 14): Previsión multiobjetivo de series temporales con STF
Características del Wizard MQL5 que debe conocer (Parte 14): Previsión multiobjetivo de series temporales con STF
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
El script del artículo da un error:
2024.11.21 15:09:16.213 Optimisation Algorithms testScript(EURUSD,M1) Zero divide, check divider for zero to avoid this error in 'D:\Market\MT5\MQL5\Scripts\Optimization Algorithms testScript.ex5'
El problema resultó ser que el script no encontró el archivo con los datos de entrenamiento. Pero, en cualquier caso, el programa debe manejar este caso si no se encuentra el archivo de datos.
Pero ahora existe tal problema:
2024.11.21 17:27:37.038 Algoritmos de optimización testScript (EURUSD,M1) 50 objetos dinámicos no eliminados encontrados:
2024.11.21 17:27:37.038 Algoritmos de optimización testScript (EURUSD,M1) 10 objetos de clase 'CTensors'
2024.11.21 17:21 17:27:37.038 Algoritmos de optimización testScript (EURUSD,M1) 40 objetos de clase 'CMatrix'
2024.11.21 17:27:37.038 Optimización Algoritmos testScript (EURUSD,M1) 14816 bytes de memoria filtrada encontrados
El problema resultó ser que el script no encontró el archivo de datos para el entrenamiento. Pero, en cualquier caso, el programa debe manejar tal caso, si no se encuentra el archivo de datos.
Pero ahora existe tal problema:
2024.11.21 17:27:37.038 Algoritmos de optimización testScript (EURUSD,M1) 50 objetos dinámicos no eliminados encontrados:
2024.11.21 17:27:37.038 Algoritmos de optimización testScript (EURUSD,M1) 10 objetos de clase 'CTensors'
2024.11.21 17:21 17:27:37.038 Algoritmos de optimización testScript (EURUSD,M1) 40 objetos de clase 'CMatrix'
2024.11.21 17:27:37.038 Optimización Algoritmos testScript (EURUSD,M1) 14816 bytes de memoria filtrada encontrados
Esto se debe a que sólo se debe llamar a una función "fit" para una instancia de una clase. He llamado a múltiples funciones de ajuste, lo que resulta en la creación de múltiples tensores en la memoria.Esto fue con fines educativos.
Debería ser así;