MetaTrader 5 / テスター
English Deutsch
preview
データサイエンスと機械学習(第21回)：ニューラルネットワークと最適化アルゴリズムの解明

データサイエンスと機械学習(第21回)：ニューラルネットワークと最適化アルゴリズムの解明

MetaTrader 5 — テスター | 24 5月 2024, 10:47
93 0
Omega J Msigwa
Omega J Msigwa

ニューラルネットワークが簡単だと言っているのではありません。それを機能させるには、専門家でなければなりません。ただし、その専門知識は、幅広いアプリケーションにわたって役に立ちます。ある意味、以前は機能設計に費やしていた努力のすべてが、今ではアーキテクチャ設計の損失関数設計と最適化スキーム設計に費やされています。手作業はより抽象度の高いレベルに引き上げられているのです。

Stefano Soatto


はじめに

最近では誰もが人工知能に興味を持っているようです。人工知能はどこにでもあります。オープンAIの背後にいるグーグルやマイクロソフトのようなハイテク業界の大物は、エンターテインメント、医療業界、芸術、創造性など、さまざまな側面や業界でAIの適応を推進しています。 

MQL5コミュニティでもこの傾向が見られます。当然です。Metatrader5に行列とベクトル、ONNXを導入したことで、あらゆる複雑さの人工知能取引モデルを作成できるようになりました。線型代数学の専門家である必要も、システムに含まれるすべてを理解できるオタクである必要もなくなったのです。

にもかかわらず、機械学習の基本を見つけることはかつてないほど難しくなっています。しかし、それらはAIについての理解を確固たるものにするのと同じくらい重要な知識です。自分の作業の理由を知ることで柔軟になり、選択肢を行使できるようになります。機械学習についてはまだお話ししていないことがたくさんあります。本日は、最適化アルゴリズムにはどのようなものがあるのか、また、最適化アルゴリズム間にどのような違いがあるのか、いつ、どの最適化アルゴリズムを選択すればニューラルネットワークのパフォーマンスと精度が向上するのかをご紹介します。

ニューラルネットワークオプティマイザ

この記事で説明する内容は、最適化アルゴリズム全般を理解するのに役立ちます。つまり、この知識はPythonのScikit-Learn、Tensorflow、Pytorchモデルを使用する場合にも役に立ちます。これらのオプティマイザは、使用するプログラミング言語に関係なく、すべてのニューラルネットワークに共通であるためです。


ニューラルネットワークオプティマイザとは

定義上、オプティマイザは、訓練中にニューラルネットワークのパラメータを微調整するアルゴリズムです。その目的は、損失関数を最小化することであり、最終的にはパフォーマンスの向上につながります。

簡単に言えば、ニューラルネットワークオプティマイザは次をおこないます。

  1. ニューラルネットワークに影響を与える重要なパラメータとして、各訓練反復において各パラメータをどのように変更するかを決定する
  2. 実際の値とニューラルネットワークの予測値との不一致を測定し、この誤差を徐々に減らすように努力する

まだの方は、以前の「フィードフォワードニューラルネットワークの解明」稿を読むことをお勧めします。今回は、この記事で0から構築したニューラルネットワークモデルを改良し、オプティマイザを追加します。

オプティマイザの種類を見る前に、バックプロパゲーションのアルゴリズムを理解する必要があります。一般に3つのアルゴリズムがあります。

  1. 確率的勾配降下法（Stochastic Gradient Descent、SGD）
  2. バッチ勾配降下法（Batch Gradient Descent、BGD）
  3. ミニバッチ勾配降下法(Mini-Batch Gradient Descent)

01：確率的勾配降下アルゴリズム(SGD)

確率的勾配降下法(SGD)は、ニューラルネットワークの学習に用いられる基本的な最適化アルゴリズムです。このアルゴリズムは、損失関数を最小化するようにネットワークの重みとバイアスを繰り返し更新します。損失関数は、ネットワークの予測値と訓練データの実際のラベル（目標値）との間の不一致を測定します。

これらの最適化アルゴリズムに関わる主なプロセスは同じで、以下のようなものがあります。

  1. 反復
  2. バックプロパゲーション
  3. 重みとバイアスの更新

これらのアルゴリズムは、反復処理の方法と重みとバイアスの更新頻度によって異なります。SGDアルゴリズムは、ニューラルネットワークのパラメータ（重みとバイアス）を一度に1つの訓練例（データポイント）ずつ更新します。

void CRegressorNets::backpropagation(const matrix& x, const vector &y)
 {   
    for (ulong epoch=0; epoch<epochs && !IsStopped(); epoch++)
      { 
        
        for (ulong iter=0; iter<rows; iter++) //iterate through all data points
          {             
             for (int layer=(int)mlp.hidden_layers-1; layer>=0 && !IsStopped(); layer--) //Loop through the network backward from last to first layer
               {    
                // find partial derivatives of each layer WRT the loss function dW and dB
                
                 
                //--- Weights updates
                 
                 optimizer_weights.update(W, dW);
                 optimizer_bias.update(B, dB);
                 
                 this.W_tensor.Add(W, layer);
                 this.B_tensor.Add(B, layer);
               }
         }
     }
 }

長所

  • 大規模なデータセットに対して計算効率が高い
  • BGDやミニバッチ勾配降下法よりも早く収束することがある（特に一度に1つの訓練サンプルを使用する非凸の損失関数の場合）
  • 局所的最小値を避けるのがうまい：SGDでは更新にノイズが含まれるため、局所的最小値から脱出し、大域的最小値に収束する能力がある

短所

  • 更新にノイズが含まれる可能性があり、訓練中にジグザグ動作になる
  • 大域的最小値に収束しない場合がある
  • 収束が遅く、各訓練例のパラメータを1つずつ更新するため、収束までに多くのエポックを必要とする場合がある
  • 学習率の選択はこのアルゴリズムにとって重要であり、学習率を高くするとアルゴリズムが大域的最小値をオーバーシュートする可能性があり、逆に低くすると収束プロセスが遅くなる
確率的勾配降下法は、局所極小を脱出して大域的極小を求めることができるため、非凸関数の最適化に適しています。


02：バッチ勾配降下アルゴリズム(BGD)

SGDとは異なり、バッチ勾配降下法(BGD)は、各反復においてデータセット全体を使用して勾配を計算します。

長所

・理論的には、損失関数が滑らかで凸であれば最小に収束する

短所

・データセット全体を繰り返し処理する必要があるため、大規模なデータセットでは計算コストが高くなる可能性がある

今あるニューラルネットワークには実装しませんが、下のミニバッチ勾配降下と同じように簡単に実装できるので、よかったら実装してみてください。


03：ミニバッチ勾配降下

このアルゴリズムはSGDとBGDの折衷案であり、各反復で訓練データの小さなサブセット（ミニバッチ）を使用してネットワークのパラメータを更新します。

長所

  • SGDやBGDと比較して、計算効率と更新の安定性のバランスが良い
  • BGDよりも大きなデータセットを効果的に扱うことができる

短所

  • SGDと比較して、ミニバッチサイズの調整がより必要になる場合がある
  • SGDに比べて計算コストが高く、バッチ保存と処理に多くのメモリを消費する
  • 大量ロットの訓練には長い時間がかかる

以下は、ミニバッチ勾配降下アルゴリズムの擬似コードです。

void CRegressorNets::backpropagation(const matrix& x, const vector &y, OptimizerSGD *sgd, const uint epochs, uint batch_size=0, bool show_batch_progress=false)
 {

  //....
    for (ulong epoch=0; epoch<epochs && !IsStopped(); epoch++)
      { 
               
            for (uint batch=0, batch_start=0, batch_end=batch_size; batch<num_batches; batch++, batch_start+=batch_size, batch_end=(batch_start+batch_size-1))
               {
                  matrix batch_x = MatrixExtend::Get(x, batch_start, batch_end-1);
                  vector batch_y = MatrixExtend::Get(y, batch_start, batch_end-1);
                  
                  rows = batch_x.Rows();              
                  
                    for (ulong iter=0; iter<rows ; iter++) //replace to rows 
                      {
                        pred_v[0] = predict(batch_x.Row(iter));
                        actual_v[0] = y[iter];
                        
                        // Find derivatives WRT weights dW and bias dB    
                        //....                    
                            
                         //--- Updating the weights using a given optimizer
                           
                           optimizer_weights.update(W, dW); 
                           optimizer_bias.update(B, dB);
                           
                           this.Weights_tensor.Add(W, layer);
                           this.Bias_tensor.Add(B, layer);  
                        }
                   }
       }
 }

これら2つのアルゴリズムの心臓部には、デフォルトで単純な勾配降下更新ルールがあり、これはしばしばSGDまたはMini-BGDオプティマイザと呼ばれます。

class OptimizerSGD
  {
protected:
   double m_learning_rate;
   
public:
                     OptimizerSGD(double learning_rate=0.01);
                    ~OptimizerSGD(void);
                     
                    virtual void update(matrix &parameters, matrix &gradients);
  };
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
OptimizerSGD::OptimizerSGD(double learning_rate=0.01):
 m_learning_rate(learning_rate)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
OptimizerSGD::~OptimizerSGD(void)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void OptimizerSGD::update(matrix &parameters, matrix &gradients)
 {
    parameters -= this.m_learning_rate * gradients; //Simple gradient descent update rule
 }
 
 
//+------------------------------------------------------------------+
//|  Batch Gradient Descent (BGD): This optimizer computes the       |
//|  gradients of the loss function on the entire training dataset   |
//|  and updates the parameters accordingly. It can be slow and      |
//|  memory-intensive for large datasets but tends to provide a      |
//|  stable convergence.                                             |
//+------------------------------------------------------------------+


class OptimizerMinBGD: public OptimizerSGD
  {
public:
                     OptimizerMinBGD(double learning_rate=0.01);
                    ~OptimizerMinBGD(void);
  };
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
OptimizerMinBGD::OptimizerMinBGD(double learning_rate=0.010000): OptimizerSGD(learning_rate)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
OptimizerMinBGD::~OptimizerMinBGD(void)
 {
 
 }

では、この2つのオプティマイザを使ってモデルを訓練し、その結果を観察してみましょう。

#include <MALE5\MatrixExtend.mqh>
#include <MALE5\preprocessing.mqh>
#include <MALE5\metrics.mqh>
#include <MALE5\Neural Networks\Regressor Nets.mqh>
CRegressorNets *nn;


StandardizationScaler scaler;
vector open_, high_, low_;

vector hidden_layers = {5};
input uint nn_epochs = 100;
input double nn_learning_rate = 0.0001;
input uint nn_batch_size =32;
input bool show_batch = false;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---

  string headers;
  matrix dataset = MatrixExtend::ReadCsv("airfoil_noise_data.csv", headers);
  
  matrix x_train, x_test;
  vector y_train, y_test;
  
  MatrixExtend::TrainTestSplitMatrices(dataset, x_train, y_train, x_test, y_test, 0.7);
  
  nn = new CRegressorNets(hidden_layers, AF_RELU_, LOSS_MSE_); 
  
  x_train = scaler.fit_transform(x_train);
  
  nn.fit(x_train, y_train, new OptimizerMinBGD(nn_learning_rate), nn_epochs, nn_batch_size, show_batch);
   
  delete nn; 
  }

nn_batch_size入力に0より大きな値が代入されると、フィット/バックプロパゲーション関数にどのオプティマイザが適用されていても、ミニバッチ勾配降下が有効になります。

backprop CRegressorNets::backpropagation(const matrix& x, const vector &y, OptimizerSGD *optimizer, const uint epochs, uint batch_size=0, bool show_batch_progress=false)
 {
//...
//...

//--- Optimizer use selected optimizer when batch_size ==0 otherwise use the batch gradient descent
      
   OptimizerSGD optimizer_weights = optimizer;
   OptimizerSGD optimizer_bias = optimizer;
   
   if (batch_size>0)
    {
      OptimizerMinBGD optimizer_weights;
      OptimizerMinBGD optimizer_bias;
    }
     
//--- Cross validation

    CCrossValidation cross_validation;      
    CTensors *cv_tensor;
    matrix validation_data = MatrixExtend::concatenate(x, y);
    matrix validation_x;
    vector validation_y;
    
    cv_tensor = cross_validation.KFoldCV(validation_data, 10); //k-fold cross validation | 10 folds selected
    
//---

    matrix DELTA = {};
    double actual=0, pred=0;
    
    matrix temp_inputs ={};
    
    matrix dB = {}; //Bias Derivatives
    matrix dW = {}; //Weight Derivatives
    
   
    for (ulong epoch=0; epoch<epochs && !IsStopped(); epoch++)
      {        
        double epoch_start = GetTickCount(); 

        uint num_batches = (uint)MathFloor(x.Rows()/(batch_size+DBL_EPSILON));
        
        vector batch_loss(num_batches), 
               batch_accuracy(num_batches);
                       
         vector actual_v(1), pred_v(1), LossGradient = {};
         if (batch_size==0) //Stochastic Gradient Descent
          {
           for (ulong iter=0; iter<rows; iter++) //iterate through all data points
             {
               pred = predict(x.Row(iter));
               actual = y[iter];
               
               pred_v[0] = pred; 
               actual_v[0] = actual; 
   //---
                
                DELTA.Resize(mlp.outputs,1);
                
                for (int layer=(int)mlp.hidden_layers-1; layer>=0 && !IsStopped(); layer--) //Loop through the network backward from last to first layer
                  {    
                    //..... backpropagation and finding derivatives code        
                    
                    //-- Observation | DeLTA matrix is same size as the bias matrix
                    
                    W = this.Weights_tensor.Get(layer);
                    B = this.Bias_tensor.Get(layer);
                  
                   //--- Derivatives wrt weights and bias
                  
                    dB = DELTA;
                    dW = DELTA.MatMul(temp_inputs.Transpose());                   
                    
                   //--- Weights updates
                    
                    optimizer_weights.update(W, dW);
                    optimizer_bias.update(B, dB);
                    
                    this.Weights_tensor.Add(W, layer);
                    this.Bias_tensor.Add(B, layer);
                  }
             }
         }
        else //Batch Gradient Descent
          {
               
            for (uint batch=0, batch_start=0, batch_end=batch_size; batch<num_batches; batch++, batch_start+=batch_size, batch_end=(batch_start+batch_size-1))
               {
                  matrix batch_x = MatrixExtend::Get(x, batch_start, batch_end-1);
                  vector batch_y = MatrixExtend::Get(y, batch_start, batch_end-1);
                  
                  rows = batch_x.Rows();              
                  
                    for (ulong iter=0; iter<rows ; iter++) //iterate through all data points
                      {
                        pred_v[0] = predict(batch_x.Row(iter));
                        actual_v[0] = y[iter];
                        
            //---
                        
                      DELTA.Resize(mlp.outputs,1);
                      
                      for (int layer=(int)mlp.hidden_layers-1; layer>=0 && !IsStopped(); layer--) //Loop through the network backward from last to first layer
                        {    
                         //..... backpropagation and finding derivatives code   
                            }
                          
                          //-- Observation | DeLTA matrix is same size as the bias matrix
                          
                          W = this.Weights_tensor.Get(layer);
                          B = this.Bias_tensor.Get(layer);
                        
                         //--- Derivatives wrt weights and bias
                        
                          dB = DELTA;
                          dW = DELTA.MatMul(temp_inputs.Transpose());                   
                          
                         //--- Weights updates
                          
                          optimizer_weights.update(W, dW);
                          optimizer_bias.update(B, dB);
                          
                          this.Weights_tensor.Add(W, layer);
                          this.Bias_tensor.Add(B, layer);
                        }
                    }
                 
                 pred_v = predict(batch_x);
                 
                 batch_loss[batch] = pred_v.Loss(batch_y, ENUM_LOSS_FUNCTION(m_loss_function));
                 batch_loss[batch] = MathIsValidNumber(batch_loss[batch]) ? (batch_loss[batch]>1e6 ? 1e6 : batch_loss[batch]) : 1e6; //Check for nan and return some large value if it is nan
                 
                 batch_accuracy[batch] = Metrics::r_squared(batch_y, pred_v);
                 
                 if (show_batch_progress)
                  printf("----> batch[%d/%d] batch-loss %.5f accuracy %.3f",batch+1,num_batches,batch_loss[batch], batch_accuracy[batch]);  
              }
          }
          
//--- End of an epoch
      
        vector validation_loss(cv_tensor.SIZE);
        vector validation_acc(cv_tensor.SIZE);
        for (ulong i=0; i<cv_tensor.SIZE; i++)
          {
            validation_data = cv_tensor.Get(i);
            MatrixExtend::XandYSplitMatrices(validation_data, validation_x, validation_y);
            
            vector val_preds = this.predict(validation_x);;
            
            validation_loss[i] = val_preds.Loss(validation_y, ENUM_LOSS_FUNCTION(m_loss_function));
            validation_acc[i] = Metrics::r_squared(validation_y, val_preds);
          }
                  
        pred_v = this.predict(x);
        
        if (batch_size==0)
          {      
              backprop_struct.training_loss[epoch] = pred_v.Loss(y, ENUM_LOSS_FUNCTION(m_loss_function));
              backprop_struct.training_loss[epoch] = MathIsValidNumber(backprop_struct.training_loss[epoch]) ? (backprop_struct.training_loss[epoch]>1e6 ? 1e6 : backprop_struct.training_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan
              backprop_struct.validation_loss[epoch] = validation_loss.Mean();
              backprop_struct.validation_loss[epoch] = MathIsValidNumber(backprop_struct.validation_loss[epoch]) ? (backprop_struct.validation_loss[epoch]>1e6 ? 1e6 : backprop_struct.validation_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan
          }
        else
          {
              backprop_struct.training_loss[epoch] = batch_loss.Mean();
              backprop_struct.training_loss[epoch] = MathIsValidNumber(backprop_struct.training_loss[epoch]) ? (backprop_struct.training_loss[epoch]>1e6 ? 1e6 : backprop_struct.training_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan
              backprop_struct.validation_loss[epoch] = validation_loss.Mean();
              backprop_struct.validation_loss[epoch] = MathIsValidNumber(backprop_struct.validation_loss[epoch]) ? (backprop_struct.validation_loss[epoch]>1e6 ? 1e6 : backprop_struct.validation_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan
          }
          
        double epoch_stop = GetTickCount();  
        printf("--> Epoch [%d/%d] training -> loss %.8f accuracy %.3f validation -> loss %.5f accuracy %.3f | Elapsed %s ",epoch+1,epochs,backprop_struct.training_loss[epoch],Metrics::r_squared(y, pred_v),backprop_struct.validation_loss[epoch],validation_acc.Mean(),this.ConvertTime((epoch_stop-epoch_start)/1000.0));
     }
     
   isBackProp = false;
   
  if (CheckPointer(optimizer)!=POINTER_INVALID)  
    delete optimizer;
    
   return backprop_struct;
 }

出力

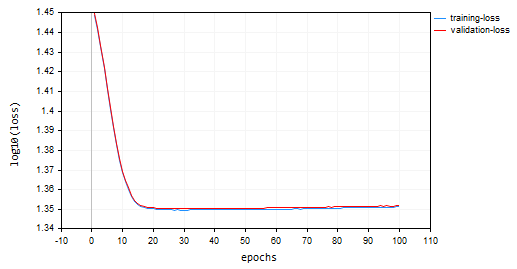
確率的勾配降下法(SGD)：学習率=0.0001

確率的勾配降下法

バッチ勾配降下(BGD)：学習率 = 0.0001、バッチサイズ = 16

バッチ勾配降下法

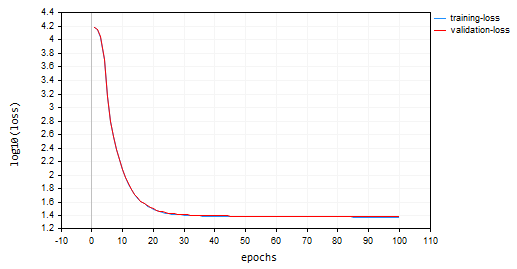
SGDはより速く収束し、約10エポックで局所的最小値に近づいた一方、BGDは約20エポックでした。SGDは訓練と検証の両方で約60%の精度に収束しましたが、BGDの精度は訓練サンプル中に15%、検証サンプル中に13%でした。BGDの学習率が最適であり、このデータセットに適したバッチ サイズであるかどうかがわからないため、まだ結論を下すことはできません。異なるオプティマイザは、異なる学習率で最も効果的に機能します。これがSGDのパフォーマンスが低下する原因の1つである可能性がありますが、極小値付近で振動することなく良好に収束しました。 これはSGDでは見られないことです。 BGDチャートは滑らかで、安定した訓練プロセスを示しています。 これは、BGDでは全体の損失が個々のバッチの損失の平均であるためです。

  backprop_struct.training_loss[epoch] = batch_loss.Mean();
  backprop_struct.training_loss[epoch] = MathIsValidNumber(backprop_struct.training_loss[epoch]) ? (backprop_struct.training_loss[epoch]>1e6 ? 1e6 : backprop_struct.training_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan
  backprop_struct.validation_loss[epoch] = validation_loss.Mean();
  backprop_struct.validation_loss[epoch] = MathIsValidNumber(backprop_struct.validation_loss[epoch]) ? (backprop_struct.validation_loss[epoch]>1e6 ? 1e6 : backprop_struct.validation_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan

プロット上でlog10がプロットの損失値に適用されていることにお気づきかもしれません。初期のエポックでは損失値がより大きな値になる場合があるため、この正規化によって損失値が適切にプロットされるようになります。目的は、より大きな値にペナルティを与え、最終的にプロットで見栄えが良くなるようにすることです。損失の実際の値は、チャートではなく[エキスパート]タブで確認できます。

void CRegressorNets::fit(const matrix &x, const vector &y, OptimizerSGD *optimizer, const uint epochs, uint batch_size=0, bool show_batch_progress=false)
 {
  trained = true; //The fit method has been called
  
  vector epochs_vector(epochs);  for (uint i=0; i<epochs; i++) epochs_vector[i] = i+1;
  
  backprop backprop_struct;
  
  backprop_struct = this.backpropagation(x, y, optimizer, epochs, batch_size, show_batch_progress); //Run backpropagation
  

  CPlots plt;
  
  backprop_struct.training_loss = log10(backprop_struct.training_loss); //Logarithmic scalling
  plt.Plot("Loss vs Epochs",epochs_vector,backprop_struct.training_loss,"epochs","log10(loss)","training-loss",CURVE_LINES);
  backprop_struct.validation_loss = log10(backprop_struct.validation_loss);
  plt.AddPlot(backprop_struct.validation_loss,"validation-loss",clrRed);
  
   while (MessageBox("Close or Cancel Loss Vs Epoch plot to proceed","Training progress",MB_OK)<0)
    Sleep(1);

  isBackProp = false;
 }

SGDオプティマイザは、損失関数を最小化するための一般的なツールであり、バックプロパゲーションのためのSGDアルゴリズムは、ニューラルネットワークの勾配を計算するために調整されたSGD内の特定の技術です。

SGDオプティマイザは大工であり、バックプロパゲーションのためのSGDまたはMin-BGDアルゴリズムは、大工の道具箱の中の特殊な道具であると考えてください。


ニューラルネットワークオプティマイザの種類

先ほど説明したSGDオプティマイザ以外にも、さまざまなニューラルネットワークオプティマイザがあり、それぞれが最適なパラメータ値を達成するために異なる戦略を採用しています。以下は、最も一般的に使用されるニューラルネットワークオプティマイザの一部です。

  1. RMSProp (Root mean square propagation)
  2. AdaGrad (Adaptive Gradient Descent)
  3. Adam (Adaptive Moment Estimation)
  4. AdaDelta
  5. Nadam (Nesterov-accelerated Adaptive Moment Estimation)
これらのオプティマイザは、バックプロパゲーション中に確率的勾配降下アルゴリズムに適用されます。


01：RMSProp (Root mean square propagation)

この最適化アルゴリズムは、確率的勾配降下法(SGD)の限界に対処することを目的としており、過去の勾配に基づいて各重みとバイアスパラメータの学習率を適応させます。

SGDの問題

SGDは、現在の勾配と固定の学習率を用いて重みとバイアスを更新します。しかし、ニューラルネットワークのような複雑な関数では、パラメータによって勾配の大きさが大きく異なることがあります。勾配が小さいパラメータの更新が非常に遅くなるため、収束が遅くなり、全体的な学習の妨げになる可能性があります。また、勾配が大きいパラメータが更新中に過度に揺れ動き、SGDは大きな振動を引き起こす可能性があり。学習プロセスが不安定になる場合があります。

理論

これがRMSPropの核となる考え方です。

  • 二乗勾配の指数移動平均(EMA)を維持する：各パラメータについて、RMSPropは勾配の二乗の指数関数的に減衰する平均を追跡する。この平均値は、パラメータがどの程度更新されるべきかの最近の履歴を反映している。
    rms prop更新二乗勾配
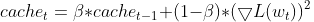
  • 勾配の正規化：各パラメータの現在の勾配は、0による除算を避けるために小さな平滑化項（通常εで示される）とともに、勾配の二乗のEMAの平方根で除算される
  • パラメータの更新：パラメータの更新を決定するために、正規化された勾配に学習率を乗じる
    rmsprop更新パラメータ

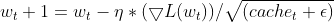
ここで

 ：時間ステップtにおける勾配の二乗のEMA

：減衰率（ハイパーパラメータ、通常0.9～0.999） - 過去の勾配の影響を制御

：時間ステップtにおけるパラメータwに関する損失関数の勾配

：時間ステップtにおけるパラメータ値

：時間ステップt+1における更新パラメータ値

η：学習率（ハイパーパラメータ）

ε：平滑化項（通常は1e-8のような小さな値）

class OptimizerRMSprop
  {
protected:
   double m_learning_rate;
   double m_decay_rate;
   double m_epsilon;
   
   matrix<double> cache;
   
   //Dividing double/matrix causes compilation error | this is the fix to the issue
   matrix divide(const double numerator, const matrix &denominator)
    {
      matrix res = denominator;
      
      for (ulong i=0; i<denominator.Rows(); i++)
        res.Row(numerator / denominator.Row(i), i);
     return res;
    }
    
public:
                     OptimizerRMSprop(double learning_rate=0.01, double decay_rate=0.9, double epsilon=1e-8);
                    ~OptimizerRMSprop(void);
                    
                    virtual void update(matrix& parameters, matrix& gradients);
  };
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
OptimizerRMSprop::OptimizerRMSprop(double learning_rate=0.01, double decay_rate=0.9, double epsilon=1e-8):
 m_learning_rate(learning_rate),
 m_decay_rate(decay_rate),
 m_epsilon(epsilon)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
OptimizerRMSprop::~OptimizerRMSprop(void)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void OptimizerRMSprop::update(matrix &parameters,matrix &gradients)
 {
 
   if (cache.Rows()!=parameters.Rows() || cache.Cols()!=parameters.Cols())
    {
     cache.Init(parameters.Rows(), parameters.Cols());
     cache.Fill(0.0);
    }
     
//---
    
    cache += m_decay_rate * cache + (1 - m_decay_rate) * MathPow(gradients, 2);
    parameters -= divide(m_learning_rate, cache + m_epsilon) * gradients;
 }

100エポックと0.0001（以前のオプティマイザで使用されたものと同じデフォルト値）を使用した場合、ニューラルネットワークは100エポックでは収束せず、訓練サンプルと検証サンプルでそれぞれ約-319と-324の精度が得られました。多数のエポックで局所的極小値をオーバーシュートしないと仮定すると、このペースで1000エポック以上が必要になる可能性があるようです。

HK      0       15:10:15.632    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [90/100] training -> loss 15164.85487215 accuracy -320.064 validation -> loss 15164.99272 accuracy -325.349 | Elapsed 0.031 Seconds 
HQ      0       15:10:15.663    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [91/100] training -> loss 15161.78717397 accuracy -319.999 validation -> loss 15161.92323 accuracy -325.283 | Elapsed 0.031 Seconds 
DO      0       15:10:15.694    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [92/100] training -> loss 15158.07142844 accuracy -319.921 validation -> loss 15158.20512 accuracy -325.203 | Elapsed 0.031 Seconds 
GE      0       15:10:15.727    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [93/100] training -> loss 15154.92004326 accuracy -319.854 validation -> loss 15155.05184 accuracy -325.135 | Elapsed 0.032 Seconds 
GS      0       15:10:15.760    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [94/100] training -> loss 15151.84229952 accuracy -319.789 validation -> loss 15151.97226 accuracy -325.069 | Elapsed 0.031 Seconds 
DH      0       15:10:15.796    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [95/100] training -> loss 15148.77653633 accuracy -319.724 validation -> loss 15148.90466 accuracy -325.003 | Elapsed 0.031 Seconds 
MF      0       15:10:15.831    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [96/100] training -> loss 15145.56414236 accuracy -319.656 validation -> loss 15145.69033 accuracy -324.934 | Elapsed 0.047 Seconds 
IL      0       15:10:15.869    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [97/100] training -> loss 15141.85430749 accuracy -319.577 validation -> loss 15141.97859 accuracy -324.854 | Elapsed 0.031 Seconds 
KJ      0       15:10:15.906    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [98/100] training -> loss 15138.40751503 accuracy -319.504 validation -> loss 15138.52969 accuracy -324.780 | Elapsed 0.032 Seconds 
PP      0       15:10:15.942    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [99/100] training -> loss 15135.31136641 accuracy -319.439 validation -> loss 15135.43169 accuracy -324.713 | Elapsed 0.046 Seconds 
NM      0       15:10:15.975    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [100/100] training -> loss 15131.73032246 accuracy -319.363 validation -> loss 15131.84854 accuracy -324.636 | Elapsed 0.032 Seconds

損失対エポックのプロット： 100エポック、学習率0.0001

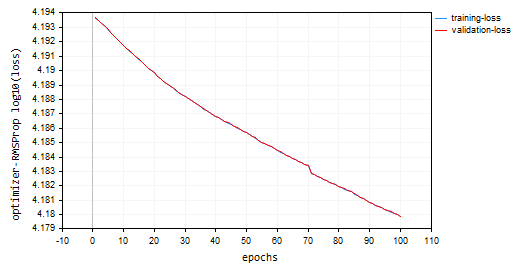
使用シナリオ

RMSPropは、非定常目的、スパースな勾配、Adamより単純な場合に適しています。


02：AdaGrad (Adaptive Gradient Algorithm)

AdaGradはニューラルネットワーク用のオプティマイザで、RMSpropに似た適応学習率を利用します。ただし、AdaGradとRMSpropには、そのアプローチにおいていくつかの重要な違いがあります。

背後にある数学

  • 過去の勾配を累積する：AdaGradは、訓練プロセスを通して、各パラメータの二乗勾配の合計を追跡します。この累積値は、パラメータが過去にどれだけ更新されたかを反映します。

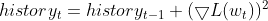
    cache += MathPow(gradients, 2);
  • 勾配を正規化する：各パラメータの現在の勾配を、累積された勾配の二乗和の平方根で除算し、0除算を避けるために小さな平滑化項（通常はεで表す）を加えます。
  • パラメータを更新する：正規化された勾配に学習率を乗じて、パラメータの更新を決定します。

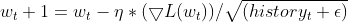
    parameters -= divide(this.m_learning_rate,  MathSqrt(cache + this.m_epsilon)) * gradients;

nn_learning_rate = 0.0001、エポック数 = 100

  nn.fit(x_train, y_train, new OptimizerAdaGrad(nn_learning_rate), nn_epochs, nn_batch_size, show_batch);

損失対エポックのプロット


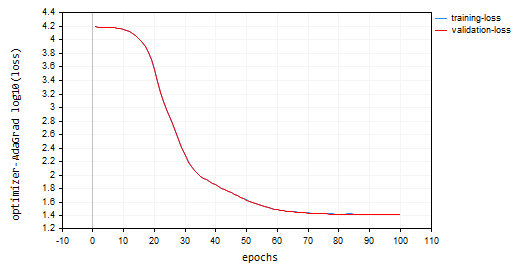
AdaGradは学習曲線がより急で、更新中も非常に安定していましたが、収束するのに100エポック以上を必要とし、訓練サンプルと検証サンプルの両方でそれぞれ約44%の精度に終わりました。

RK      0       15:15:52.202    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [90/100] training -> loss 26.22261537 accuracy 0.445 validation -> loss 26.13118 accuracy 0.440 | Elapsed 0.031 Seconds 
ER      0       15:15:52.239    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [91/100] training -> loss 26.12443561 accuracy 0.447 validation -> loss 26.03635 accuracy 0.442 | Elapsed 0.047 Seconds 
NJ      0       15:15:52.277    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [92/100] training -> loss 26.11449352 accuracy 0.447 validation -> loss 26.02561 accuracy 0.442 | Elapsed 0.032 Seconds 
IQ      0       15:15:52.316    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [93/100] training -> loss 26.09263184 accuracy 0.448 validation -> loss 26.00461 accuracy 0.443 | Elapsed 0.046 Seconds 
NH      0       15:15:52.354    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [94/100] training -> loss 26.14277865 accuracy 0.447 validation -> loss 26.05529 accuracy 0.442 | Elapsed 0.032 Seconds 
HP      0       15:15:52.393    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [95/100] training -> loss 26.09559950 accuracy 0.448 validation -> loss 26.00845 accuracy 0.443 | Elapsed 0.047 Seconds 
PO      0       15:15:52.442    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [96/100] training -> loss 26.05409769 accuracy 0.448 validation -> loss 25.96754 accuracy 0.443 | Elapsed 0.046 Seconds 
PG      0       15:15:52.479    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [97/100] training -> loss 25.98822082 accuracy 0.450 validation -> loss 25.90384 accuracy 0.445 | Elapsed 0.032 Seconds 
PN      0       15:15:52.519    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [98/100] training -> loss 25.98781231 accuracy 0.450 validation -> loss 25.90438 accuracy 0.445 | Elapsed 0.047 Seconds 
EE      0       15:15:52.559    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [99/100] training -> loss 25.91146212 accuracy 0.451 validation -> loss 25.83083 accuracy 0.446 | Elapsed 0.031 Seconds 
CN      0       15:15:52.595    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [100/100] training -> loss 25.87412572 accuracy 0.452 validation -> loss 25.79453 accuracy 0.447 | Elapsed 0.047 Seconds

長所

スパースな特徴に対してより速く収束します。データ中のスパースな特徴のために多くのパラメータが頻繁に更新されない状況では、AdaGradはそれらのパラメータの学習率を効果的に下げることができ、より速く収束することができます。

限界

AdaGradの累積二乗勾配和は時間の経過とともに増加し続け、すべてのパラメータの学習率が継続的に低下します。これでは結局、訓練の進歩が止まってしまいます。

使用場所

スパースな特徴データセットでは、多くの特徴の更新頻度が低いデータセットを扱う場合、AdaGradはそれらのパラメータの収束を速めるのに効果的です。

訓練の初期段階：シナリオによっては、訓練の後半で他のオプティマイザに切り替える前に、AdaGradによる最初の学習率調整が役に立つこともあります。


03：Adam (Adaptive Moment Estimation)

ニューラルネットワークの学習に広く使用されている、非常に効果的な最適化アルゴリズムです。AdaGradとRMSpropの長所を組み合わせ、それらの限界に対処し、効率的で安定した学習を実現します。

理論

Adamには2つの大きな特徴があります。

  • 勾配の指数移動平均(EMA)：RMSpropと同様に、Adamは、各パラメータに必要な更新の最近の履歴をキャプチャするために、二乗勾配のEMA（キャッシュ）を維持します。
  • モーメントの指数移動平均：Adamは別のEMA（モーメント）を導入し、勾配そのものの移動平均を追跡します。これは、いくつかのネットワークアーキテクチャで起こりうる勾配の消失の問題を軽減するのに役立ちます。

正規化と更新

  • モーメント更新：現在の勾配は、モーメントのEMA (m_t)を更新するために利用されます。 
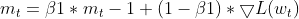
    this.moment = this.m_beta1 * this.moment + (1 -  this.m_beta1) * gradients;
  • 二乗勾配の更新：現在の二乗勾配は、二乗勾配のEMA(cache_t)を更新するために使用されます。


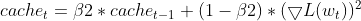
    this.cache = this.m_beta2 * this.cache + (1 -  this.m_beta2) * MathPow(gradients, 2);
  • バイアス補正：両方のEMA（moment_tとcache_t）は、指数減衰係数（β1とβ2）を用いてバイアスを補正し、真のモーメントの不偏推定値であることを保証します。


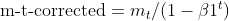
    matrix moment_hat = this.moment / (1 - MathPow(this.m_beta1, this.time_step));


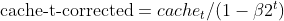
    matrix cache_hat = this.cache / (1 - MathPow(this.m_beta2, this.time_step));
  • 正規化：RMSpropと同様、現在の勾配は補正されたEMAと小さな平滑化項(ε)を使って正規化されます。
  • パラメータの更新：正規化された勾配に学習率(η)を掛けてパラメータの更新を決定します。
    parameters -= (this.m_learning_rate * moment_hat) / (MathPow(cache_hat, 0.5) + this.m_epsilon);

Adamオプティマイザのコンストラクタは次のようになっています。

OptimizerAdam(double learning_rate=0.01, double beta1=0.9, double beta2=0.999, double epsilon=1e-8);

学習率で呼び出しました。

nn.fit(x_train, y_train, new OptimizerAdam(nn_learning_rate), nn_epochs, nn_batch_size, show_batch);

その結果、損失対エポックのプロットが出来上がりました。

Adam損失対エポックのプロット

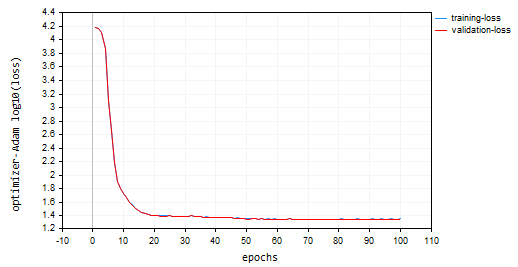
Adamは、SGDを除く先行オプティマイザよりも優れた性能を発揮し、訓練および検証訓練サンプルでそれぞれ約53%、52%の精度を示しました。

MD      0       15:23:37.651    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [90/100] training -> loss 22.05051037 accuracy 0.533 validation -> loss 21.92528 accuracy 0.529 | Elapsed 0.047 Seconds 
DS      0       15:23:37.703    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [91/100] training -> loss 22.38393234 accuracy 0.526 validation -> loss 22.25178 accuracy 0.522 | Elapsed 0.046 Seconds 
OK      0       15:23:37.756    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [92/100] training -> loss 22.12091827 accuracy 0.532 validation -> loss 21.99456 accuracy 0.528 | Elapsed 0.063 Seconds 
OR      0       15:23:37.808    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [93/100] training -> loss 21.94438889 accuracy 0.535 validation -> loss 21.81944 accuracy 0.532 | Elapsed 0.047 Seconds 
NI      0       15:23:37.862    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [94/100] training -> loss 22.41965082 accuracy 0.525 validation -> loss 22.28371 accuracy 0.522 | Elapsed 0.062 Seconds 
LQ      0       15:23:37.915    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [95/100] training -> loss 22.27254037 accuracy 0.528 validation -> loss 22.13931 accuracy 0.525 | Elapsed 0.047 Seconds 
FH      0       15:23:37.969    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [96/100] training -> loss 21.93193893 accuracy 0.536 validation -> loss 21.80427 accuracy 0.532 | Elapsed 0.047 Seconds 
LG      0       15:23:38.024    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [97/100] training -> loss 22.41523220 accuracy 0.525 validation -> loss 22.27900 accuracy 0.522 | Elapsed 0.063 Seconds 
MO      0       15:23:38.077    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [98/100] training -> loss 22.23551304 accuracy 0.529 validation -> loss 22.10466 accuracy 0.526 | Elapsed 0.046 Seconds 
QF      0       15:23:38.129    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [99/100] training -> loss 21.96662717 accuracy 0.535 validation -> loss 21.84087 accuracy 0.531 | Elapsed 0.063 Seconds 
GM      0       15:23:38.191    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [100/100] training -> loss 22.29715377 accuracy 0.528 validation -> loss 22.16686 accuracy 0.524 | Elapsed 0.062 Seconds


長所

  • AdamはSGDよりも早く収束することが多く、様々なシナリオにおいてRMSpropよりも効率的
  • 学習率の影響を受けにくい：SGDに比べ、Adamは学習率の選択に対する感度が低く、より堅牢
  • 非凸損失関数に適している：深層学習タスクで一般的な非凸損失関数を効果的に扱うことができる
  • 幅広い適用性：Adamの機能の組み合わせにより、様々なネットワークアーキテクチャやデータセットに広く適用できる

短所

  • ハイパーパラメータの調整：一般的に感度が低いが、それでも最適なパフォーマンスを得るためには、学習率や減衰率などのハイパーパラメータを調整する必要がある
  • メモリ使用量：EMAを維持すると、SGDに比べてメモリ消費量が若干多くなる可能性がある

使用シナリオ

ニューラルネットワークの訓練で以下が望まれる場合に使用します。

・より速い収束、ネットワークが学習速度にあまり影響を受けないようにしたい場合、また、勢いのある適応的な学習速度が必要な場合


04：AdaDelta (Adaptive Learning with delta)

ニューラルネットワークで使用されるもう1つの最適化アルゴリズムで、SGDやRMSPropと類似点があり、特定のモメンタム項を持つ適応学習率を提供します。

AdaDeltaは、SGDの固定学習率が収束の遅さや振動につながることに対処することを目的としており、RMSPropと同様に、過去の二乗勾配に基づいて調整する適応学習率を採用しています。

背後にある数学

  • 二乗差の指数移動平均(EMA)を維持し、各パラメータの連続したパラメータ更新間の二乗差（デルタ）のEMAを計算します。これは、パラメータがどれだけ変化したかという最近の歴史を反映しています。 


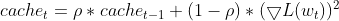
    this.cache = m_decay_rate * this.cache + (1 - m_decay_rate) * MathPow(gradients, 2);
  • 適応学習率：パラメータの現在の二乗勾配は、二乗デルタのEMA（平滑化項あり）で割られます。これは効果的に適応学習率として機能し、各パラメータの更新サイズを制御します。 


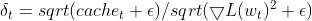
    matrix delta = lr * sqrt(this.cache + m_epsilon) / sqrt(pow(gradients, 2) + m_epsilon);

  • モメンタム：モメンタムSGDと同様に、パラメータの前回の更新を考慮するモメンタム項が組み込まれています。これにより、勾配が蓄積され、局所的な極小値から脱出できる可能性があります。

    AdaDeltaパラメータの更新 + モメンタム

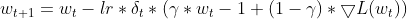
    matrix momentum_term = this.m_gamma * parameters + (1 - this.m_gamma) * gradients;

parameters -= delta * momentum_term;

ここで、

： 時間ステップtにおけるデルタの二乗のEMA

：減衰率（ハイパーパラメータ、通常は0.9から0.999の間）

：時間ステップtにおけるパラメータwに関する損失関数の勾配

：時間ステップtにおけるパラメータ値

：時間ステップt+1における更新パラメータ値

ε：平滑化項（通常は1e-8のような小さな値）

γ：モメンタム係数（ハイパーパラメータ、通常は0～1）

長所

  • より速く収束する：固定学習率を持つSGDと比較して、AdaDeltaは、特に非定常勾配を持つ問題に対して、しばしばより速く収束することができる
  • 局所最小値を脱出するためにモメンタムを使用：モメンタム項は、勾配を蓄積し、損失関数の局所的な極小値から逃れるのに役立つ
  • 学習率の影響を受けにくい：RMSpropと同様に、AdaDeltaはSGDよりも選択された特定の学習率の影響を受けにくい

短所

  • 最適なパフォーマンスを得るためには、減衰率(ρ)やモメンタム係数(γ)のようなハイパーパラメータの調整が必要 
    OptimizerAdaDelta(double learning_rate=0.01, double decay_rate=0.95, double gamma=0.9, double epsilon=1e-8);
  • 計算コストが高い：EMAを維持し、モメンタムを取り入れることで、SGDに比べて計算コストが若干高くなる

使用シナリオ

AdaDeltaは、あるシナリオにおいては貴重な代替策となりえます。

  • 非定常勾配：問題が非定常勾配を示す場合、AdaDeltaのモメンタムによる適応学習率が有効なことがある
  • 局所的最小値からの脱出が重要な状況では、AdaDeltaのモメンタム項が有利なことがある

AdaDeltaを使用して、100エポック、0.0001学習率でモデルを訓練しました。すべては他のオプティマイザで使用されているものと同じでした。

nn.fit(x_train, y_train, new OptimizerAdaDelta(nn_learning_rate), nn_epochs, nn_batch_size, show_batch);

損失とエポックのプロット

AdaDelta損失対エポックプロット

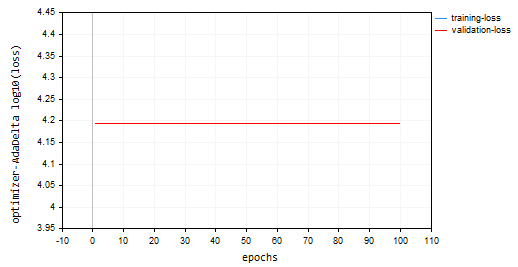
AdaDeltaオプティマイザは、訓練サンプルと検証サンプルで同じ損失値15625と約-335の精度を提供しました。何も学習できませんでした。RMSPropでおこなわれたもののようです。

NP      0       15:32:30.664    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [90/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.062 Seconds 
ON      0       15:32:30.724    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [91/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds 
IK      0       15:32:30.788    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [92/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.062 Seconds 
JQ      0       15:32:30.848    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [93/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds 
RO      0       15:32:30.914    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [94/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.062 Seconds 
PE      0       15:32:30.972    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [95/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds 
CS      0       15:32:31.029    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [96/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.047 Seconds 
DI      0       15:32:31.086    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [97/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.062 Seconds 
DG      0       15:32:31.143    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [98/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds 
FM      0       15:32:31.202    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [99/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.046 Seconds 
GI      0       15:32:31.258    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [100/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds


05：Nadam (Nesterov-accelerated Adaptive Moment Estimation)

この最適化アルゴリズムは、Adam (Adaptive Moment Estimation)とNesterovのモメンタムという2つの一般的な最適化手法の長所を組み合わせたものです。特にノイズの多い勾配がある状況において、Adamよりも収束が速く、性能が向上する可能性があります。

Nadamのアプローチ

Adamのコア機能を継承しています。

class OptimizerNadam: protected OptimizerAdam
  {
protected:
   double m_gamma;
   
    
public:
                     OptimizerNadam(double learning_rate=0.01, double beta1=0.9, double beta2=0.999, double gamma=0.9, double epsilon=1e-8);
                    ~OptimizerNadam(void);
                    
                    virtual void update(matrix &parameters, matrix &gradients);
  };
//+------------------------------------------------------------------+
//|  Initializes the Adam optimizer with hyperparameters.            |   
//|                                                                  |
//|  learning_rate: Step size for parameter updates                  |
//|  beta1: Decay rate for the first moment estimate                 |
//|     (moving average of gradients).                               |
//|  beta2: Decay rate for the second moment estimate                |
//|     (moving average of squared gradients).                       |
//|  epsilon: Small value for numerical stability.                   |
//+------------------------------------------------------------------+
OptimizerNadam::OptimizerNadam(double learning_rate=0.010000, double beta1=0.9, double beta2=0.999, double gamma=0.9, double epsilon=1e-8)
:OptimizerAdam(learning_rate, beta1, beta2, epsilon),
 m_gamma(gamma)
 {
 
 }

次が含まれます。

  • EMA（指数移動平均）の維持：Adamと同様に、二乗勾配のEMA(cache_t)とモーメントのEMA(m_t)を追跡します。



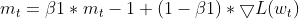
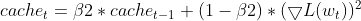
  • 適応学習率の計算：これらのEMAに基づいて、各パラメータを調整する適応学習率を計算します。
  • Nesterovのモメンタムを取り入れている：SGDから借用したNesterovのモメンタムの概念を使用します。これには以下が含まれます。 
  • 「peek」勾配：現在の勾配に基づいてパラメータを更新する前に、現在の勾配とモメンタム項を用いて「peek」勾配を推定します。 
  • Peek勾配で更新：パラメータ更新は、このpeek勾配を使用して実行されます。収束が速くなり、ノイズの多い勾配の取り扱いが改善される可能性があります。

背後にある数学

  • モーメントEMAの更新 (Adamと同じ)

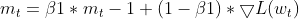
  • 二乗勾配EMAの更新（Adamと同じ）

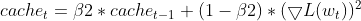
  • モーメントのバイアス補正（Adamと同じ）

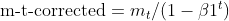
  • 二乗勾配のバイアス補正（Adamと同じ）

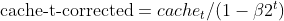
  • Nesterovのモメンタム（前の勾配推定値を使用）

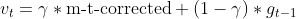
  • 前回の勾配推定値の更新
  • Nesterovのモメンタムによるパラメータの更新 
    Nesterovのモメンタムによる更新
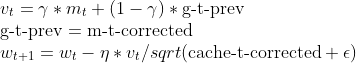
    matrix nesterov_moment = m_gamma * moment_hat + (1 - m_gamma) * gradients; // Nesterov accelerated gradient

parameters -= m_learning_rate * nesterov_moment / sqrt(cache_hat + m_epsilon); // Update parameters

長所

  • Adamと比較して、特にノイズの多い勾配を持つ問題に対して、より速い収束を達成できる可能性がある
  • Nesterovモメンタム項は、ノイズの多い勾配を平滑化するのに役立ち、パフォーマンスを向上させる
  • Adamの長所である適応性、学習率選択に対する感度の低さなどを維持している

短所

  • 最適なパフォーマンスを得るためには、学習率、減衰率、モメンタム係数などのハイパーパラメータを調整する必要がある
  • 有望であるが、すべてのシナリオでAdamを上回るとは限らない。さらなる研究と実験が必要

使用シナリオ

ノイズの多い勾配がある問題では、Adamに代わる素晴らしい選択肢となります。

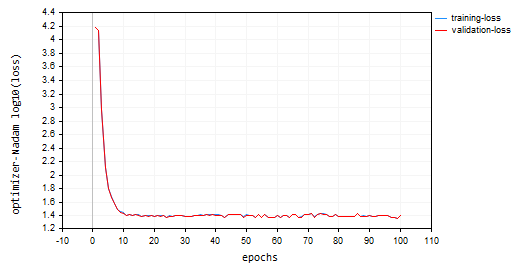
Nadamをデフォルトのパラメータと、これまで議論してきたオプティマイザと同じ学習率で呼び出しました。訓練セットと検証セットの両方で約47%の精度を出し、Adamに次いで2番手に終わりました。Nadamは、この記事で取り上げた他の方法よりも、局所最小値付近で多くの振動を起こしました。

IL      0       15:37:56.549    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [90/100] training -> loss 25.23632476 accuracy 0.466 validation -> loss 25.06902 accuracy 0.462 | Elapsed 0.062 Seconds 
LK      0       15:37:56.619    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [91/100] training -> loss 24.60851222 accuracy 0.479 validation -> loss 24.44829 accuracy 0.475 | Elapsed 0.078 Seconds 
RS      0       15:37:56.690    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [92/100] training -> loss 24.68657614 accuracy 0.477 validation -> loss 24.53442 accuracy 0.473 | Elapsed 0.078 Seconds 
IJ      0       15:37:56.761    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [93/100] training -> loss 24.89495551 accuracy 0.473 validation -> loss 24.73423 accuracy 0.469 | Elapsed 0.063 Seconds 
GQ      0       15:37:56.832    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [94/100] training -> loss 25.25899364 accuracy 0.465 validation -> loss 25.09940 accuracy 0.461 | Elapsed 0.078 Seconds 
QI      0       15:37:56.901    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [95/100] training -> loss 25.17698272 accuracy 0.467 validation -> loss 25.01065 accuracy 0.463 | Elapsed 0.063 Seconds 
FP      0       15:37:56.976    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [96/100] training -> loss 25.36663261 accuracy 0.463 validation -> loss 25.20273 accuracy 0.459 | Elapsed 0.078 Seconds 
FO      0       15:37:57.056    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [97/100] training -> loss 23.34069092 accuracy 0.506 validation -> loss 23.19590 accuracy 0.502 | Elapsed 0.078 Seconds 
OG      0       15:37:57.128    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [98/100] training -> loss 23.48894694 accuracy 0.503 validation -> loss 23.33753 accuracy 0.499 | Elapsed 0.078 Seconds 
ON      0       15:37:57.203    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [99/100] training -> loss 23.03205165 accuracy 0.512 validation -> loss 22.88233 accuracy 0.509 | Elapsed 0.062 Seconds 
ME      0       15:37:57.275    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [100/100] training -> loss 24.98193438 accuracy 0.471 validation -> loss 24.82652 accuracy 0.467 | Elapsed 0.079 Seconds

以下は、損失対エポックのグラフです。

Nadam損失対エポックグラフ

最後に

最適なオプティマイザの選択は、特定の問題、データセット、ネットワークアーキテクチャ、パラメータに依存します。ニューラルネットワークの訓練タスクに最も効果的なオプティマイザを見つけるには、実験が重要です。Adamは、収束が速く、学習速度にあまり影響されず、学習速度が勢いに応じて適応するため、多くのニューラルネットワークに最適なオプティマイザであることが証明されています。特に複雑な問題や、最初にどのオプティマイザを使用するべきかわからない場合に、最初に試してみるのに良い選択です。

幸運をお祈りします。

機械学習モデルの開発を追跡し、本連載で説明されている多くのことは、このGitHubレポに掲載されています。

添付ファイル

ファイル 説明/用途
MatrixExtend.mqh    行列操作のための追加関数
metrics.mqh         MLモデルのパフォーマンスを測定するための関数とコード 
preprocessing.mqh         生の入力データを前処理して機械学習モデルの使用に適したものにするためのライブラリ
plots.mqh  ベクトルと行列をプロットするためのライブラリ
optimizers.mqh   この記事で取り上げたすべてのニューラルネットワークオプティマイザを含むインクルードファイル
cross_validation.mqh  クロス検証テクニックを含むライブラリ 
Tensors.mqh  MQL5言語でプログラムされたテンソル、代数的3次元行列オブジェクトを含むライブラリ
Regressor Nets.mqh  回帰問題を解くためのニューラルネットワークを含む  
Optimization Algorithms testScript.mq5  すべてのインクルードファイルとデータセットからコードを実行するスクリプト
airfoil_noise_data.csv    翼型回帰問題データ


MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/14435

添付されたファイル |
ZIPをダウンロード
Code_k_Files.zip (39.41 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
MQL5で自己最適化エキスパートアドバイザーを構築する MQL5で自己最適化エキスパートアドバイザーを構築する
どのような市場にも対応できる専門的なエキスパートアドバイザー(EA)を構築します。
制約付きCustom Maxを実装するための一般的な最適化定式化(GOF) 制約付きCustom Maxを実装するための一般的な最適化定式化(GOF)
この記事では、MetaTrader 5端末の設定タブでCustom Maxを選択する際に、複数の目的と制約条件を持つ最適化問題を実装する方法を紹介します。最適化問題の例は、ドローダウンが10%未満、連敗回数が5回未満、1週間の取引回数が5回以上となるように、プロフィットファクター、ネットプロフィット、リカバリーファクターを最大化するといったものです。
MetaTrader 5用のMQTTクライアントの開発：TDDアプローチ（最終回） MetaTrader 5用のMQTTクライアントの開発：TDDアプローチ（最終回）
この記事は、MQTT 5.0プロトコルのネイティブMQL5クライアントの開発ステップを説明する連載の最終回です。ライブラリはまだ製品化されていませんが、この部分では、他の証券会社から入手したティック（またはレート）でカスタム銘柄を更新するためにクライアントを使用します。ライブラリの現在の状況、MQTT 5.0プロトコルに完全に準拠するために足りないもの、可能なロードマップ、そしてその開発をフォローし貢献する方法についての詳細は、この記事の最後をご覧ください。
MQL5入門（第6部）：MQL5における配列関数の入門ガイド MQL5入門（第6部）：MQL5における配列関数の入門ガイド
MQL5の旅の次の段階を始めましょう。この洞察に満ちて初心者に優しい記事では、残りの配列関数について調べ、複雑な概念を解明し、効率的な取引戦略を作成できるようにします。ArrayPrint、ArrayInsert、ArraySize、ArrayRange、ArrarRemove、ArraySwap、ArrayReverse、ArraySortについて説明します。アルゴリズム取引の専門知識を、これらの必要不可欠な配列関数で高めてください。一緒にMQL5マスターへの道を歩みましょう。