MetaTrader 5 / 测试者
English Русский Español Deutsch 日本語 Português
preview
数据科学和机器学习（第 21 部分）：解锁神经网络，优化算法揭秘

数据科学和机器学习（第 21 部分）：解锁神经网络，优化算法揭秘

MetaTrader 5 — 测试者 |
309 3
Omega J Msigwa
Omega J Msigwa

我并不是说神经网络很容易。您需要成为专家才能令这些事情起作用。但这些专业知识可在跨越广泛的应用中为您提供服务。从某种意义上说，以前投入到特征设计的所有努力，现在都投入到架构设计、损失函数设计、和优化制程设计。手工劳动已被提升到一个更高的抽象层次。

斯特凡诺·索托（Stefano Soatto）


概述

看似如今每个人都对人工智能感兴趣，它无处不在，openAI 背后如谷歌和微软等科技行业的大佬们正在推动人工智能在不同层面和行业的适配，譬如娱乐、医疗保健行业、艺术、创意、等等。 

我在 MQL5 社区中也看到了这种趋势，随着矩阵和向量、以及 ONNX 引入 MetaTrader5，为什么不呢。现在可以制作任何复杂的人工智能交易模型。您甚至不需要成为线性代数专家或书呆子，就足以理解塞进系统中的所有内容。

尽管如此，机器学习的基本面现在比以往任何时候都更难找到，但它们对于巩固您对 AI 的理解同样重要。它们让您知晓为什么您要这样做，这令您变得灵活、并让您行使自己的选择权。关于机器学习，我们还有很多事情需要讨论。今天，我们将看到什么是优化算法，它们如何相互竞争，您应当何时、选择哪种优化算法，以便为您的神经网络获得更好的性能和准确性。

神经网络优化

本文中讨论的内容将帮助您大致了解优化算法，这意味着即使在使用 Python 中的 Scikit-Learn、Tensorflow 或 Pytorch 模型时，这些知识也会对您有所帮助，因为无论您使用哪种编程语言，这些优化器都通用于所有神经网络。


什么是神经网络优化器？

根据定义，优化器是在训练期间优调神经网络参数的算法。它们的目标是最小化损失函数，最终提高性能。

简言之，神经网络优化器作用：

  1. 这些是影响神经网络的关键参数。优化器判定如何在每次训练迭代中修改每个参数。
  2. 优化器测量实际值与神经网络预测之间的差异。它们努力降低这种误差梯度。

如果您还没有阅读过之前的文章 《神经网络揭秘》，我建议您先阅读它。在本文中，我们将改进在这篇文章中从头开始搭建的神经网络模型，并往其中添加优化器。

在我们看到优化器有哪些不同类型之前，我们需要明白反向传播的算法。通常有三种算法；

  1. 随机梯度下降（SGD）
  2. 批量梯度下降（BGD）
  3. 小型批量梯度下降

01：随机梯度下降算法（SGD）

随机梯度下降（SGD）是一种训练神经网络的基础优化算法。它以最小化损失函数的方式迭代更新网络的权重和乖离。损失函数衡量网络预测与训练数据中的实际标签（目标值）之间的差异。

这些优化算法涉及的主要过程是相同的，它们包括：

  1. 迭代
  2. 反向传播
  3. 权重和乖离更新

这些算法在如何迭代处理、以及更新权重和乖离的频率方面有所不同。SGD 算法一次更新一个训练样本（数据点）的神经网络参数（权重和乖离）。

void CRegressorNets::backpropagation(const matrix& x, const vector &y)
 {   
    for (ulong epoch=0; epoch<epochs && !IsStopped(); epoch++)
      { 
        
        for (ulong iter=0; iter<rows; iter++) //iterate through all data points
          {             
             for (int layer=(int)mlp.hidden_layers-1; layer>=0 && !IsStopped(); layer--) //Loop through the network backward from last to first layer
               {    
                // find partial derivatives of each layer WRT the loss function dW and dB
                
                 
                //--- Weights updates
                 
                 optimizer_weights.update(W, dW);
                 optimizer_bias.update(B, dB);
                 
                 this.W_tensor.Add(W, layer);
                 this.B_tensor.Add(B, layer);
               }
         }
     }
 }

其优点：

  • 对于大型数据集，计算效率高。
  • 有时收敛速度比 BGD 和 Mini-batch 梯度下降更快，特别是对于非凸损失函数，因为它一次使用一个训练样本。
  • 善于避开局部最小值：由于 SGD 中的噪声更新，它有能力从局部最小值转义，并收敛到全局最小值。

缺点：

  • 更新可能会有噪音，导致训练期间出现之字折线行为。
  • 也许并不总能收敛到全局最小值。
  • 收敛速度较慢，可能需要更多的回合才能收敛，因为它每次更新一个训练示例的参数。
  • 学习率敏感：学习率的选择对于该算法至关重要，较高的学习率也许会导致算法越过全局最小值，而较低的学习率会减慢收敛过程。
随机梯度下降更适合优化非凸函数，因为它可以脱离局部最小值，并找到全局最小值。


02：批量梯度下降算法（BGD）：

与 SGD 不同，批量梯度下降（BGD）在每次迭代中使用到整个数据集计算梯度。

优点：

理论上，如果损失函数是平滑且凸的，则收敛到最小值。

缺点：

对于大型数据集，计算可能太昂贵，因为它需要反复处理整个数据集。

我不会在现有的神经网络中实现它，但可以像下面的小批量梯度下降一样轻松实现，若您愿意，您可自行实现它。


03：小批量梯度下降：

该算法是 SGD 和 BGD 之间的折衷方案，它在每次迭代中使用训练数据的一小部分（小批量）来更新网络参数。

优点：

  • 与 SGD 和 BGD 相比，在计算效率和更新稳定性之间提供了良好的平衡。
  • 可比 BGD 更有效地处理较大的数据集。

缺点：

  • 比之 SGD，也许需要对小批量规模进行更多调整。
  • 相比 SGD，计算更昂贵，且批量存储和处理亦会消耗大量内存。
  • 可能需要很长时间来训练许多大批量。

以下是小批量梯度下降算法的伪代码：

void CRegressorNets::backpropagation(const matrix& x, const vector &y, OptimizerSGD *sgd, const uint epochs, uint batch_size=0, bool show_batch_progress=false)
 {

  //....
    for (ulong epoch=0; epoch<epochs && !IsStopped(); epoch++)
      { 
               
            for (uint batch=0, batch_start=0, batch_end=batch_size; batch<num_batches; batch++, batch_start+=batch_size, batch_end=(batch_start+batch_size-1))
               {
                  matrix batch_x = MatrixExtend::Get(x, batch_start, batch_end-1);
                  vector batch_y = MatrixExtend::Get(y, batch_start, batch_end-1);
                  
                  rows = batch_x.Rows();              
                  
                    for (ulong iter=0; iter<rows ; iter++) //replace to rows 
                      {
                        pred_v[0] = predict(batch_x.Row(iter));
                        actual_v[0] = y[iter];
                        
                        // Find derivatives WRT weights dW and bias dB    
                        //....                    
                            
                         //--- Updating the weights using a given optimizer
                           
                           optimizer_weights.update(W, dW); 
                           optimizer_bias.update(B, dB);
                           
                           this.Weights_tensor.Add(W, layer);
                           this.Bias_tensor.Add(B, layer);  
                        }
                   }
       }
 }

默认情况下，在这两种算法的心脏中，它们具有一个简单的梯度下降更新规则，通常称为 SGD 或小-BGD 优化器。

class OptimizerSGD
  {
protected:
   double m_learning_rate;
   
public:
                     OptimizerSGD(double learning_rate=0.01);
                    ~OptimizerSGD(void);
                     
                    virtual void update(matrix &parameters, matrix &gradients);
  };
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
OptimizerSGD::OptimizerSGD(double learning_rate=0.01):
 m_learning_rate(learning_rate)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
OptimizerSGD::~OptimizerSGD(void)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void OptimizerSGD::update(matrix &parameters, matrix &gradients)
 {
    parameters -= this.m_learning_rate * gradients; //Simple gradient descent update rule
 }
 

//+------------------------------------------------------------------+
//|  Batch Gradient Descent (BGD): This optimizer computes the       |
//|  gradients of the loss function on the entire training dataset   |
//|  and updates the parameters accordingly. It can be slow and      |
//|  memory-intensive for large datasets but tends to provide a      |
//|  stable convergence.                                             |
//+------------------------------------------------------------------+


class OptimizerMinBGD: public OptimizerSGD
  {
public:
                     OptimizerMinBGD(double learning_rate=0.01);
                    ~OptimizerMinBGD(void);
  };
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
OptimizerMinBGD::OptimizerMinBGD(double learning_rate=0.010000): OptimizerSGD(learning_rate)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
OptimizerMinBGD::~OptimizerMinBGD(void)
 {
 
 }

现在我们用这两个优化器来训练一个模型，并观察结果，以便更好地理解它们：

#include <MALE5\MatrixExtend.mqh>
#include <MALE5\preprocessing.mqh>
#include <MALE5\metrics.mqh>
#include <MALE5\Neural Networks\Regressor Nets.mqh>
CRegressorNets *nn;


StandardizationScaler scaler;
vector open_, high_, low_;

vector hidden_layers = {5};
input uint nn_epochs = 100;
input double nn_learning_rate = 0.0001;
input uint nn_batch_size =32;
input bool show_batch = false;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---

  string headers;
  matrix dataset = MatrixExtend::ReadCsv("airfoil_noise_data.csv", headers);
  
  matrix x_train, x_test;
  vector y_train, y_test;
  
  MatrixExtend::TrainTestSplitMatrices(dataset, x_train, y_train, x_test, y_test, 0.7);
  
  nn = new CRegressorNets(hidden_layers, AF_RELU_, LOSS_MSE_); 
  
  x_train = scaler.fit_transform(x_train);
  
  nn.fit(x_train, y_train, new OptimizerMinBGD(nn_learning_rate), nn_epochs, nn_batch_size, show_batch);
   
  delete nn; 
  }

当 nn_batch_size 输入被分配一个大于零的数值时，无论将哪个优化器应用于 fit/backpropagation 函数，都将激活小批量梯度下降。

backprop CRegressorNets::backpropagation(const matrix& x, const vector &y, OptimizerSGD *optimizer, const uint epochs, uint batch_size=0, bool show_batch_progress=false)
 {
//...
//...

//--- Optimizer use selected optimizer when batch_size ==0 otherwise use the batch gradient descent
      
   OptimizerSGD optimizer_weights = optimizer;
   OptimizerSGD optimizer_bias = optimizer;
   
   if (batch_size>0)
    {
      OptimizerMinBGD optimizer_weights;
      OptimizerMinBGD optimizer_bias;
    }
     
//--- Cross validation

    CCrossValidation cross_validation;      
    CTensors *cv_tensor;
    matrix validation_data = MatrixExtend::concatenate(x, y);
    matrix validation_x;
    vector validation_y;
    
    cv_tensor = cross_validation.KFoldCV(validation_data, 10); //k-fold cross validation | 10 folds selected
    
//---

    matrix DELTA = {};
    double actual=0, pred=0;
    
    matrix temp_inputs ={};
    
    matrix dB = {}; //Bias Derivatives
    matrix dW = {}; //Weight Derivatives
    
   
    for (ulong epoch=0; epoch<epochs && !IsStopped(); epoch++)
      {        
        double epoch_start = GetTickCount(); 

        uint num_batches = (uint)MathFloor(x.Rows()/(batch_size+DBL_EPSILON));
        
        vector batch_loss(num_batches), 
               batch_accuracy(num_batches);
                       
         vector actual_v(1), pred_v(1), LossGradient = {};
         if (batch_size==0) //Stochastic Gradient Descent
          {
           for (ulong iter=0; iter<rows; iter++) //iterate through all data points
             {
               pred = predict(x.Row(iter));
               actual = y[iter];
               
               pred_v[0] = pred; 
               actual_v[0] = actual; 
   //---
                
                DELTA.Resize(mlp.outputs,1);
                
                for (int layer=(int)mlp.hidden_layers-1; layer>=0 && !IsStopped(); layer--) //Loop through the network backward from last to first layer
                  {    
                    //..... backpropagation and finding derivatives code        
                    
                    //-- Observation | DeLTA matrix is same size as the bias matrix
                    
                    W = this.Weights_tensor.Get(layer);
                    B = this.Bias_tensor.Get(layer);
                  
                   //--- Derivatives wrt weights and bias
                  
                    dB = DELTA;
                    dW = DELTA.MatMul(temp_inputs.Transpose());                   
                    
                   //--- Weights updates
                    
                    optimizer_weights.update(W, dW);
                    optimizer_bias.update(B, dB);
                    
                    this.Weights_tensor.Add(W, layer);
                    this.Bias_tensor.Add(B, layer);
                  }
             }
         }
        else //Batch Gradient Descent
          {
               
            for (uint batch=0, batch_start=0, batch_end=batch_size; batch<num_batches; batch++, batch_start+=batch_size, batch_end=(batch_start+batch_size-1))
               {
                  matrix batch_x = MatrixExtend::Get(x, batch_start, batch_end-1);
                  vector batch_y = MatrixExtend::Get(y, batch_start, batch_end-1);
                  
                  rows = batch_x.Rows();              
                  
                    for (ulong iter=0; iter<rows ; iter++) //iterate through all data points
                      {
                        pred_v[0] = predict(batch_x.Row(iter));
                        actual_v[0] = y[iter];
                        
            //---
                        
                      DELTA.Resize(mlp.outputs,1);
                      
                      for (int layer=(int)mlp.hidden_layers-1; layer>=0 && !IsStopped(); layer--) //Loop through the network backward from last to first layer
                        {    
                         //..... backpropagation and finding derivatives code   
                            }
                          
                          //-- Observation | DeLTA matrix is same size as the bias matrix
                          
                          W = this.Weights_tensor.Get(layer);
                          B = this.Bias_tensor.Get(layer);
                        
                         //--- Derivatives wrt weights and bias
                        
                          dB = DELTA;
                          dW = DELTA.MatMul(temp_inputs.Transpose());                   
                          
                         //--- Weights updates
                          
                          optimizer_weights.update(W, dW);
                          optimizer_bias.update(B, dB);
                          
                          this.Weights_tensor.Add(W, layer);
                          this.Bias_tensor.Add(B, layer);
                        }
                    }
                 
                 pred_v = predict(batch_x);
                 
                 batch_loss[batch] = pred_v.Loss(batch_y, ENUM_LOSS_FUNCTION(m_loss_function));
                 batch_loss[batch] = MathIsValidNumber(batch_loss[batch]) ? (batch_loss[batch]>1e6 ? 1e6 : batch_loss[batch]) : 1e6; //Check for nan and return some large value if it is nan
                 
                 batch_accuracy[batch] = Metrics::r_squared(batch_y, pred_v);
                 
                 if (show_batch_progress)
                  printf("----> batch[%d/%d] batch-loss %.5f accuracy %.3f",batch+1,num_batches,batch_loss[batch], batch_accuracy[batch]);  
              }
          }
          
//--- End of an epoch
      
        vector validation_loss(cv_tensor.SIZE);
        vector validation_acc(cv_tensor.SIZE);
        for (ulong i=0; i<cv_tensor.SIZE; i++)
          {
            validation_data = cv_tensor.Get(i);
            MatrixExtend::XandYSplitMatrices(validation_data, validation_x, validation_y);
            
            vector val_preds = this.predict(validation_x);;
            
            validation_loss[i] = val_preds.Loss(validation_y, ENUM_LOSS_FUNCTION(m_loss_function));
            validation_acc[i] = Metrics::r_squared(validation_y, val_preds);
          }
                  
        pred_v = this.predict(x);
        
        if (batch_size==0)
          {      
              backprop_struct.training_loss[epoch] = pred_v.Loss(y, ENUM_LOSS_FUNCTION(m_loss_function));
              backprop_struct.training_loss[epoch] = MathIsValidNumber(backprop_struct.training_loss[epoch]) ? (backprop_struct.training_loss[epoch]>1e6 ? 1e6 : backprop_struct.training_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan
              backprop_struct.validation_loss[epoch] = validation_loss.Mean();
              backprop_struct.validation_loss[epoch] = MathIsValidNumber(backprop_struct.validation_loss[epoch]) ? (backprop_struct.validation_loss[epoch]>1e6 ? 1e6 : backprop_struct.validation_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan
          }
        else
          {
              backprop_struct.training_loss[epoch] = batch_loss.Mean();
              backprop_struct.training_loss[epoch] = MathIsValidNumber(backprop_struct.training_loss[epoch]) ? (backprop_struct.training_loss[epoch]>1e6 ? 1e6 : backprop_struct.training_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan
              backprop_struct.validation_loss[epoch] = validation_loss.Mean();
              backprop_struct.validation_loss[epoch] = MathIsValidNumber(backprop_struct.validation_loss[epoch]) ? (backprop_struct.validation_loss[epoch]>1e6 ? 1e6 : backprop_struct.validation_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan
          }
          
        double epoch_stop = GetTickCount();  
        printf("--> Epoch [%d/%d] training -> loss %.8f accuracy %.3f validation -> loss %.5f accuracy %.3f | Elapsed %s ",epoch+1,epochs,backprop_struct.training_loss[epoch],Metrics::r_squared(y, pred_v),backprop_struct.validation_loss[epoch],validation_acc.Mean(),this.ConvertTime((epoch_stop-epoch_start)/1000.0));
     }
     
   isBackProp = false;
   
  if (CheckPointer(optimizer)!=POINTER_INVALID)  
    delete optimizer;
    
   return backprop_struct;
 }

结局：

随机梯度下降（SGD）：学习率 = 0.0001

随机梯度下降

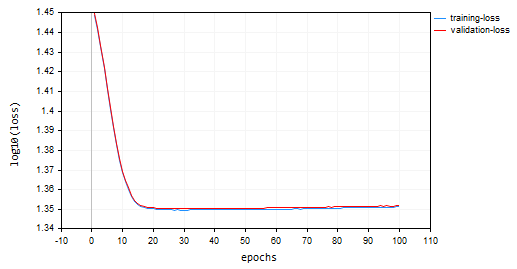
批量梯度下降（BGD）：学习率 = 0.0001，批量规模 = 16

批量梯度下降

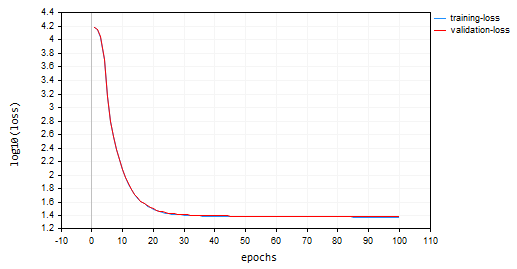
SGD 收敛得更快，在第 10 个回合左右接近局部最小值，而 BGD 在第 20 个回合左右，SGD 在训练和验证时都收敛到大约 60% 的准确率，而 BGD 在训练样本期间准确率为 15%，而在验证样本时为 13%。我们尚不能下结论，在于我们尚不确定 BGD 是否具有适合该数据集的最佳学习率、和批量规模。不同优化器的最佳工作表现也有不同的学习率。这也许是 SGD 无法执行的原因之一。然而，它收敛得很好，并未·围绕局部最小值振荡，这在 SGD 中是看不到的，BGD 图表是平滑的，表明稳定的训练过程，这是因为在 BGD 中，总体损失是独立批量的损失均值。

  backprop_struct.training_loss[epoch] = batch_loss.Mean();
  backprop_struct.training_loss[epoch] = MathIsValidNumber(backprop_struct.training_loss[epoch]) ? (backprop_struct.training_loss[epoch]>1e6 ? 1e6 : backprop_struct.training_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan
  backprop_struct.validation_loss[epoch] = validation_loss.Mean();
  backprop_struct.validation_loss[epoch] = MathIsValidNumber(backprop_struct.validation_loss[epoch]) ? (backprop_struct.validation_loss[epoch]>1e6 ? 1e6 : backprop_struct.validation_loss[epoch]) : 1e6; //Check for nan and return some large value if it is nan

您也许已经注意到，在绘图上，log10 已应用于绘图的损失值。这种常规化可确保很好地绘制损失值，因为在早期回合中，损失值有时可能更大。这旨在惩罚较大的值，如此这般它们最终在绘图中看起来不错。损失的实际值可以在智能选项卡中看到，而不是在图表上。

void CRegressorNets::fit(const matrix &x, const vector &y, OptimizerSGD *optimizer, const uint epochs, uint batch_size=0, bool show_batch_progress=false)
 {
  trained = true; //The fit method has been called
  
  vector epochs_vector(epochs);  for (uint i=0; i<epochs; i++) epochs_vector[i] = i+1;
  
  backprop backprop_struct;
  
  backprop_struct = this.backpropagation(x, y, optimizer, epochs, batch_size, show_batch_progress); //Run backpropagation
  

  CPlots plt;
  
  backprop_struct.training_loss = log10(backprop_struct.training_loss); //Logarithmic scalling
  plt.Plot("Loss vs Epochs",epochs_vector,backprop_struct.training_loss,"epochs","log10(loss)","training-loss",CURVE_LINES);
  backprop_struct.validation_loss = log10(backprop_struct.validation_loss);
  plt.AddPlot(backprop_struct.validation_loss,"validation-loss",clrRed);
  
   while (MessageBox("Close or Cancel Loss Vs Epoch plot to proceed","Training progress",MB_OK)<0)
    Sleep(1);

  isBackProp = false;
 }

SGD 优化器是最小化损失函数的通用工具，而 SGD 算法用于反向传播，是专为计算神经网络中的梯度而定制的特定技术。

将 SGD 优化器想象为木匠，将用于反向传播的 SGD 或小-BGD 算法视为其工具箱中的专用工具。


神经网络优化器的类型

除了我们刚刚讨论的 SGD 优化器之外。还有其它不同的神经网络优化器，每个优化器都采用不同的策略来达成最佳参数值，以下是一些最常用的神经网络优化器：

  1. 均方根传播（RMSProp）
  2. 自适应梯度下降（AdaGrad）
  3. 自适应矩估测（Adam）
  4. 阿达德尔塔（Adadelta）
  5. 涅斯捷罗夫（Nesterov）-加速自适应矩估测（Nadam）
这些优化器在反向传播期间应用于随机梯度下降算法。


01：均方根传播（RMSProp）

该优化算法旨在基于每个权重和乖离参数的历史梯度的适配调整学习率来解决随机梯度下降（SGD）的局限性。

SGD 的问题：

SGD 采用当前梯度和固定学习率更新权重和乖离。然而，在如神经网络这等复杂函数中，不同参数的梯度大小可能会有很大差异。这能导致收敛缓慢，因为依据小梯度参数也许会更新得非常缓慢，从而阻碍整体学习，并且 SGD 还会导致较大的振荡，因为依据大梯度参数在更新期间也许会经历过度波动，从而令学习过程不稳定。

理论：

此处是 RMSprop 背后的核心思想：

  • 保持平方梯度的指数移动平均线（EMA）。对于每个参数，RMSprop 跟踪平方梯度的指数衰减平均值。该平均值反映了最近有多少参数应当更新的历史记录。
    rms prop 更新平方梯度
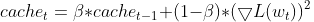
  • 常规化梯度。每个参数的当前梯度除以平方梯度的 EMA 的平方根，以及一个小的平滑项（通常用 ε 表示），从而避免除零。
  • 更新参数。将常规化梯度乘以学习率，以便判定参数的更新。
    rmsprop 更新参数

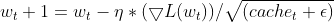
其中：

 时间步 t 处的平方梯度的 EMA

 衰减率（超参数，典型值介于 0.9 和 0.999 之间）- 控制过去梯度的影响

 损失函数在时间步 t 处相对于参数 w 的梯度

 时间步 t 处的参数值

 更新的时间步 t+1 处的参数值

η：学习率（超参数）

ε：平滑项（通常为小值，如 1e-8）

class OptimizerRMSprop
  {
protected:
   double m_learning_rate;
   double m_decay_rate;
   double m_epsilon;
   
   matrix<double> cache;
   
   //Dividing double/matrix causes compilation error | this is the fix to the issue
   matrix divide(const double numerator, const matrix &denominator)
    {
      matrix res = denominator;
      
      for (ulong i=0; i<denominator.Rows(); i++)
        res.Row(numerator / denominator.Row(i), i);
     return res;
    }
    
public:
                     OptimizerRMSprop(double learning_rate=0.01, double decay_rate=0.9, double epsilon=1e-8);
                    ~OptimizerRMSprop(void);
                    
                    virtual void update(matrix& parameters, matrix& gradients);
  };
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
OptimizerRMSprop::OptimizerRMSprop(double learning_rate=0.01, double decay_rate=0.9, double epsilon=1e-8):
 m_learning_rate(learning_rate),
 m_decay_rate(decay_rate),
 m_epsilon(epsilon)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
OptimizerRMSprop::~OptimizerRMSprop(void)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void OptimizerRMSprop::update(matrix &parameters,matrix &gradients)
 {
 
   if (cache.Rows()!=parameters.Rows() || cache.Cols()!=parameters.Cols())
    {
     cache.Init(parameters.Rows(), parameters.Cols());
     cache.Fill(0.0);
    }
     
//---
    
    cache += m_decay_rate * cache + (1 - m_decay_rate) * MathPow(gradients, 2);
    parameters -= divide(m_learning_rate, cache + m_epsilon) * gradients;
 }

与之前的优化器采用的默认值相同，100 个回合和 0.0001。神经网络 100 个回合后仍未能收敛，它在训练和验证样本中分别提供了大约 -319 和 -324 的准确率。按这样的配速，看似要需要超过 1000 个回合，假设我们采用较大的回合数量不会跨过局部最小值。

HK      0       15:10:15.632    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [90/100] training -> loss 15164.85487215 accuracy -320.064 validation -> loss 15164.99272 accuracy -325.349 | Elapsed 0.031 Seconds 
HQ      0       15:10:15.663    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [91/100] training -> loss 15161.78717397 accuracy -319.999 validation -> loss 15161.92323 accuracy -325.283 | Elapsed 0.031 Seconds 
DO      0       15:10:15.694    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [92/100] training -> loss 15158.07142844 accuracy -319.921 validation -> loss 15158.20512 accuracy -325.203 | Elapsed 0.031 Seconds 
GE      0       15:10:15.727    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [93/100] training -> loss 15154.92004326 accuracy -319.854 validation -> loss 15155.05184 accuracy -325.135 | Elapsed 0.032 Seconds 
GS      0       15:10:15.760    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [94/100] training -> loss 15151.84229952 accuracy -319.789 validation -> loss 15151.97226 accuracy -325.069 | Elapsed 0.031 Seconds 
DH      0       15:10:15.796    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [95/100] training -> loss 15148.77653633 accuracy -319.724 validation -> loss 15148.90466 accuracy -325.003 | Elapsed 0.031 Seconds 
MF      0       15:10:15.831    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [96/100] training -> loss 15145.56414236 accuracy -319.656 validation -> loss 15145.69033 accuracy -324.934 | Elapsed 0.047 Seconds 
IL      0       15:10:15.869    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [97/100] training -> loss 15141.85430749 accuracy -319.577 validation -> loss 15141.97859 accuracy -324.854 | Elapsed 0.031 Seconds 
KJ      0       15:10:15.906    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [98/100] training -> loss 15138.40751503 accuracy -319.504 validation -> loss 15138.52969 accuracy -324.780 | Elapsed 0.032 Seconds 
PP      0       15:10:15.942    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [99/100] training -> loss 15135.31136641 accuracy -319.439 validation -> loss 15135.43169 accuracy -324.713 | Elapsed 0.046 Seconds 
NM      0       15:10:15.975    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [100/100] training -> loss 15131.73032246 accuracy -319.363 validation -> loss 15131.84854 accuracy -324.636 | Elapsed 0.032 Seconds

损失与回合图：100 个回合，0.0001 学习率。

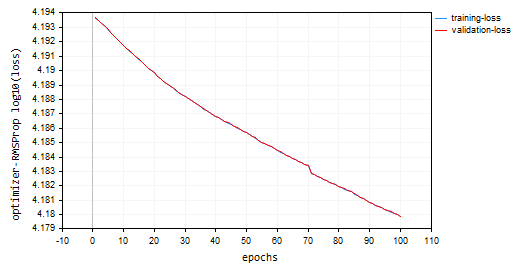
何处使用 RMSProp？

适用于非平稳目标、稀疏梯度，比 Adam 更简单。


02：Adagrad（自适应梯度算法）

Adagrad 是一种神经网络优化器，它利用类似于 RMSprop 的自适应学习率。不过，Adagrad 和 RMSprop 在方式上存在一些关键差异。

背后的数学：

  • 它累积了过去的梯度。Adagrad 在整个训练过程中跟踪每个参数的梯度平方和。该累积值反映的是有多少参数在过去已被更新。 

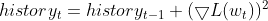
    cache += MathPow(gradients, 2);
  • 常规化梯度。每个参数的当前梯度除以累积梯度平方和的平方根，以及一个小的平滑项（通常用 ε 表示），从而避免除零。
  • 更新参数。将常规化梯度乘以学习率，以便判定参数的更新。 

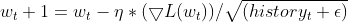
    parameters -= divide(this.m_learning_rate,  MathSqrt(cache + this.m_epsilon)) * gradients;

nn_learning_rate = 0.0001, epochs = 100

  nn.fit(x_train, y_train, new OptimizerAdaGrad(nn_learning_rate), nn_epochs, nn_batch_size, show_batch);

亏损对比回合图：


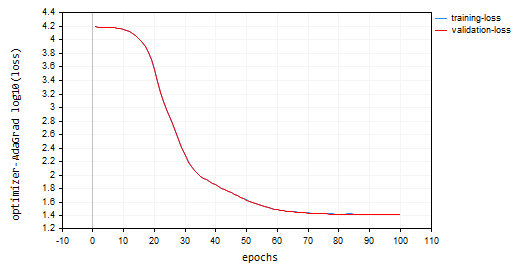
Adagrad 的学习曲线更陡峭，在更新期间非常稳定，但它需要 100 多个回合才能收敛，因为它最终的训练和验证样本准确率分别约为 44%。

RK      0       15:15:52.202    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [90/100] training -> loss 26.22261537 accuracy 0.445 validation -> loss 26.13118 accuracy 0.440 | Elapsed 0.031 Seconds 
ER      0       15:15:52.239    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [91/100] training -> loss 26.12443561 accuracy 0.447 validation -> loss 26.03635 accuracy 0.442 | Elapsed 0.047 Seconds 
NJ      0       15:15:52.277    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [92/100] training -> loss 26.11449352 accuracy 0.447 validation -> loss 26.02561 accuracy 0.442 | Elapsed 0.032 Seconds 
IQ      0       15:15:52.316    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [93/100] training -> loss 26.09263184 accuracy 0.448 validation -> loss 26.00461 accuracy 0.443 | Elapsed 0.046 Seconds 
NH      0       15:15:52.354    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [94/100] training -> loss 26.14277865 accuracy 0.447 validation -> loss 26.05529 accuracy 0.442 | Elapsed 0.032 Seconds 
HP      0       15:15:52.393    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [95/100] training -> loss 26.09559950 accuracy 0.448 validation -> loss 26.00845 accuracy 0.443 | Elapsed 0.047 Seconds 
PO      0       15:15:52.442    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [96/100] training -> loss 26.05409769 accuracy 0.448 validation -> loss 25.96754 accuracy 0.443 | Elapsed 0.046 Seconds 
PG      0       15:15:52.479    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [97/100] training -> loss 25.98822082 accuracy 0.450 validation -> loss 25.90384 accuracy 0.445 | Elapsed 0.032 Seconds 
PN      0       15:15:52.519    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [98/100] training -> loss 25.98781231 accuracy 0.450 validation -> loss 25.90438 accuracy 0.445 | Elapsed 0.047 Seconds 
EE      0       15:15:52.559    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [99/100] training -> loss 25.91146212 accuracy 0.451 validation -> loss 25.83083 accuracy 0.446 | Elapsed 0.031 Seconds 
CN      0       15:15:52.595    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [100/100] training -> loss 25.87412572 accuracy 0.452 validation -> loss 25.79453 accuracy 0.447 | Elapsed 0.047 Seconds

Adagrad 的优点：

对于稀疏特征，它收敛得更快。在由于数据中的稀疏特征而导致许多参数不会频繁更新的情况下，Adagrad 可以有效地降低它们的学习率，从而允许这些参数更快地收敛。

Adagrad 的局限性：

随着时间的推移，Adagrad 中累积的梯度平方和不断增长，导致所有参数的学习率不断降低。这最终会阻碍训练进度。

何时使用 Adagrad：

在稀疏特征数据集中：在与许多特征不会频繁更新的数据集打交道时，Adagrad 可以有效地加快这些参数的收敛速度。

在训练的早期阶段：在某些场景下，在训练后期切换到另一个优化器之前，由 Adagrad 调整初始学习率可能会有所帮助。


03：自适应矩估测（Adam）

一种广泛用于训练神经网络的高效优化算法。它结合了 AdaGrad 和 RMSprop 的优点来解决各自的局限性，并提供高效稳定的学习。

理论：

Adam 有两个关键特征;

  • 梯度的指数移动平均线（EMA）：类似于 RMSprop，Adam 维护平方梯度的 EMA（缓存）以便捕获每个参数所需的最新更新历史记录。
  • 动量指数移动平均线：Adam 引入了另一个 EMA（动量），其跟踪梯度本身的运行平均值。这有助于缓解某些网络架构中可能出现的梯度消失问题。

常规化和更新：

  • 动量更新：当前梯度用于更新动量 EMA（m_t）。 
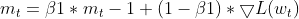
    this.moment = this.m_beta1 * this.moment + (1 -  this.m_beta1) * gradients;
  • 平方梯度更新：当前的平方梯度用于更新平方梯度 EMA（cache_t）。 


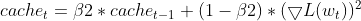
    this.cache = this.m_beta2 * this.cache + (1 -  this.m_beta2) * MathPow(gradients, 2);
  • 乖离校正：EMA（moment_t 和 cache_t）都使用指数衰减因子（β1 和 β2）进行乖离校正，从而确保它们是真实动量的无乖离估测。 


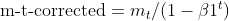
    matrix moment_hat = this.moment / (1 - MathPow(this.m_beta1, this.time_step));


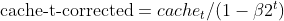
    matrix cache_hat = this.cache / (1 - MathPow(this.m_beta2, this.time_step));
  • 常规化：类似于 RMSprop，当前梯度常规化时会·采用校正后的 EMA 和小额平滑项（ε）。
  • 参数更新：常规化梯度乘以学习率（η），从而判定参数的更新。 
    parameters -= (this.m_learning_rate * moment_hat) / (MathPow(cache_hat, 0.5) + this.m_epsilon);

这是 Adam 优化器的构造函数的样子：

OptimizerAdam(double learning_rate=0.01, double beta1=0.9, double beta2=0.999, double epsilon=1e-8);

我依据学习率来调用它：

nn.fit(x_train, y_train, new OptimizerAdam(nn_learning_rate), nn_epochs, nn_batch_size, show_batch);

结果损失对比回合图：

adam 损失对比回合图

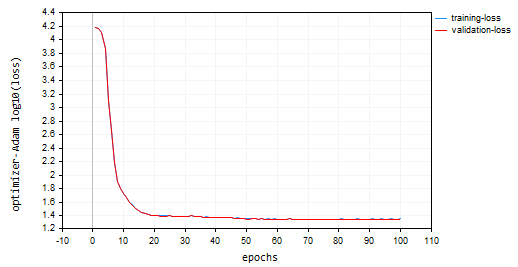
Adam 的性能优于先前来自 SGD 的优化器，在训练和验证训练样本上分别提供了大约 53% 和 52% 的准确率。

MD      0       15:23:37.651    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [90/100] training -> loss 22.05051037 accuracy 0.533 validation -> loss 21.92528 accuracy 0.529 | Elapsed 0.047 Seconds 
DS      0       15:23:37.703    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [91/100] training -> loss 22.38393234 accuracy 0.526 validation -> loss 22.25178 accuracy 0.522 | Elapsed 0.046 Seconds 
OK      0       15:23:37.756    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [92/100] training -> loss 22.12091827 accuracy 0.532 validation -> loss 21.99456 accuracy 0.528 | Elapsed 0.063 Seconds 
OR      0       15:23:37.808    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [93/100] training -> loss 21.94438889 accuracy 0.535 validation -> loss 21.81944 accuracy 0.532 | Elapsed 0.047 Seconds 
NI      0       15:23:37.862    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [94/100] training -> loss 22.41965082 accuracy 0.525 validation -> loss 22.28371 accuracy 0.522 | Elapsed 0.062 Seconds 
LQ      0       15:23:37.915    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [95/100] training -> loss 22.27254037 accuracy 0.528 validation -> loss 22.13931 accuracy 0.525 | Elapsed 0.047 Seconds 
FH      0       15:23:37.969    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [96/100] training -> loss 21.93193893 accuracy 0.536 validation -> loss 21.80427 accuracy 0.532 | Elapsed 0.047 Seconds 
LG      0       15:23:38.024    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [97/100] training -> loss 22.41523220 accuracy 0.525 validation -> loss 22.27900 accuracy 0.522 | Elapsed 0.063 Seconds 
MO      0       15:23:38.077    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [98/100] training -> loss 22.23551304 accuracy 0.529 validation -> loss 22.10466 accuracy 0.526 | Elapsed 0.046 Seconds 
QF      0       15:23:38.129    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [99/100] training -> loss 21.96662717 accuracy 0.535 validation -> loss 21.84087 accuracy 0.531 | Elapsed 0.063 Seconds 
GM      0       15:23:38.191    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [100/100] training -> loss 22.29715377 accuracy 0.528 validation -> loss 22.16686 accuracy 0.524 | Elapsed 0.062 Seconds


Adam 的优点：

  • 收敛速度更快：Adam 的收敛速度往往比 SGD 快，并且多种场景下可能比 RMSprop 更高效。
  • 对学习率低敏感：与 SGD 相比，Adam 对学习率的选择敏感度较低，令其更稳健。
  • 适用于非凸损失函数：它能有效地处理深度学习任务中常见的非凸损失函数。
  • 广泛的适用性：Adam 的功能组合令其成为广泛适用于各种网络架构和数据集的优化器。

缺点：

  • 超参数调谐：虽然通常敏感度低，但 Adam 仍然需要超参数调谐（如学习率和衰减率）来获得最优性能。
  • 内存占用：相比 SGD，维护 EMA 可能会导致内存消耗略高。

何处使用 Adam？

使用 Adam（自适应动量评测）训练神经网络的场景，当您打算：

更快的收敛。您希望您的网络对学习率不那么敏感，并且当您希望依据动量自适应学习率时。


04：Adadelta（依据增量的自适应学习）

这是神经网络中所用的另一种优化算法，它与 SGD 和 RMSProp 有一些相似之处，提供凭借特定动量项的自适应学习率。

Adadelta 旨在解决 SGD 固定学习率问题，该问题会导致收敛缓慢和振荡。它采用自适应学习率，基于过去的平方梯度进行调整，类似于 RMSProp。

背后的数学：

  • 维护平方增量的指数移动平均线（EMA），Adadelta 计算每个参数的连续参数更新（deltas）之间的平方差 EMA。这反映了近期有多少参数更新的历史记录。 


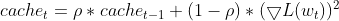
    this.cache = m_decay_rate * this.cache + (1 - m_decay_rate) * MathPow(gradients, 2);
  • 自适应学习率：参数的当前平方梯度除以平方增量 EMA（使用平滑项）。这可有效地服务于自适应学习率，控制每个参数的更新规模。 


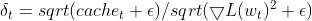
    matrix delta = lr * sqrt(this.cache + m_epsilon) / sqrt(pow(gradients, 2) + m_epsilon);

  • 动量：Adadelta 吸纳了一个动量项，其考虑到参数的上一次更新，类似于动量 SGD。这有助于累积梯度，并有脱离局部最小值的能力。

    adadelta 参数更新 + 动量

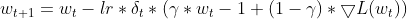
    matrix momentum_term = this.m_gamma * parameters + (1 - this.m_gamma) * gradients;

parameters -= delta * momentum_term;

其中：

：时间步 t 处平方增量 EMA

：衰减率（超参数，通常介于 0.9 和 0.999 之间）

：在时间步 t 处相对于参数 w 的损失函数梯度

：时间步 t 处的参数值

：时间步 t+1 处更新的参数值

ε：平滑项（通常为小值，如 1e-8）

γ：动量系数（超参数，典型情况介于 0 和 1 之间）

Adadelta 的优点：

  • 收敛更快：相比依据固定学习率的 SGD，Adadelta 通常收敛得更快，尤其是对于非平稳梯度的问题。
  • 它使用动量来脱离局部最小值：动量项有助于累积梯度，并有在损失函数中脱离局部最小值的潜力。
  • 对学习率敏感度低：类似于 RMSprop，Adadelta 对所选的特定学习率的敏感度低于 SGD。

Adadelta 的缺点：

  • 需要调谐衰减率（ρ）、和动量系数（γ） 等超参数，从而获得最优性能。 
    OptimizerAdaDelta(double learning_rate=0.01, double decay_rate=0.95, double gamma=0.9, double epsilon=1e-8);
  • 计算昂贵：相比 SGD，维护 EMA 并结合动量会略微增加计算成本。

何处使用 Adadelta：

在某些情况下，Adadelta 可能是一个有价值的替代方案：

  • 非平稳梯度。如果您的问题表现出非平稳梯度，则 Adadelta 依据动量的自适应学习率也许是有益的。
  • 在场景中脱离局部最小值是至关重要的，Adadelta 的动量项可能是有利的。

我使用 adadelta 训练了模型，100 个回合，学习率为 0.0001。一切都与其它优化器中所用的相同：

nn.fit(x_train, y_train, new OptimizerAdaDelta(nn_learning_rate), nn_epochs, nn_batch_size, show_batch);

亏损对比回合图：

adadelta 损失对比回合图

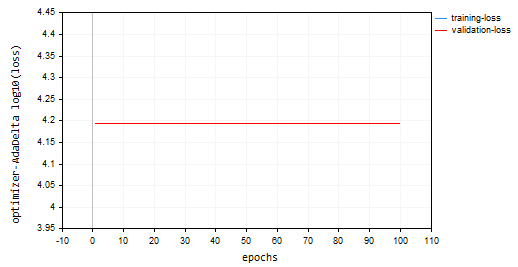
Adadelta 优化器未能学到任何东西，因为它在训练和验证样本上提供了相同的损失值 15625，和大约 -335 的准确率，看起来就像 RMSProp 所做的那样。

NP      0       15:32:30.664    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [90/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.062 Seconds 
ON      0       15:32:30.724    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [91/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds 
IK      0       15:32:30.788    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [92/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.062 Seconds 
JQ      0       15:32:30.848    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [93/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds 
RO      0       15:32:30.914    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [94/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.062 Seconds 
PE      0       15:32:30.972    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [95/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds 
CS      0       15:32:31.029    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [96/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.047 Seconds 
DI      0       15:32:31.086    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [97/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.062 Seconds 
DG      0       15:32:31.143    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [98/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds 
FM      0       15:32:31.202    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [99/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.046 Seconds 
GI      0       15:32:31.258    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [100/100] training -> loss 15625.71263806 accuracy -329.821 validation -> loss 15626.09899 accuracy -335.267 | Elapsed 0.063 Seconds


05：Nadam：涅斯捷罗夫（Nesterov）-加速自适应动量估测

该优化算法结合了两个流行的优化器的优点：Adam（自适应动量评测）和涅斯捷罗夫动量。与 Adam 相比，它旨在实现更快的收敛、和更好的性能潜力，尤其是在配以嘈杂梯度的情况下。

Nadam 的方式：

它继承了 Adam 的核心功能：

class OptimizerNadam: protected OptimizerAdam
  {
protected:
   double m_gamma;
   
    
public:
                     OptimizerNadam(double learning_rate=0.01, double beta1=0.9, double beta2=0.999, double gamma=0.9, double epsilon=1e-8);
                    ~OptimizerNadam(void);
                    
                    virtual void update(matrix &parameters, matrix &gradients);
  };
//+------------------------------------------------------------------+
//|  Initializes the Adam optimizer with hyperparameters.            |   
//|                                                                  |
//|  learning_rate: Step size for parameter updates                  |
//|  beta1: Decay rate for the first moment estimate                 |
//|     (moving average of gradients).                               |
//|  beta2: Decay rate for the second moment estimate                |
//|     (moving average of squared gradients).                       |
//|  epsilon: Small value for numerical stability.                   |
//+------------------------------------------------------------------+
OptimizerNadam::OptimizerNadam(double learning_rate=0.010000, double beta1=0.9, double beta2=0.999, double gamma=0.9, double epsilon=1e-8)
:OptimizerAdam(learning_rate, beta1, beta2, epsilon),
 m_gamma(gamma)
 {
 
 }

包括：

  • 维护 EMA（指数移动平均线）：它跟踪平方梯度 EMA（cache_t），和动量 EMA（m_t），类似于 Adam。



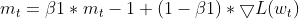
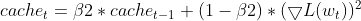
  • 自适应学习率计算：基于这些 EMA，针对每个参数调整，它会计算自适应学习率。
  • 它结合了涅斯捷罗夫动量：Nadam 借用的涅斯捷罗夫动量的概念，来自 SGD 搭配涅斯捷罗夫动量。这涉及：
  • “窥视”梯度：基于当前梯度更新参数之前，Nadam 采用当前梯度和动量项估算“窥视”梯度。 
  • 依据“窥视”梯度进行更新：然后使用该“窥视”梯度执行参数更新，潜在地会导致更快的收敛，以及改进对噪声梯度的处理。

Nadam 背后的数学：

  • 更新动量 EMA（与 Adam 相同）

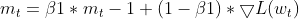
  • 更新平方梯度 EMA（与 Adam 相同）

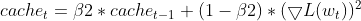
  • 动量的乖离校正（与 Adam 相同）

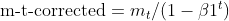
  • 平方梯度的乖离校正（与 Adam 相同）

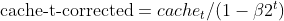
  • 涅斯捷罗夫（Nesterov）动量（采用以前的梯度估算）

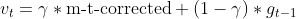
  • 更新之前的梯度估值
  • 依据涅斯捷罗夫动量更新参数 
    涅斯捷罗夫动量更新 
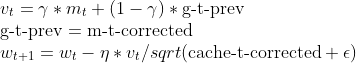
    matrix nesterov_moment = m_gamma * moment_hat + (1 - m_gamma) * gradients; // Nesterov accelerated gradient

parameters -= m_learning_rate * nesterov_moment / sqrt(cache_hat + m_epsilon); // Update parameters

Nadam 的优点：

  • 它更快：相比 Adam，Nadam 有可能达成更快的收敛，尤其是对于依据嘈杂梯度的问题。
  • 它更擅长处理嘈杂梯度：Nadam 中的涅斯捷罗夫动量项有助于平滑嘈杂梯度，并获得更好的性能。
  • 它具有 Adam 的优点：它保留了 Adam 的优点，例如自适应性、且对于学习率的选择敏感度较低。

缺点：

  • 需要调谐超参数，如学习速率、衰减速率、和动量系数，从而获得最优性能。
  • 虽然 Nadam 展现出前景，它也许并不总是在所有场景下都优于 Adam。需要进一步的研究和实验。

何处使用 Nadam？

在存在嘈杂梯度的问题中，它可以很好地替代 Adam。

我采用默认参数调用 Nadam，以及我们之前讨论优化器时所有用到的相同学习率。最终 Adam 在我的排名中位于第二，在训练集和验证集上都提供了大约 47% 的准确率。与本文中讨论的其它方法相比，Nadam 围绕局部最小值进行了多次振荡。

IL      0       15:37:56.549    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [90/100] training -> loss 25.23632476 accuracy 0.466 validation -> loss 25.06902 accuracy 0.462 | Elapsed 0.062 Seconds 
LK      0       15:37:56.619    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [91/100] training -> loss 24.60851222 accuracy 0.479 validation -> loss 24.44829 accuracy 0.475 | Elapsed 0.078 Seconds 
RS      0       15:37:56.690    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [92/100] training -> loss 24.68657614 accuracy 0.477 validation -> loss 24.53442 accuracy 0.473 | Elapsed 0.078 Seconds 
IJ      0       15:37:56.761    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [93/100] training -> loss 24.89495551 accuracy 0.473 validation -> loss 24.73423 accuracy 0.469 | Elapsed 0.063 Seconds 
GQ      0       15:37:56.832    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [94/100] training -> loss 25.25899364 accuracy 0.465 validation -> loss 25.09940 accuracy 0.461 | Elapsed 0.078 Seconds 
QI      0       15:37:56.901    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [95/100] training -> loss 25.17698272 accuracy 0.467 validation -> loss 25.01065 accuracy 0.463 | Elapsed 0.063 Seconds 
FP      0       15:37:56.976    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [96/100] training -> loss 25.36663261 accuracy 0.463 validation -> loss 25.20273 accuracy 0.459 | Elapsed 0.078 Seconds 
FO      0       15:37:57.056    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [97/100] training -> loss 23.34069092 accuracy 0.506 validation -> loss 23.19590 accuracy 0.502 | Elapsed 0.078 Seconds 
OG      0       15:37:57.128    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [98/100] training -> loss 23.48894694 accuracy 0.503 validation -> loss 23.33753 accuracy 0.499 | Elapsed 0.078 Seconds 
ON      0       15:37:57.203    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [99/100] training -> loss 23.03205165 accuracy 0.512 validation -> loss 22.88233 accuracy 0.509 | Elapsed 0.062 Seconds 
ME      0       15:37:57.275    Optimization Algorithms testScript (EURUSD,H1)  --> Epoch [100/100] training -> loss 24.98193438 accuracy 0.471 validation -> loss 24.82652 accuracy 0.467 | Elapsed 0.079 Seconds

以下是损失对比回合图：

nadam 损失对比回合图：

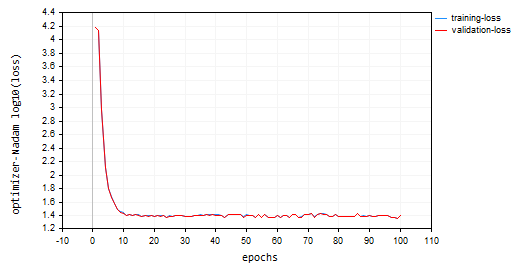
后记

最佳优化器的选择取决于您的具体问题、数据集、网络架构、和参数。实验是为神经网络训练任务找到最有效优化器的关键。Adam 被证明是许多神经网络的最佳优化器，因为它能够更快地收敛，对学习率敏感度低，并依据动量适配其学习率。首先尝试是一个不错的选择，尤其是对于复杂的问题，或当您最初不确定要用哪个优化器时。

愿您安好。

据该 GitHub 存储库，跟踪机器学习模型的开发，并讨论本系列文章中的更多内容。

附件：

文件 说明/用法
MatrixExtend.mqh    具有用于矩阵操作的附加函数。
metrics.mqh         包含用于衡量 ML 模型性能的函数和代码。 
preprocessing.mqh         预处理原始输入数据的函数库，令其适合机器学习模型的用法。
plots.mqh  绘制向量和矩阵的库
optimizers.mqh   包含本文中讨论的所有神经网络优化器的 Include 文件
cross_validation.mqh  包含交叉验证技术的库 
Tensors.mqh  一个包含张量、代数 3D 矩阵对象的函数库，以普通 MQL5 语言编程
Regressor Nets.mqh  包含用于求解回归问题的神经网络  
Optimization Algorithms testScript.mq5  用于从所有包含文件和数据集运行代码的脚本/This is the main file
airfoil_noise_data.csv    翼型回归问题数据


本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/14435

附加的文件 |
下载ZIP
Code_k_Files.zip (39.41 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.

该作者的其他文章

最近评论 | 前往讨论 (3)
Andrey Dik
Andrey Dik | 21 11月 2024 在 13:07

文章中的脚本出现错误：

2024.11.21 15:09:16.213 Optimisation Algorithms testScript(EURUSD,M1) Zero divide, check divider for zero to avoid this error in 'D:\Market\MT5\MQL5\Scripts\Optimization Algorithms testScript.ex5'.

Andrey Dik
Andrey Dik | 21 11月 2024 在 13:30
Andrey Dik (EURUSD,M1) Zero divide, check divider for zero to avoid this error in 'D:\Market\MT5\MQL5\Scripts\Optimization Algorithms testScript.ex5'.

问题原来是脚本没有找到包含训练数据的文件。但无论如何，如果找不到数据文件，程序应该会处理这种情况。

但现在出现了这样的问题：

2024.11.21 17:27:37.038 优化算法 testScript (EURUSD,M1) 找到 50 个未删除的动态对象：
2024.11.21 17:27:37.038 优化算法 testScript (EURUSD,M1) 10 个 'CTensors' 类对象
2024.11.21 17:21 17:27:37.038 优化算法 testScript (EURUSD,M1) 40 个 'CMatrix' 类对象
2024.11.21 17:27:37.038 优化算法 testScript (EURUSD,M1) 发现 14816 字节泄漏内存

看来类对象没有被删除。
Omega J Msigwa
Omega J Msigwa | 22 11月 2024 在 09:18
Andrey Dik #:

问题是脚本没有找到用于训练的数据文件。但无论如何，如果找不到数据文件，程序应该会处理这种情况。

但现在出现了这样的问题：

2024.11.21 17:27:37.038 优化算法 testScript (EURUSD,M1) 找到 50 个未删除的动态对象：
2024.11.21 17:27:37.038 优化算法 testScript (EURUSD,M1) 10 个 'CTensors' 类对象
2024.11.21 17:21 17:27:37.038 优化算法 testScript (EURUSD,M1) 40 个 'CMatrix' 类对象
2024.11.21 17:27:37.038 优化算法 testScript (EURUSD,M1) 发现 14816 字节泄漏内存

类对象似乎没有被删除。

这是因为一个类的一个实例只能调用一个 "fit "函数。我调用了多个拟合函数，结果在内存中创建了多个张量。

/*
 在一个程序中调用一个神经网络类的多个拟合函数是个坏主意，太多的对象将
 未从内存中删除，最好的办法是删除类的每个实例，并在每次
 拟合函数后再次调用它。
*/

  nn.fit(x_train, y_train, new OptimizerMinBGD(nn_learning_rate), nn_epochs, nn_batch_size, show_batch);
  nn.fit(x_train, y_train, new OptimizerRMSprop(nn_learning_rate, 0.1), nn_epochs, nn_batch_size, show_batch);
  nn.fit(x_train, y_train, new OptimizerAdaGrad(nn_learning_rate), nn_epochs, nn_batch_size, show_batch);
  nn.fit(x_train, y_train, new OptimizerAdam(nn_learning_rate), nn_epochs, nn_batch_size, show_batch);
  nn.fit(x_train, y_train, new OptimizerAdaDelta(nn_learning_rate), nn_epochs, nn_batch_size, show_batch);
  nn.fit(x_train, y_train, new OptimizerNadam(nn_learning_rate), nn_epochs, nn_batch_size, show_batch);
   
  delete nn;

应该是这样的

//---

  nn = new CRegressorNets(hidden_layers, AF_RELU_, LOSS_MSE_); 
  
  x_train = scaler.fit_transform(x_train);

  nn.fit(x_train, y_train, new OptimizerMinBGD(nn_learning_rate), nn_epochs, nn_batch_size, show_batch);
   
  delete nn; 
  
//---

  nn = new CRegressorNets(hidden_layers, AF_RELU_, LOSS_MSE_); 
  
  x_train = scaler.fit_transform(x_train);

  nn.fit(x_train, y_train, new OptimizerAdam(nn_learning_rate), nn_epochs, nn_batch_size, show_batch);
   
  delete nn;
开发多币种 EA 交易 (第 10 部分):从字符串创建对象 开发多币种 EA 交易 (第 10 部分):从字符串创建对象
EA 开发计划包括几个阶段，中间结果保存在数据库中，它们只能作为字符串或数字而不是对象再次从那里读取。因此，我们需要一种方法来根据从数据库读取的字符串重新创建 EA 中的所需对象。
开发回放系统（第 48 部分）：了解服务的概念 开发回放系统（第 48 部分）：了解服务的概念
学习些新知识怎么样？在本文中，您将了解如何将脚本转换为服务，以及为什么这样做很有用。
MQL5 简介（第 7 部分）：在 MQL5 中构建 EA 交易和使用 AI 生成代码的初级指南 MQL5 简介（第 7 部分）：在 MQL5 中构建 EA 交易和使用 AI 生成代码的初级指南
在我们的综合文章中，了解使用 MQL5 构建 EA 交易的终极初学者指南。逐步学习如何使用伪代码构建 EA，并利用 AI（人工智能）生成代码的强大功能。无论你是算法交易的新手，还是想提高自己的技能，本指南都为你提供了创建有效 EA 的清晰路径。
掌握市场动态：创建有关支撑与阻力位策略的EA 掌握市场动态：创建有关支撑与阻力位策略的EA
一个关于基于支撑位与阻力位策略开发自动化交易算法的全面指南。详细介绍了在MQL5中创建EA以及在MetaTrader 5中对其进行测试的所有方面——从分析价格区间行为到风险管理。