Processos não estacionários e regressão espúria

Conteúdo:

• Introdução
• Estudo do problema da não estacionaridade na análise de regressão
• Teste de hipóteses estatísticas sobre os parâmetros do modelo de regressão
• Especificação incorreta do modelo de regressão
• Conclusão

Introdução

A análise de regressão é uma das técnicas mais usadas na estatística aplicada para processar dados e entender as dependências entre variáveis aleatórias. Enquanto a análise de correlação nos diz se duas variáveis estão relacionadas, a regressão nos ajuda a entender como essa relação funciona. Existem diferentes tipos de regressão, como a simples e a múltipla. Para facilitar, neste estudo vou focar no modelo bem conhecido de regressão linear simples.

                                                Yt = b0 + b1Xt + et                                 (1)

• Yt é a variável dependente (resposta);
• Xt é a variável independente (ou variável explicativa);
• b0, b1 são os parâmetros do modelo; t representa o tempo (0,1,2,...n) com n sendo o número de observações;
• et é o componente aleatório, geralmente um ruído branco gaussiano.

Aqui, o índice t serve para destacar que estamos lidando com uma série temporal, onde a ordem das variáveis aleatórias faz toda a diferença.

O objetivo da análise de regressão é:

• estimar os parâmetros do modelo de regressão escolhido (no caso linear, usando o método dos mínimos quadrados);
• testar hipóteses estatísticas sobre os parâmetros do modelo;
• construir intervalos de confiança para as estimativas dos parâmetros.

Se a análise indicar que o modelo é estatisticamente significativo, ele pode ser considerado útil para prever a variável dependente. No entanto, ao aplicar a análise de regressão, especialmente em séries temporais, é importante lembrar da restrição de estacionaridade nas sequências aleatórias analisadas. A estacionaridade significa que a função de distribuição da variável aleatória permanece constante ao longo do tempo, assim como sua esperança matemática e variância dessa variável. Tentar aplicar a análise de regressão a processos não estacionários pode levar a conclusões erradas sobre a existência de uma relação significativa entre as variáveis. Nesses casos, testes estatísticos padrão, como as estatísticas F e t, não funcionam bem, o que aumenta o risco de aceitar uma dependência falsa como verdadeira.

Estudo do problema da não estacionaridade na análise de regressão

Neste artigo, quero mostrar, por meio de simulações com o método de Monte Carlo, como a regressão espúria aparece quando a suposição de estacionaridade é quebrada, além de quando existe especificação incorreta do modelo de regressão em casos estacionários. Para isso, utilizarei a biblioteca padrão do MQL5, especificamente a "Biblioteca Estatística" para gerar números aleatórios e calcular valores críticos da distribuição normal e da distribuição de Student, além da biblioteca gráfica Gráficos científicos para visualizar os resultados obtidos. Para calcular os parâmetros do modelo de regressão, é muito prático usar métodos de álgebra matricial, já que eles simplificam bastante os cálculos. Por exemplo, a fórmula para determinar os parâmetros do modelo de regressão pelo método dos mínimos quadrados em forma matricial é a seguinte:

(2) 

• X é a matriz dos valores das variáveis independentes;
• Y é o vetor-coluna da variável dependente;
• b é o vetor-coluna dos parâmetros desconhecidos que devem ser estimados a partir da amostra.

No MQL5, o vetor b (que, no caso da regressão linear simples, terá dois elementos: b0 e b1) pode ser obtido calculando a matriz pseudo-inversa PInv() da matriz X e multiplicando-a pelo vetor Y:

pinv = x.PInv(); 

Coeff = pinv.MatMul(Y);  // vector of linear regression parameters using OLS

Esta é uma versão abreviada do cálculo. É possível calcular passo a passo, conforme indicado na fórmula:

xt = x.Transpose();

xtm = xt.MatMul(x);
inv = xtm.Inv();      
invt = inv.MatMul(xt);
Coeff_B = invt.MatMul(Y); // vector of regression parameters using OLS

O resultado será o mesmo.

Para a simulação, vamos precisar de um modelo de passeio aleatório como exemplo de um processo não estacionário. Vamos construir esse modelo tanto para a variável dependente Y quanto para a variável independente X. Depois, faremos a regressão de Y sobre X, estimaremos o coeficiente de determinação (R²), calcularemos a estatística t e analisaremos os resíduos do modelo de regressão para verificar se há correlação.                                            

 Yt = Yt-1 + zt                           (3)

  Xt = Xt-1 + vt                           (4)

zt e vt são dois processos independentes de "ruído branco" gaussiano, com média zero e variância unitária N(0,1);

Duas possíveis trajetórias desse processo são ilustradas na fig. (1)

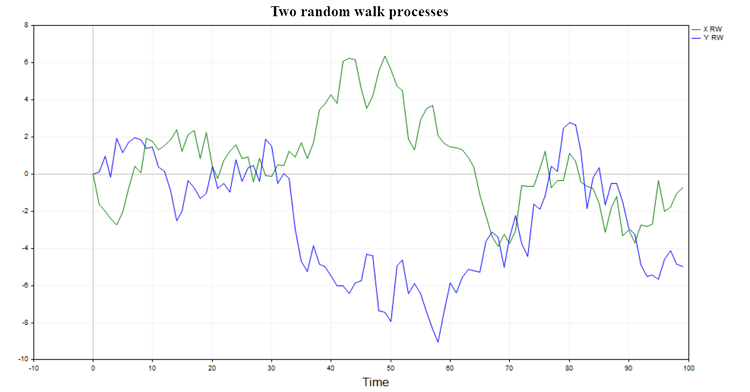
Fig.1.  Dois processos de passeio aleatório

Esses processos não têm memória e não estão ligados entre si. Por isso, é de se esperar que a regressão de um passeio aleatório sobre outro não resulte em algo significativo, e a hipótese de uma relação entre dois passeios aleatórios seja geralmente rejeitada (exceto por um pequeno percentual de casos, devido ao nível de significância escolhido).

Um exemplo de uma regressão possível é mostrado na fig.(2):

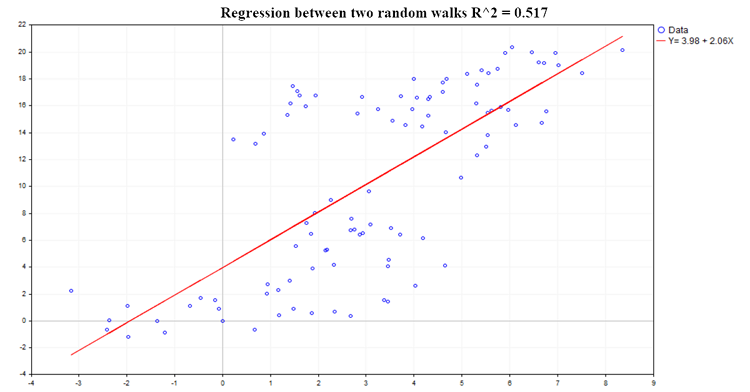
Fig.2. Regressão entre dois passeios aleatórios, R²=0.517

Essa característica da dependência de regressão analisada, como o coeficiente de determinação (R^2), é calculada pela fórmula: 

R^2 = 1 - SSE/TSS                              (5)

• SSE é a soma dos quadrados dos resíduos (Sum of Squared Errors);
• RSS é a soma dos quadrados explicada pela regressão (Regression Sum of Squares);
• TSS é a soma total dos quadrados (Total Sum of Squares), que é a soma de RSS e SSE.

Código para calcular as principais características da regressão:

      pinv = x.PInv();
      Coeff = pinv.MatMul(Y);  // vector of linear regression parameters using OLS
      yRegression = x.MatMul(Coeff);  // y regression
      res = Y-yRegression;   //  regression residuals, y - y regression
      yMean = Y.Mean();
      reg_yMean = yRegression-yMean;  // y regression - mean y
      reg_yMeanT = reg_yMean.Transpose();
      RSS = reg_yMeanT.MatMul(reg_yMean);  // Sum( y regression - y mean )^2 , sum of squares due to regression
      resT = res.Transpose();
      SSE = resT.MatMul(res);  // Sum(y - regression y)^2
      TSS = RSS[0,0]+SSE[0,0];  // Total sum of squares
      RSquare = 1-SSE[0,0]/TSS;  // R-square determination ratio
      R2_data[s] = RSquare;

      Vres = SSE[0,0]/(T-2);           // residuals variance estimate
      SEb1 = MathSqrt(Vres/SX);        // estimate of the standard deviation of the b1 ratio deviation of the regression Y = b0 + b1*X;
      t_stat[s] = (Coeff[1,0]-0)/SEb1; // find the t-statistic for the b1 ratio under the hypothesis that b1 = 0;

Os valores de R² variam de 0 a 1. Em uma regressão linear simples, R² é igual ao quadrado do coeficiente de correlação entre X e Y. Quando X não influencia Y, R² é próximo de zero, mas quando a variável dependente Y é explicada pela variável independente X, R² tende a se aproximar de um. No nosso caso, ao realizar uma regressão entre dois passeios aleatórios independentes, seria lógico esperar que o R² seja distribuído em torno de zero.  Para verificar isso, construiremos a distribuição de R² simulando, pelo método de Monte Carlo, 1000 pares de passeios aleatórios, cada um com 100 observações, e, em seguida, calcularemos o coeficiente R² para cada par. O resultado será a seguinte distribuição na figura (3):

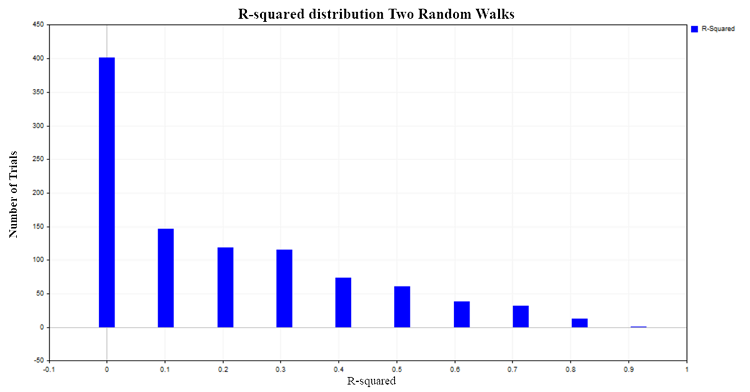
Fig.3.  Distribuição R2 para dois passeios aleatórios

Aproximadamente em 50% dos casos, o coeficiente de determinação demonstra valores superiores a 0,2, indicando a existência de uma relação entre variáveis que, na realidade, não estão relacionadas. Para comparação, vamos obter a distribuição de R² para dois processos independentes, mas agora estacionários. Um exemplo apropriado seria o modelo de ruído branco gaussiano.

                    Yt =  et                                   (6) 

 et - ruído branco gaussiano N(0,1)

Vamos gerar 1000 pares de processos aleatórios estacionários, cada um com 100 observações. O resultado será uma distribuição de R² próxima de zero, conforme esperado, na figura (4):

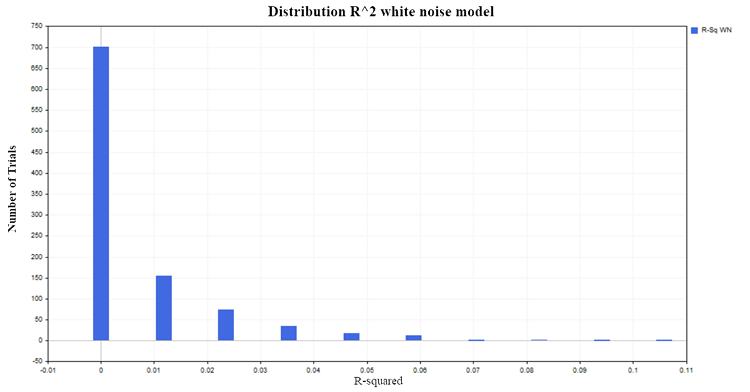
Fig.4. Distribuição R², modelo de ruído branco

Voltando ao caso dos dois passeios aleatórios, vamos agora observar o comportamento da estatística t, que é calculada para avaliar a significância dos parâmetros em nosso modelo de regressão linear.

Teste de hipóteses estatísticas sobre os parâmetros do modelo de regressão

Os coeficientes de regressão, calculados a partir da amostra, são, eles mesmos, variáveis aleatórias, o que cria a necessidade de testar a significância dessas características amostrais. Ao testar a significância do parâmetro de regressão b1, é proposta a hipótese nula (H0) de que a variável explicativa X não influencia a variável dependente Y. Ou seja, H0(i): b1 = 0 e o parâmetro b1 não difere significativamente de zero. A hipótese alternativa (H1) afirma que o parâmetro b1 difere significativamente de zero. Ou seja, H1(i): b1 ≠ 0, indicando que o preditor X influencia a variável dependente Y.

Para testar essa hipótese, utiliza-se a estatística t:

                                               t = bi /SEi                                      (7)

SEi - desvio padrão do parâmetro estimado bi 

Essa estatística segue a distribuição t de Student com a/2 (n-p) c (n-p) graus de liberdade.

• n - número de dados usados no cálculo do modelo de regressão (no nosso caso, 100);
• p - número de parâmetros estimados (no nosso caso, 2 para a regressão simples);
• a - nível de significância (1%, 5%, 10%).

Para o nosso experimento, escolhi um nível de significância de 5%. Assim, se os valores da estatística t, em módulo, ultrapassarem o valor crítico da distribuição de Student {|t| > t0,025 (98) = 1,9844}, podemos concluir que o parâmetro de regressão b1 difere de zero e, portanto, existe uma relação entre a variável explicativa X e a variável dependente Y. Como escolhi um nível de significância de 5%, devemos esperar que apenas cerca de 5% das rejeições da hipótese nula sejam falsas. No entanto, os resultados da simulação mostram que a estatística t rejeita a hipótese nula com muita frequência (falsamente, pois não há relação), aproximadamente em 75% dos casos, figura (5):

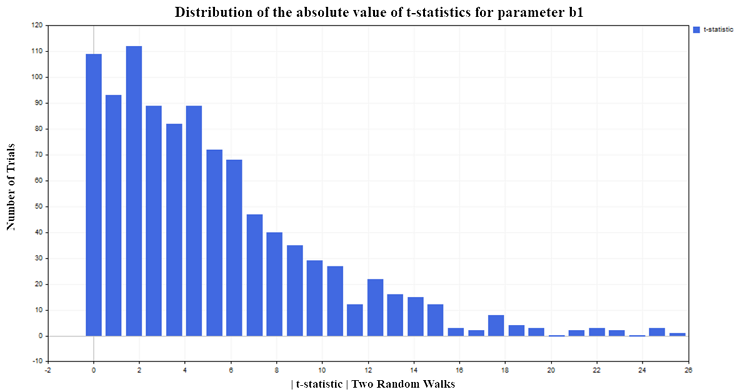
Fig.5. Distribuição do valor absoluto da estatística t para o parâmetro b1

Também é importante observar a seguinte tendência: Quanto maior o número de observações na amostra, maior o percentual de rejeição da hipótese nula. Isso cria uma situação aparentemente paradoxal, onde quanto maior a amostra, maior parece ser a influência do preditor X sobre a variável dependente Y e mais forte parece ser a relação entre as variáveis. Na verdade, não há paradoxo aqui; o problema é que estamos aplicando a análise de regressão a processos para os quais ela não é adequada. Fica claro que a estatística t padrão falha quando a regressão é aplicada à análise de séries temporais não estacionárias. Essa situação é conhecida como regressão espúria.

Especificação incorreta do modelo de regressão

Mas a não estacionaridade não é a única razão pela qual os critérios estatísticos padrão deixam de funcionar. Eles podem ser enganosos mesmo quando os dois conjuntos de dados são estacionários, mas a especificação do modelo de regressão está errada. Ou seja, quando a forma da relação funcional entre as variáveis é escolhida incorretamente (linear em vez de não linear). Ou quando uma variável independente X, que realmente afeta a variável Y, é omitida, e em seu lugar é usada erroneamente uma variável completamente irrelevante. Para ilustrar isso, construiremos dois processos estacionários independentes, X e Y. Como exemplo, vou usar o modelo de autorregressão de primeira ordem AR(1):

Yt = A*Yt-1 + zt                           (8)

 Xt = B*Xt-1 + vt                          (9)

• zt e vt são dois processos independentes de "ruído branco" gaussiano, com média zero e variância unitária N(0,1);
• A e B são os parâmetros do modelo AR(1), que devem ser estritamente menores que 1 em módulo para garantir a condição de estacionaridade.

Vamos novamente fazer a regressão de Y sobre X (por exemplo, com os parâmetros AR(1) A=0,5 e B=0,5) sob as mesmas condições usadas para o modelo de dois passeios aleatórios (100 observações em cada processo, com 1000 repetições). O resultado será a seguinte distribuição da estatística t para o parâmetro de regressão b1, conforme mostrado na figura (6):

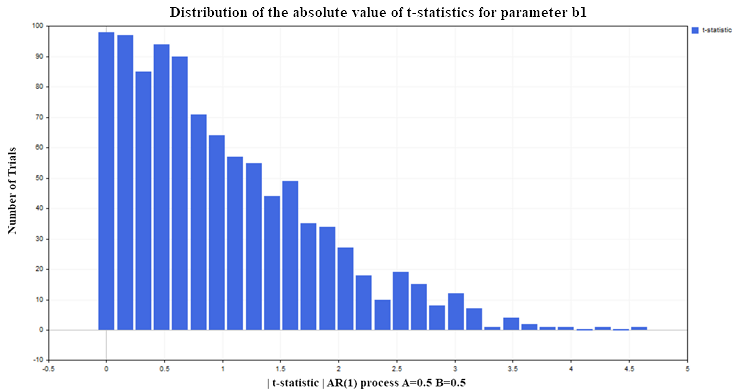
Fig. 6. Distribuição do valor absoluto da estatística t para o parâmetro b1

Como podemos ver, a situação com a rejeição da hipótese nula aqui é muito melhor do que no caso não estacionário. Apenas cerca de 12-13% das rejeições são falsas, em comparação com o nível permitido de 5% (lembre-se de que o valor crítico da distribuição de Student para 98 graus de liberdade é 1,9844). Para processos estacionários, esse percentual não aumenta com o tamanho da amostra; ele permanece no mesmo nível. Desta vez, a estatística t falha não porque as variáveis sejam não estacionárias, isso está bem, mas devido à especificação incorreta do modelo de regressão.  Embora a forma da relação tenha sido escolhida corretamente (linear), assumimos que a variável Y depende não dos valores defasados dessa mesma variável, mas dos valores da variável X, que não têm nenhuma relação com a variável Y. Se mantivermos a variável X no modelo de regressão e adicionarmos a ela os valores defasados de Y, então as propriedades estatísticas dos parâmetros de regressão melhorarão, e a estatística t deixará de produzir conclusões falsas mais frequentemente do que o nível de significância estabelecido (5% no nosso caso). Na prática, para entender se o modelo de regressão é espúrio ou mal especificado, é necessário recorrer à análise dos resíduos. 

                                         Residuals =  Yt - Yreg_t                       (10)

• Yt são os valores reais da variável dependente Y;
• Yreg_t são os valores calculados pela regressão.

Se houver uma autocorrelação significativa nos resíduos do modelo, isso indica que a regressão pode estar mal especificada ou ser espúria. 

Segue o código para calcular a função de autocorrelação (ACF) e os intervalos de confiança de 99%.

////////////////////////// ACF calculation /////////////////////////////////////////

   avgres = res.Mean();  // mean of residuals
   ArrayResize(acov,K);
   ArrayResize(acf,K);
   ArrayResize(se,K);
   ArrayResize(se2,K);

   for(i=0; i<K; i++)
     {
      ArrayResize(c,T-i);
      for(j=0; j<T-i; j++)
        {
         c[j] = (res[j,0]-avgres)*(res[j+i,0]-avgres);
        }
      acov[i] = double(MathSum(c)/T);  // Auto covariance
      acf [i] = acov [i]/acov [0];  // Auto correlation
      se[i] =   MathQuantileNormal(0.995,0,1,err)/MathSqrt(T);    // 99% confidence intervals for ACF //
      se2[i] = -MathQuantileNormal(0.995,0,1,err)/MathSqrt(T);
     }

Na fig. (7), temos o gráfico da função de autocorrelação (ACF) dos resíduos da regressão para o modelo de dois passeios aleatórios.  Também estão indicados os limites da área de confiança de 99% para a ACF, calculados pela fórmula SE = MathQuantileNormal(0.995, 0, 1, err)/MathSqrt(T); onde T é o número de observações no modelo de regressão.

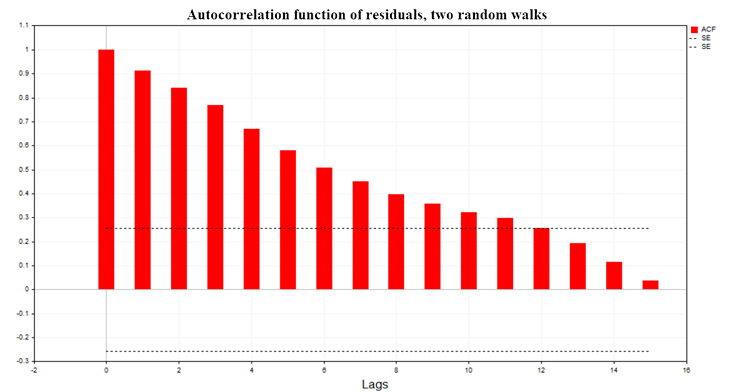
Fig. 7. Função de autocorrelação dos resíduos, dois passeios aleatórios

Na fig. (8), vemos o gráfico da ACF dos resíduos da regressão para o modelo de dois processos AR(1) com os parâmetros A=0,5 e B=0,5.

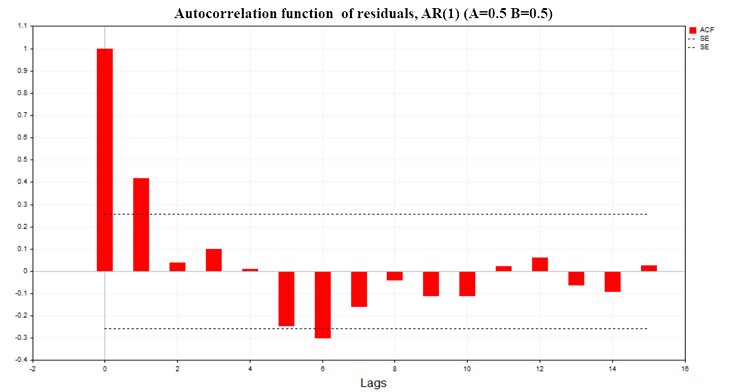
Fig. 8. Função de autocorrelação dos resíduos, AR(1) A=0,5 B=0,5

Como podemos ver nos gráficos, há uma autocorrelação significativa nos resíduos dos modelos de regressão, o que sugere que estamos lidando com um modelo de regressão mal especificado ou até mesmo com uma regressão espúria. Com base na função de autocorrelação dos resíduos, é possível aplicar o critério de Durbin-Watson (critério DW). Ele é utilizado para testar a autocorrelação dos resíduos de um modelo de regressão com defasagem de 1. 

                                            DW = 2*(1-ACF(1))                         (11)

Em casos de regressão espúria, essa estatística tende a ficar próxima de zero.

Conclusão

O principal problema que quis abordar neste artigo é a compreensão dos limites de aplicabilidade dos métodos estatísticos, em particular dos métodos de análise de regressão. Além disso, demonstrei as consequências de ultrapassar esses limites. É muito fácil realizar cálculos formais, observar uma estatística "significativa" e tirar uma conclusão equivocada sobre a existência de uma relação entre dois processos aleatórios.

A conclusão que podemos tirar de tudo o que foi exposto é a seguinte: 

• Antes de construir um modelo de regressão, é fundamental testar a estacionaridade de todas as variáveis do modelo.
• Se alguma variável não for estacionária, ela deve ser transformada para uma forma estacionária (geralmente, tomando as primeiras diferenças) e só então tentar construir o modelo com essa variável modificada.
• Após construir o modelo, é essencial analisar os resíduos para verificar a existência de autocorrelação.
• Se os valores da função de autocorrelação dos resíduos estiverem dentro dos limites da área de confiança de 99%, então podemos passar para a avaliação da significância dos parâmetros do modelo de regressão usando a estatística t.
• Se a estatística t for significativa, podemos então usar o modelo para prever a variável dependente Y.

Para reproduzir todos os resultados mencionados, no início do script, escolha os valores da variável M como 1, 0 ou 0,5, dependendo dos resultados que deseja obter para cada modelo. Em seguida, no final do script, descomente o bloco de código que exibe as estatísticas para o modelo específico. Além disso, no arquivo incluído Math.mqh, comente as duas linhas de código na função que calcula a função de densidade de probabilidade empírica (MathProbabilityDensityEmpirical) para a exibição das frequências no gráfico.

 5432  //  for(int i=0; i<count; i++)
 5433 //    pdf[i]*=coef;