
Redes neuronales: así de sencillo (Parte 92): Predicción adaptativa en los ámbitos de la frecuencia y el tiempo
Introducción
El ámbito temporal y el frecuencial son dos representaciones fundamentales utilizadas para analizar datos de series temporales. En el ámbito temporal, el análisis se centra en los cambios de amplitud a lo largo del tiempo, lo que permite identificar dependencias locales y transitorios dentro de la señal. Por el contrario, el análisis en el ámbito de la frecuencia pretende representar las series temporales en términos de sus componentes de frecuencia, lo que permite comprender las dependencias globales y las características espectrales de los datos. Combinar las ventajas de ambos campos es un enfoque prometedor para abordar el problema de la mezcla de distintos patrones periódicos en series temporales reales. El problema es cómo combinar eficazmente las ventajas de los ámbitos temporal y frecuencial.
En comparación con los logros alcanzados en el ámbito temporal, aún quedan muchas áreas inexploradas en el ámbito frecuencial. En artículos recientes hemos visto algunos ejemplos de utilización del dominio de la frecuencia para manejar mejor las dependencias globales de las series temporales. La previsión directa en el ámbito temporal permite utilizar más información espectral para mejorar la precisión de las previsiones de series temporales. Sin embargo, la predicción directa del espectro en el ámbito de la frecuencia plantea algunos problemas. Uno de estos problemas es el posible desajuste en las características de frecuencia entre el espectro de los datos conocidos que se analizan y el espectro completo de la serie temporal que se estudia, que surge como resultado del uso de la transformada discreta de Fourier (DFT). Este desajuste dificulta la representación exacta de la información sobre frecuencias específicas en todo el espectro de datos de origen, lo que provoca imprecisiones en la predicción.
Otro problema es cómo extraer eficazmente la información sobre las combinaciones de frecuencias. La extracción de características espectrales es una tarea difícil porque las series armónicas que se producen en grupos dentro del espectro contienen una cantidad significativa de información.
El artículo «ATFNet: Adaptive Time-Frequency Ensembled Network for Long-term Time Series Forecasting propone el método ATFNet como solución a los problemas mencionados. Incluye módulos del ámbito temporal y el frecuencial para el tratamiento simultáneo de las dependencias locales y globales. Además, el documento presenta un nuevo mecanismo de ponderación que distribuye dinámicamente los pesos entre los dos módulos.
Los autores del método propusieron una ponderación energética de las series armónicas dominantes, que es capaz de generar ponderaciones adecuadas para los módulos en los ámbitos temporal y frecuencial basadas en el nivel de periodicidad demostrado por los datos originales. Esto nos permite aprovechar eficazmente las ventajas de ambos campos cuando trabajamos con series temporales con diferentes patrones periódicos.
Además, los autores del método introducen una DFT ampliada para alinear el espectro de frecuencias discretas de los datos originales y la serie temporal completa, lo que aumenta la precisión de la representación de frecuencias específicas.
Los autores del método implementan el mecanismo de atención en el ámbito de la frecuencia y proponen la atención espectral compleja (CSA). Este enfoque permite recopilar información a partir de distintas combinaciones de respuestas en frecuencia, lo que constituye una forma eficaz de llamar la atención sobre las representaciones en el ámbito de la frecuencia.
El artículo presenta los resultados de experimentos con ocho conjuntos de datos reales, según los cuales ATFNet muestra resultados prometedores y supera a otros métodos de previsión de series temporales del estado del arte en muchos conjuntos de datos.
1. Algoritmo ATFNet
Los autores del método ATFNet emplean un esquema independiente del canal, que permite evitar la mezcla de espectros de diferentes canales. Dado que los canales pueden poseer patrones globales diferentes, mezclar sus espectros puede tener un impacto negativo en el rendimiento del modelo.
El bloque T procesa las series temporales univariantes de entrada directamente en el ámbito temporal. El resultado es una predicción de los valores futuros de la serie temporal analizada.
Los autores del método utilizan la transformada discreta de Fourier ampliada (Discrete Fourier Transform, DFT) para transformar los datos originales de series temporales univariantes en el ámbito de la frecuencia, generando un espectro de frecuencias ampliado. A continuación, el espectro se transforma de nuevo en el ámbito temporal mediante la DFT inversa (iDFT). Como resultado, el bloque F devuelve valores predichos de la serie temporal basados en características de frecuencia.
Los resultados de predicción del bloque T y del bloque F se combinan utilizando pesos adaptativos para obtener el resultado final de los valores predichos de las series temporales analizadas. Estas ponderaciones se determinan en función de la ponderación energética de la serie armónica dominante.
En general, el algoritmo se puede presentar de la siguiente manera:
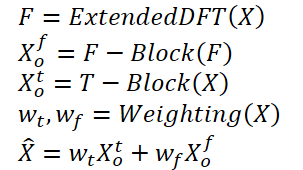
El uso de una DFT tradicional puede dar lugar a un desajuste de frecuencias entre los espectros de los datos originales y toda la serie analizada. Por lo tanto, los modelos de previsión construidos a partir del análisis de un pequeño bloque de datos iniciales pueden no tener acceso a información completa y precisa sobre las características de frecuencia de toda la serie temporal analizada. Esto da lugar a previsiones menos precisas cuando se construyen las series temporales completas.
Para resolver este problema, los autores del método proponen una DFT extendida, que supera la limitación impuesta por la longitud de los datos fuente analizados. Esto nos permite obtener el espectro original, que corresponde al grupo de frecuencias DFT de la serie completa. En concreto, los autores del método ATFNet sustituyen la base exponencial compleja original por la base DFT de la serie completa:
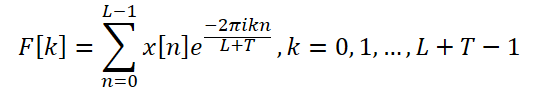
Así, obtenemos un espectro de características frecuenciales de longitud L + T, que se alinea con el espectro DFT de la serie completa analizada (datos iniciales + de previsión). Para las series de tiempo real, la simetría conjugada del espectro de salida es una propiedad importante de la DFT. Utilizando esta propiedad, podemos reducir los costes computacionales considerando sólo la primera mitad del espectro de frecuencias de los datos originales, ya que la segunda mitad proporciona información redundante.
La arquitectura del bloque F se basa en el Transformer codificador, cuyos parámetros tienen valores complejos. Todos los cálculos del bloque Fse realizan en el campo de los números complejos.
Además, los autores del método utilizan RevIN para procesar el espectro original de las características de frecuencia F. Aunque RevIN se desarrolló originalmente para eliminar los desplazamientos de distribución en el ámbito temporal, los autores del método descubrieron que también era eficaz para procesar espectros en el ámbito de la frecuencia. Este enfoque permite transformar los espectros de series con características globales diferentes en una distribución comparable. Antes del análisis, se normalizan las características de frecuencia F. Tras procesar los datos, volvemos a añadir las características estadísticas de la distribución de frecuencias.
Dado que hay pocas dependencias cronológicas en el espectro del ámbito de la frecuencia, los autores del método no utilizan la codificación posicional en el bloque F.
Además, los autores del método utilizaron un mecanismo de atención multicabeza modificado. Para cada cabeza h = 1, 2, ..., H, el espectro incorporado Fd se proyecta sobre la medición del espectro utilizando proyecciones entrenadas. A continuación, se realiza un producto escalar complejo de atención en cada cabeza.
ATFNet también utiliza capas LayerNorm y FeedForward con conexiones residuales de forma similar a Transformer, que se extienden al campo de los números complejos.
Después de M capas del codificador, los resultados del trabajo del bloque de atención se proyectan linealmente sobre el horizonte de la serie completa. Las características de frecuencia obtenidas se proyectan en el ámbito temporal mediante iDFT. Los últimos puntos T (parte de la previsión) se aceptan como resultado final del bloque F.
Cabe señalar que el bloque F utiliza la arquitectura completa de una red neuronal de valores complejos (CVNN).
El bloque T se encarga de capturar las dependencias locales en las series temporales, que son más fáciles de procesar en el ámbito temporal. En este bloque, los autores utilizan el método de segmentación de series temporales que ya nos resulta familiar. PatchTST es una forma intuitiva y eficiente de capturar dependencias locales en series temporales. También utiliza RevIN para resolver el problema del sesgo de distribución.
Las series temporales periódicas muestran sistemáticamente la existencia de al menos un grupo armónico en su espectro del ámbito de la frecuencia, siendo el grupo armónico dominante el que presenta la mayor concentración de energía espectral. Por el contrario, esta característica rara vez se observa en el espectro de las series temporales no periódicas, en las que la distribución de la energía es más uniforme. Los autores del método ATFNet demuestran que el grado de concentración de energía dentro de la serie armónica dominante en el espectro de frecuencias puede reflejar la periodicidad de la serie temporal. La relación entre la energía de la serie armónica dominante y la energía total del espectro puede servir como métrica para evaluar cuantitativamente la concentración de energía. Intuitivamente, cuando una serie temporal presenta una estructura periódica más pronunciada, puede descomponerse en componentes. Por lo tanto, una serie temporal de este tipo tiene una mayor concentración de energía dentro de la serie armónica dominante.
Basándose en esta propiedad, los autores de ATFNet utilizan la fracción de energía de la serie armónica dominante como indicador para evaluar cuantitativamente el grado de periodicidad de la serie temporal. Para identificar la serie armónica dominante, lo más importante es determinar la frecuencia fundamental. En este caso se pueden utilizar distintos enfoques:
- Un método ingenuo que identifica la frecuencia con el valor de amplitud más alto como la frecuencia fundamental.
- Algoritmos de detección de tono basados en reglas.
- Algoritmos de detección de tono basados en datos.
El algoritmo ATFNet nos permite utilizar cualquier enfoque para determinar la frecuencia fundamental. Los autores del método consideran esta componente junto con sus armónicos y calculan la energía total Eh. A continuación, los pesos del bloque F se determinan calculando la relación entre la energía de la frecuencia dominante y la energía total del espectro.
En el documento, los autores del método realizaron una serie de experimentos para evaluar la eficacia de varios métodos para determinar la frecuencia dominante. Llegaron a la conclusión de que el método ingenuo es el líder en cuanto a la relación entre la precisión de los resultados y el coste de los cálculos. Demuestra una precisión encomiable en la mayoría de los conjuntos de datos de series temporales del mundo real al tiempo que mantiene un bajo coste computacional.
Por el contrario, los enfoques alternativos se ven obstaculizados por el problema de la complejidad computacional. Además, los métodos basados en datos requieren datos de pasos etiquetados, que suelen ser difíciles de obtener, lo que supone un serio obstáculo para su uso práctico. Por ello, en sus experimentos, los autores del método ATFNet utilizan por defecto un método ingenuo para detectar la frecuencia fundamental.
A continuación se presenta la visualización original del método AFTNet.
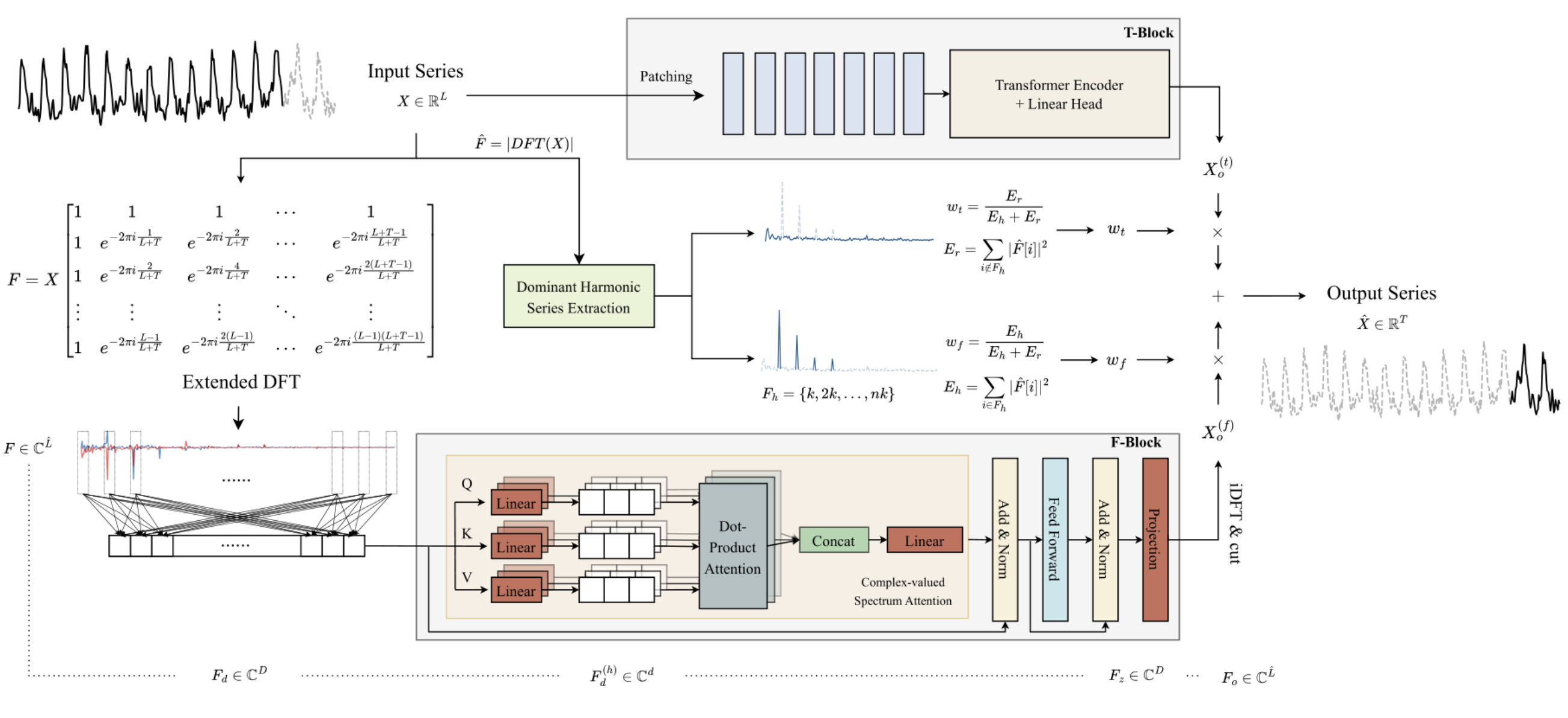
2. Operaciones básicas con números complejos
En artículos anteriores ya hemos hablado un poco de los números complejos. Son convenientes para describir el espectro de características de frecuencia. Utilizamos la parte real para representar la amplitud de la señal y la parte imaginaria para representar el desfase. Sin embargo, habiendo recibido de DFT una señal en forma compleja, trabajamos por separado con las partes real e imaginaria. A continuación, mediante iDFT, transformamos las características frecuenciales así obtenidas al dominio temporal.
A pesar de la simplicidad de aplicar el enfoque de analizar las partes real e imaginaria como entidades separadas, este enfoque no es óptimo. Los autores de ATFNet examinan en detalle ambos enfoques para procesar números complejos y llegan a la conclusión de que el análisis de las partes real e imaginaria como entidades separadas conlleva una pérdida de información. Por lo tanto, para implementar el método propuesto, necesitamos modificar el bloque de atención para trabajar con números complejos.
Por desgracia, OpenCL no admite números complejos. Por lo tanto, tenemos que implementar nosotros mismos las operaciones básicas del álgebra compleja.
Como ya se ha dicho, un número complejo consta de una parte real y una parte imaginaria:
![]()
Donde a es la parte real,
b es la parte imaginaria,
i es la unidad imaginaria.
Para guardar el número complejo en el lado OpenCL, es conveniente utilizar un vector de 2 elementos float2.
La suma y la resta de números complejos repiten casi por completo las implementadas en las operaciones vectoriales de OpenCL. Por lo tanto, no hablaremos de ellos ahora.
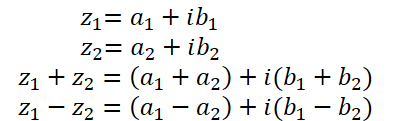
Pero la multiplicación de números complejos es un poco más complicada.
![]()
Para implementar esta operación, crearemos la función ComplexMul en el programa OpenCL.
float2 ComplexMul(const float2 a, const float2 b) { float2 result = 0; result.x = a.x * b.x - a.y * b.y; result.y = a.x * b.y + a.y * b.x; return result; }
La función toma dos vectores float2 como parámetros y devuelve el resultado en el mismo formato. De este modo creamos algo muy parecido a las operaciones correctas con variables complejas.
La división de números complejos tiene una forma más compleja:
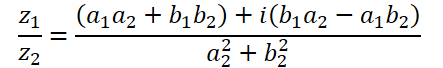
Para realizar esta operación, vamos a crear la función ComplexDiv.
float2 ComplexDiv(const float2 a, const float2 b) { float2 result = 0; float z = pow(b.x, 2) + pow(b.y, 2); if(z > 0) { result.x = (a.x * b.x + a.y * b.y) / z; result.y = (a.y * b.x - a.x * b.y) / z; } return result; }
El valor absoluto de un número complejo es un número real que indica la energía del componente de frecuencia:
![]()
Implementemos esto en la función ComplexAbs.
float ComplexAbs(float2 a) { return sqrt(pow(a.x, 2) + pow(a.y, 2)); }
La fórmula para extraer la raíz cuadrada de un número complejo es un poco más complicada:
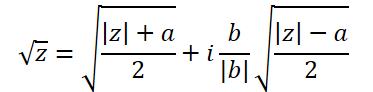
Para implementarlo, vamos a crear otra función, ComplexSqrt.
float2 ComplexSqrt(float2 a)
{
float2 result = 0;
float z = ComplexAbs(a);
result.x = sqrt((z + a.x) / 2);
result.y = sqrt((z - a.x) / 2);
if(a.y < 0)
result.y *= (-1);
//---
return result;
}
Al implementar el algoritmo Self-Attention, normalizamos los coeficientes de dependencia utilizando la función SoftMax. Para implementarlo en el dominio de los números complejos, necesitaremos el exponente del número complejo:
![]()
En el código, implementamos la función de la siguiente manera:
float2 ComplexExp(float2 a)
{
float2 result = exp(clamp(a.x, -20.0f, 20.0f));
result.x *= cos(a.y);
result.y *= sin(a.y);
return result;
}3. Capa de atención compleja
Hemos realizado los trabajos preparatorios y aplicado operaciones matemáticas básicas con números complejos. Ahora pasamos al siguiente paso, donde crearemos una clase de capa neuronal de atención utilizando matemáticas de números complejos: CNeuronComplexMLMHAttention.
Creamos la nueva clase basada en una capa de atención similar para valores reales CNeuronMLMHAttentionOCL. La ventaja de este enfoque es que podemos reutilizar al máximo la funcionalidad de primer nivel ya existente y preconfigurada. Por lo tanto, sólo tenemos que redefinir los métodos en el nivel inferior para poder trabajar con valores complejos. A continuación se muestra la estructura de la nueva clase.
class CNeuronComplexMLMHAttention : public CNeuronMLMHAttentionOCL { protected: virtual bool ConvolutionForward(CBufferFloat *weights, CBufferFloat *inputs, CBufferFloat *outputs, uint window, uint window_out, ENUM_ACTIVATION activ, uint step = 0); virtual bool AttentionScore(CBufferFloat *qkv, CBufferFloat *scores, bool mask = false); virtual bool AttentionOut(CBufferFloat *qkv, CBufferFloat *scores, CBufferFloat *out); virtual bool ConvolutuionUpdateWeights(CBufferFloat *weights, CBufferFloat *gradient, CBufferFloat *inputs, CBufferFloat *momentum1, CBufferFloat *momentum2, uint window, uint window_out, uint step = 0); virtual bool ConvolutionInputGradients(CBufferFloat *weights, CBufferFloat *gradient, CBufferFloat *inputs, CBufferFloat *inp_gradient, uint window, uint window_out, uint activ, uint shift_out = 0, uint step = 0); virtual bool AttentionInsideGradients(CBufferFloat *qkv, CBufferFloat *qkv_g, CBufferFloat *scores, CBufferFloat *gradient); virtual bool SumAndNormilize(CBufferFloat *tensor1, CBufferFloat *tensor2, CBufferFloat *out, int dimension, bool normilize = true, int shift_in1 = 0, int shift_in2 = 0, int shift_out = 0, float multiplyer = 0.5f); public: CNeuronComplexMLMHAttention(void) {}; ~CNeuronComplexMLMHAttention(void) {}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronComplexMLMHAttentionOCL; } };
Lo destacable de la estructura de la nueva clase es que no declara ni un solo objeto o variable interna. En el proceso de implementación de la funcionalidad, utilizaremos objetos y variables heredados.
Además, la estructura de la clase sólo declara la sustitución de métodos en el bloque protegido. Todos los métodos fueron declarados previamente en la clase padre. Sin embargo, no existen métodos de propagación hacia adelante y hacia atrás de alto nivel (feedForward,CalcInputGradients y updateInputWeights), en el que normalmente construimos el algoritmo de la clase. Esto se debe a que preservamos completamente la secuencia de acciones del algoritmo de la clase padre. Sin embargo, para trabajar con valores complejos, necesitamos duplicar el tamaño de los búferes de datos, porque la parte imaginaria del valor complejo se suma a cada valor real. Además, tenemos que implementar las matemáticas de números complejos en el algoritmo. Como sabes, realizamos casi todas las operaciones matemáticas en OpenCL. Por lo tanto, además de redefinir los métodos de nivel inferior, también tendremos que realizar cambios en los núcleos del programa OpenCL.
3.1 Método de inicialización de clases
El trabajo de cada clase comienza con su inicialización. Como se mencionó anteriormente, no declaramos ningún objeto anidado o variables en nuestra nueva clase. Por eso el constructor y el destructor están vacíos. La inicialización de los objetos heredados se realiza en el método Init. Como es habitual, en los parámetros de este método, recibimos del llamante las constantes principales que definen la arquitectura de la clase. Como puedes ver, la estructura de los parámetros del método es la misma que en el método similar de la clase padre. Esto no es sorprendente. Porque conservamos completamente el algoritmo de atención básico y la estructura de la clase padre. Sin embargo, reescribiremos completamente el método.
bool CNeuronComplexMLMHAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, 2 * window * units_count, optimization_type, batch)) return false;
En el cuerpo del método, como es habitual, llamamos al método de inicialización de la clase padre. Por favor, preste atención a los dos puntos siguientes:
- Llamamos al método de inicialización no del padre directo CNeuronMLMHAttentionOCL, sino de la clase base de la capa neuronal CNeuronBaseOCL. La razón es que la inicialización de objetos anidados de la clase CNeuronMLMHAttentionOCL no es necesaria ya que tenemos que redefinir todos los buffers con tamaños incrementados para poder almacenar números complejos.
- Al llamar al método de la clase padre, aumentamos el tamaño de la capa 2 veces. Esto se debe a que esperamos que la operación de capa dé como resultado valores complejos.
Asegúrese de comprobar el resultado lógico de las operaciones del método de la clase padre.
Después de inicializar con éxito los objetos heredados de la clase base de la capa neuronal, guardamos los parámetros principales de la arquitectura de la capa creada.
iWindow = window; iWindowKey = fmax(window_key, 1); iUnits = units_count; iHeads = fmax(heads, 1); iLayers = fmax(layers, 1);
En el siguiente paso, calculamos los tamaños de todos los buffers que estamos creando. Necesitamos almacenar valores complejos. Por lo tanto, todos los buffers se incrementan en 2 veces en comparación con la clase principal.
uint num = 2 * 3 * iWindowKey * iHeads * iUnits; //Size of QKV tensor uint qkv_weights = 2 * 3 * (iWindow + 1) * iWindowKey * iHeads; //Size of weights' matrix of QKV tenzor uint scores = 2 * iUnits * iUnits * iHeads; //Size of Score tensor uint mh_out = 2 * iWindowKey * iHeads * iUnits; //Size of multi-heads self-attention uint out = 2 * iWindow * iUnits; //Size of our tensore uint w0 = 2 * (iWindowKey + 1) * iHeads * iWindow; //Size W0 tensor uint ff_1 = 2 * 4 * (iWindow + 1) * iWindow; //Size of weights' matrix 1-st feed forward layer uint ff_2 = 2 * (4 * iWindow + 1) * iWindow; //Size of weights' matrix 2-nd feed forward layer
Luego organizamos un bucle según la cantidad de capas de atención anidadas creadas. En su cuerpo, inicializamos los objetos anidados.
for(uint i = 0; i < iLayers; i++) { CBufferFloat *temp = NULL;
Aquí primero creamos un bucle anidado de 2 iteraciones en el que inicializamos objetos para registrar los datos del paso de avance y los gradientes de error correspondientes.
for(int d = 0; d < 2; d++) { //--- Initilize QKV tensor temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(num, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Tensors.Add(temp)) return false;
Primero creamos un buffer concatenado de las entidades Query, Key y Value. A continuación, según el algoritmo Self-Attention, necesitamos un buffer para escribir la matriz de coeficientes de dependencia.
//--- Initialize scores temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(scores, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!S_Tensors.Add(temp)) return false;
El siguiente búfer almacenará los resultados de la atención multicabezal:
//--- Initialize multi-heads attention out temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(mh_out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!AO_Tensors.Add(temp)) return false;
A continuación, reduciremos el tamaño hasta el nivel de entrada.
//--- Initialize attention out temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false;
Al bloque de atención le sigue el bloque FeedForward, que consta de 2 capas totalmente conectadas:
//--- Initialize Feed Forward 1 temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(4 * out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false; //--- Initialize Feed Forward 2 if(i == iLayers - 1) { if(!FF_Tensors.Add(d == 0 ? Output : Gradient)) return false; continue; } temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false; }
Hemos inicializado búferes para almacenar los resultados de los pases de avance y los gradientes de error correspondientes. Sin embargo, para realizar las operaciones, necesitamos parámetros de peso aprendibles. En primer lugar, rellenamos la matriz de parámetros aprendibles para generar las entidades Query, Key y Value:
//--- Initilize QKV weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(qkv_weights)) return false; float k = (float)(1 / sqrt(iWindow + 1)); for(uint w = 0; w < qkv_weights; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Weights.Add(temp)) return false;
A continuación, generamos los parámetros de la capa de reducción de la dimensionalidad de la atención multicabezal:
//--- Initilize Weights0 temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(w0)) return false; for(uint w = 0; w < w0; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
Vamos a añadir los parámetros del bloque FeedForward:
//--- Initilize FF Weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(ff_1)) return false; for(uint w = 0; w < ff_1; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; //--- temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(ff_2)) return false; k = (float)(1 / sqrt(4 * iWindow + 1)); for(uint w = 0; w < ff_2; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
Durante el proceso de entrenamiento de los parámetros del modelo, necesitaremos buffers para registrar los momentos de entrenamiento. El número de estos búferes depende del método de aprendizaje de parámetros utilizado.
for(int d = 0; d < (optimization == SGD ? 1 : 2); d++) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(qkv_weights, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Weights.Add(temp)) return false; temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(w0, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; //--- Initilize FF Weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(ff_1, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(ff_2, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; } } //--- return true; }
Asegúrese de comprobar el resultado de cada iteración de este método, ya que durante el entrenamiento y el funcionamiento del modelo, la ausencia de uno solo de los búferes necesarios provocará un error crítico.
Después de inicializar todos los objetos anidados, terminamos el método y devolvemos el valor lógico de las operaciones realizadas a la persona que llama.
3.2 Pase hacia adelante
Después de inicializar la clase, procedemos a organizar el pase de avance. Aunque heredamos el algoritmo de alto nivel de la clase padre, todavía tenemos trabajo por hacer con los métodos de propagación hacia adelante en el nivel bajo. Ordenaremos las operaciones en la secuencia del algoritmo Self-Attention.
Los datos de entrada de la capa se transforman primero en entidades Query, Key y Value. Para generarlos en la clase padre, utilizamos el núcleo de paso directo de la capa convolucional. En esta aplicación, seguiremos el mismo planteamiento. Además, para trabajar con variables complejas, necesitamos crear un nuevo núcleo llamado FeedForwardComplexConv en el lado del programa OpenCL.
En los parámetros del núcleo, pasamos punteros a 3 búferes de datos: la matriz de parámetros de entrenamiento, los datos de entrada y un búfer para escribir los resultados.
__kernel void FeedForwardComplexConv(__global float2 *matrix_w, __global float2 *matrix_i, __global float2 *matrix_o, int inputs, int step, int window_in, int activation ) { size_t i = get_global_id(0); size_t out = get_global_id(1); size_t w_out = get_global_size(1);
Nótese que en la parte del programa principal, seguimos utilizando buffers de datos de tipo float pero de tamaño aumentado. En el kernel del lado del programa OpenCL, especificamos el tipo float2 para los búferes de datos. Este es exactamente el tipo de datos que utilizamos anteriormente al crear funciones de variables complejas.
En el cuerpo del método, identificamos el hilo actual en el espacio de tareas bidimensional. La primera dimensión indica el elemento de la secuencia de resultados, y la segunda, el filtro utilizado. En nuestro caso, indicará la posición en el vector concatenado de entidades que describen un elemento de la secuencia analizada.
A partir de los datos obtenidos, determinamos el desplazamiento en los búferes de datos:
int w_in = window_in; int shift_out = w_out * i; int shift_in = step * i; int shift = (w_in + 1) * out; int stop = (w_in <= (inputs - shift_in) ? w_in : (inputs - shift_in));
A continuación creamos un bucle para calcular el producto de vectores:
float2 sum = matrix_w[shift + w_in]; for(int k = 0; k <= stop; k ++) sum += ComplexMul(matrix_i[shift_in + k], matrix_w[shift + k]);
Tenga en cuenta que para calcular el producto de 2 cantidades complejas utilizamos la función ComplexMul creada anteriormente. Utilizamos operaciones vectoriales básicas para sumar valores.
Además, como hemos declarado el tipo de vector float2 para los búferes de datos, podemos acceder a ellos como búferes de datos normales de punto flotante sin ajuste de desplazamiento. En cada operación, se extraen dos elementos de la memoria intermedia: las partes real e imaginaria del número complejo.
A continuación comprobamos el valor calculado. En caso de desbordamiento de la variable, cambiamos su valor a 0:
if(isnan(sum.x) || isnan(sum.y) || isinf(sum.x) || isinf(sum.y)) sum = (float2)0;
Ahora sólo tenemos que calcular la función de activación y guardar el valor en el búfer de resultados.
switch(activation) { case 0: sum = ComplexTanh(sum); break; case 1: sum = ComplexDiv((float2)(1, 0), (float2)(1, 0) + ComplexExp(-sum)); break; case 2: if(sum.x < 0) sum.x *= 0.01f; if(sum.y < 0) sum.y *= 0.01f; break; default: break; } matrix_o[out + shift_out] = sum; }
Para llamar al núcleo creado anteriormente en el lado del programa principal, anularemos el método CNeuronComplexMLMHAttention::ConvolutionForward. Fíjate en que estamos sobrescribiendo el método en lugar de crear uno nuevo. Por lo tanto, es muy importante conservar toda la estructura de parámetros del método similar de la clase padre. Sólo anulando el método nos permitirá llamar a este método desde el método de paso de alimentación de nivel superior de la clase padre sin hacer ningún ajuste en él.
bool CNeuronComplexMLMHAttention::ConvolutionForward(CBufferFloat *weights, CBufferFloat *inputs, CBufferFloat *outputs, uint window, uint window_out, ENUM_ACTIVATION activ, uint step = 0) { if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(weights) == POINTER_INVALID || CheckPointer(inputs) == POINTER_INVALID || CheckPointer(outputs) == POINTER_INVALID) return false;
En el cuerpo del método, primero comprobamos la relevancia de los punteros a objetos recibidos. Y luego comprobamos si hay búferes de datos en el lado del contexto OpenCL.
if(weights.GetIndex() < 0) return false; if(inputs.GetIndex() < 0) return false; if(outputs.GetIndex() < 0) return false; if(step == 0) step = window;
Después de pasar con éxito el bloque de control, definimos el espacio de tareas para el núcleo y el desplazamiento en él:
uint global_work_offset[2] = {0, 0}; uint global_work_size[2]; global_work_size[0] = outputs.Total() / (2 * window_out); global_work_size[1] = window_out;
A continuación, pasamos todos los parámetros necesarios al núcleo, al tiempo que controlamos la ejecución de las operaciones:
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardComplexConv, def_k_ffc_matrix_w, weights.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardComplexConv, def_k_ffc_matrix_i, inputs.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardComplexConv, def_k_ffc_matrix_o, outputs.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardComplexConv, def_k_ffc_inputs, (int)(inputs.Total() / 2))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardComplexConv, def_k_ffc_step, (int)step)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardComplexConv, def_k_ffc_window_in, (int)window)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardComplexConv, def_k_ffс_window_out, (int)window_out)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardComplexConv, def_k_ffc_activation - 1, (int)activ)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Después, colocamos el núcleo en la cola de ejecución y completamos el método:
if(!OpenCL.Execute(def_k_FeedForwardComplexConv, 2, global_work_offset, global_work_size)) { string error; CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error); printf("Error of execution kernel %s: %s", __FUNCSIG__, error); return false; } //--- return true; }
El algoritmo para colocar núcleos en la cola de ejecución es bastante uniforme. Puede haber diferencias en el tamaño del espacio de tarea y variaciones con las variables. Para ahorrarle tiempo y reducir el volumen del artículo, no nos extenderemos más en los métodos de colas del kernel. Su código completo se puede encontrar en el archivo adjunto. Detengámonos en detalle en los algoritmos para construir estos núcleos.
Continuamos con el algoritmo Self-Attention. Tras definir las entidades Query, Key y Value, pasamos a definir los coeficientes de dependencia. Para definir la, necesitamos multiplicar la matriz Query por la matriz transpuesta Key. La matriz resultante se normaliza utilizando la función SoftMax.
La funcionalidad descrita se ejecuta en el núcleo ComplexMHAttentionScore, que será llamado desde el método CNeuronComplexMLMHAttention::AttentionScore.
__kernel void ComplexMHAttentionScore(__global float2 *qkv, __global float2 *score, int dimension, int mask ) { int q = get_global_id(0); int h = get_global_id(1); int units = get_global_size(0); int heads = get_global_size(1);
En los parámetros, el núcleo recibe punteros a 2 buffers de datos. Un buffer concatenado de entidades como entrada. Y un buffer para escribir los resultados.
El núcleo especificado se ejecuta en un espacio de tareas bidimensional. La primera dimensión define una fila de la matriz de consulta, y la segunda define una cabeza de atención activa. Así, cada instancia separada del núcleo de ejecución realiza operaciones para calcular 1 fila de la matriz de coeficientes de dependencia dentro de 1 cabeza de atención.
En el cuerpo del núcleo, identificamos el hilo actual en ambas dimensiones del espacio de tareas y determinamos los desplazamientos en los búferes de datos:
int shift_q = dimension * (h + 3 * q * heads); int shift_s = units * (h + q * heads);
A continuación, definimos el factor de normalización de los datos:
float2 koef = (float2)(sqrt((float)dimension), 0); if(koef.x < 1) koef.x = 1;
Crear un bucle para calcular los coeficientes de dependencia:
float2 sum = 0; for(int k = 0; k < units; k++) { if(mask > 0 && k > q) { score[shift_s + k] = (float2)0; continue; }
Cabe señalar aquí que el algoritmo presentado implementa el enmascaramiento de datos, lo que permite limitar el llamado «look-ahead». El modelo solo analiza los coeficientes de dependencia de tokens anteriores. Para los tokens posteriores, los coeficientes de dependencia se establecen en 0 para que el modelo no pueda recibir información "del futuro" durante el proceso de entrenamiento. Esta funcionalidad se activa mediante la bandera mask, que se pasa en los parámetros del kernel.
A continuación, en un bucle anidado, calculamos el siguiente elemento del vector de dependencia multiplicando 2 vectores.
float2 result = (float2)0; int shift_k = dimension * (h + heads * (3 * k + 1)); for(int i = 0; i < dimension; i++) result += ComplexMul(qkv[shift_q + i], qkv[shift_k + i]);
Calculamos el exponente para el resultado del producto:
result = ComplexExp(ComplexDiv(result, koef));
Es necesario definir el desbordamiento de variables:
if(isnan(result.x) || isnan(result.y) || isinf(result.x) || isinf(result.y)) result = (float2)0;
Escribimos el resultado en el búfer de resultados y lo añadimos a la suma total para su posterior normalización.
score[shift_s + k] = result; sum += result; }
Al final del núcleo, normalizamos la fila calculada de la matriz de coeficientes de dependencia:
if(ComplexAbs(sum) > 0) for(int k = 0; k < units; k++) score[shift_s + k] = ComplexDiv(score[shift_s + k], sum); }
La matriz Score de coeficientes de dependencia así obtenida se utiliza para calcular los resultados del bloque de atención. Aquí tenemos que multiplicar la matriz de coeficientes obtenida por la matriz de entidades Value. Este trabajo se realiza en el núcleo ComplexMHAttentionOut. Al igual que el anterior, este núcleo trabaja en el mismo espacio de tareas bidimensional.
__kernel void ComplexMHAttentionOut(__global float2 *scores, __global float2 *qkv, __global float2 *out, int dimension ) { int u = get_global_id(0); int units = get_global_size(0); int h = get_global_id(1); int heads = get_global_size(1);
En el cuerpo del núcleo, identificamos el hilo actual en el espacio de tareas y determinamos los desplazamientos en los búferes de datos:
int shift_s = units * (h + heads * u); int shift_out = dimension * (h + heads * u);
Después, creamos un sistema de bucles anidados para realizar operaciones matemáticas de multiplicación de la matriz Value por la línea de coeficientes de dependencia correspondiente:
for(int d = 0; d < dimension; d++) { float2 result = (float2)0; for(int v = 0; v < units; v++) { int shift_v = dimension * (h + heads * (3 * v + 2)) + d; result += ComplexMul(scores[shift_s + v], qkv[shift_v]); } out[shift_out + d] = result; } }
A continuación, el resultado de la atención multicabezal se consolida en un único tensor y se reduce en dimensión al tamaño del tensor de datos de entrada. A continuación realizamos las operaciones del bloque FeedForward . Estas operaciones se realizan utilizando el núcleo FeedForwardComplexConv descrito anteriormente. Con esto concluye nuestra descripción de los algoritmos del núcleo para realizar operaciones de paso hacia adelante. Puedes ver el código completo de todos los núcleos, así como los métodos que los llaman, en el archivo adjunto.
3.3 Implementación del paso de retropropagación
La funcionalidad de pase de avance está lista. A continuación, procedemos a implementar los algoritmos de retropropagación. Este trabajo es similar al realizado anteriormente para el pase de avance. Explotamos los algoritmos de alto nivel heredados de la clase padre y anulamos los métodos de bajo nivel.
Como se mencionó anteriormente, no consideraremos los algoritmos de los métodos que colocan núcleos en la cola de ejecución. Son todos iguales. Prestemos más atención al análisis de los algoritmos del núcleo en el lado del programa OpenCL.
El más utilizado en el paso feed-forward fue el núcleo FeedForwardComplexConv. Se trata de un bloque universal que utilizamos en diferentes etapas. Naturalmente, comenzamos la construcción de algoritmos de retropropagación precisamente con el núcleo para propagar el gradiente de error a través del bloque especificado. Implementamos esta funcionalidad en el núcleo CalcHiddenGradientComplexConv.
__kernel void CalcHiddenGradientComplexConv(__global float2 *matrix_w, __global float2 *matrix_g, __global float2 *matrix_o, __global float2 *matrix_ig, int outputs, int step, int window_in, int window_out, int activation, int shift_out ) { size_t i = get_global_id(0); size_t inputs = get_global_size(0);
El núcleo se ejecuta en un espacio de tareas unidimensional en función del número de elementos del búfer de datos de entrada. Cada hilo individual de un núcleo determinado recopila gradientes de error de todos los elementos que se ven afectados por el elemento de entrada analizado.
En el cuerpo del núcleo, identificamos el hilo actual y determinamos los desplazamientos en los búferes de datos. También declaramos las variables locales necesarias:
float2 sum = (float2)0; float2 out = matrix_o[shift_out + i]; int start = i - window_in + step; start = max((start - start % step) / step, 0); int stop = (i + step - 1) / step; if(stop > (outputs / window_out)) stop = outputs / window_out;
Después de esto, creamos un sistema de bucles. En su cuerpo recogeremos el gradiente de error total, teniendo en cuenta la influencia del elemento analizado en el resultado global:
for(int h = 0; h < window_out; h ++) { for(int k = start; k < stop; k++) { int shift_g = k * window_out + h; int shift_w = (stop - k - 1) * step + i % step + h * (window_in + 1); if(shift_g >= outputs || shift_w >= (window_in + 1) * window_out) break; sum += ComplexMul(matrix_g[shift_out + shift_g], matrix_w[shift_w]); } }
Después de salir del bucle, verificamos si hay desbordamiento de variables:
if(isnan(sum.x) || isnan(sum.y) || isinf(sum.x) || isinf(sum.y)) sum = (float2)0;
También ajustamos el gradiente de error obtenido por la derivada de la función de activación:
switch(activation) { case 0: sum = ComplexMul(sum, (float2)1.0f - ComplexMul(out, out)); break; case 1: sum = ComplexMul(sum, ComplexMul(out, (float2)1.0f - out)); break; case 2: if(out.x < 0.0f) sum.x *= 0.01f; if(out.y < 0.0f) sum.y *= 0.01f; break; default: break; } matrix_ig[i] = sum; }
Guardaremos el resultado final en el buffer de gradiente de error de la capa anterior.
A continuación, consideremos el kernel para propagar el gradiente de error a través del bloque de atención ComplexMHAttentionGradients. Este núcleo presenta un algoritmo bastante complejo, que puede dividirse condicionalmente en 3 bloques en función del número de entidades para las que se determina el valor del gradiente de error.
__kernel void ComplexMHAttentionGradients(__global float2 *qkv, __global float2 *qkv_g, __global float2 *scores, __global float2 *gradient) { size_t u = get_global_id(0); size_t h = get_global_id(1); size_t d = get_global_id(2); size_t units = get_global_size(0); size_t heads = get_global_size(1); size_t dimension = get_global_size(2);
En este núcleo se realizan bastantes operaciones. Para reducir el tiempo total de ejecución, durante el proceso de entrenamiento del modelo intentamos paralelizar las operaciones relacionadas con el cálculo de valores para variables individuales. Para que la identificación de hilos sea transparente e intuitiva, hemos creado un espacio de tareas tridimensional para este núcleo. Al igual que en los métodos de paso hacia delante del bloque de atención, aquí utilizamos el elemento de secuencia y la cabeza de atención. La tercera dimensión del espacio de tareas se utiliza para la posición del elemento en el tensor que describe el elemento de la secuencia. Así, a pesar del gran número de operaciones, cada subproceso individual escribirá sólo 3 valores en el búfer de resultados. En este caso, se trata de un buffer concatenado de gradientes de error para las entidades Query, Key y Value.
En el cuerpo del núcleo, primero identificamos el hilo en el espacio de tareas y determinamos los desplazamientos en los búferes de datos:
float2 koef = (float2)(sqrt((float)dimension), 0); if(koef.x < 1) koef.x = 1; //--- init const int shift_q = dimension * (heads * 3 * u + h); const int shift_k = dimension * (heads * (3 * u + 1) + h); const int shift_v = dimension * (heads * (3 * u + 2) + h); const int shift_g = dimension * (heads * u + h); int shift_score = h * units; int step_score = units * heads;
A continuación, determinamos el gradiente de error para el elemento analizado de la matriz Value. Multiplicamos una columna separada del tensor de gradiente de error a la salida del bloque de atención por la columna correspondiente de la matriz de coeficientes de dependencia:
//--- Calculating Value's gradients float2 sum = (float2)0; for(int i = 0; i < units; i++) sum += ComplexMul(gradient[(h + i * heads) * dimension + d], scores[shift_score + u + i * step_score]); qkv_g[shift_v + d] = sum;
En el siguiente paso, determinamos el gradiente de error para el elemento analizado de la entidad Query. Esta entidad no tiene influencia directa en el resultado. Sólo existe una influencia indirecta a través de la matriz de coeficientes de dependencia. Por lo tanto, primero debemos encontrar el gradiente de error para la fila correspondiente de la matriz de coeficientes de dependencia. La normalización de los datos mediante la función SoftMax complica aún más el proceso.
//--- Calculating Query's gradients shift_score = h * units + u * step_score; float2 grad = 0; float2 grad_out = gradient[shift_g + d]; for(int k = 0; k < units; k++) { float2 sc_g = (float2)0; float2 sc = scores[shift_score + k]; for(int v = 0; v < units; v++) sc_g += ComplexMul( ComplexMul(scores[shift_score + v], ComplexMul(qkv[dimension * (heads * (3 * v + 2) + h)], grad_out)), ((float2)(k == v, 0) - sc) );
El gradiente de error encontrado para un único coeficiente de dependencia se multiplica por el elemento correspondiente de la matriz de entidad Key. Los valores resultantes se suman para acumular el gradiente de error total:
grad += ComplexMul(ComplexDiv(sc_g, koef), qkv[dimension * (heads * (3 * k + 1) + h) + d]); }
Escribimos el gradiente de error acumulado en el búfer de resultados:
qkv_g[shift_q + d] = grad;
Del mismo modo, definimos el gradiente de error para los elementos de la entidad Key, que también tiene un efecto indirecto en el resultado a través de la matriz de coeficientes de dependencia. Sin embargo, esta vez trabajamos con una columna de la matriz especificada:
//--- Calculating Key's gradients grad = 0; for(int q = 0; q < units; q++) { shift_score = h * units + q * step_score; float2 sc_g = (float2)0; float2 sc = scores[shift_score + u]; float2 grad_out = gradient[dimension * (heads * q + h) + d]; for(int v = 0; v < units; v++) sc_g += ComplexMul( ComplexMul(scores[shift_score + v], ComplexMul(qkv[dimension * (heads * (3 * v + 2) + h)], grad_out)), ((float2)(u == v, 0) - sc) ); grad += ComplexMul(ComplexDiv(sc_g, koef), qkv[dimension * (heads * 3 * q + h) + d]); } qkv_g[shift_k + d] = grad; }
Esto concluye nuestra discusión de los algoritmos de construcción de núcleos de paso de retropropagación dentro de la funcionalidad de la capa de atención compleja. El código completo de todos los métodos y núcleos de la clase presentada se encuentra en el archivo adjunto.
Conclusión
En este artículo hemos tratado los aspectos teóricos de la construcción del método ATFNet, que combina enfoques de previsión de series temporales tanto en el dominio de la frecuencia como en el del tiempo.
En la parte práctica de este artículo, hicimos bastante trabajo relacionado con la construcción de una capa de atención utilizando operaciones complejas. Sin embargo, esto es sólo un objeto del bloque F del método propuesto. En el próximo artículo, seguiremos construyendo el algoritmo del método ATFNet. También veremos los resultados de su funcionamiento con datos reales.
Referencias
- ATFNet: Adaptive Time-Frequency Ensembled Network for Long-term Time Series Forecasting
- Otros artículos de esta serie
Programas utilizados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | Colección de ejemplos |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA para la recolección de ejemplos utilizando el método Real-ORL |
| 3 | Study.mq5 | Expert Advisor | EA para el entrenamiento del modelo |
| 4 | StudyEncoder.mq5 | Expert Advisor | EA de entrenamiento del codificador |
| 5 | Test.mq5 | Expert Advisor | EA de prueba de modelos |
| 6 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema |
| 7 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 8 | NeuroNet.cl | Código base | Biblioteca OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/14996
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Algoritmo de búsqueda cooperativa artificial (Artificial Cooperative Search, ACS)
Algoritmo de búsqueda cooperativa artificial (Artificial Cooperative Search, ACS)
 Desarrollo de un sistema de repetición (Parte 59): Un nuevo futuro
Desarrollo de un sistema de repetición (Parte 59): Un nuevo futuro
 Redes neuronales: así de sencillo (Parte 93): Predicción adaptativa en los ámbitos de la frecuencia y el tiempo (Parte final)
Redes neuronales: así de sencillo (Parte 93): Predicción adaptativa en los ámbitos de la frecuencia y el tiempo (Parte final)
 Operar con noticias de manera sencilla (Parte 2): Gestión de riesgos
Operar con noticias de manera sencilla (Parte 2): Gestión de riesgos
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Las redes neuronales son fáciles. Parte 92 😅
Es accesible a todo el mundo. Y el número de artículos demuestra la versatilidad y el desarrollo constante.