Продвинутый ресемплинг и выбор CatBoost моделей брутфорс методом

Введение

В предыдущей статье я постарался дать интуицию относительно основных этапов построения модели машинного обучения и внедрения её в продакшн. В этой статье я хочу перейти от наивных моделей к статистически значимым. Поскольку построение торговой системы на машинном обучении является нетривиальной задачей, мы пройдемся по ряду улучшений в плане подготовки данных, чтобы добиться оптимальных результатов. Для улучшения представления исходных данных (обучающих примеров) используются различные техники ресемплинга (resampling), одна из которых будет рассмотрена в этой статье.

В предыдущей статье я использовал простой случайный семплинг меток, который имеет ряд недостатков:

• Классы могут оказаться несбалансированными. Допустим, на периоде обучения рынок преимущественно рос, тогда как генеральная совокупность (вся история котировок) подразумевает как взлеты, так и падения. В данном случае наивный семплинг создаст больше меток на покупку, а меток на продажу окажется меньше. Соответственно, метки одного класса будут превалировать над метками другого, из-за чего модель научится чаще предсказывать сделки на покупку, чем на продажу, что окажется невалидным на новых данных.

• Автокорреляция признаков и меток. При случайном семплинге метки одного и того же класса идут друг за другом, при этом сами признаки (допустим, приращения) меняются незначительно. Если представить данный процесс на примере обучения регрессионной модели, то окажется, что в остатках модели будет наблюдаться автокорреляция, что приведет к возможному завышению оценки модели и её переобучению, как показано на изображении ниже:

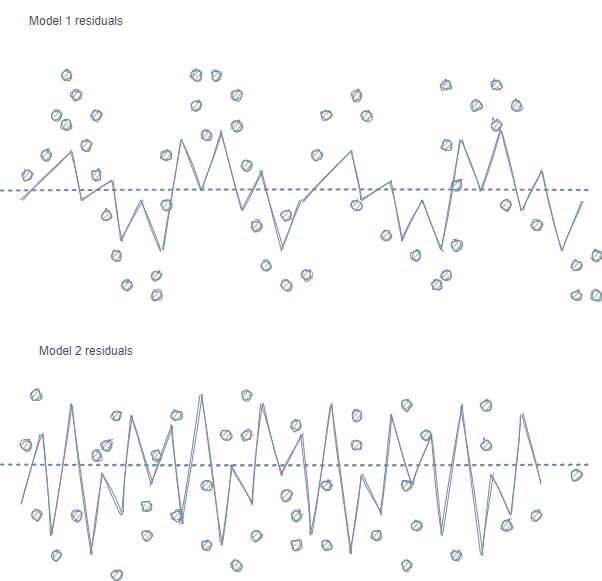
Model 1 имеет автокорреляцию остатков, что сравнимо с переобучением модели на некоторые свойства рынка (например, на волатильность на обучающих данных), тогда как другие закономерности остаются неучтенными. Model 2 имеет остатки с одинаковой дисперсией (в среднем), что говорит о том, что больше информации из временного ряда было учтено моделью, либо найдены другие зависимости (помимо корреляции соседних отсчетов).

Для классификации, этот эффект проявляется тоже, хоть и менее интуитивен из-за наличия всего нескольких классов, в отличие от непрерывной переменной в случае регрессионных моделей. Впрочем, его все равно можно оценить, например, через pearson residuals и похожие метрики. От таких зависимостей (в случае Model 1) следует избавляться.

• Классы могут значительно перекрывать друг друга. Представим гипотетическое 2D пространство признаков (поскольку представление многомерных пространств доступно немногим), каждая точка которого отнесена к классу 0 или 1. 

При случайном семплинге может возникнуть (и возникает) ситуация, когда множества примеров пересекаются. Это чревато уменьшением дистанции (допустим, эвклидова расстояния) между точками различных классов и увеличением расстояния между точками одного и того же класса, что приводит к созданию чрезмерно сложной модели на этапе обучения со множеством границ, разделяющих классы. Небольшие отклонения в показаниях признаков вызывают скачки предсказаний модели из класса в класс. Данный эффект убивает устойчивость модели на новых данных и с ним необходимо бороться.

Хотелось бы чтобы метки классов не пересекались в пространстве признаков и были разделены если не линейно (как изображено ниже), то хотя бы наиболее простым способом. Такое решение позволило бы иметь бОльшую устойчивость модели на новых данных.

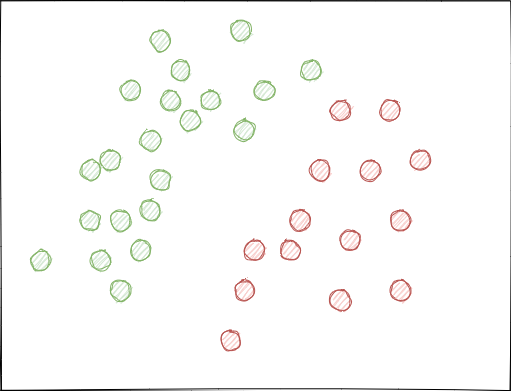
Анализ исходного GIGO датасета

В статье используются модифицированные и улучшенные функции из предыдущей. Загрузим данные:

LOOK_BACK = 5
MA_PERIODS = [15, 55, 150, 250]

SYMBOL = 'EURUSD'
MARKUP = 0.00010
TIMEFRAME = mt5.TIMEFRAME_H1
START_DATE = datetime(2020, 1, 1)
TSTART_DATE = datetime(2015, 1, 1)
STOP_DATE = datetime(2021, 1, 1)

# make dataset
pr = get_prices(START_DATE, STOP_DATE)
pr = add_labels(pr, min=10, max=25, add_noize=0)
res = tester(pr, plot=True)
pca_plot(pr)

Поскольку исходный датасет имеет размерность 20 признаков (loock_back * len(ma_periods)) или любую другую, сколь угодно большую, то его не очень-то удобно отображать на плоскости. Давайте используем метод PCA и отобразим всего 5 главных компонент, что позволит сжать пространство признаков с наименьшей потерей информации:

Для тех, кто не знает что такое PCA (principal component analysis) - гугл работает без выходных

def pca_plot(data):
    from sklearn.decomposition import PCA
    pca = PCA(n_components = 5)
    components = pd.DataFrame(pca.fit_transform(data[data.columns[1:-1]]))
    components['labels'] = data['labels'].reset_index(drop = True)
    import seaborn as sns
    g = sns.PairGrid(components, hue="labels", height=1.2)
    g.map_diag(sns.histplot)
    g.map_offdiag(sns.scatterplot)
    g.add_legend()
    plt.show()

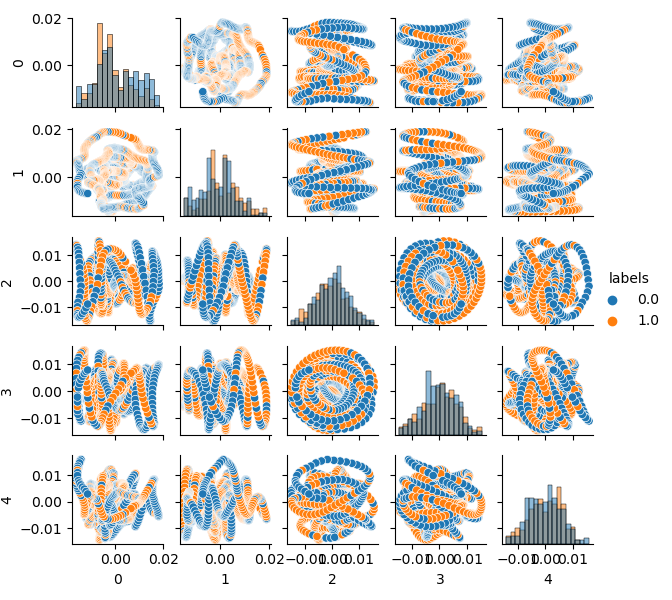
Теперь можно видеть зависимость каждой компоненты от другой, то есть 2D пространство признаков, размеченное на классы 0 и 1. Пары компонент образуют петли, непохожие на привычное облако точек. Это вызвано пресловутой автокорреляцией точек, и если проредить ряд, то кольца исчезнут. Однако нас интересует также и то, что классы сильно пересекаются. Классификатору придется создать очень сложную модель, с большим количеством разделяющих границ, чтобы классифицировать метки с наименьшей ошибкой. Можно с уверенностью заявить, что исходный датасет — это просто мусор, а, как известно, garbage in — garbage out (GIGO). Для того чтобы не следовать философии GIGO и сделать исследование более осмысленным, я предлагаю немного поразмыслить над улучшением представления исходных данных для модели машинного обучения (например, CatBoost)

Идеальное пространство признаков

Для того чтобы эффективно разделить пространство признаков на два класса, можно провести кластеризацию, допустим, методом K-means. Это даст представление относительно того, как пространство признаков могло быть идеально разделено.

Кластеризуем исходный датасет на два кластера и отобразим пять главных компонент:

# perform K-means clasterizatin over dataset
from sklearn.cluster import KMeans
pr = get_prices(look_back=LOOK_BACK)
X = pr[pr.columns[1:]]
kmeans = KMeans(n_clusters=2).fit(X)
y_kmeans = kmeans.predict(X)
pr['labels'] = y_kmeans
pca_plot(pr)

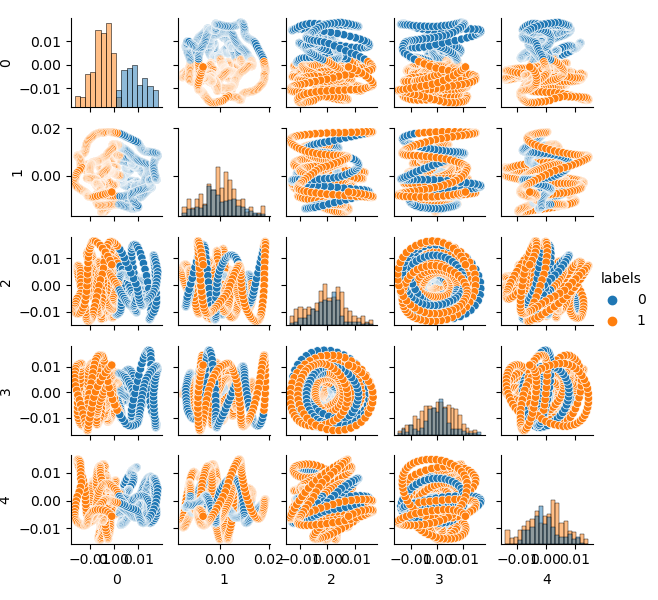
Пространство признаков выглядит идеально, но метки классов (0, 1), очевидно, не соответствуют прибыльному варианту торговли. Данный пример просто иллюстрирует более предпочтительное пространство признаков, нежели в GIGO датасете. Поэтому необходимо создать какой-то компромисс между идеальными и мусорными данными, чем и займемся дальше.

Генеративная модель для ресемплинга обучающих примеров

“What I cannot create, I do not understand.”

—Richard Feynman

В данном разделе мы рассмотрим модель, которая учится "понимать" данные и воссоздавать новые.

Метод кластеризации к-средних (k-means) является относительно простым и легким для понимания. В то же время, он имеет ряд недостатков и не подходит для нашего случая. В частности, он имеет плохую производительность во многих реальных случаях, поскольку не является вероятностным. Можно представить, что этот метод помещает окружности (или гиперсферы) вокруг заданного количества центроидов с радиусом, который определяется самой удаленной точкой кластера. Этот радиус является жестким ограничением для набора точек каждого кластера. Таким образом, все кластеры могут быть описаны только окружностями и гиперсферами, тогда как реальные кластеры не всегда удовлетворяют этому критерию (могут быть продолговатыми, в виде эллипсов). Это приведет к перекрытию значений из разных кластеров.

Более продвинутым алгоритмом является модель Гауссовских смесей (Gaussian mixture model). Данная модель ищет смесь многомерных гауссовских распределений вероятностей, которая наилучшим образом моделирует набор данных. Поскольку модель является вероятностной, то на выходе получаются вероятности отнесения примера к тому или иному кластеру. К тому же каждый кластер ассоциируется не с жестко заданной сферой, а с гладкой гауссовской моделью, которые могут представляться не только как окружности, но и как эллипсы, произвольно ориентированные в пространстве.

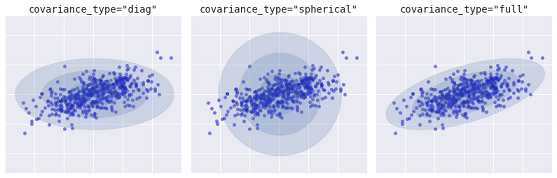
Различные виды вероятностных моделей, в зависимости от covaiance_type

Ниже приведено сравнение кластеров, полученных методами k-means и GMM (источник):

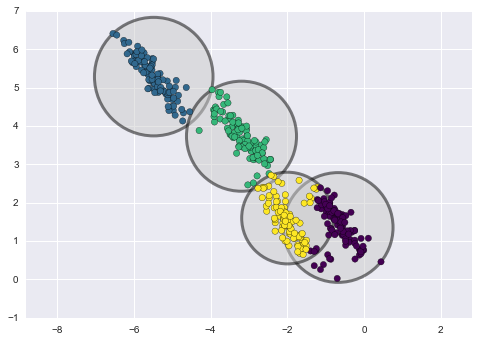
Кластеризация методом k-means

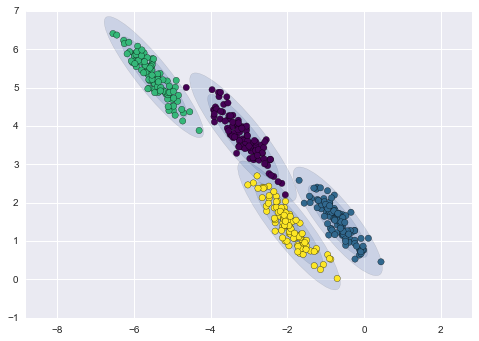
Кластеризация методом GMM

По сути, алгоритм Gaussian mixture model (GMM) не совсем кластеризатор, потому что его основной задачей является оценка плотности вероятности. Кластеры в данной модели представлены в виде данных, сгенерированных из вероятностных распределений, описывающих эти данные. Таким образом, после оценки плотности вероятности каждого кластера, мы можем сгенерировать новые наборы данных из этих распределений. Эти наборы будут являться правдоподобными, то есть, похожими на исходные данные, но обладать большей или меньшей вариативностью и меньшей склонностью к выбросам. К тому же во многих случаях будут менее коррелированы. Можно получить больше или меньше примеров случайным образом, после чего обучить на них классификатор CatBoost. 

Пайплайн для итеративного ресемплинга исходного датасета и обучения модели CatBoost

В первую очередь необходимо провести кластеризацию исходных данных, включая метки классов:

# perform GMM clasterizatin over dataset
from sklearn import mixture
pr_c = pr.copy()
X = pr_c[pr_c.columns[1:]]
gmm = mixture.GaussianMixture(n_components=75, covariance_type='full').fit(X)

В качестве основного параметра, который можно подбирать, является n_components, который эмпирическим путем был задан 75 (кластерам). Остальные параметры не так важны и здесь не рассматриваются. После того как модель обучена, можно сгенерировать некоторое количество искусственных семплов из многомерного распределения GMM модели и визуализировать несколько главных компонент:

# plot resampled components
generated = gmm.sample(5000)
gen = pd.DataFrame(generated[0])
gen.rename(columns={ gen.columns[-1]: "labels" }, inplace = True)
gen.loc[gen['labels'] >= 0.5, 'labels'] = 1
gen.loc[gen['labels'] < 0.5, 'labels'] = 0
pca_plot(gen)

Стоит отметить, что, поскольку кластеризации подверглись не только признаки, но и метки, то последние теперь не представляют собой бинаризованный ряд. В листинге выше метки снова приводятся к значениям (0;1). Теперь можно отобразить полученное пространство признаков при помощи функции pca_plot():

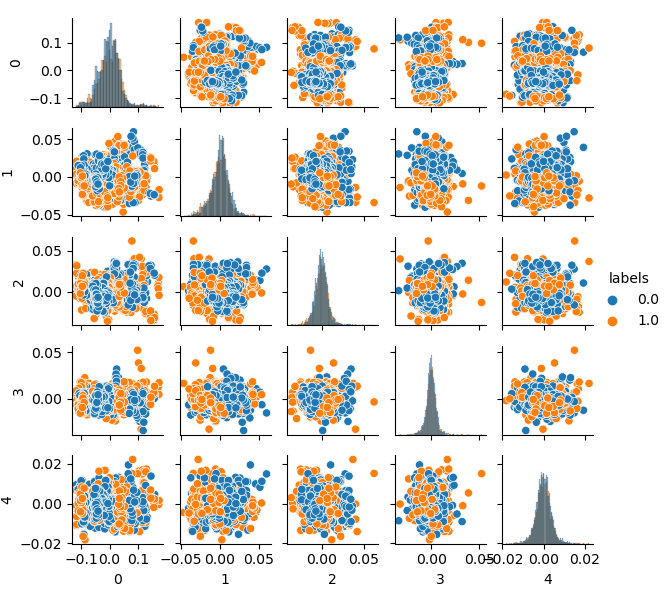
Если сравнить данную диаграмму с диаграммой GIGO датасета, которая была приведена выше, то можно заметить исчезновение петель в данных. Признаки и метки стали менее коррелированными, что должно положительно сказаться на результате обучения. В то же время метки иногда склонны формировать более плотные кластеры и, как ожидается, модель может оказаться более простой, с меньшим количеством разделяющих границ. Частично мы добились желаемого эффекта в борьбе с болезнями мусорных данных. Следует заметить, что данные, по сути, остались те же. Мы просто сделали ресемплинг.

Если вспомнить, что GMM генерирует семплы случайно, то возникает плюрализм данных и для выбора лучшей модели необходимо сделать перебор. Специально для этого была написана функция, с помощью которой можно делать брутфорс:

# brute force loop
def brute_force(samples = 5000):
    # sample new dataset
    generated = gmm.sample(samples)
    # make labels 
    gen = pd.DataFrame(generated[0])
    gen.rename(columns={ gen.columns[-1]: "labels" }, inplace = True)
    gen.loc[gen['labels'] >= 0.5, 'labels'] = 1
    gen.loc[gen['labels'] < 0.5, 'labels'] = 0
    X = gen[gen.columns[:-1]]
    y = gen[gen.columns[-1]]
    # train\test split
    train_X, test_X, train_y, test_y = train_test_split(X, y, train_size = 0.5, test_size = 0.5, shuffle=True)
    #learn with train and validation subsets
    model = CatBoostClassifier(iterations=500,
                            depth=6,
                            learning_rate=0.1,
                            custom_loss=['Accuracy'],
                            eval_metric='Accuracy',       
                            verbose=False, 
                            use_best_model=True,
                            task_type='CPU')
    model.fit(train_X, train_y, eval_set = (test_X, test_y), early_stopping_rounds=25, plot=False)
    # test on new data
    pr_tst = get_prices(TSTART_DATE, START_DATE)
    X = pr_tst[pr_tst.columns[1:]]
    X.columns = [''] * len(X.columns)

    #test the learned model
    p = model.predict_proba(X)
    p2 = [x[0]<0.5 for x in p]
    pr2 = pr_tst.iloc[:len(p2)].copy()
    pr2['labels'] = p2
    R2 = tester(pr2, MARKUP, plot=False)

    return [R2, samples, model]

Я пометил маркером основные моменты, на которые стоит обратить внимание. Сначала генерируются n-случайных примеров из распределения GMM модели. Затем обучается модель CatBoost на этих данных. Функция возвращает оценку R^2, рассчитываемую в тестере. Замечу, что модель тестируется не только на данных за период обучения, но и более ранних. Например, модель обучалась на данных с начала 2020 года, тогда как тестирование происходит с начала 2015 года. Диапазоны дат можно менять по своему усмотрению.

Напишем цикл, который будет вызывать указанную функцию несколько раз и сохранять результаты каждого прохода в список:

res = []
for i in range(50):  
    res.append(brute_force(10000))
    print('Iteration: ', i, 'R^2: ', res[-1][0])


res.sort()
test_model(res[-1])

После чего список сортируется и модель, находящаяся в конце списка, имеет наилучшую оценку R^2. Отобразим наилучший результат:

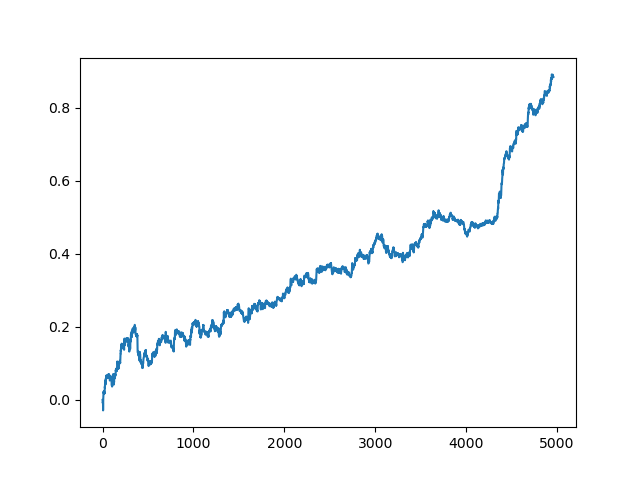
Последняя (правая) часть графика (порядка 1000 сделок) это тренировочный датасет с начала 2020 года, тогда как оставшаяся часть — новые данные, никак не учувствовавшие в обучении модели. Поскольку модели упорядочены по возрастанию метрики R^2, можно протестировать предыдущие модели с более низкой оценкой:

test_model(res[-2])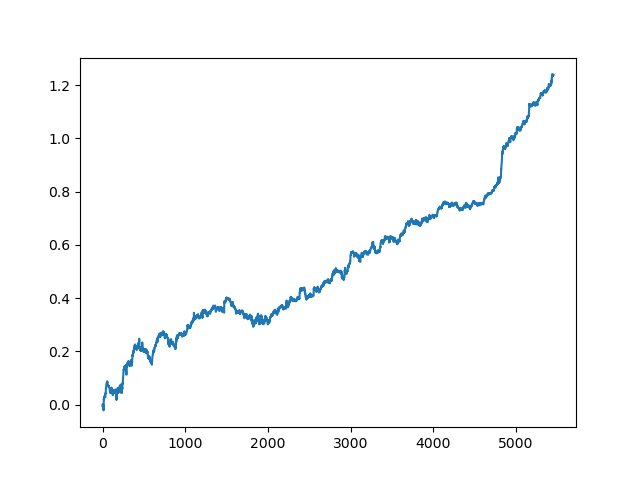

Также можно посмотреть на саму оценку R^2:

>>> res[-2][0]
0.9576444017048906

Как видно, теперь модель проходит тест на довольно длительном, пятилетнем промежутке времени, хоть и обучалась всего за один год. В завершении, можно экспортировать модель в MQH формат. Сам объект модели CatBoost находится во вложенном списке под индексом 2, тогда как первое измерение содержит номера моделей. Здесь мы экспортируем модель под индексом [-2] (вторую с конца отсортированного списка):

# export best model to mql
export_model_to_MQL_code(res[-2][2])

После экспорта, модель можно тестировать в штатном тестере MetaTrader 5. Поскольку в кастомном тестере спред стоял меньше, чем реальный, кривые несколько отличаются, однако, общая их форма совпадает.

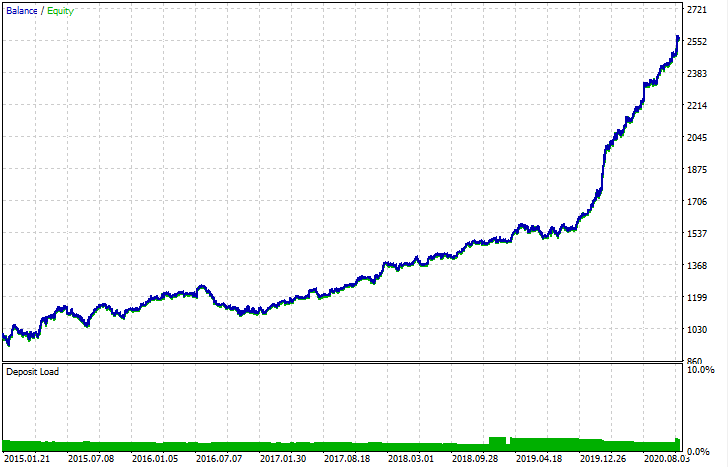
Как можно улучшить модели?

Следует понимать, что при обучении моделей существует много случайных компонент, которые меняются от раза к разу. Например, случайный семплинг сделок, затем обучение GMM (которое тоже имеет элемент случайности), затем случайный семплинг из апостериорного распределения GMM модели, затем обучение CatBoost, которое тоже содержит элемент случайности. Поэтому можно несколько раз перезапускать всю программу целиком, для получения наилучшего результата. В то же время, если не удается получить устойчивую модель, следует поиграть с параметром LOOK_BACK и количеством скользящих средних и их периодами. Имеет смысл менять количество семплов, получаемых из GMM модели, а также изменять временной интервал обучения и тестирования. 

Лог изменений и рефакторинг кода

В код Python программы были внесены некоторые изменения, которые требуют пояснений.

Теперь можно определить список скользящих средних с разными периодами усреднения. Практика показала, что комбинация нескольких МА положительно влияет на результат обучения.

MA_PERIODS = [15, 55, 150, 250]

Добавлена начальная дата для процесса тестирования, оценки модели и выбора, которую можно менять.

TSTART_DATE = datetime(2015, 1, 1)

Функция случайного семплинга претерпела ряд изменений. Добавлен параметр add_noize, который позволяет вносить шум в исходный датасет. Это нужно для того, чтобы сделать торговлю менее идеальной, внести просадки, перепутать сделки. Иногда, внеся ошибку на уровне 0.1 - 02, можно улучшить модель на новых данных. 

Теперь учитывается спред. Сделки, не покрывающие спред, помечаются меткой 2.0, а затем удаляются из датасета как неинформативные.

def add_labels(dataset, min, max, add_noize = 0.1):
    labels = []
    for i in range(dataset.shape[0]-max):
        rand = random.randint(min, max)
        curr_pr = dataset['close'][i]
        future_pr = dataset['close'][i + rand]

        if future_pr + MARKUP < curr_pr:
            labels.append(1.0)
        elif future_pr - MARKUP > curr_pr:
            labels.append(0.0)              
        else:
            labels.append(2.0)
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(dataset[dataset.labels == 2].index).reset_index(drop=True)

    if add_noize==0:
        return dataset

    # add noize to samples
    noize_b = dataset[dataset.labels == 0]['labels'].sample(frac = add_noize)
    noize_s = dataset[dataset.labels == 1]['labels'].sample(frac = add_noize)
    noize_b = noize_b+1
    noize_s = noize_s-1
    dataset.update(noize_b)
    dataset.update(noize_s)
    return dataset

Функция тестирования теперь возвращает оценку R^2:

def tester(dataset, markup = 0.0, plot = False):
    last_deal = int(2)
    last_price = 0.0
    report = [0.0]
    for i in range(dataset.shape[0]):
        pred = dataset['labels'][i]
        if last_deal == 2:
            last_price = dataset['close'][i]
            last_deal = 0 if pred <= 0.5 else 1
            continue
        if last_deal == 0 and pred > 0.5:
            last_deal = 1
            report.append(report[-1] - markup + (dataset['close'][i] - last_price))
            last_price = dataset['close'][i]
            continue
        if last_deal == 1 and pred < 0.5:
            last_deal = 0
            report.append(report[-1] - markup + (last_price - dataset['close'][i]))
            last_price = dataset['close'][i]      

    y = np.array(report).reshape(-1,1)
    X = np.arange(len(report)).reshape(-1,1)
    lr = LinearRegression()
    lr.fit(X,y)

    l = lr.coef_
    if l >= 0:
        l = 1
    else:
        l = -1

    if(plot):
        plt.plot(report)
        plt.show()

    return lr.score(X,y) * l

Добавлена вспомогательная функция для визуализации данных через метод главных компонент. Это в некоторых случаях позволяет лучше понимать ваши данные.

def pca_plot(data):
    from sklearn.decomposition import PCA
    pca = PCA(n_components = 5)
    components = pd.DataFrame(pca.fit_transform(data[data.columns[1:-1]]))
    components['labels'] = data['labels'].reset_index(drop = True)
    import seaborn as sns
    g = sns.PairGrid(components, hue="labels", height=1.2)
    g.map_diag(sns.histplot)
    g.map_offdiag(sns.scatterplot)
    g.add_legend()
    plt.show()

Дополнен парсер кода. Теперь учитываются все периоды скользящих средних, они добавляются в MQL программу, после чего специальная функция fill_arrays формирует вектор признаков.

def export_model_to_MQL_code(model):
    model.save_model('catmodel.h',
           format="cpp",
           export_parameters=None,
           pool=None)

    # add variables
    code = 'int ' + 'loock_back = ' + str(LOOK_BACK) + ';\n'
    code += 'int hnd[];\n'
    code += 'int OnInit() {\n'
    code +=     'ArrayResize(hnd,' + str(len(MA_PERIODS)) + ');\n'

    count = len(MA_PERIODS) - 1
    for i in MA_PERIODS:
        code +=     'hnd[' + str(count) + ']' + ' =' + ' iMA(NULL,PERIOD_CURRENT,' + str(i) + ',0,MODE_SMA,PRICE_CLOSE);\n'
        count -= 1

    code += 'return(INIT_SUCCEEDED);\n'
    code += '}\n\n'

    # get features
    code += 'void fill_arays(int look_back, double &features[]) {\n'
    code += '   double ma[], pr[], ret[];\n'
    code += '   ArrayResize(ret,' + str(LOOK_BACK) +');\n'
    code += '   CopyClose(NULL,PERIOD_CURRENT,1,look_back,pr);\n'
    code += '   for(int i=0;i<' + str(len(MA_PERIODS)) +';i++) {\n'
    code += '       CopyBuffer(hnd[' + 'i' + '], 0, 1, look_back, ma);\n'
    code += '       for(int f=0;f<' + str(LOOK_BACK) +';f++)\n'
    code += '           ret[f] = pr[f] - ma[f];\n'
    code += '       ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }\n'
    code += '   ArraySetAsSeries(features, true);\n'
    code += '}\n\n'

Заключение

В данной статье был продемонстрирован пример использования простой генеративной модели GMM (Gaussian mixture model) для ресемплинга исходного датасета. Показано, что можно улучшить производительность классификатора CatBoost на новых данных за счет улучшения характеристик пространства признаков. Для выбора наилучшей модели был реализован итеративный ресемплинг датасета, с возможностью последующего выбора понравившегося результата.

Мы совершили своего рода прорыв от наивных моделей к осмысленным. Затратив минимум усилий на разработку какой-то логической составляющей торговой стратегии, можно получать интересных ботов, основанных на машинном обучении.