Gradient boosting en el aprendizaje de máquinas transductivo y activo

Introducción

El aprendizaje semi-supervisado  o aprendizaje transductivo, usa los datos sin etiquetar para que el modelo pueda comprender mejor y más fácilmente la estructura general de los datos. Esto coincide con nuestro pensamiento. Con solo recordar unas pocas imágenes, el cerebro humano es capaz de extrapolar el conocimiento sobre dichas imágenes a nuevos objetos en términos generales, sin incidir en detalles poco relevantes. Esto conlleva un menor ajuste y una buena capacidad generalizadora. 

El término transducción fue introducido por Vladímir Naúmovich Vápnik, el inventor de la máquina de vectores de soporte (SVM). En su opinión, el método de transducción resulta preferible al método de inducción, ya que la inducción requiere la resolución de un problema más general (la restauración de funciones) antes que la resolución de un problema más específico (el cálculo de los resultados basados en nuevos datos). 

 «…al resolver la tarea que le interese, no resuelva un problema más general como paso intermedio. Trate de obtener la respuesta que realmente necesita, no una más general» 

Esta suposición de Vladímir Naúmovich se muestra coherente con una observación semejante que Bertrand Russell hizo con anterioridad:

«…llegaremos a la conclusión de que Sócrates es mortal con una aproximación más global a la certeza, es decir, si hacemos nuestro argumento puramente inductivo, antes que optar por la variante: "todos los hombres son mortales" y luego usar la deducción»

Es de esperar que el aprendizaje sin supervisión (sobre datos sin etiquetar) se vuelva mucho más importante a largo plazo. La enseñanza a personas y animales, en esencia, se realiza sin un maestro: estos descubren la estructura del mundo mediante la observación, y no reconociendo el nombre de cada objeto. 

Así, el aprendizaje semi-supervisado combina el aprendizaje con maestro y sin él. El aprendizaje supervisado se lleva a cabo con una pequeña cantidad de datos etiquetados, tras lo cual el modelo extrapola su conocimiento a un área más amplia no etiquetada. 

La utilización de datos sin etiquetar presupone alguna conexión con la distribución de datos subyacente. Así que se debe cumplir al menos uno de los siguientes supuestos:

• Supuesto de continuidad. Es más probable que los puntos cercanos entre sí tengan la misma etiqueta. Esto también se presupone para el aprendizaje supervisado, y da preferencia a los límites geométricamente simples que separan las clases. En el caso del aprendizaje semi-supervisado, el supuesto de continuidad ofrece además una ventaja en áreas con baja densidad de puntos, donde varios puntos son adyacentes entre sí, pero en diferentes clases.
• Supuesto de clúster. Los datos tienden a formar grupos discretos, y resulta más probable que los puntos en el mismo grupo tengan una etiqueta común (aunque los datos con una etiqueta común puedan extenderse a lo largo de varios grupos). Se trata de un caso especial del supuesto de continuidad que conlleva el aprendizaje mediante algoritmos de agrupamiento.
  
• Supuesto de redundancia de datos. Los datos se encuentran aproximadamente en un colector mucho más pequeño que el espacio de etiquetado original. En este caso, la exploración de la variedad usando datos etiquetados y no etiquetados puede evitar la maldición de la dimensionalidad. El entrenamiento puede proseguir utilizando las distancias y densidades definidas en el colector.
  

Clique en el enlace para obtener más información sobre el aprendizaje  semi-supervisado.

El método principal de aprendizaje semi-supervisado es el pseudo-etiquetado, que se efectúa de la forma siguiente:

• Se utiliza una cierta medida de proximidad (por ejemplo, la distancia euclidiana) para marcar el resto de datos usando como base la psedo-etiqueta marcada.
• Se combinan etiquetas de entrenamiento con pseudo-etiquetas y signos.
• El modelo se entrena en todo el conjunto de datos.

Los investigadores descubrieron que el uso de datos etiquetados junto con datos no etiquetados puede mejorar notablemente la precisión del modelo. Ya utilizamos una idea similar en el artículo anterior, al valorar la densidad de probabilidad de la distribución de datos etiquetados y el muestreo de esta distribución. Pero la distribución de los nuevos datos puede resultar distinta, por lo que el entrenamiento semi-supervisado es capaz de ofrecer algunos beneficios, como bien mostrará el experimento en el presente artículo.

El aprendizaje activo (active learning) es una especie de continuación lógica del aprendizaje semi-supervisado . Se trata de un proceso iterativo en el que se etiquetan los nuevos datos de tal forma que los límites que separan las clases se ubiquen de manera óptima.

La principal hipótesis del aprendizaje activo es que el algoritmo de aprendizaje puede seleccionar los datos de los que quiere aprender. Puede funcionar mejor que los métodos tradicionales con una cantidad sustancialmente menor de datos de entrenamiento. Aquí, entendemos por métodos tradicionales el aprendizaje supervisado convencional. Condicionalmente, dicho entrenamiento se puede llamar pasivo. El modelo simplemente se entrena con datos etiquetados, y cuanto más, mejor. Dentro del aprendizaje pasivo, una de las tareas que más tiempo consume es la recopilación y el etiquetado de datos. En muchos casos, pueden existir restricciones relacionadas con la recopilación de datos adicionales o, como en nuestro caso, con su correcto etiquetado. 

En el aprendizaje activo, hay tres escenarios más populares en los que el aprendiz o estudiante (el modelo de aprendizaje) solicitará nuevas etiquetas de instancia de clase del área no etiquetada:

• Solicitud de un ejemplo sintetizado artificialmente. En este caso, el modelo genera una instancia partiendo de alguna distribución que sea común a todos los ejemplos. Por ejemplo, una instancia de una clase con ruido añadido o simplemente un punto plausible en el espacio analizado. Precisamente este nuevo punto se envía al oráculo para su entrenamiento. El Oráculo es el nombre convencional para una función de valoración que evalúa el valor de una instancia con una característica determinada para un modelo.
• Muestreo selectivo basado en un flujo. Este enfoque conlleva enumerar los puntos de una muestra no marcada, después de lo cual, el Oráculo decide si desea solicitar una etiqueta de clase para un punto determinado o rechazarla basándose en algún criterio de información. 
• Muestreo basado en un pool. Como en el caso anterior, este escenario presupone un gran número de ejemplos sin etiquetar. Las instancias son seleccionadas del grupo usando como base la informatividad. Esta medida se aplica a todas las instancias del grupo, y después se seleccionan las instancias más informativas. Este es el escenario más habitual entre los adeptos del aprendizaje activo. Todos los ejemplos no etiquetados serán clasificados, seleccionándose después el más informativo.

Cada escenario puede basarse en una estrategia de consulta específica. Como hemos mencionado anteriormente, la principal diferencia entre el aprendizaje activo y el pasivo reside en la capacidad de solicitar instancias de un área no etiquetada según las solicitudes anteriores y las respuestas del modelo. Como consecuencia, todas las solicitudes requerirán alguna medida de informatividad. 

Vamos a enumerar las estrategias de consulta más populares:

• Mínima confianza (o incertidumbre de clasificación). Esta estrategia selecciona el ejemplo en el que el modelo tiene menos confianza. Por ejemplo, la probabilidad de asignar una etiqueta a una determinada clase es inferior a algún tipo de límite.
• Muestreo de margen. La desventaja del primer enfoque es que determina la probabilidad de pertenecer a una sola etiqueta, pero no se considera la probabilidad de pertenecer a otras. El enfoque de margen selecciona la menor diferencia de probabilidad entre las dos etiquetas más probables.
• Muestreo basado en la entropía. Consiste en aplicar la fórmula de la entropía a cada instancia y solicitar la instancia con el valor más alto.

Al igual que sucede con el aprendizaje semi-supervisado, el proceso de aprendizaje activo tiene varios pasos:

• El modelo se entrena con los datos etiquetados.
  
• El propio modelo se usa para marcar datos sin etiquetar, para así predecir las probabilidades (pseudo-etiquetas).
• Asimismo, se selecciona una estrategia para solicitar nuevos ejemplos.
• Se seleccionan N ejemplos del conjunto de datos según el criterio de información y se añaden al conjunto de entrenamiento. 
• Este ciclo es repitido hasta alcanzar algún criterio de parada. El criterio de parada puede ser un número de iteraciones o una valoración del error de aprendizaje, así como otros criterios externos.

Aprendizaje activo

Vamos a pasar directamente al aprendizaje activo, poniendo a prueba su efectividad en nuestros datos.

Actualmente, existen varias bibliotecas en el lenguaje Python para el aprendizaje activo, aquí tenemos tres de las más comunes:

• modAL es un paquete bastante fácil de entender y dominar, una especie de contenedor para la popular biblioteca de aprendizaje automático scikit-learn, y totalmente compatible con ella. Ofrece los métodos de aprendizaje activo más populares.
• Libact usa una estrategia de bandidos multibrazo además de las estrategias de consulta existentes para elegir de forma dinámica la mejor consulta. 
• Alipy es una especie de laboratorio de los proveedores del paquete, que contiene una gran cantidad de estrategias de consulta.

Nosotros nos decantamos por la biblioteca modAL como la más intuitiva y adecuada para familiarizarse con la filosofía del aprendizaje activo. Ofrece mucha libertad para construir modelos y crear nuestros propios diseños usando bloques estándar o creando otros propios.

Vamos a presentar el proceso de aprendizaje descrito anteriormente en un diagrama que no requiera de explicaciones detalladas:

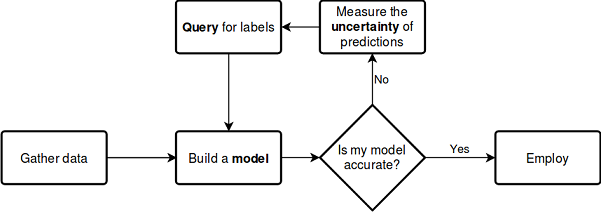
ver documentación

Lo bueno de la biblioteca es que puede utilizar cualquier clasificador de scikit-learn. El siguiente ejemplo muestra el uso de un bosque aleatorio como modelo de aprendizaje:

from modAL.models import ActiveLearner
from modAL.uncertainty import entropy_sampling
from sklearn.ensemble import RandomForestClassifier

learner = ActiveLearner(
    estimator=RandomForestClassifier(),
    query_strategy=entropy_sampling,
    X_training=X_training, y_training=y_training
)

Aquí, el bosque aleatorio ejerce como modelo de aprendizaje y evaluador, permitiendo seleccionar nuevas muestras de datos sin etiquetar según la estrategia de consulta (en este ejemplo, según la entropía). Después, se transmite al modelo un conjunto de datos que consta de una pequeña cantidad de datos etiquetados. Esto es necesario para el aprendizaje preliminar. 

La biblioteca modAL facilita la combinación de estrategias de consulta y la creación de ponderaciones compuestas partiendo de ellas:

from modAL.utils.combination import make_linear_combination, make_product
from modAL.uncertainty import classifier_uncertainty, classifier_margin

# creating new utility measures by linear combination and product
# linear_combination will return 1.0*classifier_uncertainty + 1.0*classifier_margin
linear_combination = make_linear_combination(
    classifier_uncertainty, classifier_margin,
    weights=[1.0, 1.0]
)
# product will return (classifier_uncertainty**0.5)*(classifier_margin**0.1)
product = make_product(
    classifier_uncertainty, classifier_margin,
    exponents=[0.5, 0.1]
)

Una vez generada la solicitud, los ejemplos que cumplen los criterios de solicitud son seleccionados del área de datos no etiquetados con la ayuda de los selectores multi_argmax o weighted_randm:

from modAL.utils.selection import multi_argmax

# defining the custom query strategy, which uses the linear combination of
# classifier uncertainty and classifier margin
def custom_query_strategy(classifier, X, n_instances=1):
    utility = linear_combination(classifier, X)
    query_idx = multi_argmax(utility, n_instances=n_instances)
    return query_idx, X[query_idx]

custom_query_learner = ActiveLearner(
    estimator=GaussianProcessClassifier(1.0 * RBF(1.0)),
    query_strategy=custom_query_strategy,
    X_training=X_training, y_training=y_training
)

Estrategias de consulta

Ya hemos mencionado que existen tres estrategias principales de consulta. Todas las estrategias están basadas en la incertidumbre de clasificación, por lo que se denominan medidas de incertidumbre. Vamos a ver con mayor detalle cómo funcionan.

La incertidumbre de clasificación , en el caso simple, se valora como U(x)=1−P(x^|x), donde x es el caso a predecir, y x^ es el pronóstico más probable. Por ejemplo, si tenemos tres clases y tres elementos de la muestra, las incertidumbres correspondientes se podrán calcular como:

[[0.1 , 0.85, 0.05],
 [0.6 , 0.3 , 0.1 ],
 [0.39, 0.61, 0.0 ]]

1 - proba.max(axis=1)

[0.15, 0.4 , 0.39]

Por consiguiente, el segundo ejemplo se seleccionará como el más indefinido.

El margen de clasificación supone la diferencia entre las probabilidades de la primera y segunda consultas con mayor probabilidad, determinada por la fórmula M(x)=P(x1^|x)−P(x2^|x), donde x1^ y x2^ son la primera y segunda clases más probables.

Esta estrategia de consulta elige los ejemplos con el menor margen entre las probabilidades de las dos clases más probables, porque, cuanto menor sea el margen de la solución, más incierta será.

>>> import numpy as np
>>> proba = np.array([[0.1 , 0.85, 0.05],
...                   [0.6 , 0.3 , 0.1 ],
...                   [0.39, 0.61, 0.0 ]])
>>>
>>> proba
array([[0.1 , 0.85, 0.05],
       [0.6 , 0.3 , 0.1 ],
       [0.39, 0.61, 0.  ]])
>>> part = np.partition(-proba, 1, axis=1)
>>> part
array([[-0.85, -0.1 , -0.05],
       [-0.6 , -0.3 , -0.1 ],
       [-0.61, -0.39, -0.  ]])
>>> part[:, 0]
array([-0.85, -0.6 , -0.61])
>>> part[:, 1]
array([-0.1 , -0.3 , -0.39])
>>> margin = - part[:, 0] + part[:, 1]
>>> margin
array([0.75, 0.3 , 0.22])

En este caso, se elegirá la tercera muestra (la tercera fila de la matriz), ya que el margen de probabilidad para este ejemplo es mínimo.

La entropía de clasificación se calcula usando la fórmula de entropía de la información H(x)=−∑kpklog(pk), donde pk es la probabilidad de que la muestra pertenezca a la k-ésima clase. Cuanto más cerca se encuentre la distribución respecto a la uniformidad, mayor será la entropía. Para nuestro ejemplo, la máxima entropía se obtiene para el segundo ejemplo

[0.51818621, 0.89794572, 0.66874809]

No parece complicado. Quizás esta información baste para entender las tres principales estrategias de consulta. El lector podrá leer más información sobre este tema en la documentación del paquete; aquí solo hemos traducido y enunciado los puntos básicos.

Estrategias de consulta por paquetes

Consultar elementos uno a uno y volver a entrenar el modelo no siempre resulta efectivo. Es mucho más rentable etiquetar y seleccionar varias instancias al mismo tiempo partiendo de los datos sin etiquetar. Existen varias consultas para esto, la más popular entre ellas es el muestreo de un lote clasificado basado en una función de similitud, por ejemplo, la distancia del coseno. Este método estima lo bien que se explora el espacio de rasgos en la vecindad de x (un ejemplo sin etiquetar). Después de la valoración, la instancia con la puntuación más alta se añade al conjunto de entrenamiento y se elimina del grupo de datos sin etiquetar. Después de ello, se vuelve a calcular la puntuación y se añade de nuevo la mejor instancia hasta que el número de ejemplos alcance el tamaño especificado (tamaño de lote). 

Consultas de densidad de información

Las estrategias de consulta simples que hemos descrito anteriormente no valoran de forma alguna la estructura de datos. Esto puede provocar consultas subóptimas. Para mejorar el muestreo, podemos usar medidas de densidad de información que nos ayuden a seleccionar los elementos correctos de los datos sin etiquetar. Aquí se usa el coseno o la distancia euclidiana. Cuanto mayor sea la densidad de la información, más similar resultará esta instancia seleccionada a todas las demás. 

Consultas al comité de clasificación

Este tipo de consulta nos evita algunas de las desventajas de los tipos de consulta simples. Por ejemplo, la selección de elementos suele ser sesgada debido a las peculiaridades de un clasificador particular. Es posible que falten algunos elementos de muestreo importantes. Este efecto se evita guardando varias hipótesis simultáneamente y seleccionando las consultas entre las que existen desacuerdos. Por consiguiente, cada uno de los clasificadores del comité aprende de su propia copia de la muestra, ponderándose después los resultados. El empaquetado y el bootstrapping son otros tipos de entrenamiento del comité de clasificación.

En esta breve descripción, ya hemos cubierto casi por completo la funcionalidad de la biblioteca. Si el lector desea aclarar cualquier duda, podrá consultar la documentación.

Aprendemos de forma activa

Para los experimentos, seleccionamos la estrategia de consulta por lotes, así como las consultas del comité clasificador. Inicialmente, la estrategia de consulta por lotes no mostró un buen rendimiento por sí misma con los datos nuevos; no obstante, tras enviar el conjunto de datos generados a GMM, comenzamos a obtener resultados interesantes. 

Vamos a analizar un ejemplo de implementación de la función de aprendizaje activo por lotes:

def active_learner(data, labeled_size, unlabeled_size, batch_size, max_depth):
    X_raw = data[data.columns[1:-1]].to_numpy()
    y_raw = data[data.columns[-1]].to_numpy()

    # Isolate our examples for our labeled dataset.
    training_indices = np.random.randint(low=0, high=X_raw.shape[0] + 1, size=labeled_size)

    X_train = X_raw[training_indices]
    y_train = y_raw[training_indices]

    # fit the model on all data
    cl = AdaBoostClassifier(DecisionTreeClassifier(max_depth=max_depth), n_estimators=50, learning_rate = 0.01)
    cl.fit(X_raw, y_raw)
    print('Score for the passive learning: ', cl.score(X_raw, y_raw), ' with train size: ', data.shape[0])

    # Isolate the non-training examples we'll be querying.
    X_pool = np.delete(X_raw, training_indices, axis=0)
    y_pool = np.delete(y_raw, training_indices, axis=0)

    # Pre-set our batch sampling to retrieve 3 samples at a time.
    preset_batch = partial(uncertainty_batch_sampling, n_instances=batch_size)

    # Specify our core estimator along with it's active learning model.
    cl = AdaBoostClassifier(DecisionTreeClassifier(max_depth=3), n_estimators=50, learning_rate = 0.03)
    learner = ActiveLearner(estimator=cl, query_strategy=preset_batch, X_training=X_train, y_training=y_train)

A la entrada de la función se transmiten el conjunto de datos etiquetado, el número de ejemplos etiquetados, el número de ejemplos sin etiquetar, el tamaño del lote para una solicitud de lote de etiquetas y la profundidad máxima del árbol.

Del conjunto de datos etiquetado se selecciona de forma aleatoria un número determinado de ejemplos con etiquetas para el entrenamiento previo del modelo. El resto del conjunto de datos forma un pool del que se solicitarán ejemplos. Como clasificador base, hemos elegido AdaBoost, que es similar a CatBoost. A continuación, el modelo se entrena de forma iterativa:

    # Allow our model to query our unlabeled dataset for the most
    # informative points according to our query strategy (uncertainty sampling).
    N_QUERIES = unlabeled_size // batch_size

    for index in range(N_QUERIES):
        query_index, query_instance = learner.query(X_pool)

        # Teach our ActiveLearner model the record it has requested.
        X, y = X_pool[query_index], y_pool[query_index]
        learner.teach(X=X, y=y)

        # Remove the queried instance from the unlabeled pool.
        X_pool, y_pool = np.delete(
            X_pool, query_index, axis=0), np.delete(y_pool, query_index)

        # Calculate and report our model's accuracy.
        model_accuracy = learner.score(X_raw, y_raw)
        print('Accuracy after query {n}: {acc:0.4f}'.format(
            n=index + 1, acc=model_accuracy))

        # Save our model's performance for plotting.
        performance_history.append(model_accuracy)

    print('Score for the active learning with train size: ',
          learner.X_training.shape)     

Ya que cualquier cosa puede ocurrir como resultado de dicho aprendizaje semi-supervisado, el resultado puede ser cualquiera. No obstante, tras realizar algunas manipulaciones con la configuración del aprendiz, los resultados ya eran comparables a los del artículo anterior. 

De manera ideal, la precisión de clasificación de un aprendiz activo con una pequeña cantidad de datos etiquetados debería superar la precisión de un clasificador similar si todos los datos estuvieran etiquetados.

>>> learned = active_learner(pr, 1000, 1000, 50)
Score for the passive learning:  0.5991245668429692  with train size:  5483
Accuracy after query 1: 0.5710
Accuracy after query 2: 0.5836
Accuracy after query 3: 0.5749
Accuracy after query 4: 0.5847
Accuracy after query 5: 0.5829
Accuracy after query 6: 0.5823
Accuracy after query 7: 0.5650
Accuracy after query 8: 0.5667
Accuracy after query 9: 0.5854
Accuracy after query 10: 0.5836
Accuracy after query 11: 0.5807
Accuracy after query 12: 0.5907
Accuracy after query 13: 0.5944
Accuracy after query 14: 0.5865
Accuracy after query 15: 0.5949
Accuracy after query 16: 0.5873
Accuracy after query 17: 0.5833
Accuracy after query 18: 0.5862
Accuracy after query 19: 0.5902
Accuracy after query 20: 0.6002
Score for the active learning with train size:  (2000, 8)

Por el informe, podemos entender que el clasificador entrenado con todos los datos etiquetados tiene una precisión inferior a la del aprendiz activo, entrenado con solo 2000 ejemplos. Seguramente esto sea positivo. 

Ahora podemos enviar esta muestra al modelo GMM y luego entrenar el clasificador CatBoost.

# prepare data for CatBoost
catboost_df = pd.DataFrame(learned.X_training)
catboost_df['labels'] = learned.y_training

# perform GMM clasterizatin over dataset
X = catboost_df.copy()
gmm = mixture.GaussianMixture(
    n_components=75, max_iter=500, covariance_type='full', n_init=1).fit(X)

# sample new dataset
generated = gmm.sample(10000)
# make labels
gen = pd.DataFrame(generated[0])
gen.rename(columns={gen.columns[-1]: "labels"}, inplace=True)
gen.loc[gen['labels'] >= 0.5, 'labels'] = 1
gen.loc[gen['labels'] < 0.5, 'labels'] = 0
X = gen[gen.columns[:-1]]
y = gen[gen.columns[-1]]
pr = pd.DataFrame(X)
pr['labels'] = y

# fit CatBoost model and test it
model = fit_model(pr)
test_model(model, TEST_START, END_DATE)

Podemos repetir este proceso varias veces, porque en cada etapa del procesamiento de datos hay un elemento de incertidumbre que no permite construir modelos inequívocos. Tras realizar todas las iteraciones, se obtuvieron las siguientes imágenes en el simulador (periodo de entrenamiento de 1 año y periodo de prueba de 5 años):

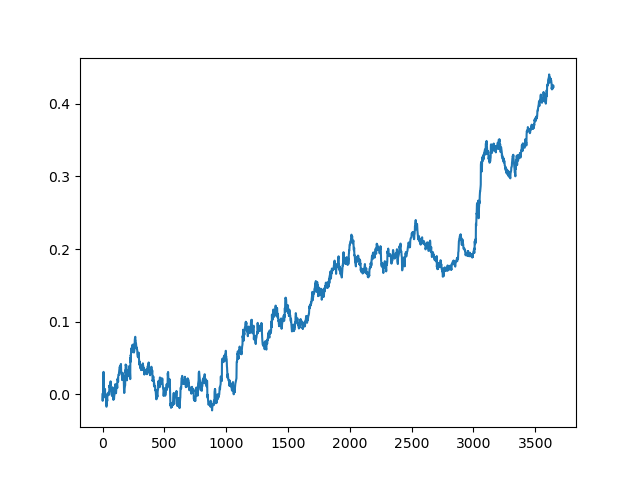
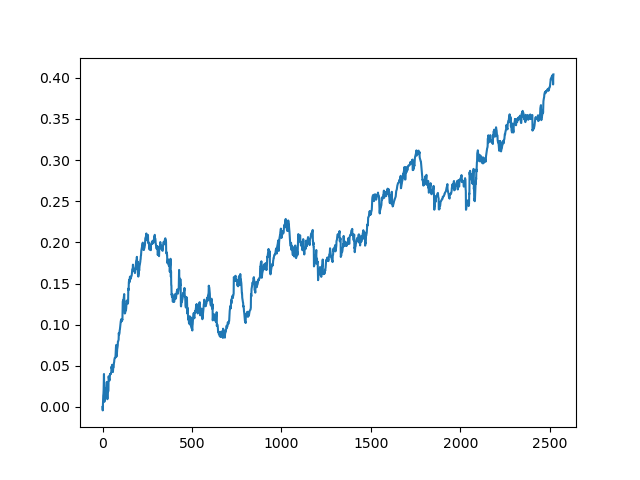
Obviamente, estas imágenes no suponen una especie de estándar: solo muestran la posibilidad de obtener modelos rentables (basados ​​en nuevos datos) que se puedan iterar. 

Vamos a implementar ahora la función de aprendizaje con el comité de clasificación, y veamos qué ocurre:

def active_learner_committee(data, learners_number, labeled_size, unlabeled_size, batch_size):
    X_pool = data[data.columns[1:-1]].to_numpy()
    y_pool = data[data.columns[-1]].to_numpy()

    cl = AdaBoostClassifier(DecisionTreeClassifier(max_depth=3), n_estimators=50, learning_rate = 0.05)
    cl.fit(X_pool, y_pool)
    print('Score for the passive learning: ', cl.score(
        X_pool, y_pool), ' with train size: ', data.shape[0])

    # initializing Committee members
    learner_list = list()

    # Pre-set our batch sampling to retrieve 3 samples at a time.
    preset_batch = partial(uncertainty_batch_sampling, n_instances=batch_size)
    
    for member_idx in range(learners_number):
        # initial training data
        train_idx = np.random.choice(range(X_pool.shape[0]), size=labeled_size, replace=False)
        X_train = X_pool[train_idx]
        y_train = y_pool[train_idx]

        # creating a reduced copy of the data with the known instances removed
        X_pool = np.delete(X_pool, train_idx, axis=0)
        y_pool = np.delete(y_pool, train_idx)

        # initializing learner
        learner = ActiveLearner(
            estimator=AdaBoostClassifier(DecisionTreeClassifier(max_depth=2), n_estimators=50, learning_rate = 0.05),
            query_strategy=preset_batch,
            X_training=X_train, y_training=y_train
        )
        learner_list.append(learner)

    # assembling the committee
    committee = Committee(learner_list=learner_list)

    unqueried_score = committee.score(X_pool, y_pool)
    performance_history = [unqueried_score]

    N_QUERIES = unlabeled_size // batch_size

    for idx in range(N_QUERIES):
        query_idx, query_instance = committee.query(X_pool)
        committee.teach(
            X=X_pool[query_idx].reshape(1, -1),
            y=y_pool[query_idx].reshape(1, )
        )
        model_accuracy = committee.score(X_pool, y_pool)
        performance_history.append(model_accuracy)
        print('Accuracy after query {n}: {acc:0.4f}'.format(
            n=idx + 1, acc=model_accuracy))

        # remove queried instance from pool
        X_pool = np.delete(X_pool, query_idx, axis=0)
        y_pool = np.delete(y_pool, query_idx)

    return committee

Aquí también elegimos la estrategia de consulta por lotes, para no volver a entrenar el modelo cada vez que se añade un solo elemento (resulta muy lento). Por lo demás, hemos creado un comité formado por un número aleatorio de clasificadores AdaBoost (no parece tener sentido añadir más de cinco, pero el lector podrá experimentar). 

A continuación, mostramos la puntuación del entrenamiento de un comité de cinco modelos con la misma configuración que el método anterior:

>>> commetee = active_learner_committee(pr, 5, 1000, 1000, 50)
Score for the passive learning:  0.6533842794759825  with train size:  5496
Accuracy after query 1: 0.5927
Accuracy after query 2: 0.5818
Accuracy after query 3: 0.5668
Accuracy after query 4: 0.5862
Accuracy after query 5: 0.5874
Accuracy after query 6: 0.5906
Accuracy after query 7: 0.5918
Accuracy after query 8: 0.5910
Accuracy after query 9: 0.5820
Accuracy after query 10: 0.5934
Accuracy after query 11: 0.5864
Accuracy after query 12: 0.5753
Accuracy after query 13: 0.5868
Accuracy after query 14: 0.5921
Accuracy after query 15: 0.5809
Accuracy after query 16: 0.5842
Accuracy after query 17: 0.5833
Accuracy after query 18: 0.5783
Accuracy after query 19: 0.5732
Accuracy after query 20: 0.5828

Aquí, el comité de aprendices activos no alcanzó el resultado de uno pasivo. Es imposible saber el motivo. Quizás solo sea un resultado aleatorio. Después ejecutamos varias veces el conjunto de datos resultante según el mismo principio que la última vez, y obtuvimos los siguientes resultados aleatorios a elegir:

Conclusión

En el presente artículo, hemos analizado el aprendizaje activo, que, sinceramente, nos ha dejado sensaciones contradictorias. Por una parte, siempre resulta tentador aprender de una pequeña cantidad de ejemplos, y estos modelos funcionan bien para algunos problemas de clasificación. No obstante, esto todavía queda lejos para la inteligencia artificial. Dicho modelo no puede encontrar patrones estables en los datos basura, y necesita una preparación más completa en cuanto a características y etiquetas, incluidas las basadas en el marcado experto. No hemos visto un aumento significativo en la calidad de los modelos, ni tampoco si ha habido una mejora en general. Al mismo tiempo, la laboriosidad y el tiempo de entrenamiento de los modelos han aumentado, lo que cual supone un factor negativo. Eso sí, al autor le han parecido atractivas la filosofía del aprendizaje activo y la adopción de las características del pensamiento humano. Adjuntamos un archivo con todas las funciones. El lector podrá experimentar por su cuenta o utilizar estos modelos de alguna otra forma original.