Выявление и классификация фрактальных паттернов посредством машинного обучения

Введение

В первой статье мы подробно рассмотрели основополагающие аспекты мультифрактальной теории рынка. В ней мы говорили о том, что графики котировок способны образовывать некие повторяющиеся структуры, под воздействием внешней организующей их информации. Участники рынка создают сложную динамическую систему, которая имеет элементы памяти, которая принимает вид определенных рыночных симметрий (паттернов). Эти паттерны могут эволюционировать во времени, а могут повторяться. Благодаря самоподобию фрактальных рыночных структур, паттерны могут быть выражены в разных временных масштабах.

В данной статье будет предложен оригинальный подход для поиска и классификации фрактальных паттернов. Исследование будет проводиться на языке Python, с возможностью экспорта финальных моделей в терминал Meta Trader 5 в формате ONNX.

Перед началом работы убедитесь, что установлены все необходимые пакеты и модули. Часть импортируемых модулей находится в приложении к статье.

import pandas as pd
import math
from datetime import datetime
from catboost import CatBoostClassifier
from sklearn.model_selection import train_test_split
from bots.botlibs.labeling_lib import *
from bots.botlibs.tester_lib import test_model
from bots.botlibs.export_lib import export_model_to_ONNX

Реализация функции поиска фрактальных паттернов

В этой статье я предлагаю простой подход для поиска симметричных мультифрактальных рыночных структур через корреляцию. Мы можем исследовать как фрактальные, так и мультифрактальные паттерны, которые отличаются масштабной инвариантностью, то есть, имеют разные размеры. Для этого необходимо реализовать поиск паттернов через корреляцию в разных временных масштабах, которые будут заданы в настройках. Ниже представлена функция, которая считает корреляцию в скользящем окне с учетом переменной величины длины паттернов.

@njit
def calculate_symmetric_correlation_dynamic(data, min_window_size, max_window_size):
    n = len(data)
    min_w = max(2, min_window_size)
    max_w = max(min_w, max_window_size)
    num_correlations = max(0, n - min_w + 1)

    if num_correlations == 0:
        return np.zeros(0, dtype=np.float64), np.zeros(0, dtype=np.int64)

    correlations = np.zeros(num_correlations, dtype=np.float64)
    best_window_sizes = np.full(num_correlations, -1, dtype=np.int64)

    for i in range(num_correlations):
        max_abs_corr_for_i = -1.0
        best_corr_for_i = 0.0
        current_best_w = -1
        current_max_w = min(max_w, n - i)
        start_w = min_w
        if start_w % 2 != 0:
            start_w += 1

        for w in range(start_w, current_max_w + 1, 2):
            if w < 2 or i + w > n:
                continue
            half_window = w // 2
            window = data[i : i + w]
            first_half = window[:half_window]
            second_half = (window[half_window:] * -1)[::-1]
            
            std1 = np.std(first_half)
            std2 = np.std(second_half)

            if std1 > 1e-9 and std2 > 1e-9:
                mean1 = np.mean(first_half)
                mean2 = np.mean(second_half)
                cov = np.mean((first_half - mean1) * (second_half - mean2))
                corr = cov / (std1 * std2)
                if  abs(corr) > max_abs_corr_for_i:
                    max_abs_corr_for_i = abs(corr)
                    best_corr_for_i =corr
                    current_best_w = w
        
        correlations[i] = best_corr_for_i
        best_window_sizes[i] = current_best_w
        
    return correlations, best_window_sizes

Для ускорения цикла с однотипными расчетами (циклы работают медленно в Python) используется декоратор @njit, который ускоряет расчеты посредством пакета Numba. 

На вход функция принимает датафрейм с ценами закрытия, а также минимальный и максимальный размер "окна" для паттернов. Например, мы хотим посчитать корреляцию для паттернов, длина которых составляет от 100 до 200 баров. Тогда мы задаем соответствующие настройки, после чего, для каждой новой точки отсчета и для каждой заданной длины паттерна, проверяется корреляция между его левой и зеркально перевернутой правой частью. Переворот правой части выделен желтым маркером. Это очень важно, поскольку мы ищем симметрию в данных.

Значения лучших абсолютных корреляций, для каждой начальной точки, записываются в массив correlations[]. Величина окна (длина паттерна), соответствующая лучшей корреляции, записывается в другой массив best_window_sizes[]. Таким образом функция возвращает максимальные значения корреляции и соответствующий ей паттерн, для каждой стартовой точки.

Визуальная проверка найденных паттернов

После того, как все паттерны посчитаны, можно визуально оценить правильность работы нашего алгоритма. Для этого я предлагаю еще одну функцию, которая будет отображать топ лучших найденных петтернов по наибольшему абсолютному коэффициенту корреляции Пирсона.

def plot_best_n_patterns(data, min_window_size, max_window_size, n_best):
    # 1. Calculate correlations and best window sizes
    corrs, window_sizes = calculate_symmetric_correlation_dynamic(data, min_window_size, max_window_size)

    # 2. Find N best patterns
    # Assuming -1 in window_sizes means invalid/not found by the calculation logic
    valid_calc_mask = window_sizes != -1 
    
    if not np.any(valid_calc_mask):
        print("No suitable patterns found (all window sizes were marked as -1 by calculation).")
        return
        
    filtered_corrs = corrs[valid_calc_mask]
    filtered_window_sizes = window_sizes[valid_calc_mask]
    
    original_indices_all = np.arange(len(corrs)) 
    filtered_start_indices = original_indices_all[valid_calc_mask]

    if len(filtered_corrs) == 0: 
        print("No suitable patterns found after filtering out -1 window_sizes.")
        return

    # Sort by absolute correlation value in descending order
    sorted_indices_of_filtered = np.argsort(np.abs(filtered_corrs))[::-1]
    
    # Determine how many of the top patterns to consider
    num_to_consider = min(n_best, len(sorted_indices_of_filtered))

    if num_to_consider == 0:
        print("No patterns to plot (either n_best is too small, or no patterns passed the initial filter).")
        return

    # Pre-filter these top candidates to find those actually plottable (even window size >= 2)
    patterns_to_plot_details = []
    for i in range(num_to_consider):
        idx_in_filtered_arrays = sorted_indices_of_filtered[i] # Index within the already filtered (by valid_calc_mask) arrays
        
        w_best_candidate = filtered_window_sizes[idx_in_filtered_arrays]
        actual_data_start_index = filtered_start_indices[idx_in_filtered_arrays]
        correlation_value = filtered_corrs[idx_in_filtered_arrays]
        
        # Check if the window size is valid for plotting (even and sufficiently large)
        if w_best_candidate >= 2 and w_best_candidate % 2 == 0 : 
            patterns_to_plot_details.append({
                "original_rank_in_consider_list": i, # Rank among the num_to_consider items
                "data_start_index": actual_data_start_index,
                "correlation": correlation_value,
                "window_size": int(w_best_candidate) # Ensure it's int
            })
        else:
            print(f"Info: Top candidate (originally rank {i+1} among considered, "
                  f"Start Index: {actual_data_start_index}) "
                  f"skipped due to invalid window size for plotting: {w_best_candidate} (must be even and >= 2).")


    num_actually_plotted = len(patterns_to_plot_details)

    fig, ax = plt.subplots(1, 1, figsize=(10, 5)) # Single axes for combined plot
    title_fontsize = 12
    label_fontsize = 10
    legend_fontsize = 8
    tick_labelsize = 9

    if num_actually_plotted == 0:
        # This message is shown if, out of the top 'num_to_consider' patterns, none had a valid window size for plotting.
        print("No patterns with valid window sizes (even, >=2) found among the top candidates to display on the chart.")
        ax.text(0.5, 0.5, "No valid patterns to display on the chart.",
                horizontalalignment='center', verticalalignment='center',
                transform=ax.transAxes, fontsize=title_fontsize, color='red')
        ax.set_xticks([])
        ax.set_yticks([])
        fig.suptitle(f"Symmetric Patterns Overlaid", fontsize=title_fontsize) # Generic title
    else:
        # Generate distinct colors for each pattern that will actually be plotted
        plot_colors = plt.cm.viridis(np.linspace(0, 1, num_actually_plotted))

        for plot_idx, pattern_info in enumerate(patterns_to_plot_details):
            actual_data_start_index = pattern_info["data_start_index"]
            correlation_value = pattern_info["correlation"]
            w_best = pattern_info["window_size"]
            
            half_window = w_best // 2
            
            # Ensure indices are within data bounds
            if actual_data_start_index + w_best > len(data):
                print(f"Warning: Pattern P{plot_idx+1} (Idx:{actual_data_start_index}, W:{w_best}) extends beyond data length {len(data)}. Skipping.")
                continue

            left_part_data = data[actual_data_start_index : actual_data_start_index + half_window]
            right_part_data = data[actual_data_start_index + half_window : actual_data_start_index + w_best]
            
            x_indices = np.arange(w_best) # X-axis relative to pattern start
            current_color = plot_colors[plot_idx]

            # Plot left part
            ax.plot(x_indices[:half_window], left_part_data, 
                    color=current_color, linestyle='-', 
                    label=f"P{plot_idx+1} (Idx:{actual_data_start_index}, W:{w_best}, C:{correlation_value:.2f})")
            
            # Plot right part
            ax.plot(x_indices[half_window:], right_part_data, 
                    color=current_color, linestyle='--') 
            
            # Add a vertical line to mark the split point for this pattern
            ax.axvline(x=half_window - 0.5, color=current_color, linestyle=':', linewidth=1, alpha=0.6)

        ax.set_xlabel("Index within Pattern Window", fontsize=label_fontsize)
        ax.set_ylabel("Data Value", fontsize=label_fontsize)
        ax.tick_params(axis='both', which='major', labelsize=tick_labelsize)
        ax.grid(True)
        
        ax.legend(fontsize=legend_fontsize, loc='best')
        # Add a text note to explain line styles
        fig.text(0.99, 0.01, 'Solid: Left Part, Dashed: Right Part (Original)', 
                 horizontalalignment='right', verticalalignment='bottom', 
                 fontsize=legend_fontsize - 1, color='dimgray', transform=fig.transFigure)

        fig.suptitle(f"Top {num_actually_plotted} Symmetric Patterns Overlaid", fontsize=title_fontsize)

    plt.tight_layout(rect=[0, 0.03, 1, 0.96]) # Adjust rect for suptitle and fig.text
    plt.show()

Данная функция достаточно большая по объему кода, но основной объем кода в ней отвечает за сортировку и отрисовку паттернов. Сначала происходит расчет самих паттернов, затем они сортируются по значениям коэффициента корреляции. Определяется позиция каждого паттерна в истории котировок, и он выводится на отрисовку. Результат работы этой функции представлен ниже.

На первом изображении мы видим один выбранный паттерн, обладающий максимальной абсолютной корреляцией. Он похож на некую вершину, локальную или глобальную, которая символизирует разворот тренда. Пунктирная вертикальная линия обозначает разделение ряда на две части одинаковой длины. Правая часть ряда переворачивается, то есть, все значения умножаются на -1, а затем инвертируются. После этого, считается корреляция между левым и правым участками. На графиках представлены не инвертированные правые части, а оригинальный исходный ряд котировок.

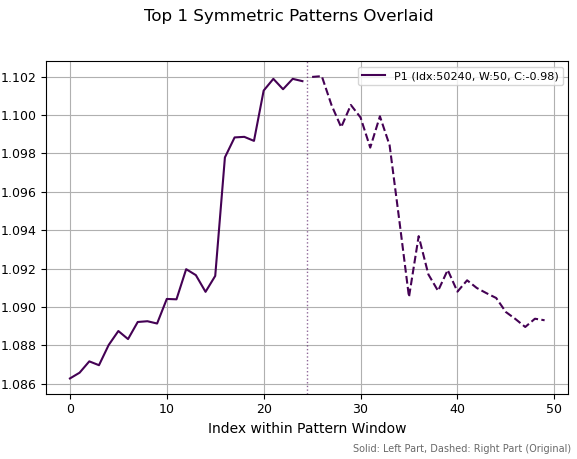
Рис 1. лучший паттерн с периодом 50 и корреляцией -0.98

На втором рисунке я отобразил пять лучших паттернов с периодом 50. Три из них похожи на вершины, два на впадину и еще один — на продолжение бычьего тренда. Шкала слева отображает исторические ценовые уровни, которым эти паттерны соответствуют.

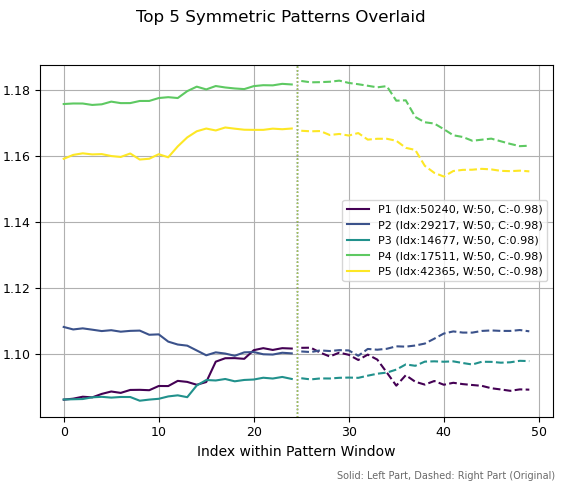
Рис 2. Топ пять паттернов с периодом 50

Если увеличить периоды паттернов до 150 баров, то наблюдаются совершенно другие структуры. Найдено три похожих паттерна (сверху). Это вызвано тем, что небольшой сдвиг в истории привел к обнаружению одной и той же структуры. Остальные два паттерна получились отличными друг от друга.

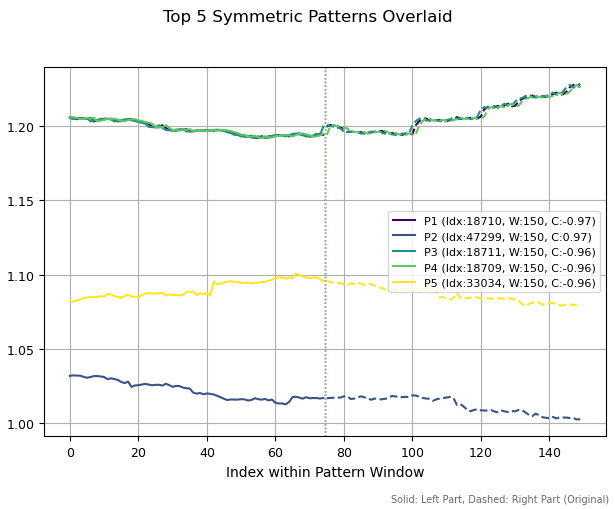
Рис 3. Топ пять паттернов с периодом 150

Если увеличить окно расчета паттернов до 250, то среди лучших снова оказались одинаковые паттерны, но с небольшим смещением в истории. Также прослеживаются некие разворотные формации, поскольку их корреляции отрицательны.

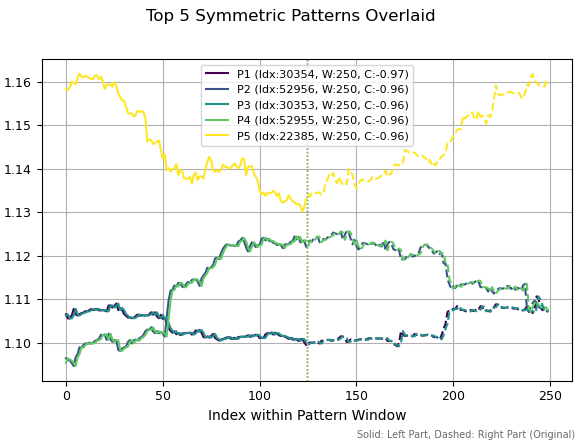
Рис 4. Топ пять паттернов с периодом 250

Данные иллюстрации демонстрируют большое разнообразие самоаффинных (самоподобных) рыночных структур. Теоретически, это разнообразие может быть ограничено только длиной исследуемого ряда. В таком случае достаточно сложно определиться, какой конкретный паттерн будет иметь прогностический потенциал, а какой нет. На исследование каждой отдельной такой структуры могли бы уйти месяцы. Здесь нам поможет машинное обучение, с помощью которого можно произвести классификацию всех паттернов одновременно.

Вполне возможно, что поиск структур через корреляцию не идеален, и следовало бы рассмотреть другие, более точные методы оценки. Но этот подход является хорошей отправной точкой для дальнейших исследований и интуитивно понятен. Теперь необходимо определиться с тем, как анализировать эти рыночные фракталы и построить на их основе торговую систему с использованием машинного обучения.

Разметка сделок на основе симметричных структур

Функция поиска симметричных структур является, своего рода, функцией дата майнинга. Мы задаем четкие критерии, что мы ищем в данных — самоподобные фрактальные структуры. Далее необходимо собрать и классифицировать полученную информацию. Но и этого окажется мало, потому что придется придумать способ разметки сделок на основе этих данных, чем мы и займемся в данном разделе.

Я предлагаю следующий способ разметки сделок для последующей классификации. Он не является единственно возможным, но отражает понимание автора как это можно реализовать. Считаю, что необходимы дополнительные исследования этой темы, но пока ограничимся существующим способом разметки.

@njit
def generate_future_outcome_labels_for_patterns(
    close_data_len,                 # Общая длина исходных данных close_data
    correlations_at_window_start,   # Массив корреляций
    window_sizes_at_window_start,   # Массив размеров окон
    source_close_data,              # Полный массив close_data
    correlation_threshold,
    min_future_horizon,             # Минимальный горизонт для определения будущей цены
    max_future_horizon,             # Максимальный горизонт
    markup_points                   # "Маркап" для определения значимого изменения цены
):
    labels = np.full(close_data_len, 2.0, dtype=np.float64)  # 2.0: нет сигнала/нейтрально/нет паттерна
    num_potential_windows = len(correlations_at_window_start)

    for idx_window_start in range(num_potential_windows):
        corr_value = correlations_at_window_start[idx_window_start]
        w = window_sizes_at_window_start[idx_window_start]

        # Условие 1: Корреляция должна быть достаточно сильной
        if abs(corr_value) < correlation_threshold:
            continue

        # Условие 2: Должно быть найдено валидное окно
        if w < 2:
            continue

        # Момент времени (индекс), когда паттерн корреляции полностью сформирован
        signal_time_idx = idx_window_start + w - 1

        if signal_time_idx >= close_data_len: # Теоретически не должно произойти
            continue
            
        # Массив для хранения меток всего паттерна (и левой, и правой части)
        pattern_labels = []
            
        # Рассчитываем индивидуальные метки для всех точек паттерна
        for point_idx in range(idx_window_start, signal_time_idx + 1):
            # Текущая цена для этой конкретной точки
            current_price = source_close_data[point_idx]
            
            # Определяем горизонт для прогноза
            current_horizon = min_future_horizon
            if max_future_horizon > min_future_horizon:
                current_horizon = random.randint(min_future_horizon, max_future_horizon)
            
            # Индекс будущей цены относительно текущей точки
            future_price_idx = point_idx + current_horizon
            
            if future_price_idx >= close_data_len:
                continue
                
            future_price = source_close_data[future_price_idx]
            
            # Определяем метку для текущей точки
            current_label = 2.0  # Нейтрально по умолчанию
            if future_price > current_price + markup_points:
                current_label = 0.0  # Цена выросла
            elif future_price < current_price - markup_points:
                current_label = 1.0  # Цена упала
                
            # Добавляем метку в массив, если она не нейтральная
            if current_label != 2.0:
                pattern_labels.append(current_label)
        
        # Если нет значимых меток в паттерне, переходим к следующему паттерну
        if len(pattern_labels) == 0:
            continue
            
        # Рассчитываем среднюю метку по всем точкам паттерна
        avg_label = 0.0
        for l in pattern_labels:
            avg_label += l
        avg_label /= len(pattern_labels)
        
        # Определяем общую метку для всего паттерна
        pattern_label = 0.0 if avg_label < 0.5 else 1.0
        
        # Присваиваем эту метку всем точкам паттерна
        for i in range(idx_window_start, signal_time_idx + 1):
            labels[i] = pattern_label
        
    return labels

Функция generate_future_outcome_labels_for_patterns() реализует следующий функционал:

• На вход принимается исходный массив цен, массив корреляций и массив длин паттернов, соответствующих наибольшим корреляциям для конкретной точки данных. Также функция принимает минимальный и максимальный горизонт прогнозирования, в барах.
• Изначально все сделки размечаются как 2.0 (не торговать).
• В цикле проверяется величина корреляции для каждой точки временного ряда. Если корреляция превышает correlation_threshhold, то это наблюдение проходит дополнительную обработку, иначе метка для этого примера остается 2.0.
• Затем, на всей длине паттерна, определенного через максимальную корреляцию, рассчитываются сделки на основе будущих ценовых изменений. Для каждой точки: если цена выросла, то это метка 0 — покупка, если цена упала, то это 1 — продажа. Находится среднее значение по сделкам, и для каждого наблюдения текущего паттерна выставляется усредненная метка.

Философия данного подхода заключается в том, что структуры с высокой корреляцией обладают "памятью" о своих начальных условиях и обладают некоторой степенью регулярности. Это означает, что наблюдения внутри них лучше предсказываются, но, чтобы предотвратить переобучение, мы ставим усредненную метку для каждого наблюдения. Наоборот, наблюдения внутри структур с низкой корреляцией предсказываются плохо, поскольку обладают меньшей регулярностью.

В итоге, мы эксплуатируем следующий принцип: одна модель будет определять качество паттерна (стоит торговать в данный момент или нет), а другая модель будет определять направление торговли. На плечи машинного обучения будет возложена задача апрроксимации всех возможных паттернов и направлений торговли.

Дальше нам потребуется еще одна функция-оркестрант, которая будет вызываться непосредственно для разметки сделок.

Финальная функция-разметчик на основе фрактальных паттернов

Настало время собрать все вместе и написать разметчик сделок, готовый к применению. 

def get_fractal_pattern_labels_from_future_outcome(
    dataset,
    min_window_size=6,
    max_window_size=60,
    correlation_threshold=0.7,
    min_future_horizon=5, 
    max_future_horizon=5,    
    markup_points=0.00010,  
):
    if 'close' not in dataset.columns:
        raise ValueError("Dataset must contain a 'close' column.")

    close_data = dataset['close'].values
    n_data = len(close_data)

    if min_window_size < 2:
        min_window_size = 2
    if max_window_size < min_window_size:
        max_window_size = min_window_size
    if min_future_horizon <= 0:
        raise ValueError("min_future_horizon must be > 0")
    if max_future_horizon < min_future_horizon:
        raise ValueError("max_future_horizon must be >= min_future_horizon")
    
    correlations_at_start, best_window_sizes_at_start = calculate_symmetric_correlation_dynamic(
        close_data,
        min_window_size,
        max_window_size,
    )

    labels = generate_future_outcome_labels_for_patterns(
        n_data,
        correlations_at_start,
        best_window_sizes_at_start,
        close_data,
        correlation_threshold,
        min_future_horizon,
        max_future_horizon,
        markup_points
    )

    result_df = dataset.copy()
    result_df['labels'] = pd.Series(labels, index=dataset.index)    
    return result_df

Функция get_fractal_pattern_labels_from_future_outcome() вызывается непосредственно для разметки вашего датасета:

• на вход подается датафрейм, который должен содержать колонку "close" с ценами закрытия, а также признаки (опционально);
• задается минимальная и максимальная длина паттернов, которые будут участвовать в разметке сделок;
• задается порог корреляции, который позволяет настраивать "точность" паттернов, участвующих в разметке;
• минимальное и  максимальное время удержания позиций (в барах) для разметки сделок также должно быть задано;
• опционально можно задать маркап.

Данная функция принимает датасет с ценами закрытия и размечает сделки на основе фрактальных паттернов, добавляя к нему колонку "labels" с размеченными метками.

Обучение модели машинного обучения на основе фрактальной разметки

Теперь все готово к экспериментам, и можно обучать модели. В качестве исходных данных я взял часовые котировки EURUSD с 2010 года по текущий момент.

В качестве признаков было решено использовать стандартные отклонения в скользящих окнах разного периода:

def get_features(data: pd.DataFrame) -> pd.DataFrame:
    pFixed = data.copy()
    pFixedC = data.copy()
    count = 0

    for i in hyper_params['periods']:
        pFixed[str(count)] = pFixedC.rolling(i).std()
        count += 1

    return pFixed.dropna()

Далее следует корректно задать гиперпараметры модели:

# set hyper parameters
hyper_params = {
    'symbol': 'EURUSD_H1',
    'export_path': '/Users/dmitrievsky/Library//drive_c/Program Files/MetaTrader 5/MQL5/Include/Trend following/',
    'model_number': 0,
    'markup': 0.00010,
    'stop_loss':  0.00500,
    'take_profit': 0.00500,
    'periods': [i for i in range(15, 300, 30)],
    'backward': datetime(2010, 1, 1),
    'forward': datetime(2024, 1, 1),
}

• стоп-лосс и тейк-профит одинаковые и равны 500 пятизначным пунктам;
• далее необходимо прописать путь для экспорта обученных моделей до вашей папки;
• периоды признаков (стандартных отклонений) установим в диапазоне от 15 до 300, с шагом 30 (всего получилось 10 признаков);
• период обучения с 2010 по 2024 годы, остальное — данные вне обучения.

Основной обучающий цикл позволяет обучать сразу много моделей, в нем также можно перебирать гиперпараметры:

# fit the models
models = []
for i in range(10):
    print('Learn ' + str(i) + ' model')
    dataset = get_features(get_prices())
    data = dataset[(dataset.index < hyper_params['forward']) & (dataset.index > hyper_params['backward'])].copy()
    data = get_fractal_pattern_labels_from_future_outcome(data, 100, 100, 0.9, 15, 25, 0.00010)
    models.append(fit_final_models(data))

В цикле мы сначала получаем цены и признаки, затем определяем временные рамки, на которых модель будет обучаться.

В функцию get_fractal_pattern_labels_from_future_outcome() передаем следующие параметры:

• исходный датафрейм с ценами и признаками
• минимальное окно для расчета корреляции
• максимальное окно для расчета корреляции
• порог КК для паттернов, по умолчанию 0.9
• минимальный горизонт прогнозирования в барах
• максимальный горизонт прогнозирования в барах
• маркап в пунктах

Затем размеченные данные передаются в функцию, которая выполняет обучение двух классификаторов:

def fit_final_models(dataset: pd.DataFrame) -> list:
    feature_columns = dataset.columns[1:-1]

    # 1. Данные для основной модели
    # Фильтруем датасет: для основной модели используются только те примеры, где 'labels' равны 0 или 1.
    main_model_df = dataset[dataset['labels'].isin([0, 1])].copy()
    
    X = main_model_df[feature_columns]
    y = main_model_df['labels'].astype('int16')

    # 2. Данные для мета-модели
    X_meta = dataset[feature_columns]
    
    # Модифицируем метки для мета-модели: если 'labels' содержит 1 или 0, то новая метка 1, если 2 - то 0.
    y_meta = dataset['labels'].apply(lambda label_val: 1 if label_val in [0, 1] else 0).astype('int16')

    # Для основной модели
    train_X, test_X, train_y, test_y = train_test_split(
        X, y, train_size=0.7, test_size=0.3, shuffle=True) 
    
    # Для мета-модели
    train_X_m, test_X_m, train_y_m, test_y_m = train_test_split(
        X_meta, y_meta, train_size=0.7, test_size=0.3, shuffle=True)
    
    # Обучение основной модели
    model = CatBoostClassifier(iterations=1000,
                               custom_loss=['Accuracy'],
                               eval_metric='Accuracy',
                               verbose=False,
                               use_best_model=True,
                               task_type='CPU',
                               )
    
    # Проверка на случай, если после split выборки оказались пустыми (маловероятно при достаточном размере X)
    if not train_X.empty and not test_X.empty:
        model.fit(train_X, train_y, eval_set=(test_X, test_y),
                  early_stopping_rounds=25, plot=False)
    elif not train_X.empty: # Если тестовая выборка пуста, но обучающая есть
        print("Предупреждение: Тестовая выборка (test_X) для основной модели пуста. Модель обучается без eval_set.")
        model.fit(train_X, train_y, early_stopping_rounds=15, plot=False) # use_best_model может работать некорректно без eval_set
    else: # Если обучающая выборка пуста
        print("Ошибка: Обучающая выборка (train_X) для основной модели пуста. Модель не может быть обучена.")
        # В этом случае test_model далее, скорее всего, вызовет ошибку.
        # Возвращаем R2=-1 и необученную модель, мета-модель тоже не будет иметь смысла без основной.
        print("R2 зафиксирован как -1.0, модели не обучены.")
        return [-1.0, model, None] # model - инстанс, но не обученный

    # Обучение мета-модели
    meta_model = CatBoostClassifier(iterations=1000,
                                    custom_loss=['F1'],
                                    eval_metric='F1',
                                    verbose=False,
                                    use_best_model=True,
                                    task_type='CPU',
                                    )

    if not train_X_m.empty and not test_X_m.empty:
        meta_model.fit(train_X_m, train_y_m, eval_set=(test_X_m, test_y_m),
                       early_stopping_rounds=25, plot=False)
    elif not train_X_m.empty:
        print("Предупреждение: Тестовая выборка (test_X_m) для мета-модели пуста. Мета-модель обучается без eval_set.")
        meta_model.fit(train_X_m, train_y_m, early_stopping_rounds=25, plot=False)
    else:
        print("Ошибка: Обучающая выборка (train_X_m) для мета-модели пуста. Мета-модель не может быть обучена.")
        print("R2 зафиксирован как -1.0.")
        return [-1.0, model, meta_model] # meta_model - инстанс, но не обученный

    data_for_test = get_features(get_prices())
    R2 = test_model(data_for_test, 
                    [model, meta_model], 
                    hyper_params['stop_loss'], 
                    hyper_params['take_profit'],
                    hyper_params['forward'],
                    hyper_params['backward'],
                    hyper_params['markup'],
                    plt=False)
    
    if math.isnan(R2):
        R2 = -1.0
        print('R2 зафиксирован как -1.0')
    print('R2: ' + str(R2))
    result = [R2, model, meta_model]
    return result

Жирным шрифтом выделены моменты, на которые стоит обратить особое внимание. Основная модель обучается предсказывать только метки 0 или 1, тогда как дополнительная мета-модель предсказывает, стоит торговать или не стоит.

Тестирование и финальные результаты

Для начала стоит сказать, что я протестировал алгоритм только на одной валютной паре — EURUSD. Мне удалось подобрать размер окна финансовых фракталов, который наиболее хорошо работает на новых данных. Он равняется 100. Оптимальные параметры алгоритма уже заданы в коде, поэтому вы можете воспроизвести результат самостоятельно.

График баланса на обучающих и тестовых данных выглядит следующим образом:

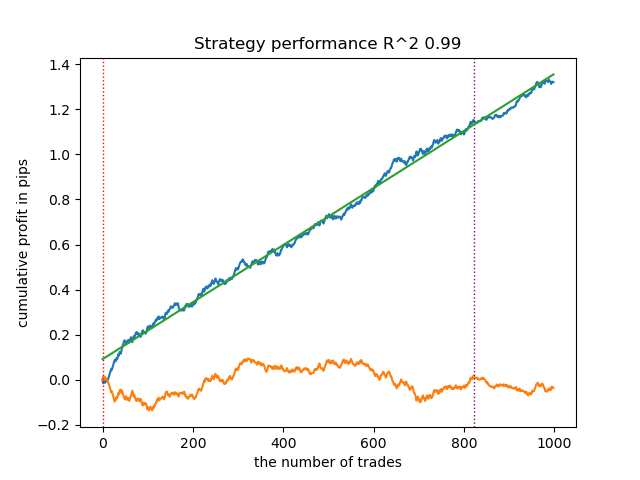
Рис 5. Тестирование алгоритма на основе фрактальной разметки

Существует прямая зависимость между порогом корреляции и результатами торговли на новых данных. Например, для порога 0.7, график баланса уже указывает на явное переобучение. Это отражает тот факт, что слабая корреляция между двумя участками временного ряда приводит к слабой зависимости. Слабая зависимость, в свою очередь, не позволяет корректно классифицировать надежные паттерны, потому что к ним подмешаны ненадежные.

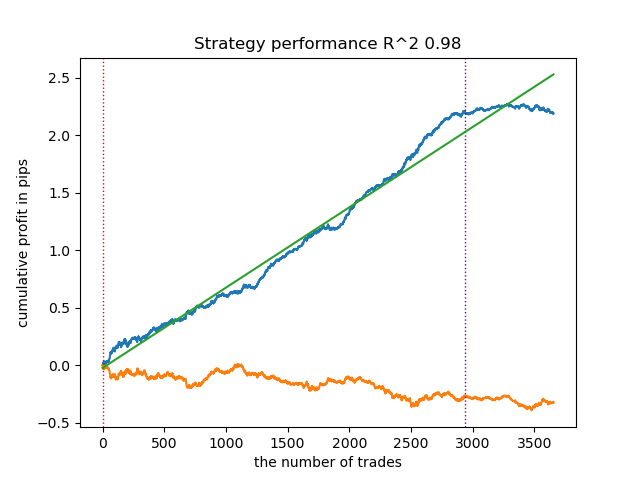
Рис 6. Тестирование алгоритма c порогом 0.7

Складывается впечатление, что корректное определение паттернов является критически важным. Необходимы дополнительные исследования и инсайты на тему того, как наиболее качественно организовать поиск фрактальных структур.

Качество и количество признаков тоже влияет на результаты классификации. Если вместо стандартных отклонений использовать приращения, то график баланса будет выглядеть иным образом.

Также необходимо подвергнуть анализу и разумной критике способ разметки сделок на основе найденных паттернов.

Анализ ошибок моделей CatBoost показывает, что модели обучаются с низкой ошибкой:

>>> models[-1][1].get_best_score()['validation']
{'Accuracy': 0.9700523560209424, 'Logloss': 0.17002244404784328}
>>> models[-1][2].get_best_score()['validation']
{'Logloss': 0.25629795409043277, 'F1': 0.8455473098330242}
>>> 

Экспорт и тестирование моделей в терминале Meta Trader 5

Для экспорта моделей необходимо вызвать функцию:

export_model_to_ONNX(model = models[-1],
                     symbol = hyper_params['symbol'],
                     periods = hyper_params['periods'],
                     periods_meta = hyper_params['periods'],
                     model_number = hyper_params['model_number'],
                     export_path = hyper_params['export_path'])

После экспорта и компиляции советника, получились следующие результаты:

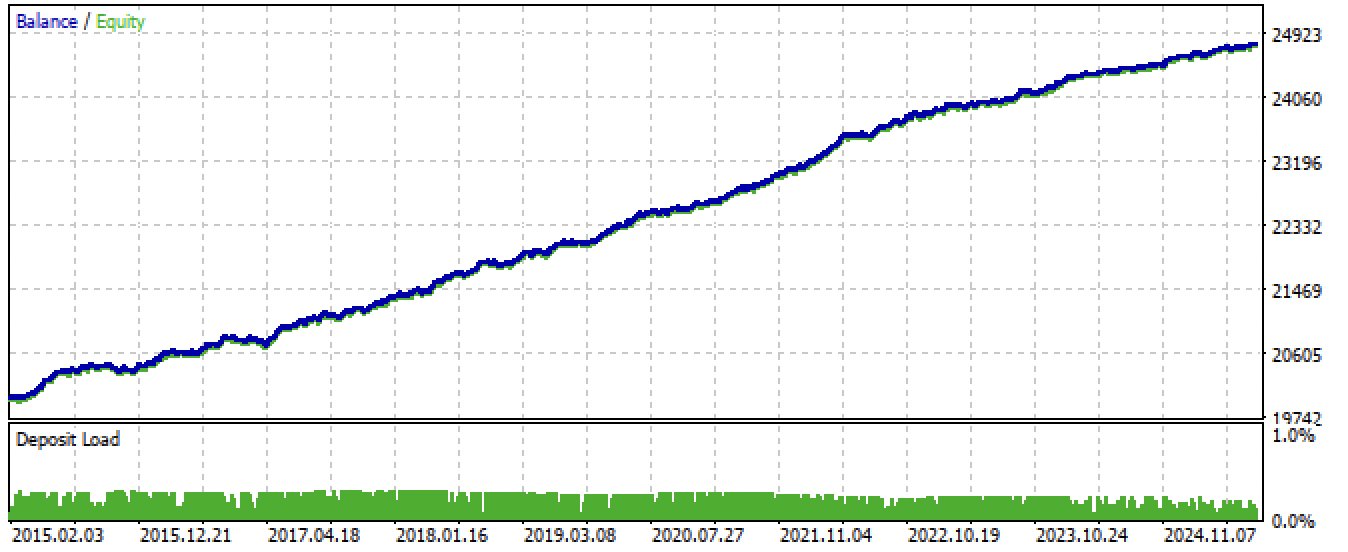
Рис 7. Тестирование советника за весь период

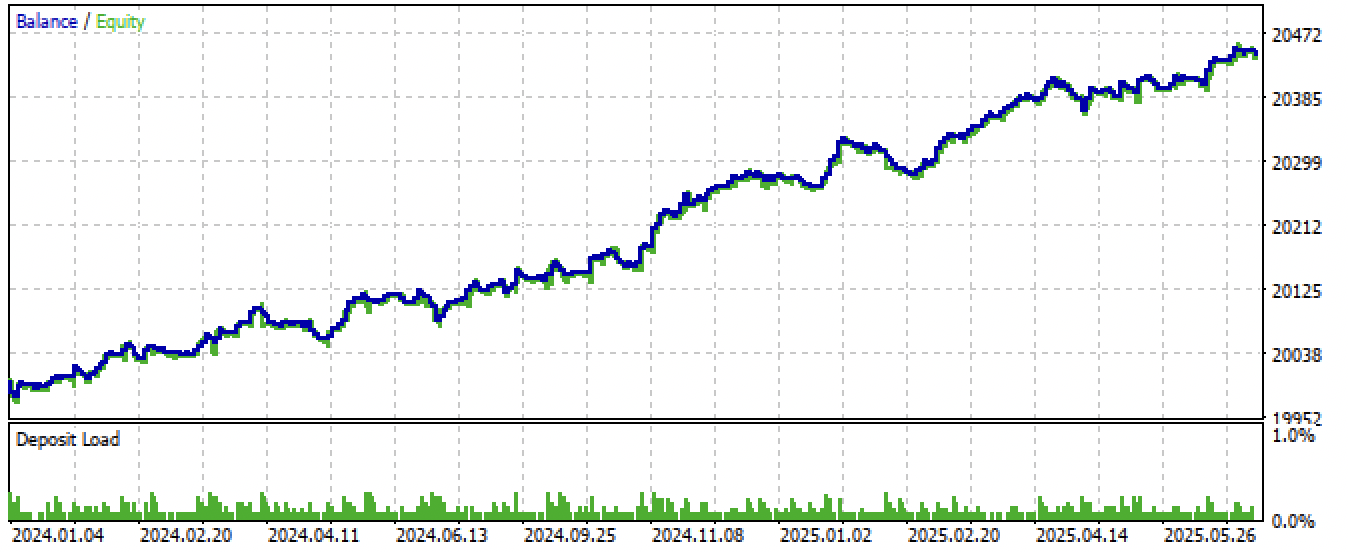
Рис 8. Тестирование советника на новых данных

Заключение

В этой статье мы затронули интригующую тему фрактального анализа и прогнозирования рынков посредством машинного обучения. Это только первые шаги на пути к исследованию многообразных фрактальных структур, которые образуются на графиках финансовых котировок.

Хочется отметить, что поиск через корреляцию может не до конца отражать зависимости между прошлым и будущим рядами котировок, и эта тема требует дополнительных исследований. Например, вместо корреляционного анализа может больше подойти регрессионный анализ. В то же время, текущий алгоритм способен демонстрировать неплохие прогностические способности при должной его настройке, что подтверждает наличие фрактальных самоподобных структур в финансовых временных рядах.

Архив Python files.zip содержит следующие файлы для разработки в среде Python:

Имя файла	Описание
fractal patterns.py	Основной скрипт для обучения моделей
labeling_lib.py	Обновленный модуль с разметчиками сделок
tester_lib.py	Обновленный кастомный тестер стратегий, основанных на машинном обучении
export_lib.py	Модуль для экспорта моделей в терминал
EURUSD_H1.csv	Файл с котировками, экспортированный из терминала MetaTrader 5

Архив MQL5 files.zip cодержит файлы для терминала MetaTrader 5:

Имя файла	Описание
fractal trader.ex5	Скомпилированный бот из данной статьи
fractal trader.mq5	Исходник бота из статьи
папка Include//Trend following	Расположены модели ONNX и заголовочный файл для подключения к боту