トランスダクション・アクティブ機械学習におけるスロープブースト

イントロダクション

半教師付きまたはトランスダクティブ学習は、モデルが一般的なデータ構造をよりよく理解できるように、ラベル付けされていないデータを使用します. これは我々のものの考え方と似ています. 人間の脳は、わずかな画像を記憶することで、取るに足らない細部に注目することなく、画像に関する知識を一般論として新たな対象物に注意することができます. その結果、オーバーフィッティングが少なくなり、より良い一般化が可能になります. 

トランスダクションは、サポートベクターマシン（SVM）の共同発明者であるVladimir Vapnik氏が紹介しています. 彼は、トランスダクションは、より具体的な問題を解く（新しいケースの出力を計算する）前に、より一般的な問題を解く（関数を推論する）必要があるので、インダクションよりも好ましいと考えています. 

「興味のある問題を解くときは、より一般的な問題を中間段階として解かない. 本当に必要としている答えを得ることを試みるが、より一般的な答えは得られない」

このヴァプニクの仮定は、Bertrand Russellが以前に行っていた観察に似ています.

"ソクラテスが死を免れないという結論に到達しなければならない、考察を純粋に帰納的にすれば、 'すべての人は死を免れない'の方法で行く場合よりも、演繹法を使用した確実に大きなアプローチである".

教師なし学習（ラベルの付いていないデータを使った）は、長期的にははるかに重要になると予想されています. 教師なし学習は、通常、人間や動物の典型的な学習法です. 

このように、半教師付き学習は両方のプロセスを組み合わせたものです：教師付き学習は少量のラベル付きデータに対して行われ、その後、モデルはその知識をラベルの付いていない大きな領域に外挿します. 

ラベルの付いていないデータを使用することは、基礎となるデータ分布との何らかの関連性を示唆します. 以下の前提条件のうち、少なくとも1つを満たす必要があります.

• 継続性の前提. 互いに近いポジションにある点はラベルを共有する可能性が高い. 教師付き学習でも想定されており、クラスを区切る幾何学的にシンプルな境界を好むことになります. 半教師付き学習の場合、平滑性の仮定は、さらに、点が互いに近くにあるが異なるクラスにある低密度領域で優先的に生成されます.
• クラスターアサンプション. データは離散的なクラスターを形成する傾向があり、同じクラスター内の点はラベルを共有しやすいです.（ラベルを共有するデータは複数のクラスターにまたがって広がることもあるが）. これは、クラスタリングアルゴリズムを用いた学習につながる平滑性の仮定の特殊なケースです.
  
• マニホールド前提. このデータは、インプット空間よりもはるかに低い次元のマニホールド上にほぼ横たわっています. この場合、ラベル付けされたデータとラベル付けされていないデータの両方を使用してマニホールドを学習することで、次元性の呪縛を回避することができます. そうすれば、多様体上に定義された距離と密度を使って学習を続けることができます.
  

セミコントロール学習の詳細はリンク先をチェックしてみてください.

半教師付き 学習の主な方法は、以下のように実装された擬似ラベリングです.

• 近接の何らかの尺度（例えば、ユークリッド距離）は、ラベル付けされたデータ領域（擬似ラベル）に基づいてデータの残りの部分をラベル付けするために使用します.
• トレーニングラベルは、疑似ラベルと標識を組み合わせたものです.
• このモデルはデータセット全体に対して学習されます.

研究者によると、ラベル付きデータとラベルなしデータを併用することで、モデルの精度を大幅に向上させることができます. 前回の記事でも似たようなアイデアを使ったのですが、その中で、ラベル付きデータの分布の確率密度の推定と、この分布からのサンプリングを使っていました. しかし、新しいデータの分布は異なる可能性があるので、半教師付き学習は、この記事の実験が示すように、利点があります.

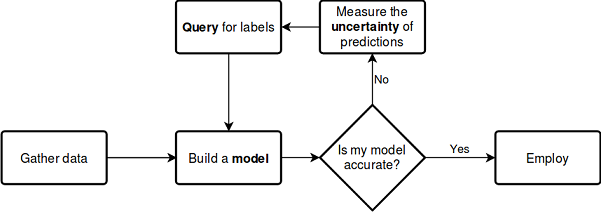
アクティブ学習は、半教師付き 学習のある種の論理的な延長線です. クラスを区切る境界が最適に配置されるように新しいデータをラベル付けする繰り返しプロセスです.

アクティブラーニングの主な仮説は、学習アルゴリズムが学習したいデータを選択できるというものです. トレーニングデータが著しく少ない従来の手法よりも優れた性能を発揮することができます. ここでいう従来の手法とは、ラベル付きデータを用いた従来の教師付き学習を指します. このようなトレーニングは、受動的なトレーニングと言えるでしょう. モデルはラベル付けされたデータに対して学習されます. データは多ければ多いほど良いです. 受動学習で最も時間のかかる問題の一つは、データの収集とラベリングです. 多くの場合、追加データの収集に関連した制限や、適切なラベリングがある場合があります. 

アクティブラーニングには、最もポピュラーな3つのシナリオがあり、学習モデルがラベルのない領域から新しいクラスインスタンスのラベルをリクエストします.

• メンバシップクエリの合成. この場合、モデルはすべての例に共通するある分布からインスタンスを生成します. ノイズが付加されたクラスインスタンスであってもよいし、問題の空間内のもっともらしい点だけであってもよいです. この新しいポイントをオラクルに送ってトレーニングを行います. Oracleは、モデルに対して与えられたフィーチャインスタンスの値を評価する評価関数の従来の名称です.
• ストリームベーストサンプリング このシナリオによると、ラベル付けされていない各データ・ポイントが一度に1つずつ検査され、その後、オラクルはこのポイントに対してクラス・ラベルを照会するか、何らかの情報基準に基づいてを拒否するかを選択します. 
• プールベースのサンプリング. このシナリオでは、先のケースと同様に、ラベル付けされていないサンプルが大量にプールされています. インスタンスは、情報性に基づいてプールから選択されます. プールから最も情報量の多いインスタンスが選択されます. アクティブラーニングファンの間では、最も人気のあるシナリオです. ラベルの付いていないインスタンスはすべてランク付けされ、その後、最も情報量の多いインスタンスが選択されます.

各シナリオは、特定のクエリ戦略に基づくことができます. 上述したように、アクティブ学習とパッシブ学習の主な差は、過去のクエリとモデルの応答に基づいて、ラベル付けされていない領域からインスタンスをクエリする関数です. したがって、すべてのクエリには何らかの情報量が必要となります. 

最も人気のあるクエリ戦略は以下の通りです.

• 不確実性のサンプリング（最小信頼度）. この戦略に従って、モデルが最も確実でないインスタンスを選択します. 例えば、あるクラスにラベルを割り当てる確率は、ある境界線以下です.
• マージンサンプリング. 最初の戦略の欠点は、他のラベルに属する確率を無視している間に、1つのラベルだけに属する確率を決定することです. マージンサンプリング戦略は、2つの最も可能性の高いラベル間の確率差が最も小さいものを選択します.
• エントロピーサンプリング. 各インスタンスにエントロピー式を適用し、最も高い値を持つインスタンスを選択します.

半教師付き学習と同様に、アクティブ学習プロセスはステップから構成されています.

• モデルはラベル付けされたデータに対してトレーニングされます.
  
• 確率を予測するためのラベル付けをしていないデータのラベル付けには、同じモデルを使用しています（擬似ラベル）.
• 新しいインスタンスクエリ戦略が選択されています.
• データプールから情報量に応じてN個のインスタンスを選択し、学習サンプルに追加します. 
• このサイクルは、あるストップ基準に達するまで繰り返されます. ストップ基準は、他の外部基準と同様に、繰り返し回数や学習誤差の推定値とすることができます.

アクティブラーニング

アクティブラーニングに直行して、その効果をデータで検証してみましょう.

Python言語でアクティブラーニングを行うためのライブラリはいくつかありますが、その中でも最も人気のあるものがです.

• modAL はシンプルで学習しやすいパッケージで、人気のある機械学習ライブラリ scikit-learn のラッパのようなものです (完全に互換性があります). このパッケージは、最も人気のあるアクティブラーニングの手法を提供しています.
• Libactは、既存のクエリ戦略よりも多腕バンディット戦略を用いて、最適なクエリを動的に選択します. 
• Alipy はパッケージプロバイダの研究室のようなもので、多くのクエリストラテジーを含んでいます.

より直感的で、アクティブラーニングの考え方を知るのに適していると判断し、modalライブラリを選択しました. 標準的なブロックを使ってモデルを設計したり、自分でモデルを作成したりと、より自由度が高くなっています.

以上説明した処理を、以下のスキームを用いて考えてみましょう.

ドキュメントを見る

このライブラリの素晴らしいところは、どのようなscikit-learn分類法を使っても良いことです. 以下の例では、学習モデルとしてランダムフォレストを使用します.

from modAL.models import ActiveLearner
from modAL.uncertainty import entropy_sampling
from sklearn.ensemble import RandomForestClassifier

learner = ActiveLearner(
    estimator=RandomForestClassifier(),
    query_strategy=entropy_sampling,
    X_training=X_training, y_training=y_training
)

ここでのランダムフォレストは、学習モデルとして、またクエリ戦略（例えば、この例のようにエントロピーに基づく）に応じて、ラベル付けされていないデータから新しいサンプルを選択することを可能にする評価体として機能します. 次に、少量のラベル付きデータからなるデータセットをモデルに渡します. これをテストトレーニングに使用します. 

modALライブラリは、クエリ戦略を組み合わせることができ、その中から複合加重戦略を作成することができます.

from modAL.utils.combination import make_linear_combination, make_product
from modAL.uncertainty import classifier_uncertainty, classifier_margin

# creating new utility measures by linear combination and product
# linear_combination will return 1.0*classifier_uncertainty + 1.0*classifier_margin
linear_combination = make_linear_combination(
    classifier_uncertainty, classifier_margin,
    weights=[1.0, 1.0]
)
# product will return (classifier_uncertainty**0.5)*(classifier_margin**0.1)
product = make_product(
    classifier_uncertainty, classifier_margin,
    exponents=[0.5, 0.1]
)

クエリが生成されると、multi_argmaxまたはweighted_randmセレクタを使用して、ラベル付けされていないデータ領域から、クエリの基準を満たすインスタンスが選択されます.

from modAL.utils.selection import multi_argmax

# defining the custom query strategy, which uses the linear combination of
# classifier uncertainty and classifier margin
def custom_query_strategy(classifier, X, n_instances=1):
    utility = linear_combination(classifier, X)
    query_idx = multi_argmax(utility, n_instances=n_instances)
    return query_idx, X[query_idx]

custom_query_learner = ActiveLearner(
    estimator=GaussianProcessClassifier(1.0 * RBF(1.0)),
    query_strategy=custom_query_strategy,
    X_training=X_training, y_training=y_training
)

クエリ戦略

クエリ戦略は主に3つあります. すべての戦略は分類の不確実性に基づいているので、不確実性対策と呼ばれています. その仕組みを見てみましょう.

分類の不確かさは、シンプルなケースでは、U(x)=1-P(x^|x)として評価され、ここでxは予測されるケース、x^は最も確率の高い予測です. 例えば、3つのクラスと3つのサンプル項目がある場合、対応する不確かさは以下のように計算することができます.

[[0.1 , 0.85, 0.05].
 [0.6 , 0.3 , 0.1 ],
 [0.39, 0.61, 0.0 ]]

1 - proba.max(axis=1)

[0.15, 0.4 , 0.39]

このように、第２実施例は、最も不確実性の高いものとして選択されます.

分類マージン は、1番目と2番目の最も確率の高いクエリの確率の差です. その差は、次の式に従って決定されます.M(x)=P(x1^|x)-P(x2^|x)であり、ここでx1^とx2^は第1と第2の確率の高いクラスです.

このクエリ戦略では、2つの最も確率の高いクラスの確率間のマージンが最も小さいインスタンスを選択します.

>>> import numpy as np
>>> proba = np.array([[0.1 , 0.85, 0.05],
...                   [0.6 , 0.3 , 0.1 ],
...                   [0.39, 0.61, 0.0 ]])
>>>
>>> proba
array([[0.1 , 0.85, 0.05],
       [0.6 , 0.3 , 0.1 ],
       [0.39, 0.61, 0.  ]])
>>> part = np.partition(-proba, 1, axis=1)
>>> part
array([[-0.85, -0.1 , -0.05],
       [-0.6 , -0.3 , -0.1 ],
       [-0.61, -0.39, -0.  ]])
>>> part[:, 0]
array([-0.85, -0.6 , -0.61])
>>> part[:, 1]
array([-0.1 , -0.3 , -0.39])
>>> margin = - part[:, 0] + part[:, 1]
>>> margin
array([0.75, 0.3 , 0.22])

この場合、このインスタンスの確率マージンは最小であるため、3番目のサンプル（配列の3行目）が選択されます.

分類エントロピーは，情報エントロピーの式を用いて計算される．H(x)=-∑-kpklog(pk), ここで，pkは標本がk番目のクラスに属する確率です. 分布が一様に近いほどエントロピーが高いです. 本実施例では、第２実施例に対して最大エントロピーが得られます.

[0.51818621, 0.89794572, 0.66874809]

これはそれほど難しそうには見えません. この記述は、3つの主要なクエリ戦略を理解するのに十分なようです. 詳細については、基本的なポイントだけを提供しているので、パッケージドキュメントを勉強してください.

バッチクエリ戦略

一度に1つの要素をクエリしてモデルを再トレーニングすることは、必ずしも効率的ではありません. より効率的なソリューションは、ラベル付けされていないデータから複数のインスタンスを一度に選択してラベル付けすることです. ここにはいくつかのクエリがあります. その中でも、コサイン距離などの類似度関数に基づくランク付き集合サンプリングが最もポピュラーです. この方法は、x（ラベルの付いていないインスタンス）の近傍で特徴空間がどの程度探索されているかを推定します. 評価後、最高ランクのインスタンスがトレーニングセットに追加され、ラベル付けされていないデータプールから削除されます. その後、ランクが再計算され、インスタンスの数が指定されたサイズ（バッチサイズ）に達するまで、最適なインスタンスが再度追加されます. 

情報密度のクエリ

上述のシンプルなクエリ戦略では、データ構造を評価しません. 最適でないクエリにつながる可能性があります. サンプリングを改善するために、ラベルの付いていないデータの要素を正しく選択するのに役立つ情報密度測定を使用することができます. 余弦距離やユークリッド距離を使用します. 情報密度が高いほど、この選択されたインスタンスは他のすべてのインスタンスと類似します. 

分類コミッションのクエリ

このクエリ型は、シンプルなクエリ型の欠点をいくつか解消します. 例えば、特定の分類器の特性により、要素の選択に偏りが生じる傾向があります. 重要なサンプリング要素が欠落している可能性があります. この効果は、複数の仮説を同時に格納し、不一致がある間のクエリを選択することで排除されます. このようにして，分類器のコミッションは，それぞれのサンプルのコピーについて学習し，その結果を加重付けします. 分類器コミッション学習の他のタイプには、バギングとブートストラップがあります.

この短い説明では、ライブラリの関数をほぼ完全に扱いています. 詳細はドキュメントを参照してください.

アクティブラーニング

分類器コミッションのクエリと同様に、バッチクエリ戦略を選択し、一連の実験を行ってきました. バッチクエリ戦略では、新しいデータではあまり良いパフォーマンスを発揮しませんでしたが、生成したデータセットをGMMに投入することで、面白い結果が得られるようになりました. 

バッチアクティブラーニング関数を実装した例を考えてみましょう.

def active_learner(data, labeled_size, unlabeled_size, batch_size, max_depth):
    X_raw = data[data.columns[1:-1]].to_numpy()
    y_raw = data[data.columns[-1]].to_numpy()

    # Isolate our examples for our labeled dataset.
    training_indices = np.random.randint(low=0, high=X_raw.shape[0] + 1, size=labeled_size)

    X_train = X_raw[training_indices]
    y_train = y_raw[training_indices]

    # fit the model on all data
    cl = AdaBoostClassifier(DecisionTreeClassifier(max_depth=max_depth), n_estimators=50, learning_rate = 0.01)
    cl.fit(X_raw, y_raw)
    print('Score for the passive learning: ', cl.score(X_raw, y_raw), ' with train size: ', data.shape[0])

    # Isolate the non-training examples we'll be querying.
    X_pool = np.delete(X_raw, training_indices, axis=0)
    y_pool = np.delete(y_raw, training_indices, axis=0)

    # Pre-set our batch sampling to retrieve 3 samples at a time.
    preset_batch = partial(uncertainty_batch_sampling, n_instances=batch_size)

    # Specify our core estimator along with its active learning model.
    cl = AdaBoostClassifier(DecisionTreeClassifier(max_depth=3), n_estimators=50, learning_rate = 0.03)
    learner = ActiveLearner(estimator=cl, query_strategy=preset_batch, X_training=X_train, y_training=y_train)

この関数には，ラベル付きデータセット，ラベル付きインスタンスの数，ラベルなしインスタンスの数，バッチラベルクエリのバッチサイズ，最大木深さがインプットされます．

モデルの事前学習に、ラベル付けされたデータセットから指定された数のラベル付けされたインスタンスがランダムに選択されます. データセットの残りの部分は、インスタンスが照会されるプールを形成します. 基本的な分類器としてAdaBoostを使ってみましたが、CatBoostと似たようなものです. その後、モデルは繰り返し的にトレーニングされます.

    # Allow our model to query our unlabeled dataset for the most
    # informative points according to our query strategy (uncertainty sampling).
    N_QUERIES = unlabeled_size // batch_size

    for index in range(N_QUERIES):
        query_index, query_instance = learner.query(X_pool)

        # Teach our ActiveLearner model the record it has requested.
        X, y = X_pool[query_index], y_pool[query_index]
        learner.teach(X=X, y=y)

        # Remove the queried instance from the unlabeled pool.
        X_pool, y_pool = np.delete(
            X_pool, query_index, axis=0), np.delete(y_pool, query_index)

        # Calculate and report our model's accuracy.
        model_accuracy = learner.score(X_raw, y_raw)
        print('Accuracy after query {n}: {acc:0.4f}'.format(
            n=index + 1, acc=model_accuracy))

        # Save our model's performance for plotting.
        performance_history.append(model_accuracy)

    print('Score for the active learning with train size: ',
          learner.X_training.shape)     

このような半教師付き学習の結果、何が起きてもおかしくないので、結果は何でもいいのです. しかし、学習者の設定を操作してみたところ、前回の記事と同等の結果が得られました. 

理想的には，少量のラベル付けされたデータに対するアクティブな学習者の分類精度が，すべてのデータがラベル付けされた状態での類似の分類器の精度を上回ることが望ましいと言えます．

>>> learned = active_learner(pr, 1000, 1000, 50)
Score for the passive learning:  0.5991245668429692  with train size:  5483
Accuracy after query 1: 0.5710
Accuracy after query 2: 0.5836
Accuracy after query 3: 0.5749
Accuracy after query 4: 0.5847
Accuracy after query 5: 0.5829
Accuracy after query 6: 0.5823
Accuracy after query 7: 0.5650
Accuracy after query 8: 0.5667
Accuracy after query 9: 0.5854
Accuracy after query 10: 0.5836
Accuracy after query 11: 0.5807
Accuracy after query 12: 0.5907
Accuracy after query 13: 0.5944
Accuracy after query 14: 0.5865
Accuracy after query 15: 0.5949
Accuracy after query 16: 0.5873
Accuracy after query 17: 0.5833
Accuracy after query 18: 0.5862
Accuracy after query 19: 0.5902
Accuracy after query 20: 0.6002
Score for the active learning with train size:  (2000, 8)

レポートによると、すべてのラベル付けされたデータに対してトレーニングされた分類器は、2000個のインスタンスのみでトレーニングされたアクティブ学習器よりも精度が低いという結果になりました. これはおそらくいいのかもしれません. 

これで、このサンプルをGMMモデルに送ることができ、その後CatBoost分類器をトレーニングすることができます.

# prepare data for CatBoost
catboost_df = pd.DataFrame(learned.X_training)
catboost_df['labels'] = learned.y_training

# perform GMM clusterization over dataset
X = catboost_df.copy()
gmm = mixture.GaussianMixture(
    n_components=75, max_iter=500, covariance_type='full', n_init=1).fit(X)

# sample new dataset
generated = gmm.sample(10000)
# make labels
gen = pd.DataFrame(generated[0])
gen.rename(columns={gen.columns[-1]: "labels"}, inplace=True)
gen.loc[gen['labels'] >= 0.5, 'labels'] = 1
gen.loc[gen['labels'] < 0.5, 'labels'] = 0
X = gen[gen.columns[:-1]]
y = gen[gen.columns[-1]]
pr = pd.DataFrame(X)
pr['labels'] = y

# fit CatBoost model and test it
model = fit_model(pr)
test_model(model, TEST_START, END_DATE)

この処理は、データ処理の各段階で、曖昧なモデルを構築できない不確実性の要素があるため、何度か繰り返す必要があります. 全ての反復（1年間のトレーニング期間と5年間のテスト期間）を行った後のテスターでは、以下のようなチャートが得られました.

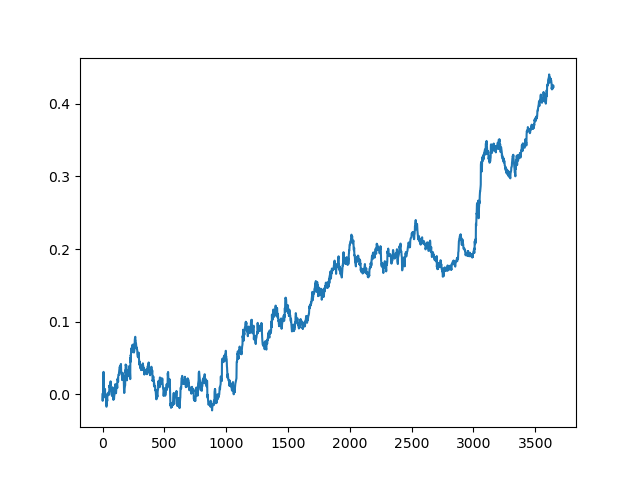
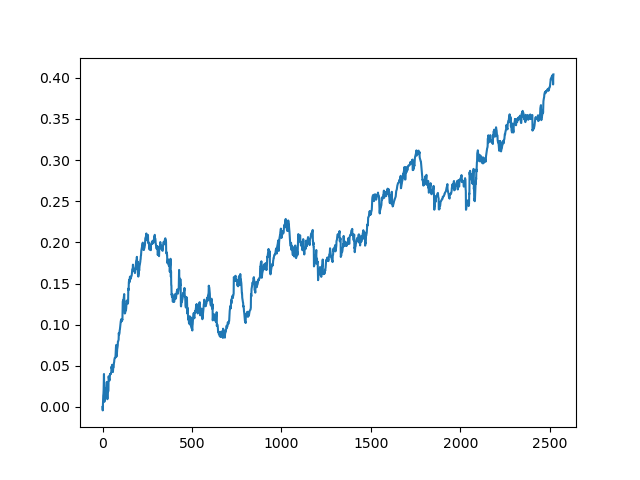
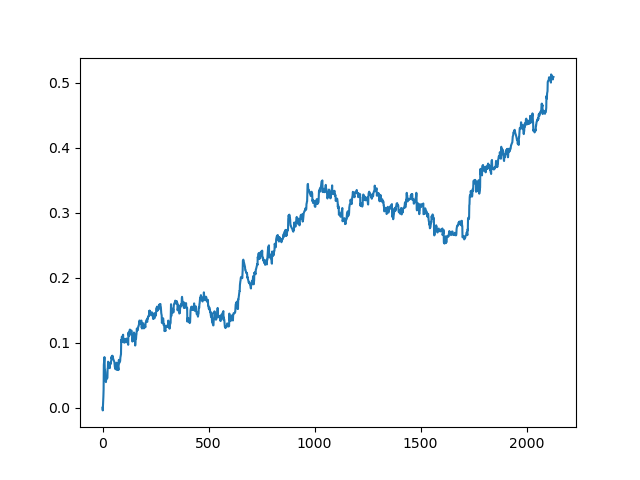
もちろん、この結果はベンチマークではなく、（新しいデータ上での）採算性の高いモデルが得られることを示しているに過ぎません. 

では、分類コミッションに学習関数を実装して、何が起こるかを見てみましょう.

def active_learner_committee(data, learners_number, labeled_size, unlabeled_size, batch_size):
    X_pool = data[data.columns[1:-1]].to_numpy()
    y_pool = data[data.columns[-1]].to_numpy()

    cl = AdaBoostClassifier(DecisionTreeClassifier(max_depth=3), n_estimators=50, learning_rate = 0.05)
    cl.fit(X_pool, y_pool)
    print('Score for the passive learning: ', cl.score(
        X_pool, y_pool), ' with train size: ', data.shape[0])

    # initializing Committee members
    learner_list = list()

    # Pre-set our batch sampling to retrieve 3 samples at a time.
    preset_batch = partial(uncertainty_batch_sampling, n_instances=batch_size)
    
    for member_idx in range(learners_number):
        # initial training data
        train_idx = np.random.choice(range(X_pool.shape[0]), size=labeled_size, replace=False)
        X_train = X_pool[train_idx]
        y_train = y_pool[train_idx]

        # creating a reduced copy of the data with the known instances removed
        X_pool = np.delete(X_pool, train_idx, axis=0)
        y_pool = np.delete(y_pool, train_idx)

        # initializing learner
        learner = ActiveLearner(
            estimator=AdaBoostClassifier(DecisionTreeClassifier(max_depth=2), n_estimators=50, learning_rate = 0.05),
            query_strategy=preset_batch,
            X_training=X_train, y_training=y_train
        )
        learner_list.append(learner)

    # assembling the committee
    committee = Committee(learner_list=learner_list)

    unqueried_score = committee.score(X_pool, y_pool)
    performance_history = [unqueried_score]

    N_QUERIES = unlabeled_size // batch_size

    for idx in range(N_QUERIES):
        query_idx, query_instance = committee.query(X_pool)
        committee.teach(
            X=X_pool[query_idx].reshape(1, -1),
            y=y_pool[query_idx].reshape(1, )
        )
        model_accuracy = committee.score(X_pool, y_pool)
        performance_history.append(model_accuracy)
        print('Accuracy after query {n}: {acc:0.4f}'.format(
            n=idx + 1, acc=model_accuracy))

        # remove queried instance from pool
        X_pool = np.delete(X_pool, query_idx, axis=0)
        y_pool = np.delete(y_pool, query_idx)

    return committee

繰り返しになりますが、1つの要素が追加されたときに毎回モデルを再教育する必要がないように、バッチクエリ戦略を選択します. あとは、任意の数のAdaBoost分類器のコミッションを作ってみました（5つ以上の分類器を追加しても意味がないと思いますが、実験してみてください）. 

下記は前回の手法で使用したのと同じ設定の5つのモデルのコミッションのトレーニングスコアです.

>>> committee = active_learner_committee(pr, 5, 1000, 1000, 50)
Score for the passive learning:  0.6533842794759825  with train size:  5496
Accuracy after query 1: 0.5927
Accuracy after query 2: 0.5818
Accuracy after query 3: 0.5668
Accuracy after query 4: 0.5862
Accuracy after query 5: 0.5874
Accuracy after query 6: 0.5906
Accuracy after query 7: 0.5918
Accuracy after query 8: 0.5910
Accuracy after query 9: 0.5820
Accuracy after query 10: 0.5934
Accuracy after query 11: 0.5864
Accuracy after query 12: 0.5753
Accuracy after query 13: 0.5868
Accuracy after query 14: 0.5921
Accuracy after query 15: 0.5809
Accuracy after query 16: 0.5842
Accuracy after query 17: 0.5833
Accuracy after query 18: 0.5783
Accuracy after query 19: 0.5732
Accuracy after query 20: 0.5828

アクティブラーニングのコミッションの結果は、一人の受動的な学習者の結果とは比べ物にならないです. その理由を推測することは不可能です. もしかしたら、ただの行き当たりばったりの結果なのかもしれません. その後、同じ原理を用いて結果のデータセットを数回実行したところ、以下のようなランダムな結果が得られました.

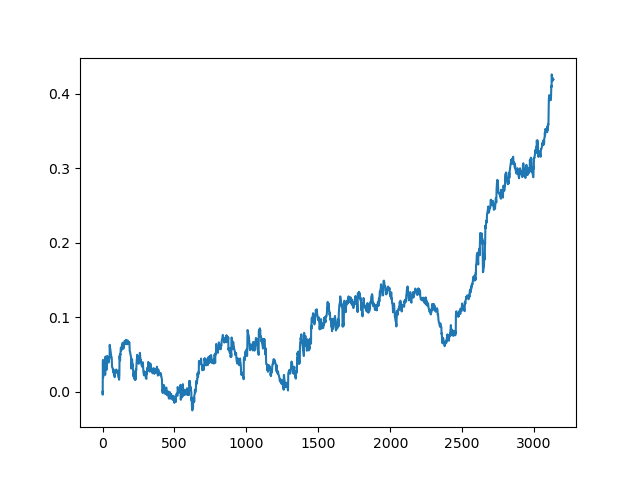
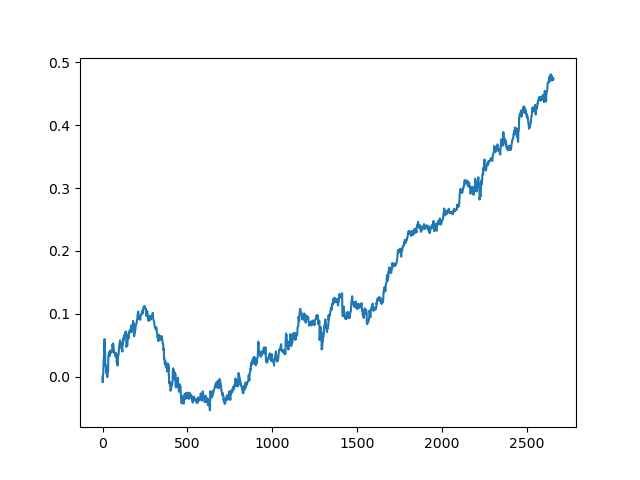
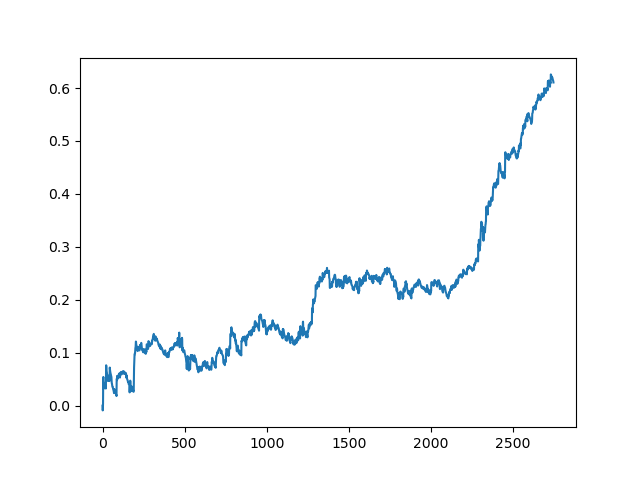
結論

今回はアクティブラーニングについて考えてみました. この印象は漠然としています. 一方では、少数のインスタンスから学習したくなるのはいつものことで、モデルは分類問題に対してうまく機能しています. しかし、まだ人工知能には程遠いでしょう. このようなモデルでは、ガベージデータの中から安定したパターンを見つけることができず、エキスパートラベリングに基づくデータの準備を含め、より徹底した特徴量やラベルの準備が必要となります. 私はモデルの質が大幅に上がっているのを見たことがありません. 同時に、モデルを鍛えるための労働強度や時間が増えたことがマイナス要因となっています. アクティブラーニングの考え方や、人間の思考の特徴を活かした考え方は好きです. 添付ファイルには、考察されているすべての関数が記載されています. モデルをさらに掘り下げて、他の独自の方法で応用してみてはいかがでしょうか.