Изучаем конформное прогнозирование финансовых временных рядов

Введение

MAPIE или "Model agnostic prediction interval estimator" — это библиотека Python с открытым исходным кодом, разработанная для количественной оценки неопределенности и контроля рисков в моделях машинного обучения. Она позволяет вычислять интервалы прогнозирования для задач регрессии, а также наборы прогнозирования для классификации и временных рядов. Эта оценка неопределенности выполняется на основе специального "набора конформизации" данных.

Одним из ключевых преимуществ MAPIE является ее модельно-агностический характер, что означает возможность использования библиотеки с любой моделью, совместимой с API scikit-learn, включая модели, разработанные с использованием TensorFlow или PyTorch, посредством соответствующих оберток. Это свойство значительно упрощает интеграцию в существующие аналитические конвейеры, поскольку трейдеры часто используют разнообразные модели машинного обучения, от традиционных статистических подходов до сложных нейронных сетей, в зависимости от конкретного класса активов или торговой стратегии. Возможность беспрепятственного использования уже проверенных моделей для включения количественной оценки неопределенности существенно сокращает затраты на внедрение и ускоряет адаптацию, что особенно ценно в динамичной финансовой среде.

Библиотека является частью экосистемы scikit-learn-contrib и опирается на области конформного прогнозирования и инференса, не зависящих от распределения. Она реализует рецензируемые алгоритмы, которые не зависят от модели и варианта использования, и обладают теоретическими гарантиями при минимальных предположениях о данных и модели. Помимо стандартной классификации, MAPIE также способна контролировать риски для более сложных задач, таких как многоклассовая классификация и сегментация изображений в компьютерном зрении, предоставляя вероятностные гарантии по таким метрикам, как полнота и точность.

Способность контролировать риски и предоставлять вероятностные гарантии позиционирует MAPIE не просто как инструмент количественной оценки неопределенности, а как полноценную структуру управления рисками. В финансах точечные прогнозы недостаточны, поскольку они не передают уровень уверенности или потенциальную ошибку. Предоставление гарантированных показателей ошибок, например, 95% охвата, напрямую переводится в количественно измеримый риск. Это позволяет управляющим рисками устанавливать явные допуски на риск.

Например, если модель выдает сигнал "покупка", но конформный прогноз указывает на высокую вероятность ошибки, управляющий риском может принять решение о сокращении позиции или воздержаться от сделки, непосредственно контролируя потенциальные потери. Это способствует принятию более надежных решений в условиях неопределенности, выходя за рамки простой точности прогнозирования.

Основные принципы конформного прогнозирования: модельно-агностические гарантии, не зависящие от распределения

Конформное прогнозирование (КП) представляет собой статистическую основу, которая генерирует наборы прогнозирования для задач классификации или интервалы прогнозирования для регрессии с гарантированной вероятностью охвата. Это означает, что при заданном уровне достоверности, например, 90%, истинный результат будет находиться в предсказанном наборе или интервале, по крайней мере, в 90% случаев.

Ключевое преимущество КП заключается в его "независимости от распределения": метод не опирается на строгие предположения о базовом распределении данных или самой модели. Единственное фундаментальное предположение состоит в том, что данные (обучающие и тестовые точки) являются обмениваемыми, то есть они взяты из одного и того же распределения, и их порядок не имеет значения.

Это предположение слабее, чем предположение о независимости и идентичной распределенности (i.i.d.), и часто может быть обосновано на практике. В отличие от традиционных интервалов прогнозирования, которые могут лишь аппроксимировать охват, КП предлагает гарантии для конечных выборок, обеспечивая достижение заданного уровня охвата даже при ограниченных данных.

Не зависящая от распределения гарантия конформного прогнозирования напрямую решает фундаментальную проблему финансового моделирования. Финансовые данные, как известно, не являются нормально распределенными, демонстрируют тяжелые хвосты и часто нарушают типичные статистические предположения, такие как гомоскедастичность или независимость приращений.

Традиционные интервалы прогнозирования часто полагаются на эти предположения, например, нормальные остатки, и, таким образом, обеспечивают лишь приблизительный охват. Способность КП предоставлять гарантированный охват без таких предположений делает его по своей природе более надежным и заслуживающим доверия для финансовых приложений, где неверно заданные распределения могут привести к значительной недооценке риска. Это означает, что сообщаемые уровни достоверности более надежны в реальных, сложных финансовых наборах данных.

Процесс конформного прогнозирования обычно включает в себя использование обученной модели машинного обучения, создание калибровочного набора данных (невидимого для модели во время обучения), вычисление "оценок конформности" на этом наборе, а затем, использование квантиля этих оценок для определения наборов прогнозирования. Переход от приблизительного охвата к гарантированному охвату конечной выборки принципиально меняет ландшафт регулирования и управления рисками для моделей машинного обучения в финансах.

В высокорискованных отраслях, таких как финансы, модели часто должны демонстрировать количественную надежность и контроль над показателями ошибок. Это отличается от традиционных статистических методов, где "90% уверенности" может быть лишь асимптотическим свойством или аппроксимацией. Для количественного трейдера это обеспечивает более прочную основу для обоснования торговых стратегий или распределения рискового капитала.

Наборы прогнозирования против точечных прогнозов в бинарной классификации

Традиционные модели бинарной классификации выдают одну предсказанную метку (например, "Купить" или "Продать") или оценку вероятности (например, 0.8 для "Купить"). Это точечные прогнозы. Однако конформное прогнозирование предоставляет набор прогнозирования, который является подмножеством возможных классов (например, {Купить}, {Продать} или {Купить, Продать}). Этот набор гарантированно содержит истинную метку с заданной вероятностью.

Для бинарной классификации набор прогнозирования может быть:

• Единым классом (например, {Купить} или {Продать}), что указывает на высокую степень уверенности.
• Обоими классами (например, {Купить, Продать}), что указывает на неопределенность или двусмысленность.
• Пустым набором {} (хотя это менее распространено при использовании некоторых методов, таких как APS, и часто нежелательно), что указывает на крайнюю неопределенность или на то, что ни один класс не соответствует порогу достоверности.

"Информативность" набора прогнозирования обратно пропорциональна его размеру: меньшие наборы (например, одноклассовые) более информативны, чем более широкие (например, оба класса). Явный вывод набора, а не одной точки, принципиально меняет процесс принятия решений в бинарной классификации для финансов. Вместо простого сигнала "да/нет" или "купить/продать", набор прогнозирования предоставляет прямую меру уверенности модели.

Одноклассовый набор, такой как {Купить}, предполагает сильный сигнал, в то время как двухклассовый набор {Купить, Продать} указывает на значительную двусмысленность. Это позволяет применять более тонкую торговую стратегию: выполнять сделки с сигналами высокой уверенности и либо воздерживаться, либо уменьшать размер позиции, либо искать дополнительную информацию для двусмысленных сигналов. Это прямой механизм для интеграции неопределенности в действенные финансовые решения.

"Информативность" наборов прогнозирования становится прямой мерой действенности и толерантности к риску в финансовой торговле. Широкий, неинформативный набор прогнозирования (например, {Купить, Продать}) для транзакции означает, что модель не может надежно различить покупку и продажу на желаемом уровне достоверности. Для количественного аналитика это не ошибка прогнозирования, которую нужно исправлять, а сигнал не действовать или действовать с крайней осторожностью. Это позволяет динамически управлять рисками: выделять больше капитала для сделок с узкими, высоконадежными наборами и сохранять капитал, избегая или минимизируя подверженность сделкам с широкими, неопределенными наборами. Это напрямую приводит к оптимизации профиля риск-доходность торговой стратегии.

Теоретические гарантии: маргинальное и условное покрытие

Конформные предикторы "автоматически действительны" в том смысле, что их наборы прогнозирования имеют вероятность охвата, равную или превышающую заданный уровень достоверности (1 - α) в среднем по всем данным. Эта гарантия сохраняется независимо от базовой модели или процесса генерации данных, при условии соблюдения предположения об обмениваемости. Это свойство известно как маргинальное покрытие.

В то время как маргинальное покрытие гарантировано, оно является средним показателем. Более строгие понятия, такие как условная валидность, стремятся к гарантиям покрытия, обусловленным конкретными свойствами данных (например, по классу, по объекту, по метке). Индуктивные конформные предикторы (вычислительно эффективная версия) в первую очередь контролируют безусловную вероятность покрытия. Достижение условной валидности часто требует модификаций метода.

Различие между маргинальным и условным покрытием имеет первостепенное значение для финансовой бинарной классификации, особенно с несбалансированными наборами данных, распространенными в финансах (например, много сигналов "нет сделки" или "держать" по сравнению с меньшим количеством сигналов "купить" или "продать").

Маргинальное покрытие гарантирует, что в среднем 90% прогнозов будут верными. Однако, если сигналы "купить" редки, модель может достичь 90% маргинального покрытия, будучи очень точной по сигналам "продать", но плохо работая по сигналам "купить". Это может привести к значительным упущенным возможностям или потерям, если сигналы "купить" критически важны.

Условное покрытие, особенно покрытие по классам, гарантирует, что желаемый уровень достоверности достигается для каждого класса индивидуально. Это имеет решающее значение для обеспечения надежности прогнозов как для сделок "купить", так и для сделок "продать", предотвращая систематические смещения, которые могут подорвать торговую стратегию.

Стремление к условной валидности с помощью таких методов, как Mondrian Conformal Prediction, напрямую решает проблему справедливости и надежности по различным классам результатов в финансовых приложениях. В финансах ошибки прогнозирования по определенным классам (например, редкая, но очень прибыльная возможность "купить" или критическая "продать" для избежания больших потерь) могут иметь непропорционально высокие затраты по сравнению с ошибками прогнозирования по более распространенным сценариям "нет сделки".

Обеспечивая условное покрытие, система гарантирует минимальный уровень надежности для каждого типа транзакции, а не только в среднем. Это позволяет более справедливо относиться к различным торговым сигналам и повышает доверие к способности модели обрабатывать разнообразные рыночные условия и редкие события, что важно для надежной алгоритмической торговли.

Оценки конформности: ядро конформного прогнозирования

Оценки конформности (conformity scores) являются ядром конформного прогнозирования; они количественно определяют, насколько "необычной" или "несоответствующей" является новая точка данных по сравнению с калибровочными данными. Единственное требование к функции оценки состоит в том, что более высокие оценки должны кодировать худшее соответствие между входными данными и их гипотетической меткой. Эти оценки используются для вычисления квантиля (точки отсечения) из калибровочного набора, который затем определяет набор прогнозирования для новых тестовых точек.

MAPIE реализует различные оценки конформности, включая симметричные (например, Absolute Residual Score для регрессии) и асимметричные (например, Gamma Score для регрессии), которые влияют на то, как рассчитываются границы интервала прогнозирования. Для классификации используются специфические оценки, такие как LAC, APS и RAPS.

Выбор оценки конформности — это не просто техническая деталь, а стратегическое решение, которое влияет на практическую полезность и интерпретируемость наборов прогнозирования. Различные оценки конформности (например, LAC, APS) приводят к различному поведению при формировании наборов прогнозирования.

Например, LAC может производить пустые наборы при высокой неопределенности, что может быть нежелательно в финансах, поскольку это не дает никаких указаний. APS по своей конструкции избегает пустых наборов, всегда предоставляя некоторый набор правдоподобных результатов. Это означает, что выбор оценки напрямую влияет на то, как представлены "плохие" образцы, и может ли система всегда предоставлять действенный (пусть и неопределенный) ответ. Количественный трейдер должен выбрать оценку, которая соответствует желаемому уровню информативности и толерантности к риску.

Концепция "конформности" позволяет определить "выброс" или "необычное" наблюдение в контексте прогнозов модели на основе данных, что весьма актуально для обнаружения аномальных торговых условий. На финансовых рынках необычные движения цен, внезапные всплески объемов или неожиданные новости могут привести к появлению точек данных, которые значительно отклоняются от исторических закономерностей.

Высокая оценка конформности для нового наблюдения будет сигнализировать о том, что это наблюдение "не соответствует" закономерностям, наблюдаемым в калибровочных данных. Это может служить системой раннего предупреждения о рыночных аномалиях или смене режимов, побуждая к пересмотру торговой стратегии или временной приостановке автоматизированной торговли, тем самым выступая в качестве важнейшего инструмента управления рисками, выходящего за рамки простой точности модели.

Подробное рассмотрение соответствующих оценок конформности для классификации

MAPIE предлагает различные оценки конформности, каждая из которых имеет свои особенности и применимость.

• Least Ambiguous Set-valued Classifier (LAC):

1. Расчет: оценка конформности определяется как 1 - softmax_score_of_the_true_label.
2. Свойства: простой подход, теоретически гарантирует маргинальное покрытие. Обычно приводит к небольшим наборам прогнозирования.
3. Применимость/Ограничения: имеет тенденцию к формированию пустых наборов прогнозирования при высокой неопределенности модели (например, около границ принятия решений). Это может быть проблематично в финансах, так как пустой набор не дает действенных указаний.

• Adaptive Prediction Sets (APS):

1. Расчет: оценки конформности вычисляются путем суммирования ранжированных оценок softmax каждой метки, от самой высокой до самой низкой, пока не будет достигнута истинная метка.
2. Свойства: преодолевает проблему пустых наборов LAC; наборы прогнозирования по определению не пусты. Предоставляет гарантии маргинального покрытия.
3. Применимость: Более надежен для финансовых приложений, где некоторая форма прогнозирования (даже если она неопределенная) всегда предпочтительнее пустого набора.

• Regularized Adaptive Prediction Sets (RAPS):

1. Расчет: аналогичен APS, но включает член регуляризации для уменьшения размера наборов прогнозирования.
2. Свойства: направлен на балансирование охвата и эффективности путем регуляризации размера набора при сохранении гарантий охвата.
3. Применимость: полезен в сценариях, где размер набора прогнозирования (эффективность) так же важен, как и охват, поскольку меньшие наборы более действенны в торговле.

• Mondrian Conformal Prediction:

1. Расчет: этот метод вычисляет отдельные квантили оценок конформности для каждого класса. Это позволяет включать в набор прогнозирования с учетом класса.
2. Свойства: обеспечивает условное покрытие (1 - α) для каждого класса, что жизненно важно для несбалансированных многоклассовых или бинарных задач.
3. Применимость: настоятельно рекомендуется для финансовой бинарной классификации (купить/продать), где классы могут быть несбалансированы (например, меньше сигналов "купить", чем "держать" или "продать") или иметь различные допуски на ошибки. Это гарантирует, что надежность сигнала "купить" гарантируется независимо от сигнала "продать".

Эволюция оценок конформности от LAC до APS/RAPS отражает практическую потребность в действенных и информативных наборах прогнозирования в реальных приложениях. Хотя LAC концептуально прост, его склонность к созданию пустых наборов является существенным недостатком в финансах. Пустой набор прогнозирования для решения о покупке/продаже не дает никаких указаний, фактически останавливая процесс принятия решения. APS и RAPS, гарантируя непустые наборы, обеспечивают, что даже в условиях высокой неопределенности модель предоставляет некоторые правдоподобные результаты, что позволяет принимать решение по умолчанию "держать" или "переоценить", а не полностью останавливаться. Это обеспечивает непрерывную работу и управление рисками.

Метод Mondrian является критически важным достижением для финансовой бинарной классификации, напрямую решающим проблему несбалансированных классов и дифференциального влияния ошибок. В сценариях покупки/продажи сигналы "покупки" могут быть редкими, но очень прибыльными, в то время как сигналы "продажи" могут быть более частыми, но менее значимыми индивидуально. Стандартные конформные методы обеспечивают маргинальное покрытие, что может означать, что покрытие для редкого класса "покупки" ниже желаемого, если общий средний показатель достигнут. Способность Мондриана вычислять квантили для конкретных классов гарантирует, что желаемый уровень достоверности поддерживается для каждого класса.

Это имеет решающее значение для предотвращения систематического недопокрытия критических, редких событий (например, сильных сигналов на покупку) и, таким образом, приводит к более надежным и потенциально более прибыльным торговым стратегиям. Это гарантирует, что надежность модели не является просто средним показателем, но сохраняется для конкретного типа рассматриваемой транзакции.

Этапы формирования конформных предиктивных множеств для классификации

Давайте разберем процесс шаг за шагом:

1. Выбор меры неконформности (или "функции оценки"): Это крайне важно. Для классификации часто используется вывод предварительно обученного классификатора (например, логистической регрессии, опорных векторов, нейронной сети или случайного леса). Пусть f(x) — это вывод классификатора для входных данных x. Если f(x) выдает вероятности (например, из слоя softmax), хорошей мерой неконформности для точки данных (xi ,yi ) может быть:
• 1 - Предсказанная вероятность истинного класса: αi =1−P^(yi ∣xi ). Здесь P^(yi ∣xi ) — это предсказанная вероятность истинной метки yi  для входных данных xi . Малое значение αi  означает, что модель уверена в своем предсказании для истинного класса, что указывает на "конформность". Большое αi  означает, что модель менее уверена, что указывает на "неконформность".
• На основе температурного масштабирования softmax: если модель выдает логиты, можно применить softmax для получения вероятностей. Тогда оценка неконформности снова будет 1−P(yi ∣xi ).
• Расстояние до разделяющей поверхности (для SVM): для моделей, подобных SVM, которые выдают знаковое расстояние до разделяющей поверхности, мера неконформности может быть связана с отрицательным значением этого расстояния для правильно классифицированных точек или положительным значением этого расстояния для неправильно классифицированных точек.
2. Разделение данных для калибровки: чтобы сделать предсказания статистически достоверными, необходимо откалибровать наши оценки неконформности. Обычно это делается путем разделения исходного набора данных на две части:
• Обучающая выборка: используется для обучения базового классификатора (например, нейронной сети, SVM).
• Калибровочная выборка: отдельный набор точек данных, не используемый для обучения классификатора, но используемый для расчета оценок неконформности и определения порога достоверности.
3. Расчет оценок неконформности для калибровочных данных: для каждой точки данных (xj ,yj ) в калибровочной выборке рассчитывается ее оценка неконформности αj  с помощью предварительно обученного классификатора.
4. Сортировка оценок неконформности и определение квантиля (1−δ): упорядочиваются все оценки неконформности из калибровочной выборки в порядке возрастания: α(1) ≤α(2) ≤⋯≤α(m) , где m — размер калибровочной выборки.
   Теперь выбирается желаемый уровень значимости δ∈(0,1). Это δ представляет вероятность того, что предиктивное множество не содержит истинную метку. И наоборот, 1−δ — это желаемая вероятность охвата. Нужно найти (1−δ)-й квантиль этих оценок. Точнее, находится наименьшее значение q такое, что по крайней мере (1−δ)×(m+1) оценок калибровки меньше или равны q. Распространенный способ расчета этого порога: q=α(⌈(m+1)(1−δ)⌉)
   Однако для конечных выборок, чтобы гарантировать точное покрытие, часто более надежным является рассмотрение эмпирического квантиля (1−δ), скорректированного для конечных выборок. Более практичный подход состоит в том, чтобы найти наименьшее α(k)  такое, что k/(m+1)≥1−δ. Пусть это значение будет q^ .
5. Формирование предиктивного множества для новой тестовой точки: пусть xtest  — это новый вход, для которого мы хотим сделать предсказание. Для каждой возможной метки k в наборе классов (например, 1,2,…,C для C классов) представьте, что ytest =k.
   Теперь рассчитывается оценка неконформности αtest,k  для пары (xtest ,k) с помощью выбранной меры неконформности (например, 1−P^(k∣xtest )).
   Предиктивное множество Ytest  для xtest  формируется путем включения всех меток k, для которых оценка неконформности αtest,k  меньше или равна порогу q^ , определенному на шаге 4: Ytest ={k∈{1,…,C}∣αtest,k ≤q^ }

Ключевые компоненты MapieClassifier

MapieClassifier является основным классом в MAPIE для генерации наборов прогнозирования в задачах классификации. Он разработан для совместимости с любым оценщиком scikit-learn, который имеет методы fit, predict и predict_proba. Если оценщик не предоставлен, по умолчанию используется LogisticRegression.

Параметр cv позволяет использовать различные стратегии кросс-валидации (например, "split", "crossval", "prefit") для вычисления оценок конформности, влияя на различие между методами jackknife и CV. Опция "prefit" предполагает, что оценщик уже обучен, и все предоставленные данные используются для калибровки прогнозов посредством вычисления оценок. Процесс включает разделение данных на обучающий, калибровочный и тестовый наборы, обучение базовой модели на обучающем наборе, а затем использование MAPIE для "конформизации" модели на калибровочном наборе.

Опция cv="prefit" очень практична для финансовых приложений, где модели часто непрерывно обучаются или переобучаются на больших наборах данных. В реальном времени или при высокочастотной торговле модели часто обновляются или обучаются на потоковых данных. Возможность использовать предварительно обученную модель, а затем калибровать ее с помощью отдельного набора данных означает, что вычислительно интенсивный этап обучения не нужно повторять для конформизации. Это позволяет эффективно интегрировать количественную оценку неопределенности в существующие высокопроизводительные торговые системы без значительных задержек.

Параметр method (теперь устаревший в пользу conformity_score) задает метод конформного прогнозирования. Отказ от параметра method в пользу conformity_score означает переход к большей модульности и явному контролю над основным механизмом конформного прогнозирования. Это архитектурное решение позволяет пользователям точно определять, как измеряется "несоответствие" для их конкретной проблемы. Для финансовых данных, где различные типы ошибок или неопределенностей могут быть более критичными (например, неправильная классификация "покупки" по сравнению с "продажей"), эта модульность позволяет точно настроить процесс количественной оценки неопределенности для лучшего соответствия конкретным финансовым метрикам риска или торговым целям. Это дает опытным пользователям возможность настраивать процесс конформизации за пределами предопределенных методов.

Выводы по теоретической части и рекомендации

Библиотека MAPIE представляет собой мощный инструмент для количественной оценки неопределенности в моделях машинного обучения, особенно в контексте конформной бинарной классификации для финансовых приложений. Ее способность предоставлять не зависящие от распределения, конечные выборочные гарантии покрытия и явно идентифицировать "хорошие" и "плохие" образцы существенно повышает надежность и управляемость рисков в высокорисковых финансовых средах.

Возможность MAPIE интегрироваться с любой моделью, совместимой со scikit-learn, обеспечивает гибкость и снижает барьеры для внедрения в существующие финансовые системы. Переход от точечных прогнозов к наборам прогнозирования позволяет принимать более тонкие и информированные решения, явно учитывая степень неопределенности модели. В частности, различие между маргинальным и условным покрытием имеет решающее значение для финансовых приложений, где надежность прогнозов для редких, но критически важных классов (например, сильных сигналов на покупку) может иметь несоразмерно большое значение.

Рекомендации:

• Приоритет оценок конформности: для бинарной классификации в финансах рекомендуется отдавать предпочтение оценкам конформности, таким как APS или RAPS, поскольку они гарантируют непустые наборы прогнозирования, что обеспечивает непрерывность процесса принятия решений и всегда предоставляет некоторую форму действенного вывода, даже в условиях высокой неопределенности.
• Использование Mondrian Conformal Prediction: в сценариях с несбалансированными классами или когда условное покрытие для конкретных типов транзакций (например, редких сигналов на покупку) является критическим, следует рассмотреть использование метода Mondrian Conformal Prediction. Этот метод обеспечивает гарантии надежности для каждого класса индивидуально, что предотвращает систематическое недопокрытие важных, но редких событий.
• Тщательная валидация временных рядов: применение конформного прогнозирования к финансовым временным рядам требует тщательной валидации и учета нарушения предположения об обмениваемости. Несмотря на наличие специализированных инструментов в MAPIE для временных рядов, таких как MapieTimeSeriesRegressor, их следует сочетать с другими методами, специфичными для временных рядов, и строгим бэктестингом, чтобы обеспечить надежность в условиях нестационарности и внезапных рыночных изменений.
• Разработка многоуровневых торговых стратегий: следует разрабатывать торговые стратегии, которые используют интерпретируемость наборов прогнозирования. Это позволит динамически корректировать подверженность риску: например, выполнять высокоуверенные сделки (одноклассовые наборы) с полным капиталом, а для сделок с низкой уверенностью (многоклассовые наборы) уменьшать размер позиции, применять хеджирование или воздерживаться.

Практическое применение библиотеки MAPIE

В библиотеке MAPIE реализовано два способа "конформизации" предсказаний моделей:

• Split conformal predictions
• Cross conformal predictions

Первый способ разделяет исходные данные на тренировочную и валидационную подвыборки. Первая используется для обучения басового классификатора, а вторая для калибровки и вывода наборов прогнозирования. Второй способ разделяет датасет на несколько фолдов и использует перекрестное обучение и калибровку. Мы сразу будем использовать второй, поскольку он должен быть более надежным ввиду перекрестной проверки. Это аналог walk-forward в машинном обучении - пояснение для тех, кто не знаком с кросс-валидацией.

Сначала необходимо установить пакет MAPIE и импортировать модуль:

pip install mapie
from mapie.classification import CrossConformalClassifier

Также должны быть установлены и импортированы дополнительные библиотеки, список которых представлен ниже.

import pandas as pd
import math
from datetime import datetime
from catboost import CatBoostClassifier
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_predict
from sklearn.model_selection import StratifiedKFold
from bots.botlibs.labeling_lib import *
from bots.botlibs.tester_lib import test_model
from mapie.classification import CrossConformalClassifier
from sklearn.ensemble import RandomForestClassifier

Далее я написал тестовую функцию, которая реализует процесс конформизации, а затем вывод плохих и хороших примеров на основе наборов прогнозирования.

def meta_learners_mapie(n_estimators_rf: int,
                       max_depth_rf: int,
                       confidence_level: float = 0.9):
    
    dataset = get_labels(get_features(get_prices()), markup=hyper_params['markup'])
    data = dataset[(dataset.index < hyper_params['forward']) & 
                  (dataset.index > hyper_params['backward'])].copy()
    
    # Extract features and target
    feature_columns = list(data.columns[1:-2])
    X = data[feature_columns]
    y = data['labels']

    mapie_classifier = CrossConformalClassifier(
                        estimator=RandomForestClassifier(n_estimators=n_estimators_rf, 
                                                         max_depth=max_depth_rf),
                        confidence_level=confidence_level,
                        cv=5,
                        ).fit_conformalize(X, y)
    predicted, y_prediction_sets = mapie_classifier.predict_set(X)
    
    
    y_prediction_sets = np.squeeze(y_prediction_sets, axis=-1)
    # Calculate set sizes (sum across classes for each sample)
    set_sizes = np.sum(y_prediction_sets, axis=1)
    # Initialize meta_labels
    data['meta_labels'] = 0.0
    # Mark labels as "good" (1.0) only where prediction set size is exactly 1
    data.loc[set_sizes == 1, 'meta_labels'] = 1.0
    # Report statistics on prediction sets
    empty_sets = np.sum(set_sizes == 0)
    single_element_sets = np.sum(set_sizes == 1)
    multi_element_sets = np.sum(set_sizes >= 2)
    
    print(f"Empty sets (meta_labels=0): {empty_sets}")
    print(f"Single element sets (meta_labels=1): {single_element_sets}")
    print(f"Multi-element sets (meta_labels=0): {multi_element_sets}")

    # Return the dataset with features, original labels, and meta labels
    return data[feature_columns + ['labels', 'meta_labels']]

В качестве базового классификатора будем использовать случайный лес из поставки scikit-learn, поскольку пакет MAPIE поддерживает все классификаторы из этого пакета. Случайный лес является достаточно сильной моделью с гибкими настройками, но вы можете использовать другую модель, которую посчитаете уместной для своих задач. Для этого следует в качестве estimator в выделенном коде передать любой другой классификатор. Стоит отметить, что данный классификатор будет использоваться только для вывода предиктивных множеств, а в качестве финальных моделей по прежнему обучается CatBoost. 

Давайте разберем функцию meta_learners_mapie() по шагам.

Определение функции и ее параметров:

def meta_learners_mapie(n_estimators_rf: int,
                       max_depth_rf: int,
                       confidence_level: float = 0.9):

Функция принимает три аргумента:  

1. n_estimators_rf: количество деревьев в случайном лесе (Random Forest), который будет использоваться как базовая модель.  
2. max_depth_rf: максимальная глубина каждого дерева в случайном лесе.  
3. confidence_level: уровень доверия для конформного предсказания (по умолчанию 0.9, т.е. 90%). Этот параметр определяет, насколько "широкими" будут предсказательные множества.

Загрузка и подготовка данных:

dataset = get_labels(get_features(get_prices()), markup=hyper_params['markup'])
data = dataset[(dataset.index < hyper_params['forward']) &
              (dataset.index > hyper_params['backward'])].copy()

Сначала происходит загрузка и предварительная обработка данных.

Предполагается, что есть три вспомогательные функции:  

• get_prices(): загружает исходные данные (цены) 
• get_features(): извлекает или вычисляет признаки (фичи) из данных, полученных от get_prices() 
• get_labels(): генерирует целевые метки (labels) на основе признаков и параметра markup из словаря hyper_params.  

Затем данные фильтруются по временному индексу. Оставляются только те записи, индекс которых находится между hyper_params['backward'] и hyper_params['forward'].  .copy() используется для создания копии отфильтрованного DataFrame, чтобы избежать проблем с SettingWithCopyWarning.

Извлечение признаков X и целевой переменной y:

feature_columns = list(data.columns[1:-2])
X = data[feature_columns]
y = data['labels']

• feature_columns: cоздается список имен столбцов, которые будут использоваться как признаки. Берутся все столбцы, кроме первого (индекс 0) и двух последних. Это специфично для структуры data. 
• X: cоздается DataFrame с признаками, выбирая столбцы из feature_columns.  
• y: cоздается Series с целевыми метками из столбца 'labels'.

Инициализация и обучение конформного классификатора MAPIE:

mapie_classifier = CrossConformalClassifier(
                    estimator=RandomForestClassifier(n_estimators=n_estimators_rf,
                                                     max_depth=max_depth_rf),
                    confidence_level=confidence_level,
                    cv=5,
                    ).fit_conformalize(X, y)

• Создается экземпляр CrossConformalClassifier из библиотеки MAPIE. Это обертка, которая добавляет возможности конформного прогнозирования к любой модели, совместимой с scikit-learn.  
• estimator: в качестве базовой модели (оценщика) используется RandomForestClassifier из scikit-learn. Ему передаются параметры n_estimators_rf и max_depth_rf, полученные функцией.  
• confidence_level: используется уровень доверия, переданный в функцию.  cv=5: Указывает на использование 5-кратной перекрестной проверки (cross-validation) для калибровки конформного предиктора. Это стандартный подход в MAPIE для разделения данных на обучающие и калибровочные наборы.  
• .fit_conformalize(X, y): метод обучает базовый RandomForestClassifier на данных (X, y) и одновременно калибрует конформный предиктор. После этого шага mapie_classifier готов делать конформные предсказания.

Получение предсказаний и предсказательных множеств:

predicted, y_prediction_sets = mapie_classifier.predict_set(X)

mapie_classifier.predict_set(X): этот метод генерирует два выхода для входных данных X:  

• predicted: точечные предсказания (один класс для каждого примера), аналогично стандартному методу .predict().  
• y_prediction_sets: это ключевой результат конформного прогнозирования. Для каждого примера данных это массив (или список массивов), указывающий, какие классы включены в предсказательное множество с заданным confidence_level. Предсказательное множество – это набор классов, который с вероятностью не менее confidence_level содержит истинный класс. Его форма обычно (n_samples, n_classes, 1) или (n_samples, n_classes), где значения - булевы (True/False) или 0/1, указывающие на включение класса в множество.

Обработка предсказанных множеств:

y_prediction_sets = np.squeeze(y_prediction_sets, axis=-1)
set_sizes = np.sum(y_prediction_sets, axis=1)

• np.squeeze(y_prediction_sets, axis=-1): если y_prediction_sets имеет лишнее измерение размером 1 в конце (например, форму (n_samples, n_classes, 1)), эта операция удаляет его, приводя к форме (n_samples, n_classes).  
• set_sizes = np.sum(y_prediction_sets, axis=1): для каждого примера (по оси 0) суммируются значения в y_prediction_sets по классам (по оси 1). Если y_prediction_sets содержит 0/1, то эта сумма дает количество классов, включенных в предсказательное множество для каждого примера. То есть set_sizes – это массив размеров предсказательных множеств для каждого наблюдения.

Генерация Мета-меток:

data['meta_labels'] = 0.0
data.loc[set_sizes == 1, 'meta_labels'] = 1.0

• data['meta_labels'] = 0.0: в DataFrame data добавляется новый столбец 'meta_labels', который инициализируется нулями.  
• data.loc[set_sizes == 1, 'meta_labels'] = 1.0: это ключевой шаг для создания мета-меток. Для тех примеров, где размер предсказательного множества (set_sizes) равен точно 1 (т.е. модель с заданной уверенностью предсказывает ровно один класс), значение в столбце 'meta_labels' устанавливается в 1.0. Это означает, что для этих примеров модель очень уверена в своем единственном предсказанном классе. Если предсказательное множество пустое (размер 0) или содержит несколько классов (размер >= 2), мета-метка остается 0.0.

Отчет по статистике предсказанных множеств:

empty_sets = np.sum(set_sizes == 0)
single_element_sets = np.sum(set_sizes == 1)
multi_element_sets = np.sum(set_sizes >= 2)

print(f"Empty sets (meta_labels=0): {empty_sets}")
print(f"Single element sets (meta_labels=1): {single_element_sets}")
print(f"Multi-element sets (meta_labels=0): {multi_element_sets}")

Подсчитывается количество:  

• empty_sets: пустых предсказательных множеств (модель не может выбрать ни один класс с заданной уверенностью).  
• single_element_sets: множеств, содержащих ровно один класс (высокоуверенные предсказания, для которых meta_labels=1).  
• multi_element_sets: множеств, содержащих два или более класса (модель не уверена в одном конкретном классе).  

Эта статистика выводится на печать, давая представление о том, насколько часто модель генерирует уверенные однозначные предсказания.

Возврат результата:

return data[feature_columns + ['labels', 'meta_labels']]

Функция возвращает DataFrame, содержащий исходные признаки (feature_columns), оригинальные метки ('labels') и новые сгенерированные мета-метки ('meta_labels'). Эти мета-метки затем могут быть использованы, например, для обучения другой модели (мета-модели) или для выбора только наиболее надежных предсказаний для дальнейших действий.

В итоге, функция использует конформное прогнозирование для идентификации тех наблюдений, для которых базовая модель (Random Forest) делает предсказание с высокой степенью уверенности, указывая ровно один возможный класс. Эти наблюдения помечаются "мета-меткой" равной 1.

Доработка функции конформизации

Протестировав функцию и оценив результаты я пришел к выводу, что она имеет один существенный недостаток. Несмотря на то, что она отлично справляется с выводом предиктивных множеств, на которых обучается финальная мета-модель, базовая модель все еще обучается на исходном датасете, который может содержать много ошибок, из-за чего она плохо обобщает на новых данных. Мета-модель корректирует ошибки базовой модели, запрещая ей торговать в ситуациях с высокой неопределенностью, однако из-за слабого обобщения основной модели, вся система все еще плохо работает на нестационарном рынке.

Вспомним, что после обучения классификатора MAPIE, мы получаем два набора меток: предсказания модели (сами метки) и предиктивные сеты.

predicted, y_prediction_sets = mapie_classifier.predict_set(X)

В первоначальной функции конформизации используются только предиктивные сеты для обучения мета-модели, тогда как базовая модель обучается на метках из исходного датасета. Но мы можем исправить метки также для базовой модели, оставив только те, в которых классификатор MAPIE больше всего уверен.

# Initialize meta_labels column with zeros
data['meta_labels'] = 0.0
# Set meta_labels to 1 where predicted labels match original labels
# Compare predicted values with the original labels in the dataset
data.loc[predicted == data['labels'], 'meta_labels'] = 1.0

В представленном выше коде мы сравниваем предсказанные метки с исходными и формируем новую колонку 'meta_labels', которая содержит единицы если метки совпали и ноли если не совпали. Затем мы обучим базовый классификатор только на тех примерах, метки которых совпали.

Первая часть функции обучения финальных моделей теперь будет выглядеть следующим образом:

def fit_final_models(dataset) -> list:
    # features for model\meta models. We learn main model only on filtered labels 
    X = dataset[dataset['meta_labels']==1]
    X = X[X.columns[1:-3]]
    X_meta = dataset[dataset.columns[1:-3]]
    # labels for model\meta models
    y = dataset[dataset['meta_labels']==1]
    y = y[y.columns[-3]]
    y_meta = dataset['conformal_labels']

Таким образом, обе модели будут возвращать качественные оценки после обучения, насколько это возможно на нестационарных временных рядах.

Обучение и тестирование алгоритма

Для проверки метода, обучим 10 моделей в цикле на валютной паре EURUSD с начала 2020 года до начала 2025 года. Оставшиеся данные - форвард период.

hyper_params = {
    'symbol': 'EURUSD_H1',
    'export_path': '/Users/dmitrievsky/Library/Program Files/MetaTrader 5/MQL5/Include/Trend following/',
    'model_number': 0,
    'markup': 0.00010,
    'stop_loss':  0.00500,
    'take_profit': 0.00200,
    'periods': [i for i in range(5, 300, 30)],
    'backward': datetime(2020, 1, 1),
    'forward': datetime(2025, 1, 1),
}

models = []
for i in range(10):
    print('Learn ' + str(i) + ' model')
    models.append(fit_final_models(meta_learners_mapie(15, 5, confidence_level=0.90, CV_folds=5)))

Функция meta_leaners_mapie будет вызываться со следующими аргументами:

• 15 решающих деревьев в составе Random Forest (базовый классификатор)
• 5: глубина каждого дерева принятия решения
• уровень уверенности модели 90%
• количество фолдов для кросс-валидации равно пяти

В процессе обучения выводится следующая информация:

Learn 9 model
Empty sets (meta_labels=0): 0
Single element sets (meta_labels=1): 6715
Multi-element sets (meta_labels=0): 22948
Correct predictions (meta_labels=1): 16638
Incorrect predictions (meta_labels=0): 13025
R2: 0.9931613891107195

• Empty sets: количество пустых предиктивных сетов, когда модель не уверена ни в одном из классов
• Single element sets: количество предиктивных сетов, которые содержат один элемент. В этих прогнозах модель уверена с вероятностью 0.9
• Multi-element sets: количество предиктивных сетов, которые содержат несколько классов. В этих примерах модель не уверена
• Correct predictions: количество правильно предсказанных меток
• Incorrect predictions: количество неправильно предсказанных меток
• R2: оценка кривой баланса

На основании предоставленного отчета можно сделать вывод, что датасет содержит много мусорных данных: 6715 надежных предсказаний против 22948 ненадежных. Но наша модель постарается это исправить и будет использовать только надежные. В результате график баланса в тестере будет выглядеть следующим образом.

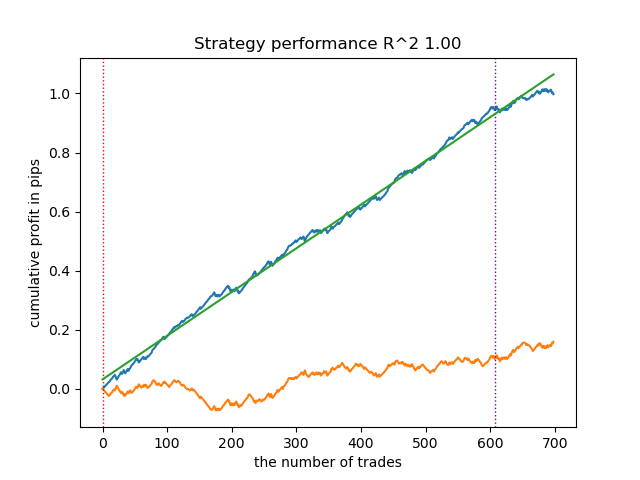
Отличительной особенностью такого алгоритма является то, что обе модели (основная и мета) обучаются с высоким Accuracy:

>>> models[-1][1].get_best_score()['validation']
{'Accuracy': 0.92, 'Logloss': 0.1990666082064606}

>>> models[-1][2].get_best_score()['validation']
{'Accuracy': 0.9647435897435898, 'Logloss': 0.10955056411224594}

Это означает, что теперь из моделей удалена большая часть неопределенности по сравнению с исходным датасетом, который содержит много мусорных данных. Дополнительно, финальные модели можно откалибровать, для получения более надежных порогов принятия решений, что выходит за рамки этой статьи.

Что произойдет, если уровень уверенности (confidence_level) снизить с 0.9 до 0.6? Мы получим больше множеств, которые с вероятностью 60% содержат истинную метку класса, это отражено в отчете.

Learn 8 model
Empty sets (meta_labels=0): 0
Single element sets (meta_labels=1): 28647
Multi-element sets (meta_labels=0): 991
Correct predictions (meta_labels=1): 16999
Incorrect predictions (meta_labels=0): 12639
R2: 0.9850582205528567

Если в предыдущем примере Single Element sets содержали мало примеров, теперь их количество превалирует над Multi-element sets. Но уверенность в удачном исходе гораздо ниже. График баланса отражает эту неопределенность, потому что содержит больше просадок.

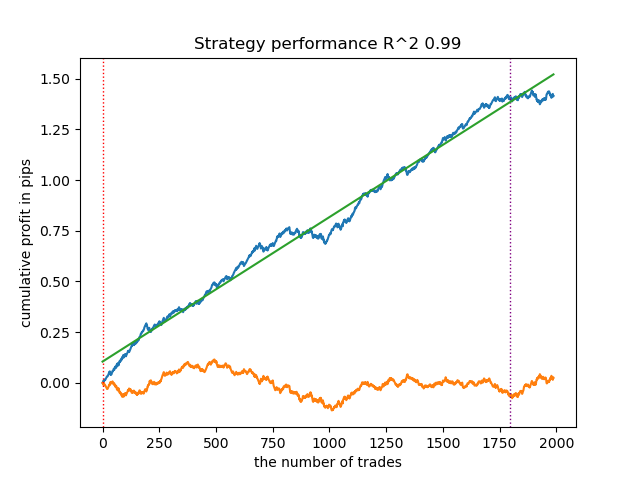
Таким образом, регулируя уровень уверенности модели, можно контролировать риски, связанные с неудачными торговыми операциями. Благодаря этому можно искать компромисс между количеством сделок и эффективностью торговли, либо вероятностью наступления черного лебедя.

Экспорт и тестирование моделей в терминале Meta Trader 5

Экспорт моделей реализован точно таким же образом, как во всех предыдущих статьях. Для более подробного ознакомления рекомендую их прочесть.

export_model_to_ONNX(model = models[-1],
                     symbol = hyper_params['symbol'],
                     periods = hyper_params['periods'],
                     periods_meta = hyper_params['periods'],
                     model_number = hyper_params['model_number'],
                     export_path = hyper_params['export_path'])

Теперь можно протестировать алгоритм уже в терминале Meta Trader 5. Торговая система оказалась устойчивой не только на форвард периоде, но и на периоде в прошлом, с 2017 по 2020 год.

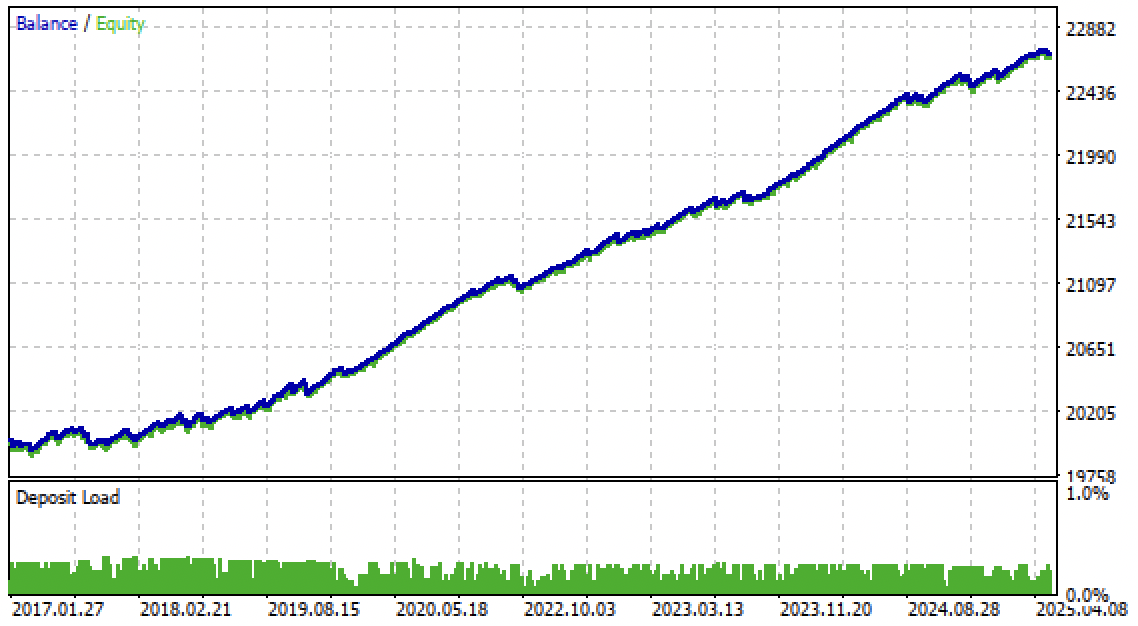
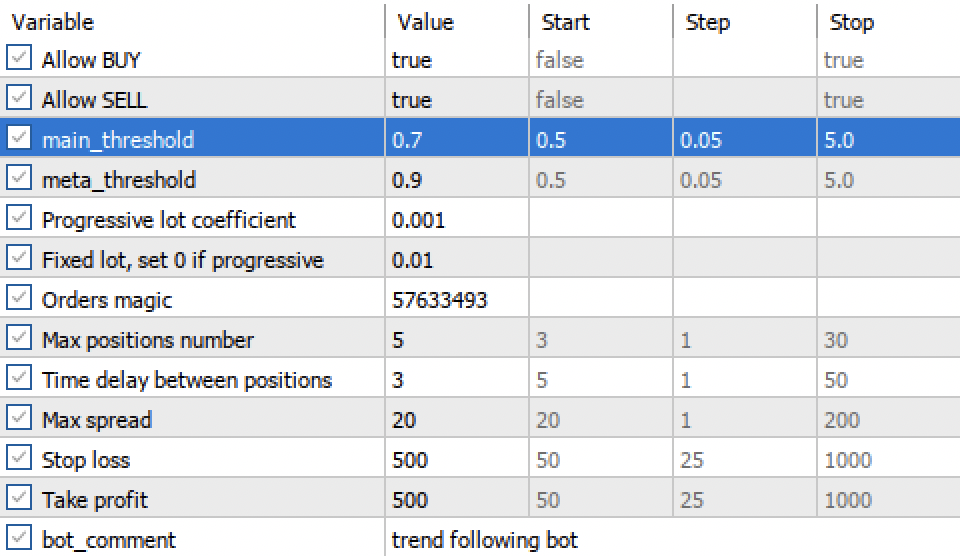
Настройки порогов main threshold и meta threshold теперь позволяют фильтровать сигналы моделей по уверенности. Чем выше порог, тем более уверенная торговля, но меньше сделок.

Заключение

В этой статье мы познакомились с конформными предсказаниями и библиотекой MAPIE, которая их реализует. Данный подход является одним из самых современных в машинном обучении и позволяет сосредоточиться на контроле рисков для уже существующих разнообразных моделей машинного обучения. Конформные предсказания, сами по себе, не являются способом поиска закономерностей в данных. Они лишь определяют степень уверенности существующих моделей в предсказании конкретных примеров и позволяют фильтровать надежные предсказания. Это важное свойство позволяет контролировать риск в трейдинге через настройку порога уверенности еще на этапе обучения моделей.

Архив Python files.zip содержит следующие файлы для разработки в среде Python:

Имя файла	Описание
mapie causal.py	Основной скрипт для обучения моделей
labeling_lib.py	Обновленный модуль с разметчиками сделок
tester_lib.py	Обновленный кастомный тестер стратегий, основанных на машинном обучении
export_lib.py	Модуль для экспорта моделей в терминал
EURUSD_H1.csv	Файл с котировками, экспортированный из терминала MetaTrader 5

Архив MQL5 files.zip cодержит файлы для терминала MetaTrader 5:

Имя файла	Описание
mapie trader.ex5	Скомпилированный бот из данной статьи
mapie trader.mq5	Исходник бота из статьи
папка Include//Trend following	Расположены модели ONNX и заголовочный файл для подключения к боту