Скрытые марковские модели в торговых системах на машинном обучении

Содержание

• Введение
• Алгоритмы, представленные в библиотеке hmmlearn
• Описание класса hmm.GaussianHMM
• Описание класса hmm.GMMHMM
• Описание класса vhmm.VariationalGaussianHMM
• Сравнение эффективности моделей
• Методы определения априорных матриц
• Определение рыночных режимов c помощью HMM
• Создание априорных матриц
• Экспорт моделей в Meta Trader 5
• Заключение

Введение

Скрытые марковские модели (СММ) представляют собой мощный класс вероятностных моделей, предназначенных для анализа последовательных данных, где наблюдаемые события зависят от некоторой последовательности ненаблюдаемых (скрытых) состояний, которые формируют марковский процесс.СММ являются двойным стохастическим процессом, характеризующимся конечным набором скрытых состояний и последовательностью наблюдаемых событий, вероятность которых зависит от текущего скрытого состояния.Основные предположения СММ включают марковское свойство для скрытых состояний, означающее, что вероятность перехода в следующее состояние зависит только от текущего состояния, и независимость наблюдений при условии знания текущего скрытого состояния.

Скрытые марковские модели находят широкое применение в различных областях, включая распознавание речи и образов, обработку естественного языка (например, частеречная разметка), биоинформатику (анализ последовательностей ДНК и белков) и анализ временных рядов (прогнозирование, выявление аномалий).Возможность моделировать системы, внутренняя структура которых непосредственно не наблюдается, но оказывает влияние на наблюдаемые выходные данные, делает СММ ценным инструментом для анализа сложных временных зависимостей. Наблюдения в таких моделях являются лишь косвенным отражением скрытых процессов, и понимание этих процессов может предоставить важную информацию о динамике системы.

Библиотека hmmlearn представляет собой набор алгоритмов на языке Python для обучения без учителя (скрытых марковских моделей). Она разработана с целью предоставить простые и эффективные инструменты для работы с СММ, следуя API библиотеки scikit-learn, что облегчает интеграцию в существующие проекты машинного обучения и упрощает процесс обучения для пользователей, знакомых с scikit-learn. Hmmlearn построена на базе таких фундаментальных библиотек научного Python, как NumPy, SciPy и Matplotlib.

Основные возможности hmmlearn включают реализацию различных моделей СММ с разными типами эмиссионных распределений, обучение параметров моделей по наблюдаемым данным, вывод наиболее вероятных последовательностей скрытых состояний, генерацию выборок из обученных моделей, а также возможность сохранения и загрузки обученных моделей. Разнообразие реализованных моделей позволяет пользователям выбирать наиболее подходящий тип эмиссионного распределения, в зависимости от характера их данных. Тип данных (непрерывные, дискретные, счетчики) определяет, какое вероятностное распределение лучше всего описывает процесс генерации наблюдений в каждом скрытом состоянии.

Алгоритмы, представленные в библиотеке hmmlearn

В библиотеке hmmlearn реализованы следующие основные модели СММ:

• hmm.CategoricalHMM: для моделирования последовательностей категориальных (дискретных) наблюдений.
• hmm.GaussianHMM: для моделирования последовательностей непрерывных наблюдений, предполагающих гауссовское распределение в каждом скрытом состоянии.
• hmm.GMMHMM: для моделирования последовательностей непрерывных наблюдений, где эмиссии из каждого скрытого состояния описываются смесью гауссовских распределений.
• hmm.MultinomialHMM: для моделирования последовательностей дискретных наблюдений, где каждое состояние имеет распределение вероятностей по фиксированному набору символов.
• hmm.PoissonHMM: для моделирования последовательностей данных, представляющих собой счетчики событий, где эмиссии из каждого скрытого состояния подчиняются распределению Пуассона.
• vhmm.VariationalCategoricalHMM: вариационная версия CategoricalHMM, использующая методы вариационного вывода для обучения.
• vhmm.VariationalGaussianHMM: вариационная версия GaussianHMM, предназначенная для непрерывных наблюдений, распределенных по многомерному нормальному закону, и обучаемая с использованием вариационного вывода.

Нас интересуют алгоритмы, работающие с непрерывными данными, поэтому будут рассмотрены только они.

Подробное описание класса hmm.GaussianHMM

Класс hmm.GaussianHMM в библиотеке hmmlearn реализует скрытую марковскую модель с гауссовскими эмиссиями. Эта модель применяется, когда наблюдаемые переменные являются непрерывными и предполагается, что в каждом скрытом состоянии они подчиняются многомерному нормальному (гауссовскому) распределению.

GaussianHMM широко используется для моделирования различных временных рядов, таких как финансовые данные (например, цены на акции), показания различных датчиков, а также другие непрерывные процессы, где наблюдаемые значения могут быть описаны гауссовским распределением в каждом из скрытых состояний.

Конструктор класса hmm.GaussianHMM принимает следующие параметры:

• n_components (int, по умолчанию 1): определяет количество скрытых состояний в модели. Каждое состояние будет связано со своим гауссовским распределением.
• covariance_type ({"spherical", "diag", "full", "tied"}, по умолчанию "diag"): задает тип ковариационной матрицы, используемой для каждого состояния. Выбор типа ковариации напрямую влияет на сложность модели и количество оцениваемых параметров.

1. "spherical": каждое состояние использует одну и ту же дисперсию для всех признаков. Ковариационная матрица является кратной единичной матрице.
2. "diag": каждое состояние использует диагональную ковариационную матрицу, предполагая, что признаки внутри состояния статистически независимы, но могут иметь различные дисперсии.
3. "full": каждое состояние использует полную (неограниченную) ковариационную матрицу, что позволяет моделировать корреляции между признаками внутри каждого состояния. Этот вариант является наиболее гибким, но требует большего количества данных для оценки и может быть подвержен переобучению.
4. "tied": все скрытые состояния совместно используют одну и ту же полную ковариационную матрицу. Это позволяет учитывать корреляции между признаками, но предполагает, что структура этих корреляций одинакова во всех состояниях.

• min_covar (float, по умолчанию 1e-3): устанавливает минимальное значение для диагональных элементов ковариационной матрицы, чтобы предотвратить ее вырождение (например, нулевую дисперсию) во время обучения и избежать переобучения.
• startprob_prior (array, форма (n_components,), необязательный): параметры априорного распределения Дирихле для начальных вероятностей startprob_, которые определяют вероятность начала последовательности наблюдений в каждом из скрытых состояний.
• transmat_prior (array, форма (n_components, n_components), необязательный): параметры априорного распределения Дирихле для каждой строки матрицы переходных вероятностей transmat_, которая определяет вероятность перехода между скрытыми состояниями.
• means_prior (array, форма (n_components,), необязательный): среднее значение нормального априорного распределения для средних значений (means_) каждого скрытого состояния.
• means_weight (array, форма (n_components,), необязательный): вес (или точность, обратная дисперсия) нормального априорного распределения для средних значений (means_) каждого скрытого состояния.
• covars_prior (array, форма (n_components,), необязательный): параметры априорного распределения для ковариационной матрицы covars_. Тип этого распределения зависит от параметра covariance_type. Для "spherical" и "diag" это параметры обратного гамма-распределения, а для "full" и "tied" — параметры, связанные с обратным распределением Уишарта.
• covars_weight (array, форма (n_components,), необязательный): вес параметров априорного распределения для ковариационной матрицы covars_. Аналогично covars_prior, интерпретация зависит от covariance_type (параметры масштаба для обратного гамма или обратного распределения Уишарта).
• algorithm ({"viterbi", "map"}, необязательный): алгоритм, используемый для декодирования, то есть, для нахождения наиболее вероятной последовательности скрытых состояний, соответствующих наблюдаемой последовательности. "viterbi" реализует алгоритм Витерби, а "map" (maximum a posteriori estimation) выполняет сглаживание (forward-backward) для нахождения наиболее вероятного состояния в каждый момент времени.
• random_state (RandomState или int, необязательный): объект генератора случайных чисел или целочисленный seed для инициализации параметров модели случайным образом, что обеспечивает воспроизводимость результатов.
• n_iter (int, необязательный): максимальное количество итераций, выполняемых алгоритмом Expectation-Maximization (EM) при обучении модели. По умолчанию установлено значение 10.
• tol (float, необязательный): порог сходимости алгоритма EM. Если изменение логарифмической правдоподобности между двумя последовательными итерациями становится меньше этого значения, обучение прекращается. По умолчанию 0.01.
• verbose (bool, необязательный): если установлено значение True, в стандартный поток ошибок будет выводиться информация о сходимости на каждой итерации. Также сходимость можно отслеживать через атрибут monitor_.
• params (string, необязательный): строка, указывающая, какие параметры модели будут обновляться во время обучения. Может содержать комбинацию символов: 's' для начальных вероятностей (startprob_), 't' для переходных вероятностей (transmat_), 'm' для средних (means_) и 'c' для ковариаций (covars_). По умолчанию 'stmc' (обновляются все параметры).
• init_params (string, необязательный): строка, указывающая, какие параметры модели будут инициализированы перед началом обучения. Символы имеют то же значение, что и в параметре params. По умолчанию 'stmc' (инициализируются все параметры).
• implementation (string, необязательный): определяет, какая реализация алгоритма forward-backward будет использоваться: логарифмическая ("log") или с использованием масштабирования ("scaling"). По умолчанию используется "log", для обеспечения обратной совместимости, однако, реализация "scaling" обычно работает быстрее.

Инициализация параметров GaussianHMM происходит перед началом обучения модели с использованием алгоритма EM. Параметры инициализации определяют начальное состояние модели. Параметр init_params контролирует, какие параметры будут инициализированы. Если какой-либо параметр не включен в init_params, предполагается, что его значение уже установлено вручную.

Начальные значения параметров могут быть заданы случайным образом или вычислены на основе предоставленных данных. Правильная инициализация параметров может существенно повлиять на скорость сходимости алгоритма EM и качество итоговой модели, поскольку алгоритм EM может застревать в локальных оптимумах.

Оптимизация параметров GaussianHMM осуществляется с помощью итеративного алгоритма Expectation-Maximization (EM). Этот алгоритм состоит из двух основных шагов, выполняемых итеративно до достижения сходимости:

1. E-шаг (Expectation): на этом шаге, при текущих оценках параметров модели и наблюдаемой последовательности данных, вычисляются апостериорные вероятности того, что в каждый момент времени система находилась в определенном скрытом состоянии. Это обычно делается с использованием алгоритма forward-backward.
2. M-шаг (Maximization): на этом шаге параметры модели (начальные вероятности, вероятности перехода между состояниями, средние значения и ковариации для каждого состояния) обновляются таким образом, чтобы максимизировать ожидаемую логарифмическую правдоподобность наблюдаемых данных, при условии вычисленных на E-шаге апостериорных вероятностей.

Процесс повторяется до тех пор, пока не будет достигнута сходимость, которая определяется либо достижением максимального количества итераций, заданного параметром n_iter, либо, когда изменение логарифмической правдоподобности между последовательными итерациями становится меньше заданного порога tol. Алгоритм EM гарантированно увеличивает (или оставляет неизменной) логарифмическую правдоподобность на каждой итерации, однако, он не гарантирует нахождения глобального максимума, и результат может зависеть от начальной инициализации параметров.

Выбор параметра covariance_type оказывает непосредственное влияние на структуру ковариационной матрицы, используемой для моделирования эмиссий в каждом скрытом состоянии.

• При выборе "spherical" предполагается изотропная ковариация, то есть, дисперсия всех признаков в данном состоянии одинакова, и ковариационная матрица пропорциональна единичной.
• "diag" указывает на использование диагональной ковариационной матрицы, что означает, что признаки в каждом состоянии считаются статистически независимыми, хотя и могут иметь различные дисперсии.
• "full" позволяет использовать полную ковариационную матрицу, учитывая корреляции между различными признаками внутри каждого скрытого состояния.
• "tied" означает, что все скрытые состояния совместно используют одну и ту же полную ковариационную матрицу. Выбор типа ковариации должен основываться на предположениях о структуре данных в каждом скрытом состоянии. Более сложные типы ковариации, такие как "full", могут лучше соответствовать данным, имеющим сложные зависимости между признаками, но требуют большего количества параметров для оценки, что может привести к переобучению при недостаточном объеме данных.

Гибкость, обеспечиваемая различными параметрами hmm.GaussianHMM, позволяет исследователям адаптировать модель к специфическим характеристикам финансовых временных рядов. В частности, параметр `covariance_type` дает возможность делать различные предположения о взаимосвязях между признаками в каждом скрытом состоянии.

При настройке параметров hmm.GaussianHMM для финансовых временных рядов следует учитывать их специфические характеристики, такие как волатильность, скачки цен и возможное отклонение распределений от нормального закона. Количество скрытых состояний (n_components) следует выбирать, исходя из предполагаемого числа рыночных режимов. Это может быть определено на основе экспертных знаний или с использованием критериев выбора модели, таких как AIC или BIC.

Рекомендуется начинать с небольшого числа состояний (например, 2 или 3) и увеличивать его при необходимости, контролируя при этом риск переобучения. Для одномерных финансовых временных рядов (например, доходностей) может быть достаточно типов ковариации "diag" или "spherical". Для многомерных рядов (например, доходности нескольких активов или такие признаки, как цена и объем) "full" позволяет моделировать корреляции, но увеличивает сложность модели. Тип ковариации "tied" предполагает одинаковую структуру корреляции для всех состояний.

Параметр min_covar помогает предотвратить переобучение, гарантируя, что дисперсии не станут слишком малыми. Значение по умолчанию 1e-3 часто является хорошей отправной точкой. Установка информативных априорных распределений (например, с использованием startprob_prior и transmat_prior для отражения предварительных представлений о начальных вероятностях состояний и тенденциях переходов) может быть полезной, особенно при ограниченном объеме данных. Например, можно ожидать устойчивости рыночных режимов, что может быть закодировано в априорном распределении для матрицы переходов.

Параметры n_iter и tol контролируют максимальное количество итераций и порог сходимости EM-алгоритма. Большее значение n_iter может привести к лучшей сходимости, но также увеличит время обучения. Меньшее значение tol приводит к более строгим критериям сходимости.

Предварительная обработка финансовых данных имеет решающее значение. Рекомендуется использовать доходности (процентные изменения) вместо цен и, возможно, включать технические индикаторы, такие как скользящие средние, меры волатильности (например, ATR) и индикаторы объема, в качестве признаков. Нормализация или стандартизация признаков также рекомендуется. Финансовые временные ряды часто являются нестационарными. Следует рассмотреть возможность дифференцирования данных или использования скользящего окна для оценки параметров, чтобы адаптироваться к изменяющейся динамике рынка.

Для поиска оптимальной комбинации гиперпараметров для конкретного финансового набора данных, следует использовать такие методы, как поиск по сетке, или байесовская оптимизация (например, с помощью Optuna). Нестационарная природа финансовых временных рядов требует тщательной предварительной обработки и, возможно, использования адаптивных методов, таких как обучение с использованием скользящего окна. Настройка гиперпараметров также имеет решающее значение для обеспечения эффективного захвата моделью GaussianHMM базовой динамики рынка без переобучения на исторических данных.

Подробное описание класса hmm.GMMHMM

Класс hmm.GMMHMM предназначен для работы с непрерывными эмиссиями, которые лучше представляются смесью нескольких гауссовских распределений. Это позволяет моделировать более сложные закономерности эмиссий, по сравнению с использованием одного гауссовского распределения, что особенно полезно для данных с выраженными кластерами внутри каждого скрытого состояния.

hmm.GMMHMM может быть полезен, когда распределение финансовых данных в рамках определенного режима является мультимодальным или существенно отличается от гауссовского. Например, доходности в режиме высокой волатильности могут демонстрировать различные характеристики в зависимости от направления движения цены. hmm.GMMHMM расширяет возможности hmm.GaussianHMM, позволяя связывать каждое скрытое состояние со смесью гауссовских распределений. Это особенно выгодно для финансовых временных рядов, которые могут демонстрировать более сложное и ненормально распределенное поведение в различных рыночных режимах.

• Конструктор класса hmm.GMMHMM включает все параметры класса hmm.GaussianHMM, а также добавляет параметр n_mix (целое число, по умолчанию 1), определяющий количество компонент смеси в каждом состоянии, и априорные распределения, связанные с весами смеси. 
• Параметр covariance_type в GMMHMM имеет несколько отличную опцию "tied": все компоненты смеси каждого состояния используют одну и ту же полную ковариационную матрицу. 
• Параметры params и init_params также включают символ 'w' для управления весами смеси GMM. 
• Ключевое отличие в параметрах заключается в n_mix и связанных с ним априорных распределениях для весов смеси, что обеспечивает более гибкое моделирование вероятностей эмиссий в каждом скрытом состоянии. Более тонкая опция "tied" для ковариации в GMMHMM также предоставляет дополнительный способ ограничения модели.

При настройке параметров hmm.GMMHMM для финансовых временных рядов, выбор количества компонент смеси (n_mix) является критически важным шагом. Количество компонент смеси должно наилучшим образом представлять распределение финансовых данных в каждом скрытом состоянии. Это может потребовать экспериментов. Рекомендуется начинать с небольшого числа компонент (например, 2 или 3) и увеличивать его, если модель недообучается, но следует избегать переобучения.

Для определения оптимального значения n_mix можно использовать информационные критерии, такие как AIC или BIC. Другие параметры могут быть настроены аналогично параметрам hmm.GaussianHMM, с учетом специфических характеристик финансовых данных. Например, выбор covariance_type повлияет на способ моделирования дисперсии внутри каждого компонента смеси. Выбор оптимального числа компонент смеси (n_mix) является важным этапом эффективного использования hmm.GMMHMM для финансовых временных рядов. Это включает в себя балансирование способности модели захватывать сложные распределения данных с риском переобучения и может потребовать использования таких методов, как кросс-валидация или информационные критерии для получения робастных оценок.

Подробное описание класса vhmm.VariationalGaussianHMM

Класс vhmm.VariationalGaussianHMM представляет собой скрытую марковскую модель с многомерными гауссовскими эмиссиями, обучение которой производится с использованием вариационного вывода, а не алгоритма ожидания-максимизации (EM), применяемого в hmm.GaussianHMM. 

Вариационный вывод направлен на поиск параметров такого распределения, которое было бы наиболее близко к истинному апостериорному распределению скрытых переменных и параметров модели. В отличие от EM, который предоставляет точечные оценки параметров, вариационный вывод обеспечивает апостериорные распределения для параметров модели, что может быть полезно для оценки неопределенности.

Основное отличие vhmm.VariationalGaussianHMM заключается в использовании вариационного вывода для обучения. Этот байесовский подход имеет преимущества перед оценкой максимального правдоподобия в hmm.GaussianHMM, особенно в части предоставления меры неопределенности через апостериорные распределения параметров модели.

• Конструктор класса vhmm.VariationalGaussianHMM включает параметры n_components, covariance_type, algorithm, random_state, n_iter, tol, verbose, params, init_params и implementation, аналогичные параметрам hmm.GaussianHMM. 
• Ключевыми дополнительными параметрами, связанными с априорными распределениями, являются startprob_prior, transmat_prior, means_prior, beta_prior, dof_prior, scale_prior. Если эти параметры имеют значение None, используются априорные распределения по умолчанию. Параметр beta_prior связан с точностью нормального априорного распределения для средних значений. Параметры dof_prior и scale_prior определяют априорное распределение для ковариационной матрицы (обратное распределение Уишарта или обратное гамма-распределение в зависимости от covariance_type). 
• Инициализация vhmm.VariationalGaussianHMM требует указания априорных распределений для всех параметров модели. Эти априорные распределения играют важную роль в процессе обучения, особенно при ограниченном объеме данных, и позволяют включать предварительные знания или убеждения относительно параметров.

При настройке параметров vhmm.VariationalGaussianHMM для финансовых временных рядов выбор априорных распределений имеет важное значение. Априорные распределения действуют как форма регуляризации, предотвращая переобучение модели на обучающих данных. Они также позволяют включать существующие знания или убеждения относительно параметров модели.

Например, если есть основания полагать, что начальное распределение состояний (startprob_) должно быть относительно равномерным, можно использовать априорное распределение Дирихле с симметричными параметрами, близкими к 1. Аналогично, убеждения относительно вероятностей переходов (transmat_), средних значений (means_prior) или ковариаций (scale_prior,  dof_prior) могут быть закодированы через соответствующие выборы априорных распределений.

Выбор априорных распределений влияет на результирующие апостериорные распределения параметров модели после обучения на данных. Информативные априорные распределения (например, с малой дисперсией вокруг определенного значения) будут оказывать более сильное влияние, смещая апостериорное распределение в сторону априорного. Неинформативные или слабые априорные распределения (например, с большой дисперсией или равномерные распределения) будут оказывать меньшее влияние, позволяя данным доминировать в апостериорном распределении.

Сравнение эффективности моделей для финансовых временных рядов

Модель hmm.GaussianHMM является базовой моделью, которая предполагает, что наблюдаемые финансовые данные в каждом скрытом состоянии распределены по гауссовскому закону. Ее сильной стороной является простота и вычислительная эффективность, что делает ее подходящей для больших наборов данных и случаев, когда нет оснований полагать, что распределения сильно отличаются от нормального.

Однако, ее слабостью является предположение о нормальности распределений, которое может не выполняться для многих финансовых временных рядов, характеризующихся асимметрией, эксцессом и тяжелыми хвостами. В сценариях, где финансовые данные в каждом режиме относительно хорошо аппроксимируются нормальным распределением, hmm.GaussianHMM может показать хорошие результаты, например, при моделировании основных рыночных режимов на дневных или недельных данных. Она также может показать худшие результаты при моделировании высокочастотных данных или данных, подверженных резким скачкам и ненормальным распределениям.

Модель hmm.GMMHMM расширяет возможности hmm.GaussianHMM, позволяя использовать смесь гауссовских распределений для моделирования эмиссий в каждом скрытом состоянии. Ее сильной стороной является способность моделировать более сложные, мультимодальные распределения, что делает ее более подходящей для финансовых данных, которые могут демонстрировать различные подпаттерны в рамках одного рыночного режима. Например, в периоды высокой волатильности доходности могут вести себя по-разному в зависимости от направления движения рынка.

Слабой стороной hmm.GMMHMM является увеличение количества параметров, что может привести к переобучению, особенно при ограниченном объеме данных. Кроме того, обучение может быть более вычислительно затратным, по сравнению с hmm.GaussianHMM.

hmm.GMMHMM может показать лучшие результаты при моделировании финансовых временных рядов, где распределения в рамках режимов являются ненормальными или мультимодальными, например, при анализе внутридневных данных или данных о волатильности. Она может показать худшие результаты при моделировании простых режимов с приблизительно нормальным распределением или при очень малых объемах данных, когда риск переобучения высок.

Модель vhmm.VariationalGaussianHMM использует вариационный вывод для обучения, что является байесовским подходом. Ее сильной стороной является способность предоставлять апостериорные распределения параметров, что позволяет оценивать неопределенность модели. Байесовский подход также может быть полезен при ограниченном объеме данных, благодаря использованию априорных распределений, которые могут регуляризовать модель и включать предварительные знания. 

Слабой стороной vhmm.VariationalGaussianHMM является сложность настройки априорных распределений, которая может существенно повлиять на результаты. Кроме того, вариационный вывод является методом приближения, и полученное апостериорное распределение может отличаться от истинного апостериорного распределения.

vhmm.VariationalGaussianHMM может показать лучшие результаты при моделировании финансовых временных рядов, где важна оценка неопределенности параметров или когда доступно ограниченное количество данных и необходимо использовать априорные знания. Она может показать худшие результаты, если априорные распределения выбраны неудачно или если требуется очень высокая точность оценки параметров, которую может обеспечить метод максимального правдоподобия при достаточном количестве данных.

На выбор модели влияют такие факторы, как объем доступных данных, сложность динамики рынка и требования к интерпретируемости модели. При большом объеме данных и относительно простой динамике рынка, hmm.GaussianHMM может быть достаточным и предпочтительным из-за своей простоты и вычислительной эффективности. При более сложной динамике, или ненормальных распределениях, может потребоваться hmm.GMMHMM. Если важна оценка неопределенности, или доступно мало данных, следует рассмотреть vhmm.VariationalGaussianHMM.

Заключение и рекомендации

Для финансовых временных рядов потенциально лучшая или худшая модель зависит от конкретной задачи и характеристик данных.

В целом, если финансовые данные в рамках рыночных режимов могут быть разумно аппроксимированы гауссовским распределением, hmm.GaussianHMM представляет собой простой и эффективный выбор. Если распределения более сложные или мультимодальные, hmm.GMMHMM может обеспечить лучшую подгонку, но требует более тщательной настройки и может быть более склонен к переобучению. vhmm.VariationalGaussianHMM предлагает байесовский подход с возможностью оценки неопределенности, что может быть полезно в определенных сценариях, но требует понимания и правильного выбора априорных распределений.

Важно подчеркнуть, что выбор модели не может быть сделан исключительно на теоретических основаниях. Эмпирическая проверка и бэктестирование на реальных финансовых данных являются необходимыми шагами для определения того, какая модель лучше всего подходит для конкретной задачи. Различные метрики эффективности, такие как логарифмическое правдоподобие, точность прогнозирования и специфические для финансов метрики (например, MAPE, R^2), должны использоваться для сравнения производительности моделей и выбора наиболее подходящей для решения конкретной проблемы анализа финансовых временных рядов.

Способы определения априорных ковариационных матриц для временных рядов в библиотеке hmmlearn

Одним из распространенных типов HMM являются модели с гауссовскими эмиссиями, где предполагается, что наблюдаемые данные в каждом скрытом состоянии распределены по многомерному нормальному закону. Параметрами этого распределения являются вектор средних значений и ковариационная матрица, которая определяет форму, ориентацию и степень зависимости между компонентами наблюдаемых данных. 

При обучении гауссовских HMM, особенно при использовании байесовских подходов, таких как вариационный вывод, важную роль играет определение априорных ковариационных матриц. Априорные знания о структуре ковариации временного ряда могут существенно помочь в процессе обучения модели, особенно в ситуациях, когда объем доступных данных ограничен. Неправильно заданные априорные данные могут привести к неоптимальным результатам, проблемам сходимости алгоритмов обучения или к переобучению модели.

Библиотека hmmlearn в Python предоставляет классы hmm.GaussianHMM (и hmm.GMMHMM) и vhmm.VariationalGaussianHMM для работы с HMM с гауссовскими эмиссиями. Класс hmm.GaussianHMM реализует обучение модели с использованием классического алгоритма Expectation-Maximization (EM), в то время как vhmm.VariationalGaussianHMM предлагает байесовский подход на основе вариационного вывода. 

Оба класса предоставляют параметры для влияния на процесс обучения и инициализацию модели, включая возможность задания априорных распределений на ковариационные матрицы. В частности, параметр covariance_type позволяет выбирать тип ковариационной матрицы (сферическая, диагональная, полная или связанная), а параметры covars_prior и covars_weight в hmm.GaussianHMM, а также scale_prior и dof_prior в vhmm.VariationalGaussianHMM дают возможность задавать априорные распределения на ковариации. Корректное использование этих параметров требует понимания различных методов определения априорных ковариационных матриц для временных рядов.

Методы определения априорных ковариационных матриц для временных рядов

Существует несколько подходов к определению априорных ковариационных матриц для временных рядов, каждый из которых основан на различных предположениях о данных и доступной предварительной информации.

Эмпирическая оценка. Одним из наиболее прямых способов является оценка ковариационной матрицы непосредственно на основе предварительно собранных данных временного ряда. Выборочная ковариационная матрица отражает ковариацию между различными компонентами временного ряда, где каждый элемент (i, j) матрицы представляет собой выборочную ковариацию между i-м и j-м компонентами, а диагональные элементы — выборочные дисперсии. 

Для временного ряда X длиной T и размерностью p, выборочная ковариационная матрица Σ̂ может быть рассчитана по стандартной формуле. Однако, применение эмпирической оценки для временных рядов имеет свои ограничения.

Во-первых, предполагается, что временной ряд является стационарным, то есть, его статистические свойства, такие как среднее и ковариация, не меняются со временем.

Во-вторых, для получения надежной оценки, требуется достаточный объем данных по сравнению с размерностью временного ряда.

В-третьих, при малом размере выборки по сравнению с размерностью, может возникнуть проблема сингулярности ковариационной матрицы, что делает ее непригодной для использования в некоторых алгоритмах.

Несмотря на эти ограничения, эмпирическая оценка может служить разумной отправной точкой при наличии достаточного количества стационарных данных.

Методы сжатия (Shrinkage). В ситуациях, когда эмпирическая оценка ковариационной матрицы может быть ненадежной, из-за ограниченного объема данных или высокой размерности, могут быть использованы методы сжатия. Эти методы комбинируют выборочную ковариационную матрицу с некоторой целевой матрицей, используя коэффициент сжатия для определения веса каждой матрицы. 

Целевая матрица может представлять собой, например, единичную матрицу (предполагая независимость компонентов), диагональную матрицу (предполагая отсутствие корреляции между компонентами), или матрицу постоянной дисперсии. Формула линейного сжатия имеет вид Rα = (1 − α)S + αT, где S - выборочная ковариационная матрица, T - целевая матрица, а α ∈ - коэффициент сжатия. 

Методы сжатия особенно полезны при ограниченном объеме данных, так как они позволяют уменьшить ошибку оценки ковариационной матрицы, повысить ее устойчивость и предотвратить переобучение модели. Выбор целевой структуры предполагает наличие некоторой априорной информации о характере зависимостей в данных.

Использование информативных априорных распределений. Если имеется предварительное знание о предметной области или о ковариационной структуре временного ряда, это знание может быть формально включено в модель путем использования информативных априорных распределений. 

Для ковариационных матриц часто используется обратное распределение Уишарта (Inverse Wishart), которое является сопряженным априорным распределением для ковариационных матриц в многомерном нормальном распределении. Параметрами обратного распределения Уишарта являются матрица масштаба (scale matrix) и степени свободы (degrees of freedom). 

Выбор параметров априорного распределения должен отражать имеющиеся априорные убеждения о ковариационной структуре. Информативные априорные распределения могут быть сформированы на основе результатов предыдущих исследований, экспертных знаний или анализа аналогичных временных рядов. Использование таких априорных данных может значительно улучшить качество обучения модели, особенно при наличии обоснованных предварительных знаний.

Неинформативные априорные распределения. В случаях, когда отсутствуют сильные предварительные убеждения о ковариационной структуре временного ряда, могут быть использованы неинформативные априорные распределения. Целью таких априорных данных является минимизация их влияния на апостериорное распределение, позволяя данным в большей степени определять результаты обучения. 

Примером неинформативного априорного распределения для ковариационной матрицы может служить распределение Джеффриса. Для корреляционных матриц часто используется LKJ prior, которое обеспечивает равномерное распределение по пространству корреляционных матриц или позволяет задавать различные уровни концентрации вокруг нулевой корреляции. Однако, следует учитывать, что определение истинно неинформативного априора может быть сложной задачей, и даже слабоинформативные априорные данные могут оказывать влияние на результаты, особенно при ограниченном объеме данных.

Структурные предположения о временных рядах. Если временной ряд демонстрирует известные автокорреляционные свойства, эти знания могут быть использованы для формирования априорной ковариационной матрицы. Например, анализ автокорреляционной функции (ACF) и частичной автокорреляционной функции (PACF) может помочь выявить порядок авторегрессионных (AR) или скользящего среднего (MA) процессов, которые могут описывать временной ряд. 

На основе параметров этих моделей можно построить априорную ковариационную матрицу, отражающую известные временные зависимости. Например, для AR(1) процесса структура ковариационной матрицы будет зависеть от параметра автокорреляции. Этот подход предполагает, что временной ряд может быть адекватно описан некоторой моделью временных рядов, и что параметры этой модели могут быть оценены на основе предварительных данных.

Применение методов определения априорных ковариационных матриц в hmmlearn

Библиотека hmmlearn предоставляет различные возможности для определения априорных ковариационных матриц при использовании классов hmm.GaussianHMM и vhmm.VariationalGaussianHMM.

Эмпирическая оценка ковариационной матрицы, полученная на основе предварительных данных, может быть использована для прямой инициализации атрибута covars_ как в классе hmm.GaussianHMM, так и в классе vhmm.VariationalGaussianHMM. Аналогично, результаты применения методов сжатия к эмпирической ковариационной матрице могут быть использованы для инициализации covars_.

Для задания информативных априорных распределений, класс hmm.GaussianHMM предоставляет параметры covars_prior и covars_weight. Эти параметры контролируют параметры априорного распределения для ковариационной матрицы covars_. Тип априорного распределения зависит от значения параметра covariance_type. Если covariance_type установлено в "spherical" или "diag", то используется обратное гамма-распределение. Если же covariance_type установлено в "full" или "tied", то используется обратное распределение Уишарта.

Параметр covars_prior интерпретируется как параметр формы для обратного гамма-распределения и связан со степенями свободы для обратного распределения Уишарта. Параметр covars_weight является параметром масштаба для обратного гамма-распределения и связан с матрицей масштаба для обратного распределения Уишарта.

Класс vhmm.VariationalGaussianHMM также позволяет задавать информативные априорные распределения на ковариационные матрицы с помощью параметров scale_prior и dof_prior. Параметр dof_prior определяет степени свободы для распределения Уишарта (для "full" и "tied") или обратного гамма-распределения (для "spherical" и "diag"). Параметр scale_prior задает матрицу масштаба для распределения Уишарта (для "full" и "tied") или параметр масштаба для обратного гамма-распределения (для "spherical" и "diag"). Эти параметры определяют априорные убеждения о ковариационной структуре в байесовской модели, реализованной с помощью вариационного вывода.

Для задания неинформативных априорных распределений, можно использовать соответствующие параметры covars_prior, covars_weight, scale_prior и dof_prior, устанавливая их значения таким образом, чтобы априорное распределение было слабым или диффузным. Например, можно задать очень малые значения для параметров, связанных с точностью или обратным масштабом, или очень большие значения для параметров, связанных с масштабом.

Наконец, структурные предположения о временных рядах могут быть учтены путем построения соответствующей ковариационной матрицы на основе анализа автокорреляций и использования этой матрицы для инициализации атрибута covars_ в обоих классах hmmlearn.

Определение рыночных режимов с помощью HMM: переходим к практике

Перед прочтением данного раздела, я рекомендую ознакомиться с двумя предыдущими статьями:

• Машинное обучение в однонаправленной трендовой торговле на примере золота

• Торговля по алгоритму: ИИ и его путь к золотым вершинам

В этих статьях описан основной принцип построения торговых систем, который будет использоваться. Но вместо причинно-следственного вывода или кластеризации рыночных режимов, будут использоваться скрытые марковские модели для определения рыночных режимов. Так вы сможете протестировать и сравнить эти подходы между собой и составить свое мнение относительно их эффективности.

Перед началом работы убедитесь, что установлены необходимые пакеты:

import math
import pandas as pd
from datetime import datetime
from catboost import CatBoostClassifier

from sklearn.model_selection import train_test_split
from sklearn.cluster import KMeans
from hmmlearn import hmm, vhmm

from bots.botlibs.labeling_lib import *
from bots.botlibs.tester_lib import tester_one_direction
from bots.botlibs.export_lib import export_model_to_ONNX

Алгоритм будет определять рыночные режимы посредством обучения скрытых марковских моделей по тому же принципу, как это было описано в статьях про кластеризацию рыночных режимов. Поэтому изменения в коде будут касаться только самого процесса определения рыночных режимов.

Ниже представлена функция, которая определяет рыночные режимы:

def markov_regime_switching(dataset, n_regimes: int, model_type="GMMHMM") -> pd.DataFrame:
    data = dataset[(dataset.index < hyper_params['forward']) & (dataset.index > hyper_params['backward'])].copy()
    
    # Extract meta features
    meta_X = data.loc[:, data.columns.str.contains('meta_feature')]
    
    if meta_X.shape[1] > 0:
        # Format data for HMM (requires 2D array)
        X = meta_X.values
        
        # Features normalization before training
        from sklearn.preprocessing import StandardScaler
        scaler = StandardScaler()
        X_scaled = scaler.fit_transform(X)
        
        # Create and train the HMM model
        if model_type == "HMM":
            model = hmm.GaussianHMM(
                n_components=n_regimes,
                covariance_type="spherical",
                n_iter=10,
            )
        elif model_type == "GMMHMM":
            model = hmm.GMMHMM(
                n_components=n_regimes,
                covariance_type="spherical",
                n_iter=10,
                n_mix=3,
            )
        elif model_type == "VARHMM":
            model = vhmm.VariationalGaussianHMM(
                n_components=n_regimes,
                covariance_type="spherical",
                n_iter=10,
            )
           
        # Fit the model
        model.fit(X_scaled)     
        # Predict the hidden states (regimes)
        hidden_states = model.predict(X_scaled)
        # Assign states to clusters
        data['clusters'] = hidden_states
        
    return data

В коде представлены 3 модели, описанные в теоретической части, которые имеют дефолтные параметры. Сначала нужно убедиться, что они вообще работают, а затем, перейти к настройке параметров. Вы можете выбрать одну из моделей при вызове функции и сразу же протестировать качество кластеризации.

Обучающий цикл остался прежним, за исключением функции определения рыночных режимов:

for i in range(1):
    data = markov_regime_switching(dataset, n_regimes=hyper_params['n_clusters'], model_type="HMM")
    sorted_clusters = data['clusters'].unique()
    sorted_clusters.sort()
    for clust in sorted_clusters:
        clustered_data = data[data['clusters'] == clust].copy()
        if len(clustered_data) < 500:
            print('too few samples: {}'.format(len(clustered_data)))
            continue
    
        clustered_data = get_labels_one_direction(clustered_data,
                                       markup=hyper_params['markup'],
                                       min=1,
                                       max=15,
                                       direction=hyper_params['direction'])
        
        print(f'Iteration: {i}, Cluster: {clust}')
        clustered_data = clustered_data.drop(['close', 'clusters'], axis=1)

        meta_data = data.copy()
        meta_data['clusters'] = meta_data['clusters'].apply(lambda x: 1 if x == clust else 0)
        models.append(fit_final_models(clustered_data, meta_data.drop(['close'], axis=1)))

Гиперпараметры обучения заданы следующим образом:

hyper_params = {
    'symbol': 'XAUUSD_H1',
    'export_path': '/drive_c/Program Files/MetaTrader 5/MQL5/Include/Trend following/',
    'model_number': 0,
    'markup': 0.2,
    'stop_loss':  10.000,
    'take_profit': 5.000,
    'periods': [i for i in range(5, 300, 30)],
    'periods_meta': [5],
    'backward': datetime(2000, 1, 1),
    'forward': datetime(2024, 1, 1),
    'full forward': datetime(2026, 1, 1),
    'direction': 'buy',
    'n_clusters': 5,
}

• Период признаков, на которых будет производиться обучение скрытых марковских моделей равен пяти.
• Направление на покупку для золота.
• Предполагаемое количество режимов равно пяти.

Все модели будут тестироваться на стандартных отклонениях в скользящем окне (волатильности) в качестве признаков:

def get_features(data: pd.DataFrame) -> pd.DataFrame:
    pFixed = data.copy()
    pFixedC = data.copy()
    count = 0

    for i in hyper_params['periods']:
        pFixed[str(count)] = pFixedC.rolling(i).std()
        count += 1
    
    for i in hyper_params['periods_meta']:
        pFixed[str(count)+'meta_feature'] = pFixedC.rolling(i).std()
        count += 1

    return pFixed.dropna()

Результаты обучения с дефолтными параметрами

• Алгоритм GaussianHMM с дефолтными параметрами продемонстрировал способность эффективно находить скрытые состояния (режимы), благодаря чему, кривая баланса на тестовых данных выглядит приемлемо.

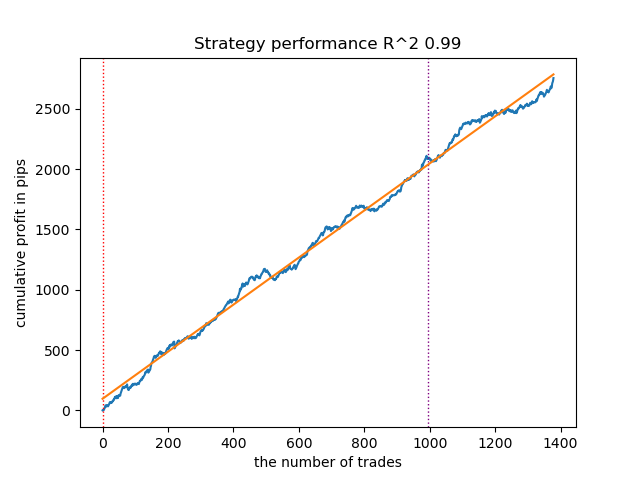
Рис 1. Тестирование GaussianHMM с дефолтными настройками

• Алгоритм GMMHMM также неплохо показал себя, заметных изменений в качестве моделей не наблюдается.

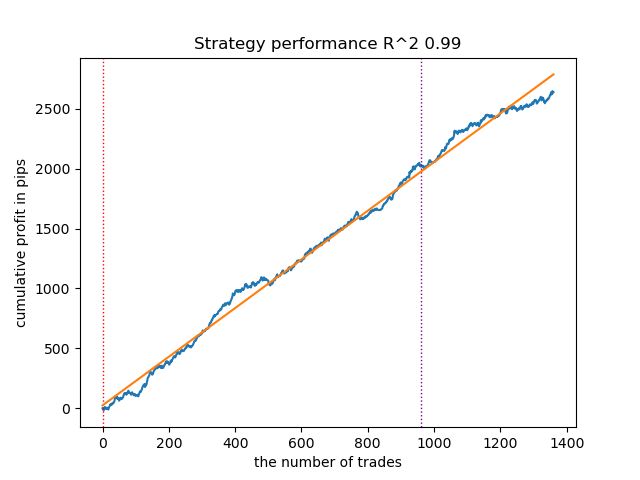
Рис 2. Тестирование GMMHMM с дефолтными настройками

• Алгоритм VariationalGaussianHMM может показаться аутсайдером, однако, после нескольких переобучений, можно добиться более красивых кривых.

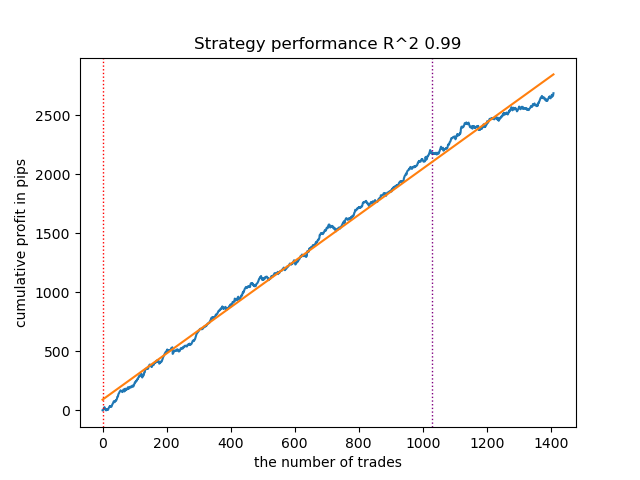
Рис 3. Тестирование VariationalGaussianHMM с дефолтными настройками

В целом, все алгоритмы доказали свою работоспособность, а это значит, что можно перейти к тюнингу их параметров.

Увеличение количества итераций запуска (n_iter = 100)

При увеличении количества итераций обучения марковских моделей, результаты на новых данных несколько улучшились для всех модификаций алгоритма. Связано это по-видимому с тем, что алгоритмы нашли более выгодные локальные оптимумы. В целом, на данном этапе, не было замечено серьезных отличий в качестве получаемых моделей для разных алгоритмов. Но GaussianHMM обучался несколько быстрее, ввиду своей простоты.

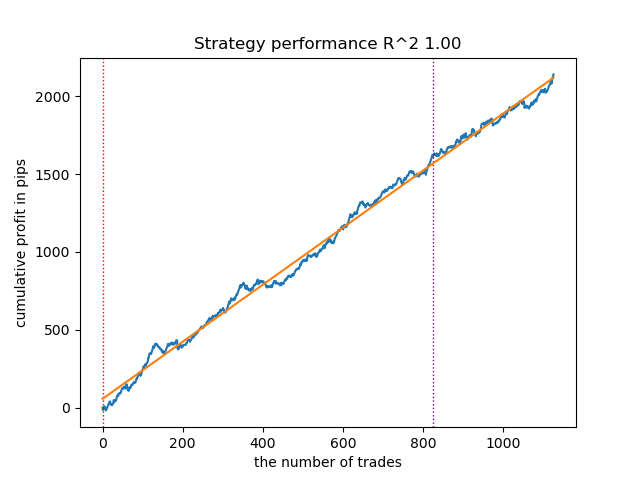
Рис 4. Тестирование GaussianHMM с n_iter = 100

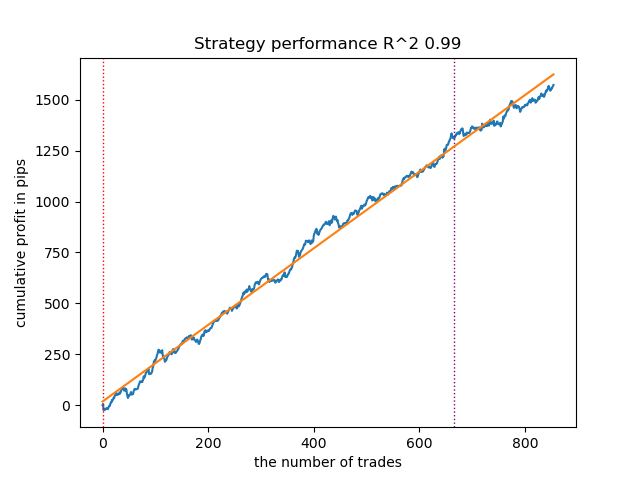
Рис 5. Тестирование GMMHMM с n_iter = 100

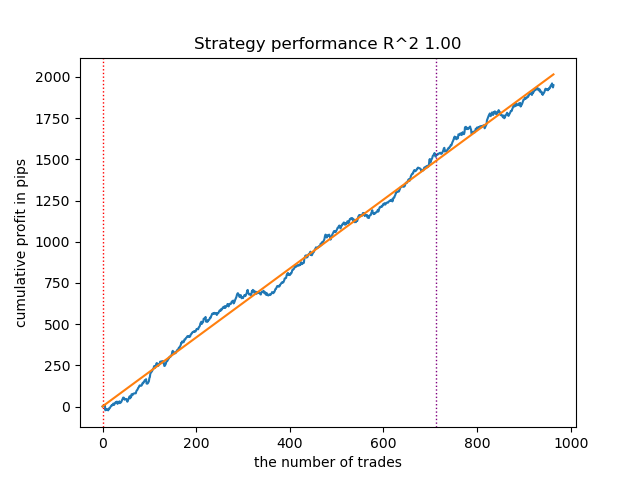
Рис 6. Тестирование VariationalGaussianHMM с n_iter = 100

Уменьшение количества рыночных режимов до трех

Количество итераций влияет на качество моделей, оставим этот параметр равным 100 итерациям. Давайте попробуем уменьшить количество режимов (скрытых состояний моделей) до трех и посмотрим на результаты.

hyper_params = {
    'symbol': 'XAUUSD_H1',
    'export_path': '/drive_c/Program Files/MetaTrader 5/MQL5/Include/Trend following/',
    'model_number': 0,
    'markup': 0.2,
    'stop_loss':  10.000,
    'take_profit': 5.000,
    'periods': [i for i in range(5, 300, 30)],
    'periods_meta': [5],
    'backward': datetime(2000, 1, 1),
    'forward': datetime(2024, 1, 1),
    'full forward': datetime(2026, 1, 1),
    'direction': 'buy',
    'n_clusters': 3,
}

GaussianHMM, GMMHMM и VariationalGaussianHMM показали отличные результаты в определении трех рыночных режимов, но для последнего потребовалось сделать несколько перезапусков обучения.

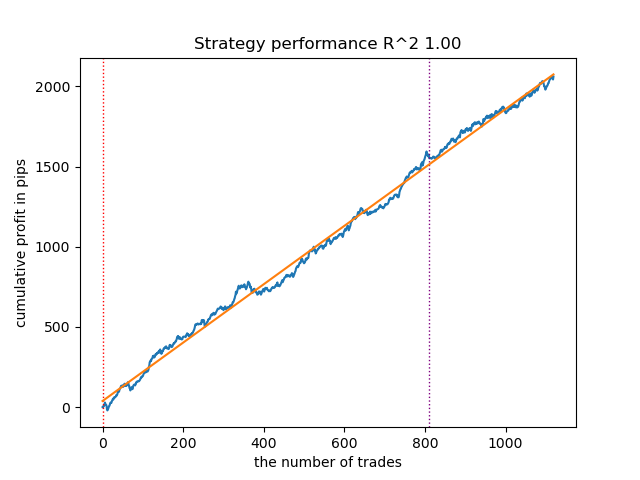
Рис 7. Тестирование VariationalHMM с n_iter = 100 и тремя режимами

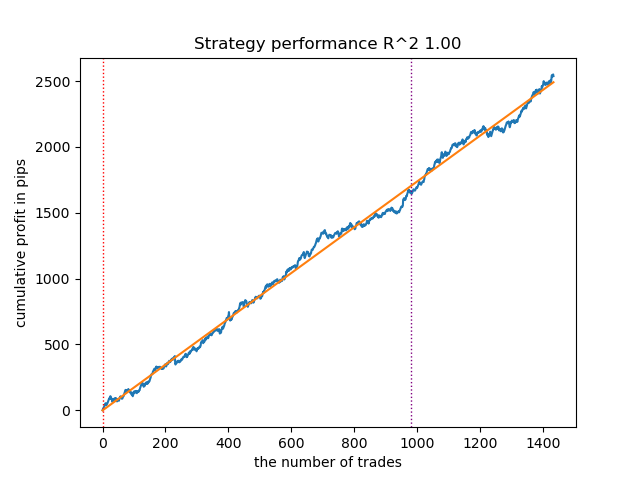
Рис 8. Тестирование GMMHMM с n_iter = 100 и тремя режимами

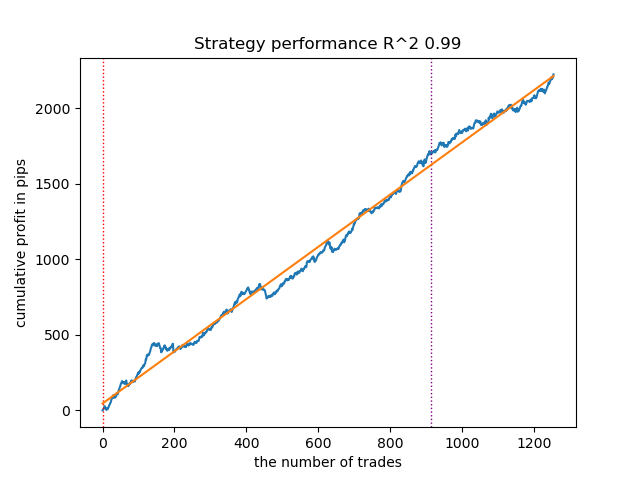
Рис 9. Тестирование VariationalGaussianHMM с n_iter = 100 и тремя режимами

Создание априорных ковариационных матриц для скрытых марковских моделей

В теоретической части статьи были рассмотрены пять методов определения априорных ковариационных матриц для временных рядов. Больше всего нам подходят первый и последний методы, давайте вспомним их:

• Эмпирическая оценка. Одним из наиболее прямых способов является оценка ковариационной матрицы непосредственно на основе предварительно собранных данных временного ряда. Выборочная ковариационная матрица отражает ковариацию между различными компонентами временного ряда, где каждый элемент (i, j) матрицы представляет собой выборочную ковариацию между i-м и j-м компонентами, а диагональные элементы - выборочные дисперсии. Для временного ряда X длиной T и размерностью p выборочная ковариационная матрица Σ̂ может быть рассчитана по стандартной формуле. Однако, применение эмпирической оценки для временных рядов имеет свои ограничения. Во-первых, предполагается, что временной ряд является стационарным, то есть его статистические свойства, такие как среднее и ковариация, не меняются со временем. Во-вторых, для получения надежной оценки требуется достаточный объем данных по сравнению с размерностью временного ряда. В-третьих, при малом размере выборки по сравнению с размерностью может возникнуть проблема сингулярности ковариационной матрицы, что делает ее непригодной для использования в некоторых алгоритмах. Несмотря на эти ограничения, эмпирическая оценка может служить разумной отправной точкой при наличии достаточного количества стационарных данных.
• Структурные предположения о временных рядах. Если временной ряд демонстрирует известные автокорреляционные свойства, эти знания могут быть использованы для формирования априорной ковариационной матрицы. Например, анализ автокорреляционной функции (ACF) и частичной автокорреляционной функции (PACF) может помочь выявить порядок авторегрессионных (AR) или скользящего среднего (MA) процессов, которые могут описывать временной ряд. На основе параметров этих моделей можно построить априорную ковариационную матрицу, отражающую известные временные зависимости. Например, для AR(1) процесса структура ковариационной матрицы будет зависеть от параметра автокорреляции. Этот подход предполагает, что временной ряд может быть адекватно описан некоторой моделью временных рядов, и что параметры этой модели могут быть оценены на основе предварительных данных.

Однако, мы не можем c уверенностью утверждать, что финансовый временной ряд может быть адекватно описан такими простыми моделями. Эксперименты показали, что такие приоры не всегда улучшают результат определения скрытых марковских состояний. Кроме этого, я провел эксперименты с предварительной кластеризацией посредством k-means для инициализации матриц перехода полученными значениями. Это привело к тому, что скрытые марковские модели начали выдавать результаты, похожие на результаты из предыдущей статьи, где происходила кластеризация рыночных режимов, немного улучшая или вообще не улучшая кривую баланса на новых данных.

Создание приоров на основе кластеризации

В обучающем скрипте представлена экспериментальная функция для предварительного расчета приоров просредтством кластеризации и последующего обучения скрытых марковских моделей.

def markov_regime_switching_prior(dataset, n_regimes: int, model_type="HMM", n_iter=100) -> pd.DataFrame:
    data = dataset[(dataset.index < hyper_params['forward']) & (dataset.index > hyper_params['backward'])].copy()
    
    # Extract meta features
    meta_X = data.loc[:, data.columns.str.contains('meta_feature')]
    
    if meta_X.shape[1] > 0:
        # Format data for HMM (requires 2D array)
        X = meta_X.values
        
        # Features normalization before training
        scaler = StandardScaler()
        X_scaled = scaler.fit_transform(X)
        
        # Calculate priors from meta_features using k-means clustering
        from sklearn.cluster import KMeans
        
        # Use k-means to cluster the data into n_regimes groups
        kmeans = KMeans(n_clusters=n_regimes, n_init=10)
        cluster_labels = kmeans.fit_predict(X_scaled)
        
        # Calculate cluster-specific means and covariances to use as priors
        prior_means = kmeans.cluster_centers_  # Shape: (n_regimes, n_features)
        
        # Calculate empirical covariance for each cluster
        from sklearn.covariance import empirical_covariance
        prior_covs = []
        
        for i in range(n_regimes):
            cluster_data = X_scaled[cluster_labels == i]
            if len(cluster_data) > 1:  # Need at least 2 points for covariance
                cluster_cov = empirical_covariance(cluster_data)
                prior_covs.append(cluster_cov)
            else:
                # Fallback to overall covariance if cluster is too small
                prior_covs.append(empirical_covariance(X_scaled))
        
        prior_covs = np.array(prior_covs)  # Shape: (n_regimes, n_features, n_features)
        
        # Calculate initial state distribution from cluster proportions
        initial_probs = np.bincount(cluster_labels, minlength=n_regimes) / len(cluster_labels)
        
        # Calculate transition matrix based on cluster sequences
        trans_mat = np.zeros((n_regimes, n_regimes))
        for t in range(1, len(cluster_labels)):
            trans_mat[cluster_labels[t-1], cluster_labels[t]] += 1
            
        # Normalize rows to get probabilities
        row_sums = trans_mat.sum(axis=1, keepdims=True)
        # Avoid division by zero
        row_sums[row_sums == 0] = 1
        trans_mat = trans_mat / row_sums
    
        # Initialize model parameters based on model type
        if model_type == "HMM":
            model_params = {
                'n_components': n_regimes,
                'covariance_type': "full",
                'n_iter': n_iter,
                'init_params': ''  # Don't use default initialization
            }
            
            from hmmlearn import hmm
            model = hmm.GaussianHMM(**model_params)
            
            # Set the model parameters directly with our k-means derived priors
            model.startprob_ = initial_probs
            model.transmat_ = trans_mat
            model.means_ = prior_means
            model.covars_ = prior_covs
            
                
        # Fit the model
        model.fit(X_scaled)
        
        # Predict the hidden states (regimes)
        hidden_states = model.predict(X_scaled)
        
        # Assign states to clusters
        data['clusters'] = hidden_states    
        return data
    
    return data

Подготовка априорных распределений, на примере модели GaussianHMM, выглядит следующим образом:

• Нормализация данных. Мета-признаки масштабируются с помощью StandardScaler для устранения влияния масштаба на результаты кластеризации.
• Кластеризация K-means. Определяет начальные параметры для скрытых состояний (режимов). Данные кластеризуются на n_regimes кластеров. Полученные метки кластеров cluster_labels используются для расчета средних значений prior_means (центры кластеров) и ковариационных матриц proir_covs - эмпирическая ковариация внутри кластеров или общая ковариация, если кластер слишком мал.
• Расчет начальных вероятностей. Начальное распределение initial_probs: доля точек в каждом кластере. Например, если 30% данных принадлежит кластеру 0, то initial_probs[0] = 0.3. 
• Матрица переходов. Подсчитывается, как часто один кластер следует за другим по времени. 
• Затем, этими приорами инициализируется скрытая мартовская модель и обучается.

Остальные методы дают еще более слабые предположения о зависимостях, поэтому вовсе не рассматривались. Вероятно, это не полный список возможных методов определения приоров. Другие методы могут быть использованы, но должны быть основаны на экспертных оценках.

Тестирование скрытых марковских моделей с априорными распределениями

Было замечено, что разброс результатов уменьшился. Модели стали меньше застревать в локальных минимумах, но их разнообразие снизилось. Также для определения рыночных режимов посредством скрытых марковских моделей обычно требуется меньшее количество режимов (кластеров), в отличие от k-means.

Результаты тестирования трех моделей с заданными приорами приведены ниже:

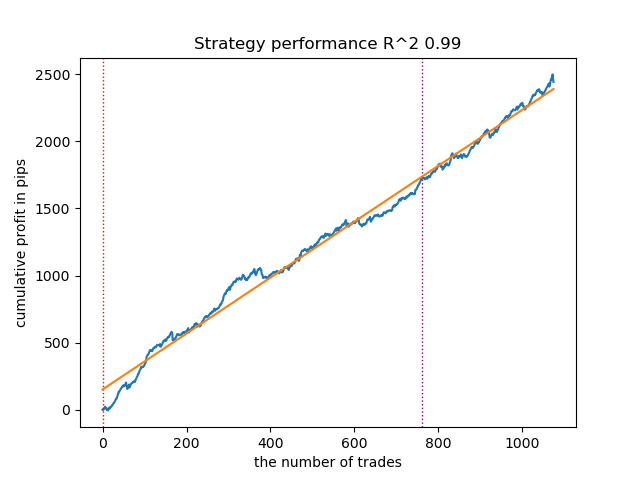
Рис 10. Тестирование GaussianHMM с априорными распределениями

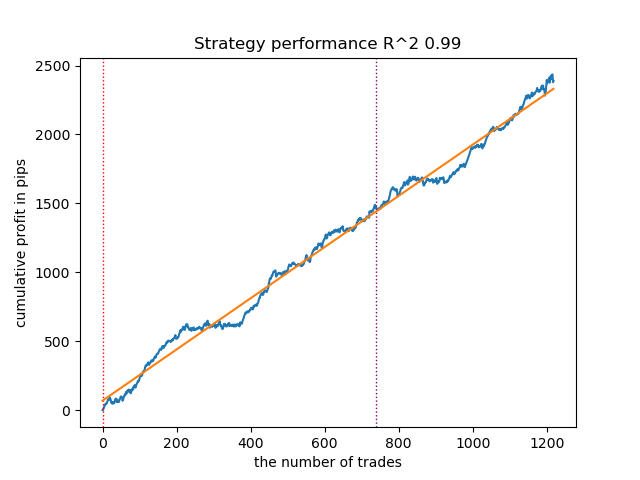
Рис 11. Тестирование GMMHMM с априорными распределениями

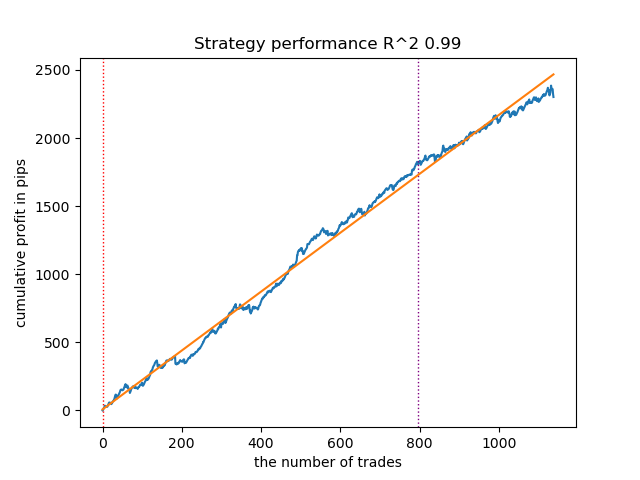
Рис 12. Тестирование VariationalGaussianHMM с априорными распределениями

Экспорт моделей и компиляция бота для платформы Meta Trader 5

Экспорт моделей происходит точно таким же способом, который был предложен в предыдущих статьях. Модуль с экспортом приложен в прикрепленном архиве.

Предположим, что мы выбрали модель, используя кастомный тестер стратегий.

# TESTING & EXPORT
models.sort(key=lambda x: x[0])
test_model_one_direction(models[-1][1:],
                        hyper_params['stop_loss'],
                        hyper_params['take_profit'],
                        hyper_params['forward'],
                        hyper_params['backward'],
                        hyper_params['markup'],
                        hyper_params['direction'],
                        plt=True)

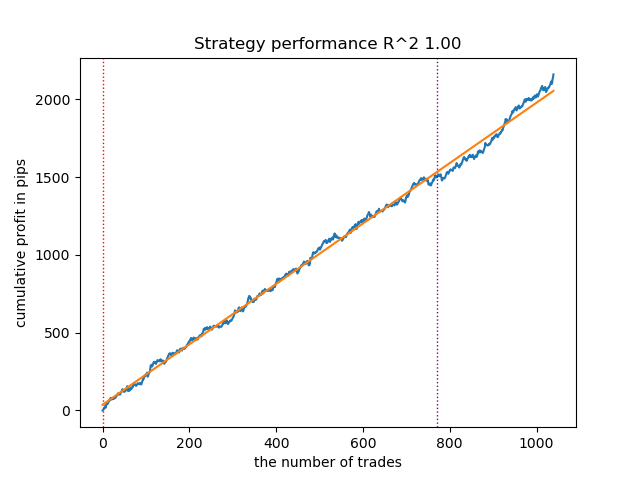
Рис 13. Тестирование лучшей модели с помощью кастомного тестера стратегий

Теперь необходимо вызвать функцию экспорта, которая сохранит модели в папку терминала.

export_model_to_ONNX(model = models[-1],
                     symbol = hyper_params['symbol'],
                     periods = hyper_params['periods'],
                     periods_meta = hyper_params['periods_meta'],
                     model_number = hyper_params['model_number'],
                     export_path = hyper_params['export_path'])

Затем, следует скомпилировать приложенного в конце статьи бота и протестировать его в тестере MetaTrader 5.

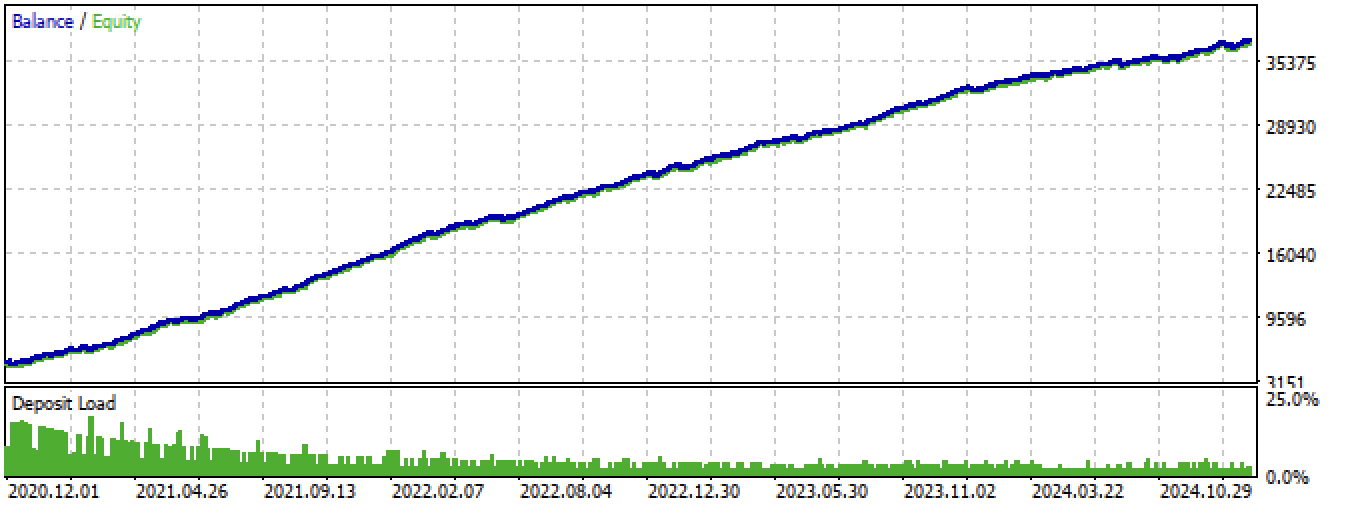
Рис 14. тестирование лучшей модели в терминале Meta Trader 5 за весь период

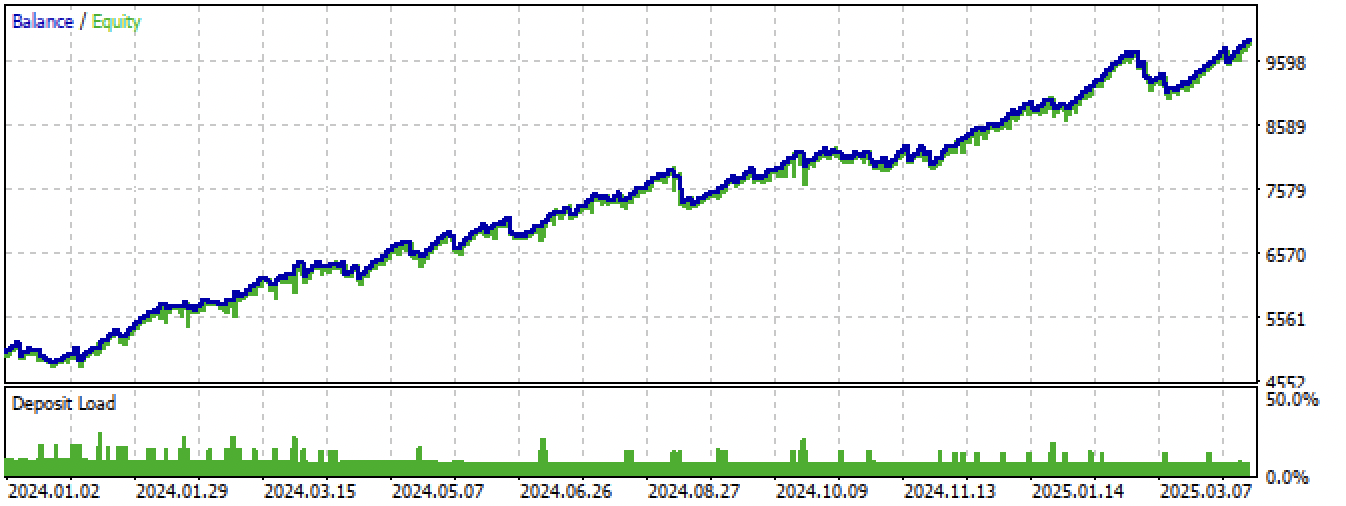
Рис 15. Тестирование лучшей модели в терминале Meta Trader 5 на новых данных

Заключение

Скрытые марковские модели — это интересный метод определения рыночных режимов. Но как и все модели машинного обучения, они склонны к переобучению на нестационарных временных рядах.

Качественное задание априорных матриц позволяет находить более устойчивые рыночные режимы, которые продолжают работать на новых данных. Обычно требуется меньшее рыночных режимов, чем это было в случае кластеризации. Если, в первом случае, понадобилось 10 кластеров, то во втором, бывает достаточно задать 3-5 скрытых состояния.

Я не обнаружил большой разницы в работе трех алгоритмов, все они показывают примерно одинаковые результаты. Поэтому можно использовать GaussianHMM, как наиболее простой и быстрый. GMMHMM, теоретически, позволяет получать более гладкие кривые баланса из-за наличия смеси распределений, что помогает находить подпаттерны в каждом рыночном режиме, но может из-за этого сильнее переобучаться. Для VariationalGaussianHMM требуется более вдумчивое задание приоров, в то же время, параметры этой модели сложнее задавать и интерпретировать.

Еще одним полезным подходом может являться кросс-валидация моделей через оценку параметров распределений режимов на разных фолдах, но такой подход в данной статье не рассматривался.

Архив Python files.zip содержит следующие файлы для разработки в среде Python:

Имя файла	Описание
one direction HMM.py	Основной скрипт для обучения моделей
labeling_lib.py	Обновленный модуль с разметчиками сделок
tester_lib.py	Обновленный кастомный тестер стратегий, основанных на машинном обучении
export_lib.py	Модуль для экспорта моделей в терминал
XAUUSD_H1.csv	Файл с котировками, экспортированный из терминала MetaTrader 5

Архив MQL5 files.zip cодержит файлы для терминала MetaTrader 5:

Имя файла	Описание
one direction HMM.ex5	Скомпилированный бот из данной статьи
one direction HMM.mq5	Исходник бота из статьи
папка Include//Trend following	Расположены модели ONNX и заголовочный файл для подключения к боту