Gradient Boosting beim transduktiven und aktiven maschinellen Lernen

Einführung

Semi-überwachtes oder transduktives Lernen verwendet unmarkierte Daten, die es dem Modell ermöglichen, die allgemeine Datenstruktur besser zu verstehen. Das ist ähnlich wie bei unserem Denken. Indem sich das menschliche Gehirn nur an einige wenige Bilder erinnert, ist es in der Lage, das Wissen über diese Bilder auf neue Objekte im Allgemeinen zu extrapolieren, ohne sich auf unwichtige Details zu konzentrieren. Dies führt zu weniger Überanpassung und zu einer besseren Generalisierung. 

Die Transduktion wurde von Vladimir Vapnik eingeführt, der Miterfinder der Support-Vector Machine (SVM) ist. Er glaubt, dass die Transduktion der Induktion vorzuziehen ist, da die Induktion die Lösung eines allgemeineren Problems (Ableiten einer Funktion) vor der Lösung eines spezifischeren Problems (Berechnen von Ausgaben für neue Fälle) erfordert. 

"Wenn Sie ein Problem von Interesse lösen, lösen Sie nicht ein allgemeineres Problem als Zwischenschritt. Versuchen Sie, die Antwort zu bekommen, die Sie wirklich brauchen, aber nicht eine allgemeinere." 

Diese Annahme Vapniks ähnelt der Beobachtung, die schon Bertrand Russell gemacht hatte:

"Wir werden mit größerer Annäherung an die Gewissheit zu dem Schluss kommen, dass Sokrates sterblich ist, wenn wir rein induktiv argumentieren, als wenn wir den Weg über 'alle Menschen sind sterblich' gehen und dann die Deduktion benutzen."

Es wird erwartet, dass unüberwachtes Lernen (mit unmarkierten Daten) auf lange Sicht viel wichtiger wird. Unüberwachtes Lernen ist in der Regel typisch für Menschen und Tiere: Sie entdecken die Struktur der Welt durch Beobachten, nicht durch das Erkennen der Namen der einzelnen Objekte. 

Semi-überwachtes Lernen kombiniert also beide Prozesse: überwachtes Lernen findet auf einer kleinen Menge von gelabelten Daten statt, danach extrapoliert das Modell sein Wissen auf einen großen unmarkierten Bereich. 

Die Verwendung von unmarkierten Daten impliziert eine gewisse Verbindung mit der zugrunde liegenden Datenverteilung. Mindestens eine der folgenden Annahmen muss erfüllt sein:

• Kontinuitätsannahme. Punkte, die nahe beieinander liegen, haben mit größerer Wahrscheinlichkeit die gleiche Kennzeichnung. Dies wird auch beim überwachten Lernen angenommen und führt zu einer Präferenz für geometrisch einfache Grenzen, die die Klassen trennen. Beim semi-überwachten Lernen führt die Glattheitsannahme zusätzlich zu einer Bevorzugung von Regionen mit geringer Dichte, in denen wenige Punkte nahe beieinander, aber in verschiedenen Klassen liegen.
• Cluster-Annahme. Die Daten neigen dazu, diskrete Cluster zu bilden, und es ist wahrscheinlicher, dass Punkte im selben Cluster ein Label teilen (obwohl Daten, die ein Label teilen, über mehrere Cluster verteilt sein können). Dies ist ein Spezialfall der Glattheitsannahme, die zum Lernen mit Clustering-Algorithmen führt.
  
• Mannigfaltigkeitsannahme. Die Daten liegen näherungsweise auf einer Mannigfaltigkeit von viel geringerer Dimension als der Eingaberaum. In diesem Fall kann das Lernen der Mannigfaltigkeit unter Verwendung sowohl der beschrifteten als auch der unbeschrifteten Daten den Fluch der Dimensionalität vermeiden. Dann kann das Lernen mit Abständen und Dichten fortgesetzt werden, die auf der Mannigfaltigkeit definiert sind.
  

Unter dem Link finden Sie weitere Details zum semi-überwachten Lernen.

Die Hauptmethode beim semi-überwachten Lernen ist das Pseudo-Labeling (Pseudo-Kennzeichnung), das wie folgt implementiert wird:

• Ein gewisses Maß an Nähe (z. B. euklidischer Abstand) wird verwendet, um den Rest der Daten basierend auf der gelabelten Datenregion (Pseudo-Label) zu labeln.
• Trainings-Labels werden mit Pseudo-Labels und Vorzeichen kombiniert.
• Das Modell wird auf dem gesamten Datensatz trainiert.

Den Forschern zufolge kann die Verwendung von gelabelten Daten in Kombination mit nicht gelabelten Daten die Modellgenauigkeit deutlich verbessern. Ich habe eine ähnliche Idee in meinem vorherigen Artikel verwendet, in dem ich die Schätzung der Wahrscheinlichkeitsdichte der Verteilung der gelabelten Daten und das Sampling aus dieser Verteilung verwendet habe. Aber die Verteilung der neuen Daten kann anders sein, so dass semi-überwachten Lernen einige Vorteile bieten kann, wie das Experiment in diesem Artikel zeigen wird.

Aktives Lernen ist eine gewisse logische Fortführung des semi-überwachten Lernens. Es ist ein iterativer Prozess, neue Daten so zu beschriften, dass die Grenzen zwischen den Klassen optimal gefunden werden.

Die Haupthypothese des aktiven Lernens besagt, dass der Lernalgorithmus die Daten auswählen kann, aus denen er lernen will. Er kann mit deutlich weniger Trainingsdaten bessere Leistungen erbringen als traditionelle Methoden. Traditionelle Methoden beziehen sich hier auf das konventionelle überwachte Lernen mit gelabelten Daten. Ein solches Training kann als passiv bezeichnet werden. Das Modell wird einfach auf gelabelten Daten trainiert. Je mehr Daten, desto besser. Eines der zeitaufwändigsten Probleme beim passiven Lernen ist die Datenerfassung und -beschriftung. In vielen Fällen können Einschränkungen mit der Sammlung zusätzlicher Daten oder mit deren adäquater Beschriftung verbunden sein. 

Beim aktiven Lernen gibt es drei populäre Szenarien, in denen das Lernmodell neue Klasseninstanz-Labels aus dem unbeschrifteten Bereich anfordert:

• Synthese von Zugehörigkeitsanfragen. In diesem Fall generiert das Modell eine Instanz aus einer bestimmten Verteilung, die allen Beispielen gemeinsam ist. Dies kann eine Klasseninstanz mit hinzugefügtem Rauschen sein, oder einfach ein plausibler Punkt im fraglichen Raum. Dieser neue Punkt wird zum Training an das Orakel gesendet. Orakel ist der konventionelle Name für eine Evaluatorfunktion, die den Wert einer gegebenen Merkmalsinstanz für das Modell auswertet.
• Datenstrombasiertes Sampling. Bei diesem Szenario wird jeder unbeschriftete Datenpunkt einzeln untersucht, woraufhin das Orakel entscheidet, ob es für diesen Punkt ein Klassenlabel abfragen oder ihn aufgrund eines Informationskriteriums verwerfen möchte. 
• Pool-basiertes Sampling. In diesem Szenario gibt es, wie im vorherigen Fall, einen großen Pool von unbeschrifteten Beispielen. Die Instanzen werden aus dem Pool auf Basis der Informativität ausgewählt. Die informativsten Instanzen werden aus dem Pool ausgewählt. Dies ist das beliebteste Szenario unter Fans des aktiven Lernens. Alle unbeschrifteten Instanzen werden in eine Rangfolge gebracht, und dann werden die informativsten Instanzen ausgewählt.

Jedes Szenario kann auf einer bestimmten Abfragestrategie basieren. Wie bereits erwähnt, besteht der Hauptunterschied zwischen aktivem und passivem Lernen in der Möglichkeit, Instanzen aus einer un-gelabelten Region abzufragen, basierend auf vergangenen Abfragen und Modellantworten. Daher erfordern alle Abfragen ein gewisses Maß an Informiertheit. 

Die gängigsten Abfragestrategien sind die folgenden

• Geringstes Vertrauen (oder Unsicherheit bei der Klassifizierung). Bei dieser Strategie wird die Instanz ausgewählt, für die das Modell am wenigsten sicher ist. Zum Beispiel liegt die Wahrscheinlichkeit, ein Label einer bestimmten Klasse zuzuordnen, unterhalb einer bestimmten Grenze.
• Abstabds-Sampling. Der Nachteil des ersten Ansatzes ist, dass er die Wahrscheinlichkeit der Zugehörigkeit zu nur einem Label ermittelt, während die Wahrscheinlichkeiten der Zugehörigkeit zu anderen nicht berücksichtigt werden. Das Abstands-Sampling wählt die kleinste Wahrscheinlichkeitsdifferenz zwischen den beiden wahrscheinlichsten Bezeichnungen aus.
• Entropie-basiertes Sampling. Die Entropieformel wird auf jede Instanz angewendet und die Instanz mit dem höchsten Wert wird abgefragt.

Wie beim semi-überwachtem Lernen hat auch der aktive Lernprozess mehrere Schritte:

• Das Modell wird auf gelabelten Daten trainiert.
  
• Dasselbe Modell wird zur Beschriftung von nicht beschrifteten Daten verwendet, um Wahrscheinlichkeiten (Pseudo-Labels) vorherzusagen.
• Die Strategie für die Abfrage neuer Instanzen wird gewählt.
• N Instanzen werden entsprechend der Informativität aus dem Datenpool ausgewählt und der Trainingsstichprobe hinzugefügt. 
• Dieser Zyklus wird wiederholt, bis ein Stoppkriterium erreicht ist. Ein Stoppkriterium kann die Anzahl der Iterationen oder die Schätzung des Lernfehlers sein, sowie andere externe Kriterien.

Aktives Lernen

Lassen Sie uns direkt zum aktiven Lernen übergehen und dessen Effektivität mit unseren Daten testen.

Es gibt mehrere Bibliotheken für aktives Lernen in der Sprache Python, die bekanntesten davon sind:

• modAL ist ein recht einfaches und leicht zu erlernendes Paket. Das ist eine Art Wrapper für scikit-learn, die beliebte Bibliothek für maschinelles Lernen (sie sind vollständig kompatibel). Das Paket stellt die populärsten aktiven Lernmethoden zur Verfügung.
• Libact verwendet die Strategie des mehrarmigen Banditen über bestehende Abfragestrategien für eine dynamische Auswahl der besten Abfrage. 
• Alipy ist eine Art Labor von Paketanbietern, das eine große Anzahl von Abfragestrategien enthält.

Ich habe die Bibliothek modAL ausgewählt, da sie intuitiver ist und sich für den Einstieg in die Philosophie des aktiven Lernens eignet. Sie bietet eine größere Freiheit bei der Gestaltung von Modellen und bei der Erstellung eigener Modelle durch die Verwendung von Standardblöcken oder durch die Erstellung eigener Modelle.

Betrachten wir den oben beschriebenen Prozess anhand des folgenden Schemas, das keiner weiteren Erklärungen bedarf:

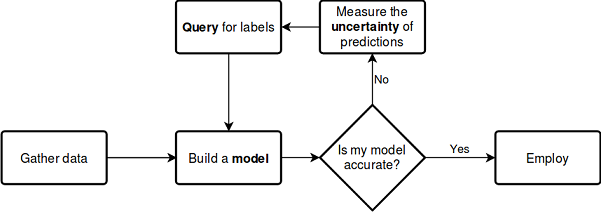
Siehe die Dokumentation

Das Tolle an der Bibliothek ist, dass Sie jeden beliebigen Scikit-Learn-Klassifikator verwenden können. Das folgende Beispiel demonstriert die Verwendung eines Random Forest als Lernmodell:

from modAL.models import ActiveLearner
from modAL.uncertainty import entropy_sampling
from sklearn.ensemble import RandomForestClassifier

learner = ActiveLearner(
    estimator=RandomForestClassifier(),
    query_strategy=entropy_sampling,
    X_training=X_training, y_training=y_training
)

Der Random Forest fungiert hier als Lernmodell und als Evaluator, der je nach Abfragestrategie (z. B. basierend auf Entropie, wie in diesem Beispiel) die Auswahl neuer Stichproben aus unbeschrifteten Daten ermöglicht. Als Nächstes wird ein Datensatz, der aus einer kleinen Menge gelabelter Daten besteht, an das Modell übergeben. Dieser wird für das vorläufige Training verwendet. 

Die Bibliothek modAL ermöglicht eine einfache Kombination von Abfragestrategien und erlaubt es, daraus zusammengesetzte gewichtete Strategien zu machen:

from modAL.utils.combination import make_linear_combination, make_product
from modAL.uncertainty import classifier_uncertainty, classifier_margin

# creating new utility measures by linear combination and product
# linear_combination will return 1.0*classifier_uncertainty + 1.0*classifier_margin
linear_combination = make_linear_combination(
    classifier_uncertainty, classifier_margin,
    weights=[1.0, 1.0]
)
# product will return (classifier_uncertainty**0.5)*(classifier_margin**0.1)
product = make_product(
    classifier_uncertainty, classifier_margin,
    exponents=[0.5, 0.1]
)

Sobald die Abfrage generiert ist, werden Instanzen, die die Abfragekriterien erfüllen, aus der unbeschrifteten Datenregion ausgewählt, wobei die Selektoren multi_argmax oder weighted_randm verwendet werden:

from modAL.utils.selection import multi_argmax

# defining the custom query strategy, which uses the linear combination of
# classifier uncertainty and classifier margin
def custom_query_strategy(classifier, X, n_instances=1):
    utility = linear_combination(classifier, X)
    query_idx = multi_argmax(utility, n_instances=n_instances)
    return query_idx, X[query_idx]

custom_query_learner = ActiveLearner(
    estimator=GaussianProcessClassifier(1.0 * RBF(1.0)),
    query_strategy=custom_query_strategy,
    X_training=X_training, y_training=y_training
)

Abfragestrategien

Es gibt drei Hauptabfragestrategien. Alle Strategien basieren auf der Klassifizierungsunsicherheit, weshalb sie auch Unsicherheitsmaß genannt wird. Schauen wir uns an, wie sie funktionieren.

Klassifizierungsunsicherheit wird in einem einfachen Fall als U(x)=1-P(x^|x) bewertet, wobei x der vorherzusagende Fall ist, während x^ die wahrscheinlichste Vorhersage ist. Wenn es z. B. drei Klassen und drei Stichprobenpositionen gibt, können die entsprechenden Unsicherheiten wie folgt berechnet werden:

[[0.1 , 0.85, 0.05],
 [0.6 , 0.3 , 0.1 ],
 [0.39, 0.61, 0.0 ]]

1 - proba.max(axis=1)

[0.15, 0.4 , 0.39]

Somit wird das zweite Beispiel als das unsicherste ausgewählt.

Klassifizierungsspanne ist die Differenz der Wahrscheinlichkeiten der ersten und zweiten wahrscheinlichsten Abfrage. Die Differenz wird nach der folgenden Formel ermittelt: M(x)=P(x1^|x)-P(x2^|x), wobei x1^ und x2^ die erste und zweitwahrscheinlichste Klasse sind.

Diese Abfragestrategie wählt Instanzen mit der kleinsten Spanne zwischen den Wahrscheinlichkeiten der beiden wahrscheinlichsten Klassen aus, denn je kleiner die Spanne der Lösung ist, desto unsicherer ist sie.

>>> import numpy as np
>>> proba = np.array([[0.1 , 0.85, 0.05],
...                   [0.6 , 0.3 , 0.1 ],
...                   [0.39, 0.61, 0.0 ]])
>>>
>>> proba
array([[0.1 , 0.85, 0.05],
       [0.6 , 0.3 , 0.1 ],
       [0.39, 0.61, 0.  ]])
>>> part = np.partition(-proba, 1, axis=1)
>>> part
array([[-0.85, -0.1 , -0.05],
       [-0.6 , -0.3 , -0.1 ],
       [-0.61, -0.39, -0.  ]])
>>> part[:, 0]
array([-0.85, -0.6 , -0.61])
>>> part[:, 1]
array([-0.1 , -0.3 , -0.39])
>>> margin = - part[:, 0] + part[:, 1]
>>> margin
array([0.75, 0.3 , 0.22])

In diesem Fall wird das dritte Ergebnis (die dritte Zeile des Arrays) ausgewählt, da die Wahrscheinlichkeitsspanne für diese Instanz minimal ist.

Die Klassifikationsentropie wird mit der Informationsentropie-Formel berechnet: H(x)=-∑kpklog(pk), wobei pk die Wahrscheinlichkeit ist, dass das Ergebnis zur k-ten Klasse gehört. Je näher die Verteilung an der Gleichverteilung ist, desto größer ist die Entropie. In unserem Beispiel ergibt sich die maximale Entropie für das 2 Beispiel.

[0.51818621, 0.89794572, 0.66874809]

Es sieht nicht sehr schwierig aus. Diese Beschreibung scheint ausreichend zu sein, um die drei wichtigsten Abfragestrategien zu verstehen. Für weitere Details studieren Sie bitte die Dokumentation des Pakets, denn ich gebe nur die grundlegenden Punkte wieder.

Die Strategien der Abfrage mit Batch-Jobs

Ein Element nach dem anderen abzufragen und das Modell neu zu trainieren ist nicht immer effizient. Eine effizientere Lösung ist es, mehrere Instanzen aus den unmarkierten Daten auf einmal zu markieren und auszuwählen. Hierfür gibt es eine Reihe von Abfragen. Die verbreitetste davon ist das Ranked Set Sampling, das auf einer Ähnlichkeitsfunktion wie der Cosinus-Distanz basiert. Diese Methode schätzt, wie gut der Merkmalsraum in der Nähe von x (unbeschriftete Instanz) erforscht ist. Nach der Auswertung wird die Instanz mit dem höchsten Rang zum Trainingsset hinzugefügt und aus dem Pool der unbeschrifteten Daten entfernt. Danach wird der Rang neu berechnet und die beste Instanz wird erneut hinzugefügt, bis die Anzahl der Instanzen die angegebene Größe (Batch-Größe) erreicht. 

Abfragen der Informationsdichte

Die oben beschriebenen einfachen Abfragestrategien werten die Datenstruktur nicht aus. Dies kann zu suboptimalen Abfragen führen. Um das Sampling zu verbessern, können Sie Informationsdichtemaße verwenden, die bei der korrekten Auswahl der Elemente der unbeschrifteten Daten helfen. Dabei wird die Kosinus- oder Euklidische Distanz verwendet. Je höher die Informationsdichte ist, desto ähnlicher ist diese ausgewählte Instanz allen anderen. 

Abfragen der Klassifizierungsjury

Dieser Abfragetyp beseitigt einige der Nachteile der einfachen Abfragetypen. Zum Beispiel neigt die Auswahl der Elemente dazu, aufgrund der Eigenschaften eines bestimmten Klassifizierers verzerrt zu sein. Einige wichtige Stichprobenelemente können fehlen. Dieser Effekt wird eliminiert, indem mehrere Hypothesen gleichzeitig gespeichert werden und Abfragen ausgewählt werden, zwischen denen Unstimmigkeiten bestehen. Auf diese Weise lernt die Jury von Klassifikatoren jeweils auf seiner eigenen Kopie der Stichprobe, und dann werden die Ergebnisse gewichtet. Andere Arten des Jury-Lernens von Klassifikatoren sind Bagging und Bootstrapping.

Diese kurze Beschreibung deckt die Funktionen der Bibliothek fast vollständig ab. Für weitere Details können Sie die Dokumentation zu Rate ziehen.

Aktives Lernen

Ich habe sowohl die Strategie mit Batch-Abfragen als auch die Abfragen Klassifikationsjury ausgewählt und eine Reihe von Experimenten durchgeführt. Die Batch-Abfragestrategie zeigte bei neuen Daten keine gute Leistung, aber indem ich den von ihr erzeugten Datensatz an GMM übermittelte, erhielt ich interessante Ergebnisse. 

Betrachten wir ein Beispiel für die Implementierung einer Batch-Active-Learning-Funktion:

def active_learner(data, labeled_size, unlabeled_size, batch_size, max_depth):
    X_raw = data[data.columns[1:-1]].to_numpy()
    y_raw = data[data.columns[-1]].to_numpy()

    # Isolate our examples for our labeled dataset.
    training_indices = np.random.randint(low=0, high=X_raw.shape[0] + 1, size=labeled_size)

    X_train = X_raw[training_indices]
    y_train = y_raw[training_indices]

    # fit the model on all data
    cl = AdaBoostClassifier(DecisionTreeClassifier(max_depth=max_depth), n_estimators=50, learning_rate = 0.01)
    cl.fit(X_raw, y_raw)
    print('Score for the passive learning: ', cl.score(X_raw, y_raw), ' with train size: ', data.shape[0])

    # Isolate the non-training examples we'll be querying.
    X_pool = np.delete(X_raw, training_indices, axis=0)
    y_pool = np.delete(y_raw, training_indices, axis=0)

    # Pre-set our batch sampling to retrieve 3 samples at a time.
    preset_batch = partial(uncertainty_batch_sampling, n_instances=batch_size)

    # Specify our core estimator along with its active learning model.
    cl = AdaBoostClassifier(DecisionTreeClassifier(max_depth=3), n_estimators=50, learning_rate = 0.03)
    learner = ActiveLearner(estimator=cl, query_strategy=preset_batch, X_training=X_train, y_training=y_train)

Die Funktion erhält folgende Eingaben: einen gelabelten Datensatz, die Anzahl der gelabelten Instanzen, die Anzahl der nicht gelabelten Instanzen, die Batchgröße für die Batch-Label-Abfrage und die maximale Baumtiefe.

Aus dem gelabelten Datensatz wird eine bestimmte Anzahl von gelabelten Instanzen zufällig für das Vortraining des Modells ausgewählt. Der Rest des Datensatzes bildet einen Pool, aus dem die Instanzen abgefragt werden. Als Basisklassifikator habe ich AdaBoost verwendet, der ähnlich wie CatBoost arbeitet. Danach wird das Modell iterativ trainiert:

    # Allow our model to query our unlabeled dataset for the most
    # informative points according to our query strategy (uncertainty sampling).
    N_QUERIES = unlabeled_size // batch_size

    for index in range(N_QUERIES):
        query_index, query_instance = learner.query(X_pool)

        # Teach our ActiveLearner model the record it has requested.
        X, y = X_pool[query_index], y_pool[query_index]
        learner.teach(X=X, y=y)

        # Remove the queried instance from the unlabeled pool.
        X_pool, y_pool = np.delete(
            X_pool, query_index, axis=0), np.delete(y_pool, query_index)

        # Calculate and report our model's accuracy.
        model_accuracy = learner.score(X_raw, y_raw)
        print('Accuracy after query {n}: {acc:0.4f}'.format(
            n=index + 1, acc=model_accuracy))

        # Save our model's performance for plotting.
        performance_history.append(model_accuracy)

    print('Score for the active learning with train size: ',
          learner.X_training.shape)     

Da alles Mögliche als Ergebnis eines solchen semi-überwachten Lernens auftreten kann, kann das Ergebnis beliebig sein. Nach einigen Manipulationen mit den Einstellungen des Lerners erhielt ich jedoch Ergebnisse, die mit denen aus dem vorherigen Artikel vergleichbar sind. 

Im Idealfall sollte die Klassifizierungsgenauigkeit eines aktiven Lerners bei einer kleinen Menge an gelabelten Daten die Genauigkeit eines ähnlichen Klassifizierers mit allen gelabelten Daten übertreffen.

>>> learned = active_learner(pr, 1000, 1000, 50)
Score for the passive learning:  0.5991245668429692  with train size:  5483
Accuracy after query 1: 0.5710
Accuracy after query 2: 0.5836
Accuracy after query 3: 0.5749
Accuracy after query 4: 0.5847
Accuracy after query 5: 0.5829
Accuracy after query 6: 0.5823
Accuracy after query 7: 0.5650
Accuracy after query 8: 0.5667
Accuracy after query 9: 0.5854
Accuracy after query 10: 0.5836
Accuracy after query 11: 0.5807
Accuracy after query 12: 0.5907
Accuracy after query 13: 0.5944
Accuracy after query 14: 0.5865
Accuracy after query 15: 0.5949
Accuracy after query 16: 0.5873
Accuracy after query 17: 0.5833
Accuracy after query 18: 0.5862
Accuracy after query 19: 0.5902
Accuracy after query 20: 0.6002
Score for the active learning with train size:  (2000, 8)

Dem Bericht zufolge hat der Klassifikator, der auf allen gelabelten Daten trainiert wurde, eine geringere Genauigkeit als der aktive Lerner, der nur mit 2000 Instanzen trainiert wurde. Dies ist wahrscheinlich gut. 

Nun kann diese Probe an das GMM-Modell gesendet werden, wonach der Klassifikator CatBoost trainiert werden kann.

# prepare data for CatBoost
catboost_df = pd.DataFrame(learned.X_training)
catboost_df['labels'] = learned.y_training

# perform GMM clusterization over dataset
X = catboost_df.copy()
gmm = mixture.GaussianMixture(
    n_components=75, max_iter=500, covariance_type='full', n_init=1).fit(X)

# sample new dataset
generated = gmm.sample(10000)
# make labels
gen = pd.DataFrame(generated[0])
gen.rename(columns={gen.columns[-1]: "labels"}, inplace=True)
gen.loc[gen['labels'] >= 0.5, 'labels'] = 1
gen.loc[gen['labels'] < 0.5, 'labels'] = 0
X = gen[gen.columns[:-1]]
y = gen[gen.columns[-1]]
pr = pd.DataFrame(X)
pr['labels'] = y

# fit CatBoost model and test it
model = fit_model(pr)
test_model(model, TEST_START, END_DATE)

Dieser Vorgang kann mehrmals wiederholt werden, da in jeder Phase der Datenverarbeitung ein Element der Unsicherheit vorhanden ist, das keine eindeutigen Modelle ermöglicht. Die folgenden Charts wurden im Tester nach allen Iterationen erhalten (Trainingsperiode von 1 Jahr gefolgt von einer 5-jährigen Testperiode):

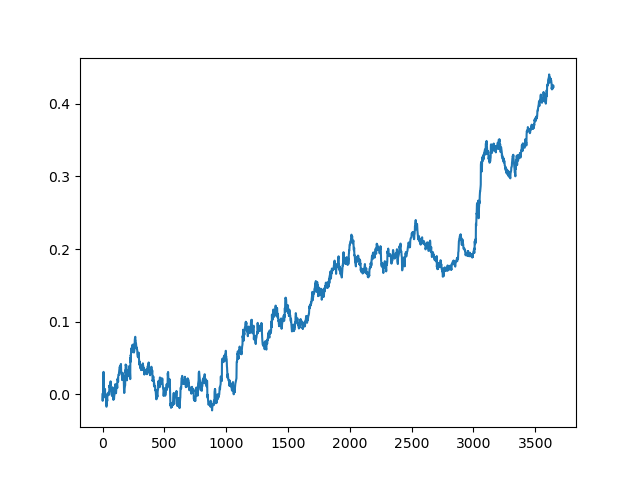
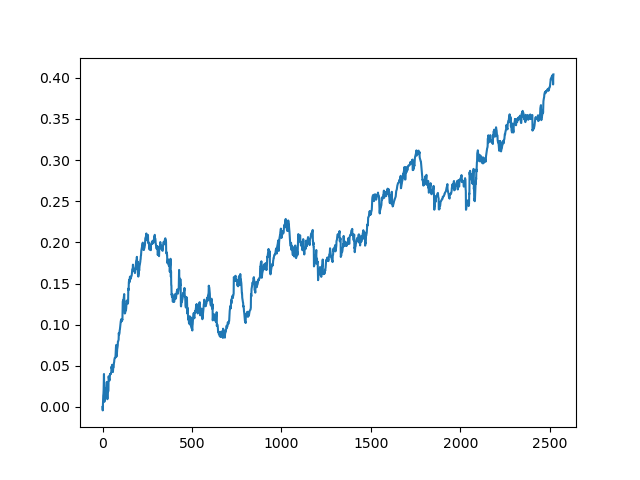
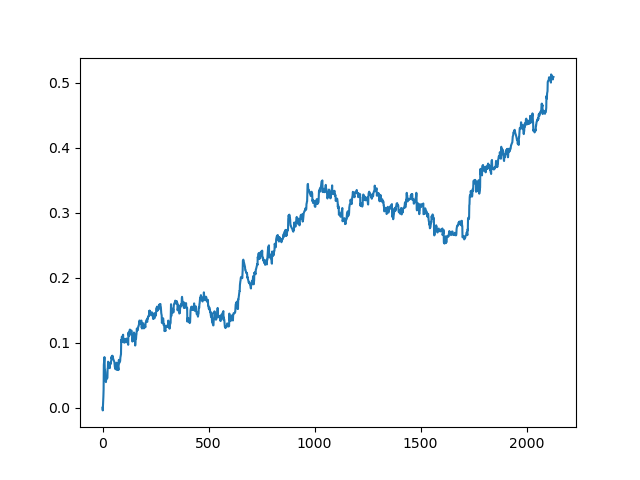
Natürlich sind diese Ergebnisse kein Benchmark, sie zeigen nur, dass profitable (auf neuen Daten) Modelle erhalten werden können. 

Lassen Sie uns nun die Lernfunktion auf dem Klassifizierer-Komitee implementieren und sehen, was passiert:

def active_learner_committee(data, learners_number, labeled_size, unlabeled_size, batch_size):
    X_pool = data[data.columns[1:-1]].to_numpy()
    y_pool = data[data.columns[-1]].to_numpy()

    cl = AdaBoostClassifier(DecisionTreeClassifier(max_depth=3), n_estimators=50, learning_rate = 0.05)
    cl.fit(X_pool, y_pool)
    print('Score for the passive learning: ', cl.score(
        X_pool, y_pool), ' with train size: ', data.shape[0])

    # initializing Committee members
    learner_list = list()

    # Pre-set our batch sampling to retrieve 3 samples at a time.
    preset_batch = partial(uncertainty_batch_sampling, n_instances=batch_size)
    
    for member_idx in range(learners_number):
        # initial training data
        train_idx = np.random.choice(range(X_pool.shape[0]), size=labeled_size, replace=False)
        X_train = X_pool[train_idx]
        y_train = y_pool[train_idx]

        # creating a reduced copy of the data with the known instances removed
        X_pool = np.delete(X_pool, train_idx, axis=0)
        y_pool = np.delete(y_pool, train_idx)

        # initializing learner
        learner = ActiveLearner(
            estimator=AdaBoostClassifier(DecisionTreeClassifier(max_depth=2), n_estimators=50, learning_rate = 0.05),
            query_strategy=preset_batch,
            X_training=X_train, y_training=y_train
        )
        learner_list.append(learner)

    # assembling the committee
    committee = Committee(learner_list=learner_list)

    unqueried_score = committee.score(X_pool, y_pool)
    performance_history = [unqueried_score]

    N_QUERIES = unlabeled_size // batch_size

    for idx in range(N_QUERIES):
        query_idx, query_instance = committee.query(X_pool)
        committee.teach(
            X=X_pool[query_idx].reshape(1, -1),
            y=y_pool[query_idx].reshape(1, )
        )
        model_accuracy = committee.score(X_pool, y_pool)
        performance_history.append(model_accuracy)
        print('Accuracy after query {n}: {acc:0.4f}'.format(
            n=idx + 1, acc=model_accuracy))

        # remove queried instance from pool
        X_pool = np.delete(X_pool, query_idx, axis=0)
        y_pool = np.delete(y_pool, query_idx)

    return committee

Auch hier habe ich die Strategie der Batch-Abfrage gewählt, damit das Modell nicht jedes Mal neu trainiert werden muss, wenn ein Element hinzugefügt wird. Für den Rest habe ich eine Art Bewertungskomitee aus einer beliebigen Anzahl von AdaBoost-Klassifikatoren erstellt (ich denke, es macht keinen Sinn, mehr als fünf Klassifikatoren hinzuzufügen, aber Sie können experimentieren). 

Unten ist ein Trainingsergebnis für ein Komitee von fünf Modellen mit den gleichen Einstellungen, die für die vorherige Methode verwendet wurden:

>>> committee = active_learner_committee(pr, 5, 1000, 1000, 50)
Score for the passive learning:  0.6533842794759825  with train size:  5496
Accuracy after query 1: 0.5927
Accuracy after query 2: 0.5818
Accuracy after query 3: 0.5668
Accuracy after query 4: 0.5862
Accuracy after query 5: 0.5874
Accuracy after query 6: 0.5906
Accuracy after query 7: 0.5918
Accuracy after query 8: 0.5910
Accuracy after query 9: 0.5820
Accuracy after query 10: 0.5934
Accuracy after query 11: 0.5864
Accuracy after query 12: 0.5753
Accuracy after query 13: 0.5868
Accuracy after query 14: 0.5921
Accuracy after query 15: 0.5809
Accuracy after query 16: 0.5842
Accuracy after query 17: 0.5833
Accuracy after query 18: 0.5783
Accuracy after query 19: 0.5732
Accuracy after query 20: 0.5828

Die Ergebnisse des Komitees der aktiven Lerner sind nicht so gut wie die eines passiven Lerners. Es ist unmöglich, die Gründe dafür zu erraten. Vielleicht ist dies nur ein Zufallsergebnis. Dann habe ich den resultierenden Datensatz mehrmals nach demselben Prinzip durchlaufen lassen und erhielt die folgenden Zufallsergebnisse:

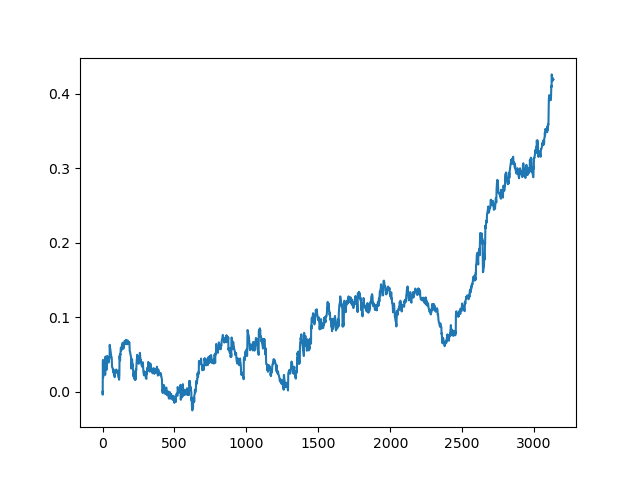
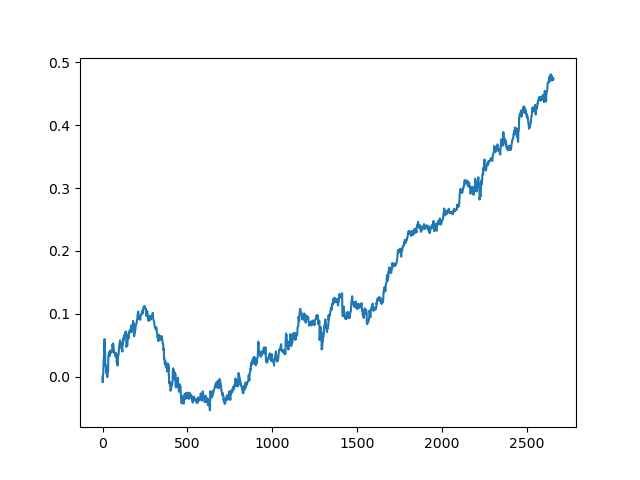
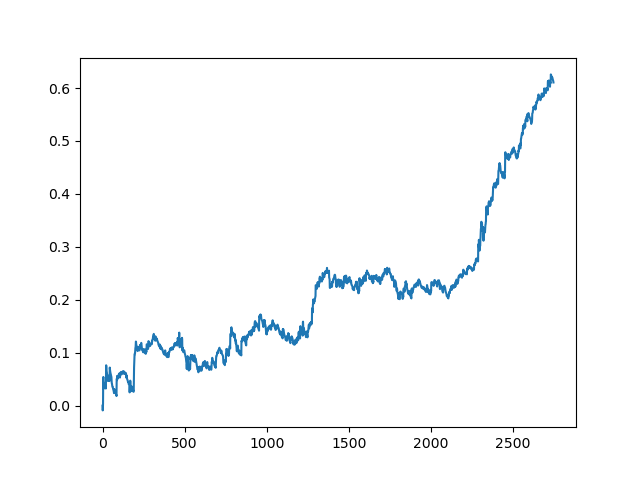
Schlussfolgerungen

In diesem Artikel haben wir aktives Lernen betrachtet. Der Eindruck ist unklar. Einerseits ist es immer verlockend, aus einer kleinen Anzahl von Instanzen zu lernen, und diese Modelle funktionieren bei einigen Klassifizierungsproblemen auch gut. Allerdings ist dies noch weit von künstlicher Intelligenz entfernt. Ein solches Modell kann keine stabilen Muster unter Mülldaten finden, und es erfordert eine gründlichere Aufbereitung von Merkmalen und Beschriftungen, einschließlich einer Datenaufbereitung auf Basis von Expertenbeschriftungen. Ich habe keine signifikante Steigerung der Qualität der Modelle gesehen. Gleichzeitig ist der Arbeits- und Zeitaufwand für das Training der Modelle gestiegen, was ein negativer Faktor ist. Mir gefällt die Philosophie des aktiven Lernens und die Ausnutzung der Eigenschaften des menschlichen Denkens. Die angehängte Datei enthält alle besprochenen Funktionen. Sie können diese Modelle weiter erforschen und versuchen, sie auf eine andere originelle Weise anzuwenden.