Redes neurais em trading: Framework híbrido de negociação com codificação preditiva (StockFormer)

Introdução

O aprendizado por reforço (Reinforcement Learning, RL) está sendo cada vez mais usado para resolver tarefas complexas na área financeira, incluindo o desenvolvimento de estratégias de negociação e a gestão de portfólios de investimento. Os modelos são treinados para analisar dados históricos de preços de ativos financeiros, volumes de operações e indicadores técnicos. No entanto, a maioria dos métodos existentes assume que os dados analisados refletem completamente todas as interdependências entre os ativos. Na prática, isso nem sempre ocorre, especialmente em dados de mercado ruidosos e altamente voláteis.

Métodos tradicionais muitas vezes não consideram previsões de retorno de ativos de longo e curto prazo, nem suas correlações mútuas. Ao mesmo tempo, estratégias de investimento bem-sucedidas geralmente se baseiam em uma análise profunda desses fatores. Para modelar essas dependências complexas, no trabalho "StockFormer: Learning Hybrid Trading Machines with Predictive Coding" foi proposto o sistema de negociação híbrido StockFormer, que combina as capacidades de modelagem preditiva (predictive coding) com a flexibilidade de RL-agentes. A modelagem preditiva, amplamente usada em processamento de linguagem natural e visão computacional, permite extrair estados ocultos informativos a partir de dados brutos ruidosos, o que é especialmente relevante em aplicações financeiras.

O framework StockFormer une três ramos modificados da arquitetura Transformer, cada um responsável por estudar diferentes aspectos da dinâmica de mercado:

• tendências de longo prazo;
• tendências de curto prazo;
• interdependências entre ativos.

Todos os ramos são equipados com o mecanismo "Diversified Multi-Head Attention" (DMH-Attn), que aprimora o módulo Transformer utilizando blocos FeedForward. Isso permite identificar padrões variados de séries temporais em diferentes subespaços, preservando informações criticamente importantes.

Para otimizar as estratégias de negociação, três tipos de estados latentes das diferentes ramificações são combinados de forma adaptativa por meio de mecanismos de atenção multicabeça em um subespaço unificado de estados, que é então utilizado pelo RL-agente.

Os autores do framework propõem que o aprendizado da política seja realizado com métodos Actor-Critic. Nesse processo, a propagação reversa dos gradientes de erro vindos do Crítico tem como objetivo aprimorar o módulo de codificação preditiva, o que garante uma integração estreita entre as fases de treinamento.

Experimentos realizados pelos autores do framework em três conjuntos de dados públicos mostraram, que StockFormer supera significativamente os métodos existentes tanto em previsão quanto em maximização do lucro de investimento.

Algoritmo StockFormer

O framework StockFormer resolve tarefas de previsão e tomada de decisões de negociação nos mercados financeiros utilizando abordagens de aprendizado por reforço (RL). Um dos principais problemas dos métodos tradicionais está na ausência de um mecanismo eficaz para analisar as dependências dinâmicas entre ativos e suas tendências futuras. Isso é especialmente crítico nos mercados financeiros, onde mudanças podem ocorrer de forma rápida e imprevisível. Para lidar com esse desafio, StockFormer adota duas etapas principais: codificação preditiva e aprendizado da estratégia de negociação.

Na primeira etapa, StockFormer treina o modelo usando abordagens de aprendizado autossupervisionado para extrair eficientemente padrões ocultos dos dados de mercado, mesmo na presença de ruído. Isso permite que o modelo leve em conta tanto tendências de curto quanto de longo prazo, assim como as interdependências entre os ativos. Usando essa abordagem, o modelo extrai importantes estados ocultos, que são então utilizados na próxima etapa para a tomada de decisões de negociação.

A variedade de padrões temporais entre sequências de múltiplos ativos nos mercados financeiros aumenta significativamente a complexidade da extração de representações eficazes a partir dos dados brutos. Para resolver esse problema, os autores do StockFormer modificam o módulo de atenção multicabeça do Transformer padrão, substituindo um único bloco FeedForward (FFN) por um grupo de blocos semelhantes. Sem alterar o número total de parâmetros, esse mecanismo melhora a capacidade do módulo de atenção multicabeça de decompor características, o que facilita o modelamento de diversos padrões temporais em diferentes subespaços.

Esse módulo modificado foi chamado de "Diversified Multi-Head Attention" (DMH-Attn — DMH-Attn). Para as entidades Query, Key e Value com dimensionalidade dmodel, o processo no módulo de atenção multicabeça diversificada pode ser descrito da seguinte forma: inicialmente, dividimos as características de saída Z do mecanismo de atenção multicabeça em h grupos ao longo da dimensão de canais, onde h é o número de cabeças de atenção paralelas, a então aplicamos um FFN separado a cada grupo de características divididas em Z:

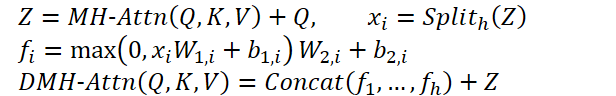
Onde MH-Attn representa o mecanismo de atenção multicabeça. E 𝑓𝑖 refere-se às características de saída de cada cabeça FFN, que contêm duas projeções lineares com ativação ReLU entre elas.

Cada ramo do Transformer modificado no StockFormer é dividido em dois módulos: codificador e decodificador. Ambos os módulos são usados no processo de treinamento da codificação preditiva com diferentes finalidades, no entanto, apenas o codificador é utilizado na otimização da estratégia. O modelo utiliza L camadas de codificador e M camadas de decodificador. As representações latentes obtidas na última camada do codificador XLenc servem como uma das entradas para cada camada do decodificador. O processo de cálculo na l-camada do codificador e na m-camada do decodificador pode ser descrito da seguinte maneira:

• camada do codificador:

• camada do decodificador:

Aqui, Xl,enc e Xm,dec representam os resultados das camadas do codificador e do decodificador, respectivamente. Os dados brutos com incorporações posicionais adicionadas são fornecidos como entradas para a primeira camada do codificador e do decodificador. E os resultados da última camada do decodificador são enviados para uma camada de projeção, que gera o resultado final para a tarefa de codificação preditiva.

O módulo de extração de interdependências é projetado para identificar correlações dinâmicas entre séries temporais. A cada instante de tempo t, o módulo utiliza os mesmos dados brutos tanto no codificador quanto no decodificador. Para lidar com dados do mercado de ações, os autores do framework utilizaram como estatísticas indicadores técnicos, como MACD, RSI e SMA.

Durante o processo de treinamento, os dados brutos são divididos em duas partes:

1. Matriz de covariância. Matriz de covariâncias entre as sequências de preços de fechamento diário de todos os ativos durante um período fixo anterior ao momento t.
2. Estatísticas mascaradas. Nessa parte, metade das séries temporais é selecionada aleatoriamente e suas estatísticas brutas são mascaradas com zeros. Na fase de teste, são usados os dados completos, sem mascaramento.

O principal objetivo do módulo de extração de interdependências é reconstruir as estatísticas mascaradas com base na matriz de covariância e nas estatísticas visíveis restantes. Esse método de codificação preditiva força o codificador Transformer a aprender a identificar dependências entre as séries temporais analisadas.

Os módulos de previsão de curto e longo prazo no StockFormer têm como foco a previsão dos coeficientes de retorno para cada ativo em diferentes horizontes temporais.

A tarefa do módulo de previsão de curto prazo é prever o coeficiente de retorno do ativo para o dia seguinte (H = 1). Para isso, são fornecidas ao codificador as estatísticas analisadas dos últimos T dias. O decodificador recebe os mesmos indicadores, mas apenas para o momento analisado.

O módulo de previsão de longo prazo funciona de maneira semelhante, mas com um horizonte de planejamento maior para os coeficientes de retorno do ativo. Isso estimula o modelo a capturar a dinâmica do mercado em um intervalo temporal mais estendido.

Para treinar os módulos de previsão de curto e longo prazo, utiliza-se uma função de perda combinada que inclui erro de regressão e erro de ranqueamento de ações. A primeira minimiza a diferença entre os retornos previstos e os reais, enquanto o erro de ranqueamento assegura que os ativos com maior retorno tenham prioridade superior.

Assim, os dois ramos do modelo ajudam StockFormer a capturar a dinâmica do mercado em diferentes horizontes temporais, o que permite ao agente RL tomar decisões de negociação mais precisas e informadas.

Na segunda etapa do treinamento, StockFormer combina três tipos de representações latentes srelat,t, slong,t, sshort,t em um espaço unificado de estados St por meio de uma cascata de blocos de atenção multicabeça. Inicialmente, ocorre a fusão das previsões de curto e longo prazo. Nesse processo, a representação de longo prazo é usada como Query, pois é menos afetada por ruídos de curto prazo. Os resultados dessa etapa são alinhados com o estado latente das interdependências entre ativos, que é utilizado como Key e Value no módulo de atenção seguinte.

Depois disso, o modelo é treinado para determinar a estratégia de negociação ideal utilizando a abordagem Ator–Crítico. Um dos principais diferenciais do StockFormer é a integração entre as fases de codificação preditiva e otimização da política. As avaliações do Crítico ajudam a melhorar a qualidade da extração das representações latentes, permitindo que o modelo analise mais profundamente as conexões entre ativos e lide melhor com ruídos nos dados brutos.

A visualização original do framework StockFormer é apresentada abaixo.

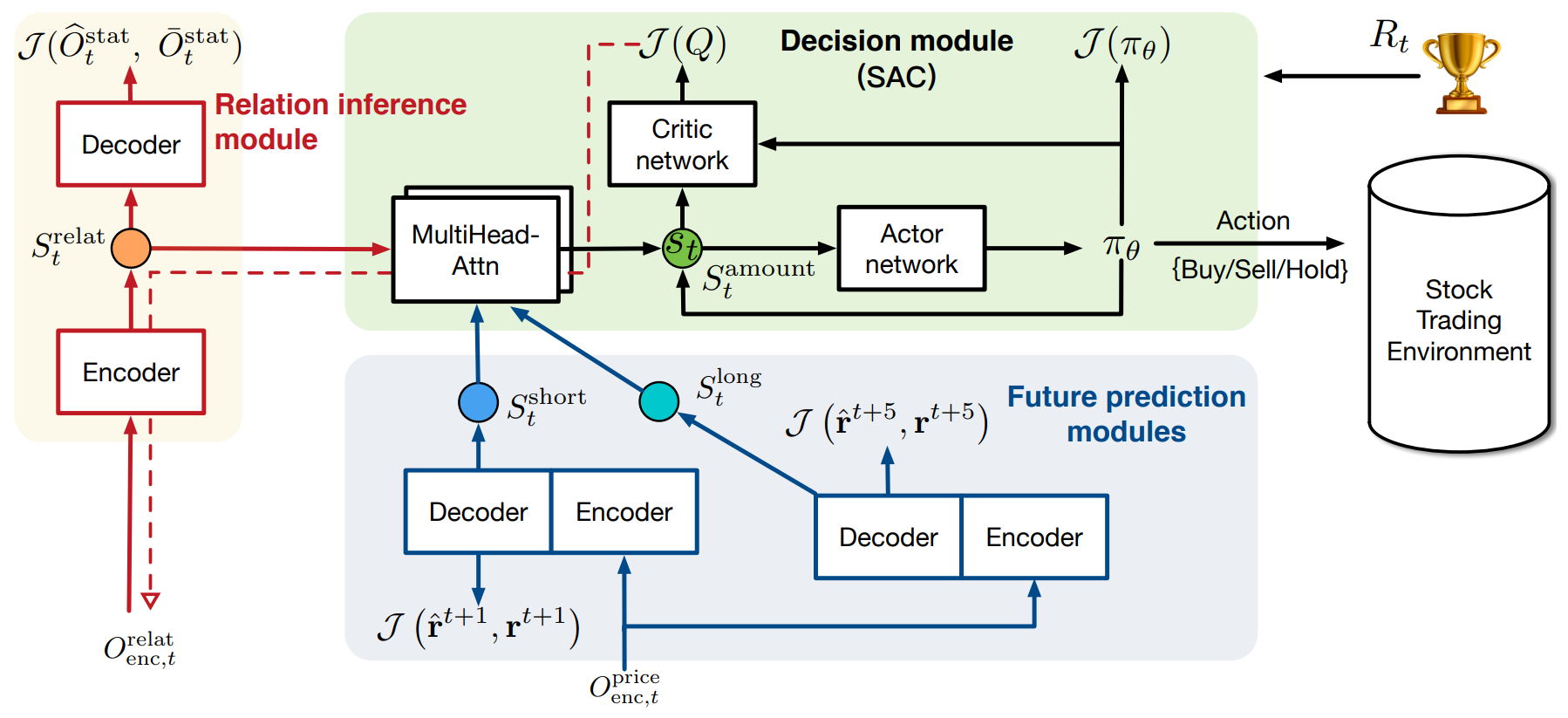
Implementação com MQL5

Após abordarmos os aspectos teóricos do framework StockFormer, passamos à implementação da nossa própria interpretação das abordagens propostas usando MQL5. Como pode ser observado na descrição teórica apresentada, a principal modificação estrutural na arquitetura dos módulos de atenção utilizados é a introdução do bloco multicabeça FeedForward. A implementação desse bloco será a primeira etapa do nosso trabalho.

Na implementação proposta pelos autores do framework StockFormer para o bloco multicabeça FeedForward, os resultados do bloco de Self-Attention multicabeça para cada elemento da sequência são divididos em h grupos iguais, e a cada grupo é aplicado um MLP com parâmetros treináveis únicos.

É importante notar que aqui a abordagem para formar as cabeças difere daquela usada anteriormente no nosso bloco de atenção multicabeça. No Multi-Head Self-Attention, a partir de uma única incorporação de um elemento da sequência, gerávamos múltiplas variantes das entidades Query, Key e Value. Neste caso, os autores do StockFormer propõem dividir diretamente o vetor de descrição de um único elemento da sequência em vários grupos iguais de elementos. Em seguida, aplica-se um MLP diferente a cada grupo. Essa abordagem, de fato, permite organizar várias cabeças sem aumentar o número de parâmetros treináveis. E na saída, obtemos um tensor com a mesma dimensionalidade, sem a necessidade de uma camada de projeção, como é feito no MH Self-Attention. No entanto, isso nos impede de utilizar as camadas convolucionais existentes, como fazíamos antes. Precisamos, portanto, encontrar uma solução alternativa.

Por um lado, poderíamos considerar opções de transposição do tensor tridimensional com o objetivo de “ajustar” a solução para uso de uma camada convolucional com análise independente de sequências unitárias. Mas sabemos que haverá um número razoável dessas camadas no StockFormer. Consequentemente, transpor os dados antes e depois do bloco FeedForward em cada camada aumentaria significativamente o tempo de treinamento e de execução do modelo. Por isso, decidiu-se criar uma versão multicabeça da camada convolucional. Mas antes de começar a construir esse novo objeto do lado do programa principal, precisamos fazer alguns ajustes em nosso programa OpenCL.

Complemento do programa OpenCL

E começamos esse trabalho com a construção do kernel de propagação para frente da nossa nova camada convolucional FeedForwardMHConv multicabeça. Vale mencionar que a estrutura de parâmetros e parte do algoritmo foram aproveitadas de um kernel existente de camada convolucional semelhante. E o identificador da cabeça da convolução, assim como o número total de cabeças, foi introduzido como uma dimensão adicional no espaço de tarefas.

__kernel void FeedForwardMHConv(__global float *matrix_w,
                                __global float *matrix_i,
                                __global float *matrix_o,
                                const int inputs,
                                const int step,
                                const int window_in,
                                const int window_out,
                                const int activation
                               )
  {
   const size_t i = get_global_id(0);
   const size_t h = get_global_id(1);
   const size_t v = get_global_id(2);
   const size_t total = get_global_size(0);
   const size_t heads = get_global_size(1);

No corpo do kernel, realizamos a identificação da thread atual por todas as dimensões do espaço de tarefas. Em seguida, definimos as dimensões de entrada e saída de cada cabeça de convolução e o deslocamento nos buffers de dados globais até os elementos analisados.

   const int window_in_h = (window_in + heads - 1) / heads;
   const int window_out_h = (window_out + heads - 1) / heads;
   const int shift_out = window_out * i + window_out_h * h;
   const int shift_in = step * i + window_in_h * h;
   const int shift_var_in = v * inputs;
   const int shift_var_out = v * window_out * total;
   const int shift_var_w = v * window_out * (window_in_h + 1);
   const int shift_w_h = h * window_out_h * (window_in_h + 1);

Após concluir o trabalho preparatório, passamos à construção das operações do algoritmo de convolução dos dados brutos com o filtro treinável. Dentro de uma única thread, executaremos as operações de convolução de uma cabeça dos dados brutos com o filtro correspondente. Para isso, organizamos um sistema de laços aninhados. O laço externo percorre os elementos na camada de resultados do elemento analisado para a respectiva cabeça de convolução.

   float sum = 0;
   float4 inp, weight;
   int stop = (window_in_h <= (inputs - shift_in) ? window_in_h : (inputs - shift_in));
//---
   for(int out = 0; (out < window_out_h && (window_out_h * h + out) < window_out); out++)
     {
      int shift = (window_in_h + 1) * out + shift_w_h;

No corpo do laço externo, primeiro definimos o deslocamento no buffer dos parâmetros treináveis. Em seguida, organizamos o laço que percorre os elementos da janela dos dados brutos.

      for(int k = 0; k <= stop; k += 4)
        {
         switch(stop - k)
           {
            case 0:
               inp = (float4)(1, 0, 0, 0);
               weight = (float4)(matrix_w[shift_var_w + shift + window_in_h], 0, 0, 0);
               break;
            case 1:
               inp = (float4)(matrix_i[shift_var_in + shift_in + k], 1, 0, 0);
               weight = (float4)(matrix_w[shift_var_w + shift + k], matrix_w[shift_var_w + shift + window_in_h], 0, 0);
               break;
            case 2:
               inp = (float4)(matrix_i[shift_var_in + shift_in + k],
                              matrix_i[shift_var_in + shift_in + k + 1], 1, 0);
               weight = (float4)(matrix_w[shift_var_w + shift + k], matrix_w[shift_var_w + shift + k + 1],
                                 matrix_w[shift_var_w + shift + window_in_h], 0);
               break;
            case 3:
               inp = (float4)(matrix_i[shift_var_in + shift_in + k], matrix_i[shift_var_in + shift_in + k + 1],
                              matrix_i[shift_var_in + shift_in + k + 2], 1);
               weight = (float4)(matrix_w[shift_var_w + shift + k], matrix_w[shift_var_w + shift + k + 1],
                                 matrix_w[shift_var_w + shift + k + 2], matrix_w[shift_var_w + shift + shift_w_h]);
               break;
            default:
               inp = (float4)(matrix_i[shift_var_in + shift_in + k], matrix_i[shift_var_in + shift_in + k + 1],
                              matrix_i[shift_var_in + shift_in + k + 2], matrix_i[shift_var_in + shift_in + k + 3]);
               weight = (float4)(matrix_w[shift_var_w + shift + k], matrix_w[shift_var_w + shift + k + 1],
                                 matrix_w[shift_var_w + shift + k + 2], matrix_w[shift_var_w + shift + k + 3]);
               break;
           }

Com o objetivo de otimizar os processos computacionais das operações de convolução, utilizamos a multiplicação embutida de variáveis vetoriais, o que permite um uso mais eficiente dos recursos do processador. Por isso, primeiro transferimos os dados dos buffers externos para variáveis vetoriais locais, depois realizamos a multiplicação vetorial e prosseguimos para a próxima iteração do laço aninhado.

         sum += IsNaNOrInf(dot(inp, weight), 0);
        }

Após executar todas as iterações do laço interno, realizamos as operações da função de ativação e salvamos o valor obtido no elemento correspondente do buffer de resultados. Em seguida, passamos para a próxima iteração do laço externo.

      sum = IsNaNOrInf(sum, 0);
      //---
      matrix_o[shift_var_out + out + shift_out] = Activation(sum, activation);;
     }
  }

Ao final de todas as iterações do sistema de laços, os valores necessários estarão salvos no buffer de resultados, e encerramos a execução do kernel.

A seguir, passamos à construção dos algoritmos de propagação reversa. E aqui, é importante destacar que não podemos mais introduzir o identificador da cabeça de convolução como uma dimensão do espaço de tarefas.

Lembro que, durante a execução do algoritmo de distribuição do gradiente de erro, coletamos os valores de influência de cada elemento dos dados brutos sobre o resultado. E no caso em que o passo da janela de convolução analisada for menor que seu tamanho, um único elemento dos dados brutos pode influenciar elementos do tensor de resultados de diferentes cabeças de convolução.

Portanto, neste caso, introduzimos o número de cabeças de atenção como um parâmetro externo adicional no kernel CalcHiddenGradientMHConv. E o identificador da cabeça de convolução específica é definido no processo de coleta dos gradientes de erro.

__kernel void CalcHiddenGradientMHConv(__global float *matrix_w,
                                       __global float *matrix_g,
                                       __global float *matrix_o,
                                       __global float *matrix_ig,
                                       const int outputs,
                                       const int step,
                                       const int window_in,
                                       const int window_out,
                                       const int activation,
                                       const int shift_out,
                                       const int heads
                                      )
  {
   const size_t i = get_global_id(0);
   const size_t inputs = get_global_size(0);
   const size_t v = get_global_id(1);

No corpo do kernel, identificamos a thread atual em um espaço de tarefas bidimensional, que aponta para o elemento dos dados brutos e para o identificador da sequência unitária. Em seguida, determinamos os valores das constantes, incluindo os deslocamentos nos buffers de dados, bem como as dimensões da janela e o número de filtros para uma única cabeça de convolução. 

   const int shift_var_in = v * inputs;
   const int shift_var_out = v * outputs;
   const int shift_var_w = v * window_out * (window_in + 1);
   const int window_in_h = (window_in + heads - 1) / heads;
   const int window_out_h = (window_out + heads - 1) / heads;

Neste ponto, também definimos o intervalo da janela de resultados que sofre influência do elemento dos dados brutos analisado.

   float sum = 0;
   float out = matrix_o[shift_var_in + i];
   const int w_start = i % step;
   const int start = max((int)((i - window_in + step) / step), 0);
   int stop = (w_start + step - 1) / step;
   stop = min((int)((i + step - 1) / step + 1), stop) + start;
   if(stop > (outputs / window_out))
      stop = outputs / window_out;

Após concluir o trabalho preparatório, passamos à coleta dos gradientes de erro de todos os elementos dependentes do tensor de resultados. Para isso, organizamos um sistema de laços. O laço externo percorre os elementos dependentes dentro da janela definida anteriormente.

   for(int k = start; k < stop; k++)
     {
      int head = (k % window_out) / window_out_h;

No corpo do laço externo, primeiro identificamos a cabeça de convolução para o elemento específico do tensor de resultados e, em seguida, organizamos um laço aninhado que percorre os filtros.

      for(int h = 0; h < window_out_h; h ++)
        {
         int shift_g = k * window_out + head * window_out_h + h;
         int shift_w = (stop - k - 1) * step + (i % step) / window_in_h +
                       head * (window_in_h + 1) + h * (window_in_h + 1);
         if(shift_g >= outputs || shift_w >= (window_in_h + 1) * window_out)
            break;
         float grad = matrix_g[shift_out + shift_g + shift_var_out];
         sum += grad * matrix_w[shift_w + shift_var_w];
        }
     }

É no corpo do laço aninhado que coletamos o gradiente de erro de todos os filtros de uma cabeça de convolução e então seguimos para a próxima iteração do sistema de laços.

Após a coleta bem-sucedida dos gradientes de erro de todos os elementos dependentes, ajustamos o valor coletado pela derivada da função de ativação e salvamos o resultado obtido no elemento correspondente do buffer de dados.

   matrix_ig[shift_var_in + i] = Deactivation(sum, out, activation);
  }

Com isso, encerramos as operações do kernel de distribuição de gradiente de erro. Quanto ao kernel de atualização dos parâmetros do modelo, deixo a sugestão de que você o explore por conta própria. O código completo do programa OpenCL está disponível no anexo do artigo. Agora avançamos para a próxima etapa do nosso trabalho, que é a construção do objeto de camada neural de convolução multicabeça no lado do programa principal.

Camada de convolução multicabeça

Para implementar a funcionalidade da convolução no lado do programa principal, criaremos um novo objeto CNeuronMHConvOCL. E, como se pode imaginar, utilizamos como classe-mãe uma camada convolucional já existente. A estrutura do novo objeto está apresentada abaixo.

class CNeuronMHConvOCL  :  public CNeuronConvOCL
  {
protected:
   uint              iHeads;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMHConvOCL(void)  :  iHeads(1)   {};
                    ~CNeuronMHConvOCL(void)  {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint step, uint window_out, 
                          uint units_count, uint variables, uint heads, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const override   {  return defNeuronMHConvOCL;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
  };

Na estrutura apresentada do objeto, apenas declaramos uma variável interna para armazenar o número definido de cabeças de convolução. Todos os demais objetos e variáveis necessários para organizar os processos são herdados da classe-mãe. Além disso, sobrescrevemos os métodos de propagação para frente e propagação reversa, que funcionam como "wrappers" para a chamada dos kernels descritos anteriormente. O algoritmo para enfileiramento dos kernels para execução permanece o mesmo. Por isso, não entraremos em detalhes sobre esses métodos. Nesta etapa do artigo, vamos nos concentrar apenas no método de inicialização do novo objeto Init, que foi praticamente criado "do zero".

Na estrutura de parâmetros do método de inicialização, apenas um elemento foi adicionado para permitir que o número de cabeças de convolução seja transmitido a partir do programa chamador.

bool CNeuronMHConvOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                            uint window, uint step, uint window_out, 
                            uint units_count, uint variables, uint heads, 
                            ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronProofOCL::Init(numOutputs, myIndex, open_cl, window, step, 
                             units_count * window_out * variables, ADAM, batch))
      return false;

No corpo do método, invocamos diretamente o método homônimo da camada base, que neste caso é o objeto ancestral. Em seguida, armazenamos os valores dos parâmetros externos em variáveis locais.

   iWindowOut = window_out;
   iVariables = variables;
   iHeads = MathMax(MathMin(heads, window), 1);

Depois, precisamos inicializar o tensor de parâmetros treináveis com valores aleatórios. Mas antes disso, definimos a dimensionalidade desse tensor. Ela depende da quantidade de sequências unitárias na sequência multimodal analisada, do número total de filtros e do tamanho da janela analisada por uma cabeça de convolução.

   const int window_h = int((iWindow + heads - 1) / heads);
   const int count = int((window_h + 1) * iWindowOut * iVariables);

Observe que estamos falando do número total de filtros de todas as cabeças de convolução, mas utilizamos apenas a janela analisada por uma única cabeça. É fácil perceber que a quantidade de parâmetros treináveis para uma única cabeça de convolução é igual ao produto do número de filtros por cabeça e o tamanho da janela de dados analisada por ela, somado a um elemento de viés bayesiano (Fi * (Wi + 1)). Então, para obter o número total de parâmetros de uma sequência unitária, basta multiplicar esse valor pelo número de cabeças de convolução (Fi * (Wi + 1) * H). E aqui fica evidente que o número de filtros por cabeça, multiplicado pelo número de cabeças, nos fornece o total de filtros definido pelo usuário.

O próximo passo é verificar a validade do ponteiro para o objeto do buffer de parâmetros treináveis e, se necessário, criar um novo objeto.

   if(!WeightsConv)
     {
      WeightsConv = new CBufferFloat();
      if(!WeightsConv)
         return false;
     }

Reservamos a quantidade necessária de elementos no buffer e organizamos um laço para preenchê-lo com valores aleatórios.

   if(!WeightsConv.Reserve(count))
      return false;
   float k = (float)(1 / sqrt(window_h + 1));
   for(int i = 0; i < count; i++)
     {
      if(!WeightsConv.Add((GenerateWeight() * 2 * k - k) * WeightsMultiplier))
         return false;
     }
   if(!WeightsConv.BufferCreate(OpenCL))
      return false;

Após preencher com sucesso o buffer com valores aleatórios, transferimos seu conteúdo para a memória do contexto OpenCL. Nesse momento também criamos os buffers de momentos, preenchendo-os com valores nulos.

   if(!FirstMomentumConv)
     {
      FirstMomentumConv = new CBufferFloat();
      if(!FirstMomentumConv)
         return false;
     }
   if(!FirstMomentumConv.BufferInit(count, 0.0))
      return false;
   if(!FirstMomentumConv.BufferCreate(OpenCL))
      return false;
//---
   if(!SecondMomentumConv)
     {
      SecondMomentumConv = new CBufferFloat();
      if(!SecondMomentumConv)
         return false;
     }
   if(!SecondMomentumConv.BufferInit(count, 0.0))
      return false;
   if(!SecondMomentumConv.BufferCreate(OpenCL))
      return false;
   if(!!DeltaWeightsConv)
      delete DeltaWeightsConv;
//---
   return true;
  }

Com isso, encerramos a análise dos métodos do objeto de camada convolucional multicabeça CNeuronMHConvOCL. O código completo dessa classe e de todos os seus métodos está disponível no anexo.

Bloco FeedForward multicabeça

Já construímos o primeiro “bloco de construção” no caminho da implementação do framework StockFormer. E agora iremos utilizá-lo para criar o bloco FeedForward multicabeça dentro do novo objeto CNeuronMHFeedForward, cuja estrutura está apresentada abaixo.

class CNeuronMHFeedForward   :  public CNeuronBaseOCL
  {
protected:
   CNeuronMHConvOCL  acConvolutions[2];
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMHFeedForward(void) {};
                    ~CNeuronMHFeedForward(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_out,
                          uint units_count, uint variables, uint heads,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const override   {  return defNeuronMHFeedForward;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Na estrutura do novo objeto, declaramos um array com duas camadas convolucionais multicabeça internas e sobrescrevemos o conjunto já conhecido de métodos virtuais. Os objetos internos são declarados de forma estática, o que permite manter o construtor e o destrutor da classe vazios. A inicialização de todos os objetos declarados e herdados é feita no método Init.

bool CNeuronMHFeedForward::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                uint window, uint window_out,
                                uint units_count, uint variables, uint heads,
                                ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count * variables, optimization_type, batch))
      return false;

Nos parâmetros do método de inicialização, recebemos as constantes que definem a arquitetura do objeto a ser criado. Parte desses parâmetros é imediatamente repassada para o método homônimo da classe-mãe, com o objetivo de inicializar as interfaces base herdadas.

Depois, inicializamos a primeira camada convolucional, definindo a função de ativação GELU.

   if(!acConvolutions[0].Init(0, 0, OpenCL, window, window, window_out, units_count, variables, heads, 
                                                                                  optimization, iBatch))
      return false;
   acConvolutions[0].SetActivationFunction(GELU);

Em seguida, inicializamos a segunda camada convolucional, desta vez sem função de ativação.

   if(!acConvolutions[1].Init(0, 1, OpenCL, window_out, window_out, window, units_count, variables, heads, 
                                                                                     optimization, iBatch))
      return false;
   acConvolutions[1].SetActivationFunction(None);

E observe que, ao chamar o método de inicialização da segunda camada convolucional, trocamos a ordem dos parâmetros referentes ao número de filtros e ao tamanho da janela dos dados brutos analisados.

Na saída do bloco FeedForward são utilizadas conexões residuais com normalização dos dados, por isso não sobrescrevemos o buffer da interface de resultados do nosso bloco. No entanto, sobrescrevemos o buffer de gradientes de erro, o que permite a transferência direta dos gradientes das interfaces para o buffer correspondente da segunda camada convolucional.

   if(!SetGradient(acConvolutions[1].getGradient(), true))
      return false;
   SetActivationFunction(None);
//---
   return true;
  }

Também desativamos a função de ativação para o nosso bloco e finalizamos o método retornando à rotina chamadora o resultado lógico da execução das operações.

Após concluir a inicialização do novo objeto, passamos à construção do algoritmo de propagação para frente no método feedForward. E é preciso dizer que, neste caso, sua implementação não apresenta dificuldades. Apenas chamamos, em sequência, os métodos homônimos das camadas convolucionais internas.

bool CNeuronMHFeedForward::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   CObject *prev = NeuronOCL;
   for(uint i = 0; i < acConvolutions.Size(); i++)
     {
      if(!acConvolutions[i].FeedForward(prev))
         return false;
      prev = GetPointer(acConvolutions[i]);
     }

Depois, somamos os valores obtidos aos dados brutos com normalização dos resultados dentro de cada elemento da sequência multimodal analisada.

   if(!SumAndNormilize(NeuronOCL.getOutput(), acConvolutions[acConvolutions.Size() - 1].getOutput(),
                       Output, acConvolutions[0].GetWindow(), true, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

E finalizamos o método retornando à rotina chamadora o resultado lógico da execução das operações.

O algoritmo do método de distribuição de gradiente de erro calcInputGradients é um pouco mais complexo, o que se deve à necessidade de propagação dos gradientes por dois fluxos de informação.

bool CNeuronMHFeedForward::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

Nos parâmetros do método, recebemos um ponteiro para o objeto dos dados brutos, no buffer do qual devemos transferir o gradiente de erro, refletindo a influência desses dados no resultado final da execução do modelo. No corpo do método, verificamos imediatamente a validade do ponteiro recebido.

Após passar com sucesso pelo bloco de verificações, organizamos um laço para percorrer em ordem reversa as camadas convolucionais internas, chamando sucessivamente seus métodos homônimos.

   for(int i = (int)acConvolutions.Size() - 2; i >= 0; i--)
     {
      if(!acConvolutions[i].calcHiddenGradients(acConvolutions[i + 1].AsObject()))
         return false;
     }

Após a distribuição do gradiente de erro ao longo dos objetos internos, realizamos sua transferência para o nível dos dados brutos. Essa operação encerra o fluxo principal de informações.

   if(!NeuronOCL.calcHiddenGradients(acConvolutions[0].AsObject()))
      return false;

Em seguida, propagamos o gradiente de erro através do segundo fluxo de informação. Aqui, o algoritmo se divide em dois ramos, dependendo da presença ou não de função de ativação nos dados brutos. Na ausência dessa função, basta somar o gradiente de erro acumulado no nível dos dados brutos com os valores correspondentes na saída do nosso bloco.

   if(NeuronOCL.Activation() == None)
     {
      if(!SumAndNormilize(NeuronOCL.getGradient(), Gradient, NeuronOCL.getGradient(),
                          acConvolutions[0].GetWindow(), false, 0, 0, 0, 1))
         return false;
     }
   else
     {
      if(!DeActivation(NeuronOCL.getOutput(), NeuronOCL.getPrevOutput(), Gradient, NeuronOCL.Activation()) ||
         !SumAndNormilize(NeuronOCL.getGradient(), NeuronOCL.getPrevOutput(), NeuronOCL.getGradient(),
                          acConvolutions[0].GetWindow(), false, 0, 0, 0, 1))
         return false;
     }
//---
   return true;
  }

Caso contrário, é necessário primeiro ajustar o gradiente de erro no nível dos resultados do nosso bloco pela derivada da função de ativação dos dados brutos. E só então realizar a soma dos dados dos dois fluxos de informação.

Agora só nos resta retornar o resultado lógico da execução à rotina chamadora e encerrar o método.

O método de ajuste dos parâmetros treináveis do bloco para reduzir o erro total do modelo, updateInputWeights, deixo como sugestão para estudo independente. Seu algoritmo é bastante simples: apenas chamamos sequencialmente os métodos homônimos dos objetos internos. O código completo do objeto do bloco FeedForward multicabeça CNeuronMHFeedForward e todos os seus métodos podem ser encontrados no anexo do artigo.

Decodificador de atenção multicabeça diversificada

Após a criação do bloco multicabeça FeedForward, passamos à construção dos objetos codificador e decodificador de atenção multicabeça diversificada. Para desenvolver os algoritmos desses módulos, criaremos dois novos objetos CNeuronDMHAttention e CNeuronCrossDMHAttention, respectivamente. A estrutura de construção desses objetos é bastante similar. O segundo se diferencia por conter um bloco interno de atenção cruzada e por operar com duas fontes de dados brutos. Neste artigo, vamos focar na análise dos algoritmos do decodificador, por ser o objeto mais complexo. Após compreendê-los, acredito que entender os algoritmos do codificador será uma tarefa simples.

Como classe-mãe em ambos os casos, utilizamos o objeto CNeuronRMAT, dentro do qual está organizado o algoritmo do modelo sequencial.

class CNeuronCrossDMHAttention   :  public CNeuronRMAT
  {
protected:
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer) override { return false; }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput,
                                                                   CBufferFloat *SecondGradient, 
                                                        ENUM_ACTIVATION SecondActivation = None) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override;

public:
                     CNeuronCrossDMHAttention(void)  {};
                    ~CNeuronCrossDMHAttention(void)  {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count,
                          uint window_cross, uint units_cross,
                          uint heads, uint layers,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronCrossDMHAttention; }
  };

Na estrutura do objeto decodificador, observamos apenas a sobrescrição de métodos virtuais. A estrutura dos objetos internos é definida no método de inicialização Init, cujos parâmetros recebem as principais constantes que determinam a arquitetura do objeto.

bool CNeuronCrossDMHAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                    uint window, uint window_key, uint units_count,
                                    uint window_cross, uint units_cross, uint heads,
                                    uint layers, ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

No corpo do método, primeiro chamamos o método homônimo do objeto base de camada totalmente conectada para inicializar as interfaces herdadas.

Em seguida, limpamos o array dinâmico que armazena os ponteiros dos objetos internos do módulo e criamos algumas variáveis locais para armazenar dados temporários.

   cLayers.Clear();
   cLayers.SetOpenCL(OpenCL);
   CNeuronRelativeSelfAttention *attention = NULL;
   CNeuronRelativeCrossAttention *cross = NULL;
   CNeuronMHFeedForward *conv = NULL;
   bool use_self = units_count > 0;
   int layer = 0;

Com isso, finalizamos o trabalho preparatório e organizamos um laço com número de iterações igual ao número de camadas internas do decodificador de atenção multicabeça diversificada.

   for(uint i = 0; i < layers; i++)
     {
      if(use_self)
        {
         attention = new CNeuronRelativeSelfAttention();
         if(!attention ||
            !attention.Init(0, layer, OpenCL, window, window_key, units_count, heads, optimization, iBatch) ||
            !cLayers.Add(attention)
           )
           {
            delete attention;
            return false;
           }
         layer++;
        }

No corpo do laço, criamos primeiro o bloco de Self-Attention relativo para analisar as dependências nos dados brutos do fluxo principal. No entanto, observe que o bloco Self-Attention só é criado quando o comprimento da sequência do fluxo principal é maior que “1”. Caso contrário, não há dados suficientes para buscar dependências.

Em seguida, adicionamos o módulo de atenção cruzada relativa.

      cross = new CNeuronRelativeCrossAttention();
      if(!cross ||
         !cross.Init(0, layer, OpenCL, window, window_key, units_count, heads, 
                              window_cross, units_cross, optimization, iBatch) ||
         !cLayers.Add(cross)
        )
        {
         delete cross;
         return false;
        }
      layer++;

E cada camada interna do decodificador é finalizada com o bloco multicabeça FeedForward. Em seguida, passamos para a próxima iteração do laço.

      conv = new CNeuronMHFeedForward();
      if(!conv ||
         !conv.Init(0, layer, OpenCL, window, 2 * window, units_count, 1, heads, optimization, iBatch) ||
         !cLayers.Add(conv)
        )
        {
         delete conv;
         return false;
        }
      layer++;
     }

Após completar a inicialização de todos os objetos internos, realizamos a substituição dos ponteiros dos objetos de interface e encerramos o método, retornando à rotina chamadora o resultado lógico da execução das operações.

   SetOutput(conv.getOutput(), true);
   SetGradient(conv.getGradient(), true);
//---
   return true;
  }

O algoritmo do método de propagação para frente feedForward não apresenta pontos complexos e consiste em chamadas sequenciais aos métodos homônimos dos objetos internos. Recomendo deixá-lo para estudo independente. No entanto, vamos dedicar um momento à análise do algoritmo de distribuição do gradiente de erro calcInputGradients.

bool CNeuronCrossDMHAttention::calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                                   CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = -1)
  {
   if(!NeuronOCL || !SecondInput || !SecondGradient)
      return false;

Nos parâmetros do método, recebemos ponteiros para os objetos dos dados brutos e seus gradientes de erro, nos quais escreveremos os resultados das operações. Portanto, no corpo do método, verificamos imediatamente a validade dos ponteiros recebidos.

Em seguida, é importante notar que o segundo conjunto de dados brutos foi utilizado igualmente por todos os módulos de atenção cruzada nas camadas internas do decodificador durante a propagação para frente. Assim, precisamos coletar o gradiente de erro de todos os fluxos de informação, e, como de costume nesse tipo de situação, será necessário um buffer de armazenamento interno, o qual não criamos dentro do novo objeto. Por isso, utilizamos um dos buffers não utilizados herdados da classe-mãe.

Primeiramente, verificamos o tamanho do buffer herdado e, se necessário, ajustamos suas dimensões.

   if(PrevOutput.Total() != SecondGradient.Total())
     {
      PrevOutput.BufferFree();
      if(!PrevOutput.BufferInit(SecondGradient.Total(), 0) ||
         !PrevOutput.BufferCreate(OpenCL))
         return false;
     }

Depois, preenchemos o buffer de gradientes de erro do segundo conjunto de dados com valores nulos. Essa operação é essencial para evitar a soma dos gradientes da execução atual com dados acumulados anteriormente.

   if(!SecondGradient.Fill(0))
      return false;

Também criamos variáveis locais para armazenamento temporário dos dados.

   CObject *next = cLayers[-1];
   CNeuronBaseOCL *current = NULL;

Com isso, concluímos a etapa de preparação e iniciamos o laço de iteração reversa sobre os objetos internos.

   for(int i = cLayers.Total() - 2; i >= 0; i--)
     {
      current = cLayers[i];
      if(!current ||
         !current.calcHiddenGradients(next, SecondInput, PrevOutput, SecondActivation))
         return false;
      if(next.Type() == defNeuronCrossDMHAttention)
         if(!SumAndNormilize(SecondGradient, PrevOutput, SecondGradient, 1, false, 0, 0, 0, 1))
            return false;
      next = current;
     }

No corpo do laço, chamamos sucessivamente os métodos homônimos dos objetos internos, verificando continuamente o tipo de objeto que está realizando a distribuição do gradiente de erro. No caso de um bloco de atenção cruzada, somamos o gradiente de erro obtido do segundo conjunto de dados com os valores previamente acumulados.

Após concluir com sucesso todas as iterações do laço, transmitimos o gradiente de erro para o nível dos dados brutos da via principal.

   if(!NeuronOCL.calcHiddenGradients(next, SecondInput, PrevOutput, SecondActivation))
      return false;
   if(next.Type() == defNeuronCrossDMHAttention)
      if(!SumAndNormilize(SecondGradient, PrevOutput, SecondGradient, 1, false, 0, 0, 0, 1))
         return false;
//---
   return true;
  }

Nesse processo, verificamos novamente o tipo do objeto responsável pela distribuição do gradiente e, se necessário, somamos o gradiente do segundo fluxo de informação aos dados acumulados anteriormente. Em seguida, finalizamos o método retornando à rotina chamadora o resultado lógico da execução das operações.

Com isso, encerramos a análise dos algoritmos de construção dos métodos do decodificador de atenção multicabeça diversificada. O código completo desse objeto e de todos os seus métodos pode ser consultado no anexo. Lá também está disponível o código completo de todos os objetos apresentados neste artigo.

Concluímos, portanto, a implementação da principal unidade arquitetônica do framework StockFormer — módulo diversificado de atenção multicabeça sob a forma de codificador e decodificador da arquitetura Transformer. No entanto, os autores do StockFormer propuseram um processo de treinamento em dois níveis, com um mecanismo complexo de interação entre os modelos treináveis. Esse será o tema da próxima parte deste trabalho.

Considerações finais

Apresentamos o framework StockFormer, cujos autores propuseram uma abordagem inovadora para o treinamento de estratégias de negociação nos mercados financeiros. StockFormer combina técnicas de codificação preditiva com aprendizado profundo por reforço. Sua principal vantagem está na capacidade de treinar políticas flexíveis que consideram dependências dinâmicas entre múltiplos ativos e conseguem prever seus comportamentos em horizontes de tempo curtos e longos. 

A codificação preditiva em três ramificações garante a extração de representações latentes associadas a tendências de curto prazo, dinâmicas de longo prazo e interdependências entre ativos. Já o mecanismo de atenção multicabeça em cascata permite integrar de forma eficiente diferentes tipos de representações em um espaço unificado de estados.

Na parte prática do artigo, implementamos com MQL5 a modificação do algoritmo Transformer padrão proposta pelos autores e a incorporamos nos módulos codificador e decodificador de atenção multicabeça diversificada. Na próxima parte do artigo, daremos continuidade a esse trabalho e abordaremos a arquitetura dos modelos treináveis, bem como seu processo de treinamento.

Links

• StockFormer: Learning Hybrid Trading Machines with Predictive Coding
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA para coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA para coleta de exemplos com método Real-ORL
3	Study1.mq5	Expert Advisor	EA para treinamento com codificação preditiva
4	Study2.mq5	Expert Advisor	EA para treinamento de política
5	Test.mq5	Expert Advisor	EA para testes do modelo
6	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema
7	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de rede neural
8	NeuroNet.cl	Biblioteca	Biblioteca com código do programa OpenCL