Redes neurais em trading: Conjunto de agentes com uso de mecanismos de atenção (Conclusão)

MetaTrader 5 — Sistemas de negociação | 28 maio 2025, 11:10

133

Dmitriy Gizlyk

Introdução

O gerenciamento de portfólio de instrumentos financeiros desempenha um papel importante nas decisões de investimento voltadas para o aumento da rentabilidade e a redução de riscos por meio da redistribuição dinâmica de capital entre os ativos. No trabalho "Developing an attention-based ensemble learning framework for financial portfolio optimisation" foi proposto um framework adaptativo multiagente inovador, MASAAT, que combina mecanismos de atenção e análise de séries temporais. Dentro dessa abordagem, são criados diversos agentes de trading para análise cruzada das variações direcionais nos preços dos ativos considerando diferentes níveis de detalhamento. Essa solução permite revisar a estrutura do portfólio de investimentos, buscando um equilíbrio eficaz entre rentabilidade e risco em cenários de alta volatilidade nos mercados financeiros.

Para capturar mudanças significativas nos preços, os agentes utilizam filtros de movimento direcional com diferentes limiares. Além disso, são extraídas características-chave das tendências nas séries temporais de preços analisadas, o que melhora a compreensão das transições de mercado com diferentes intensidades. A abordagem proposta introduz uma nova metodologia para gerar tokens de sequência, permitindo que os módulos de análise cruzada com base em atenção (CSA) e análise temporal (TA) identifiquem de forma eficiente diversas correlações. Especificamente, ao reconstruir os mapas de características, os tokens de sequência no módulo CSA são formados com base nos indicadores de ativos individuais, otimizados através de mecanismos de atenção. Ao mesmo tempo, os tokens no módulo TA são construídos com base nas características dos pontos temporais, o que permite destacar conexões significativas entre momentos específicos no tempo.

As avaliações de correlação entre ativos e pontos temporais, reunidas nos módulos CSA e TA, são combinadas pelos agentes MASAAT utilizando o mecanismo de atenção, com o objetivo de encontrar dependências de cada ativo em relação a cada ponto no tempo durante o período de observação.

A visualização original do framework MASAAT é apresentada abaixo.

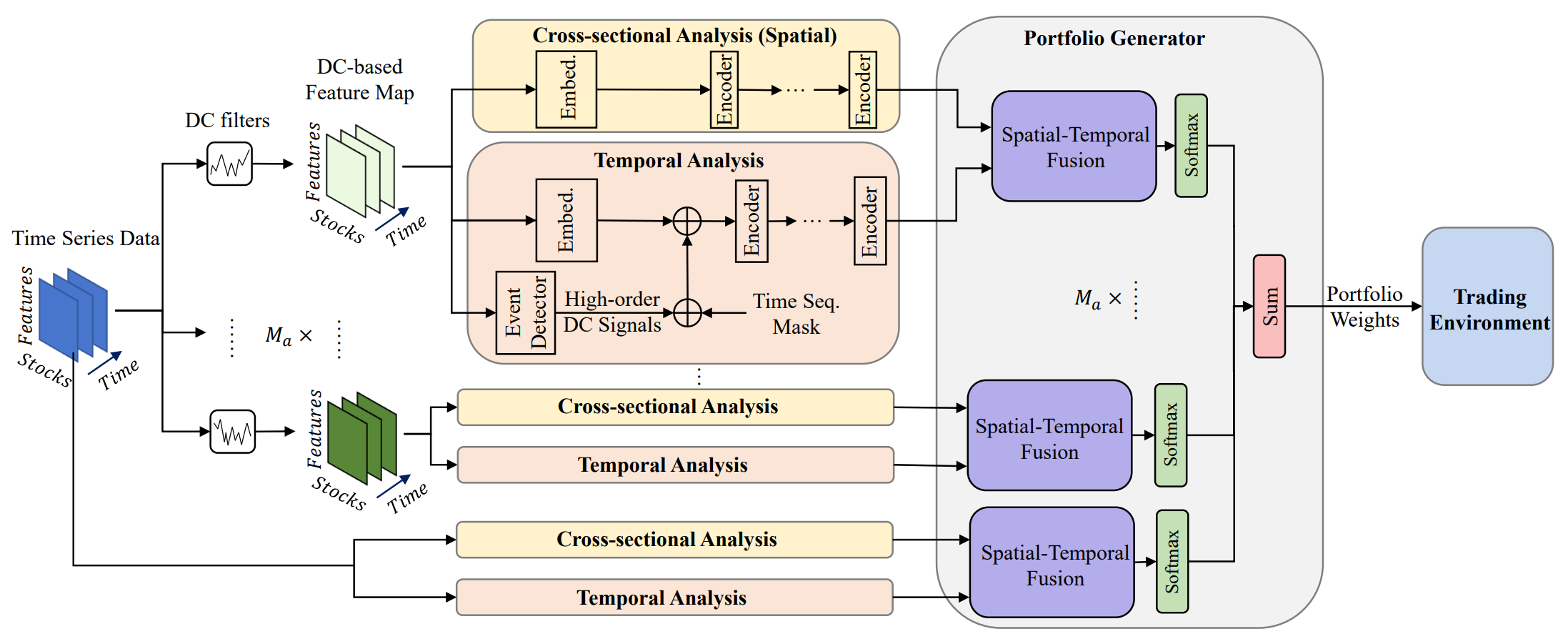
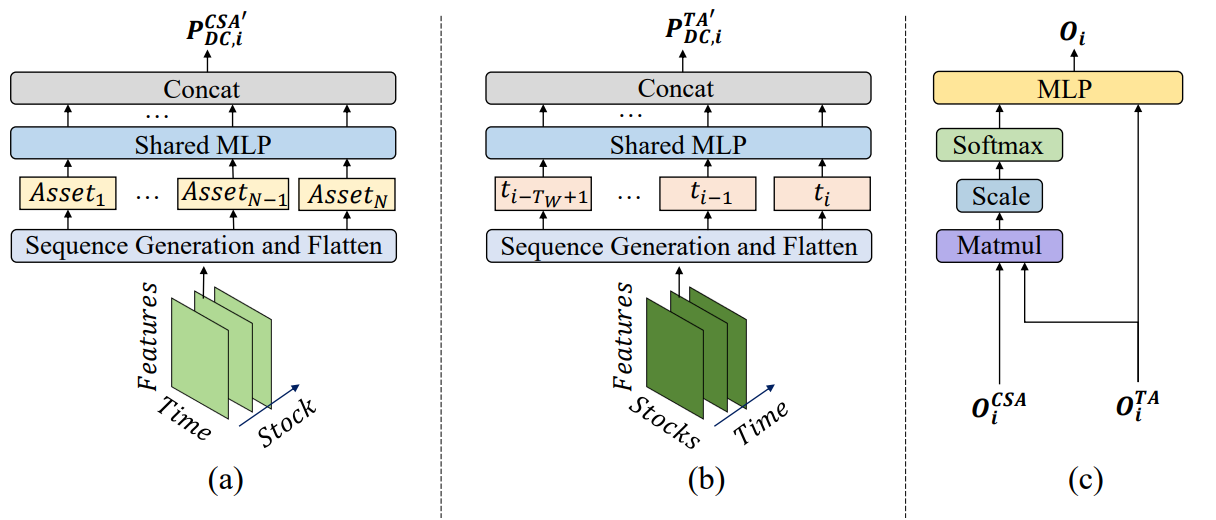
O framework MASAAT possui uma estrutura modular bem definida. Isso nos permite implementar cada módulo como uma classe separada e, em seguida, unir os objetos criados em uma única estrutura. No artigo anterior, já foram apresentados os algoritmos de implementação do objeto multiagente de transformação paralela da série temporal multimodal analisada em representações segmentadas lineares de diferentes escalas, CNeuronPLRMultiAgentsOCL. Também foi analisado o algoritmo do módulo de atenção cruzada entre ativos, CSACNeuronCrossSectionalAnalysis. Neste artigo, damos continuidade ao trabalho iniciado.

Módulo de análise temporal

Encerramos o artigo anterior com a análise do objeto CNeuronCrossSectionalAnalysis, no qual está implementada a funcionalidade do módulo CSA. Paralelamente a ele, dentro da estrutura do framework MASAAT, opera o módulo de análise temporal TA. Nele, é realizado o mapeamento de dependências entre pontos temporais individuais da sequência multimodal analisada. Ao examinarmos detalhadamente a estrutura desses dois módulos, podemos observar uma semelhança quase completa entre eles. No entanto, eles realizam análise cruzada dos dados brutos. Em outras palavras, observam a sequência analisada de diferentes ângulos.

Aqui surge uma solução evidente: transpor a sequência original antes de alimentar com dados o objeto CNeuronCrossSectionalAnalysis criado anteriormente. E nesse ponto, deparamo-nos com a necessidade de transpor duas dimensões dentro de um tensor tridimensional. Lembrando que devemos realizar análise paralela de várias sequências temporais multimodais. Mais precisamente, cada agente analisa sua própria escala da representação segmentada linear da sequência multimodal original. Assim, planejamos receber um tensor tridimensional de entrada [Agente, Ativo, Tempo] para o objeto, e para fins de análise das dependências entre os pontos temporais, precisaremos transpor os dados brutos nas duas últimas dimensões. Nossa biblioteca ainda não possui essa funcionalidade. Portanto, teremos que criá-la.

O problema de transposição de um tensor tridimensional nas duas últimas dimensões pode ser abordado de diversas formas. É claro que a primeira abordagem seria resolvê-lo de forma direta, isto é, criando um novo kernel no lado do programa OpenCL, com posterior construção de uma nova classe no programa principal para dar suporte a esse kernel. Essa provavelmente seria a solução mais eficiente do ponto de vista do uso de recursos computacionais. No entanto, ao mesmo tempo, é a solução mais custosa para o programador. Optamos por reduzir o esforço do programador em detrimento do uso de recursos computacionais, e organizar o processo utilizando três camadas de transposição previamente criadas, de forma sequencial. Mais precisamente, primeiro utilizamos uma camada de transposição de matriz bidimensional, unificando as duas últimas dimensões em uma só:

[Agente, [Ativo, Tempo]] → [[Tempo, Ativo], Agente]

Em seguida, usamos o objeto CNeuronTransposeRCDOCL para transpor o tensor tridimensional nas duas primeiras dimensões:

[Tempo, Ativo, Agente] → [Ativo, Tempo, Agente]

E por fim, usamos novamente a camada de transposição de matriz para retornar a dimensão dos agentes à primeira posição, unificando as outras duas dimensões em uma só:

[[Ativo, Tempo], Agente] → [Agente, [Tempo, Ativo]]

Esse processo descrito será estruturado dentro da nova classe CNeuronTransposeVRCOCL, cuja estrutura é apresentada a seguir.

class CNeuronTransposeVRCOCL  :  public CNeuronTransposeOCL
  {
protected:
   CNeuronTransposeOCL     cTranspose;
   CNeuronTransposeRCDOCL  cTransposeRCD;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer) override;

public:
                     CNeuronTransposeVRCOCL(void) {};
                    ~CNeuronTransposeVRCOCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint variables, uint count, uint window, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)  const override    {  return defNeuronTransposeVRCOCL; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Como objeto pai, utilizamos a camada de transposição de matriz bidimensional, que ao mesmo tempo desempenha a função da etapa final de reorganização dos dados. Isso nos permite declarar apenas dois objetos estáticos no corpo da nova classe. A inicialização de todos os objetos é feita no método Init, no qual os três tamanhos do tensor a ser transposto são passados como parâmetros.

bool CNeuronTransposeVRCOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                  uint variables, uint count, uint window,
                                  ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronTransposeOCL::Init(numOutputs, myIndex, open_cl, count * window, variables, optimization_type, batch))
      return false;

No corpo do método, chamamos o método homônimo da classe pai. No entanto, é importante observar que o objeto pai será utilizado para a etapa final da reorganização dos dados. Portanto, ao chamar o método da classe pai, devemos fornecer os parâmetros corretos. Nesse caso, a primeira dimensão é definida como o produto das duas últimas dimensões do tensor original. A dimensão restante, acredito que seja evidente.

Após a execução bem-sucedida das operações do método da classe pai, passamos para a inicialização dos objetos internos. Primeiro, inicializamos a camada primária de transposição de matriz. Seus parâmetros são inversos ao método da classe pai que acabamos de executar.

   if(!cTranspose.Init(0, 0, OpenCL, variables, count * window, optimization, iBatch))
      return false;

Em seguida, inicializamos o objeto de transposição das duas primeiras dimensões do tensor tridimensional. É exatamente aqui que trocaremos as posições das dimensões de ativos e tempo.

   if(!cTransposeRCD.Init(0, 1, OpenCL, count, window, variables, optimization, iBatch))
      return false;
//---
   return true;
  }

Resta-nos retornar o resultado lógico da execução das operações para o programa chamador e encerrar o método.

O método de inicialização apresentado é bastante simples e compreensível. O mesmo pode ser dito sobre os demais métodos da classe de transposição de tensor tridimensional apresentada. Por exemplo, no método de propagação para frente feedForward, chamamos sequencialmente os métodos homônimos dos objetos internos, e encerramos com o método homônimo da classe pai.

bool CNeuronTransposeVRCOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cTranspose.FeedForward(NeuronOCL))
      return false;
   if(!cTransposeRCD.FeedForward(cTranspose.AsObject()))
      return false;
//---
   return CNeuronTransposeOCL::feedForward(cTransposeRCD.AsObject());
  }

Quanto aos algoritmos dos métodos de propagação reversa, sugiro que você os analise por conta própria no anexo. Até porque o objeto não contém parâmetros treináveis.

E agora que temos o objeto necessário para a transposição dos dados, podemos prosseguir com a implementação do módulo de análise temporal TA, cujos algoritmos serão implementados na classe CNeuronTemporalAnalysis. A funcionalidade da nova classe será a mais simples possível. Apenas transpor os dados originais e, em seguida, utilizar os recursos do módulo de atenção cruzada entre ativos. A estrutura do novo objeto é apresentada a seguir.

class CNeuronTemporalAnalysis :  public CNeuronCrossSectionalAnalysis
  {
protected:
   CNeuronTransposeVRCOCL  cTranspose;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronTemporalAnalysis(void) {};
                    ~CNeuronTemporalAnalysis(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint heads, uint heads_kv,
                          uint units_count, uint layers, uint layers_to_one_kv,
                          uint variables, ENUM_OPTIMIZATION optimization_type, uint batch) override;
   //---
   virtual int       Type(void)   const override   {  return defNeuronTemporalAnalysis;   }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Como classe pai, utilizamos o objeto do módulo de atenção cruzada entre ativos. Como foi mencionado anteriormente, a funcionalidade desse objeto será utilizada na implementação do algoritmo principal. Apenas adicionamos um objeto interno de transposição de tensor tridimensional pelas duas últimas dimensões. A inicialização do novo objeto e dos herdados é realizada no método Init, que herda totalmente a estrutura de parâmetros do método equivalente da classe pai.

bool CNeuronTemporalAnalysis::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                   uint window, uint window_key, uint heads, uint heads_kv,
                                   uint units_count, uint layers, uint layers_to_one_kv, uint variables,
                                   ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronCrossSectionalAnalysis::Init(numOutputs, myIndex, open_cl, 3 * units_count, window_key, heads, heads_kv,
                                           window / 3, layers, layers_to_one_kv, variables, optimization_type, batch))
      return false;

No corpo do método, chamamos diretamente o método homônimo da classe pai, passando todos os parâmetros recebidos.

E aqui, vale a pena destacar alguns detalhes da nossa implementação. Em primeiro lugar, nos parâmetros externos recebemos as dimensões dos dados originais. E quero lembrar que planejamos transpor o tensor tridimensional dos dados brutos pelas duas últimas dimensões. Portanto, ao passar os parâmetros para o método de inicialização da classe pai, invertemos essas dimensões.

Em segundo lugar, é importante lembrar a estrutura dos dados originais recebidos. Na entrada desse objeto, esperamos receber os resultados do bloco multiagente de detecção de tendências. Ou seja, a cada vez, na entrada do modelo, fornecemos um tensor de representação segmentada linear da série temporal multimodal. A versão que implementamos dessa representação segmentada linear considera a extração de 3 elementos para armazenar os parâmetros de um único segmento direcionado da série temporal unitária. A lógica nos diz que, durante a análise, devemos tratá-los como uma unidade. Por isso, aumentamos em 3 vezes o tamanho da janela analisada e, proporcionalmente, reduzimos em 3 vezes o comprimento da sequência.

Após a execução bem-sucedida do método de inicialização da classe pai, chamamos o método homônimo do objeto interno de transposição de tensor tridimensional.

   if(!cTranspose.Init(0, 0, OpenCL,variables, units_count, window, optimization_type, batch))
      return false;
//---
   return true;
  }

E encerramos o método retornando o resultado lógico da execução das operações ao programa chamador.

Os algoritmos dos métodos de propagação para frente e propagação reversa do objeto de análise temporal CNeuronTemporalAnalysis são extremamente simples. Por isso, não vamos nos aprofundar neles agora, e deixamos sua análise para estudo individual. O código completo dessa classe e de todos os seus métodos pode ser encontrado no anexo do artigo.

Módulo de geração de portfólios

Na saída dos blocos CSA e TA, obtemos os dados brutos enriquecidos com informações sobre as dependências entre os ativos e os pontos temporais, respectivamente. Essas informações são combinadas por meio do mecanismo de atenção para que cada agente forme sua própria versão de portfólio de investimentos. Mais precisamente, cada agente primeiro gera suas próprias incorporações (embeddings) dos ativos levando em conta as dependências temporais, e então, utilizando uma camada totalmente conectada, é gerado um vetor de distribuição proporcional do pacote de investimentos, em que a soma de todos os elementos do vetor é igual a 1.

Recordando a representação matemática da função de geração do pacote de investimentos:

Com base nas sugestões de portfólio, é formada a representação final do pacote de investimentos.

Aqui, nos afastamos ligeiramente da apresentação original do framework MASAAT. No entanto, é importante destacar que esse afastamento é mais lógico do que matemático. Na prática, embora repitamos quase integralmente a função acima mencionada, mudamos um pouco nossa interpretação dos resultados obtidos.

A questão é que nosso objetivo difere ligeiramente do objetivo dos autores do framework. Na saída do modelo, gostaríamos de obter um vetor de ações do Agente contendo a direção da operação, o seu volume, bem como os níveis de stop loss e take profit. Para determinar o volume da operação, além dos dados sobre a dinâmica do ativo financeiro analisado, também precisamos de informações sobre o estado da conta, que estão ausentes nos dados brutos. Portanto, esperamos que, na saída do nosso objeto de implementação das abordagens do framework MASAAT, seja produzido um estado oculto contendo a incorporação de uma análise abrangente da situação atual do mercado.

A parte final da funcionalidade do framework MASAAT será implementada no objeto CNeuronPortfolioGenerator, cuja estrutura é apresentada abaixo.

class CNeuronPortfolioGenerator  :  public CNeuronBaseOCL
  {
protected:
   uint              iAssets;
   uint              iTimePoints;
   uint              iAgents;
   uint              iDimension;
   //---
   CNeuronBaseOCL          cAssetTime[2];
   CNeuronTransposeVRCOCL  cTransposeVRC;
   CNeuronSoftMaxOCL       cSoftMax;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)  override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer) override { return false; }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                                                                   CBufferFloat *SecondGradient, 
                                                ENUM_ACTIVATION SecondActivation = None) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronPortfolioGenerator(void) {};
                    ~CNeuronPortfolioGenerator(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint assets, uint time_points, uint dimension,
                          uint agents,  uint projection,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const override   {  return defNeuronPortfolioGenerator;   }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Na estrutura da nova classe, declaramos diversos objetos internos, cuja funcionalidade será explorada durante a implementação dos métodos. Todos os objetos internos são declarados de forma estática, o que nos permite deixar os métodos construtor e destrutor da classe vazios. A inicialização de todos os objetos declarados e herdados é feita no método Init. E aqui, vale dizer, há uma série de particularidades.

bool CNeuronPortfolioGenerator::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                     uint assets, uint time_points, uint dimension,
                                     uint agents, uint projection,
                                     ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(assets <= 0 || time_points <= 0 || dimension <= 0 || agents <= 0)
      return false;

Nos parâmetros do método, recebemos diversos valores cujo significado precisa ser explicado:

assets — quantidade de ativos analisados no módulo CSA;
time_points — quantidade de pontos temporais analisados no módulo TA;
dimension — dimensionalidade do vetor de incorporação de um elemento da sequência analisada (comum aos módulos CSA e TA);
agents — quantidade de agentes;
projection — tamanho da projeção do estado analisado na saída do módulo.

No corpo do método, verificamos imediatamente os valores dos parâmetros. Todos eles devem ser, no mínimo, maiores que "0". Em seguida, chamamos o método de inicialização da classe pai, passando a ele a dimensionalidade da projeção do estado analisado. Esse é exatamente o tipo de tensor que esperamos obter na saída do módulo.

   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, projection, optimization_type, batch))
      return false;

Após a execução bem-sucedida das operações do método da classe pai, armazenamos os valores dos parâmetros externos em variáveis internas.

   iAssets = assets;
   iTimePoints = time_points;
   iDimension = dimension;
   iAgents = agents;

Em seguida, passamos à inicialização dos objetos internos. E aqui é necessário retomar a fórmula apresentada anteriormente. Dela, depreendemos que os resultados do módulo de análise temporal TA são utilizados duas vezes. Primeiro na forma transposta, e outra, não.

Gostaria de lembrar que, na saída do módulo TA, obtemos um tensor tridimensional com dimensões [Agente, Tempo, Incorporação]. Portanto, neste caso, precisamos utilizar o objeto de transposição do tensor tridimensional nas duas últimas dimensões.

   if(!cTransposeVRC.Init(0, 0, OpenCL, iAgents, iTimePoints, iDimension, optimization, iBatch))
      return false;

Depois, é necessário multiplicar os resultados do módulo CSA pelos dados transpostos do módulo TA. O método de multiplicação de matrizes foi herdado da classe pai. No entanto, para registrar os resultados, inicializamos uma camada totalmente conectada.

   if(!cAssetTime[0].Init(0, 1, OpenCL, iAssets * iTimePoints * iAgents, optimization, iBatch))
      return false;
   cAssetTime[0].SetActivationFunction(None);

Os valores obtidos são normalizados por meio da função SoftMax.

   if(!cSoftMax.Init(0, 2, OpenCL, cAssetTime[0].Neurons(), optimization, iBatch))
      return false;
   cSoftMax.SetHeads(iAssets * iAgents);

Deve-se observar que a normalização dos dados é feita no contexto de cada ativo individual para cada agente. Por isso, o número de cabeças de normalização será definido como o produto entre o número de ativos e o número de agentes.

Os coeficientes normalizados, obtidos como resultado dessa operação, representam os pesos de atenção atribuídos a cada ponto temporal no nível de cada ativo, separados por agente. Multiplicando a matriz desses coeficientes pelos resultados do módulo TA, obtemos as incorporações dos ativos analisados. Para registrar essas incorporações, inicializamos uma camada totalmente conectada.

   if(!cAssetTime[1].Init(Neurons(), 3, OpenCL, iAssets * iDimension * iAgents, optimization, iBatch))
      return false;
   cAssetTime[1].SetActivationFunction(None);
//---
   return true;
  }

Para projetar o conjunto de incorporações obtidas de todos os agentes em uma única representação do estado analisado do ambiente, utilizamos uma camada totalmente conectada. E aqui vale destacar o fato de que utilizamos exatamente o objeto da camada totalmente conectada como classe pai. Aproveitando essa estrutura, não criamos uma camada totalmente conectada interna adicional. Sua funcionalidade será executada pelos recursos herdados da classe pai. Apenas no último nível interno, indicamos o número de conexões de saída como sendo igual ao tamanho da projeção fornecido pelo programa externo.

E após a inicialização bem-sucedida de todos os objetos internos, encerramos o método retornando previamente os resultados da execução das operações ao programa chamador.

Na etapa seguinte do nosso trabalho, passamos à construção dos algoritmos de propagação para frente no método feedForward. Aqui, vale destacar que estamos lidando com duas fontes de dados brutos. Ao mesmo tempo, lembramos do uso duplo dos resultados do módulo de análise temporal. Esse fato nos obriga a utilizar exatamente esse fluxo de informações como o principal.

bool CNeuronPortfolioGenerator::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
  {
   if(!SecondInput)
      return false;
//---
   if(!cTransposeVRC.FeedForward(NeuronOCL))
      return false;

No corpo do método, verificamos a validade do ponteiro para a segunda fonte de dados e realizamos a transposição da primeira. Após essa preparação, partimos para os cálculos propriamente ditos. Primeiro, multiplicamos o tensor da segunda fonte de dados pelos dados transpostos da primeira.

   if(!MatMul(SecondInput, cTransposeVRC.getOutput(), cAssetTime[0].getOutput(), iAssets, iDimension, 
                                                                                 iTimePoints, iAgents))
      return false;

Os resultados são normalizados pela função SoftMax.

   if(!cSoftMax.FeedForward(cAssetTime[0].AsObject()))
      return false;

E então multiplicamos pelos dados brutos do fluxo principal de informações.

   if(!MatMul(cSoftMax.getOutput(), NeuronOCL.getOutput(), cAssetTime[1].getOutput(), iAssets, iTimePoints,
                                                                                      iDimension, iAgents))
      return false;

Agora, com os recursos da classe pai, projetamos os dados obtidos no subespaço especificado.

   return CNeuronBaseOCL::feedForward(cAssetTime[1].AsObject());
  }

Retornamos o resultado lógico da execução das operações ao programa chamador e encerramos o método.

Após concluir a organização do processo de propagação para frente, passamos à construção dos algoritmos de propagação reversa. E aqui, começamos analisando o método de distribuição do gradiente do erro calcInputGradients.

bool CNeuronPortfolioGenerator::calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                                     CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = -1)
  {
   if(!NeuronOCL || !SecondGradient || !SecondInput)
      return false;

Nos parâmetros do método, recebemos ponteiros para os objetos de dados brutos e seus respectivos gradientes de erro para ambos os fluxos de informação. No corpo do método, verificamos imediatamente a validade dos ponteiros recebidos, Pois, caso contrário, todas as operações subsequentes seriam inviáveis.

Como se sabe, a propagação do gradiente de erro ocorre seguindo exatamente o fluxo informacional da propagação para frente, porém no sentido inverso. As operações desse método começam com a chamada ao método homônimo de distribuição do gradiente de erro da classe pai até o objeto interno.

   if(!CNeuronBaseOCL::calcInputGradients(cAssetTime[1].AsObject()))
      return false;

Em seguida, chamamos o método de distribuição do gradiente de erro da operação de multiplicação de matrizes, onde encaminhamos os dados ao nível dos dados brutos e da camada interna SoftMax.

   if(!MatMulGrad(cSoftMax.getOutput(), cSoftMax.getGradient(),
                  NeuronOCL.getOutput(), cTransposeVRC.getPrevOutput(),
                  cAssetTime[1].getGradient(),
                  iAssets, iTimePoints, iDimension, iAgents))
      return false;

No entanto, lembramos que o gradiente de erro deve chegar ao nível dos dados brutos do fluxo principal por meio de dois fluxos de informação. Por isso, os valores obtidos nesta etapa são armazenados em um buffer livre de transposição de dados.

Depois, transmitimos o gradiente de erro pela camada da função SoftMax até o nível dos coeficientes não normalizados.

   if(!cAssetTime[0].calcHiddenGradients(cSoftMax.AsObject()))
      return false;

E então distribuímos o gradiente de erro obtido até o nível da segunda fonte de dados e da nossa camada de transposição.

   if(!MatMulGrad(SecondInput, SecondGradient,
                  cTransposeVRC.getOutput(), cTransposeVRC.getGradient(),
                  cAssetTime[0].getGradient(),
                  iAssets, iDimension, iTimePoints, iAgents))
      return false;

Aqui, verificamos imediatamente a função de ativação da segunda fonte de dados e, se necessário, ajustamos o gradiente de erro com a derivada correspondente.

   if(SecondActivation != None)
      if(!DeActivation(SecondInput, SecondGradient, SecondGradient, SecondActivation))
         return false;

Neste ponto, o gradiente de erro foi transferido ao nível do módulo CSA (neste caso, a segunda fonte de dados). Resta concluir a transmissão do gradiente de erro ao módulo de atenção temporal (fonte principal de dados brutos). Este módulo recebe dados por dois fluxos de informação: a partir dos coeficientes de atenção e diretamente dos resultados. Os dados de ambos os fluxos estão agora armazenados em buffers distintos do objeto de transposição de dados. No buffer principal de gradientes, encontram-se os valores transpostos do fluxo informacional dos coeficientes de atenção. Utilizaremos a funcionalidade principal do objeto de transposição de tensor tridimensional para reverter esses dados ao nível dos dados brutos.

   if(!NeuronOCL.calcHiddenGradients(cTransposeVRC.AsObject()) ||
      !SumAndNormilize(NeuronOCL.getGradient(), cTransposeVRC.getPrevOutput(), NeuronOCL.getGradient(),
                                                                        iDimension, false, 0, 0, 0, 1))
      return false;

Em seguida, somamos os dados provenientes dos dois fluxos de informação. Para concluir as operações do método, ajustamos o gradiente de erro com a derivada da função de ativação do fluxo informacional principal.

   if(NeuronOCL.Activation() != None)
      if(!DeActivation(NeuronOCL.getOutput(), cTransposeVRC.getPrevOutput(), cTransposeVRC.getPrevOutput(), 
                                                                                   NeuronOCL.Activation()))
         return false;
//---
   return true;
  }

E saímos do método, retornando o resultado lógico da execução das operações ao programa chamador.

Quanto ao método de atualização dos parâmetros do modelo, sugiro que você o explore por conta própria. O código completo da classe CNeuronPortfolioGenerator e de todos os seus métodos está incluído no anexo.

Montando o framework MASAAT

Já implementamos o funcionamento dos blocos individuais do framework MASAAT e chegou o momento de reuni-los em uma estrutura única. Essa tarefa será realizada dentro da classe CNeuronMASAAT. Como classe pai, foi escolhido o CNeuronPortfolioGenerator, criado anteriormente, que representa o último bloco da nossa implementação das abordagens do framework MASAAT. Isso nos permite não declarar esse módulo entre os objetos internos da nossa classe. Toda a funcionalidade necessária será herdada do objeto pai. A estrutura da nova classe é apresentada a seguir.

class CNeuronMASAAT  :  public CNeuronPortfolioGenerator
  {
protected:
   CNeuronTransposeOCL              cTranspose;
   CNeuronPLRMultiAgentsOCL         cPLR;
   CNeuronBaseOCL                   cConcat;
   CNeuronCrossSectionalAnalysis    cCrossSectionalAnalysis;
   CNeuronTemporalAnalysis          cTemporalAnalysis;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)  override
     { return        feedForward(NeuronOCL); }
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                       CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None) override
     { return        calcInputGradients(NeuronOCL); }
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMASAAT(void)  {};
                    ~CNeuronMASAAT(void)  {};
   //---
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint heads, uint units_cout,
                          uint layers, vector<float> &min_distance, uint projection,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const override   {  return defNeuronMASAAT;   }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Na estrutura apresentada da nova classe, vemos a declaração de todos os objetos criados anteriormente. E não é difícil imaginar que o algoritmo de todos os métodos dessa classe será baseado na chamada sequencial dos métodos homônimos dos objetos internos. E a sequência dessas chamadas será esclarecida durante a implementação dos métodos.

Todos os objetos internos são declarados de forma estática, o que nos permite deixar o construtor e o destrutor da classe “vazios”. A inicialização de todos os objetos declarados e herdados, como de costume, é realizada no método Init.

bool CNeuronMASAAT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                         uint window, uint window_key, uint heads, uint units_cout,
                         uint layers, vector<float> &min_distance, uint projection,
                         ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronPortfolioGenerator::Init(numOutputs, myIndex, open_cl, window, units_cout / 3,
                                       window_key, (uint)min_distance.Size() + 1, projection, optimization_type, batch))
      return false;

Nos parâmetros deste método, recebemos as constantes principais que indicam a estrutura dos dados brutos e definem a arquitetura do objeto que será inicializado.

No corpo do método, como já virou tradição, chamamos imediatamente o método homônimo da classe pai, onde já está estruturado o processo de inicialização dos objetos herdados e das interfaces básicas. No entanto, é importante observar que, neste caso, utilizamos a classe pai como um bloco funcional completo dentro dos algoritmos que estamos construindo. Esse módulo será utilizado na saída da nossa implementação do framework MASAAT. Por isso, precisamos antecipar mentalmente a definição dos parâmetros de inicialização do objeto pai.

Assim, na entrada do objeto pai, planejamos fornecer os resultados dos nossos módulos CSA e TA. Nestes, a quantidade de ativos analisados é igual ao tamanho da janela dos dados brutos, e a quantidade de pontos temporais é esperada com base no comprimento da sequência dos dados brutos. Mas espere: estamos planejando transformar a sequência temporal multimodal original em uma representação segmentada linear. Isso significa que o número de pontos temporais será três vezes menor. Como resultado, ao passarmos os parâmetros para o método da classe pai, dividimos o tamanho da sequência original por 3.

Analisando os parâmetros do método pai, chegamos ao número de agentes. Como discutido anteriormente, ao construir o objeto de transformação multiagente da série temporal em uma representação segmentada linear, a quantidade de agentes é determinada pelo tamanho do vetor de desvios máximos dos indicadores. Mas se observarmos a análise feita pelos autores do MASAAT sobre o impacto dos diferentes componentes do framework no resultado, veremos que utilizar a representação segmentada linear da série temporal em conjunto com a original melhora a eficiência do modelo. Portanto, aumentamos o número de agentes em 1. Esse último agente trabalhará com a representação original da série temporal analisada.

Os demais parâmetros são passados sem alterações.

Após a execução bem-sucedida das operações do método da classe pai, passamos à inicialização dos objetos recém-declarados. E aqui, iniciamos com a inicialização do objeto de transposição dos dados brutos.

   if(!cTranspose.Init(0, 0, OpenCL, units_cout, window, optimization, iBatch))
      return false;

Em seguida, inicializamos o objeto de transformação multiagente da sequência analisada para uma representação segmentada linear.

   if(!cPLR.Init(0, 1, OpenCL, window, units_cout, false, min_distance, optimization, iBatch))
      return false;

Resultados dessa transformação são concatenados com os dados brutos. Para isso, inicializamos uma camada totalmente conectada com tamanho correspondente.

   if(!cConcat.Init(0, 2, OpenCL, cTranspose.Neurons() + cPLR.Neurons(), optimization, iBatch))
      return false;

E resta apenas inicializar os objetos dos módulos CSA e TA. Ambos os módulos trabalham com a mesma fonte de dados, portanto recebem os mesmos parâmetros.

   if(!cCrossSectionalAnalysis.Init(0, 3, OpenCL, units_cout, window_key, heads, heads / 2, window, layers, 1, 
                                                                                 iAgents, optimization, iBatch))
      return false;
   if(!cTemporalAnalysis.Init(0, 4, OpenCL, units_cout, window_key, heads, heads / 2, window, layers, 1, 
                                                                                  iAgents, optimization, iBatch))
      return false;
//---
   return true;
  }

Após a inicialização bem-sucedida de todos os objetos internos, retornamos o resultado lógico da execução das operações ao programa chamador e encerramos o método.

Em seguida, passamos à construção do algoritmo de propagação para frente no método feedForward. Aqui tudo é relativamente simples. Nos parâmetros do método, recebemos um ponteiro para o objeto de dados brutos, que é imediatamente passado para o método homônimo do objeto de transposição de dados.

bool CNeuronMASAAT::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cTranspose.FeedForward(NeuronOCL))
      return false;

Depois, transformamos os dados brutos recebidos em várias versões da representação segmentada linear da série temporal e concatenamos os valores obtidos com os dados brutos, utilizando sua forma transposta.

   if(!cPLR.FeedForward(cTranspose.AsObject()))
      return false;
   if(!Concat(cTranspose.getOutput(), cPLR.getOutput(), cConcat.getOutput(), cTranspose.Neurons(), cPLR.Neurons(), 1))
      return false;

Os dados assim preparados são passados aos módulos CSA e TA, e os resultados obtidos são enviados ao método homônimo da classe pai.

   if(!cCrossSectionalAnalysis.FeedForward(cConcat.AsObject()))
      return false;
   if(!cTemporalAnalysis.FeedForward(cConcat.AsObject()))
      return false;
//---
   return CNeuronPortfolioGenerator::feedForward(cTemporalAnalysis.AsObject(), cCrossSectionalAnalysis.getOutput());
  }

Em seguida, finalizamos o método, retornando previamente o resultado lógico da execução das operações ao programa chamador.

Por trás da aparente simplicidade do método de propagação para frente, há uma complexa ramificação dos fluxos informacionais. Observe que utilizamos duas vezes os dados brutos transpostos e o tensor concatenado. Isso leva a algumas complicações na organização do processo de distribuição do gradiente de erro no método calcInputGradients.

Nos parâmetros do método de distribuição do gradiente de erro, recebemos um ponteiro para o objeto de dados brutos, ao qual devemos transmitir o gradiente de erro. No corpo do método, verificamos imediatamente a validade do ponteiro recebido.

bool CNeuronMASAAT::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
   if(!prevLayer)
      return false;

Depois, chamamos o método homônimo da classe pai para distribuir o gradiente de erro entre os módulos CSA e TA, de acordo com a influência de cada um no resultado do modelo.

   if(!CNeuronPortfolioGenerator::calcInputGradients(cTemporalAnalysis.AsObject(),
         cCrossSectionalAnalysis.getOutput(),
         cCrossSectionalAnalysis.getGradient(),
         (ENUM_ACTIVATION)cCrossSectionalAnalysis.Activation()))
      return false;

Ambos os módulos mencionados operam com os dados do tensor concatenado. Portanto, devemos transmitir o gradiente de erro ao nível do tensor concatenado por dois fluxos informacionais. Primeiro, passamos o gradiente de erro de um dos módulos.

   if(!cConcat.calcHiddenGradients(cCrossSectionalAnalysis.AsObject()))
      return false;

Em seguida, usamos um truque com a substituição do buffer de gradiente de erro e obtemos os valores do segundo fluxo de informação, realizando a soma das informações de ambas as fontes.

   CBufferFloat *grad = cConcat.getGradient();
   if(!cConcat.SetGradient(cConcat.getPrevOutput(), false) ||
      !cConcat.calcHiddenGradients(cTemporalAnalysis.AsObject()) ||
      !SumAndNormilize(grad, cConcat.getGradient(), grad, 1, 0, 0, 0, 0, 1) ||
      !cConcat.SetGradient(grad, false))
      return false;

O gradiente de erro do tensor concatenado é então distribuído entre os objetos que o compõem. Lembrando que os dados devem ser enviados ao nível do objeto de transposição de dados brutos por outro fluxo informacional. Por isso, neste estágio, utilizamos um buffer de dados livre.

   if(!DeConcat(cTranspose.getPrevOutput(), cPLR.getGradient(), cConcat.getGradient(), cTranspose.Neurons(), 
                                                                                         cPLR.Neurons(), 1))
      return false;

E antes de prosseguir com o processo de distribuição do gradiente de erro entre os objetos, verificamos a necessidade de ajustá-lo com a derivada da função de ativação correspondente.

   if(cPLR.Activation() != None)
      if(!DeActivation(cPLR.getOutput(), cPLR.getGradient(), cPLR.getGradient(), cPLR.Activation()))
         return false;

Na etapa seguinte, transmitimos o gradiente de erro pelo objeto de transformação multiagente em representação segmentada linear da série temporal e somamos os valores provenientes dos dois fluxos de informação.

   if(!cTranspose.calcHiddenGradients(cPLR.AsObject()) ||
      !SumAndNormilize(cTranspose.getGradient(), cTranspose.getPrevOutput(), cTranspose.getGradient(), iDimension, 
                                                                                               false, 0, 0, 0, 1))
      return false;

Se necessário, ajustamos o gradiente de erro com a derivada da função de ativação e o transmitimos ao nível dos dados brutos.

   if(cTranspose.Activation() != None)
      if(!DeActivation(cTranspose.getOutput(), cTranspose.getGradient(), cTranspose.getGradient(), 
                                                                         cTranspose.Activation()))
         return false;
   if(!prevLayer.calcHiddenGradients(cTranspose.AsObject()))
      return false;
//---
   return true;
  }

Para finalizar o método, retornamos ao programa chamador o resultado lógico da execução das operações.

Com isso, encerramos a análise dos algoritmos de implementação das abordagens do framework MASAAT. O código completo de todas as classes e seus métodos apresentados está disponível no anexo. Também estão incluídos todos os programas utilizados na preparação do artigo, bem como as arquiteturas dos modelos. Faremos apenas uma breve observação sobre a arquitetura dos modelos. Nossa implementação do framework MASAAT foi incorporada ao modelo do Ator. Não entraremos agora na arquitetura completa do modelo. Ela foi praticamente mantida a partir dos trabalhos anteriores. Vamos apenas observar a declaração da nova camada.

No array dinâmico de dimensões da janela, indicamos o tamanho da janela dos dados analisados e o comprimento do tensor de estado oculto obtido na saída da camada.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMASAAT;
//--- Windows
     {
      int temp[] = {BarDescr, LatentCount};
      if(ArrayCopy(descr.windows, temp) < (int)temp.Size())
         return false;
     }

Os valores-limite para nossos 3 agentes foram definidos como uma progressão geométrica.

//--- Min Distance
     {
      vector<float> ones = vector<float>::Ones(3);
      vector<float> cs = ones.CumSum() - 1;
      descr.radius = pow(ones * 2, cs) * 0.01f;
     }

Os demais parâmetros mantêm valores usuais.

   descr.window_out = 32;
   descr.count = HistoryBars;
   descr.step = 4;               //Heads
   descr.layers = 3;             //Layers
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

A arquitetura completa dos modelos, como já mencionado, pode ser consultada no anexo.

Testes

Nosso trabalho de implementação das abordagens propostas pelos autores do framework MASAAT com os recursos do MQL5 chegou ao seu encerramento lógico. E agora partimos para a etapa mais crítica: a avaliação da eficácia das abordagens implementadas em dados históricos reais.

É importante destacar que estamos avaliando as abordagens implementadas, e não o framework MASAAT em sua apresentação original. Pois durante a implementação foram feitas alterações na versão original do framework.

Os modelos foram treinados com dados históricos do ano de 2023 para o ativo financeiro EURUSD, no timeframe H1. Todos os parâmetros dos indicadores analisados foram utilizados com as configurações padrão.

Para a fase inicial do treinamento, foi usada uma amostra de dados de treino reunida em pesquisas anteriores, que foi atualizada periodicamente ao longo do processo de treinamento para permitir adaptação à estratégia atual do Ator.

Após vários ciclos de treinamento e atualização da amostra, foi obtida uma política que demonstrou lucratividade tanto na amostra de treino quanto na amostra de teste.

Os testes da política final treinada foram realizados com dados históricos de janeiro de 2024, mantendo todos os demais parâmetros inalterados. Os resultados do teste são apresentados a seguir.

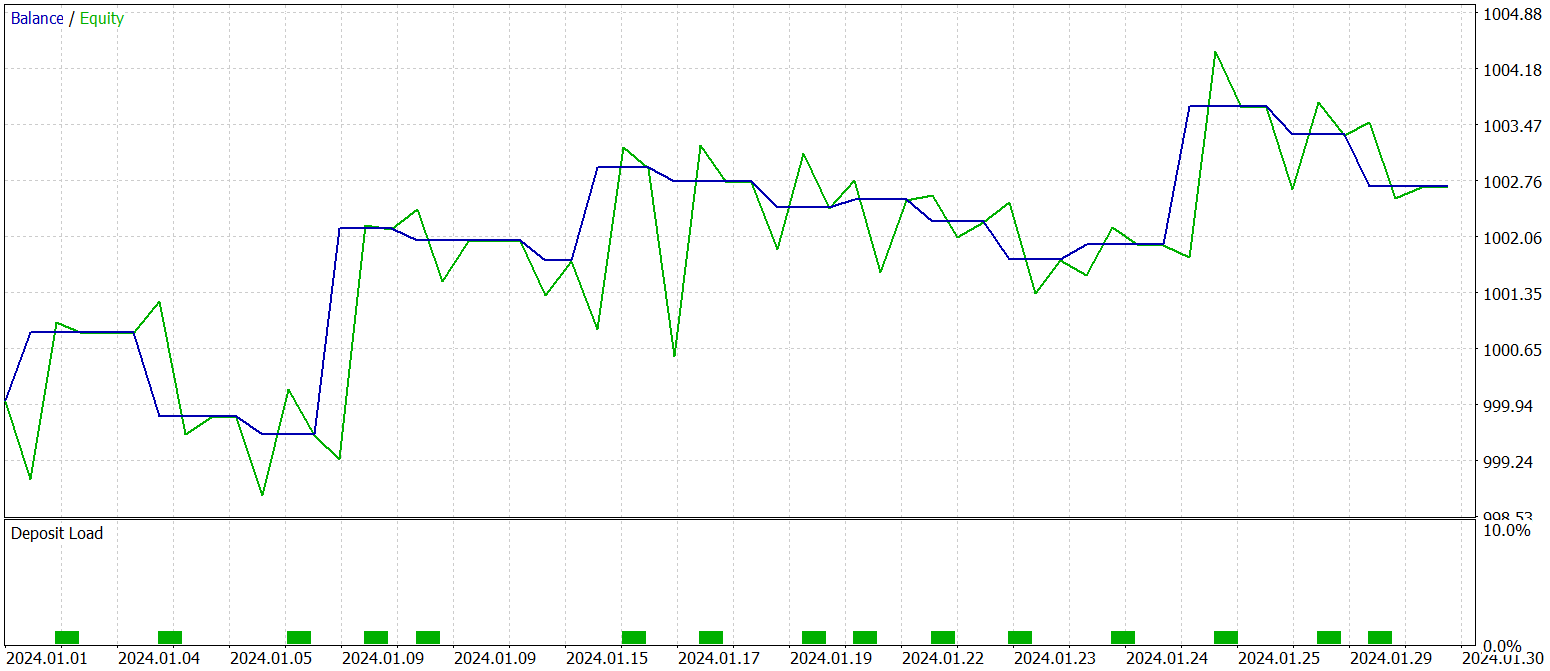
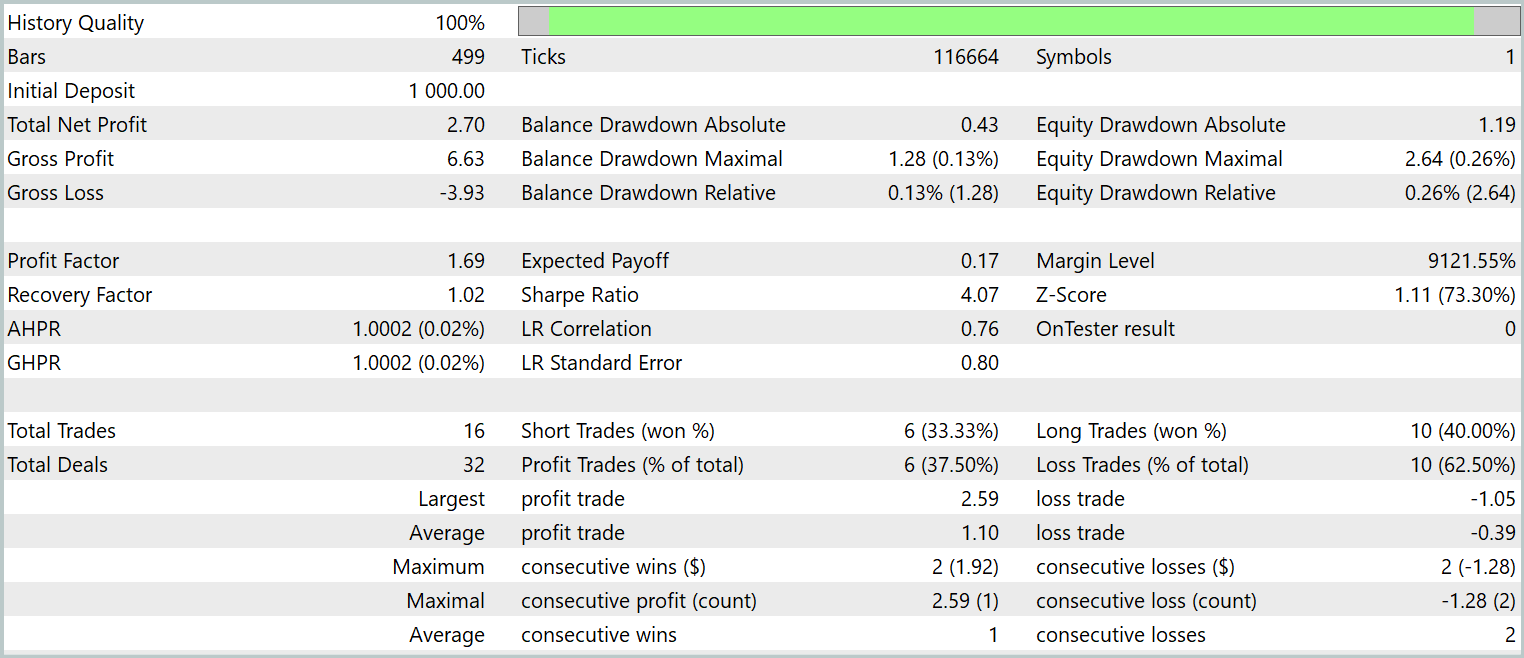
Como pode ser visto nos dados apresentados, durante o período de testes, o modelo realizou 16 operações de trading. E apenas pouco mais de um terço dessas operações foi encerrado com lucro. No entanto, a operação mais lucrativa supera o resultado equivalente das operações com prejuízo em 2,5 vezes. E, considerando os valores médios das operações, há um aumento de três vezes. Como consequência, observamos uma tendência clara de crescimento do saldo.

Considerações finais

Neste trabalho, exploramos a estrutura adaptativa multiagente MASAAT, desenvolvida para otimização de portfólios de investimento. MASAAT combina mecanismos de atenção e análise de séries temporais. Esse framework utiliza um conjunto de agentes de trading para análise multifacetada de dados de preços, o que contribui para reduzir vieses nas decisões de trading geradas. Cada agente aplica um mecanismo de análise cruzada baseado em atenção para identificar correlações entre ativos e pontos temporais dentro do período observado. As informações obtidas são então combinadas por meio de um módulo de fusão espaço-temporal, o que permite integrar dados de forma eficiente e melhorar a qualidade das estratégias de trading.

Na parte prática, implementamos nossa própria visão das abordagens propostas utilizando os recursos do MQL5. Incorporamos essas abordagens em um modelo e o treinamos com dados históricos reais. Os resultados dos testes da versão treinada do modelo indicam o potencial das abordagens propostas.

Referências

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA de coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA de coleta de exemplos com o método Real-ORL
3	Study.mq5	Expert Advisor	EA de treinamento de modelos
4	Test.mq5	Expert Advisor	EA para testes do modelo
5	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema
6	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de rede neural
7	NeuroNet.cl	Biblioteca	Biblioteca de código para o programa OpenCL

Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/16631

Arquivos anexados |

Baixar como ZIP

MQL5.zip (2222.68 KB)

Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.

Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.

Outros artigos do autor

Últimos Comentários | Ir para discussão (1)

Alexey Volchanskiy | 15 dez. 2024 em 20:23

Por que eles publicam artigos tão vergonhosos? O lucro do mês é de 0,27%, meu gato, batendo a pata acidentalmente, ganhará 50 vezes mais.

EA baseado em um aproximador universal MLP

Este artigo apresenta uma forma simples e acessível de usar uma rede neural em um EA, que não exige conhecimento aprofundado em aprendizado de máquina. O método elimina a necessidade de normalizar a função alvo e evita problemas como “explosão de pesos” e “paralisação da rede”, oferecendo um aprendizado intuitivo com controle visual dos resultados.

Reimaginando Estratégias Clássicas em MQL5 (Parte II): FTSE100 e Títulos Públicos do Reino Unido

Nesta série de artigos, exploramos estratégias de negociação populares e tentamos melhorá-las usando IA. No artigo de hoje, revisitamos a estratégia clássica de negociação baseada na relação entre o mercado de ações e o mercado de títulos.

Redes neurais em trading: Framework híbrido de negociação com codificação preditiva (StockFormer)

Apresentamos o sistema de negociação híbrido StockFormer, que combina codificação preditiva e algoritmos de aprendizado por reforço (RL). O framework utiliza 3 ramos Transformer com mecanismo integrado Diversified Multi-Head Attention (DMH-Attn), que melhora o módulo de atenção padrão com um bloco Feed-Forward multicabeça, permitindo capturar padrões de séries temporais em diferentes subespaços.

Otimização de portfólio em Forex: Síntese de VaR e teoria de Markowitz

Como se realiza o trading com portfólio em Forex? Como pode ser feita a síntese entre a teoria de portfólio de Markowitz para otimizar as proporções do portfólio e o modelo VaR para otimizar o risco do portfólio? Vamos criar um código baseado na teoria de portfólio, onde, de um lado, obtemos um risco reduzido e, do outro, uma rentabilidade de longo prazo aceitável.