Rede neural na prática: A prática leva a perfeição

Introdução

Olá pessoal, e sejam bem-vindos a mais um artigo sobre Rede Neural.

No artigo anterior Rede neural na prática: O primeiro neurônio, construímos o nosso primeiro neurônio. Porém nem tudo são flores, quando o assunto é programação. Muita gente simplesmente criar, ou melhor cópia um código e começar a usar. Definitivamente, isto não é, nem de longe, um problema. Fazer isto não é errado. Muito pelo contrário. É uma prática bastante inteligente, desde é claro você, estude o código e tente melhorar ele de forma que ele se adeque as suas necessidades. Errado é você querer usar algo sem entender. Ou pior, reclamar de algo, ou sair falando de algo do qual você definitivamente não tem nenhum conhecimento.

Aquele mesmo código, que foi visto no artigo anterior. Apesar de funcionar. Não é de forma alguma algo que você deva usar em uma aplicação mais complexa. Isto para que as coisas sejam executadas em um tempo adequado. Ou até mesmo dentro de uma certa perspectiva de resultados.

Para que você, meu caro e estimado leitor, consiga entender do que estou falando. Vamos ver como as coisas estão. E os problemas que podemos ter se as mudarmos só um pouco. Mas para que fique mais claro, vamos ver isto em um novo tópico.

Inviabilizando o tempo de execução

Muito bem, nosso singelo e único neurônio, pode ser visto no código abaixo.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define macroRandom (rand() / (double)SHORT_MAX)
05. #define macroSigmoid(a) (1.0 / (1 + MathExp(-a)))
06. //+------------------------------------------------------------------+
07. double Train[][3] {
08.                     {0, 0, 0},
09.                     {0, 1, 0},
10.                     {1, 0, 0},
11.                     {1, 1, 1},
12.                   };
13. //+------------------------------------------------------------------+
14. const uint nTrain = Train.Size() / 3;
15. const double eps = 1e-3;
16. //+------------------------------------------------------------------+
17. double Cost(const double w0, const double w1, const double b)
18. {
19.     double err;
20. 
21.     err = 0;
22.     for (uint c = 0; c < nTrain; c++)
23.         err += MathPow((macroSigmoid((Train[c][0] * w0) + (Train[c][1] * w1) + b) - Train[c][2]), 2);
24. 
25.     return err / nTrain;
26. }
27. //+------------------------------------------------------------------+
28. void OnStart()
29. {
30.     double  w0, w1, err, ew0, ew1, eb, bias;
31.     ulong count, it0, it1;
32. 
33.     Print("The Neuron - Tutor ...");
34.     MathSrand(512);
35.     w0 = (double)macroRandom;
36.     w1 = (double)macroRandom;
37.     bias = (double)macroRandom;
38. 
39.     it0 = GetTickCount();
40. 
41.     for (count = 0; (count < ULONG_MAX) && ((err = Cost(w0, w1, bias)) > eps); count++)
42.     {
43.         ew0 = (Cost(w0 + eps, w1, bias) - err) / eps;
44.         ew1 = (Cost(w0, w1 + eps, bias) - err) / eps;
45.         eb  = (Cost(w0, w1, bias + eps) - err) / eps;
46.         w0 -= (ew0 * eps);
47.         w1 -= (ew1 * eps);
48.         bias -= (eb * eps);
49.     }
50. 
51.     it1 = GetTickCount();
52.     Print("Time: ", (it1 - it0) / 1000.0, " seconds.");
53.     PrintFormat("%I64u > w0: %.4f %.4f || w1: %.4f %.4f || b: %.4f %.4f || %.4f", count, w0, ew0, w1, ew1, bias, eb, err);
54.     Print("w0 = ", w0, " || w1 = ", w1, " || Bias = ", bias);
55.     Print("Error Weight 0: ", ew0);
56.     Print("Error Weight 1: ", ew1);
57.     Print("Error Bias: ", eb);
58.     Print("Error: ", err);
59. 
60.     Print("Testing the neuron...");
61.     for (uchar p0 = 0; p0 < 2; p0++)
62.         for (uchar p1 = 0; p1 < 2; p1++)
63.             PrintFormat("%d AND %d IS %f", p0, p1, macroSigmoid((p0 * w0) + (p1 * w1) + bias));
64. 
65.     Print("************************************");
66. }
67. //+------------------------------------------------------------------+

Mudei algumas coisas no código, frente ao que foi postado no artigo anterior. E o motivo para isto ter sido feito é bem simples. Quero mostrar como uma simples mudança pode afetar de maneira gritante, todo o tempo de execução. Assim como também os resultados esperados. Este código acima, se for executado, no MetaTrader 5. Irá gerar algo muito parecido com o que pode ser visto na imagem abaixo.

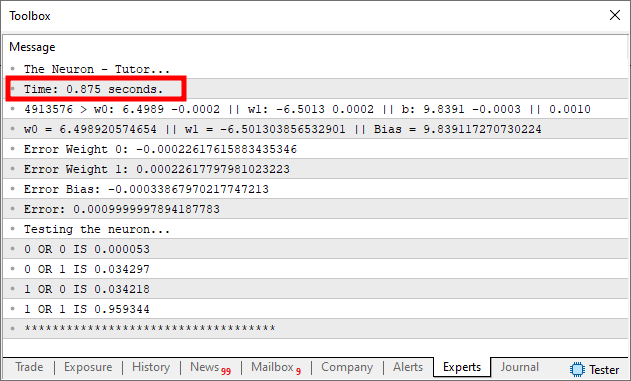
Preste atenção a algumas informações vistas nesta imagem acima. A mais evidente, é claro, estou colocando em destaque. Que é justamente o tempo de execução do código. Este tempo leva em consideração apenas o fato de estarmos fatorando as coisas. Você pode ver isto, olhando o código. Veja que na linha 39, capturamos o exato momento, antes de começarmos a fatorar os dados de treinamento do neurônio. E na linha 51, capturamos novamente o exato momento em que o treinamento terminou. A diferença entre estes dois valores, nos dá o tempo de execução do treinamento. Note que na linha 52, fazemos um pequeno cálculo. Como o tempo capturado gira na casa dos milissegundos. Dividindo a diferença de valor entre os tempos por mil, temos um valor aproximado do tempo em termos de segundos. Este mesmo tempo é o que está sendo destacado na imagem acima.

Agora veja o que vamos fazer. Na linha 15 deste mesmo código visto acima, estamos definindo o erro como 0,001. Agora o que acontece em termos de tempo de execução para este mesmo código, se mudarmos o erro para 0,0001 ou 1e-4?

Bem, faça isto em sua máquina para sentir o que acontece. Mas de qualquer forma, você terá algo muito próximo do que é visto na imagem abaixo.

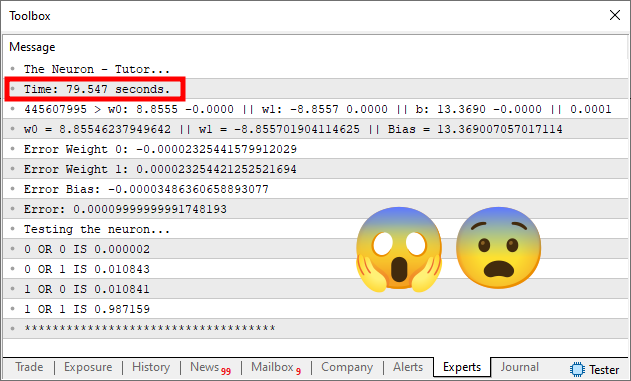
Agora observe o seguinte. O simples fato de termos mudado o erro de 1e-3 para 1e-4, faz com que o tempo de execução venha a saltar de menos de 1 segundo para quase 80 segundos. Isto mesmo que você está vendo. O simples fato de termos mudado a precisão em apenas 10 vezes, fez com que o tempo de execução viesse a aumentar em mais de 80 vezes.

E justamente este tipo de coisa, que acaba destruindo os sonhos de muitos iniciantes. Mas principalmente de pessoas que não fazem a mínima ideia de como, programação não é uma das tarefas mais simples. Quando dizemos que cada programa, muitas das vezes é voltado para executar uma dada tarefa. Muitos ficam perplexos em ouvir tal coisa. Ainda mais quando diversas outras pessoas dizem que uma rede neural, consegue fazer qualquer coisa de forma muito rápida. Sendo que na verdade não é bem assim.

Quero chamar a sua atenção para este fato, meu caro leitor. Antes de entrarmos na questão de adicionar mais neurônios na rede. Saber como a rede será construída e para qual propósito, faz toda a diferença. Para provar isto, vamos pegar este mesmo simples e singelo neurônio e o mudar para algo que uma pouco diferente. Porém voltado para resolver o mesmo problema visto no código. Ou seja, vamos fazer com que este neurônio se torne especialista no que precisa fazer. Não em termos de fatoração, mas em termos de número de entradas. Para separar as coisas, vamos ver isto em um outro tópico.

Ajustando o código para melhores resultados

Muito bem, vamos pensar o seguinte: Qual o sentido em um único neurônio, gastar 80 vezes mais tempo, para melhorar a precisão em apenas 10 vezes? Não faz nenhum sentido este tipo de coisa. Porém, caso saibamos de antemão que o neurônio, em todo o seu tempo de existência, irá trabalhar com duas entradas e uma saída. Podemos melhorar o código dele. Isto fará com que ele seja mais rápido, a fim de conseguir aprender as coisas de uma forma mais prática.

Fazer tal mudança pode parecer ser algo extremamente complicado, e só quem tem um grande conhecimento irá conseguir tal façanha. Porém, não é bem assim. Tudo que você precisa entender, meu caro leitor, é como o programa funciona e qual o seu propósito. Se você souber isto, e entender como o programa foi escrito em uma dada linguagem. Conseguirá, mesmo que demore um pouco, implementar uma solução bem melhor.

E para provar isto. Vamos modificar o código do tópico anterior. Mas mantendo o código original ainda presente. O objetivo disto é entender se estamos no caminho certo ou não. Um bom programador, nunca tenta mudar um código desconhecido. Ele tenta primeiro entender o código, entender como ele funciona e assim tentar promover alguma melhoria no mesmo. Seguindo estas premissas, o novo código pode ser visto logo abaixo:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define macroRandom (rand() / (double)SHORT_MAX)
05. #define macroSigmoid(a) (1.0 / (1 + MathExp(-a)))
06. //+------------------------------------------------------------------+
07. #define def_Fast
08. //+------------------------------------------------------------------+
09. double Train[][3] {
10.                     {0, 0, 0},
11.                     {0, 1, 0},
12.                     {1, 0, 0},
13.                     {1, 1, 1},
14.                   };
15. //+------------------------------------------------------------------+
16. const uint nTrain = Train.Size() / 3;
17. const double eps = 1e-4;
18. //+------------------------------------------------------------------+
19. double Cost(const double w0, const double w1, const double b)
20. {
21.     double err;
22. 
23.     err = 0;
24.     for (uint c = 0; c < nTrain; c++)
25.         err += MathPow((macroSigmoid((Train[c][0] * w0) + (Train[c][1] * w1) + b) - Train[c][2]), 2);
26. 
27.     return err / nTrain;
28. }
29. //+------------------------------------------------------------------+
30. double Cost_2(double &w0, double &w1, double &b)
31. {
32.     double err, ew0, ew1, eb;
33. 
34.     err = ew0 = ew1 = eb = 0;
35.     for (uint c = 0; c < nTrain; c++)
36.     {
37.         err += MathPow((macroSigmoid((Train[c][0] * w0) + (Train[c][1] * w1) + b) - Train[c][2]), 2);
38.         ew0 += MathPow((macroSigmoid((Train[c][0] * (w0 + eps)) + (Train[c][1] * w1) + b) - Train[c][2]), 2);
39.         ew1 += MathPow((macroSigmoid((Train[c][0] * w0) + (Train[c][1] * (w1 + eps)) + b) - Train[c][2]), 2);
40.         eb += MathPow((macroSigmoid((Train[c][0] * w0) + (Train[c][1] * w1) + (b + eps)) - Train[c][2]), 2);
41.     }
42. 
43.     w0 -= (((ew0 - err)/ eps) * eps);
44.     w1 -= (((ew1 - err)/ eps) * eps);
45.     b  -= (((eb - err)/ eps) * eps);
46. 
47.     return err / nTrain;
48. }
49. //+------------------------------------------------------------------+
50. void OnStart()
51. {
52.     double  w0, w1, err, ew0, ew1, eb, bias;
53.     ulong count, it0, it1;
54. 
55.     Print("The Neuron - Tutor...");
56.     MathSrand(512);
57.     w0 = (double)macroRandom;
58.     w1 = (double)macroRandom;
59.     bias = (double)macroRandom;
60. 
61.     it0 = GetTickCount();
62. #ifdef def_Fast    
63.     for (count = 0; (count < ULONG_MAX) && ((err = Cost_2(w0, w1, bias)) > eps); count++);
64. #else
65.     for (count = 0; (count < ULONG_MAX) && ((err = Cost(w0, w1, bias)) > eps); count++)
66.     {
67.         ew0 = (Cost(w0 + eps, w1, bias) - err) / eps;
68.         ew1 = (Cost(w0, w1 + eps, bias) - err) / eps;
69.         eb  = (Cost(w0, w1, bias + eps) - err) / eps;
70.         w0 -= (ew0 * eps);
71.         w1 -= (ew1 * eps);
72.         bias -= (eb * eps);
73.     }
74. #endif
75.     it1 = GetTickCount();
76.     Print("Time: ", (it1 - it0) / 1000.0, " seconds.");
77.     PrintFormat("%I64u > w0: %.4f %.4f || w1: %.4f %.4f || b: %.4f %.4f || %.4f", count, w0, ew0, w1, ew1, bias, eb, err);
78.     Print("w0 = ", w0, " || w1 = ", w1, " || Bias = ", bias);
79.     Print("Error Weight 0: ", ew0);
80.     Print("Error Weight 1: ", ew1);
81.     Print("Error Bias: ", eb);
82.     Print("Error: ", err);
83. 
84.     Print("Testing the neuron...");
85.     for (uchar p0 = 0; p0 < 2; p0++)
86.         for (uchar p1 = 0; p1 < 2; p1++)
87.             PrintFormat("%d AND %d IS %f", p0, p1, macroSigmoid((p0 * w0) + (p1 * w1) + bias));
88. 
89.     Print("************************************");
90. }
91. //+------------------------------------------------------------------+

Não se preocupe em digitar este código. Caso você deseje, pode fazer isto para fixar melhor a forma de codificar em MQL5. Já que quando digitamos um código, conseguimos entender melhor como ele está sendo criado. Além do que, fixamos também, diversas outras questões envolvidas na sintaxe da linguagem, da qual estamos programando. Mas no anexo, você terá acesso a ele. Então fica ao seu critério como fazer uso deste conhecimento.

Ok, então vamos ver o que obteremos em termos de tempo de execução. Isto pode ser visto na imagem abaixo.

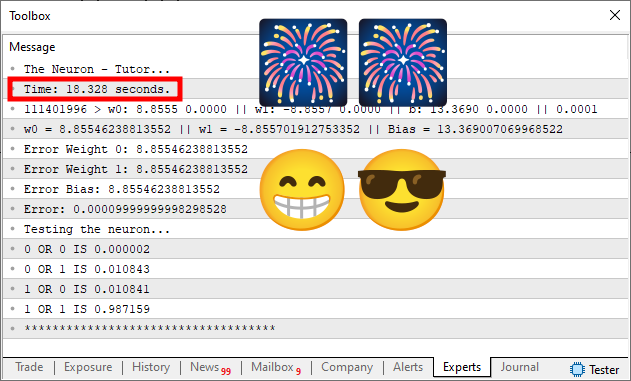
Oque? Mas como isto foi possível de ser feito? Como o tempo gasto despencou de quase 80 segundos, para pouco mais de 18 segundos? Isto é completamente e totalmente impossível de ser feito. Há já sei, você mudou de computador, usou um computador melhor para fazer isto. Ou ainda, muito provavelmente, e é quase certo que você tenha feito algum tipo de trapaça. Colocando um erro diferente no sistema, ou mudando alguma outra coisa. Assim na primeira execução, você gastaria mais tempo, como pode ser visto na primeira imagem. Mas depois gastaria muito menos tempo, usando algum tipo de trapaça. E assim produziria o que pode ser visto nesta segunda imagem.

Bem meu caro leitor. Talvez até poderia ter feito isto. Mas não, por isto estou deixando o código no anexo. Assim você conseguirá entender o que aconteceu. Experimentando em sua máquina este mesmo código. Mas antes de fazer isto, vamos primeiro entender o que está acontecendo, para que o código que antes era executado em quase 80 segundos, passasse a ser executado em pouco mais de 18 segundos. E antes de começarmos, não existe mágica ou coisa do gênero. É conhecimento do que o neurônio precisa aprender.

Se você observar o código poderá achar que ele é muito complicado. Ainda mais se você está começando na programação. Porém não se assuste, ele é bem simples, e tenho feito questão de mantê-lo assim. Desta forma fica mais didático e prático de explicar como ele funciona.

Vamos começar pela linha sete. Ali temos uma definição. Sendo um dos poucos pontos dos quais, você iniciante e entusiasta deverá mexer no código. Isto sem perigo de torna-lo instável. Se você remover esta linha sete, você tornará o código exatamente como visto no tópico anterior. Ou seja, lento e desajeitado, porém genérico. No entanto, caso esta linha sete, esteja da forma como é vista aqui no artigo, o código a ser usado será a versão rápida do mesmo. Mostrando assim o resultado visto na imagem acima.

Agora quero que você compare esta imagem neste tópico, com as imagens do tópico anterior. Mas quero que você observe o valor do erro. Veja que eles são bem parecidos. Principalmente na última imagem do tópico anterior, para a vista neste tópico. Ou seja, estamos usando um erro de 1e-4 em ambos os casos. Então espere um pouco, aí. Você está dizendo que apesar de estarmos usando a mesma precisão, o tempo de execução acabou caindo bruscamente? Sim, meu caro leitor. É justamente isto que aconteceu. Mas por que aconteceu isto, você saberia me dizer?

Bem, para entender, é preciso olhar algumas coisas no código. Vamos pular grande parte do código, e nos dirigir para o procedimento OnStart, que se encontra presente na linha 50. Agora é preciso um pouco de calma. Mas não é nada complicado entender o que está acontecendo. Note que dentro deste procedimento, grande parte do código pode ser visto no tópico anterior. Estas partes iguais, são o que torna o neurônio idêntico ao que foi visto até então. Porém, justamente na linha 62, pedimos ao compilador para fazer um teste. Isto quando ele for criar o executável final. Este teste, checará se a linha sete existe ou não.

Caso ela não exista, o código a ser criado é igual ao visto no tópico anterior. Caso a linha sete exista. O código do tópico anterior será substituído pelo código presente na linha 63. Preste atenção a isto. Estamos substituindo o código entre as linhas 65 a 73, pelo código da linha 63. Todo o restante irá permanecer idêntico e intacto.

Mas agora olhando o conteúdo da linha 63, você nota que se trata de um laço for. Este se parece em muito com o código da linha 65. Claro, que a diferença está no fato de que na linha 65 estamos chamando Cost e na linha 63 estamos chamando Cost_2. Fora isto o código é idêntico. Mas isto não explica o motivo de em uma execução ser necessário quase 80 segundos enquanto na outra ser necessários 18 segundos. Este tipo de coisa, não faz o menor sentido. Mas é aí que você se engana meu caro leitor. Esta mera mudança faz toda a diferença. Observe que apesar de você estar olhando apenas a linha 65, na verdade a função Cost é chamada em quatro momentos diferentes. Na linha 65, na 67, na 68 e na 69.

Em cada uma destas chamadas, toda a tabela, banco de dados, ou no nosso caso, o array de treinamento precisa ser analisado. Pense por um instante nesta questão. Veja que nosso array de treinamento, contém apenas quatro linhas de dados. Isto pode ser visto na linha nove do código. Apenas e tão somente quatro linhas de dados. Porém, cada vez que a função Cost, presente na linha 19, precisa ser chamada. O laço na linha 24 irá ler e calcular tudo novamente. Isto para cada uma das chamadas presentes no procedimento OnStart.

Apesar de ser muito mais simples de programar as coisas desta forma. Isto em termos gerais não é nada eficiente. Porém, este mesmo modo de programar, torna o neurônio, muito mais genérico. Isto por que, podemos colocar tantas quantas forem necessárias as entradas ou saídas do mesmo. E tudo isto, sem precisar mudar absolutamente nada no código. Neste ponto é onde saber o que está fazendo, ou conhecer o tipo de resultado planejado ou esperado, faz toda a diferença. Muitos iriam pegar e transformar esta função da linha 19 em um código OpenCL. Ou mesmo um código que poderia ser executado em sistemas paralelos. Em alguns casos, máquinas que executam aplicações paralelas podem ser bastante caras.

Em outros, uma boa GPU consegue dar cabo da coisa toda. De qualquer forma, estaríamos apenas trocando seis por meia dúzia. Já que o código ainda assim seria pouco eficiente. E estou dizendo isto, pelo fato de que a cada chamada a fim de calcular o custo, teríamos a varredura de todo o banco usado para o treinamento. Pense em um banco contendo milhares de megabytes de dados.

Agora vamos voltar a questão da linha 63. Apesar de ela não ser a maravilha das maravilhas. Temos nela uma chamada a uma função especializada. Isto torna a execução muito mais rápida em comparação a uma execução não especializada. Porém o fato de termos um neurônio especializado, torna a coisa um tanto quanto mais complicada em termos de programação. Visto que se precisamos mudar algo no neurônio. Seja o número de entradas, seja o número de saídas. Precisaríamos mudar completamente o código da função Cost_2, que é chamada um número menor de vezes na linha 63. E o motivo de ela ser menos chamada, está justamente na forma como ela trabalha. Vamos ver como as coisas funcionam, indo para a linha 30. Onde Cost_2 está sendo implementada. Porém para tornar a explicação mais didática, vamos ver esta função em um novo tópico.

Tornando um único neurônio especializado em algo

Bem, para quem deseja estudar as coisas com mais calma. E de fato entender como funcionam, vamos desmembrar a função Cost_2 em duas partes. Assim será mais simples de explicar por que ela é mais rápida do que a versão genérica.

Bem a primeira parte está entre as linhas 35 e 41. E o que o código presente nestas linhas está fazendo? Bem, ele está fazendo o que antes estava sendo feito pelas linhas 65, 67, 68 e 69. Além é claro, do que era feito no laço for, presente na linha 24. Ou seja, no final das contas estamos executando a linha 25. Só que ao contrário do que era feito antes. Agora estamos fazendo tudo ao mesmo tempo. Então precisamos de mais variáveis do que era preciso antes. Cada uma das variáveis, declaradas na linha 32, serve para ajudar a acelerar o código. Assim, na linha 37, estamos calculando o erro geral do neurônio. Isto não acelera as coisas. Mas, porém, toda via e entretanto. Nas linhas 38, 39 e 40, calculamos todos os demais erros. Que antes eram feitos lá no laço for, presente a linha 65.

Agora vem a parte complicada da coisa. A linha 40, faz parte de qualquer neurônio. Sendo que ela é exclusiva de todo e qualquer neurônio. Ou seja, um código genérico, assim como a linha 37. Porém as linhas 38 e 39, não. Elas é que tornam o neurônio especializado. Ou seja, se você precisar adicionar, mais entradas no neurônio, precisará adicionar mais destas linhas no código. Sendo que um neurônio criado para um propósito. Muito provavelmente não servirá para outra coisa. Porém o fato de tornarmos o código como ele pode ser visto. Faz com que ele seja bem mais rápido do que seria um código muito parecido. Porém mal otimizado para um propósito específico.

A segunda parte do código, é justamente as linhas 43, 44 e 45. Ali reajustamos os valores para uma próxima chamada a função de custo. Isto antes era feito nas linhas 70, 71 e 72.

O simples fato de termos feito, estas simples e singelas mudanças no código, tornaram possível que o neurônio ficasse extremamente mais rápido. Aprendendo, ou melhor dizendo, retornando um conjunto de valores, que tornasse possível armazenar um banco de conhecimento prévio. E esta é a verdadeira graça em se programar tais coisas. Não é pelo desafio em si. Mas pelo prazer de ver que podemos fazer as coisas de uma forma muito mais eficiente. E observe, que se quer foi preciso usar OpenCL, ou uma programação visando paralelismo nos cálculos. Tudo muito mais empolgante e divertido, do que toda aquela chatice que muitos ficam mostrando por aí. Ainda mais quando o assunto é redes neurais.

Muito bem, este foi um exemplo bastante simples de como podemos fazer as coisas. Mas podemos avançar um pouco mais, sobre esta mesma questão. Pois apesar de este simples e singelo neurônio, conseguir fazer diversas coisas e ter como única limitação o fato de precisamos sempre adicionar ou reduzir o número de entradas nele. Visando é claro tornar ele sempre o mais rápido possível. Ele ainda não é suficientemente "esperto" para conseguir lidar com certos tipos de situação. Por isto está coisa de inteligência artificial ou redes neurais, não é um assunto tão simples como muitos acreditam. Da mesma forma também não podemos considerar que um neurônio conseguirá lidar com qualquer tipo de situação, dentro de um dado cenário.

Para conseguir poder exemplificar isto, vamos fazer um pequeno exercício mental. Nada muito complicado, apenas quero mostrar, para você meu caro leitor, algo que muitos desconsideram ao estudar sobre redes neurais. Trata-se de uma coisa da qual muitos não dizem ou que não querem dizer. Mas que se você conseguir entender, perceberá que nada programado, realmente conseguirá superar a mente que a programou.

Vamos pensar nos dados usados para treinamento. Existem situações em que não conseguimos fazer com que um neurônio consiga lidar com os dados. Não que sejam dados extremamente complicados ou algo do tipo. Na verdade, são dados simples. Porém um neurônio, não, e vou repetir, NÃO consegue solucionar o problema. Sendo necessário que usemos mais de um neurônio para isto. Então já vou dar uma rápida pincelada no assunto que será abordado mais para frente. Porém em casos específicos, é admissível simularmos uma pequena rede neural, usando apenas um único neurônio. Tudo depende do tipo de coisa da qual estamos procurando uma solução.

Assim, em muitos dos casos, e na maior parte das vezes, um neurônio pode ser construído, ou melhor dizendo, programado, de forma a ser usado no futuro, para implementar uma rede neural. E não estou falando em uma rede neural do tipo ChatBot, ou coisa do tipo. Estou falando de algo infinitamente mais simples. Porém existem casos, em que podemos forçar um único neurônio, a resolver um tipo de problema, onde seria preciso uma pequena rede neural. E não precisaremos criar um BIG DATA, com um apanhado enorme de informações, para encontrar uma situação onde isto acontece. Podemos fazer isto usando este mesmo código que está sendo mostrado neste artigo.

Xi, agora complicou de vez. Como assim? Deixe-me ver se consegui entender a sua colocação. Você está me dizendo. Que este neurônio, em que estamos trabalhando. Não conseguirá lidar com algo que podemos representar neste mesmo banco de dados. Mas que se soubermos como trabalhar com ele, podemos forçar ele a simular uma pequena rede neural. E assim conseguir solucionar algo que ele não conseguiria sozinho. É isto? Sim, é isto mesmo. Note que este banco de dados, que estamos usando. Se parece com portas lógicas. Ou seja, podemos colocar nele combinações de zeros e uns, e pedir para o neurônio venha a tentar encontrar uma equação. Ou melhor dizendo, alguma regressão linear, que possa conseguir representar a porta lógica.

Porém existem dois casos, se bem que podemos tratar eles como sendo um. Isto por que ambos são inversos um do outro. Onde este singelo neurônio não conseguirá encontrar a equação correta. Porém se você o forçar a trabalhar de uma dada forma ele conseguirá encontrar a equação correta.

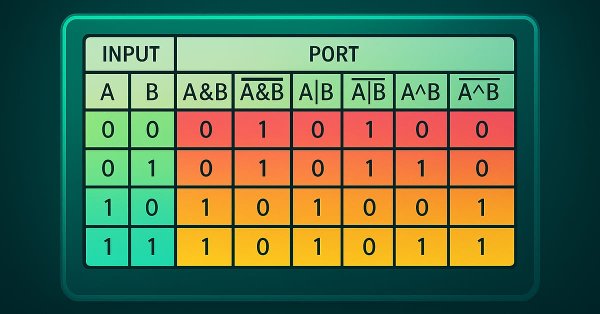
Para entender de forma mais simples o que quero explicar. Veja a imagem abaixo.

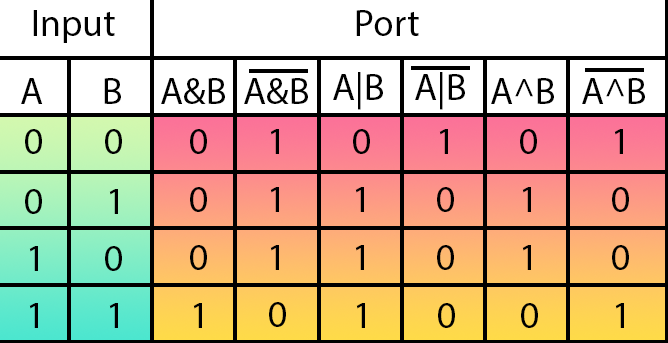
Esta imagem mostra, todas as portas lógicas que existem. Na parte em verde estão as entradas da porta. Na parte em tons de vermelho e laranja estão as saídas de cada uma das portas. Na parte superior de cada saída, está sendo definida o tipo de porta lógica.

Pois bem, vamos entender o que isto quer dizer. Da esquerda para a direita temos as portas na seguinte ordem: AND, NAND, OR, NOR, XOR e NXOR.

E no que esta tabela, mostrada na imagem acima, tem de importante para nós aqui. Se o assunto é rede neurais? Para compreender, olhe novamente no código do neurônio. Veja que na linha nove, onde definimos as regras de treinamento. Temos exatamente algo parecido com esta tabela mostrada na imagem acima.

Agora vem a parte interessante. Os dois primeiros valores são as entradas. Já o terceiro valor é a saída. Compare o que é visto no código, com a tabela mostrada na imagem. O que você consegue notar, meu caro leitor? Bem, se você prestar um pouco atenção, acabará notando que estamos definindo no treinamento uma porta do tipo AND.

Você pode experimentar mudando os valores do terceiro argumento usado no treinamento. E verá que conseguirá que o neurônio aprenda, ou gere uma equação que consiga representar, quase todas as portas. Digo quase, por que duas delas não serão possíveis de serem aprendidas pelo neurônio. Tais postas são justamente a XOR e sua inversa, que é a NXOR.

Opá. Mas espere um momento aí. Como assim, o neurônio não vai conseguir aprender a gerar as portas XOR e NXOR? Você só pode estar brincando. Todas os valores são apenas compostos por zeros e uns. Isto só pode ser uma piada ou uma brincadeira. Você está me zoando.

Eu até queria estar de brincadeira, fazendo uma pegadinha do malandro. Mas não. Isto é fato, e você pode experimentar. Se você tentar treinar um único neurônio, usando apenas zeros e uns. Irá existir casos em que o neurônio não conseguirá aprender a tratar a situação. Isto por conta que a solução é muito mais complicada do que o neurônio consegue aprender.

Este tipo de coisa, dificilmente você verá alguém falando ou se quer mencionando. Isto quando o assunto no qual estamos lendo, está de alguma forma relacionado a inteligência artificial, redes neurais ou programação de neurônios. As pessoas não pensam em tentar todas as alternativas. Se funciona para um caso específico, elas logo começam a divulgar e a falar sobre o assunto. Mas se você começar a questionar elas sobre determinados cenários, elas começam a enrolar ou ignoram o questionamento.

Porém, existe uma forma de forçar o neurônio a aprender, como lidar com estas situações. Como é o caso onde precisamos resolver o problema da porta XOR ou de sua inversa, a NXOR. Como este tema é um tanto quanto complicado de explicar no que resta de tempo neste artigo. Veremos no próximo artigo como resolver este tipo de questão. Mas até que o próximo artigo venha a ser publicado. Quem sabe, você meu caro leitor e entusiasta sobre o tema, consiga pensar em uma forma de resolver o problema da porta XOR e usa inversa, a porta NXOR. Detalhe: Não vale usar mais de um neurônio. Pois fazer sito seria trapaça. A regra é: Só pode usar um neurônio para implementar a solução.

Considerações finais

Neste artigo mostrei como, uma simples mudança no código, a fim de tornar o neurônio um pouco mais especializado. Pode tornar a fase de treinamento consideravelmente mais rápida. Visto que uma vez que o neurônio, ou rede neural, como será visto mais para frente. Já estiver sido treinada. O trabalho executado por ela, será feito de maneira muito mais rápida. Tanto que no código presente, tanto no artigo, quanto no anexo. Você pode notar que a geração dos resultados a partir da entrada é feita de maneira muito rápida. Desde é claro, já venhamos a saber quais os valores a serem usados no cálculo.

Aqui também mencionei um problema que existe, do qual quase ninguém fala ou menciona. Que é justamente o fato, de que um neurônio, não consegue lidar com todos os tipos de cenários existentes. Diferente do que muitos acreditam. A máquina não é assim tão melhor, ou capaz de superar um ser vivo. Um único neurônio vivo, consegue resolver qualquer tipo de cenário simples. Porém um neurônio programado, ou implementado em silício, não consegue tal façanha.

Então no próximo artigo, continuaremos a ver mais sobre este assunto. Até mais. E nos vemos em breve.