Нейросети в трейдинге: Модели с использованием вейвлет-преобразовании и многозадачного внимания

MetaTrader 5 — Торговые системы | 25 декабря 2024, 18:57

907

Dmitriy Gizlyk

Введение

Прогнозирование доходности активов является широко исследуемой темой в области финансов. Проблема прогнозирования доходности возникает из-за нескольких проблем. Во-первых, множество факторов, влияющих на доходность активов, и низкое отношение сигнал/шум в разреженных матрицах большой размерности затрудняют извлечение значимой информации традиционными эконометрическими моделями. Во-вторых, функциональные связи между прогностическими характеристиками и доходностью активов неясны, что создает проблемы при захвате нелинейных структур между ними.

В последние годы глубокое обучение стало незаменимым инструментом в количественных инвестициях, особенно в совершенствовании многофакторных стратегий, которые формируют основу для понимания движения цен финансовых активов. Автоматизируя обучение признакам и фиксируя нелинейные взаимосвязи в данных финансового рынка, алгоритмы глубокого обучения эффективно выявляют сложные закономерности, тем самым повышая точность прогнозирования. Мировое исследовательское сообщество признает потенциал глубоких нейронных сетей, таких как рекуррентные нейронные сети (RNN) и сверточные нейронные сети (CNN), для прогнозирования цен на акции и фьючерсы. Тем не менее использование моделей глубокого обучения, таких как RNN и CNN, хотя и широко распространено, редко исследует более глубокие модели нейронных сетей, которые добывают и конструируют рыночную и выдающую информацию о последовательностях, что предполагает возможности для дальнейшего развития применения глубокого обучения на фондовых рынках.

Сегодня предлагаем познакомиться с фреймворком Multitask-Stockformer, представленном в статье "Stockformer: A Price-Volume Factor Stock Selection Model Based on Wavelet Transform and Multi-Task Self-Attention Networks". Несмотря на созвучность названия с ранее рассмотренным фреймворком StockFormer, фреймворки не имеют ничего общего. Кроме, конечно, цели — генерации прибыльного портфеля акций для работы на фондовом рынке.

Фреймворк Multitask-Stockformer создает многозадачную модель прогнозирования акций на основе вейвлет-преобразования и моделей Self-Attention.

Алгоритм Multitask-Stockformer

Архитектура фреймворка Multitask-Stockformer разделена на 3 блока: модуль разделения потока, двухчастотный пространственно-временной энкодер и двухчастотный декодер. Анализируемые исторические данные об активах 𝒳 ∈ RT1×N×362 обрабатывается в модуле разделения потока. На данном этапе тензор ряда доходности активов разделяется на высокочастотные и низкочастотные компоненты с помощью дискретного вейвлет-преобразования. При этом признак тренда и коэффициенты цена-объем остаются неизменными. Затем эти компоненты объединяются с неизмененными частями сигнала по последнему измерению.

Низкочастотная составляющая отражает долгосрочные тренды, а высокочастотная составляющая фиксирует краткосрочные колебания и резкие события. Они обозначаются как 𝒳l, 𝒳h ∈ RT1×N×362, соответственно. Затем 𝒳h и 𝒳l линейно преобразуются через полносвязный слой в размерность RT1×N×D. В данном случае T1 обозначает глубину анализируемой истории.

Двухчастотный пространственно-временной Энкодер предназначен для представления этих различных паттернов временных рядов: низкочастотные объекты подаются в модуль временного внимание (обозначаемое как tatt), а высокочастотные признаки обрабатываются через расширенный причинно-следственный сверточный слой (обозначаемый как conv). Эти компоненты затем вводятся в графовые сети внимания (обозначаемые как gat). Взаимодействие с информацией графов позволяет модели фиксировать сложные отношения и зависимости между активами и временем. В этом модуле пространственный граф Aspa и темпоральный граф Atem преобразуются с помощью полносвязного слоя и операций тензорной трансляции в многомерные вложения, обозначенные как ρspa, ρtem ∈ RT1×N×D, которые затем объединяются с 𝒳l,tatt, 𝒳h,conv при помощи сложение и операций графового внимания для получения 𝒳l,gat, 𝒳h,gat ∈ RT1×N×D. Двухчастотный пространственно-временной энкодер состоит из L слоев, направленных на эффективное представление двух масштабных пространственно-временных паттернов низко- и высокочастотных волн. Наконец, в двухчастотном Декодере предикторы генерируют 𝒴l,f, 𝒴h,f ∈ RT2×N×D, которые агрегируются с помощью взаимодействий Fusion Attention для получения скрытого представления двухмасштабных временных паттернов. С помощью отдельных полносвязных слоев (слой регрессии FC1 и классификационный слой FC2) создаются многозадачные результаты, включая прогнозы доходности акций (результат регрессии, обозначаемый как reg) и вероятности прогнозирования тренда акций (результат классификации, обозначаемый как cla).

Кроме того, выводятся значения регрессии и вероятности прогнозирования тренда для низкочастотной составляющей, что позволяет улучшить обучение низкочастотного сигнала.

Авторская визуализация фреймворка Multitask-Stockformer представлена ниже.

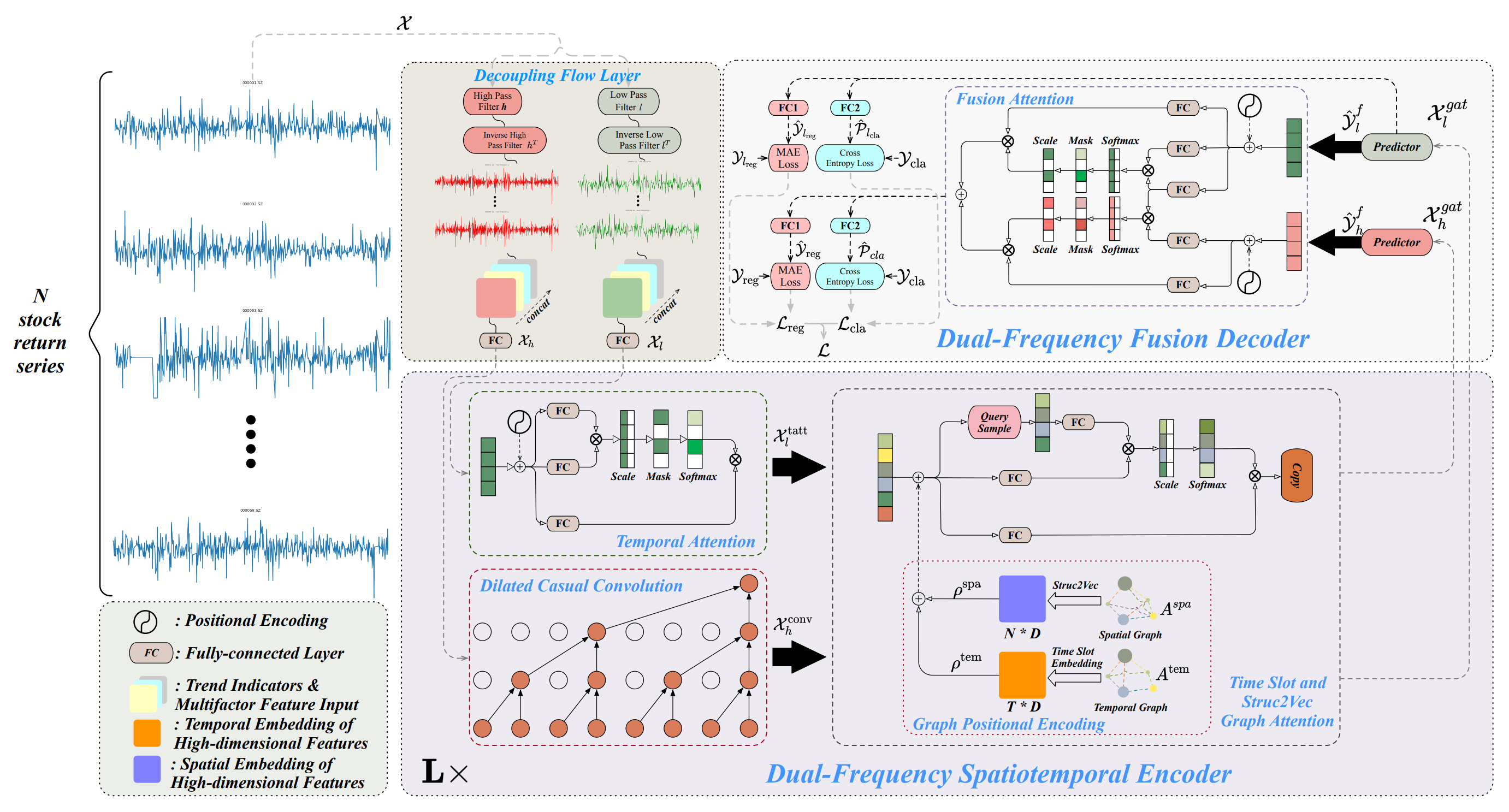
Реализация средствами MQL5

Выше представлено лишь краткое описание фреймворка Multitask-Stockformer. Фреймворк довольно сложный. И я думаю, что более эффективно будет познакомиться с отдельными алгоритмами в процессе их реализации. И начнем мы работу с модуля разделения потока исходных данных.

Модуль декомпозиции сигнала

Для разделения анализируемого сигнала на низкочастотную и высокочастотную составляющую авторы фреймворка предлагают использовать дискретное вейвлет-преобразование. В отличие от разложения Фурье, вейвлет-преобразование способно захватывать не только частотную составляющую, но и структуру сигнала. Это делает его более выгодным для анализа финансовых рынков, когда важна не только частота, но и порядок сигналов.

Ранее мы уже использовали дискретное вейвлет-преобразование при построении фреймворка FEDformer, но тогда мы выделяли только низкочастотную составляющую. Сейчас же нам необходима и высокочастотная составляющая. Тем не менее мы можем воспользоваться существующими наработками.

Дискретное вейвлет-преобразование по существу является операцией свертки с определенным вейвлетом, используемым в качестве фильтра. Это позволяет нам использовать алгоритмы сверточного слоя, в качестве базового функционала. При этом стоит учесть, что в процессе преобразования мы используем статичные вейвлеты, параметры которых не изменяются в процессе обучения. Следовательно, нам необходимо отключить механизм оптимизации параметров нашего объекта.

Имея выше представленные вводные мы создаем новый объект для выделения высоко- и низкочастотной составляющей сигнала при помощи дискретного вейвлет-преобразования CNeuronLegendreWaveletsHL.

class CNeuronLegendreWaveletsHL :  public CNeuronConvOCL
  {
protected:
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL)   { return true; }

public:
                     CNeuronLegendreWaveletsHL(void) {};
                    ~CNeuronLegendreWaveletsHL(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint step, uint units_count, 
                          uint filters, uint variables, 
                          ENUM_OPTIMIZATION optimization_type, uint batch) override;
   //---
   virtual int       Type(void)   const   {  return defNeuronLegendreWaveletsHL;   }
   //---
   virtual uint      GetFilters(void)  const {return (iWindowOut / 2); }
   virtual uint      GetVariables(void)  const {return (iVariables); }
   virtual uint      GetUnits(void)  const {return (Neurons() / (iVariables * iWindowOut)); }
  };

Как уже было сказано выше, дискретное вейвлет-преобразование является сверткой с вейвлетом-фильтром. Это позволяет нам полностью использовать функционал родительского класса сверточного слоя для построения алгоритма. Достаточно лишь переопределить метод инициализации, задав вместо случайных параметров фильтров данные вейвлетов.

Однако используемые вейвлеты-фильтры статичны. Поэтому мы переопределяем метод оптимизации параметров updateInputWeights положительной заглушкой.

Инициализация нового объекта осуществляется в методе Init. Как обычно, в параметрах данного метода мы получаем от внешней программы ряд констант, позволяющих однозначно идентифицировать архитектуру создаваемого объекта. В данном случае это:

window — размер анализируемого окна;
step — шаг анализируемого окна;
units_count — количество операций свертки для одной унитарной последовательности;
filters — количество используемых фильтров;
variables — количество унитарных последовательностей в анализируемом мультимодальном временном ряде.

bool CNeuronLegendreWaveletsHL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                     uint window, uint step, uint units_count, 
                                     uint filters, uint variables, 
                                     ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronConvOCL::Init(numOutputs, myIndex, open_cl, window, step, 2 * filters, 
                                  units_count, variables, optimization_type, batch))
      return false;

В теле метода мы сразу передаем полученные параметры в одноименный метод родительского класса. Однако стоит обратить внимание, что при вызове метода родительского класса мы увеличиваем количество фильтров в 2 раза. Это связано с необходимостью создания фильтров для выделения высоко- и низкочастотной составляющей.

После успешного выполнения метода родительского класса мы очищаем буфер параметров свертки, заполнив его нулевыми значениями, и определим константу смещения в буфере между элементами низко- и высокочастотного фильтра.

   WeightsConv.BufferInit(WeightsConv.Total(), 0);
   const uint shift_hight = (iWindow + 1) * filters;

После чего организуем систему вложенных циклов генерации нужного количества фильтров. Здесь мы воспользуемся рекурсивностью генерации вейвлетов Лежандра. И будем последовательно заполнять матрицу фильтров вейвлетами более высокого порядка.

   for(uint i = 0; i < iWindow; i++)
     {
      uint shift = i;
      float k = float(2.0 * i - 1.0) / iWindow;
      for(uint f = 1; f <= filters; f++)
        {
         float value = 0;
         switch(f)
           {
            case 1:
               value = k;
               break;
            case 2:
               value = (3 * k * k - 1) / 2;
               break;
            default:
               value = ((2 * f - 1) * k * WeightsConv.At(shift - (iWindow + 1)) - 
                       (f - 1) * WeightsConv.At(shift - 2 * (iWindow + 1))) / f;
               break;
           }

Для каждого элемента анализируемого окна мы создаем вложенный цикл генерации элементов фильтра. В котором мы сначала генерируем элемент соответствующего фильтра низкой частоты.

А затем организовываем ещё один вложенный цикл, в теле которого распространим сгенерированный элемент в фильтры всех независимых переменных мультимодальной последовательности. И тут же добавим элемент фильтра высокой частоты, формируемый на основании соответствующего элемента низкочастотного фильтра.

         for(uint v = 0; v < iVariables; v++)
           {
            uint shift_var = 2 * shift_hight * v;
            if(!WeightsConv.Update(shift + shift_var, value))
               return false;
            if(!WeightsConv.Update(shift + shift_var + shift_hight, 
                                    MathPow(-1.0f, float(i))*value))
               return false;
           }

Затем мы корректируем смещение до элемента фильтра и переходим к следующей итерации системы циклов.

         shift += iWindow + 1;
        }
     }

Дальнейший алгоритм данного метода инициализации объекта отличается от всех ранее рассмотренных. До этого мы не использовали фрагменты OpenCL-программы в процессе инициализации объектов. Но данный метод станет исключением. Здесь мы нормализуем полученные вейвлет-фильтры.

   if(!!OpenCL)
     {
      if(!WeightsConv.BufferWrite())
         return false;
      uint global_work_size[] = {iWindowOut * iVariables};
      uint global_work_offset[] = {0};
      OpenCL.SetArgumentBuffer(def_k_NormilizeWeights, def_k_norm_buffer, WeightsConv.GetIndex());
      OpenCL.SetArgument(def_k_NormilizeWeights, def_k_norm_dimension, (int)iWindow + 1);
      if(!OpenCL.Execute(def_k_NormilizeWeights, 1, global_work_offset, global_work_size))
        {
         string error;
         CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error);
         printf("Error of execution kernel %s Normalize: %s", __FUNCSIG__, error);
         return false;
        }
     }
//---
   return true;
  }

После успешного выполнения операции нормализации параметров завершаем работу метода, передав логический результат выполнения операций вызывающей программе.

С полным кодом представленного объекта и всех его методов Вы можете ознакомиться во вложении.

Здесь стоит отметить, что функционал модуля декомпозиции анализируемых данных несколько шире дискретного вейвлет-преобразования, хотя это его основная часть. Мы планируем использование объекта в реализации наших моделей, где на вход подается двухмерный тензор мультимодальной временной последовательности с размерностью {Bar, Indicator Value}. Но для корректной работы нашего объекта дискретного вейвлет-преобразование необходимо их транспонировать. Конечно, эту операцию можно осуществить и перед подачей исходных данных в объект. Но наша цель построить объекты максимально удобные в эксплуатации. Поэтому мы создадим объект модуля декомпозиции потока с немного расширенным функционалом CNeuronDecouplingFlow. А в качестве родительского класса воспользуемся выше созданным объектом дискретного вейвлет-преобразования.

class CNeuronDecouplingFlow   :  public   CNeuronLegendreWaveletsHL
  {
protected:
   CNeuronTransposeOCL  cTranspose;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronDecouplingFlow(void) {};
                    ~CNeuronDecouplingFlow(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint step, uint units_count,
                          uint filters, uint variables,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronDecouplingFlow;   }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

В теле нового объекта мы добавляем слой предварительного транспонирования данных и меняем понимание внешнего параметра метода инициализации units_count. Мы делаем его более дружелюбным для пользователя и воспринимаем как длину анализируемой последовательности. Таким образом параметр units_count соответствует глубине анализируемой истории (количество баров), а variables — количество анализируемых параметров (индикаторов).

Рассмотрим реализацию такого подхода в методе инициализации Init. В теле метода мы сначала пересчитываем количество операций свертки для одной унитарной последовательности, исходя из размера исходной последовательности, окна свертки и его шага. И только потом вызываем одноименный метод родительского класса, передав ему скорректированные параметры.

bool CNeuronDecouplingFlow::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                 uint window, uint step, uint units_count,
                                 uint filters, uint variables,
                                 ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   uint units_out = (units_count - window + step) / step;
   if(!CNeuronLegendreWaveletsHL::Init(numOutputs, myIndex, open_cl, window, step, units_out, 
                                                filters, variables, optimization_type, batch))
      return false;

А после успешного выполнения метода родительского класса мы выполняем инициализацию слоя транспонирования исходных данных.

   if(!cTranspose.Init(0, 0, OpenCL, units_count, variables, optimization, iBatch))
      return false;
//---
   return true;
  }

И завершаем работу метода, предварительно вернув логический результат выполнения операций вызывающей программе.

Алгоритм метода прямого и обратного прохода довольно прост. К примеру, для осуществления прямого прохода мы сначала транспонируем исходные данные, а затем полученный тензор подаем на вход одноименного метода родительского класса.

bool CNeuronDecouplingFlow::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cTranspose.FeedForward(NeuronOCL))
      return false;
   if(!CNeuronLegendreWaveletsHL::feedForward(cTranspose.AsObject()))
      return false;
//---
   return true;
  }

Поэтому позвольте не останавливаться на их рассмотрения. А с полным кодом данного объекта и всех его методов Вы можете самостоятельно ознакомиться во вложении.

В завершении рассмотрения модуля декомпозиции сигнала несколько слов надо сказать о результатах его работы. Дело в том, что построенный нами поток операций не позволяет получать на выходе нейронного слоя 2 тензора. Поэтому было принято решение выводить результаты работы низко- и высокочастотных фильтров в едином тензоре данных. И, как следствие, на выходе модуля декомпозиции сигнала мы получаем подобие четырехмерного тензора {Variables, Units, [Low, High], Filters}. Разделения тензора на отдельные потоки обработки данных мы планируем осуществлять в двухчастотном пространственно-временном Энкодере.

После построения модуля декомпозиции исходных данных мы переходим к работе по реализации подходов двухчастотного пространственно-временного Энкодера, который состоит из трех основных компонентов: временного внимания, расширенной причинно-следственной свертки и временного слота с графовыми сетями внимания Struc2Vec.

Здесь стоит обратить внимание, что авторы фреймворка Multitask-Stockformer организовывают 2 независимых потока для низко- и высокочастотной составляющей. Более того, эти потоки отличаются архитектурными решениями, что позволяет сосредоточиться на тенденциях и сезонных компонентах.

Низкочастотная составляющая поступает на вход блока пространственно-временного внимания, который фиксирует долгосрочные низкочастотные тренды, рассматривая глобальные отношения последовательностей.

В то же время высокочастотная часть сигнала обрабатывается расширенным причинно-следственным сверточным слоем. Это позволяет сфокусироваться на локальных закономерностях, эффективно моделируя высокочастотные компоненты и резкие события.

Ожидается, что такой подход к двойному моделированию повышает точность прогнозирования сложных финансовых последовательностей.

В качестве блока пространственно-временного внимания мы можем воспользоваться одним из уже существующих объектов, построенных с использованием архитектуры Энкодера Transformer. А вот над алгоритмом причинно-следственного сверточного слоя нам предстоит поработать.

Причинно-следственный сверточный слой

Предложенная авторами фреймворка расширенная причинно-следственная свертка — это специфический тип одномерной свертки, который скользит по исходным данным, пропуская значения на определенном шаге, как показано на рисунке выше. Теоретически, при заданной одномерной последовательности x ∈ RT и фильтре f ∈ RJ, операция расширенной причинной свертки на временном шаге t определяется как:

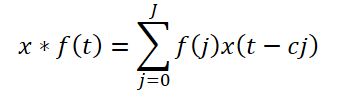
Здесь c — фактор расширения. Расширенная причинно-следственная свертка высокочастотной составляющей выражается как:

Стоит обратить внимание, что в предложенной реализации добавляется ещё один гиперпараметр — фактор расширения. Боле того, он постоянен. Но является ли фиксированным расстояние между зависимыми элементами на протяжении всей анализируемой последовательности. Ситуация усугубляется использованием одного коэффициента для различных унитарных последовательностей.

В своей реализации мы решили немного изменить архитектуру расширенного причинно-следственного модуля. Вместо пропусков предлагаем воспользоваться алгоритмом Segment, Shuffle, Stitch (S3). А за ним использовать обычный сверточный слой.

S3 позволяет настроить обучаемую перестановку сегментов в исходных данных. Таким образом мы уходим от фиксированного пропуска значений в тензоре исходных данных, предлагая модели самостоятельно выучить зависимости между отдельными элементами анализируемых последовательностей. А создание стека из нескольких подобных блоков позволяет адаптивно обнаруживать и фиксировать зависимости высокочастотной компоненты.

Предложенный подход мы реализуем в рамках объекта CNeuronDilatedCasualConv. Думаю, очевидно, что выше описанный алгоритм является линейным. Поэтому в качестве родительского объекта мы используем класс CNeuronRMAT, в рамках которого уже организованы основной функционал и интерфейсы реализации линейных алгоритмов. Структура нового объекта представлена ниже.

class CNeuronDilatedCasualConv   :  public CNeuronRMAT
  {
public:
                     CNeuronDilatedCasualConv(void) {};
                    ~CNeuronDilatedCasualConv(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint step, uint dimension,
                          uint units_count, uint variables, uint layers,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronDilatedCasualConv; }
  };

Как можно заметить, из представленной структуры нового объекта, выбор "правильного" родительского класса позволяет нам ограничиться указанием архитектуры объекта в методе инициализации. Весь остальной функционал уже реализован в методах родительского класса, которые мы успешно унаследовали.

В параметрах метода инициализации Init мы, как обычно, получаем набор констант, позволяющих однозначно определить архитектур создаваемого объекта:

window — размер анализируемого окна;
step — шаг анализируемого окна;
dimension — размерность вектора одного элемента последовательности;
units_count — количество элементов последовательности;
variables — количество анализируемых элементов в мультимодальной последовательности;
layers — количество слоев свертки.

Здесь стоит обратить внимание, на особенности использования указанных переменных. Но вначале вспомним о размерности тензора анализируемых исходных данных. Как было сказано выше, из модуля декомпозиции анализируемого сигнала мы получаем четырехмерный тензор {Variables, Units, [Low, High], Filters}. После разложения тензора на составляющие высоко- и низкочастотного сигнала в третьем измерении мы получаем только одно значение, что практически делает тензор трехмерным {Variables, Units, Filters}.

Напомню, что в OpenCL-контексте мы работаем с одномерными буферами данных. И разложение буфера на измерения носит условный характер, но подразумевает соответствующую последовательность значений.

Имея понимание о размерности тензора исходных данных, мы можем сопоставить с ними получаемые от внешней программы параметры. Очевидно, что параметр variables соответствует размерности первого измерения Variables. А units_count укажет длину анализируемой последовательности по второму измерению Units. И dimension определит последнее измерение Filters. Все указанные параметры определяют размер тензора исходных данных в чистом виде.

Дополнительно скажем, что размер анализируемого окна (window) и его шаг (step) указываются в единицах второго измерения Units. То есть при указании размера окна равным 2 (window = 2), для свертки берется 2*dimension элементов из буфера исходных данных.

Но вернемся к алгоритму метода инициализации объекта.

bool CNeuronDilatedCasualConv::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                    uint window, uint step, uint dimension, uint units_count,
                                    uint variables, uint layers,
                                    ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, 1, optimization_type, batch))
      return false;

Как обычно, в теле метода мы первым делом вызываем одноименный метод родительского класса, в котором организованы необходимые контроли и инициализация унаследованных объектов. И тут мы сталкиваемся с 2 моментами. Во-первых, структура объектов родительского класса CNeuronRMAT сильно отличается от необходимой нам. Поэтому мы вызываем метод не прямого родительского класса, а базового полносвязного слоя. Как Вы помните, он является основой для создания всех нейронных слоев нашей библиотеки.

Однако есть второй момент — в процессе свертки изменяется объем тензора результатов. И на данный момент у нас нет его финального размера для указания размерностей базовых интерфейсов. Поэтому мы инициализируем базовые интерфейсы с условным одним элементом на выходе.

Затем очистим динамический массив хранения указателей на внутренние объекты и подготовим вспомогательные переменные.

   cLayers.Clear();
   cLayers.SetOpenCL(OpenCL);
   uint units = units_count;
   CNeuronConvOCL *conv = NULL;
   CNeuronS3 *s3 = NULL;

После завершения подготовительной работы мы переходим к непосредственному созданию архитектуры нашего объекта. Для этого организуем цикл с числом итераций, равным количеству внутренних слоев.

   for(uint i = 0; i < layers; i++)
     {
      s3 = new CNeuronS3();
      if(!s3 ||
         !s3.Init(0, i*2, OpenCL, dimension, dimension*units*variables, optimization, iBatch) ||
         !cLayers.Add(s3))
        {
         if(!!s3)
            delete s3;
         return false;
        }
      s3.SetActivationFunction(None);

В теле цикла мы вначале инициализируем объект S3. Однако следует обратить внимание, что данный объект работает только с одномерным тензором. Поэтому, чтобы не допустить "разрыв" вектора описания элемента последовательности необходимо указывать величину сегмента кратной размерности такого вектора. В данном случае мы указываем их равными. При этом в качестве величины последовательности указывается полный размер тензора с учетом всех анализируемых переменных.

После успешной инициализации объекта мы добавляем указатель на него в наш динамический массив хранения указателей на внутренние объекты. И отключаем функцию активации.

Следующим идет процесс инициализации сверточного слоя. Здесь перед началом процесса инициализации нового объекта мы рассчитываем количество операций свертки для создаваемого слоя. И сохраним полученное значение в локальную переменную. Значение именно этой переменной мы использовали на предыдущем этапе при указании размерности анализируемой последовательности. Следовательно, на следующей итерации цикла мы создадим объект S3 актуализированного размера.

      conv = new CNeuronConvOCL();
      units = MathMax((units - window + step) / step, 1);
      if(!conv ||
         !conv.Init(0, i * 2 + 1, OpenCL, window * dimension, step * dimension, dimension,
                                                   units, variables, optimization, iBatch) ||
         !cLayers.Add(conv))
        {
         if(!!conv)
            delete conv;
         return false;
        }
      conv.SetActivationFunction(GELU);
     }

Используемый нами сверочный слой, в отличие от объекта S3, может работать в разрезе унитарных последовательностей. Это позволяет нам не только осуществлять свертку каждого унитарного временного ряда отдельно, но и использовать различные фильтры для унитарных последовательностей. Что делает их анализ полностью независимым.

На выходе сверточного слоя мы используем функцию активации GELU, вместо ReLU, предложенной авторами фреймворка.

Добавляем указатель на инициализированный объект в наш динамический массив и переходим к следующей итерации цикла для создания следующего слоя.

После успешной инициализации всех внутренних слоев нашего объекта мы вновь вызываем метод инициализации базового полносвязного слоя для создания корректных буферов внешних интерфейсов с указанием размерности последнего внутреннего слоя нашего блока.

  if(!CNeuronBaseOCL::Init(numOutputs, myIndex, OpenCL, conv.Neurons(), optimization_type, batch))
      return false;

И в завершении осуществим подмену указателей на буферы внешних интерфейсов соответствующими буферами последнего внутреннего слоя.

   if(!SetGradient(conv.getGradient(), true) ||
      !SetOutput(conv.getOutput(), true))
      return false;
   SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
//---
   return true;
  }

Скопируем указатель функции активации, вернем логический результат выполнения операций вызывающей программе и завершим работу метода.

Как Вы заметили, в рамках архитектуры данного блока мы использовали внутренние объекты работающие с тензорами разной размерности. Вначале слой S3 осуществляет перестановку элементов в рамках всего буфера данных, без оглядки на унитарные последовательности. И в таком варианте вполне возможна "перетасовка" элементов между унитарными последовательности. С одной стороны, мы не ограничиваем перестановку элементов рамками унитарных последовательностей. С другой стороны, последовательность перестановки обучается на основе данных обучающей выборки. И если модель найдет зависимости между элементами различных унитарных последовательностей, то возможно это повысит эффективность модели. Довольно интересно будет посмотреть на результат обучения.

Объём статьи подходит к своему пределу, но наша работа на этом не заканчивается. Мы продолжим её в следующей статье нашей серии.

Заключение

В данной работе мы познакомились с фреймворком Multitask-Stockformer — инновационной моделью выбора акций, которая объединяет преобразование вейвлетов с мультизадачными модулями Self-Attention. Использование вейвлет-преобразования позволяет выявлять временные и частотные особенности рыночных данных, а механизмы Self-Attention обеспечивают точное моделирование сложных взаимодействий между анализируемыми факторами.

В практической части мы реализовали собственное видение отдельных блоков предложенного фреймворка средствами MQL5. И в следующей работе мы завершим реализацию рассмотренного фреймворка. А так же проверим эффективность реализованных подходов на реальных исторических данных.

Ссылки

Программы, используемые в статье

#	Имя	Тип	Описание
1	Research.mq5	Советник	Советник сбора примеров
2	ResearchRealORL.mq5	Советник	Советник сбора примеров методом Real-ORL
3	Study.mq5	Советник	Советник обучения моделей
4	Test.mq5	Советник	Советник для тестирования модели
5	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
6	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
7	NeuroNet.cl	Библиотека	Библиотека кода программы OpenCL

Прикрепленные файлы |

Загрузить ZIP

MQL5.zip (2279.1 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.

Другие статьи автора

Последние комментарии | Перейти к обсуждению на форуме трейдеров (1)

Rorschach | 26 дек. 2024 в 18:00

Про Gramian Angular Difference Field ничего не планируется?

Разработка интерактивного графического пользовательского интерфейса на MQL5 (Часть 1): Создание панели

В статье рассматриваются основные этапы создания и реализации панели графического пользовательского интерфейса (Graphical User Interface, GUI) с помощью языка MetaQuotes Language 5 (MQL5). Пользовательские панели утилит повышают качество взаимодействия с системой при торговле, упрощая типовые задачи и визуализируя важную торговую информацию. Создавая пользовательские панели, трейдеры могут оптимизировать рабочий процесс и сэкономить время при торговых операциях.

Разработка системы репликации (Часть 57): Анализируем тестовый сервис

И заключительный момент: хотя он и не включен в эту статью, я объясню код сервиса, который будет использоваться в следующей, поскольку мы будем использовать этот же код в качестве трамплина для того, что мы на самом деле разрабатываем. Так что, наберитесь терпения и ждите следующей статьи, ведь с каждым днем все становится еще интереснее.

Нейросети в трейдинге: Модели с использованием вейвлет-преобразования и многозадачного внимания (Окончание)

В предыдущей статье мы рассмотрели теоретические основы и приступили к реализации подходов фреймворка Multitask-Stockformer, объединяющего вейвлет-преобразование и многозадачную модель Self-Attention. Продолжаем реализацию алгоритмов указанного фреймворка и оценим их эффективность на реальных исторических данных.

Возможности Мастера MQL5, которые вам нужно знать (Часть 26): Скользящие средние и показатель Херста

Показатель Херста — это мера того, насколько сильно временной ряд автокоррелирует в долгосрочной перспективе. Предполагается, что он отражает долгосрочные свойства временного ряда и поэтому имеет определенный вес в анализе временных рядов даже за пределами экономических/финансовых временных рядов. Однако мы сосредоточимся на его потенциальной пользе для трейдеров, изучив, как этот показатель можно объединить со скользящими средними для формирования потенциально надежного сигнала.