Redes neurais de maneira fácil (Parte 94): Otimização da sequência de dados iniciais

Introdução

A abordagem tradicional na análise de séries temporais é manter os passos temporais na sequência original, acreditando-se que a ordem histórica seja a mais otimizada. No entanto, a maioria dos modelos não possui mecanismos claros para explorar relações entre segmentos distantes dentro de cada série, os quais podem, na verdade, ter fortes dependências. Por exemplo, redes neurais convolucionais (CNN) aplicadas em séries temporais capturam padrões em uma janela temporal limitada. Consequentemente, em séries temporais onde padrões importantes se estendem por períodos mais longos, esses modelos têm dificuldade em capturar a informação de forma eficaz. O uso de redes profundas aumenta o campo receptivo e resolve o problema parcialmente. Porém, o número de camadas convolucionais necessário para cobrir toda a sequência pode ser muito alto, levando à atenuação dos gradientes.

Na arquitetura de Transformer, a eficiência para captar dependências de longo prazo depende de vários fatores, como o comprimento da sequência, estratégias de codificação posicional e tokenização dos dados.

Essas considerações levaram os autores do artigo "Segment, Shuffle, and Stitch: A Simple Mechanism for Improving Time-Series Representations" a questionar a eficácia da sequência histórica. Será que existe uma forma mais eficaz de organizar as séries temporais para treinar representações mais robustas para cada tarefa?

Neste artigo, os autores apresentam um mecanismo simples e pronto para uso, chamado Segment, Shuffle, Stitch (S3), projetado para otimizar a representação de séries temporais. Como o nome sugere, S3 funciona segmentando a série temporal em partes não sobrepostas, embaralhando esses segmentos na ordem mais eficiente e, em seguida, unindo-os em uma nova sequência. Vale ressaltar que a ordem de rearranjo dos segmentos é ajustada para cada tarefa específica.

Além disso, S3 integra a série temporal original mediante uma operação treinável de soma ponderada com a versão embaralhada, permitindo preservar informações-chave da sequência original.

O mecanismo S3 é modular, fácil de integrar a qualquer modelo de análise de séries temporais e proporciona uma curva de aprendizagem mais suave, com redução do erro. Como S3 é treinado com a rede principal, os parâmetros de embaralhamento são atualizados de forma direcionada, adaptando-se às características dos dados iniciais e ao modelo base para refletir melhor a dinâmica temporal. Além disso, S3 pode ser empilhado, permitindo um embaralhamento com maior detalhamento.

O algoritmo proposto tem poucos hiperparâmetros para ajuste e exige recursos computacionais adicionais mínimos.

Para avaliar a eficácia dos métodos propostos, os autores integraram S3 em várias arquiteturas neurais, incluindo modelos baseados em CNN e Transformer. A análise de desempenho em diferentes conjuntos de dados de classificação univariada e previsão multivariada demonstra que a introdução de S3 resulta em uma melhora significativa na eficácia dos modelos, mantendo as mesmas condições. Os resultados indicam que integrar S3 em métodos modernos pode aumentar o desempenho em até 39,59% nas tarefas de classificação. Em tarefas de previsão de séries temporais univariadas e multivariadas, a eficácia do modelo pode aumentar em 68,71% e 51,22%, respectivamente.

1. O Algoritmo S3

Vamos conhecer o método S3 em detalhes.

Os dados iniciais são uma série temporal multivariada X, com T passos temporais e C canais, divididos em N segmentos não sobrepostos.

Consideramos o caso geral da série temporal multivariada, mas o método também é eficaz com séries univariadas. Basicamente, uma série temporal univariada pode ser vista como um caso particular de uma série multivariada, onde o número de canais C é igual a 1.

O objetivo do método é reorganizar os segmentos de forma ótima para criar uma nova sequência X', que capte melhor as relações e dependências temporais essenciais da série. Isso, por sua vez, melhora as representações para a tarefa-alvo.

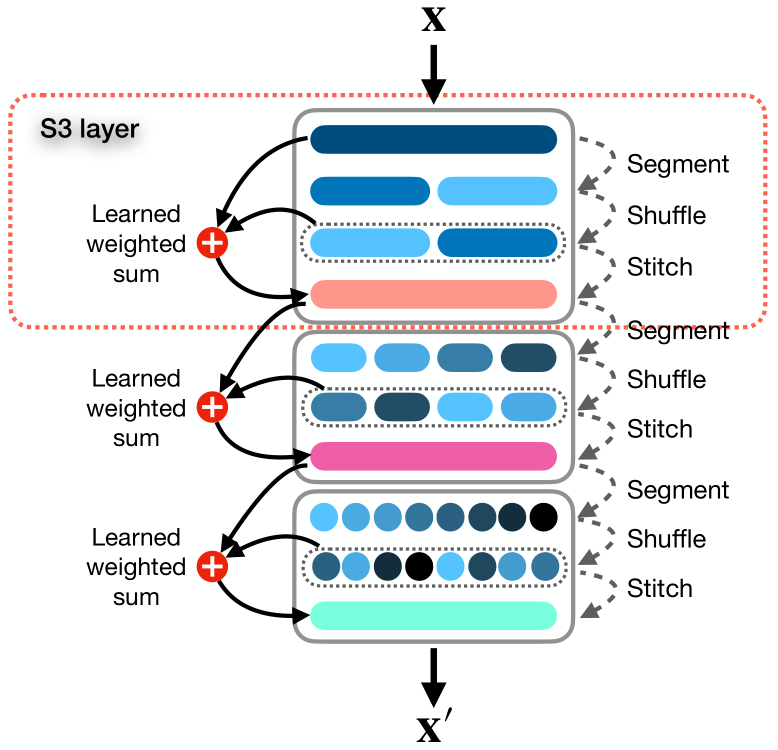
Os autores do método S3 propõem resolver o problema em três etapas: "Segmentação", "Embaralhamento" e "Unificação".

O módulo Segment divide a sequência original X em N segmentos não sobrepostos, cada um com τ passos temporais, onde τ = T/N. O conjunto de segmentos pode ser representado como S = {s1, s2, . . . , sn}.

Os segmentos são passados para o módulo Shuffle, que usa um vetor de embaralhamento P = {p1, p2, . . . , pn} para reorganizar os segmentos na ordem ideal. Cada parâmetro de embaralhamento pj no vetor P corresponde ao segmento sj na matriz S. Em essência, P é um conjunto de pesos treináveis, otimizados pela rede, que controla a posição e a prioridade do segmento na sequência reordenada.

O processo de embaralhamento é simples e intuitivo: quanto maior o valor de pj, maior a prioridade do segmento sj na sequência embaralhada. A sequência embaralhada Sshuffledpode ser representada como:

A reorganização do vetor S com base na ordem de classificação P não é diferenciável por padrão, pois envolve operações discretas e introduz descontinuidades. Métodos de ordenação "suave" aproximam a ordem de classificação, atribuindo probabilidades que refletem o quanto cada elemento é maior em relação aos outros. Embora essa aproximação seja naturalmente diferenciável, ela pode adicionar ruído e imprecisões, tornando a classificação menos intuitiva. Para obter uma ordenação diferenciável precisa e intuitiva, assim como nos métodos tradicionais, os autores introduzem etapas intermediárias. Essas etapas criam um caminho para que os gradientes passem pelos parâmetros de embaralhamento P durante o aprendizado.

Primeiro, obtemos os índices que ordenam os elementos P, usando σ = Argsort(P). Temos uma lista de tensores S = {s1, s2, s3, ...sn}, que queremos reordenar com base nos índices da lista σ = {σ1, σ2, ..., σn} de forma diferenciável. Depois, criamos uma matriz U de dimensão (τ × C) × n × n, onde repetimos cada si N vezes.

A seguir, formamos a matriz Ω com dimensão n × n, onde cada linha j tem um único elemento não nulo na posição k = σj. Convertendo Ω em uma matriz binária, escalamos cada elemento não nulo para 1 usando um coeficiente de escala. Esse processo cria um caminho para os gradientes passarem por P na retropropagação do erro.

Realizando o produto de Hadamard entre U e Ω, obtemos a matriz V, onde cada linha j contém um único elemento não nulo k, igual a sk. Ao somar sobre a última dimensão e transpor a matriz resultante, obtemos a matriz embaralhada final Sshuffled.

O uso de uma matriz multidimensional P' permite incluir parâmetros adicionais que ajudam o modelo a capturar representações mais complexas. Assim, os autores introduzem o hiperparâmetro λ para definir a dimensionalidade da matriz P'. Em seguida, soma-se P' sobre os primeiros λ − 1 eixos para obter um vetor unidimensional P, , que é então usado para calcular os índices de permutação σ = Argsort(P).

Essa abordagem permite aumentar o número de parâmetros de embaralhamento, capturando dependências mais complexas nos dados de séries temporais sem afetar as operações de ordenação.

Na etapa final, o módulo Stitch combina os segmentos embaralhados Sshuffled para criar uma única sequência embaralhada X'.

Para manter a informação do ordenamento original da série temporal, realiza-se uma soma ponderada entre as sequências original e embaralhada, com os parâmetros w1 2 w2, que também são otimizados durante o treinamento do modelo principal.

Considerando S3 como um módulo, podemos empilhá-los sequencialmente na arquitetura neural. Definimos ϕ como hiperparâmetro que determina o número de camadas S3. Para simplificar e evitar definir um hiperparâmetro separado por segmento, os autores definem o parâmetro θ como multiplicador do número de segmentos nas camadas subsequentes de S3.

Quando várias camadas de S3 são empilhadas, cada nível ℓ de 1 a ϕ segmenta e embaralha os dados com base nos resultados do nível anterior.

Todos os parâmetros treináveis de S3 são atualizados junto com os parâmetros do modelo, sem introduzir perdas intermediárias nas camadas de S3. Isso garante que os níveis S3 sejam treinados conforme a tarefa específica e o nível de base.

Caso a sequência original X não seja divisível pelo número de segmentos N, truncamos os primeiros T mod N passos da sequência de entrada. Para assegurar que nenhum dado se perca e manter as mesmas dimensões de entrada e saída, adicionamos as amostras truncadas de volta ao início dos dados de saída da última camada de S3.

A visualização do método está disponível na ilustração do artigo.

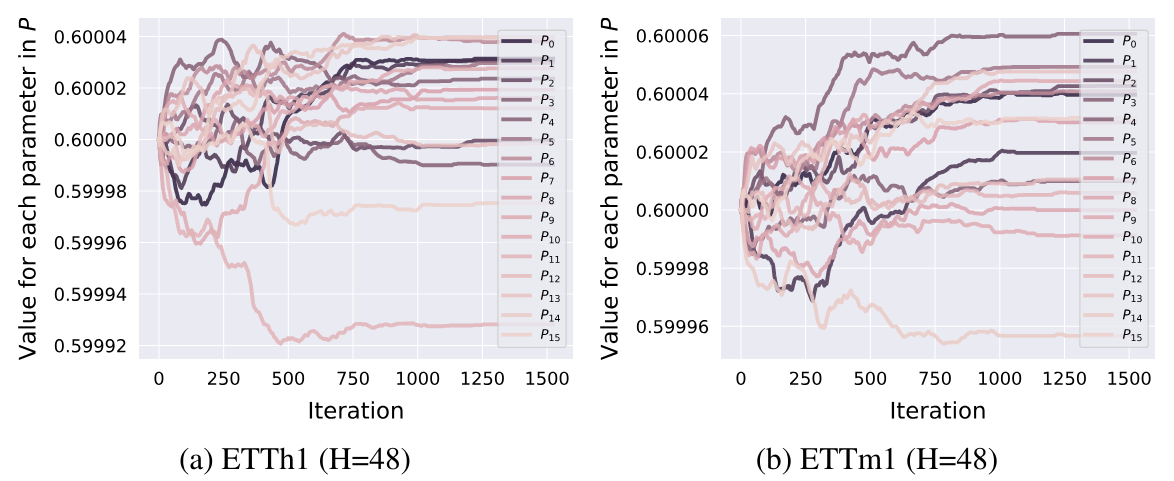
Os experimentos indicam que os parâmetros de permutação são ajustados no estágio inicial de treinamento e, em seguida, são fixados sem alterações posteriores.

2. Implementação com MQL5

Após revisar os aspectos teóricos do método S3, passamos para a parte prática, onde exploraremos uma implementação em MQL5. Antes de escrever o código, vamos refletir sobre a arquitetura dos métodos propostos à luz das nossas ferramentas disponíveis.

2.1 Arquitetura de construção

Para definir a ordem de classificação dos dados, os autores usam um vetor de parâmetros treináveis P. Na nossa biblioteca, parâmetros treináveis só existem em camadas neurais. Em princípio, podemos usar uma camada neural para gerar os parâmetros de prioridade dos segmentos. Assim, o treinamento dos parâmetros pode ser feito com as ferramentas da camada neural utilizada. Contudo, surge um detalhe: é necessário fornecer dados de entrada, o que não é previsto para parâmetros treináveis. Resolvemos isso de forma simples: passamos um vetor fixo preenchido com "1" para a camada.

Esse método permite resolver também a questão da matriz multidimensional de permutação P'. Para alterar a dimensão dessa matriz (definida pelo hiperparâmetro λ pelos autores), basta modificar o tamanho do vetor de entrada. O restante da funcionalidade permanece inalterado. A soma dos parâmetros para cada segmento já é realizada na camada neural. O tamanho dos resultados dessa camada neural é igual ao número de segmentos.

Para transformar as prioridades dos segmentos em valores probabilísticos, usamos a função SoftMax.

Aplicaremos um método similar para os parâmetros de ponderação da influência das sequências original e embaralhada. Neste caso, o tamanho dos resultados da camada será 2, e a função de ativação escolhida é a sigmoide.

Os parâmetros treináveis estão definidos. No entanto, precisamos implementar o algoritmo de classificação dos segmentos em ordem crescente ou decrescente de probabilidades.

Teoricamente, a ordem de classificação das prioridades dos segmentos não é relevante, pois treinaremos a ordem de permutação dos segmentos. Assim, durante o treinamento, o modelo distribuirá as prioridades conforme a ordem de classificação estabelecida. É crucial que a ordem de classificação permaneça a mesma no treinamento e na execução do modelo.

Para permitir a distribuição do gradiente de erro no vetor de prioridades P, os autores propuseram um algoritmo complexo, envolvendo matrizes multidimensionais e várias duplicações dos dados iniciais. Isso aumenta os custos computacionais e o consumo de memória. Podemos encontrar uma alternativa mais econômica?

Vamos examinar o processo proposto pelos autores do S3, analisando ações e resultados.

Primeiro, é formada a matriz U, que representa múltiplas cópias dos dados iniciais. Gostaria de evitar essa etapa, pois isso reduziria o uso de memória para armazenar a grande matriz e os recursos computacionais gastos na cópia dos dados.

A segunda matriz Ω é binária, majoritariamente preenchida com zeros. A quantidade de valores não nulos equivale ao número de segmentos na sequência analisada (N), enquanto o número de elementos nulos é N - 1 vezes maior. Seria ideal usar uma matriz esparsa, economizando tanto memória quanto poder computacional ao multiplicar as matrizes.

Em seguida, o algoritmo S3 aplica a multiplicação elemento a elemento entre as matrizes, somando pelo último eixo e transpondo a matriz resultante.

Essas operações resultam simplesmente em um tensor embaralhado dos dados iniciais. Uma permutação direta dos elementos do tensor exigiria menos recursos e seria mais rápida.

O algoritmo “elaborado” de permutação foi desenvolvido para viabilizar a distribuição do gradiente de erro até o vetor de prioridades P. Isso ocorre devido a uma “armadilha” do processo automático de diferenciação do PyTorch, que os autores usaram.

Como estamos construindo os algoritmos de propagação para fente e inversa, isso aumenta o trabalho de desenvolvimento, mas nos oferece mais flexibilidade. Portanto, na propagação para fente, podemos substituir essas operações por uma permutação direta dos dados. É evidente que esta é uma abordagem mais eficiente.

Mas permanece a questão da distribuição dos gradientes de erro. Creio que todos concordamos que, ao reorganizar os dados iniciais, cada segmento participa no tensor de resultados apenas uma vez. Consequentemente, todo o gradiente de erro é transmitido para o segmento correspondente. Em outras palavras, ao distribuir o gradiente de erro sobre os dados iniciais, precisamos realizar uma permutação inversa dos segmentos. Desta vez, no entanto, trabalharemos com o tensor de gradientes de erro.

A segunda questão é a distribuição do gradiente de erro para o vetor de prioridades. Aqui, o algoritmo é um pouco mais complexo. Na propagação para frente, utilizamos uma prioridade única para todo o segmento. Portanto, na propagação reversa, precisamos somar o gradiente de erro de todo o segmento em uma única prioridade. Para isso, multiplicamos o vetor de dados iniciais do segmento relevante pelo segmento correspondente do tensor de gradientes de erro.

Além disso, na construção da matriz binária Ω, foram usados coeficientes de escala para ajustar os elementos não nulos para 1. É claro que, para ajustar um número não nulo para 1, é preciso dividi-lo por ele mesmo ou multiplicá-lo pelo seu inverso. Portanto, os coeficientes de escala são iguais aos inversos das prioridades. Assim, o valor do gradiente de erro obtido acima deve ser dividido pela prioridade do segmento.

Vale notar que a prioridade do segmento não deve ser igual a "0". O uso de SoftMax elimina essa possibilidade. Contudo, não exclui valores muito pequenos, cuja divisão pode gerar gradientes de erro relativamente altos.

Além disso, a utilização da função SoftMax para formar as probabilidades de prioridade dos segmentos garante que todos os valores estejam no intervalo (0, 1). E aqui torna-se evidente que segmentos com prioridade menor recebem um gradiente de erro maior. Pois a divisão por um número menor que 1 resulta em um valor maior que o dividendo.

Definindo os pontos críticos do algoritmo em desenvolvimento, podemos prosseguir para a sua implementação direta no código. Começaremos com a implementação no contexto do OpenCL.

2.2 Construção dos kernels OpenCL

Como sempre, iniciamos o trabalho com a implementação dos algoritmos de propagação para frente. No lado do programa OpenCL, primeiro criaremos o kernel FeedForwardS3.

Aqui, quero lembrar que a geração das probabilidades de distribuição dos segmentos e dos pesos para a soma ponderada da sequência original e embaralhada será realizada nas camadas neurais aninhadas. Portanto, neste kernel, os dados já chegam prontos na forma de parâmetros.

Assim, nosso kernel recebe nos parâmetros ponteiros para 5 buffers de dados e 2 constantes. Em 3 buffers estão contidos os dados iniciais: sequência original, probabilidades dos segmentos e coeficientes de ponderação. Outros 2 buffers destinam-se ao registro dos resultados do kernel. Em um deles, registraremos a sequência resultante, e no outro, os índices de permutação dos segmentos, que serão necessários para realizar as operações de propagação reversa.

Nas constantes, especificaremos o tamanho da janela de um segmento e a quantidade total de elementos na sequência.

Vale ressaltar que, na segunda constante, indicamos o tamanho exato do vetor de dados iniciais, e não a quantidade de segmentos ou passos temporais. No tamanho da janela de segmentos, também indicamos o número de elementos do array, e não os passos temporais. É evidente que ambas as constantes devem ser divisíveis sem resto pelo tamanho do vetor de um único passo temporal.

__kernel void FeedForwardS3(__global float* inputs,
                            __global float* probability,
                            __global float* weights,
                            __global float* outputs,
                            __global float* positions,
                            const int window,
                            const int total
                           )
  {
   int pos = get_global_id(0);
   int segments = get_global_size(0);

Pretendemos iniciar o kernel em um espaço de tarefas unidimensional, com base no número de segmentos da sequência analisada. No corpo do kernel, identificamos imediatamente o fluxo atual e determinamos o número total de segmentos com base na quantidade de tarefas iniciadas.

Para o caso em que o tamanho total dos dados iniciais não seja múltiplo do tamanho da janela de um segmento, reduzimos o total de segmentos em 1.

   if((segments * window) > total)
      segments--;

O próximo passo é ordenar as prioridades dos segmentos para definir a sequência deles. No entanto, não implementaremos um algoritmo de ordenação em sua forma pura. Em vez disso, definiremos a posição do segmento analisado na sequência. Pode parecer uma “jogada de palavras”, mas para definir a posição de um único elemento, precisamos apenas de uma passagem pelo vetor de probabilidades dos segmentos. Já ao ordenar o vetor, precisaríamos de várias passagens pelo vetor de probabilidades e da sincronização dos fluxos de cálculo.

Neste ponto, dividimos o algoritmo em duas ramificações, dependendo do índice do fluxo atual. A primeira ramificação é o caso geral, usada quando o índice do fluxo atual é menor que o número de segmentos. Considerando que o índice do primeiro fluxo é 0, essa condição pode parecer incomum. Mas vale lembrar que, conforme mencionado anteriormente, no caso de o tamanho dos dados iniciais não ser múltiplo do tamanho da janela dos segmentos, reduzimos o valor da variável que representa o número de segmentos. Assim, o último fluxo segue a segunda ramificação do algoritmo para determinar a posição do segmento.

No caso geral, para definir a posição do segmento correspondente ao fluxo de operações atual, fixamos em uma constante local sua prioridade. Configuramos um laço que vai do primeiro até o segmento atual, no qual contamos os elementos com prioridade menor ou igual à do segmento atual. No caso de uma ordenação decrescente, contamos o número de elementos com prioridade maior ou igual ao segmento atual.

Em seguida, realizamos um laço do próximo segmento até o último, somando o número de elementos com prioridade estritamente menor (estritamente maior em ordenação decrescente).

Após completar as operações de ambos os laços, obtemos a posição do segmento atual na sequência geral.

   int segment = 0;
   if(pos < segments)
     {
      const float prob = probability[pos];
      for(int i = 0; i < pos; i++)
        {
         if(probability[i] <= prob)
            segment++;
        }
      for(int i = pos + 1; i < segments; i++)
        {
         if(probability[i] < prob)
            segment++;
        }
     }

A divisão da passagem pelo vetor de prioridades em dois laços é feita para o caso específico de haver dois ou mais elementos com a mesma prioridade. Nesse caso, a prioridade é atribuída ao elemento que aparece primeiro na sequência original. É claro que é possível construir o algoritmo com um único laço, mas, nesse caso, antes de comparar as prioridades, seria necessário verificar em cada iteração se o segmento está antes ou depois do atual na sequência original.

Na segunda ramificação do algoritmo para o caso especial, simplesmente atribuímos o número do segmento à sua ordem na sequência. É fácil deduzir que, no caso especial mencionado acima, todos os segmentos completos serão embaralhados, enquanto o último (incompleto) permanecerá em sua posição original.

   else
      segment = pos;

Agora que determinamos a posição do segmento na sequência embaralhada, podemos movê-lo. Para isso, definiremos os deslocamentos nos buffers de dados iniciais e de resultados.

   const int shift_in = segment * window;
   const int shift_out = pos * window;

Imediatamente, armazenamos a posição determinada no buffer correspondente.

   positions[pos] = (float)segment;

E aqui lembramos da soma ponderada das sequências original e embaralhada. Naturalmente, para evitar cópia desnecessária de dados no buffer de resultados, salvamos diretamente a soma ponderada dos dois segmentos das sequências original e embaralhada. Para isso, armazenamos em constantes locais os parâmetros de ponderação.

   const float w1 = weights[0];
   const float w2 = weights[1];

Fazemos um laço com um número de iterações igual ao tamanho da janela de um segmento, no qual somamos os elementos das duas sequências com os coeficientes de ponderação, e salvamos os valores obtidos no buffer de resultados.

   for(int i = 0; i < window; i++)
     {
      if((shift_in + i) >= total || (shift_out + i) >= total)
         break;
      outputs[shift_out + i] = w1 * inputs[shift_in + i] + w2 * inputs[shift_out + i];
     }
  }

Após construir o kernel de propagação para frente, passamos a trabalhar na propagação reversa. Aqui, começamos com a construção do kernel InsideGradientS3, no qual distribuímos o gradiente de erro até o nível da camada anterior e das prioridades dos segmentos. Nos parâmetros desse kernel, além dos buffers já conhecidos, adicionamos ponteiros para os buffers dos gradientes de erro correspondentes.

__kernel void InsideGradientS3(__global float* inputs,
                               __global float* inputs_gr,
                               __global float* probability,
                               __global float* probability_gr,
                               __global float* weights,
                               __global float* outputs_gr,
                               __global float* positions,
                               const int window,
                               const int total
                              )
  {
   size_t pos = get_global_id(0);

O kernel será iniciado em um espaço de tarefas unidimensional com base no número de segmentos da sequência analisada. No corpo do kernel, identificamos de imediato o fluxo atual de operações. Determinar o número total de segmentos neste caso é desnecessário.

Em seguida, carregamos das constantes definidas durante a propagação para frente nos buffers de dados.

   int segment = (int)positions[pos];
   float prob = probability[pos];
   const float w1 = weights[0];
   const float w2 = weights[1];

Após isso, definimos o deslocamento nos buffers de dados.

   const int shift_in = segment * window;
   const int shift_out = pos * window;

Declaramos variáveis locais para armazenar dados intermediários.

   float grad = 0;
   float temp = 0;

No próximo passo, realizamos um laço com número de iterações igual ao tamanho da janela do segmento, no qual acumulamos o gradiente de erro para a prioridade do segmento.

   for(int i = 0; i < window; i++)
     {
      if((shift_out + i) >= total)
         break;
      temp = outputs_gr[shift_out + i] * w1;
      grad += temp * inputs[shift_in + i];

Simultaneamente, transmitimos o gradiente de erro ao buffer da camada anterior. Lembro que, na propagação para frente, somamos a sequência original e a embaralhada. Portanto, cada elemento dos dados iniciais deve receber o gradiente de erro de dois fluxos, com o respectivo coeficiente de ponderação.

      inputs_gr[shift_in + i] = temp + outputs_gr[shift_in + i] * w2;
     }

Antes de registrar o gradiente de erro da prioridade do segmento no buffer de dados correspondente, dividimos o valor obtido pela probabilidade do segmento atual.

   probability_gr[segment] = grad / prob;
  }

No kernel de distribuição de gradiente de erro analisado anteriormente, falta um detalhe — a distribuição do gradiente de erro sobre os coeficientes de ponderação das sequências original e embaralhada. Para realizar essa funcionalidade, criaremos um kernel separado WeightGradientS3.

É importante notar que a abordagem geral que estamos usando, onde cada fluxo individual coleta o gradiente de erro de um elemento, neste caso, é pouco eficiente. Isso ocorre devido ao pequeno número de elementos no vetor de coeficientes de ponderação. Como se pode observar, aqui temos apenas dois. Mas gostaríamos de ter mais fluxos paralelos para reduzir o tempo total de treinamento do modelo. Para alcançar esse efeito, criaremos 2 grupos de trabalho de fluxos, cada um dos quais irá coletar o gradiente de erro para seu respectivo parâmetro.

__kernel void WeightGradientS3(__global float *inputs,
                               __global float *positions,
                               __global float *outputs_gr,
                               __global float *weights_gr,
                               const int window,
                               const int total
                              )
  {
   size_t l = get_local_id(0);
   size_t w = get_global_id(1);

Assim, o kernel será configurado para ser executado em um espaço de tarefas bidimensional. A primeira dimensão define o número de fluxos paralelos em um grupo. A segunda dimensão indicará o índice do parâmetro para o qual o gradiente de erro está sendo coletado.

Em seguida, declararemos um array local, no qual cada fluxo do grupo de trabalho armazenará sua parte do trabalho.

   __local float temp[LOCAL_ARRAY_SIZE];

Como a quantidade de fluxos de trabalho não pode ser maior que o tamanho do array local declarado, somos obrigados a limitar a quantidade de “trabalhadores”.

   size_t ls = min((uint)get_local_size(0), (uint)LOCAL_ARRAY_SIZE);

No primeiro estágio, cada fluxo coleta sua parte dos gradientes de erro de forma independente dos outros fluxos do grupo de trabalho. Para isso, organizamos um laço que percorre os elementos do buffer de gradientes de erro na saída da camada atual, desde o elemento com o índice do fluxo atual até o último no array, com um passo igual ao número de “trabalhadores”.

No corpo do laço, primeiro definimos o deslocamento até o elemento correspondente no buffer de dados iniciais. E vale mencionar que esse deslocamento depende do índice do coeficiente de ponderação para o qual estamos coletando o gradiente de erro. Para o segundo coeficiente de ponderação, o deslocamento nos buffers de gradientes de erro da camada e dos dados iniciais é o mesmo.

   if(l < ls)
     {
      float val = 0;
      //---
      for(int i = l; i < total; i += ls)
        {
         int shift_in = i;

Já para o primeiro, inicialmente identificamos o segmento no buffer de gradientes de erro. Em seguida, extraímos o segmento correspondente da sequência original a partir do vetor de permutações. Só então podemos calcular o deslocamento no buffer de dados iniciais até o elemento requerido.

         if(w == 0)
           {
            int pos = i / window;
            shift_in = positions[pos] * window + i % window;
           }

Com os índices dos elementos correspondentes em ambos os buffers, calculamos o gradiente de erro para o coeficiente de ponderação na posição dada e o adicionamos a uma variável acumulativa.

         val += outputs_gr[i] * inputs[shift_in];
        }
      temp[l] = val;
     }
   barrier(CLK_LOCAL_MEM_FENCE);

Após todas as iterações do laço, a soma acumulada do gradiente de erro é registrada no elemento correspondente do array de memória local e organizamos uma barreira de sincronização dos fluxos do grupo de trabalho.

No segundo estágio, somamos os valores dos elementos do array local.

   int t = ls;
   do
     {
      t = (t + 1) / 2;
      if(l < t && (l + t) < ls)
        {
         temp[l] += temp[l + t];
         temp[l + t] = 0;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(t > 1);

Para finalizar as operações do kernel, o primeiro fluxo do grupo de trabalho transfere o gradiente de erro somado para o elemento correspondente no buffer global.

   if(l == 0)
      weights_gr[w] = temp[0];
  }

Após a distribuição dos gradientes de erro para todos os elementos, de acordo com sua influência no resultado geral, passamos geralmente a trabalhar nos algoritmos de atualização dos parâmetros. Contudo, no contexto deste artigo, todos os parâmetros treináveis foram organizados nas camadas neurais aninhadas. Portanto, os algoritmos de atualização de parâmetros já estão implementados nesses objetos mencionados. Desta forma, encerramos o trabalho no contexto do OpenCL e passamos para a implementação na parte principal do programa.

2.3 Criação da classe CNeuronS3

Para implementar as abordagens propostas na parte principal do programa, criamos uma nova classe de camada neural chamada CNeuronS3. A estrutura desta classe é apresentada a seguir.

class CNeuronS3   :  public CNeuronBaseOCL
  {
protected:
   uint              iWindow;
   uint              iSegments;
   //---
   CNeuronBaseOCL    cOne;
   CNeuronConvOCL    cShufle;
   CNeuronSoftMaxOCL cProbability;
   CNeuronConvOCL    cWeights;
   CBufferFloat      cPositions;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      feedForwardS3(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradientsS3(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronS3(void)   {};
                    ~CNeuronS3(void)   {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint numNeurons, ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronS3;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   virtual CLayerDescription* GetLayerInfo(void);
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

Na nossa classe, declaramos 2 variáveis e 5 objetos aninhados. Nas variáveis, armazenaremos o tamanho da janela de um segmento e o número total de segmentos na sequência. À medida que atribuirmos funções aos objetos aninhados, iremos conhecê-los melhor durante a implementação dos métodos da nossa classe.

Todos os objetos da classe são declarados estaticamente, o que nos permite manter o construtor e o destrutor da classe "vazios". A inicialização de todos os objetos aninhados é realizada no método Init. Como sempre, nos parâmetros deste método, recebemos os principais parâmetros de arquitetura da classe criada a partir do programa chamador. E aqui devemos atentar para dois parâmetros:

• window — tamanho da janela de um segmento;
• numNeurons — número de neurônios na camada.

A particularidade desses parâmetros é que indicam a quantidade de elementos do array, e não os passos da série temporal. Além disso, seus valores devem ser múltiplos do tamanho do vetor que descreve um único passo temporal. Em outras palavras, para simplificar a implementação, construímos uma classe para trabalhar com séries temporais unidimensionais, e a responsabilidade por manter a integridade dos passos temporais de uma série multidimensional dentro dos segmentos recai sobre o usuário.

bool CNeuronS3::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                     uint window, uint numNeurons, 
                     ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, numNeurons, optimization_type, batch))
      return false;

No corpo do método, chamamos imediatamente o método homônimo da classe pai, no qual os parâmetros recebidos são validados e os objetos herdados são inicializados. E claro, não deixamos de verificar o resultado lógico do método chamado.

Após a inicialização bem-sucedida dos objetos herdados, armazenamos o tamanho da janela de um segmento e imediatamente definimos o número total de segmentos.

   iWindow = MathMax(window, 1);
   iSegments = (numNeurons + window - 1) / window;

Em seguida, procedemos à inicialização dos objetos internos da classe. Primeiro, inicializamos uma camada neural fixa de valores unitários, que será usada como base para gerar as prioridades de permutação dos segmentos e os parâmetros de soma ponderada das sequências. Primeiro, inicializamos a camada neural e depois preenchemos o buffer de resultados com valores unitários de forma forçada.

   if(!cOne.Init(0, 0, OpenCL, 1, optimization, iBatch))
      return false;
   CBufferFloat *buffer = cOne.getOutput();
   if(!buffer || !buffer.BufferInit(buffer.Total(),1))
      return false;
   if(!buffer.BufferWrite())
     return false;

Aqui, é importante destacar dois pontos. Primeiro, criamos uma camada com apenas um neurônio. Como você deve lembrar, ao projetar a arquitetura de nossa implementação, mencionamos que o número de neurônios nesta camada indica a dimensionalidade da matriz de permutação. Pessoalmente, não vejo a necessidade de utilizar uma matriz multidimensional. Do ponto de vista matemático, sem o uso de funções de ativação intermediárias, a função linear de soma do produto de várias variáveis por uma constante se reduz ao produto de uma única variável pela constante utilizada.

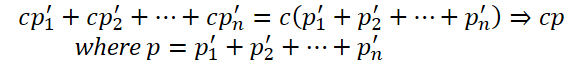
Sob essa perspectiva, o aumento dos parâmetros leva apenas ao crescimento da complexidade computacional, com impacto questionável na eficiência do modelo.

Por outro lado, essa é apenas minha opinião. Deixo a você a oportunidade de testar isso experimentalmente.

O segundo ponto a ser observado é a indicação de "0" conexões de saída para esta camada aninhada. Lembro que planejamos utilizar esse objeto como dados de entrada para duas camadas neurais. A presença dessas duas camadas subsequentes nos levou a uma pequena adaptação. Nossa camada neural básica foi construída de forma que contém uma matriz de coeficientes de ponderação apenas para uma camada subsequente. Temos, no entanto, uma classe de camadas neurais convolucionais, que contém suas próprias matrizes de coeficientes de ponderação para conexões de entrada. O uso de um único elemento na entrada e vários valores de prioridade de permutação na saída, por assim dizer, não é exatamente o cenário ideal para uma camada convolucional. Mas não vamos nos precipitar.

Um único elemento na entrada nos garante um parâmetro treinável no filtro de convolução. E podemos facilmente definir o tamanho do vetor de permutação especificando a quantidade necessária de filtros de convolução. Assim, indicamos apenas um elemento de convolução. Dessa forma, transferimos os parâmetros treináveis para as camadas neurais subsequentes.

   if(!cShufle.Init(0, 1, OpenCL, 1, 1, iSegments, 1, optimization, iBatch))
      return false;
   cShufle.SetActivationFunction(None);

Como discutido anteriormente, as prioridades de permutação são convertidas em probabilidades por meio da função SoftMax.

   if(!cProbability.Init(0, 2, OpenCL, iSegments, optimization, iBatch))
      return false;
   cProbability.SetActivationFunction(None);
   cProbability.SetHeads(1);

Procedemos de maneira similar com o objeto de geração dos parâmetros de soma ponderada das sequências. Aqui, apenas utilizamos a função sigmoide como função de ativação.

   if(!cWeights.Init(0, 3, OpenCL, 1, 1, 2, 1, optimization, iBatch))
      return false;
   cWeights.SetActivationFunction(SIGMOID);

E, ao final do método de inicialização, criamos um buffer para registrar os índices de permutação dos segmentos.

   if(!cPositions.BufferInit(iSegments, 0) || !cPositions.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

Entre os métodos da classe, podemos observar dois novos métodos (feedForwardS3 e calcInputGradientsS3). Neles, a fila de execução dos kernels do programa OpenCL é organizada. É fácil deduzir que o primeiro método enfileira o kernel de propagação para frente, enquanto o segundo enfileira os dois kernels restantes para a distribuição dos gradientes de erro. Em artigos anteriores, já descrevemos diversas vezes o algoritmo de enfileiramento de um kernel para execução. Esses métodos são construídos de maneira semelhante, então não nos aprofundaremos neles agora. Você pode consultar o código desses métodos no anexo. Lá também está o código completo de todas as classes e programas usados na preparação deste artigo.

O algoritmo de propagação para frente da nossa classe é construído no método feedForward. Assim como o método homônimo da classe pai, ele recebe, nos parâmetros, um ponteiro para o objeto da camada neural anterior, que contém os dados iniciais.

Gostaria de lembrar que, antes de chamar o método para enfileirar o kernel de propagação para frente, precisamos preparar as prioridades de permutação dos segmentos e os parâmetros de soma ponderada das sequências original e embaralhada. Vale notar que o vetor fixo de valores unitários é usado como dados de entrada para esses processos. Portanto, esses valores não dependem dos dados iniciais e não se alteram durante o uso do modelo. Eles podem mudar apenas se houver uma alteração nos parâmetros treináveis durante o processo de aprendizado. Isso significa que o recálculo desses valores é necessário apenas no treinamento. O recálculo é realizado por meio da chamada do método de propagação para frente dos objetos aninhados correspondentes.

bool CNeuronS3::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(bTrain)
     {
      if(!cWeights.FeedForward(cOne.AsObject()))
         return false;
      if(!cShufle.FeedForward(cOne.AsObject()))
         return false;
      if(!cProbability.FeedForward(cShufle.AsObject()))
         return false;
     }

Em seguida, realizamos o embaralhamento da sequência original chamando o método de enfileiramento do kernel de propagação para frente na fila de execução.

   if(!feedForwardS3(NeuronOCL))
      return false;
//---
   return true;
  }

E, claro, acompanhamos o progresso das operações.

No algoritmo do método de distribuição dos gradientes, não há "armadilhas". O próprio método é chamado apenas durante o processo de treinamento, de modo que não precisamos verificar o modo atual de operação do modelo.

Nos parâmetros, o método recebe um ponteiro para o objeto da camada anterior, para o qual o gradiente de erro deve ser transmitido, e chamamos imediatamente o método de enfileiramento dos kernels de distribuição de gradientes de erro previamente criados.

bool CNeuronS3::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!calcInputGradientsS3(NeuronOCL))
      return false;

Em seguida, passamos o gradiente de erro para a camada de parâmetros de prioridade de permutação dos segmentos.

   if(!cShufle.calcHiddenGradients(cProbability.AsObject()))
      return false;

Passar o gradiente de erro até o nível da camada fixa não faz sentido. Portanto, omitiremos esse procedimento. Resta apenas ajustar o gradiente de erro resultante para as possíveis funções de ativação.

   if(cWeights.Activation() != None)
      if(!DeActivation(cWeights.getOutput(), cWeights.getGradient(), cWeights.getGradient(), cWeights.Activation()))
         return false;
   if(NeuronOCL.Activation() != None)
      if(!DeActivation(NeuronOCL.getOutput(),NeuronOCL.getGradient(),NeuronOCL.getGradient(),NeuronOCL.Activation()))
         return false;
//---
   return true;
  }

Observe que chamamos o método de desativação de gradientes de erro somente se tal função estiver presente no objeto correspondente.

Após a distribuição do gradiente de erro para todos os elementos de nosso modelo, de acordo com sua influência no resultado geral, devemos ajustar os parâmetros do modelo para reduzir o erro total. Aqui, o processo é bastante simples. Para ajustar os parâmetros da camada CNeuronS3, basta chamar os métodos de atualização de parâmetros dos objetos aninhados correspondentes.

bool CNeuronS3::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cWeights.UpdateInputWeights(cOne.AsObject()))
      return false;
   if(!cShufle.UpdateInputWeights(cOne.AsObject()))
      return false;
//---
   return true;
  }

Com isso, concluímos a análise dos métodos da nova classe. O escopo deste artigo não permite descrever o algoritmo de todos os métodos da nossa nova classe, mas você pode consultá-los por conta própria no anexo. Lá, o código completo desta classe e todos os seus métodos estão disponíveis.

2.4 Arquitetura dos Modelos

Após criar a nova classe de camada, a integramos na arquitetura do nosso modelo. Acredito que seja evidente que a classe CNeuronS3 será adicionada à arquitetura do Codificador do Estado do Ambiente. Nesta seção, não abordaremos em detalhes a arquitetura do Codificador, pois ela foi totalmente transferida do artigo anterior. Vamos nos concentrar apenas nas camadas neurais adicionadas, que colocamos logo após a camada de dados iniciais.

Lembro que nossos modelos de teste foram construídos para análise de dados históricos no timeframe H1. Para a análise, usamos os últimos 120 candles de histórico, cada um descrito por 9 parâmetros.

#define        HistoryBars             120           //Depth of history
#define        BarDescr                9             //Elements for 1 bar description

Durante a preparação deste artigo, adicionamos ao Codificador 3 camadas sequenciais para embaralhar os dados iniciais. Para a primeira camada, usamos segmentos de 12 passos temporais (horas).

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronS3;
   descr.count = prev_count;
   descr.window = 12*BarDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Na segunda camada, reduzimos o tamanho do segmento para 4 passos temporais.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronS3;
   descr.count = prev_count;
   descr.window = 4*BarDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

E na última camada, embaralhamos cada passo temporal individualmente.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronS3;
   descr.count = prev_count;
   descr.window = BarDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Em seguida, transferimos a arquitetura dos modelos do artigo anterior sem nenhuma alteração. Consequentemente, também não fizemos mudanças no algoritmo dos programas de interação com o ambiente, treinamento e teste dos modelos. Você pode consultar o código completo de todos os programas utilizados na preparação deste artigo no anexo.

3. Testes

Após finalizar a construção dos algoritmos dos métodos propostos, passamos, possivelmente, para a etapa mais empolgante — os testes e a avaliação dos resultados obtidos.

Como mencionado anteriormente, no processo de desenvolvimento deste artigo, não fizemos alterações nos programas de interação com o ambiente. Isso significa que podemos usar a amostra de dados de treinamento previamente coletada para treinar as modelos.

Lembro que, para o treinamento das modelos, usamos registros de execuções do programa de interação com o ambiente no testador de estratégias MetaTrader 5, com dados históricos reais do instrumento EURUSD no timeframe H1 para todo o ano de 2023.

Na primeira etapa, realizamos o treinamento do Codificador do estado do ambiente. Este modelo é treinado para prever os dados dos 24 elementos subsequentes da série temporal analisada.

#define        NForecast               24            //Number of forecast

Em outras palavras, nossa modelo tenta prever o movimento de preço para o próximo dia. De antemão, digo que, ao construir a política de comportamento do nosso Agente, nos baseamos não na previsão obtida, mas no estado oculto do Codificador. Portanto, no processo de treinamento da modelo, o mais importante não é a previsão exata do movimento futuro, mas a capacidade do Codificador de captar e codificar em seu estado oculto as principais tendências e movimentos futuros do preço.

A modelo do Codificador é treinada apenas para analisar o estado do mercado, sem considerar o saldo da conta e as posições abertas. Assim, atualizar a amostra de treinamento no processo de treinamento desse modelo não fornece informações adicionais. Isso permite treinar a modelo com a amostra criada anteriormente até atingir o resultado desejado.

E claro, ao final da primeira etapa de treinamento, nos interessa o impacto da nova camada sobre os dados de entrada recebidos pela modelo. Devo notar que a modelo dedica atenção quase igual às sequências embaralhada e original. A sequência original recebe um pouco mais de atenção.

Na primeira camada, o coeficiente da sequência embaralhada foi de 0,5039, enquanto o da sequência original foi de 0,5679. Ao mesmo tempo, observa-se um embaralhamento quase completo da sequência. Apenas o segmento com índice 7 permaneceu em sua posição original por acaso. Esse embaralhamento não é simétrico. Não há pares de elementos que simplesmente trocam de lugar.

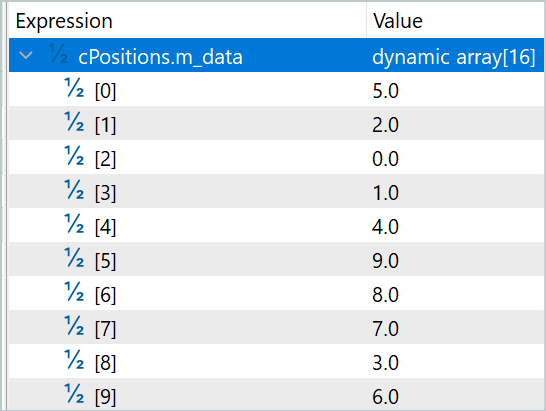
Na camada seguinte, ambos os coeficientes aumentaram ligeiramente para 0,6386 e 0,6574, respectivamente. Não incluí a lista de permutações aqui, pois ela aumentou três vezes. Mas já não há segmentos que permaneçam sem deslocamento.

Na terceira camada, mais atenção é dada à sequência original, mas o coeficiente da sequência embaralhada permanece bastante alto. Os parâmetros mudaram para 0,5064 e 0,7089, respectivamente.

Os resultados obtidos podem ser interpretados de diversas formas. A meu ver, a modelo busca uma lógica racional na comparação entre pares de segmentos.

O resultado é bastante interessante, mas o que mais nos interessa é o impacto sobre a política final do Agente. Após o treinamento do Codificador, passamos para a segunda etapa de treinamento das nossas modelos. Nesta etapa, realizamos o treinamento da política do Ator e do modelo do Crítico. O desempenho desses modelos depende fortemente do saldo da conta e das posições abertas no momento analisado. Portanto, nosso processo de treinamento será iterativo, alternando o treinamento das modelos com a coleta de dados adicionais de interação com o ambiente, permitindo refinar e otimizar a política de comportamento do Agente.

No processo de treinamento, conseguimos desenvolver uma política capaz de gerar lucro tanto no período de treinamento quanto no de teste. Os resultados do treinamento são apresentados a seguir.

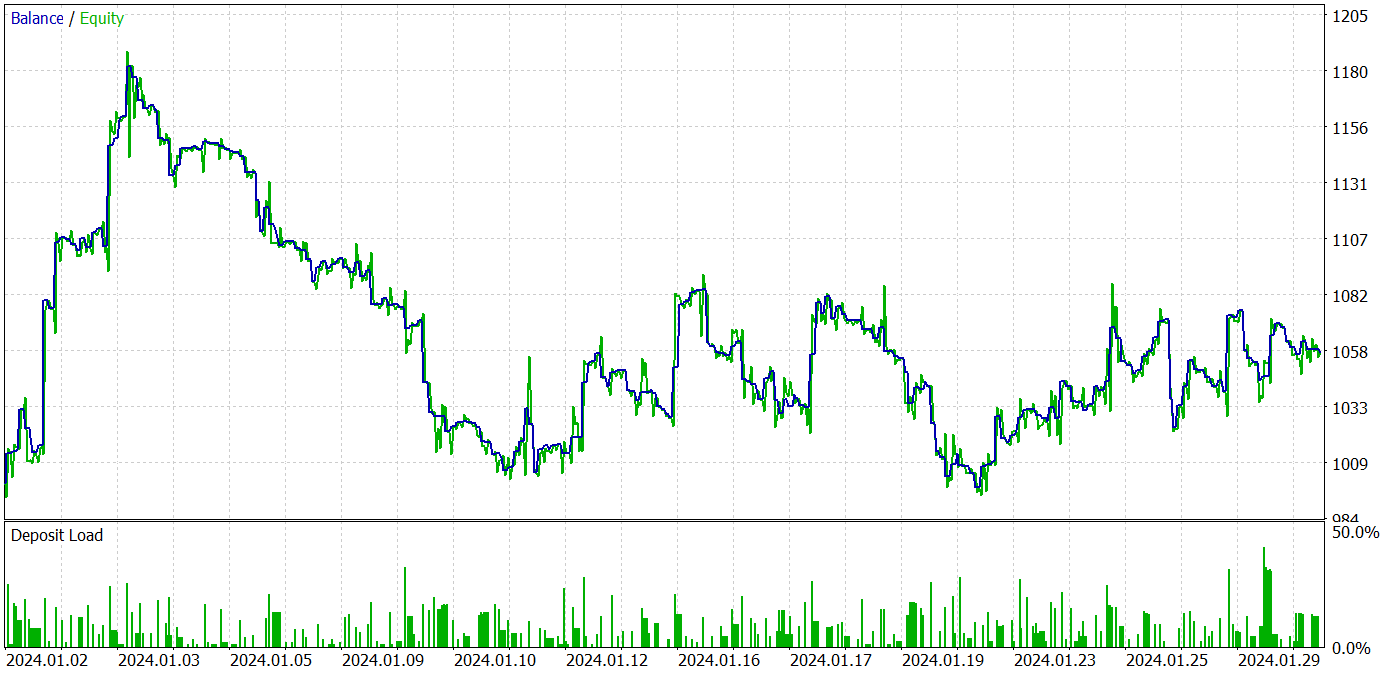
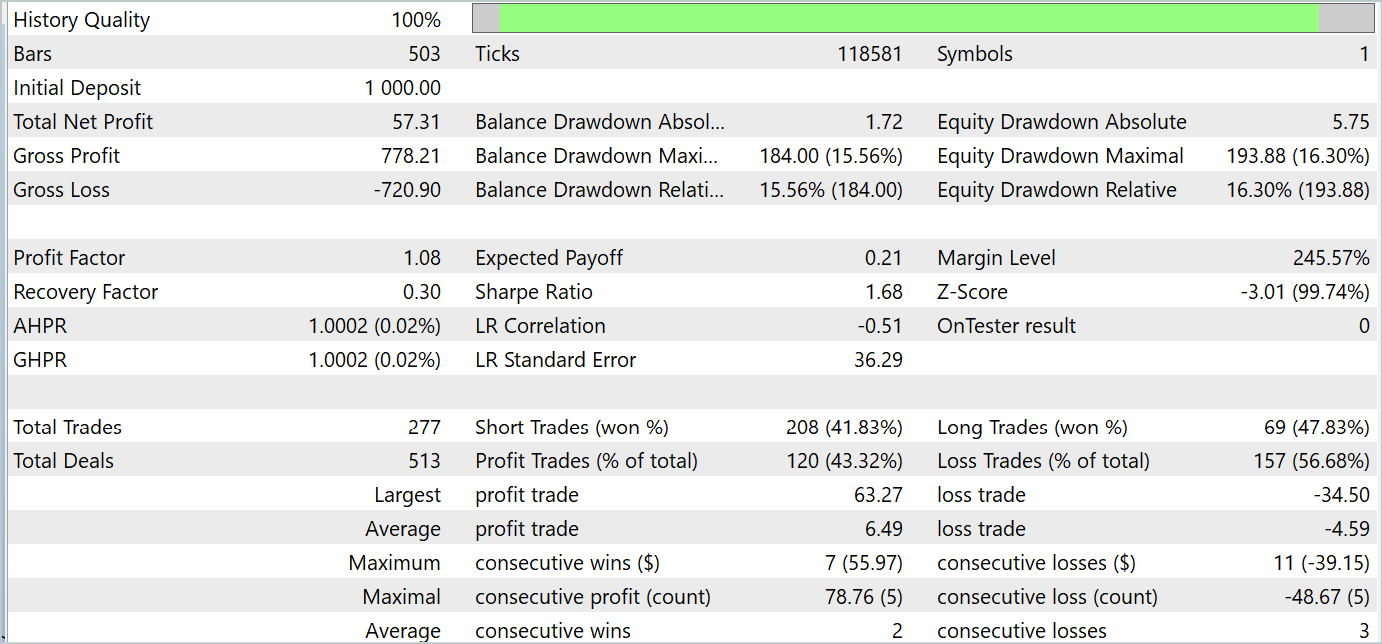
Apesar do lucro obtido, o gráfico de saldo está longe do desejado. E o modelo ainda necessita de ajustes. Ao observar o relatório de teste com mais atenção, podemos destacar que segunda e sexta-feira foram os dias mais deficitários. Na quarta-feira, ao contrário, o modelo gerou o máximo de lucro.

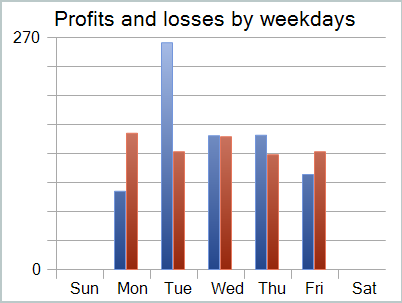
Portanto, limitar a atuação do modelo a dias específicos da semana pode aumentar a rentabilidade geral do modelo. Mas essa hipótese requer testes mais detalhados com uma amostra de dados mais representativa.

Considerações finais

Neste artigo, exploramos um método interessante de otimização de sequência de séries temporais S3, apresentado no artigo "Segment, Shuffle, and Stitch: A Simple Mechanism for Improving Time-Series Representations". A ideia central do método é aprimorar a qualidade da representação das séries temporais. A aplicação do S3 leva ao aumento da precisão de classificação e da robustez dos modelos.

Na parte prática do nosso artigo, apresentamos nossa visão dos métodos propostos utilizando MQL5. Realizamos o treinamento e teste dos modelos usando os métodos sugeridos. E os resultados são bastante interessantes.

Referências

• Segment, Shuffle, and Stitch: A Simple Mechanism for Improving Time-Series Representations
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA para coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA para coleta de exemplos com o método Real-ORL
3	Study.mq5	Expert Advisor	EA para treinamento das Modelos
4	StudyEncoder.mq5	Expert Advisor	EA para treinamento do Codificador
5	Test.mq5	Expert Advisor	EA para teste do modelo
6	Trajectory.mqh	Biblioteca de classes	Estrutura para descrição do estado do sistema
7	NeuroNet.mqh	Biblioteca de classes	Biblioteca de classes para criação de rede neural
8	NeuroNet.cl	Biblioteca	Biblioteca de código para o programa OpenCL