Redes neuronales en el trading: Modelos con transformada de wavelet y atención multitarea

Introducción

La previsión del rendimiento de los activos es un tema extensamente investigado en finanzas. El problema de la previsión del rendimiento se debe a varias cuestiones. En primer lugar, la multitud de factores que afectan a los rendimientos de los activos y la baja relación señal-ruido en matrices dispersas y de alta dimensionalidad dificultan que los modelos econométricos tradicionales extraigan información significativa. En segundo lugar, las relaciones funcionales entre las características predictivas y los rendimientos de los activos no están claras, lo cual crea problemas para captar las estructuras no lineales entre ellas.

En los últimos años, el aprendizaje profundo se ha convertido en una herramienta indispensable en la inversión cuantitativa, sobre todo para perfeccionar las estrategias multifactoriales que constituyen la base para comprender los movimientos de los precios de los activos financieros. Al automatizar el aprendizaje de características y captar las relaciones no lineales en los datos de los mercados financieros, los algoritmos de aprendizaje profundo identifican eficazmente patrones complejos, mejorando así la precisión de las previsiones. La comunidad investigadora mundial reconoce el potencial de las redes neuronales profundas, como las redes neuronales recurrentes (RNN) y las redes neuronales convolucionales (CNN), para predecir los precios de las acciones y los futuros. Sin embargo, el uso de modelos de aprendizaje profundo como RNN y CNN, aunque generalizado, rara vez explora modelos de redes neuronales más profundos, capaces de extraer y construir información de mercado y secuencias de emisión, lo cual sugiere oportunidades para un mayor desarrollo de aplicaciones de aprendizaje profundo en los mercados de valores.

Hoy le proponemos familiarizarse con el framework Multitask-Stockformer presentado en el artículo "Stockformer: A Price-Volume Factor Stock Selection Model Based on Wavelet Transform and Multi-Task Self-Attention Networks". A pesar de la semejanza del nombre con el framework StockFormer anteriormente discutido, los frameworks no tienen nada en común. Salvo, por supuesto, el objetivo de generar un portafolio de valores rentable para el rendimiento bursátil.

El framework Multitask-Stockformer construye un modelo de predicción bursátil multitarea basado en la transformada de wavelet y los modelos de Self-Attention.

El algoritmo Multitask-Stockformer

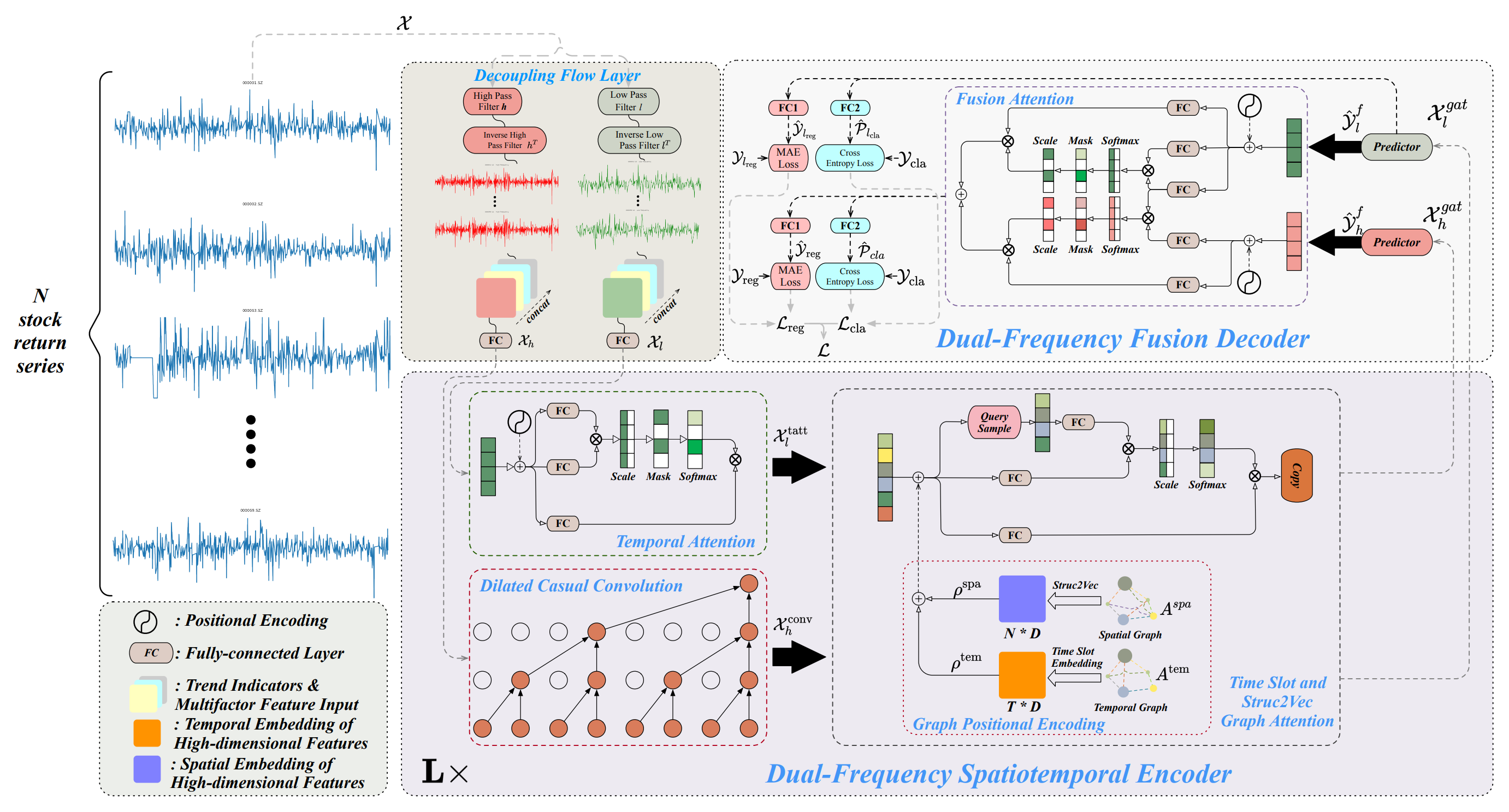
La arquitectura del framework Multitask-Stockformer se divide en 3 bloques: un módulo de división de flujos, un codificador espaciotemporal de doble frecuencia y un decodificador de doble frecuencia. Los datos históricos de activos analizados 𝒳 ∈ RT1×N×362 se procesan en el módulo de separación de flujos. En esta fase, el tensor de las series de rendimientos de los activos se separa en componentes de alta y baja frecuencia usando una transformada de wavelet discreta. Al mismo tiempo, el signo de la tendencia y las relaciones precio-volumen permanecen invariables. Luego estos componentes se combinan con las partes inalteradas de la señal de la última medición.

El componente de baja frecuencia muestra las tendencias a largo plazo, mientras que el componente de alta frecuencia capta las fluctuaciones a corto plazo y los acontecimientos bruscos. Se denotan como 𝒳l, 𝒳h ∈ RT1×N×362, respectivamente. Entonces 𝒳h y 𝒳l se transforman linealmente a través de una capa totalmente conectada en la dimensionalidad de RT1×N×D. En este caso, T1 denota la profundidad de la historia analizada.

El codificador espaciotemporal de doble frecuencia está diseñado para representar estos diferentes patrones de series temporales: las características de baja frecuencia se introducen en un módulo de atención temporal (denominado tatt), mientras que las características de alta frecuencia se procesan a través de una capa convolucional causal ampliada (denominada conv). A continuación, estos componentes se introducen en redes de atención basadas en grafos (denominadas gat). La interacción con la información de los grafos permite al modelo captar relaciones y dependencias complejas entre activos y tiempo. En este módulo, el grafo espacialAspa y el grafo temporal Atem se transforman usando una capa completamente conectada y operaciones de traslación tensorial en incorporaciones multidimensionales, denotadas como ρspa, ρtem ∈ RT1×N×D, que luego se combinan con 𝒳l,tatt, 𝒳h,conv utilizando operaciones de adición y atención al grafo para obtener 𝒳l,gat, 𝒳h,gat ∈ RT1×N×D. El codificador espaciotemporal de doble frecuencia consta de L capas destinadas a representar eficazmente dos patrones espaciotemporales a gran escala de ondas de baja y alta frecuencia. Por último, en el decodificador de doble frecuencia, los predictores generan 𝒴l,f, 𝒴h,f ∈ RT2×N×D, que se añaden mediante interacciones de Fusion Attention para obtener una representación latente de patrones temporales a dos escalas. Utilizando capas completamente conectadas separadas (la capa de regresión FC1 y la capa de clasificación FC2), se generan resultados multitarea que incluyen las previsiones de los rendimientos de las acciones (resultado de la regresión, denotado como reg), así como las probabilidades de previsión de la tendencia de las acciones (el resultado de la clasificación, denotado como cla).

Asimismo, los valores de regresión y las probabilidades de predicción de tendencias para el componente de baja frecuencia también se emiten para mejorar la formación de la señal de baja frecuencia.

A continuación le mostramos la visualización del framework Multitask-Stockformer realizada por el autor.

Implementación con MQL5

Lo anterior supone solo una breve descripción del framework Multitask-Stockformer. El framework es bastante complejo. Así que creo que resultará más eficaz familiarizarse con los algoritmos individuales a medida que se vayan aplicando. Y comenzaremos nuestro trabajo con el módulo de división del flujo de datos de origen.

Módulo de descomposición de señales

Para separar la señal analizada en componentes de baja y alta frecuencia, los autores del framework proponen usar una transformada de wavelet discreta. A diferencia de la descomposición de Fourier, la transformada de wavelet es capaz de captar no solo el componente de frecuencia, sino también la estructura de la señal. Esto la hace más ventajosa para analizar los mercados financieros, cuando no solo resulta importante la frecuencia, sino también el orden de las señales.

Ya habíamos utilizado antes la transformada de wavelet discreta para construir el framework FEDformer, pero entonces solo extrajimos el componente de baja frecuencia. Ahora también necesitaremos el componente de alta frecuencia. No obstante, podemos aprovechar los avances existentes.

La transformada de wavelet discreta supone en esencia una operación de convolución con una wavelet concreta utilizada como filtro. Esto nos permite usar algoritmos de capas convolucionales como base funcional. Debemos considerar que durante la transformación utilizaremos wavelets estáticas cuyos parámetros no cambiarán durante el entrenamiento. En consecuencia, deberemos desactivar el mecanismo de optimización de los parámetros de nuestro objeto.

Con las entradas anteriores crearemos un nuevo objeto para extraer el componente de alta y baja frecuencia de la señal utilizando la transformada de wavelet discreta CNeuronLegendreWaveletsHL.

class CNeuronLegendreWaveletsHL :  public CNeuronConvOCL
  {
protected:
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL)   { return true; }

public:
                     CNeuronLegendreWaveletsHL(void) {};
                    ~CNeuronLegendreWaveletsHL(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint step, uint units_count, 
                          uint filters, uint variables, 
                          ENUM_OPTIMIZATION optimization_type, uint batch) override;
   //---
   virtual int       Type(void)   const   {  return defNeuronLegendreWaveletsHL;   }
   //---
   virtual uint      GetFilters(void)  const {return (iWindowOut / 2); }
   virtual uint      GetVariables(void)  const {return (iVariables); }
   virtual uint      GetUnits(void)  const {return (Neurons() / (iVariables * iWindowOut)); }
  };

Como ya hemos mencionado, la transformada de wavelet discreta es una convolución con un filtro wavelet. Esto nos permitirá utilizar plenamente la funcionalidad de la clase padre de la capa convolucional para construir el algoritmo. Bastará con redefinir el método de inicialización estableciendo los datos de wavelets en lugar de parámetros de filtro aleatorios.

Sin embargo, los filtros de wavelets utilizados serán estáticos. Por lo tanto, redefiniremos el método de optimización de parámetros updateInputWeights con un stub positivo.

La inicialización de un nuevo objeto se realizará en el método Init. Como es habitual, en los parámetros de este método obtendremos del programa externo una serie de constantes que nos permitirán identificar unívocamente la arquitectura del objeto creado. En este caso serán:

• window — tamaño de la ventana analizada;
• step — paso de la ventana analizada;
• units_count — número de operaciones de convolución para una secuencia unitaria;
• filtros — número de filtros utilizados;
• variables — número de secuencias unitarias en las series temporales multimodales analizadas. 

bool CNeuronLegendreWaveletsHL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                     uint window, uint step, uint units_count, 
                                     uint filters, uint variables, 
                                     ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronConvOCL::Init(numOutputs, myIndex, open_cl, window, step, 2 * filters, 
                                  units_count, variables, optimization_type, batch))
      return false;

En el cuerpo del método transmitiremos directamente los parámetros recibidos al método homónimo de la clase padre. Sin embargo, vale la pena señalar que cuando llamemos al método de la clase padre, aumentaremos el número de filtros en 2 veces. Esto se debe a la necesidad de crear filtros para separar el componente de alta y baja frecuencia.

Después de ejecutar con éxito el método de la clase padre, limpiaremos el búfer de parámetros de convolución, rellenándolo con valores nulos, y determinaremos la constante de desplazamiento en el búfer entre los elementos del filtro de baja y alta frecuencia.

   WeightsConv.BufferInit(WeightsConv.Total(), 0);
   const uint shift_hight = (iWindow + 1) * filters;

A continuación, organizaremos un sistema de ciclos anidados para generar el número necesario de filtros. Aquí aprovecharemos la recursividad de la generación de wavelets de Legendre. Y sucesivamente rellenaremos la matriz del filtro con wavelets de orden superior.

   for(uint i = 0; i < iWindow; i++)
     {
      uint shift = i;
      float k = float(2.0 * i - 1.0) / iWindow;
      for(uint f = 1; f <= filters; f++)
        {
         float value = 0;
         switch(f)
           {
            case 1:
               value = k;
               break;
            case 2:
               value = (3 * k * k - 1) / 2;
               break;
            default:
               value = ((2 * f - 1) * k * WeightsConv.At(shift - (iWindow + 1)) - 
                       (f - 1) * WeightsConv.At(shift - 2 * (iWindow + 1))) / f;
               break;
           }

Para cada elemento de la ventana analizada, crearemos un ciclo anidado de generación de elementos de filtro, en el que primero generaremos un elemento del filtro de baja frecuencia correspondiente.

Y a continuación organizaremos otro ciclo anidado, en cuyo cuerpo propagaremos el elemento generado a los filtros de todas las variables independientes de la secuencia multimodal. Y luego añadiremos un elemento de filtro de alta frecuencia formado a partir del elemento de filtro de baja frecuencia correspondiente.

         for(uint v = 0; v < iVariables; v++)
           {
            uint shift_var = 2 * shift_hight * v;
            if(!WeightsConv.Update(shift + shift_var, value))
               return false;
            if(!WeightsConv.Update(shift + shift_var + shift_hight, 
                                    MathPow(-1.0f, float(i))*value))
               return false;
           }

A continuación, corregiremos el desplazamiento hasta el elemento del filtro y pasaremos a la siguiente iteración del sistema de ciclos.

         shift += iWindow + 1;
        }
     }

El algoritmo adicional de este método de inicialización de objetos se distingue de todos los métodos discutidos anteriormente. Hasta ahora no habíamos utilizado fragmentos de programa OpenCL en el proceso de inicialización de objetos. Pero este método será una excepción. Aquí normalizaremos los filtros wavelet obtenidos.

   if(!!OpenCL)
     {
      if(!WeightsConv.BufferWrite())
         return false;
      uint global_work_size[] = {iWindowOut * iVariables};
      uint global_work_offset[] = {0};
      OpenCL.SetArgumentBuffer(def_k_NormilizeWeights, def_k_norm_buffer, WeightsConv.GetIndex());
      OpenCL.SetArgument(def_k_NormilizeWeights, def_k_norm_dimension, (int)iWindow + 1);
      if(!OpenCL.Execute(def_k_NormilizeWeights, 1, global_work_offset, global_work_size))
        {
         string error;
         CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error);
         printf("Error of execution kernel %s Normalize: %s", __FUNCSIG__, error);
         return false;
        }
     }
//---
   return true;
  }

Una vez ejecutada con éxito la operación de normalización de parámetros, finalizaremos el método pasando el resultado lógico de las operaciones al programa que realiza la llamada.

Podrá ver el código completo del objeto presentado y todos sus métodos en el archivo adjunto.

Aquí cabe señalar que la funcionalidad del módulo para la descomposición de los datos analizados es algo más amplia que la transformada de wavelet discreta, aunque esta sea su parte principal. Planeamos usar el objeto en la implementación de nuestros modelos, donde la entrada es un tensor de secuencia temporal multimodal bidimensional con dimensionalidad {Bar, Indicator Value}. Pero para que nuestro objeto de transformada de wavelet discreta funcione correctamente, necesitaremos transponerlos. Obviamente, esta operación también puede realizarse antes de introducir los datos de origen en el objeto. Pero nuestro objetivo es construir objetos lo más fáciles de usar posible. Así que crearemos un objeto módulo de descomposición de flujo con una funcionalidad CNeuronDecouplingFlow ligeramente ampliada. Y utilizaremos como clase padre el objeto de transformada de wavelet discreta creado anteriormente.

class CNeuronDecouplingFlow   :  public   CNeuronLegendreWaveletsHL
  {
protected:
   CNeuronTransposeOCL  cTranspose;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronDecouplingFlow(void) {};
                    ~CNeuronDecouplingFlow(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint step, uint units_count,
                          uint filters, uint variables,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronDecouplingFlow;   }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

En el cuerpo del nuevo objeto, añadiremos una capa de datos de transposición previa y cambiaremos la comprensión del parámetro externo del método de inicialización units_count. Lo haremos más fácil de usar y lo tomaremos como la longitud de la secuencia a analizar. Así, el parámetro units_count se corresponderá con la profundidad de la historia (número de barras) analizada, mientras que variables se corresponderá con el número de parámetros (indicadores) analizados.

Consideraremos la implementación de este enfoque en el método de inicialización Init. En el cuerpo del método, primero recalcularemos el número de operaciones de convolución para una secuencia unitaria según el tamaño de la secuencia original, la ventana de convolución y su paso. Y solo entonces llamaremos al método homónimo de la clase padre, transmitiéndole los parámetros corregidos.

bool CNeuronDecouplingFlow::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                 uint window, uint step, uint units_count,
                                 uint filters, uint variables,
                                 ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   uint units_out = (units_count - window + step) / step;
   if(!CNeuronLegendreWaveletsHL::Init(numOutputs, myIndex, open_cl, window, step, units_out, 
                                                filters, variables, optimization_type, batch))
      return false;

Y después de ejecutar con éxito el método de la clase padre, inicializaremos la capa de transposición de los datos de origen.

   if(!cTranspose.Init(0, 0, OpenCL, units_count, variables, optimization, iBatch))
      return false;
//---
   return true;
  }

Y finalizaremos el método, devuelto previamente el resultado lógico de las operaciones al programa que realiza la llamada.

El algoritmo del método de pasada directa e inversa es bastante sencillo. Por ejemplo, para realizar una pasada directa, primero transpondremos los datos de origen y luego introduciremos el tensor resultante en la entrada del método homónimo de la clase padre.

bool CNeuronDecouplingFlow::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cTranspose.FeedForward(NeuronOCL))
      return false;
   if(!CNeuronLegendreWaveletsHL::feedForward(cTranspose.AsObject()))
      return false;
//---
   return true;
  }

Por tanto, no nos detendremos a analizarlos. Podrá ver el código completo de este objeto y todos sus métodos en el archivo adjunto.

Para finalizar el análisis del módulo de descomposición de señales, conviene decir unas palabras sobre los resultados de su trabajo. La cuestión es que el flujo de operaciones que hemos construido no nos permite obtener 2 tensores a la salida de la capa neuronal. Por lo tanto, hemos decidido incluir los resultados de los filtros de alta y baja frecuencia en un único tensor de datos. Y, como consecuencia, a la salida del módulo de descomposición de la señal obtendremos algo semejante a un tensor de cuatro dimensiones {Variables, Units, [Low, High], Filters}. El tensor en flujos individuales de procesamiento de datos lo dividiremos más tarde en un Codificador espaciotemporal de doble frecuencia.

Tras construir el módulo de descomposición de datos de origen, trabajaremos en la implementación de los enfoques del Codificador espaciotemporal de doble frecuencia, que constará de tres componentes principales: la atención temporal, la convolución causal ampliada y la ranura temporal con redes de grafos de atención Struc2Vec.

Aquí cabe señalar que los autores del framework Multitask-Stockformer organizan 2 flujos independientes para los componentes de baja y alta frecuencia. Además, estos flujos son diferentes desde el punto de vista de su construcción, lo que le permite centrarse en las tendencias y los componentes estacionales.

El componente de baja frecuencia se introduce en la unidad de atención espaciotemporal, que capta las tendencias de baja frecuencia a largo plazo analizando las relaciones de secuencia globales.

Al mismo tiempo, la parte de alta frecuencia de la señal es procesada por la capa convolucional causal ampliada, lo cual nos permite centrarnos en los patrones locales, modelizando eficazmente los componentes de alta frecuencia y los sucesos abruptos.

Esperamos que este enfoque de modelización dual mejore la precisión de las previsiones de secuencias financieras complejas.

Como unidad de atención espacio-temporal, podemos usar uno de los objetos ya existentes construidos mediante la arquitectura del Codificador del Transformer. Pero tenemos que trabajar en el algoritmo de la capa convolucional causal.

Capa convolucional causal

La convolución causal ampliada propuesta por los autores del framework es un tipo específico de convolución univariante que recorre los datos de origen, saltándose valores en un determinado paso, como se muestra en la figura anterior. Teóricamente, dada una secuencia unidimensional x ∈ RT y un filtro f ∈ RJ, la operación de convolución causal ampliada en el paso de tiempo t se definirá como:

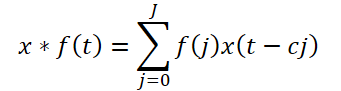
Aquí c será el factor de expansión. La convolución causal ampliada del componente de alta frecuencia se expresará como:

Cabe destacar que la implementación propuesta añadirá un hiperparámetro más, el factor de expansión. Y lo que es más, será permanente. Pero, ¿será la distancia entre los elementos dependientes fija a lo largo de la secuencia analizada? La situación se agrava por el uso de un único coeficiente para secuencias unitarias distintas.

En nuestra aplicación, hemos decidido modificar ligeramente la arquitectura del módulo causal ampliado. En lugar de saltos fijos, le proponemos utilizar el algoritmo Segment, Shuffle, Stitch (S3). Y tras él, usar una capa de convolución normal.

El S3 nos permitirá establecer una permutación entrenable de segmentos con los datos de origen. De este modo, evitaremos los saltos fijos de valores en el tensor de datos de origen, sugiriendo al modelo que aprenda por sí mismo las dependencias entre los elementos individuales de las secuencias analizadas. Por otra parte, la creación de una pila de varios bloques de este tipo permitirá detectar y captar de forma adaptativa las dependencias del componente de alta frecuencia.

Implementaremos el enfoque propuesto dentro del objeto CNeuronDilatedCasualConv. A mi juicio, resulta obvio que el algoritmo anterior es lineal. Por lo tanto, utilizaremos como objeto padre la clase CNeuronRMAT, dentro de la cual ya estarán organizadas las principales funcionalidades e interfaces para implementar los algoritmos lineales. Más abajo resumiremos la estructura del nuevo objeto.

class CNeuronDilatedCasualConv   :  public CNeuronRMAT
  {
public:
                     CNeuronDilatedCasualConv(void) {};
                    ~CNeuronDilatedCasualConv(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint step, uint dimension,
                          uint units_count, uint variables, uint layers,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronDilatedCasualConv; }
  };

Como puede ver en la estructura presentada del nuevo objeto, la elección de la clase padre "correcta" nos permite limitarnos a especificar la arquitectura del objeto en el método de inicialización. El resto de funcionalidades ya están implementadas en los métodos de la clase padre, que hemos heredado correctamente.

En los parámetros del método de inicialización Init obtendremos, como es habitual, un conjunto de constantes que nos permitirán definir de forma inequívoca la arquitectura del objeto a crear:

• window — tamaño de la ventana analizada;
• step — paso de la ventana analizada;
• dimension — dimensionalidad del vector de un elemento de la secuencia;
• units_count — número de elementos de la secuencia;
• variables — número de elementos analizados en la secuencia multimodal;
• layers — número de capas de convolución.

Aquí debemos prestar atención a las peculiaridades de uso de estas variables. Pero antes recordaremos la dimensionalidad del tensor de los datos de origen analizados. Como hemos mencionado antes, a partir del módulo de descomposición de la señal analizada obtendremos el tensor tetradimensional {Variables, Units, [Low, High], Filters}. Tras descomponer el tensor en componentes de señal de alta y baja frecuencia en la tercera dimensión, obtendremos un único valor, lo que prácticamente convertirá el tensor en tridimensional {Variables, Units, Filters}.

Permítame recordarle que en el contexto OpenCL trabajamos con búferes de datos unidimensionales. Y la descomposición del búfer en dimensiones es condicional, pero implica la secuencia de valores correspondiente.

Conociendo la dimensionalidad del tensor de datos de origen, podemos asignarles los parámetros obtenidos del programa externo. Obviamente, el parámetro variables se corresponderá con la dimensionalidad de la primera dimensión de Variables, mientras que units_count especificará la longitud de la secuencia analizada mediante la segunda dimensión Units. Y dimension definirá la última dimensión de Filters. Todos los parámetros anteriores definen el tamaño del tensor de datos de origen en forma pura.

Además, el tamaño de la ventana analizada (window) y su paso (step) se especifican en unidades de la segunda dimensión Units. Es decir, si se especifica un tamaño de ventana igual a 2 (window = 2), para la convolución se tomará 2*dimension elementos del búfer de datos de origen.

Pero volvamos al algoritmo del método de inicialización del objeto.

bool CNeuronDilatedCasualConv::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                    uint window, uint step, uint dimension, uint units_count,
                                    uint variables, uint layers,
                                    ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, 1, optimization_type, batch))
      return false;

Como es habitual, en el cuerpo del método llamaremos primero al método homónimo de la clase padre, que organizará el control y la inicialización necesarios de los objetos heredados. Y aquí nos enfrentaremos a dos puntos. En primer lugar, la estructura de los objetos de la clase padre CNeuronRMAT es muy diferente de la que necesitamos. Por lo tanto, no estaremos llamando al método de la clase padre directa, sino de la capa básica completamente conectada. Como recordará, es la base para crear todas las capas neuronales de nuestra biblioteca.

Sin embargo, hay un segundo punto a considerar: el proceso de convolución cambia el volumen del tensor resultante. Y de momento no tenemos su tamaño final para indicar las dimensiones de las interfaces básicas. Por lo tanto, inicializaremos las interfaces básicas con un único elemento condicional en la salida.

A continuación, borraremos el array dinámico de almacenamiento de los punteros a los objetos internos y prepararemos las variables auxiliares.

   cLayers.Clear();
   cLayers.SetOpenCL(OpenCL);
   uint units = units_count;
   CNeuronConvOCL *conv = NULL;
   CNeuronS3 *s3 = NULL;

Una vez terminado el trabajo preparatorio, crearemos directamente la arquitectura de nuestro objeto. Para ello, organizaremos un ciclo con un número de iteraciones igual al número de capas internas.

   for(uint i = 0; i < layers; i++)
     {
      s3 = new CNeuronS3();
      if(!s3 ||
         !s3.Init(0, i*2, OpenCL, dimension, dimension*units*variables, optimization, iBatch) ||
         !cLayers.Add(s3))
        {
         if(!!s3)
            delete s3;
         return false;
        }
      s3.SetActivationFunction(None);

En el cuerpo del ciclo, primero inicializaremos el objeto S3. Tenga en cuenta, sin embargo, que este objeto solo funcionará con un tensor unidimensional. Por consiguiente, para evitar que se "rompa" el vector de descripción de los elementos de la secuencia, deberemos especificar el tamaño del segmento como múltiplo de la dimensionalidad de dicho vector. En este caso especificaremos que sean iguales. Además, como valor de la secuencia, se dará el tamaño completo del tensor, incluidas todas las variables analizadas.

Una vez que el objeto se haya inicializado correctamente, añadiremos el puntero al mismo a nuestro array dinámico encargado de almacenar los punteros a los objetos internos. Y desactivaremos la función de activación.

A continuación vendrá el proceso de inicialización de la capa de convolución. Aquí, antes de iniciar el proceso de inicialización de un nuevo objeto, calcularemos el número de operaciones de convolución para la capa a crear. Y guardemos el valor obtenido en una variable local. Ya hemos utilizado el valor de esta variable en el paso anterior, al especificar la dimensionalidad de la secuencia analizada. Por lo tanto, en la siguiente iteración del ciclo crearemos un objeto S3 del tamaño actualizado.

      conv = new CNeuronConvOCL();
      units = MathMax((units - window + step) / step, 1);
      if(!conv ||
         !conv.Init(0, i * 2 + 1, OpenCL, window * dimension, step * dimension, dimension,
                                                   units, variables, optimization, iBatch) ||
         !cLayers.Add(conv))
        {
         if(!!conv)
            delete conv;
         return false;
        }
      conv.SetActivationFunction(GELU);
     }

La capa convolucional usada, a diferencia del objeto S3, puede operar en la sección de secuencias unitarias. Esto nos permitirá no solo realizar la convolución de cada serie temporal unitaria por separado, sino también utilizar distintos filtros para las secuencias unitarias, lo que hace que su análisis completamente independiente.

En la salida de la capa de convolución, utilizaremos la función de activación GELU en lugar de la ReLU propuesta por los autores del framework.

Luego añadiremos el puntero al objeto inicializado a nuestro array dinámico y pasaremos a la siguiente iteración del ciclo para crear la siguiente capa.

Una vez inicializadas correctamente todas las capas internas de nuestro objeto, volveremos a llamar al método de inicialización de la capa básica completamente conectada para crear los búferes de interfaz externos correctos, especificando la dimensionalidad de la última capa interna de nuestro bloque.

  if(!CNeuronBaseOCL::Init(numOutputs, myIndex, OpenCL, conv.Neurons(), optimization_type, batch))
      return false;

Y, por último, sustituiremos los punteros a los búferes de las interfaces externas por los correspondientes búferes de la última capa interna.

   if(!SetGradient(conv.getGradient(), true) ||
      !SetOutput(conv.getOutput(), true))
      return false;
   SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
//---
   return true;
  }

Luego copiaremos el puntero de la función de activación, retornaremos el resultado lógico de las operaciones al programa que realiza la llamada y finalizaremos el método.

Como habrá notado, dentro de la arquitectura de este bloque utilizamos objetos internos que trabajan con tensores de diferentes dimensiones. De inicio, la capa S3 realiza la permutación de elementos dentro de todo el búfer de datos, sin tener en cuenta las secuencias unitarias. Y en esta variante resulta muy posible "barajar" elementos entre secuencias unitarias. Por un lado, nosotros no restringimos la permutación de elementos mediante marcos de secuencias unitarias. Por otro lado, la secuencia de permutación se entrena partiendo de los datos de la muestra de entrenamiento. Y si el modelo encuentra dependencias entre los elementos de diferentes secuencias unitarias, quizá esto mejore la eficacia del modelo. Será muy interesante ver el resultado del entrenamiento.

Ya casi hemos llegado al final del artículo, pero no al final de nuestro tema. Lo continuaremos en el próximo artículo.

Conclusión

En este artículo, nos hemos familiarizado con el framework Multitask-Stockformer, un innovador modelo de selección de valores que combina transformadas de wavelet con módulos multitarea Self-Attention. El uso de transformadas de wavelet permite identificar las características temporales y frecuenciales de los datos de mercado, mientras que los mecanismos de Self-Attention posibilitan una modelización precisa de las complejas interacciones entre los factores analizados.

En la parte práctica, hemos implementado nuestra propia visión de bloques separados del framework propuesto utilizando las herramientas MQL5. Y en el próximo artículo, completaremos la aplicación del framework analizado. También comprobaremos la eficacia de los enfoques aplicados con datos históricos reales.

Enlaces

• Stockformer: A Price-Volume Factor Stock Selection Model Based on Wavelet Transform and Multi-Task Self-Attention Networks
• Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de recopilación de ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de modelos
4	Test.mq5	Asesor	Asesor para la prueba de modelos
5	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema y la arquitectura de modelos
6	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
7	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL