Técnicas do MQL5 Wizard que você deve conhecer (Parte 33): Kernels de Processos Gaussianos

Introdução

Os Kernels de Processos Gaussianos são funções de covariância usadas em processos gaussianos para medir as relações entre pontos de dados, como em uma série temporal. Esses kernels geram matrizes que capturam a relação intra-dados, permitindo que o Processo Gaussiano faça projeções ou previsões assumindo que os dados seguem uma distribuição normal. Como essas séries buscam explorar novas ideias enquanto examinam como essas ideias podem ser exploradas, os Kernels de Processos Gaussiano (GP) estão servindo como nosso tópico para a construção de um sinal personalizado.

Recentemente, cobrimos muitos artigos relacionados a aprendizado de máquina nos últimos cinco artigos, então, para este, "fazemos uma pausa" e olhamos para a boa e velha estatística. Na natureza de desenvolvimento de sistemas, frequentemente os dois estão casados, no entanto, ao desenvolver este sinal personalizado, não estaremos suplementando ou considerando nenhum algoritmo de aprendizado de máquina. Os kernels GP são notáveis por sua flexibilidade.

Eles podem ser usados para modelar uma grande variedade de padrões de dados que variam de periodicidade, a tendências ou até mesmo relações não-lineares. No entanto, mais significativo do que isso é que, ao prever, eles fazem mais do que fornecer um único valor. Em vez disso, fornecem uma estimativa de incerteza que incluiria o valor desejado, bem como um valor limite superior e inferior. Esses intervalos de limites são frequentemente fornecidos com uma classificação de confiança, o que facilita ainda mais o processo de tomada de decisão de um trader ao ser apresentado com um valor de previsão. Essas classificações de confiança também podem ser perspicazes e ajudar a entender melhor os títulos negociados ao comparar diferentes faixas de previsões que estão marcadas com níveis de confiança díspares.

Além disso, eles são bons em lidar com dados ruidosos, pois permitem que um valor de ruído seja incrementado na matriz K criada (veja abaixo), e também são capazes de serem usados enquanto incorporam conhecimento prévio, além de serem muito escaláveis. Há uma quantidade considerável de diferentes kernels para escolher por aí. A lista inclui (mas não se limita a): Kernel Exponencial Quadrado (RBF), Kernel Linear, Kernel Periódico, Kernel Quadrático Racional, Kernel Matern, Kernel Exponencial, Kernel Polinomial, Kernel de Ruído Branco, Kernel de Produto Escalar, Kernel de Mistura Espectral, Kernel Constante, Kernel Cosseno, Kernel de Rede Neural (Arccosseno), e Kernels de Produto & Soma.

Para este artigo, vamos apenas olhar para o kernel RBF, também conhecido como Kernel de Função de Base Radial. Como a maioria dos kernels, ele mede a similaridade entre dois pontos de dados focando em sua distância, com a suposição básica subjacente de que quanto mais distantes os pontos, menos semelhantes eles são, e vice-versa. Isso é regido pela seguinte equação:

Onde

• x e x′: Estes são os vetores de entrada ou pontos no espaço de entrada.
• σ f ²: Este é o parâmetro de variância do kernel, que serve como um parâmetro pré-determinado ou otimizado.
• l é frequentemente referido como o parâmetro de escala de comprimento. Ele controla a suavidade da função resultante. Um valor menor de l (ou uma escala de comprimento menor) resulta em uma função que varia rapidamente, enquanto um valor maior de l (escala de comprimento maior) resulta em uma função mais suave.
• exp: Esta é a função exponencial.

Este kernel pode ser codificado facilmente em MQL5 como:

//+------------------------------------------------------------------+
// RBF Kernel Function
//+------------------------------------------------------------------+
matrix CSignalGauss::RBF_Kernel(vector &Rows, vector &Cols)
{  matrix _rbf;
   _rbf.Init(Rows.Size(), Cols.Size());
   for(int i = 0; i < int(Rows.Size()); i++)
   {  for(int ii = 0; ii < int(Cols.Size()); ii++)
      {  _rbf[i][ii] = m_variance * exp(-0.5 * pow(Rows[i] - Cols[ii], 2.0) / pow(m_next, 2.0));
      }
   }
   return(_rbf);
}

Processos Gaussianos em Séries Temporais Financeiras

Os processos gaussianos são uma estrutura probabilística onde as previsões são feitas em termos de distribuições, em vez de valores fixos. Por isso, também são chamados de estrutura não-paramétrica. As previsões de saída incluem uma previsão média e uma variância (ou incerteza) em torno dessa previsão. A variância dos GPs representa a incerteza ou confiança na previsão realizada. Essa incerteza é, em princípio, aleatória, já que se baseia na distribuição normal do GP. No entanto, porque implica um intervalo e uma classificação de confiança (geralmente baseada em 95%), nem todas as suas previsões precisam ser seguidas. Comparado com outros métodos estatísticos de previsão, como o ARIMA, o GP é altamente flexível e capaz de modelar relações não-lineares complexas com incerteza quantificada, enquanto o ARIMA funciona melhor com séries temporais estacionárias com estruturas definidas. A principal desvantagem do GP é seu custo computacional, enquanto métodos como o ARIMA não são tão exigentes.

O Kernel RBF

Calcular o kernel GP envolve, principalmente, 6 matrizes e 2 vetores. Essas matrizes e vetores são todos usados na nossa função ‘GetOutput’, cujo código é resumidamente fornecido abaixo:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalGauss::GetOutput(double BasisMean, vector &Output)
{  
   ...

   matrix _k = RBF_Kernel(_past_time, _past_time);
   matrix _noise;
   _noise.Init(_k.Rows(), _k.Cols());
   _noise.Fill(fabs(0.05 * _k.Min()));
   _k += _noise;
   matrix _norm;
   _norm.Init(_k.Rows(), _k.Cols());
   _norm.Identity();
   _norm *= 0.0005;
   _k += _norm;
   vector _next_time;
   _next_time.Init(m_next);
   for(int i = 0; i < m_next; i++)
   {  _next_time[i] = _past_time[_past_time.Size() - 1] + i + 1;
   }
   matrix _k_s = RBF_Kernel(_next_time, _past_time);
   matrix _k_ss = RBF_Kernel(_next_time, _next_time);
// Compute K^-1 * y
   matrix _k_inv = _k.Inv();
   if(_k_inv.Rows() > 0 && _k_inv.Cols() > 0)
   {  vector _alpha = _k_inv.MatMul(_past);
      // Compute mean predictions: mu_* = K_s * alpha
      vector _mu_star = _k_s.MatMul(_alpha);
      vector _mean;
      _mean.Init(_mu_star.Size());
      _mean.Fill(BasisMean);
      _mu_star += _mean;
   // Compute covariance: Sigma_* = K_ss - K_s * K_inv * K_s^T
      matrix _v = _k_s.MatMul(_k_inv);
      matrix _sigma_star = _k_ss - (_v.MatMul(_k_s.Transpose()));
      vector _variances = _sigma_star.Diag();
      //Print(" sigma star: ",_sigma_star);
      Print(" pre variances: ",_variances);
      Output = _mu_star;
      SetOutput(Output);
      SetOutput(_variances);
      Print(" variances: ",_variances);
   }
}

Para listar, são eles:

• _k
• _k_s
• _k_ss
• _k_inv
• _v
• e _sigma_star

_k é a matriz de covariância âncora e principal. Ela captura as relações entre os pares de vetores de entrada para a função kernel em uso. Estamos utilizando o kernel Radial Basis Function (RBF), e sua origem já foi compartilhada acima. Como estamos fazendo uma previsão para uma série temporal, a entrada para nosso kernel RBF seria dois vetores temporais semelhantes que registram os índices de tempo da série de dados que estamos procurando prever. Codificando as similaridades entre os pontos de tempo registrados, isso serve como uma base para determinar a estrutura geral. Lembre-se de que existem muitos outros formatos de kernel, como visto nos quatorze listados acima, e em artigos futuros poderíamos considerar essas alternativas como uma classe de sinal personalizada.

Isso nos leva à matriz de covariância _k_s. Esta matriz atua como uma ponte para os próximos índices de tempo, também via um kernel RBF, como a _k. O comprimento ou número desses índices de tempo define o número de projeções a serem feitas, e é definido pelo parâmetro de entrada de escala de comprimento. Nos referimos a esse parâmetro como m_next na classe de sinal personalizada. Através da ponte entre os índices de tempo passados e os próximos índices de tempo, _k_s serve para projetar uma relação entre dados conhecidos e os próximos dados desconhecidos, e isso, como se espera, é útil na previsão. Esta matriz em particular é altamente sensível à projeção feita, então sua precisão precisa ser exata, e felizmente nosso código e a função kernel RBF lidam com isso perfeitamente. No entanto, os dois parâmetros ajustáveis de variância e escala de comprimento precisam ser ajustados com cuidado para garantir que a precisão da projeção seja maximizada.

Esta matriz pode ser definida como:

Onde

• k(x i , y i ) é uma Função de Base Radial entre dois valores nos vetores x e y no índice i. No nosso caso, x e y são o mesmo vetor temporal de entrada, portanto, ambos os vetores são rotulados como x. x é geralmente os dados de treinamento, enquanto y é um espaço reservado para os dados de teste.
• k s é o vetor de covariância (ou matriz, caso o número de projeções ou escala de comprimento seja maior que 1) entre os dados de treinamento e o ponto de teste x∗.
• x1, x2,…, xn são os pontos de dados de treinamento.
• x∗ é o ponto de dados de teste onde as previsões devem ser feitas.

Isso leva à matriz _k_ss, que essencialmente é uma imagem espelhada da matriz _k, com a principal diferença sendo que é uma covariância dos índices de tempo da previsão. Suas dimensões, portanto, correspondem ao parâmetro de entrada de escala de comprimento. Ela é instrumental para calcular a estimativa de incerteza da previsão. It measures the variance over the forecast time indices before data is incorporated. This can be captured in a formula as:

Onde

• k ss é a matriz de covariância dos pontos de dados de teste.
• x∗, x∗′ são os pontos de dados de teste onde as previsões devem ser feitas.
• k(x∗,x∗′) é a função kernel aplicada ao par de pontos de teste 𝑥∗ e 𝑥∗′.

A matriz _k_inv, como o nome sugere, é a inversa da matriz k. A inversão das matrizes é tratada por funções internas, no entanto, não é infalível, pois a inversão pode não ser possível. Por isso, em nosso código, verificamos se a matriz invertida tem linhas ou colunas. Se não houver, isso implica que a inversão falhou. Essa inversão é importante para calcular os pesos aplicados aos dados de treinamento durante a previsão. Métodos alternativos personalizados para realizar essa inversão, como a decomposição de Cholesky, poderiam ser considerados (desde que não seja a abordagem interna), mas a codificação deles como opções fica a critério do leitor.

O vetor de pesos é usado para combinar as saídas do treinamento com base em sua estrutura de covariância. _alpha determina o quanto os novos pontos de dados influenciam a previsão sobre os pontos de teste/escala de comprimento. Obtivemos alpha a partir do produto matricial da matriz k invertida e os dados antigos brutos para os quais buscamos uma previsão. Isso nos leva ao nosso objetivo, o vetor _mu_star. Ele finalmente registra as previsões sobre o período da escala de comprimento de entrada com base nos dados anteriores, cujo tamanho é definido pelo parâmetro de entrada m_past na classe de sinal personalizada. Assim, o número de médias projetadas é determinado pela escala de comprimento, que nos referimos como m_next na classe, e como vetores em MQL5 não são ordenados como séries (ao copiar e lidar com taxas), o índice mais alto desse vetor de previsão é projetado para ocorrer por último, enquanto o índice zero deve ocorrer de forma imediata. Isso implica que, além de estimar quais valores ocorrerão a seguir na série, também podemos projetar a tendência que seguirá, dependendo do tamanho do parâmetro de escala de comprimento. Esses valores projetados também são chamados de pontos de teste.

Uma vez que temos as médias indicativas, o processo GP também fornece uma noção de incerteza em torno desses valores através da matriz _sigma_star. O que ela captura é a covariância entre diferentes previsões em pontos diferentes no futuro ou ao longo dos pontos de teste. Como estamos fazendo um número específico de previsões, uma para cada ponto de teste, estamos interessados apenas nos valores diagonais dessa matriz. Não estamos interessados na covariância entre previsões. A fórmula para essa matriz é dada por:

Onde

• k ss é a matriz de covariância dos novos pontos de dados conforme descrito acima como _k_ss.
• k s é a matriz de covariância entre os novos pontos de dados e os dados de treinamento, também como já mencionado acima como _k_s.
• K é a matriz de covariância dos dados de treinamento, a primeira matriz que definimos.

A partir da nossa equação acima, a matriz _v é indicada como o produto entre k_s e a inversa K^-1. Estamos testando para uma confiança de 95%, e graças às tabelas de distribuição normal, isso significa que, para cada ponto de teste, o valor do limite superior é a previsão média mais 1.96 vezes o respectivo valor de variância na matriz. Por outro lado, o valor do limite inferior é a média prevista menos 1.96 vezes o valor de variância de nossa matriz _sigma_star. Essa variância ajuda a quantificar nossa confiança com as previsões médias, e, isso é importante, valores maiores indicam maior incerteza. Portanto, quanto maior o intervalo de confiança (do valor limite superior ao inferior), menos confiante se deve estar!

Como nota lateral, mas ponto importante, os cálculos de kernel GP envolvem encontrar a inversão de matrizes e, como mencionado acima, isso pode ser personalizado ainda mais pelo leitor ao considerar abordagens como a decomposição de Cholesky para minimizar erros e NaNs. Além disso, uma técnica comum de normalização que é aplicada à matriz _k no início do processo do kernel GP é a adição de um pequeno valor diferente de zero em sua diagonal para evitar ou prevenir valores negativos na matriz _sigma_star. Lembre-se de que essa matriz contém valores de desvio padrão ao quadrado ou os valores de variância, portanto todos os seus valores precisam ser positivos. E curiosamente, a omissão dessa pequena adição ao longo da diagonal da matriz _k pode levar a essa matriz contendo valores negativos! Portanto, é uma etapa importante, e está indicada na listagem da função de saída acima.

Portanto, nossas projeções estão nos dando duas coisas, a previsão e o quanto 'confiantes devemos estar' sobre essa previsão. Para este artigo, como pode ser visto abaixo, estamos realizando testes confiando exclusivamente na projeção bruta sem levar em consideração os níveis de confiança implícitos pela matriz _sigma_star. Isso, de muitas maneiras, é uma grande sub-representação dos kernels GP, então, como poderíamos incorporar a confiança implícita de uma previsão no nosso sinal personalizado? Existem várias maneiras de isso ser feito, mas antes mesmo de considerar essas opções, uma solução rápida seria geralmente fora da classe de sinal personalizada, usando a magnitude da confiança para orientar o dimensionamento da posição.

Isso implicaria que, além de ter um kernel GP em uma classe de sinal personalizada, também teríamos outro kernel GP em uma classe personalizada de gerenciamento de dinheiro. E nesta situação, tanto a classe de sinal quanto a de gerenciamento de dinheiro teriam que usar conjuntos de dados de entrada semelhantes, bem como parâmetros de variância e escala de comprimento. No entanto, dentro da classe de sinal personalizada, uma fácil incorporação seria criar um vetor de variâncias que copie a diagonal da matriz _sigma_star, normalize-o com nossa função ‘SetOutput’ e depois determine o índice com o menor valor. Esse índice seria então usado no vetor _mu_star para determinar a condição do sinal personalizado. Como _mu_star também é normalizado com a mesma função, então qualquer valor abaixo de 0.5 se mapearia para mudanças negativas, o que seria um sinal de baixa, enquanto qualquer valor acima de 0.5 seria de alta.

Outro método de usar a incerteza quantificada de uma previsão dentro de uma classe de sinal personalizada poderia ser se pegássemos a média ponderada de todas as previsões ou projeções através de todos os pontos de teste, mas usássemos o valor de variância normalizado como um peso inverso. Seria inverso, significando que o subtrairíamos de um ou inverteríamos enquanto adicionamos um pequeno valor ao denominador. Essa inversão é importante porque, como enfatizado acima, uma maior variância implica mais incerteza. Essas abordagens de uso de incerteza são apenas mencionadas aqui, mas não foram implementadas no código ou durante nosso teste. O leitor fica à vontade para levar isso adiante, realizando seus próprios testes independentes.

Pré-processamento de Dados e Normalização

Os kernels GP podem ser usados para uma variedade de dados financeiros em séries temporais, de forma ampla, esses dados podem estar em um formato absoluto, como preços absolutos, ou podem estar em um formato incremental, como variações de preços. Para este artigo, vamos testar o kernel GP RBF com o último. Para esse fim, como pode ser visto na listagem ‘GetOutput’ acima, começamos preenchendo o vetor ‘_past’ com a diferença entre dois outros vetores que copiaram preços de fechamento de diferentes pontos, separados por 1 barra.

Além disso, poderíamos ter normalizado essas variações de preço convertendo-as de seus pontos brutos e colocando-as em uma faixa de -1.0 a +1.0. A função ‘SetOutput’ que é usada para pós-normalização ou outro método personalizado, poderia ser usada para esse pré-processamento de dados também. No entanto, para nossos testes, estamos usando as variações de preço brutas em formato de ponto flutuante (double) e aplicando normalização apenas nos valores de previsão (aquilo que chamamos de pontos de teste acima). Isso é realizado com a função ‘SetOutput’, cujo código está listado abaixo:

//+------------------------------------------------------------------+
//|
//+------------------------------------------------------------------+
void CSignalGauss::SetOutput(vector &Output)
{  vector _copy;
   _copy.Copy(Output);
   if(Output.HasNan() == 0 && _copy.Max() - _copy.Min() > 0.0)
   {  for (int i = 0; i < int(Output.Size()); i++)
      {  if(_copy[i] >= 0.0)
         {  Output[i] = 0.5 + (0.5 * ((_copy[i] - _copy.Min()) / (_copy.Max() - _copy.Min())));
         }
         else if(_copy[i] < 0.0)
         {  Output[i] = (0.5 * ((_copy[i] - _copy.Min()) / (_copy.Max() - _copy.Min())));
         }
      }
   }
   else
   {  Output.Fill(0.5);
   }
}

Usamos essa normalização em artigos anteriores dentro desta série e tudo o que estamos fazendo é reescalar os valores do vetor projetado para ficarem na faixa de 0.0 a +1.0, com a principal ressalva de que qualquer valor abaixo de 0.5 teria sido negativo na série desnormalizada, enquanto qualquer valor acima de 0.5 teria sido positivo.

Testes e Avaliação

Para nossos testes com o kernel GP RBF, estamos testando o par EURUSD para o ano de 2023 no intervalo de tempo diário. Como é frequentemente o caso, mas nem sempre, essas configurações foram obtidas a partir de uma otimização muito curta, e não foram verificadas com uma caminhada futura. A aplicação do nosso Expert Advisor montado pelo wizard nas condições reais de mercado exigirá mais diligência independente da parte do leitor para garantir que testes extensivos em mais históricos e com caminhadas futuras (validação cruzada) sejam realizados. Os resultados da nossa execução estão abaixo:

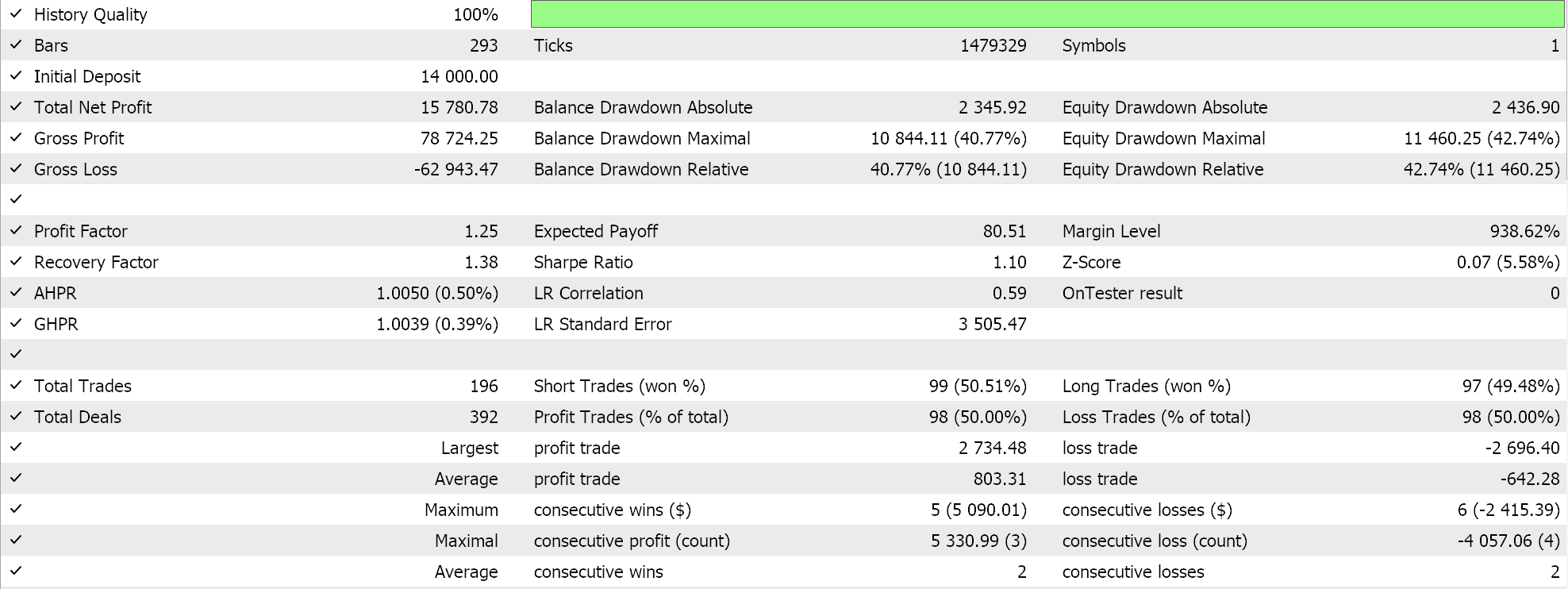
Conclusão

Em conclusão, examinamos os kernels de Processos Gaussianos como um sinal potencial para um sistema de negociação. ‘Gaussiano’ frequentemente invoca o aleatório ou a presunção de que um sistema usado assume que seu ambiente é aleatório, e, portanto, aposta em probabilidades de 50–50 para ganhar dinheiro. No entanto, seus defensores argumentam que eles usam uma amostra de dados fornecida para prever ao longo de um período pré-definido com uma estrutura probabilística. Este método, argumenta-se, permite mais flexibilidade, já que nenhuma suposição é feita sobre o que os dados estudados aderem (ou seja, é não-paramétrico). A única suposição abrangente é que os dados seguem uma distribuição Gaussiana. Portanto, por que a incerteza é incorporada no processo e nos resultados, argumenta-se que o processo não é centrado no aleatório.

Além disso, a partir da nossa codificação e testes dos kernels de Processos Gaussianos, não exploramos a quantificação da incerteza, que pode ser argumentada como o que os diferencia de outros métodos de previsão. Dito isso, o uso e a dependência de distribuições normais levanta a questão de saber se os kernels de Processos Gaussianos devem ser usados de forma independente ou funcionam melhor quando emparelhados com um sinal alternativo. O wizard MQL5, para o qual os novos leitores podem encontrar orientações aqui e aqui, permite facilmente testar mais de um sinal em um único Expert Advisor, pois cada sinal selecionado pode ser otimizado para um peso adequado. Qual sinal alternativo vale a pena emparelhar com esses kernels? Bem, a melhor resposta para essa pergunta só pode ser fornecida pelo leitor a partir de seus próprios testes, no entanto, se eu fosse sugerir, deveria ser osciladores como o RSI, ou o oscilador estocástico ou volume em equilíbrio e até alguns indicadores de sentimento de notícias. Além disso, indicadores como médias móveis simples, cruzamentos de médias móveis, canais de preço e indicadores em geral com um atraso substancial podem não funcionar bem quando emparelhados com os kernels de Processos Gaussianos.

Também examinamos apenas um tipo de kernel, o Radial Basis Function, os outros formatos serão examinados em artigos futuros com configurações alteradas.