
Redes neuronales: así de sencillo (Parte 96): Extracción multinivel de características (MSFformer)
Introducción
Los datos de series temporales están muy extendidos en el mundo real y desempeñan un papel clave en diversos campos, incluidas las finanzas. Estos datos suponen secuencias de observaciones recogidas en distintos momentos. El análisis en profundidad de las series temporales y el modelado permiten a los investigadores predecir tendencias y patrones futuros, lo cual se utiliza en el proceso de toma de decisiones.
En los últimos años, muchos investigadores han centrado sus esfuerzos en el aprendizaje de series temporales usando modelos de aprendizaje profundo. Estos métodos han demostrado su eficacia para captar relaciones no lineales y procesar dependencias a largo plazo, lo que resulta especialmente útil para modelar sistemas complejos. No obstante, a pesar de los importantes avances, persisten retos significativos a la hora de extraer e integrar eficazmente las dependencias a largo plazo y las características a corto plazo. Comprender y combinar adecuadamente estos dos tipos de dependencias resulta fundamental para crear modelos predictivos precisos y fiables.
Una de las soluciones a este problema se presentó en el artículo "Time Series Prediction Based on Multi-Scale Feature Extraction". En este se propone un modelo de previsión de series temporales, el MSFformer (Multi-Scale Feature Transformer), basado en una arquitectura de atención piramidal mejorada. Este modelo está diseñado para extraer e integrar características de varios niveles de forma eficaz.
Los autores del método destacan las siguientes innovaciones del MSFformer:
- La introducción del mecanismo Skip-PAM, que permite al modelo captar eficazmente las características tanto a largo como a corto plazo de las series temporales largas.
- El módulo mejorado para crear una estructura piramidal de datos CSCM.
Los autores del MSFformer presentan los resultados experimentales en tres conjuntos de datos de series temporales que demuestran el rendimiento superior del modelo propuesto. Los mecanismos propuestos permiten al modelo MSFformer procesar los datos de series temporales complejas con mayor precisión y eficacia, garantizando una gran exactitud y fiabilidad de las previsiones.
1. Algoritmo MSFformer
Los autores del modelo MSFformer proponen la novedosa arquitectura de un mecanismo de atención piramidal en diferentes intervalos temporales, que supone la base de su método. Además, para construir información temporal multinivel en los datos de origen, utilizan la convolución de características en el Módulo de construcción a gran escala CSCM (Coarser-Scale Construction Module). Esto permite extraer información temporal a un nivel más grueso.
El módulo CSCM construye el árbol de características de las series temporales analizadas. En primer lugar, los datos de origen pasan por la capa completamente conectada para transformar la dimensionalidad de las características a un tamaño fijo. A continuación, se usan varios bloques de convolución de características FCNN consecutivos, especialmente diseñados.
En el bloque FCNN, los vectores de características se generan en primer lugar extrayendo los datos de la secuencia original mediante un paso de cruce concreto. A continuación, se combinan dichos vectores, y se realizan operaciones de convolución sobre ellos. Más abajo se presenta la visualización de autor del bloque FCNN.
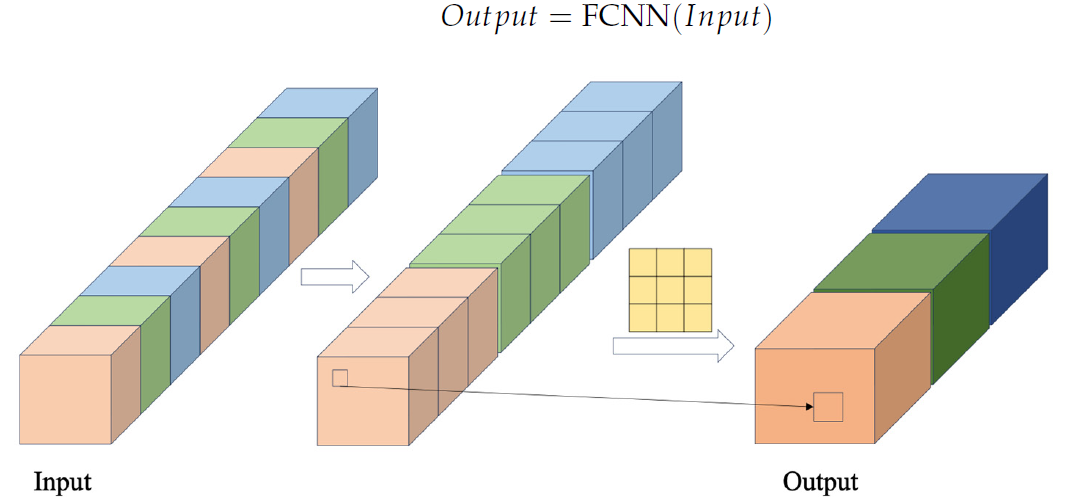
El módulo propuesto por los autores del método CSCM usa múltiples bloques FCNN consecutivos. Y cada uno de ellos, usando los resultados del bloque anterior como datos de entrada, extrae indicios de una escala mayor.
Las características de diferentes escalas obtenidas de este modo se combinan en un único vector cuyo tamaño se reduce usando una capa lineal hasta el nivel de los datos de origen.
A continuación le presentamos la visualización del módulo CSCM realizada por el autor.
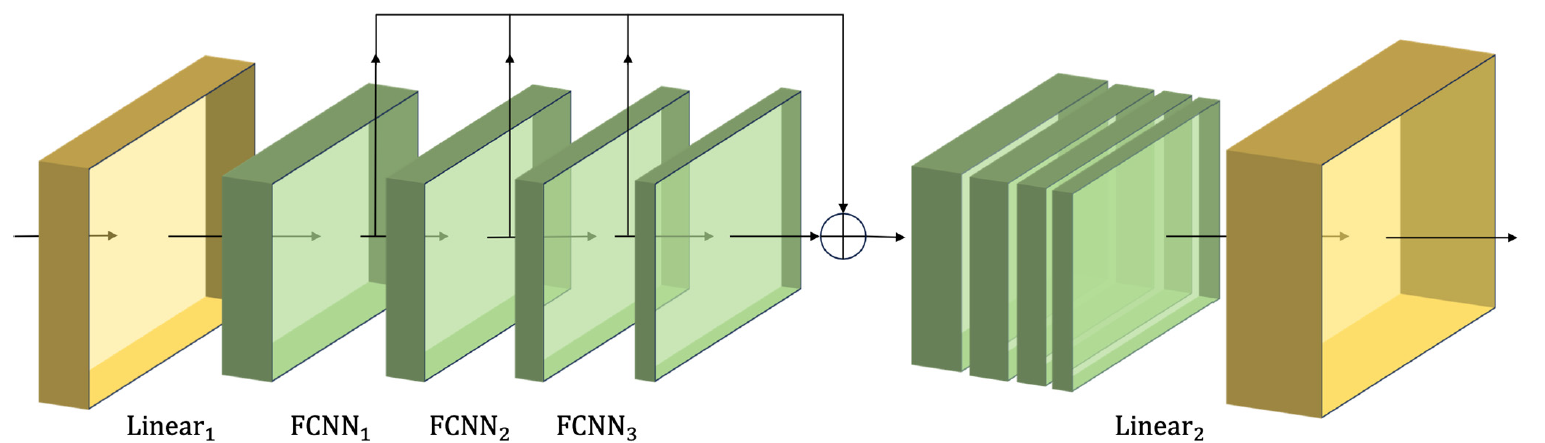
Al pasar los datos de las series temporales analizadas por un CSCM de este tipo, obtendremos información temporal sobre características con distintos niveles de detalle. Construiremos un árbol de características piramidal superponiendo capas de FCNN, lo que permitirá comprender los datos en múltiples niveles y ofrecerá una base sólida para aplicar la innovadora estructura de atención piramidal Skip-PAM (Skip-Pyramidal Attention Module).
La idea básica de Skip-PAM consiste en procesar los datos de origen en distintos intervalos de tiempo, lo cual permite al modelo captar dependencias temporales de distintos niveles de detalle. En los niveles inferiores, el modelo puede centrarse en patrones detallados a corto plazo, mientras que los niveles superiores son capaces de captar tendencias y periodicidades más macroscópicas. El método Skip-PAM presta más atención a las dependencias periódicas, como cada lunes o a principios de cada mes. Este enfoque multinivel permite al modelo captar una variedad de relaciones temporales a diferentes niveles.
Skip-PAM extrae información de series temporales a múltiples escalas usando un mecanismo de atención basado en un árbol de características temporales. Este proceso implica conexiones intraescalares e interescalares. Las conexiones intraescalares implican la realización de cálculos de atención entre un nodo y sus nodos vecinos de la misma capa. Las conexiones interescalares implican cómputos de atención entre un nodo y su nodo padre.
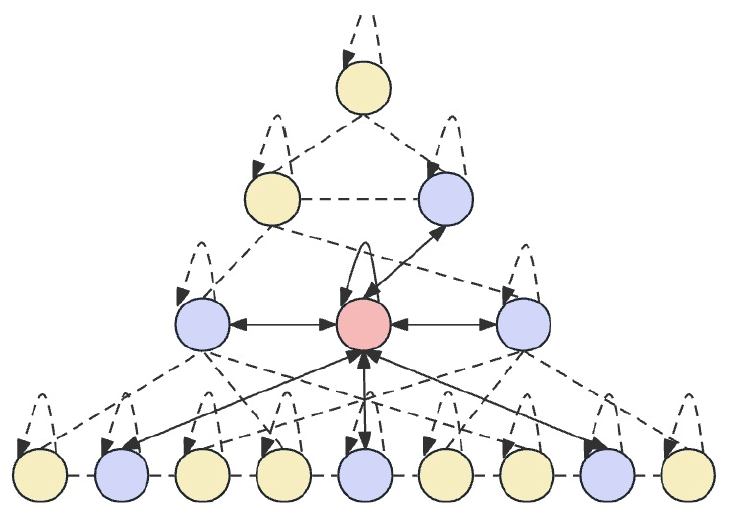
Usando este mecanismo de atención piramidal Skip-PAM, combinado con la convolución de características multinivel en CSCM, se forma una potente red de extracción de características que puede adaptarse a cambios dinámicos en diferentes escalas temporales, ya sean fluctuaciones a corto plazo o evoluciones a largo plazo.
Los autores del método combinan los 2 módulos descritos antes en un potente modelo MSFformer, cuya visualización de autor se presenta a continuación.
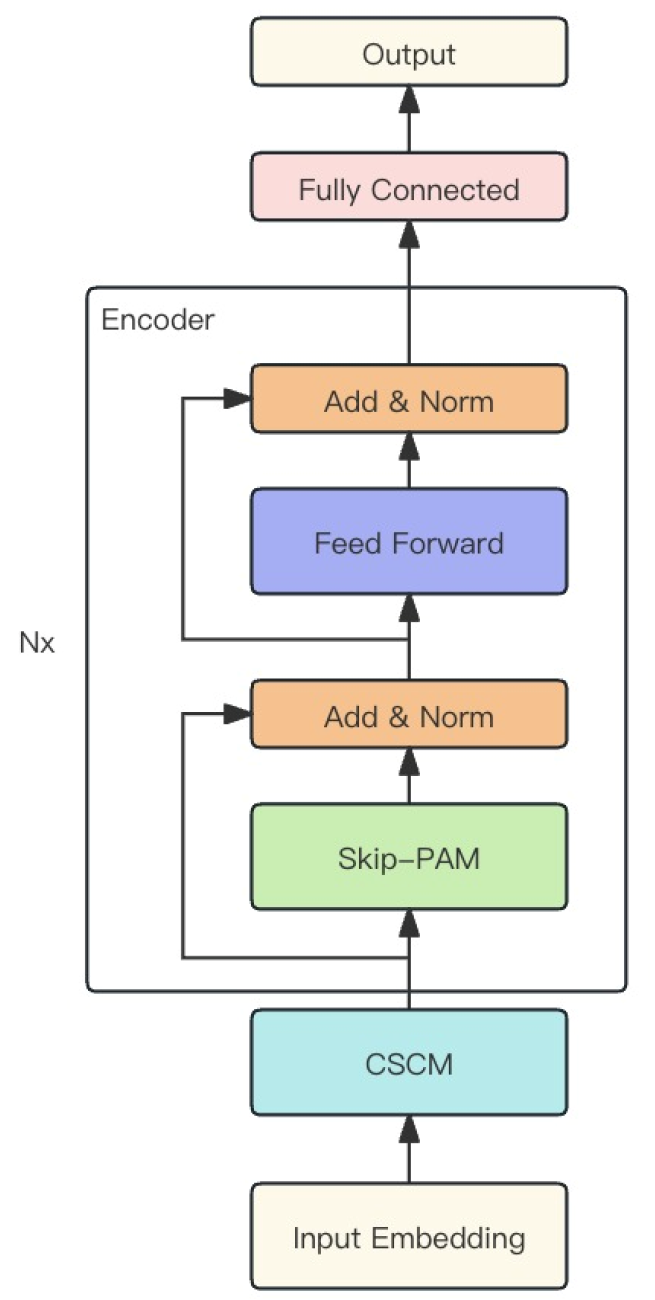
2. Implementación con MQL5
Tras familiarizarnos con los aspectos teóricos del método MSFformer, vamos a pasar a la parte práctica de nuestro artículo, donde implementaremos nuestra visión de los enfoques propuestos con ayuda de MQL5.
Como ya hemos mencionado, el método MSFformer propuesto se basa en 2 módulos: CSCM y Skip-PAM. Precisamente esto implementaremos en el marco de este artículo. Tenemos mucho trabajo por hacer. Lo dividiremos en 2 partes, según los módulos que deberían implementarse.
2.1. Creamos el módulo CSCM
Empezaremos nuestro trabajo construyendo el módulo CSCM. Para implementar la arquitectura de este módulo, crearemos la clase CNeuronCSCMOCL, que hereda la funcionalidad básica de la clase básica de la capa neuronal CNeuronBaseOCL. A continuación, mostraremos la estructura de la nueva clase.
class CNeuronCSCMOCL : public CNeuronBaseOCL { protected: uint i_Count; uint i_Variables; bool b_NeedTranspose; //--- CArrayInt ia_Windows; CArrayObj caTranspose; CArrayObj caConvolutions; CArrayObj caMLP; CArrayObj caTemp; CArrayObj caConvOutputs; CArrayObj caConvGradients; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); //--- virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronCSCMOCL(void) {}; ~CNeuronCSCMOCL(void) {}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint &windows[], uint variables, uint inputs_count, bool need_transpose, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronCSCMOCL; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
En la estructura de clases CNeuronCSCMOCL presentada podemos observar un conjunto bastante estándar de métodos redefinidos y un gran número de arrays dinámicos que nos ayudarán a organizar una estructura de extracción de características multicapa. Nos familiarizaremos con el propósito de los arrays dinámicos y las variables declaradas durante la implementación de métodos.
Todos los objetos de la clase se declaran de forma estática, lo que nos permitirá dejar el constructor y el destructor de la clase "vacíos". La inicialización directa de todos los objetos y variables anidados se realizará en el método Init.
Como es habitual, en los parámetros del método Init obtendremos las principales constantes que nos permitirán definir de forma inequívoca la arquitectura del objeto a crear.
Para ofrecer al usuario flexibilidad al determinar el número de capas de extracción de características y el tamaño de la ventana de convolución, utilizaremos un array dinámico windows. El número de elementos del array indicará el número de bloques de extracción de características FCNN que deberán crearse, mientras que el valor de cada elemento indicará el tamaño de la ventana de convolución del bloque correspondiente.
El número de secuencias temporales unitarias en la serie temporal multidimensional de los datos de origen, así como el tamaño de la secuencia de origen, se especificarán en los parámetros variables y inputs_count, respectivamente.
Además, añadiremos una variable booleana need_transpose para indicar la necesidad de transponer los datos de origen antes de la extracción de características.
bool CNeuronCSCMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint &windows[], uint variables, uint inputs_count, bool need_transpose, ENUM_OPTIMIZATION optimization_type, uint batch) { const uint layers = windows.Size(); if(layers <= 0) return false; if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, inputs_count * variables, optimization_type, batch)) return false;
En el cuerpo del método, organizaremos un pequeño bloque de control. Aquí comprobaremos primero la necesidad de crear al menos un bloque de extracción de características. Después llamaremos al método homónimo de la clase padre, que ya implementa una parte de las funciones de control e inicialización de los objetos heredados. Controlaremos el resultado de las operaciones de los métodos de la clase padre usando el valor lógico retornado.
El siguiente paso consistirá en guardar los parámetros obtenidos en las variables internas y el array correspondientes.
if(!ia_Windows.AssignArray(windows)) return false; i_Variables = variables; i_Count = inputs_count / ia_Windows[0]; b_NeedTranspose = need_transpose;
Después iniciaremos el proceso de inicialización de los objetos anidados. Y aquí, en caso de que necesitemos transponer los datos de origen, crearemos 2 capas anidadas de transposición de datos. La primera servirá para transponer los datos de origen,
if(b_NeedTranspose) { CNeuronTransposeOCL *transp = new CNeuronTransposeOCL(); if(!transp) return false; if(!transp.Init(0, 0, OpenCL, inputs_count, i_Variables, optimization, iBatch)) { delete transp; return false; } if(!caTranspose.Add(transp)) { delete transp; return false; }
mientras que la segunda servirá para transponer los resultados, devolviéndolos a la dimensionalidad de los datos de origen.
transp = new CNeuronTransposeOCL(); if(!transp) return false; if(!transp.Init(0, 1, OpenCL, i_Variables, inputs_count, optimization, iBatch)) { delete transp; return false; } if(!caTranspose.Add(transp)) { delete transp; return false; } if(!SetOutput(transp.getOutput()) || !SetGradient(transp.getGradient()) ) return false; }
Y tenga en cuenta que cuando necesitamos transponer datos, sobreescribiremos los búferes de resultados y gradientes de nuestra clase a los búferes correspondientes de la capa de transposición del resultado. Esta medida nos permitirá eliminar operaciones innecesarias de copiado de datos.
A continuación, crearemos una capa de alineación del tamaño de los datos de origen dentro de las secuencias unitarias individuales.
uint total = ia_Windows[0] * i_Count; CNeuronConvOCL *conv = new CNeuronConvOCL(); if(!conv.Init(0, 0, OpenCL, inputs_count, inputs_count, total, 1, i_Variables, optimization, iBatch)) { delete conv; return false; } if(!caConvolutions.Add(conv)) { delete conv; return false; }
Y en un ciclo crearemos el número necesario de capas de convolución de extracción de características.
total = 0; for(uint i = 0; i < layers; i++) { conv = new CNeuronConvOCL(); if(!conv.Init(0, i + 1, OpenCL, ia_Windows[i], ia_Windows[i], (i < (layers - 1) ? ia_Windows[i + 1] : 1), i_Count, i_Variables, optimization, iBatch)) { delete conv; return false; } if(!caConvolutions.Add(conv)) { delete conv; return false; } if(!caConvOutputs.Add(conv.getOutput()) || !caConvGradients.Add(conv.getGradient()) ) return false; total += conv.Neurons(); }
Obsérvese que en el array caConvolutions hemos combinado la capa de alineación del tamaño de los datos de origen y la convolución de extracción de características. Por consiguiente, tendremos un objeto más que el número dado de bloques FCNN.
Recordemos que el algoritmo del módulo CSCM supone la concatenación de las características de todas las escalas analizadas en un único tensor. Por ello, paralelamente a la creación de capas de convolución, calcularemos el tamaño total del tensor de sus resultados. Además, hemos almacenado los punteros a los búferes de datos de resultados y gradientes de error de las capas de extracción de características creadas en arrays dinámicos independientes, lo cual nos permitirá acceder más rápidamente a su contenido durante el entrenamiento y el funcionamiento del modelo.
Y ahora, con el valor que necesitamos, crearemos una capa para grabar el tensor concatenado.
CNeuronBaseOCL *comul = new CNeuronBaseOCL(); if(!comul.Init(0, 0, OpenCL, total, optimization, iBatch)) { delete comul; return false; } if(!caMLP.Add(comul)) { delete comul; return false; }
Y aquí preveremos un caso especial de creación de 1 capa de extracción de características. No resulta difícil adivinar que en tal caso no tendremos nada que combinar, y el tensor concatenado será una copia completa del tensor único de extracción de características. Por consiguiente, para eliminar las operaciones de copiado innecesarias, redefiniremos los búferes de gradiente de resultados y errores.
if(layers == 1) { comul.SetOutput(conv.getOutput()); comul.SetGradient(conv.getGradient()); }
A continuación, crearemos una capa para ajustar linealmente la dimensionalidad del tensor de características concatenado al tamaño de la secuencia original.
conv = new CNeuronConvOCL(); if(!conv.Init(0, 0, OpenCL, total / i_Variables, total / i_Variables, inputs_count, 1, i_Variables, optimization, iBatch)) { delete conv; return false; } if(!caMLP.Add(conv)) { delete conv; return false; }
Arriba, hemos sobrescrito los búferes de datos de origen y de resultados de nuestra clase cuando necesitamos transponer los datos de origen. Si no, los redefiniremos ahora.
if(!b_NeedTranspose) { if(!SetOutput(conv.getOutput()) || !SetGradient(conv.getGradient()) ) return false; }
De este modo, hemos eliminado las operaciones innecesarias de copiado de datos en ambos casos, tanto si es necesario transponer los datos de origen como si no.
Al final del método, crearemos 3 búferes auxiliares para almacenar los datos intermedios que utilizaremos al concatenar características y desconcatenar los gradientes de error correspondientes.
CBufferFloat *buf = new CBufferFloat(); if(!buf) return false; if(!buf.BufferInit(total, 0) || !buf.BufferCreate(OpenCL) || !caTemp.Add(buf)) { delete buf; return false; } buf = new CBufferFloat(); if(!buf) return false; if(!buf.BufferInit(total, 0) || !buf.BufferCreate(OpenCL) || !caTemp.Add(buf)) { delete buf; return false; } buf = new CBufferFloat(); if(!buf) return false; if(!buf.BufferInit(total, 0) || !buf.BufferCreate(OpenCL) || !caTemp.Add(buf)) { delete buf; return false; } //--- caConvOutputs.FreeMode(false); caConvGradients.FreeMode(false); //--- return true; }
No olvide controlar el proceso de creación de todos los objetos anidados. Y después de inicializar con éxito todos los objetos anidados, retornar el resultado lógico de las operaciones al programa que realiza la llamada.
Después de construir el método de inicialización del objeto de nuestra clase CNeuronCSCMOCL, organizaremos su método de pasada directa. Aquí vale la pena decir que dentro de esta clase no realizaremos trabajos en el lado OpenCL del programa. La implementación completa se basará en el uso de métodos de objetos anidados, cuyo algoritmo ya está implementado en la parte OpenCL. Y en tales condiciones, solo necesitaremos construir un algoritmo de nivel superior a partir de los métodos de los objetos anidados y heredados de la clase padre.
Como ya sabe, la pasada directa se organizará en el método feedForward, en cuyos parámetros el programa que realiza la llamada nos ha proporcionado el puntero al objeto de la capa precedente.
bool CNeuronCSCMOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { CNeuronBaseOCL *inp = NeuronOCL; CNeuronBaseOCL *current = NULL;
En el cuerpo del método declararemos dos variables para almacenar los punteros a los objetos de la capa neuronal. En esta fase, transmitiremos el puntero recibido del programa que realiza la llamada a la variable de datos de origen. Dejaremos la segunda variable vacía.
A continuación, comprobaremos si es necesario transponer los datos de origen. Y si es necesario, llevaremos a cabo esta operación.
if(b_NeedTranspose) { current = caTranspose.At(0); if(!current || !current.FeedForward(inp)) return false; inp = current; }
Luego transmitiremos la serie temporal de origen por las sucesivas capas convolucionales de extracción de características de diferentes escalas cuyos punteros hemos almacenado en el array caConvolutions.
int layers = caConvolutions.Total() - 1; for(int l = 0; l <= layers; l++) { current = caConvolutions.At(l); if(!current || !current.FeedForward(inp)) return false; inp = current; }
Recordemos que la primera capa de este array está diseñada para alinear el tamaño de la secuencia de datos de origen. Su resultado no lo usaremos en la concatenación de características extraídas, que realizaremos en el siguiente paso.
Debemos decir que construiremos el algoritmo sin restringir el límite superior de capas convolucionales de extracción de características. Incluso permitiremos como mínimo 1 capa de extracción de características. Y probablemente el algoritmo más simple que podamos utilizar en este caso sea la creación de un ciclo con la adición secuencial de 1 array de características al tensor a la vez. Pero este enfoque dará lugar a posibles copiados múltiples de los mismos datos, lo que aumentará significativamente nuestra sobrecarga de recursos computacionales en la pasada directa. Para minimizar estas operaciones, hemos creado un algoritmo de ramificación según el número de bloques de extracción de características.
Como ya hemos dicho, deberá haber al menos una capa de extracción de características. Si no está presente, retornaremos una señal de error al programa de llamada en forma de resultado negativo.
current = caMLP.At(0); if(!current) return false; switch(layers) { case 0: return false;
Con una sola capa de extracción de características, no tendremos nada que concatenar. Y como recordará, en el método de inicialización de la clase hemos redefinido los búferes de datos de las capas de extracción y concatenación de características para tal caso, lo cual nos ha permitido reducir las operaciones de copiado innecesarias. Simplemente pasaremos a las siguientes operaciones.
case 1: break;
La presencia de entre 2 y 4 capas de extracción de características provocará la selección del método de concatenación de datos correspondiente.
case 2: if(!Concat(caConvOutputs.At(0), caConvOutputs.At(1), current.getOutput(), ia_Windows[1], 1, i_Variables * i_Count)) return false; break; case 3: if(!Concat(caConvOutputs.At(0), caConvOutputs.At(1), caConvOutputs.At(2), current.getOutput(), ia_Windows[1], ia_Windows[2], 1, i_Variables * i_Count)) return false; break; case 4: if(!Concat(caConvOutputs.At(0), caConvOutputs.At(1), caConvOutputs.At(2), caConvOutputs.At(3), current.getOutput(), ia_Windows[1], ia_Windows[2], ia_Windows[3], 1, i_Variables * i_Count)) return false;
Si hay más capas de este tipo, concatenaremos las 4 primeras capas de extracción de características, pero el resultado se escribirá en un búfer de almacenamiento temporal.
default: if(!Concat(caConvOutputs.At(0), caConvOutputs.At(1), caConvOutputs.At(2), caConvOutputs.At(3), caTemp.At(0), ia_Windows[1], ia_Windows[2], ia_Windows[3], ia_Windows[4], i_Variables * i_Count)) return false; break; }
Nótese que cuando realizamos operaciones de concatenación, no accedemos a los objetos de las capas de convolución desde el array caConvolutions, sino directamente a los búferes de sus resultados, los punteros a los que hemos almacenado cuidadosamente en el array dinámico caConvOutputs.
A continuación, organizaremos un ciclo a partir de la capa 4 de extracción de características y con un paso de 3 capas. En el cuerpo de este ciclo, primero calcularemos el tamaño de ventana de los datos almacenados en el búfer temporal.
uint last_buf = 0; for(int i = 4; i < layers; i += 3) { uint buf_size = 0; for(int j = 1; j <= i; j++) buf_size += ia_Windows[j];
Y, a continuación, organizaremos el algoritmo de selección de la función de concatenación de forma similar a la anterior, solo que en este caso, el búfer temporal con los datos recogidos anteriormente siempre será el primero, y el siguiente lote de características extraídas ya se añadirá a él.
switch(layers - i) { case 1: if(!Concat(caTemp.At(last_buf), caConvOutputs.At(i), current.getOutput(), buf_size, 1, i_Variables * i_Count)) return false; break; case 2: if(!Concat(caTemp.At(last_buf), caConvOutputs.At(i), caConvOutputs.At(i + 1), current.getOutput(), buf_size, ia_Windows[i + 1], 1, i_Variables * i_Count)) return false; break; case 3: if(!Concat(caTemp.At(last_buf), caConvOutputs.At(i), caConvOutputs.At(i + 1), caConvOutputs.At(i + 2), current.getOutput(), buf_size, ia_Windows[i + 1], ia_Windows[i + 2], 1, i_Variables * i_Count)) return false; break; default: if(!Concat(caTemp.At(last_buf), caConvOutputs.At(i), caConvOutputs.At(i + 1), caConvOutputs.At(i + 2), caTemp.At((last_buf + 1) % 2), buf_size, ia_Windows[i + 1], ia_Windows[i + 2], ia_Windows[i + 3], i_Variables * i_Count)) return false; break; } last_buf = (last_buf + 1) % 2; }
Tenga en cuenta que cuando se añaden las últimas capas de características (1 a 3), el resultado de la operación se guarda en el búfer de capas de concatenación de datos. En otros casos, utilizaremos otro búfer de almacenamiento temporal. Los búferes se intercalarán en cada iteración del ciclo para evitar la corrupción y pérdida de datos.
Tras concatenar todas las características en un único tensor, nos quedará ajustar el tamaño del tensor de resultados.
inp = current; current = caMLP.At(1); if(!current || !current.FeedForward(inp)) return false;
Y si es necesario, transponer estos a la dimensionalidad de los datos de origen.
if(b_NeedTranspose) { inp = current; current = caTranspose.At(1); if(!current || !current.FeedForward(inp)) return false; } //--- return true; }
Permítame recordarle que en el método de inicialización hemos organizado el intercambio de búferes de datos. Por ello, el copiado de los resultados de las operaciones en el correspondiente búfer heredado de nuestra clase se realizará "automáticamente".
Tras construir el método de pasada directa, procederemos a implementar los algoritmos de pasada inversa. Y primero crearemos un método para distribuir el gradiente de error a todos los objetos según su influencia en el resultado global (calcInputGradients). Como es habitual, en los parámetros de este método obtendremos el puntero al objeto de la capa neuronal precedente. En este caso, tendremos que transmitirle la fracción correspondiente del gradiente de error.
bool CNeuronCSCMOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!prevLayer) return false;
En el cuerpo del método comprobaremos directamente la relevancia del puntero recibido. Después crearemos los punteros locales de las dos capas de neuronas con las que trabajaremos secuencialmente.
CNeuronBaseOCL *current = caMLP.At(0); CNeuronBaseOCL *next = caMLP.At(1);
Recordemos que durante la distribución del gradiente de error, nos moveremos a lo largo del algoritmo de pasada directa, pero en la dirección opuesta. Por lo tanto, primero transmitiremos el gradiente por la capa de transposición de datos, por supuesto, si existe la necesidad de realizar tal operación.
if(b_NeedTranspose) { if(!next.calcHiddenGradients(caTranspose.At(1))) return false; }
A continuación, transmitiremos el gradiente de error a una capa concatenada de características extraídas de diferentes escalas.
if(!current.calcHiddenGradients(next.AsObject())) return false; next = current;
Después, tendremos que distribuir el gradiente de error a las capas de extracción de características correspondientes.
No nos olvidaremos del caso especial en el que tenemos 1 capa de extracción de características. Aquí solo necesitaremos ajustar el gradiente de error usando la derivada de la función de activación.
int layers = caConvGradients.Total(); if(layers == 1) { next = caConvolutions.At(1); if(next.Activation() != None) { if(!DeActivation(next.getOutput(), next.getGradient(), next.getGradient(), next.Activation())) return false; } }
En el caso general, sin embargo, primero separaremos el gradiente de error de la última capa de extracción de características y corregiremos la derivada de la función de activación.
else { int prev_window = 0; for(int i = 1; i < layers; i++) prev_window += int(ia_Windows[i]); if(!DeConcat(caTemp.At(0), caConvGradients.At(layers - 1), next.getGradient(), prev_window, 1, i_Variables * i_Count)) return false; next = caConvolutions.At(layers); int current_buf = 0;
Después, organizaremos un ciclo de iteración inversa de capas de extracción de características, en cuyo cuerpo obtendremos primero el gradiente de error de la capa posterior de extracción de características.
for(int l = layers; l > 1; l--) { current = caConvolutions.At(l - 1); if(!current.calcHiddenGradients(next.AsObject())) return false;
A continuación, extraeremos la fracción de la capa analizada del búfer de gradiente de error del tensor de características concatenado.
int window = int(ia_Windows[l - 1]); prev_window -= window; if(!DeConcat(caTemp.At((current_buf + 1) % 2), caTemp.At(2), caTemp.At(current_buf), prev_window, window, i_Variables * i_Count)) return false;
La corregiremos según la derivada de la función de activación.
if(current.Activation() != None) { if(!DeActivation(current.getOutput(), caTemp.At(2), caTemp.At(2), current.Activation())) return false; }
Y sumaremos los gradientes de error de los 2 flujos de datos.
if(!SumAndNormilize(current.getGradient(), caTemp.At(2), current.getGradient(), 1, false, 0, 0, 0, 1)) return false; next = current; current_buf = (current_buf + 1) % 2; } }
Después, pasaremos a la siguiente iteración de nuestro ciclo.
De este modo, distribuiremos el gradiente de error entre todas las capas de extracción de características. Y luego transmitiremos el gradiente de error a la capa de alineación del tamaño de los datos de origen.
current = caConvolutions.At(0); if(!current.calcHiddenGradients(next.AsObject())) return false; next = current;
Si es necesario, transmitiremos el gradiente de error por la capa de transposición de datos.
if(b_NeedTranspose) { current = caTranspose.At(0); if(!current.calcHiddenGradients(next.AsObject())) return false; next = current; }
Y para completar las operaciones del método, transmitiremos el gradiente de error a la capa neuronal precedente, cuyo puntero hemos obtenido en los parámetros de este método.
if(!prevLayer.calcHiddenGradients(next.AsObject())) return false; //--- return true; }
Como ya sabemos, la distribución del gradiente de error no es el objetivo del entrenamiento del modelo: es solo un medio para determinar la dirección y la magnitud del ajuste de los parámetros del modelo. Por ello, una vez que hayamos distribuido con éxito el gradiente de error, deberemos ajustar los parámetros del modelo para minimizar su error de rendimiento en general. Esta funcionalidad se implementará en el método updateInputWeights.
bool CNeuronCSCMOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { CObject *prev = (b_NeedTranspose ? caTranspose.At(0) : NeuronOCL); CNeuronBaseOCL *current = NULL;
En los parámetros del método, como antes, obtendremos el puntero al objeto de la capa neuronal precedente. No obstante, en este caso, no comprobaremos la relevancia del puntero obtenido. Lo guardaremos en una variable local. Pero aquí hay un matiz a considerar. La capa de transposición de datos no contiene ningún parámetro. Por consiguiente, no llamaremos al método de ajuste de parámetros del modelo para ello. Salvo que para la capa de alineación del tamaño de los datos de origen, seleccionaremos la capa precedente dependiendo del parámetro de necesidad de transposición de los datos de origen b_NeedTranspose.
A continuación, organizaremos un ciclo de ajuste sucesivo de los parámetros de las capas de convolución, incluida la capa inicial de ajuste del tamaño de la secuencia y los bloques de extracción de características.
for(int i = 0; i < caConvolutions.Total(); i++) { current = caConvolutions.At(1); if(!current || !current.UpdateInputWeights(prev) ) return false; prev = current; }
Después deberemos ajustar los parámetros de la capa de alineación de la dimensionalidad de los resultados.
current = caMLP.At(1); if(!current || !current.UpdateInputWeights(caMLP.At(0)) ) return false; //--- return true; }
Los demás objetos anidados de nuestra clase CNeuronCSCMOCL no contendrán parámetros entrenables.
La implementación de los algoritmos básicos del módulo CSCM puede considerarse finalizada. Obviamente, la funcionalidad de nuestra clase no estará completa sin la implementación adicional de algoritmos de métodos auxiliares. Pero para reducir la extensión del artículo, los dejaremos para un estudio aparte. El código completo de todos los métodos de esta clase se ofrece en el archivo adjunto. Ahí encontrará también el código completo de todas las clases y programas utilizados en la preparación de este artículo. Ahora procederemos a construir los algoritmos para el siguiente módulo, Skip-PAM.
2.2 Aplicación de los algoritmos Skip-PAM
La segunda parte del trabajo que deberemos hacer es implementar el algoritmo de atención piramidal. La innovación de los autores del método MSFformer consiste en la aplicación de algoritmos de atención al árbol de características en diferentes intervalos. Los autores del método usan pasos fijos entre características dentro del mismo nivel de atención. En nuestra aplicación haremos las cosas de forma un poco distinta. ¿Y si dejamos que el modelo aprenda por sí solo qué atributos analizará cada pirámide de atención individual en cada nivel de atención aparte? Parece divertido. Sí, y la aplicación, en mi opinión, resulta obvia y sencilla. Simplemente añadiremos antes de cada nivel de atención una capa S3.
Construiremos los algoritmos de nuestra implementación del módulo Skip-PAM dentro de la clase CNeuronSPyrAttentionOCL, cuya estructura mostramos a continuación.
class CNeuronSPyrAttentionOCL : public CNeuronBaseOCL { protected: uint iWindowIn; uint iWindowKey; uint iHeads; uint iHeadsKV; uint iCount; uint iPAMLayers; //--- CArrayObj caS3; CArrayObj caQuery; CArrayObj caKV; CArrayInt caScore; CArrayObj caAttentionOut; CArrayObj caW0; CNeuronConvOCL cFF1; CNeuronConvOCL cFF2; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool AttentionOut(CBufferFloat *q, CBufferFloat *kv, int scores, CBufferFloat *out, int window); virtual bool AttentionInsideGradients(CBufferFloat *q, CBufferFloat *q_g, CBufferFloat *kv, CBufferFloat *kv_g, int scores, CBufferFloat *gradient); //--- virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); virtual void ArraySetOpenCL(CArrayObj *array, COpenCLMy *obj); public: CNeuronSPyrAttentionOCL(void) {}; ~CNeuronSPyrAttentionOCL(void) {}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window_in, uint window_key, uint heads, uint heads_kv, uint units_count, uint pam_layers, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronSPyrAttentionMLKV; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
Como podemos ver en la estructura presentada, la nueva clase contiene arrays y parámetros aún más dinámicos. Sus nombres estarán en consonancia con los objetos de otras clases de atención. Y como podemos ver, no se trata de una casualidad. Con el uso de los objetos y variables creados nos familiarizaremos durante la implementación.
Al igual que antes, comenzaremos nuestro análisis de los algoritmos de la nueva clase con el método de inicialización del objeto Init.
bool CNeuronSPyrAttentionOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window_in, uint window_key, uint heads, uint heads_kv, uint units_count, uint pam_layers, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_in * units_count, optimization_type, batch)) return false;
En los parámetros del método obtendremos las constantes principales que definen las arquitecturas del objeto a crear, mientras que en el cuerpo del método llamaremos directamente al método homónimo de la clase padre, que implementará el mínimo necesario de control e inicialización de los objetos heredados.
Obsérvese también que en este método analizaremos los pasos temporales individuales dentro de una secuencia temporal multimodal global. Aunque en este caso probablemente sea difícil llamar series temporales multimodales a los datos de origen introducidos en la entrada del módulo Skip-PAM. Al fin y al cabo, los resultados del módulo CSCM anterior supondrán un conjunto de características extraídas de diferentes escalas de datos, no una secuencia temporal.
Una vez ejecutado con éxito el método de inicialización de objetos de la clase padre, guardaremos las constantes obtenidas en variables locales.
iWindowIn = window_in; iWindowKey = MathMax(window_key, 1); iHeads = MathMax(heads, 1); iHeadsKV = MathMax(heads_kv, 1); iCount = units_count; iPAMLayers = MathMax(pam_layers, 2);
Aquí deberemos prestar atención a la aparición de un nuevo parámetro iPAMLayers, que determinará el número de niveles de atención piramidal. El resto de parámetros, sin embargo, implicarán la misma funcionalidad que los métodos de atención comentados anteriormente. También dejaremos el parámetro iHeadsKV para permitir que el número de cabezas Key-Value sea diferente de la dimensionalidad de la cabeza de atención Query, como se comenta en el método MLKV.
A continuación, limpiaremos los arrays dinámicos.
caS3.Clear(); caQuery.Clear(); caKV.Clear(); caScore.Clear(); caAttentionOut.Clear(); caW0.Clear();
Vamos a crear las variables locales necesarias.
CNeuronBaseOCL *base = NULL; CNeuronConvOCL *conv = NULL; CNeuronS3 *s3 = NULL;
También organizaremos un ciclo de inicialización de objetos del bloque de atención piramidal. Como podemos adivinar, el número de iteraciones del ciclo será igual al número de niveles de atención creados.
for(uint l = 0; l < iPAMLayers; l++) { //--- S3 s3 = new CNeuronS3(); if(!s3) return false; if(!s3.Init(0, l, OpenCL, iWindowIn, iCount, optimization, iBatch) || !caS3.Add(s3)) return false; s3.SetActivationFunction(None);
En el cuerpo del ciclo, crearemos primero la capa S3, en la que se organizará la permutación de la secuencia que vamos a analizar. En este caso, utilizaremos una sola capa de mezcla de datos con una ventana igual al número de parámetros analizados en la secuencia multimodal original.
A continuación crearemos los objetos de generación de entidades Query, Key y Value Tenga en cuenta que, al formar entidades, usaremos el mismo objeto de datos de origen, pero diferentes parámetros de la cabeza de atención.
//--- Query conv = new CNeuronConvOCL(); if(!conv) return false; if(!conv.Init(0, 0, OpenCL, iWindowIn, iWindowIn, iWindowKey*iHeads, iCount, optimization, iBatch) || !caQuery.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(None); //--- KV conv = new CNeuronConvOCL(); if(!conv) return false; if(!conv.Init(0, 0, OpenCL, iWindowIn, iWindowIn, 2*iWindowKey*iHeadsKV, iCount, optimization, iBatch) || !caKV.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(None);
Crearemos la matriz de coeficientes de dependencia solo en el lado del contexto OpenCL. Aquí guardaremos solo el puntero al búfer.
//--- Score int temp = OpenCL.AddBuffer(sizeof(float) * iCount * iCount * iHeads, CL_MEM_READ_WRITE); if(temp < 0) return false; if(!caScore.Add(temp)) return false;
A continuación, crearemos una capa para registrar los resultados de la atención multicabeza.
//--- MH Attention Out base = new CNeuronBaseOCL(); if(!base) return false; if(!base.Init(0, 0, OpenCL, iWindowKey * iHeadsKV * iCount, optimization, iBatch) || !caAttentionOut.Add(conv)) { delete base; return false; } base.SetActivationFunction(None);
Y completaremos las iteraciones del ciclo con una capa de reducción de la dimensionalidad al nivel de los datos de origen.
//--- W0 conv = new CNeuronConvOCL(); if(!conv) return false; if(!conv.Init(0, 0, OpenCL, iWindowKey * iHeadsKV, iWindowKey * iHeadsKV, iWindowIn, iCount, optimization, iBatch) || !caW0.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(None); }
Una vez completadas con éxito todas las iteraciones para crear los niveles de atención piramidal, añadiremos una capa en cuyo búfer registraremos la suma de los resultados del bloque de atención piramidal y los datos de origen.
//--- Residual base = new CNeuronBaseOCL(); if(!base) return false; if(!base.Init(0, 0, OpenCL, iWindowIn * iCount, optimization, iBatch) || !caW0.Add(conv)) { delete base; return false; } base.SetActivationFunction(None);
Y ahora solo nos quedará inicializar las capas del bloque FeedForward.
//--- FeedForward if(!cFF1.Init(0, 0, OpenCL, iWindowIn, iWindowIn, 4 * iWindowIn, iCount, optimization, iBatch)) return false; cFF1.SetActivationFunction(LReLU); if(!cFF2.Init(0, 0, OpenCL, 4 * iWindowIn, 4 * iWindowIn, iWindowIn, iCount, optimization, iBatch)) return false; cFF2.SetActivationFunction(None); if(!SetGradient(cFF2.getGradient())) return false;
Al final del método, eliminaremos forzosamente la función de activación de nuestra capa.
SetActivationFunction(None); //--- return true; }
Tras inicializar los objetos de nuestra clase, procederemos a implementar los algoritmos de pasada directa. Y debemos decir que aquí tendremos que hacer un poco de trabajo preparatorio en el lado OpenCL del programa. Así, crearemos el nuevo kernel MH2PyrAttentionOut, que en esencia supone una versión corregida del kernel MH2AttentionOut.
__kernel void MH2PyrAttentionOut(__global float *q, __global float *kv, __global float *score, __global float *out, const int dimension, const int heads_kv, const int window ) { //--- init const int q_id = get_global_id(0); const int k = get_global_id(1); const int h = get_global_id(2); const int qunits = get_global_size(0); const int kunits = get_global_size(1); const int heads = get_global_size(2);
Además del nombre del kernel, se distinguirá del anterior en la presencia del parámetro adicional de ventana de atención window. Invocaremos el kernel en un espacio de tareas tridimensional. Y como siempre, al principio del kernel, realizaremos la identificación del flujo en todas las dimensiones del espacio de tareas.
A continuación, efectuaremos el cálculo de las constantes necesarias.
const int h_kv = h % heads_kv; const int shift_q = dimension * (q_id * heads + h); const int shift_k = dimension * (2 * heads_kv * k + h_kv); const int shift_v = dimension * (2 * heads_kv * k + heads_kv + h_kv); const int shift_s = kunits * (q_id * heads + h) + k; const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE); const int delta_win = (window + 1) / 2; float koef = sqrt((float)dimension); if(koef < 1) koef = 1;
E inicializaremos un array local para registrar los valores intermedios.
__local float temp[LOCAL_ARRAY_SIZE];
Primero deberemos determinar los coeficientes de dependencia de cada elemento de la secuencia. Como ya sabemos, en el bloque de atención, las relaciones de dependencia se normalizarán usando la función SoftMax. Para ello, calcularemos primero la suma de los exponentes de los coeficientes de dependencia.
En la primera etapa, cada flujo recopilará su parte de la suma de valores exponenciales en el elemento correspondiente del conjunto de datos local. Y aquí deberemos prestar atención a un pequeño añadido: calcularemos los coeficientes de dependencia solo dentro de la ventana de atención del elemento actual. Para los demás elementos, el coeficiente de dependencia será "0".
//--- sum of exp uint count = 0; if(k < ls) do { if((count * ls) < (kunits - k)) { float sum = 0; if(abs(count * ls + k - q_id) <= delta_win) { for(int d = 0; d < dimension; d++) sum = q[shift_q + d] * kv[shift_k + d]; sum = exp(sum / koef); if(isnan(sum)) sum = 0; } temp[k] = (count > 0 ? temp[k] : 0) + sum; } count++; } while((count * ls + k) < kunits); barrier(CLK_LOCAL_MEM_FENCE);
Para sincronizar los flujos del grupo local, utilizaremos una barrera.
En la siguiente etapa, tendremos que recopilar la suma de los valores de todos los elementos del array local. Para ello, organizaremos otro ciclo con flujos locales sincronizados en cada iteración. Aquí deberemos tener cuidado de que cada flujo visite el mismo número de barreras. De lo contrario, algunos flujos podrían que darse "colgados".
count = min(ls, (uint)kunits); //--- do { count = (count + 1) / 2; if(k < ls) temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0); if(k + count < ls) temp[k + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Tras determinar la suma de los exponentes, podremos calcular los coeficientes de dependencia normalizados. Y aquí no deberemos olvidarnos de la presencia de dependencias solo dentro de la ventana de atención.
//--- score float sum = temp[0]; float sc = 0; if(sum != 0 && abs(k - q_id) <= delta_win) { for(int d = 0; d < dimension; d++) sc = q[shift_q + d] * kv[shift_k + d]; sc = exp(sc / koef) / sum; if(isnan(sc)) sc = 0; } score[shift_s] = sc; barrier(CLK_LOCAL_MEM_FENCE);
Y, obviamente, sincronizaremos los flujos locales tras calcular los coeficientes de dependencia.
A continuación, tendremos que determinar el valor de los elementos considerando las dependencias. Aquí utilizaremos el mismo algoritmo para sumar los valores en flujos paralelos, como se ha hecho para determinar la suma de los valores exponenciales de las dependencias. Primero recopilaremos las sumas de los valores individuales de los elementos del array local.
//--- out for(int d = 0; d < dimension; d++) { uint count = 0; if(k < ls) do { if((count * ls) < (kunits - k)) { float sum = 0; if(abs(count * ls + k - q_id) <= delta_win) { sum = kv[shift_v + d] * (count == 0 ? sc : score[shift_s + count * ls]); if(isnan(sum)) sum = 0; } temp[k] = (count > 0 ? temp[k] : 0) + sum; } count++; } while((count * ls + k) < kunits); barrier(CLK_LOCAL_MEM_FENCE);
Y luego recopilaremos la suma de los valores de los elementos del array.
//--- count = min(ls, (uint)kunits); do { count = (count + 1) / 2; if(k < ls) temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0); if(k + count < ls) temp[k + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); //--- out[shift_q + d] = temp[0]; } }
La suma resultante la guardaremos en el elemento correspondiente del búfer de resultados.
De este modo, hemos creado un nuevo kernel de atención dentro de una ventana determinada. Tenga en cuenta que hemos especificado que los coeficientes de dependencia sean "0" para los elementos fuera de la ventana de atención. Este movimiento sin complicaciones nos permitirá usar el kernel MH2AttentionInsideGradients creado anteriormente para distribuir el gradiente de error dentro de la pasada inversa.
Los métodos AttentionOut y AttentionInsideGradients se han creado en el lado del programa principal para poner en la cola los kernels especificados para su ejecución, respectivamente. Su algoritmo no diferirá mucho de otros métodos similares analizados en los artículos anteriores de esta serie, por lo que no nos detendremos ahora en ellos. Le sugiero que se familiarice con ellos en los anexos. Ahora pasaremos a implementar los algoritmos del método feedForward.
En los parámetros, el método de pasada directa recibirá el puntero al objeto de la capa neuronal precedente que contiene los datos de origen.
bool CNeuronSPyrAttentionOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { CNeuronBaseOCL *prev = NeuronOCL; CNeuronBaseOCL *current = NULL; CBufferFloat *q = NULL; CBufferFloat *kv = NULL;
En el cuerpo del método, crearemos una serie de variables locales para almacenar los punteros a los objetos procesados de las capas neuronales anidadas.
A continuación, crearemos un ciclo de iteración de niveles de atención. En el cuerpo del ciclo, primero mezclaremos los datos de origen.
for(uint l = 0; l < iPAMLayers; l++) { //--- Mix current = caS3.At(l); if(!current || !current.FeedForward(prev.AsObject()) ) return false; prev = current;
Después, generaremos los tensores de entidad Query, Key y Value para implementar el algoritmo de atención multicabeza.
//--- Query current = caQuery.At(l); if(!current || !current.FeedForward(prev.AsObject()) ) return false; q = current.getOutput(); //--- Key and Value current = caKV.At(l); if(!current || !current.FeedForward(prev.AsObject()) ) return false; kv = current.getOutput();
Y ejecutaremos el algoritmo del kernel de atención para este nivel.
//--- PAM current = caAttentionOut.At(l); if(!current || !AttentionOut(q, kv, caScore.At(l), current.getOutput(), iPAMLayers - l)) return false; prev = current;
Observe que en cada nivel sucesivo reduciremos la ventana de atención, creando así un efecto piramidal. Para ello, utilizaremos la diferencia "iPAMLayers - l".
Al final de las iteraciones del ciclo, reduciremos el tamaño del tensor de resultados de atención multicabeza al tamaño de los datos de origen.
//--- W0 current = caW0.At(l); if(!current || !current.FeedForward(prev.AsObject()) ) return false; prev = current; }
Una vez se hayan ejecutado con éxito todos los niveles de atención piramidal, sumaremos y normalizaremos los resultados de la atención con los datos de referencia.
//--- Residual current = caW0.At(iPAMLayers); if(!SumAndNormilize(NeuronOCL.getOutput(), prev.getOutput(), current.getOutput(), iWindowIn, true)) return false;
Completará la capa de atención piramidal el bloque FeedForward, similar al Transformer vainilla.
//---FeedForward if(!cFF1.FeedForward(current.AsObject()) || !cFF2.FeedForward(cFF1.AsObject()) ) return false;
A continuación, resumiremos y normalizaremos los datos de los dos flujos de operaciones.
//--- Residual if(!SumAndNormilize(current.getOutput(), cFF2.getOutput(), getOutput(), iWindowIn, true)) return false; //--- return true; }
Obviamente, no nos olvidaremos de controlar el proceso de ejecución de las operaciones. Y en la finalización del método, retornaremos el resultado lógico de las operaciones al programa que realiza la llamada.
Como es habitual, tras implementar la pasada directa, procederemos a construir los algoritmos de pasada inversa. El proceso constará de 2 pasos: la distribución del gradiente de error y la optimización de los parámetros del modelo.
La distribución de los gradientes de error se implementará en el método calcInputGradients.
bool CNeuronSPyrAttentionOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!prevLayer) return false;
En los parámetros de este método obtendremos el puntero al objeto de la capa neuronal precedente, a cuyo búfer deberemos transmitir el gradiente de error según la influencia de los datos iniciales en el resultado global.
A continuación, crearemos algunas variables locales para almacenar temporalmente los punteros a los objetos internos.
CNeuronBaseOCL *next = NULL; CNeuronBaseOCL *current = NULL; CNeuronBaseOCL *q = NULL; CNeuronBaseOCL *kv = NULL;
La distribución de los gradientes de error se realizará según las operaciones de pasada directa, pero en orden inverso. Primero pasaremos el gradiente de error por el bloque FeedForward.
//--- FeedForward current = caW0.At(iPAMLayers); if(!current || !cFF1.calcHiddenGradients(cFF2.AsObject()) || !current.calcHiddenGradients(cFF1.AsObject()) ) return false; next = current;
A continuación, tendremos que sumar los gradientes de error de los 2 flujos de operaciones.
//--- Residual current = caW0.At(iPAMLayers - 1); if(!SumAndNormilize(getGradient(), next.getGradient(), current.getGradient(), iWindowIn, false)) return false; CBufferFloat *residual = next.getGradient(); next = current;
Después, organizaremos un ciclo de iteración inversa de los niveles de atención con un descenso sucesivo del gradiente de error.
for(int l = int(iPAMLayers - 1); l >= 0; l--) { //--- W0 current = caAttentionOut.At(l); if(!current || !current.calcHiddenGradients(next.AsObject()) ) return false;
En el cuerpo del ciclo, primero distribuiremos el gradiente de error por las cabezas de atención. Y luego lo distribuiremos hasta el nivel de las entidades Query, Key y Value.
//--- MH Attention q = caQuery.At(l); kv = caKV.At(l); if(!q || !kv || !AttentionInsideGradients(q.getOutput(), q.getGradient(), kv.getOutput(), kv.getGradient(), caScore.At(l), current.getGradient()) ) return false;
El siguiente paso consistirá en descender el gradiente de error hasta la capa de mezcla de datos. Y aquí tendremos que combinar los datos de 2 flujos, los de Query y Key-Value. Para ello, primero obtendremos el gradiente de error de Query, y luego lo desplazaremos al búfer temporal.
//--- Query current = caS3.At(l); if(!current || !current.calcHiddenGradients(q.AsObject()) || !Concat(current.getGradient(), current.getGradient(), residual, iWindowIn,0, iCount) ) return false;
Luego tomaremos el gradiente Key-Value y sumaremos los resultados de los 2 flujos de datos.
//--- Key and Value if(!current || !current.calcHiddenGradients(kv.AsObject()) || !SumAndNormilize(current.getGradient(), residual, current.getGradient(), iWindowIn, false) ) return false; next = current;
A continuación, transmitiremos el gradiente de error a través de la capa de mezcla de datos y pasaremos a la siguiente iteración del ciclo.
//--- S3 current = (l == 0 ? prevLayer : caW0.At(l - 1)); if(!current || !current.calcHiddenGradients(next.AsObject()) ) return false; next = current; }
Al final de las operaciones del método, todo lo que deberemos hacer es combinar el gradiente de error de los 2 flujos. Aquí, primero corregiremos la derivada de la función de activación de la capa anterior según el gradiente del error de enlace residual. Cuando el gradiente de error descienda directamente al nivel de la capa, la corrección del gradiente de error a la función de activación será automática.
current = caW0.At(iPAMLayers - 1); if(!DeActivation(prevLayer.getOutput(), current.getGradient(), residual, prevLayer.Activation()) || !SumAndNormilize(prevLayer.getGradient(), residual, prevLayer.getGradient(), iWindowIn, false) ) return false; //--- return true; }
Y luego sumaremos los gradientes de error de ambos flujos.
Tras distribuir los gradientes de error, procederemos a ajustar los parámetros del modelo. Esta funcionalidad se implementará en el método updateInputWeights. El algoritmo de este método será bastante prosaico y predecible: simplemente llamaremos secuencialmente a los métodos homónimos de los objetos anidados que contengan los parámetros que debemos entrenar.
bool CNeuronSPyrAttentionOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { CNeuronBaseOCL *prev = NeuronOCL; CNeuronBaseOCL *current = NULL; for(uint l = 0; l < iPAMLayers; l++) { //--- S3 current = caS3.At(l); if(!current || !current.UpdateInputWeights(prev) ) return false; //--- Query prev = current; current = caQuery.At(l); if(!current || !current.UpdateInputWeights(prev) ) return false; //--- Key and Value current = caKV.At(l); if(!current || !current.UpdateInputWeights(prev) ) return false; //--- W0 prev = caAttentionOut.At(l); current = caW0.At(l); if(!current || !current.UpdateInputWeights(prev) ) return false; prev = current; } //--- FeedForward prev = caW0.At(iPAMLayers); if(!cFF1.UpdateInputWeights(prev) || !cFF2.UpdateInputWeights(cFF1.AsObject()) ) return false; //--- return true; }
No deberemos olvidarnos de controlar el proceso de ejecución de todas las operaciones del método y de devolver el resultado lógico de las operaciones ejecutadas al programa que realiza la llamada.
Con esto daremos por concluido nuestro trabajo sobre la aplicación de los enfoques propuestos del método MSFformer. Podrá ver el código completo de las clases creadas y sus métodos en el archivo adjunto.
Conclusión
En este artículo, nos hemos familiarizado con otro interesante y prometedor método de previsión de series temporales, el MSFformer (Multi-Scale Feature Transformer), presentado en el artículo "Time Series Prediction Based on Multi-Scale Feature Extraction". El algoritmo propuesto se basa en una arquitectura de atención piramidal mejorada y en un novedoso enfoque de extracción de características multinivel de distintas escalas a partir de los datos de origen.
En la parte práctica del artículo, hemos implementado los 2 módulos principales del algoritmo propuesto. Veremos los resultados de este trabajo en el próximo artículo.
Enlaces
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | ResearchRealORL.mq5 | Asesor | Asesor de recopilación de ejemplos con el método Real-ORL |
| 3 | Study.mq5 | Asesor | Asesor de entrenamiento de Modelos |
| 4 | StudyEncoder.mq5 | Asesor | Asesor de entrenamiento del Codificador |
| 5 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 6 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema. |
| 7 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 8 | NeuroNet.cl | Biblioteca | Biblioteca de código de programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/15156
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Introducción a MQL5 (Parte 8): Guía del trading algorítmico para principiantes (II)
Introducción a MQL5 (Parte 8): Guía del trading algorítmico para principiantes (II)
 Del básico al intermedio: Operadores
Del básico al intermedio: Operadores
 Aprendizaje automático y Data Science (Parte 26): La batalla definitiva en la previsión de series temporales: redes neuronales LSTM frente a GRU
Aprendizaje automático y Data Science (Parte 26): La batalla definitiva en la previsión de series temporales: redes neuronales LSTM frente a GRU
 Del básico al intermedio: Variables (III)
Del básico al intermedio: Variables (III)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso