Neuronale Netze leicht gemacht (Teil 96): Mehrskalige Merkmalsextraktion (MSFformer)

Einführung

Zeitreihendaten sind in der realen Welt weit verbreitet und spielen in verschiedenen Bereichen, darunter auch im Finanzwesen, eine wichtige Rolle. Diese Daten stellen Sequenzen von Beobachtungen dar, die zu verschiedenen Zeitpunkten gesammelt wurden. Tiefgreifende Zeitreihenanalysen und -modelle ermöglichen es den Forschern, künftige Trends und Muster vorherzusagen, die dann in den Entscheidungsprozess einfließen.

In den letzten Jahren haben viele Forscher ihre Bemühungen auf die Untersuchung von Zeitreihen mit Hilfe von Deep-Learning-Modellen konzentriert. Diese Methoden haben sich bei der Erfassung nichtlinearer Beziehungen und der Handhabung langfristiger Abhängigkeiten bewährt, was besonders bei der Modellierung komplexer Systeme von Nutzen ist. Trotz bedeutender Erfolge stellt sich jedoch immer noch die Frage, wie langfristige Abhängigkeiten und kurzfristige Merkmale effizient extrahiert und integriert werden können. Das Verständnis und die richtige Kombination dieser beiden Arten von Abhängigkeiten ist entscheidend für die Erstellung genauer und zuverlässiger Vorhersagemodelle.

Eine der Möglichkeiten, dieses Problem zu lösen, wurde in dem Papier „Time Series Prediction Based on Multi-Scale Feature Extraction“. Der Beitrag stellt ein Zeitreihenvorhersagemodell MSFformer (Multi-Scale Feature Transformer) vor, das auf einer verbesserten pyramidalen Aufmerksamkeitsarchitektur basiert. Dieses Modell ist für die effiziente Extraktion und Integration von Merkmalen mit mehreren Maßstäben konzipiert.

Die Autoren der Methode heben die folgenden Innovationen von MSFformer hervor:

• Einführung des Mechanismus Skip-PAM, der es dem Modell ermöglicht, sowohl langfristige als auch kurzfristige Merkmale in langen Zeitreihen effektiv zu erfassen.
• Verbessertes Modul CSCM zur Erstellung einer Pyramiden-Datenstruktur.

Die Autoren von MSFformer präsentierten experimentelle Ergebnisse zu drei Zeitreihendatensätzen, die die überlegene Leistung des vorgeschlagenen Modells belegen. Die vorgeschlagenen Mechanismen ermöglichen es dem Modell MSFformer, komplexe Zeitreihendaten genauer und effizienter zu verarbeiten und eine hohe Prognosegenauigkeit und -zuverlässigkeit zu gewährleisten.

1. Der Algorithmus MSFformer

Die Autoren des Modells MSFformer schlagen eine innovative Architektur des pyramidalen Aufmerksamkeitsmechanismus in verschiedenen Zeitintervallen vor, die ihrer Methode zugrunde liegt. Um mehrstufige, zeitliche Informationen in den Eingabedaten zu konstruieren, verwenden sie außerdem die Merkmalsfaltung im großräumigen Konstruktionsmodul CSCM (Coarser-Scale Construction Module). Dies ermöglicht es ihnen, zeitliche Informationen auf einer gröberen Ebene zu extrahieren.

Das Modul CSCM konstruiert einen Baum von Merkmalen der analysierten Zeitreihen. Hier werden die Eingaben zunächst durch eine voll verknüpfte Schicht geleitet, um die Dimensionalität der Merkmale auf eine feste Größe zu transformieren. Dann werden mehrere aufeinander folgende, speziell entwickelte FCNN-Merkmalsfaltungsblöcke verwendet.

Im Block FCNN werden zunächst Merkmalsvektoren gebildet, indem Daten aus der Eingabesequenz unter Verwendung eines bestimmten Kreuzschritts extrahiert werden. Diese Vektoren werden dann kombiniert. Die kombinierten Vektoren werden dann einer Faltungsoperation unterzogen. Die Visualisierung des Blocks FCNN durch den Autor ist unten dargestellt.

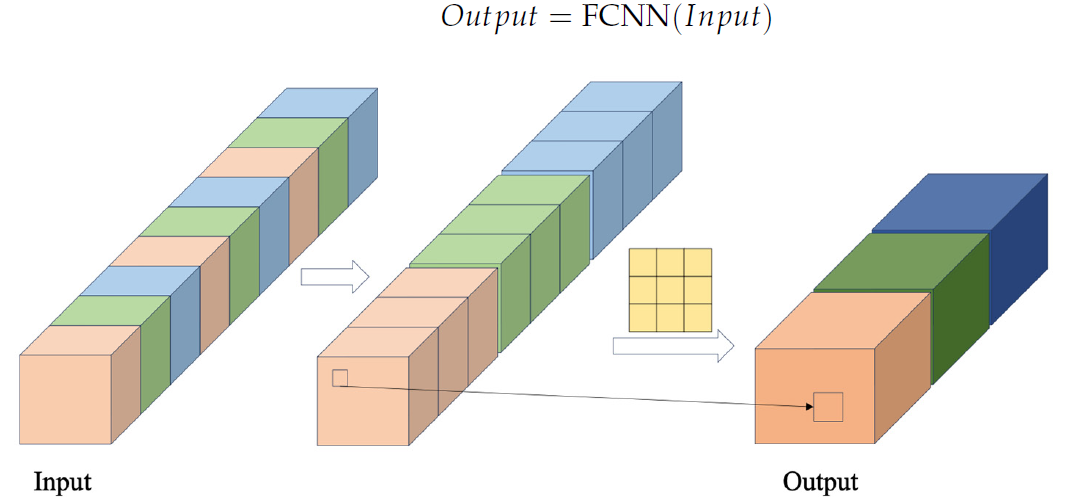
Das von den Autoren vorgeschlagene Modul CSCM verwendet mehrere aufeinanderfolgende FCNN-Blöcke. Jeder dieser Blöcke verwendet die Ergebnisse des vorhergehenden Blocks als Eingabe und extrahiert Merkmale in größerem Umfang.

Die auf diese Weise gewonnenen Merkmale verschiedener Maßstäbe werden zu einem einzigen Vektor kombiniert, dessen Größe durch eine lineare Schicht auf den Maßstab der Eingabedaten reduziert wird.

Im Folgenden wird die Visualisierung des Moduls CSCM durch den Autor vorgestellt.

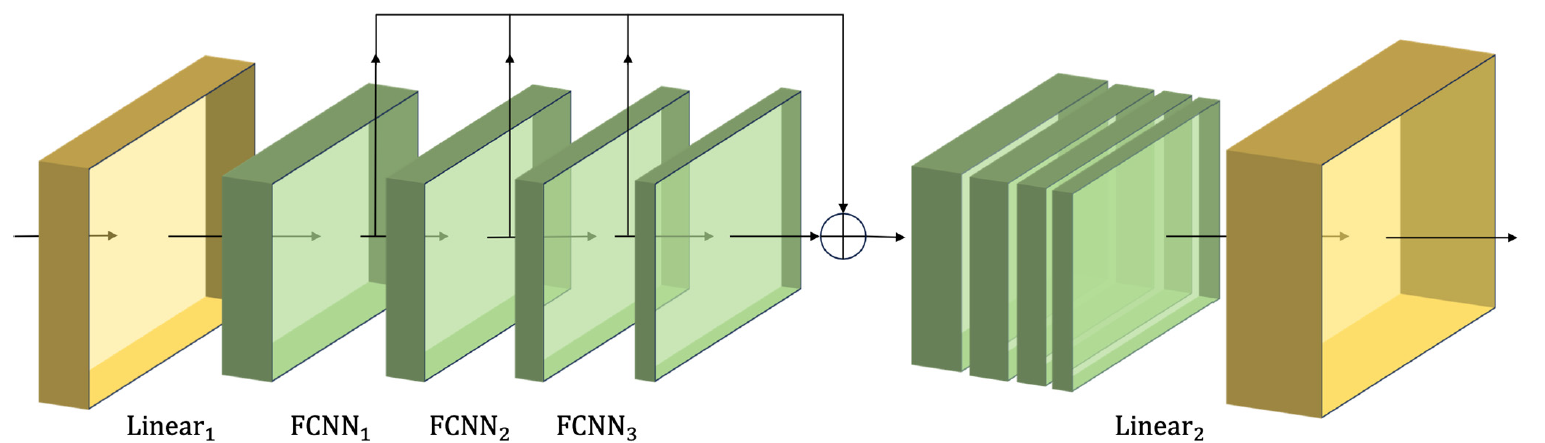
Indem wir die Daten der analysierten Zeitreihen durch ein solches CSCM leiten, erhalten wir zeitliche Informationen über Merkmale auf verschiedenen Granularitätsebenen. Wir bauen einen pyramidenförmigen Baum von Merkmalen auf, indem wir Schichten von FCNN stapeln. Dies ermöglicht es uns, die Daten auf mehreren Ebenen zu verstehen und bietet eine solide Grundlage für die Implementierung der innovativen pyramidalen Aufmerksamkeitsstruktur Skip-PAM (Skip-Pyramidal Attention Module).

Der Grundgedanke von Skip-PAM besteht darin, die Eingabedaten in verschiedenen Zeitintervallen zu verarbeiten, wodurch das Modell zeitliche Abhängigkeiten auf verschiedenen Granularitätsebenen erfassen kann. Auf niedrigeren Ebenen kann sich das Modell auf kurzfristige, detaillierte Muster konzentrieren. Die oberen Ebenen sind in der Lage, mehr makroskopische Trends und Periodizitäten zu erfassen. Das vorgeschlagene Skip-PAM berücksichtigt eher periodische Abhängigkeiten wie z.B. jeden Montag oder jeden Monatsanfang. Dieser mehrskalige Ansatz ermöglicht es dem Modell, eine Vielzahl von zeitlichen Beziehungen auf verschiedenen Ebenen zu erfassen.

Skip-PAM extrahiert Informationen aus Zeitreihen auf verschiedenen Ebenen durch einen Aufmerksamkeitsmechanismus, der auf einem zeitlichen Merkmalsbaum aufbaut. Dieser Prozess umfasst Verbindungen innerhalb und zwischen den Skalen. Intra-Skalen-Verbindungen beinhalten die Durchführung von Aufmerksamkeitsberechnungen zwischen einem Knoten und seinen Nachbarknoten in derselben Schicht. Skalenübergreifende Verbindungen beinhalten Aufmerksamkeitsberechnungen zwischen einem Knoten und seinem übergeordneten Knoten.

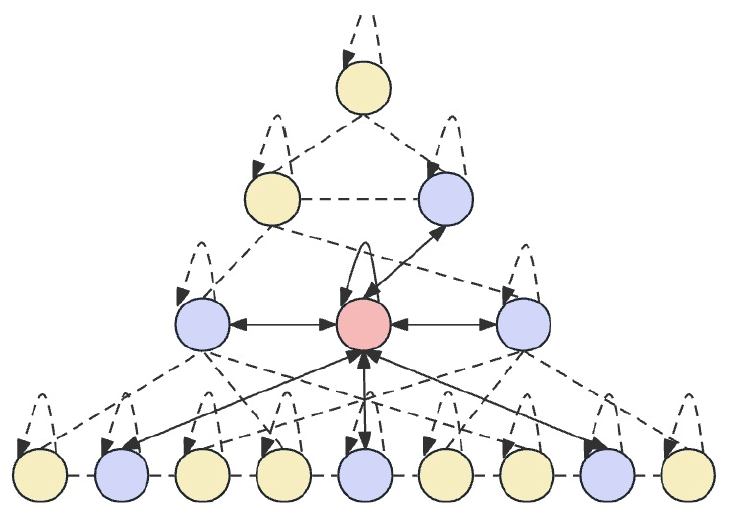
Durch diesen pyramidalen Aufmerksamkeitsmechanismus Skip-PAM in Kombination mit der multiskaligen Merkmalsfaltung in CSCM wird ein leistungsfähiges Merkmalsextraktionsnetzwerk gebildet, das sich an dynamische Veränderungen auf verschiedenen Zeitebenen anpassen kann, seien es kurzfristige Schwankungen oder langfristige Entwicklungen.

Die Autoren der Methode kombinieren die beiden oben beschriebenen Module zu einem leistungsstarken MSFformer-Modell. Die ursprüngliche Visualisierung ist unten dargestellt.

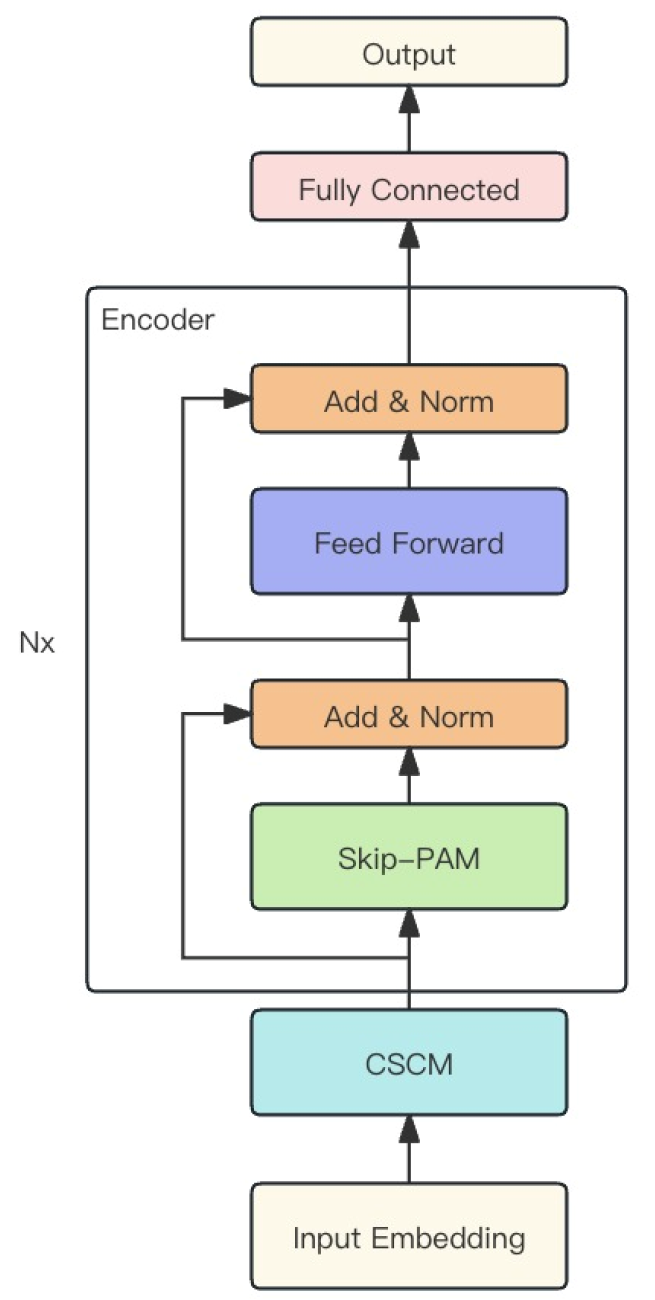
2. Implementierung in MQL5

Nach der Betrachtung der theoretischen Aspekte der Methode MSFformer gehen wir zum praktischen Teil unseres Artikels über, in dem wir unsere Vision der vorgeschlagenen Ansätze mit MQL5 umsetzen.

Wie bereits erwähnt, basiert die vorgeschlagene Methode MSFformer auf 2 Modulen: CSCM und Skip-PAM. Wir werden sie im Rahmen dieses Artikels umsetzen. Es gibt eine Menge Arbeit zu tun. Unterteilen wir sie in 2 Teile, je nach den zu implementierenden Modulen.

2.1. Aufbau des Moduls CSCM

Beginnen wir mit dem Aufbau des ModulsCSCM. Um die Architektur dieses Moduls zu implementieren, erstellen wir die Klasse CNeuronCSCMOCL, die die Hauptfunktionalität von der Basisklasse CNeuronBaseOCL der neuronalen Schicht erbt. Die Struktur der neuen Klasse ist unten dargestellt.

class CNeuronCSCMOCL :  public CNeuronBaseOCL
  {
protected:
   uint              i_Count;
   uint              i_Variables;
   bool              b_NeedTranspose;
   //---
   CArrayInt         ia_Windows;
   CArrayObj         caTranspose;
   CArrayObj         caConvolutions;
   CArrayObj         caMLP;
   CArrayObj         caTemp;
   CArrayObj         caConvOutputs;
   CArrayObj         caConvGradients;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronCSCMOCL(void) {};
                    ~CNeuronCSCMOCL(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint &windows[], uint variables, uint inputs_count, 
                          bool need_transpose, ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronCSCMOCL;   }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

Die vorgestellte Struktur der Klasse CNeuronCSCMOCL verfügt über eine Reihe von Standardmethoden, die überschrieben werden können, sowie über eine große Anzahl von dynamischen Arrays, die uns bei der Organisation einer mehrstufigen Merkmalsextraktionsstruktur helfen werden. Der Zweck von dynamischen Arrays und deklarierten Variablen wird während der Implementierung der Methode erklärt.

Alle Objekte der Klasse werden als statisch deklariert. So können wir den Konstruktor und den Destruktor der Klasse „leer“ lassen. Alle verschachtelten Objekte und Variablen werden in der Methode Init initialisiert.

Wie üblich erhalten wir in den Parametern der Methode Init die grundlegenden Konstanten, mit denen wir die Architektur des zu erstellenden Objekts eindeutig bestimmen können.

Um dem Nutzer die Flexibilität zu geben, die Anzahl der Merkmalsextraktionsschichten und die Größe des Faltungsfensters zu bestimmen, verwenden wir ein dynamisches Array der Fenster. Die Anzahl der Elemente im Array gibt die Anzahl der zu erstellenden FCNN-Merkmalsextraktionsblöcke an. Der Wert der einzelnen Elemente gibt die Größe des Faltungsfensters des entsprechenden Blocks an.

Die Anzahl der unitären Zeitsequenzen in der multidimensionalen Eingabezeitreihe und die Größe der ursprünglichen Sequenz werden in den Parametern variables und inputs_count angegeben.

Außerdem fügen wir eine logische Variable need_transpose hinzu, die angibt, ob die Eingaben vor der Merkmalsextraktion transponiert werden müssen.

bool CNeuronCSCMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint &windows[], uint variables, uint inputs_count, bool need_transpose, 
                          ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   const uint layers = windows.Size();
   if(layers <= 0)
      return false;
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, inputs_count * variables, optimization_type, batch))
      return false;

Im Hauptteil der Methode implementieren wir einen kleinen Kontrollblock. Hier prüfen wir zunächst, ob es notwendig ist, mindestens einen Merkmalsextraktionsblock zu erstellen. Danach rufen wir die gleichnamige Methode der Elternklasse auf, in der ein Teil der Kontrollfunktionen und die Initialisierung der geerbten Objekte bereits implementiert sind. Wir kontrollieren das Ergebnis der Ausführung von Operationen der übergeordneten Klassenmethode durch den zurückgegebenen logischen Wert.

Im nächsten Schritt speichern wir die empfangenen Parameter in den entsprechenden internen Variablen und Arrays.

   if(!ia_Windows.AssignArray(windows))
      return false;
   i_Variables = variables;
   i_Count = inputs_count / ia_Windows[0];
   b_NeedTranspose = need_transpose;

Danach beginnen wir mit der Initialisierung der verschachtelten Objekte. Wenn die Eingabedaten transponiert werden müssen, erstellen wir hier 2 verschachtelte Datentranspositionsebenen. Die erste dient der Transposition der Eingabedaten.

   if(b_NeedTranspose)
     {
      CNeuronTransposeOCL *transp = new CNeuronTransposeOCL();
      if(!transp)
         return false;
      if(!transp.Init(0, 0, OpenCL, inputs_count, i_Variables, optimization, iBatch))
        {
         delete transp;
         return false;
        }
      if(!caTranspose.Add(transp))
        {
         delete transp;
         return false;
        }

Die zweite ist für die Transponierung der Ausgänge, um sie in die Dimension der Eingänge zurückzuführen.

      transp = new CNeuronTransposeOCL();
      if(!transp)
         return false;
      if(!transp.Init(0, 1, OpenCL, i_Variables, inputs_count, optimization, iBatch))
        {
         delete transp;
         return false;
        }
      if(!caTranspose.Add(transp))
        {
         delete transp;
         return false;
        }
      if(!SetOutput(transp.getOutput()) ||
         !SetGradient(transp.getGradient())
        )
         return false;
     }

Wenn wir Daten transponieren müssen, überschreiben wir die Ergebnis- und Gradientenpuffer unserer Klasse mit den entsprechenden Puffern der Ergebnistranspositionsebene. Dieser Schritt ermöglicht es uns, unnötige Datenkopiervorgänge zu vermeiden.

Dann erstellen wir eine Schicht, um die Größe der Eingabedaten innerhalb der einzelnen, unitären Sequenzen anzugleichen.

   uint total = ia_Windows[0] * i_Count;
   CNeuronConvOCL *conv = new CNeuronConvOCL();
   if(!conv.Init(0, 0, OpenCL, inputs_count, inputs_count, total, 1, i_Variables, optimization, iBatch))
     {
      delete conv;
      return false;
     }
   if(!caConvolutions.Add(conv))
     {
      delete conv;
      return false;
     }

In einer Schleife erstellen wir die erforderliche Anzahl von Faltungsschichten zur Merkmalsextraktion.

   total = 0;
   for(uint i = 0; i < layers; i++)
     {
      conv = new CNeuronConvOCL();
      if(!conv.Init(0, i + 1, OpenCL, ia_Windows[i], ia_Windows[i], 
                    (i < (layers - 1) ? ia_Windows[i + 1] : 1), 
                    i_Count, i_Variables, optimization, iBatch))
        {
         delete conv;
         return false;
        }
      if(!caConvolutions.Add(conv))
        {
         delete conv;
         return false;
        }
      if(!caConvOutputs.Add(conv.getOutput()) ||
         !caConvGradients.Add(conv.getGradient())
        )
         return false;
      total += conv.Neurons();
     }

Beachten Sie, dass wir im Array caConvolutions die Schicht zur Anpassung der Eingangsdatengröße und die Faltungsschicht zur Merkmalsextraktion kombinieren. Er enthält daher ein Objekt mehr als die angegebene Anzahl von FCNN-Blöcken.

In Übereinstimmung mit dem Algorithmus des CSCM-Moduls müssen wir die Merkmale aller analysierten Skalen zu einem einzigen Tensor zusammenfügen. Daher berechnen wir zusammen mit der Erstellung von Faltungsschichten die Gesamtgröße des entsprechenden Ausgabentensors. Darüber hinaus haben wir Zeiger auf die Ausgabedatenpuffer und Fehlergradienten der erstellten Merkmalsextraktionsschichten in separaten dynamischen Arrays gespeichert. Dies ermöglicht einen schnelleren Zugriff auf ihre Inhalte während der Modellschulung und des Betriebs.

Jetzt, da wir den Wert haben, den wir brauchen, können wir eine Ebene erstellen, um den verketteten Tensor zu schreiben.

   CNeuronBaseOCL *comul = new CNeuronBaseOCL();
   if(!comul.Init(0, 0, OpenCL, total, optimization, iBatch))
     {
      delete comul;
      return false;
     }
   if(!caMLP.Add(comul))
     {
      delete comul;
      return false;
     }

Hier bieten wir auch einen Sonderfall für die Erstellung von 1 Merkmalsextraktionsschicht an. In diesem Fall haben wir nichts zu kombinieren, und der verkettete Tensor ist eine vollständige Kopie des einzelnen Merkmalsextraktionstensors. Um unnötige Kopiervorgänge zu vermeiden, definieren wir daher die Ergebnis- und Fehlergradientenpuffer neu.

   if(layers == 1)
     {
      comul.SetOutput(conv.getOutput());
      comul.SetGradient(conv.getGradient());
     }

Danach erstellen wir eine Schicht zur linearen Anpassung der Dimension des verketteten Merkmalstensors an die Größe der Eingabesequenz.

   conv = new CNeuronConvOCL();
   if(!conv.Init(0, 0, OpenCL, total / i_Variables, total / i_Variables, inputs_count, 1, 
                                                        i_Variables, optimization, iBatch))
     {
      delete conv;
      return false;
     }
   if(!caMLP.Add(conv))
     {
      delete conv;
      return false;
     }

Wir haben die Eingabe- und Ergebnispuffer unserer Klasse für den Fall überschrieben, dass wir die Eingabedaten transponieren müssen. Für einen anderen Fall werden wir sie jetzt außer Kraft setzen.

   if(!b_NeedTranspose)
     {
      if(!SetOutput(conv.getOutput()) ||
         !SetGradient(conv.getGradient())
        )
         return false;
     }

Auf diese Weise konnten wir in beiden Fällen unnötige Datenkopiervorgänge vermeiden, unabhängig davon, ob die Eingabedaten transponiert werden müssen oder nicht.

Am Ende der Methode erstellen wir 3 Hilfspuffer für die Speicherung von Zwischendaten, die wir bei der Verkettung von Merkmalen und der Entkettung der entsprechenden Fehlergradienten verwenden werden.

   CBufferFloat *buf = new CBufferFloat();
   if(!buf)
      return false;
   if(!buf.BufferInit(total, 0) || !buf.BufferCreate(OpenCL) ||
      !caTemp.Add(buf))
     {
      delete buf;
      return false;
     }
   buf = new CBufferFloat();
   if(!buf)
      return false;
   if(!buf.BufferInit(total, 0) || !buf.BufferCreate(OpenCL) ||
      !caTemp.Add(buf))
     {
      delete buf;
      return false;
     }
   buf = new CBufferFloat();
   if(!buf)
      return false;
   if(!buf.BufferInit(total, 0) || !buf.BufferCreate(OpenCL) ||
      !caTemp.Add(buf))
     {
      delete buf;
      return false;
     }
//---
   caConvOutputs.FreeMode(false);
   caConvGradients.FreeMode(false);
//---
   return true;
  }

Vergessen Sie nicht, den Prozess der Erstellung aller verschachtelten Objekte zu kontrollieren. Nach erfolgreicher Initialisierung aller verschachtelten Objekte geben wir das logische Ergebnis der Operationen an den Aufrufer zurück.

Nach der Initialisierung des Objekts unserer Klasse CNeuronCSCMOCL fahren wir mit der Erstellung des Algorithmus für den Vorwärtsdurchgang fort. Bitte beachten Sie, dass wir im Rahmen dieser Klasse keine Operationen auf der OpenCL-Programmseite implementieren. Die gesamte Implementierung basiert auf der Verwendung von verschachtelten Objektmethoden. Ihr Algorithmus ist bereits auf der Seite von OpenCL implementiert. In solchen Fällen brauchen wir nur einen High-Level-Algorithmus aus den Methoden der verschachtelten Objekte zu erstellen und von der übergeordneten Klasse zu erben.

Wir organisieren den Vorwärtsdurchlauf in der Methode FeedForward, in deren Parametern das aufrufende Programm einen Zeiger auf das Objekt der vorherigen Schicht bereitstellt.

bool CNeuronCSCMOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   CNeuronBaseOCL *inp = NeuronOCL;
   CNeuronBaseOCL *current = NULL;

Im Hauptteil der Methode werden 2 Variablen deklariert, um Zeiger auf Objekte der neuronalen Schicht zu speichern. In diesem Stadium übergeben wir den vom aufrufenden Programm erhaltenen Zeiger an die Quelldatenvariable. Und die zweite Variable lassen wir leer.

Als Nächstes wird geprüft, ob die Eingabedaten transponiert werden müssen. Falls erforderlich, führen wir diese Operation durch.

   if(b_NeedTranspose)
     {
      current = caTranspose.At(0);
      if(!current ||
         !current.FeedForward(inp))
         return false;
      inp = current;
     }

Danach wird die Eingabezeitreihe durch aufeinanderfolgende Faltungsschichten mit unterschiedlichen Skalen geleitet, deren Zeiger im Array caConvolutions gespeichert werden.

   int layers = caConvolutions.Total() - 1;
   for(int l = 0; l <= layers; l++)
     {
      current = caConvolutions.At(l);
      if(!current ||
         !current.FeedForward(inp))
         return false;
      inp = current;
     }

Die erste Schicht in diesem Array dient dazu, die Größe der Eingabedatenfolge anzupassen. Wir verwenden das Ergebnis nicht bei der Verkettung der extrahierten Merkmale, die wir in der nächsten Phase durchführen werden.

Bitte beachten Sie, dass wir einen Algorithmus entwickeln, ohne die Obergrenze der Faltungsebenen für die Merkmalsextraktion zu begrenzen. In diesem Fall ist sogar ein Minimum von einer Schicht der Merkmalsextraktion zulässig. Der einfachste Algorithmus, den wir in diesem Fall verwenden können, ist die Erstellung einer Schleife mit sequentieller Addition von einem Eigenschafts-Array zum Tensor. Dieser Ansatz führt jedoch dazu, dass dieselben Daten möglicherweise mehrfach kopiert werden. Dadurch erhöht sich der Rechenaufwand beim Vorwärtsdurchgang erheblich. Um solche Operationen zu minimieren, haben wir einen Verzweigungsalgorithmus entwickelt, der auf der Anzahl der Merkmalsextraktionsblöcke basiert.

Wie bereits erwähnt, muss es mindestens eine Merkmalsextraktionsschicht geben. Ist sie nicht vorhanden, geben wir ein Fehlersignal in Form eines negativen Ergebnisses an das aufrufende Programm zurück.

   current = caMLP.At(0);
   if(!current)
      return false;
   switch(layers)
     {
      case 0:
         return false;

Bei der Verwendung einer einzigen Merkmalsextraktionsschicht gibt es nichts zu verketten. Wie Sie sich erinnern, haben wir in diesem Fall in der Klasseninitialisierungsmethode die Datenpuffer der Merkmalsextraktions- und Verkettungsschichten neu definiert, wodurch wir unnötige Kopiervorgänge reduzieren konnten. Wir gehen also einfach zu den nächsten Vorgängen über.

      case 1:
         break;

Das Vorhandensein von 2 bis 4 Merkmalsextraktionsschichten führt zur Wahl einer geeigneten Datenverkettungsmethode.

      case 2:
         if(!Concat(caConvOutputs.At(0),
                    caConvOutputs.At(1),
                    current.getOutput(),
                    ia_Windows[1], 1,
                    i_Variables * i_Count))
            return false;
         break;
      case 3:
         if(!Concat(caConvOutputs.At(0),
                    caConvOutputs.At(1),
                    caConvOutputs.At(2),
                    current.getOutput(),
                    ia_Windows[1], ia_Windows[2], 1,
                    i_Variables * i_Count))
            return false;
         break;
      case 4:
         if(!Concat(caConvOutputs.At(0),
                    caConvOutputs.At(1),
                    caConvOutputs.At(2),
                    caConvOutputs.At(3),
                    current.getOutput(),
                    ia_Windows[1], ia_Windows[2], ia_Windows[3], 1,
                    i_Variables * i_Count))
            return false;

Wenn es mehr solcher Ebenen gibt, werden die ersten 4 Ebenen der Merkmalsextraktion miteinander verknüpft, das Ergebnis wird jedoch in einen Zwischenspeicher geschrieben.

      default:
         if(!Concat(caConvOutputs.At(0),
                    caConvOutputs.At(1),
                    caConvOutputs.At(2),
                    caConvOutputs.At(3),
                    caTemp.At(0),
                    ia_Windows[1], ia_Windows[2], ia_Windows[3], ia_Windows[4],
                    i_Variables * i_Count))
            return false;
         break;
     }

Beachten Sie, dass wir bei der Durchführung von Verkettungsoperationen nicht auf die Objekte der Faltungsschichten aus dem Array caConvolutions zugreifen, sondern direkt auf die Puffer ihrer Ergebnisse, deren Zeiger wir vorsichtshalber in dem dynamischen Array caConvOutputs gespeichert haben.

Als Nächstes wird eine Schleife erstellt, die mit der 4. Schicht der Merkmalsextraktion beginnt und in 3 Schichten fortschreitet. Im Hauptteil dieser Schleife wird zunächst die Größe des im temporären Puffer gespeicherten Datenfensters berechnet.

   uint last_buf = 0;
   for(int i = 4; i < layers; i += 3)
     {
      uint buf_size = 0;
      for(int j = 1; j <= i; j++)
         buf_size += ia_Windows[j];

Dann organisieren wir einen Algorithmus für die Auswahl einer Verkettungsfunktion ähnlich dem oben genannten. In diesem Fall steht jedoch der temporäre Puffer mit den zuvor gesammelten Daten immer an erster Stelle, und der nächste Stapel von extrahierten Merkmalen wird diesem hinzugefügt.

      switch(layers - i)
        {
         case 1:
            if(!Concat(caTemp.At(last_buf),
                       caConvOutputs.At(i),
                       current.getOutput(),
                       buf_size, 1,
                       i_Variables * i_Count))
               return false;
            break;
         case 2:
            if(!Concat(caTemp.At(last_buf),
                       caConvOutputs.At(i),
                       caConvOutputs.At(i + 1),
                       current.getOutput(),
                       buf_size, ia_Windows[i + 1], 1,
                       i_Variables * i_Count))
               return false;
            break;
         case 3:
            if(!Concat(caTemp.At(last_buf),
                       caConvOutputs.At(i),
                       caConvOutputs.At(i + 1),
                       caConvOutputs.At(i + 2),
                       current.getOutput(),
                       buf_size, ia_Windows[i + 1], ia_Windows[i + 2], 1,
                       i_Variables * i_Count))
               return false;
            break;
         default:
            if(!Concat(caTemp.At(last_buf),
                       caConvOutputs.At(i),
                       caConvOutputs.At(i + 1),
                       caConvOutputs.At(i + 2),
                       caTemp.At((last_buf + 1) % 2),
                       buf_size, ia_Windows[i + 1], ia_Windows[i + 2], ia_Windows[i + 3],
                       i_Variables * i_Count))
               return false;
            break;
        }
      last_buf = (last_buf + 1) % 2;
     }

Beachten Sie, dass beim Hinzufügen der letzten Merkmalsschichten (1 bis 3) das Ergebnis der Operation im Puffer der Datenverkettungsschicht gespeichert wird. In anderen Fällen verwenden wir einen anderen Puffer für die vorübergehende Speicherung von Daten. Bei jeder Iteration der Schleife werden die Puffer gewechselt, um Datenbeschädigungen und -verluste zu vermeiden.

Nach der Verkettung aller Merkmale zu einem einzigen Tensor müssen wir nur noch die Größe des Ergebnistensors anpassen.

   inp = current;
   current = caMLP.At(1);
   if(!current ||
      !current.FeedForward(inp))
      return false;

Falls erforderlich, transponieren wir sie in die Dimension der Eingabedaten.

   if(b_NeedTranspose)
     {
      inp = current;
      current = caTranspose.At(1);
      if(!current ||
         !current.FeedForward(inp))
         return false;
     }
//---
   return true;
  }

Ich möchte Sie daran erinnern, dass wir in der Initialisierungsmethode die Ersetzung von Datenpuffern organisiert haben. Daher werden die Ergebnisse von Operationen „automatisch“ in den entsprechenden geerbten Puffer unserer Klasse kopiert.

Nach der Konstruktion der Methode für den Vorwärtsdurchgang gehen wir zur Implementierung der Algorithmen für den Rückwärtsdurchgang über. Zunächst erstellen wir eine Methode zur Weitergabe des Fehlergradienten an alle Objekte, je nach ihrem Einfluss auf das Gesamtergebnis (calcInputGradients). Wie üblich, erhalten wir in den Parametern dieser Methode einen Zeiger auf das Objekt der vorherigen neuronalen Schicht. In diesem Fall müssen wir den entsprechenden Anteil des Fehlergradienten an ihn weitergeben.

bool CNeuronCSCMOCL::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
   if(!prevLayer)
      return false;

Im Hauptteil der Methode wird sofort die Relevanz des empfangenen Zeigers geprüft. Danach erstellen wir lokale Zeiger von 2 neuronalen Schichten, mit denen wir nacheinander arbeiten werden.

   CNeuronBaseOCL *current = caMLP.At(0);
   CNeuronBaseOCL *next = caMLP.At(1);

Ich möchte daran erinnern, dass wir uns bei der Verteilung des Fehlergradienten den Algorithmus des Vorwärtsdurchgangs verwenden, allerdings in umgekehrter Richtung. Daher propagieren wir den Gradienten zunächst durch eine Datentranspositionsebene, natürlich nur, wenn ein solcher Vorgang erforderlich ist.

   if(b_NeedTranspose)
     {
      if(!next.calcHiddenGradients(caTranspose.At(1)))
         return false;
     }

Anschließend speisen wir den Fehlergradienten in die verkettete Schicht der extrahierten Merkmale verschiedener Skalen ein.

   if(!current.calcHiddenGradients(next.AsObject()))
      return false;
   next = current;

Danach müssen wir den Fehlergradienten auf die entsprechenden Merkmalsextraktionsschichten verteilen.

Vergessen wir nicht den Sonderfall, dass es nur eine Merkmalsextraktionsschicht gibt. Hier müssen wir nur den Fehlergradienten durch die Ableitung der Aktivierungsfunktion anpassen.

   int layers = caConvGradients.Total();
   if(layers == 1)
     {
      next = caConvolutions.At(1);
      if(next.Activation() != None)
        {
         if(!DeActivation(next.getOutput(), next.getGradient(), next.getGradient(), next.Activation()))
            return false;
        }
     }

Im Allgemeinen trennen wir zunächst den Fehlergradienten der letzten Merkmalsextraktionsschicht und korrigieren ihn durch die Ableitung der Aktivierungsfunktion.

   else
     {
      int prev_window = 0;
      for(int i = 1; i < layers; i++)
         prev_window += int(ia_Windows[i]);
      if(!DeConcat(caTemp.At(0), caConvGradients.At(layers - 1), next.getGradient(), 
                                              prev_window, 1, i_Variables * i_Count))
         return false;
      next = caConvolutions.At(layers);
      int current_buf = 0;

Danach erstellen wir eine Rückwärtsschleife durch die Ebenen der Merkmalsextraktion. Im Hauptteil dieser Schleife erhalten wir zunächst den Fehlergradienten aus der nachfolgenden Merkmalsextraktionsschicht.

      for(int l = layers; l > 1; l--)
        {
         current = caConvolutions.At(l - 1);
         if(!current.calcHiddenGradients(next.AsObject()))
            return false;

Dann extrahieren wir den Anteil der analysierten Schicht aus dem Puffer der Fehlergradienten des verketteten Merkmalstensors.

         int window = int(ia_Windows[l - 1]);
         prev_window -= window;
         if(!DeConcat(caTemp.At((current_buf + 1) % 2), caTemp.At(2), caTemp.At(current_buf), 
                                                  prev_window, window, i_Variables * i_Count))
            return false;

Wir passen sie an die Ableitung der Aktivierungsfunktion an.

         if(current.Activation() != None)
           {
            if(!DeActivation(current.getOutput(), caTemp.At(2), caTemp.At(2), current.Activation()))
               return false;
           }

Und wir summieren die Fehlergradienten aus den zwei Datenströmen.

         if(!SumAndNormilize(current.getGradient(), caTemp.At(2), current.getGradient(), 1, false, 0, 0, 0, 1))
            return false;
         next = current;
         current_buf = (current_buf + 1) % 2;
        }
     }

Danach fahren wir mit der nächsten Iteration unserer Schleife fort.

Auf diese Weise wird der Fehlergradient auf alle Ebenen der Merkmalsextraktion verteilt. Dann geben wir den Fehlergradienten an die Schicht zur Anpassung der Eingangsdatengröße weiter.

   current = caConvolutions.At(0);
   if(!current.calcHiddenGradients(next.AsObject()))
      return false;
   next = current;

Falls erforderlich, propagieren wir den Fehlergradienten durch eine Datentranspositionsschicht.

   if(b_NeedTranspose)
     {
      current = caTranspose.At(0);
      if(!current.calcHiddenGradients(next.AsObject()))
         return false;
      next = current;
     }

Am Ende der Methodenoperationen übergeben wir den Fehlergradienten an die vorherige neuronale Schicht, deren Zeiger wir in den Parametern dieser Methode erhalten haben.

   if(!prevLayer.calcHiddenGradients(next.AsObject()))
      return false;
//---
   return true;
  }

Wie Sie wissen, ist die Ausbreitung des Fehlergradienten nicht das Ziel der Modellbildung. Sie ist lediglich ein Mittel, um die Richtung und den Umfang der Anpassung der Modellparameter zu bestimmen. Daher müssen wir nach erfolgreicher Ausbreitung des Fehlergradienten die Modellparameter so anpassen, dass der Gesamtfehler der Operation minimiert wird. Diese Funktion ist in der Methode updateInputWeights implementiert.

bool CNeuronCSCMOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   CObject *prev = (b_NeedTranspose ? caTranspose.At(0) : NeuronOCL);
   CNeuronBaseOCL *current = NULL;

In den Methodenparametern erhalten wir, wie zuvor, einen Zeiger auf das Objekt der vorherigen neuronalen Schicht. In diesem Fall prüfen wir jedoch nicht die Relevanz des erhaltenen Indexes. Wir speichern sie einfach in einer lokalen Variablen. Allerdings gibt es hier eine Nuance. Die Datenumsetzungsschicht enthält keine Parameter. Daher wird die Methode der Modellparameteranpassung für sie nicht aufgerufen. Für die Schicht zur Anpassung der Eingabegröße wird jedoch die vorherige Schicht ausgewählt, je nach dem Parameter b_NeedTranspose, der angibt, ob die Eingabedaten transponiert werden müssen.

Als Nächstes organisieren wir eine Schleife zur sequentiellen Anpassung der Parameter der Faltungsschichten, einschließlich einer Schicht zur Anpassung der Größe der ursprünglichen Sequenz und der Merkmalsextraktionsblöcke.

   for(int i = 0; i < caConvolutions.Total(); i++)
     {
      current = caConvolutions.At(1);
      if(!current ||
         !current.UpdateInputWeights(prev)
        )
         return false;
      prev = current;
     }

Als Nächstes müssen wir die Parameter der Ebene zum Ausrichten der Ergebnisgröße anpassen.

   current = caMLP.At(1);
   if(!current ||
      !current.UpdateInputWeights(caMLP.At(0))
     )
      return false;
//---
   return true;
  }

Andere verschachtelte Objekte unserer Klasse CNeuronCSCMOCL enthalten keine trainierbaren Parameter.

An diesem Punkt kann die Implementierung der wichtigsten Algorithmen des Moduls CSCM als abgeschlossen betrachtet werden. Natürlich ist die Funktionalität unserer Klasse ohne zusätzliche Implementierung von Hilfsmethodenalgorithmen nicht vollständig. Um den Umfang des Artikels zu reduzieren, verzichte ich jedoch auf eine Beschreibung. Den vollständigen Code für alle Methoden dieser Klasse finden Sie im Anhang. Der Anhang enthält auch den vollständigen Code für alle im Artikel verwendeten Programme. Und wir machen weiter mit der Entwicklung der Algorithmen des nächsten Moduls - Skip-PAM.

2.2 Implementierung der Algorithmen von Skip-PAM

Der zweite Teil unserer Arbeit besteht darin, den pyramidalen Aufmerksamkeitsalgorithmus zu implementieren. Die Innovation der Autoren der MSFformer-Methode ist die Anwendung von Aufmerksamkeitsalgorithmen auf einen Merkmalsbaum mit unterschiedlichen Intervallen. Die Autoren der Methode verwenden feste Schritte zwischen den Merkmalen innerhalb einer Aufmerksamkeitsebene. Bei unserer Umsetzung werden wir etwas anders vorgehen. Wie wäre es, wenn wir das Modell selbst lernen lassen, welche Merkmale jede einzelne Aufmerksamkeitspyramide auf jeder einzelnen Aufmerksamkeitsebene analysieren wird? Klingt vielversprechend. Auch die Umsetzung ist meiner Meinung nach offensichtlich und einfach. Wir fügen einfach eine S3 Ebene vor jeder Aufmerksamkeitsebene.

Wir werden Algorithmen für unsere Implementierung des Moduls von Skip-PAM innerhalb der Klasse CNeuronSPyrAttentionOCL erstellen. Seine Struktur wird im Folgenden dargestellt.

class CNeuronSPyrAttentionOCL :  public CNeuronBaseOCL
  {
protected:
   uint              iWindowIn;
   uint              iWindowKey;
   uint              iHeads;
   uint              iHeadsKV;
   uint              iCount;
   uint              iPAMLayers;
   //---
   CArrayObj         caS3;
   CArrayObj         caQuery;
   CArrayObj         caKV;
   CArrayInt         caScore;
   CArrayObj         caAttentionOut;
   CArrayObj         caW0;
   CNeuronConvOCL    cFF1;
   CNeuronConvOCL    cFF2;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      AttentionOut(CBufferFloat *q, CBufferFloat *kv, int scores, CBufferFloat *out, int window);
   virtual bool      AttentionInsideGradients(CBufferFloat *q, CBufferFloat *q_g, CBufferFloat *kv, 
                                              CBufferFloat *kv_g, int scores, CBufferFloat *gradient);
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);
   virtual void      ArraySetOpenCL(CArrayObj *array, COpenCLMy *obj);

public:
                     CNeuronSPyrAttentionOCL(void) {};
                    ~CNeuronSPyrAttentionOCL(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window_in, uint window_key, uint heads, uint heads_kv, 
                          uint units_count, uint pam_layers, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronSPyrAttentionMLKV;   }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

Wie Sie aus der dargestellten Struktur ersehen können, enthält die neue Klasse noch mehr dynamische Arrays und Parameter. Ihre Namen stehen im Einklang mit den Objekten der anderen Aufmerksamkeitsklassen. Sie werden verstehen, dass dies mit Absicht geschieht. Wir werden uns mit der Verwendung von erstellten Objekten und Variablen während des Implementierungsprozesses vertraut machen.

Wie bisher beginnen wir unsere Überlegungen zu den Algorithmen der neuen Klasse mit dem Objekt der Initialisierungsmethode Init.

bool CNeuronSPyrAttentionOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                   uint window_in, uint window_key, uint heads,
                                   uint heads_kv, uint units_count, uint pam_layers,
                                   ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_in * units_count, optimization_type, batch))
      return false;

In den Methodenparametern erhalten wir die wichtigsten Konstanten, die die Architektur des zu erstellenden Objekts bestimmen. Im Körper der Methode rufen wir die entsprechende Methode der Elternklasse auf, in der die minimal notwendigen Kontrollen und die Initialisierung der geerbten Objekte implementiert sind.

Zu beachten ist auch, dass im Rahmen dieser Methode einzelne Zeitschritte innerhalb der gesamten multimodalen Zeitsequenz analysiert werden. In diesem Fall ist es jedoch wahrscheinlich schwierig, die in das Modul Skip-PAM eingegebenen Originaldaten als multimodale Zeitreihen zu bezeichnen. Denn die Ergebnisse des vorangegangenen Moduls CSCM stellen keine zeitliche Abfolge, sondern eine Reihe von extrahierten Merkmalen verschiedener Datenskalen dar.

Nach erfolgreicher Ausführung der Initialisierungsmethode der übergeordneten Klassenobjekte speichern wir die erhaltenen Konstanten in lokalen Variablen.

   iWindowIn = window_in;
   iWindowKey = MathMax(window_key, 1);
   iHeads = MathMax(heads, 1);
   iHeadsKV = MathMax(heads_kv, 1);
   iCount = units_count;
   iPAMLayers = MathMax(pam_layers, 2);

Achten Sie auf das Erscheinen eines neuen Parameters iPAMLayers, der die Anzahl der Ebenen der pyramidalen Aufmerksamkeit bestimmt. Die übrigen Parameter haben die gleiche Funktion wie die bereits erwähnten Aufmerksamkeitsmethoden. Wir haben auch den Parameter iHeadsKV beibehalten, um die Möglichkeit zu haben, die Anzahl der Köpfe von Key-Value (Schlüssel-Wert) zu verwenden, die sich von den Dimensionen der Köpfe Query-Attention (Abfrage-Aufmerksamkeit) unterscheiden, wie es in der Methode MLKV berücksichtigt wurde.

Dann löschen wir die dynamischen Arrays.

   caS3.Clear();
   caQuery.Clear();
   caKV.Clear();
   caScore.Clear();
   caAttentionOut.Clear();
   caW0.Clear();

Legen wir die erforderlichen lokalen Variablen an.

   CNeuronBaseOCL *base = NULL;
   CNeuronConvOCL *conv = NULL;
   CNeuronS3      *s3 = NULL;

Wir erstellen die Initialisierungsschleife für die Objekte des pyramidalen Aufmerksamkeitsblocks. Wie Sie sich denken können, ist die Anzahl der Iterationen der Schleife gleich der Anzahl der erzeugten Aufmerksamkeitsstufen.

   for(uint l = 0; l < iPAMLayers; l++)
     {
      //--- S3
      s3 = new CNeuronS3();
      if(!s3)
         return false;
      if(!s3.Init(0, l, OpenCL, iWindowIn, iCount, optimization, iBatch) ||
         !caS3.Add(s3))
         return false;
      s3.SetActivationFunction(None);

Im Hauptteil der Schleife erstellen wir zunächst die Schicht S3, in der die Permutation der analysierten Sequenz organisiert wird. In diesem Fall verwenden wir nur eine Datenmischungsschicht mit einem Fenster, das der Anzahl der analysierten Parameter in der ursprünglichen multimodalen Sequenz entspricht.

Dann erstellen wir die Objekte Query, Key und Value (Abfrage, Schlüssel und Wert) zur Erzeugung von Entitäten. Bitte beachten Sie, dass wir bei der Bildung von Entitäten ein einziges INPUT-Datenobjekt verwenden, aber unterschiedliche Parameter für den Aufmerksamkeitskopf.

      //--- Query
      conv = new CNeuronConvOCL();
      if(!conv)
         return false;
      if(!conv.Init(0, 0, OpenCL, iWindowIn, iWindowIn, iWindowKey*iHeads, iCount, optimization, iBatch) ||
         !caQuery.Add(conv))
        {
         delete conv;
         return false;
        }
      conv.SetActivationFunction(None);
      //--- KV
      conv = new CNeuronConvOCL();
      if(!conv)
         return false;
      if(!conv.Init(0, 0, OpenCL, iWindowIn, iWindowIn, 2*iWindowKey*iHeadsKV, iCount, optimization, iBatch) ||
         !caKV.Add(conv))
        {
         delete conv;
         return false;
        }
      conv.SetActivationFunction(None);

Wir werden die Matrix der Abhängigkeitskoeffizienten nur auf der Kontextseite von OpenCL erstellen. Hier wird nur ein Zeiger auf den Puffer gespeichert.

      //--- Score
      int temp = OpenCL.AddBuffer(sizeof(float) * iCount * iCount * iHeads, CL_MEM_READ_WRITE);
      if(temp < 0)
         return false;
      if(!caScore.Add(temp))
         return false;

Im nächsten Schritt erstellen wir eine Ebene, um die Ergebnisse der mehrköpfigen Aufmerksamkeit zu erfassen.

      //--- MH Attention Out
      base = new CNeuronBaseOCL();
      if(!base)
         return false;
      if(!base.Init(0, 0, OpenCL, iWindowKey * iHeadsKV * iCount, optimization, iBatch) ||
         !caAttentionOut.Add(conv))
        {
         delete base;
         return false;
        }
      base.SetActivationFunction(None);

Die Iterationen der Schleife werden durch eine Ebene der Dimensionalitätsreduktion bis auf die Ebene der Eingabedaten abgeschlossen.

      //--- W0
      conv = new CNeuronConvOCL();
      if(!conv)
         return false;
      if(!conv.Init(0, 0, OpenCL, iWindowKey * iHeadsKV, iWindowKey * iHeadsKV, iWindowIn, iCount, 
                                                                              optimization, iBatch) ||
         !caW0.Add(conv))
        {
         delete conv;
         return false;
        }
      conv.SetActivationFunction(None);
     }

Nach erfolgreichem Abschluss aller Iterationen zur Schaffung pyramidaler Aufmerksamkeitsebenen fügen wir eine Ebene hinzu. Im Puffer dieser Schicht wird die Summe der Ergebnisse des pyramidalen Aufmerksamkeitsblocks und der Eingangsdaten gespeichert.

//--- Residual
   base = new CNeuronBaseOCL();
   if(!base)
      return false;
   if(!base.Init(0, 0, OpenCL, iWindowIn * iCount, optimization, iBatch) ||
      !caW0.Add(conv))
     {
      delete base;
      return false;
     }
   base.SetActivationFunction(None);

Jetzt müssen wir nur noch die Blockebenen der Vorwärtsdurchgänge initialisieren.

//--- FeedForward
   if(!cFF1.Init(0, 0, OpenCL, iWindowIn, iWindowIn, 4 * iWindowIn, iCount, optimization, iBatch))
      return false;
   cFF1.SetActivationFunction(LReLU);
   if(!cFF2.Init(0, 0, OpenCL, 4 * iWindowIn, 4 * iWindowIn, iWindowIn, iCount, optimization, iBatch))
      return false;
   cFF2.SetActivationFunction(None);
   if(!SetGradient(cFF2.getGradient()))
      return false;

Am Ende der Methode entfernen wir zwangsweise die Aktivierungsfunktion unserer Schicht.

   SetActivationFunction(None);
//---
   return true;
  }

Nachdem wir die Objekte unserer Klasse initialisiert haben, gehen wir zur Implementierung der Algorithmen der Vorwärtsdurchgänge über. Hier müssen wir ein wenig Vorarbeit auf der Programmseite von OpenCL leisten. Wir werden einen neuen Kernel MH2PyrAttentionOut erstellen, der im Wesentlichen eine modifizierte Version des Kernels von MH2AttentionOut ist.

__kernel void MH2PyrAttentionOut(__global float *q,
                                 __global float *kv,
                                 __global float *score,
                                 __global float *out,
                                 const int dimension,
                                 const int heads_kv,
                                 const int window
                                )
  {
//--- init
   const int q_id = get_global_id(0);
   const int k = get_global_id(1);
   const int h = get_global_id(2);
   const int qunits = get_global_size(0);
   const int kunits = get_global_size(1);
   const int heads = get_global_size(2);

Neben dem Kernel-Namen unterscheidet er sich von dem vorherigen durch das Vorhandensein eines zusätzlichen Fensterparameters für das Aufmerksamkeitsfenster. Wir planen, den Kernel in einem 3-dimensionalen Aufgabenraum aufzurufen. Wie immer identifizieren wir zu Beginn des Kernels Threads in allen Dimensionen des Aufgabenraums.

Als Nächstes berechnen wir die notwendigen Konstanten.

   const int h_kv = h % heads_kv;
   const int shift_q = dimension * (q_id * heads + h);
   const int shift_k = dimension * (2 *  heads_kv * k + h_kv);
   const int shift_v = dimension * (2 *  heads_kv * k + heads_kv + h_kv);
   const int shift_s = kunits * (q_id *  heads + h) + k;
   const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE);
   const int delta_win = (window + 1) / 2;
   float koef = sqrt((float)dimension);
   if(koef < 1)
      koef = 1;

Wir initialisieren auch ein lokales Array, um Zwischenwerte zu speichern.

   __local float temp[LOCAL_ARRAY_SIZE];

Zunächst müssen wir die Abhängigkeitskoeffizienten für jedes Element der Sequenz bestimmen. Wie Sie wissen, werden im Aufmerksamkeitsblock die Abhängigkeitskoeffizienten durch die Funktion SoftMax normalisiert. Dazu berechnen wir zunächst die Summe der Exponenten der Abhängigkeitskoeffizienten.

In der ersten Phase sammelt jeder Thread seinen Anteil an der Summe der Exponentialwerte in dem entsprechenden Element des lokalen Datenarrays. Bitte beachten Sie den folgenden Zusatz: Wir berechnen die Abhängigkeitskoeffizienten nur innerhalb des Aufmerksamkeitsfensters des aktuellen Elements. Für alle anderen Elemente ist der Abhängigkeitskoeffizient „0“.

//--- sum of exp
   uint count = 0;
   if(k < ls)
      do
        {
         if((count * ls) < (kunits - k))
           {
            float sum = 0;
            if(abs(count * ls + k - q_id) <= delta_win)
              {
               for(int d = 0; d < dimension; d++)
                  sum = q[shift_q + d] * kv[shift_k + d];
               sum = exp(sum / koef);
               if(isnan(sum))
                  sum = 0;
              }
            temp[k] = (count > 0 ? temp[k] : 0) + sum;
           }
         count++;
        }
      while((count * ls + k) < kunits);
   barrier(CLK_LOCAL_MEM_FENCE);

Zur Synchronisierung lokaler Gruppen-Threads wird eine Barriere verwendet.

Im nächsten Schritt müssen wir die Summe der Werte aller Elemente des lokalen Arrays ermitteln. Hierfür erstellen wir eine weitere Schleife, in der wir bei jeder Iteration lokale Threads synchronisieren. Hier müssen Sie darauf achten, dass jeder Thread die gleiche Anzahl von Barrieren besucht. Andernfalls kann es zum „Einfrieren“ einzelner Fäden kommen.

   count = min(ls, (uint)kunits);
//---
   do
     {
      count = (count + 1) / 2;
      if(k < ls)
         temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0);
      if(k + count < ls)
         temp[k + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Nach Bestimmung der Summe der Exponenten können wir die normierten Abhängigkeitskoeffizienten berechnen. Vergessen Sie nicht, dass Abhängigkeiten nur innerhalb des Aufmerksamkeitsfensters vorhanden sind.

//--- score
   float sum = temp[0];
   float sc = 0;
   if(sum != 0 && abs(k - q_id) <= delta_win)
     {
      for(int d = 0; d < dimension; d++)
         sc = q[shift_q + d] * kv[shift_k + d];
      sc = exp(sc / koef) / sum;
      if(isnan(sc))
         sc = 0;
     }
   score[shift_s] = sc;
   barrier(CLK_LOCAL_MEM_FENCE);

Natürlich synchronisieren wir die lokalen Threads nach der Berechnung der Abhängigkeits-Koeffizienten.

Als Nächstes müssen wir den Wert der Elemente unter Berücksichtigung der Abhängigkeiten bestimmen. Hier wird derselbe Algorithmus für die Summierung von Werten in parallelen Threads verwendet wie bei der Ermittlung der Summe von Exponentialwerten von Abhängigkeiten. Zunächst werden die Summen der einzelnen Werte in den Elementen des lokalen Arrays gebildet.

//--- out
   for(int d = 0; d < dimension; d++)
     {
      uint count = 0;
      if(k < ls)
         do
           {
            if((count * ls) < (kunits - k))
              {
               float sum = 0;
               if(abs(count * ls + k - q_id) <= delta_win)
                 {
                  sum = kv[shift_v + d] * (count == 0 ? sc : score[shift_s + count * ls]);
                  if(isnan(sum))
                     sum = 0;
                 }
               temp[k] = (count > 0 ? temp[k] : 0) + sum;
              }
            count++;
           }
         while((count * ls + k) < kunits);
      barrier(CLK_LOCAL_MEM_FENCE);

Und dann wird die Summe der Werte der Array-Elemente gebildet.

      //---
      count = min(ls, (uint)kunits);
      do
        {
         count = (count + 1) / 2;
         if(k < ls)
            temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0);
         if(k + count < ls)
            temp[k + count] = 0;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);
      //---
      out[shift_q + d] = temp[0];
     }
  }

Die sich daraus ergebende Summe wird in dem entsprechenden Element des Ergebnispuffers gespeichert.

Wir haben also einen neuen Aufmerksamkeitskern innerhalb des gegebenen Fensters geschaffen. Bitte beachten Sie, dass wir für Elemente außerhalb des Aufmerksamkeitsfensters die Abhängigkeitskoeffizienten auf „0“ gesetzt haben. Dieser einfache Schritt ermöglicht es uns, den zuvor erstellten Kernel von MH2AttentionInsideGradients zu verwenden, um den Fehlergradienten innerhalb des Rückwärtsdurchgangs zu verteilen.

Um die angegebenen Kernel in die Ausführungswarteschlange auf der Seite des Hauptprogramms zu stellen, habe ich die Methoden AttentionOut und AttentionInsideGradients erstellt. Ihr Algorithmus unterscheidet sich nicht wesentlich von ähnlichen Methoden, die in früheren Artikeln dieser Reihe besprochen wurden, sodass wir jetzt nicht näher darauf eingehen werden. Sie können den Code selbst im Anhang finden. Nun geht es an die Umsetzung der Algorithmen der Methode FeedForward.

In den Parametern erhält die Vorwärtsdurchgangs-Methode einen Zeiger auf das Objekt der vorherigen neuronalen Schicht, das die Eingabedaten enthält.

bool CNeuronSPyrAttentionOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   CNeuronBaseOCL *prev = NeuronOCL;
   CNeuronBaseOCL *current = NULL;
   CBufferFloat   *q = NULL;
   CBufferFloat   *kv = NULL;

Im Hauptteil der Methode erstellen wir eine Reihe von lokalen Variablen, um Zeiger auf die verarbeiteten Objekte der verschachtelten neuronalen Schichten zu speichern.

Als Nächstes erstellen wir eine Schleife durch die Aufmerksamkeitsstufen. Im Hauptteil der Schleife werden zunächst die Quelldaten gemischt.

   for(uint l = 0; l < iPAMLayers; l++)
     {
      //--- Mix
      current = caS3.At(l);
      if(!current ||
         !current.FeedForward(prev.AsObject())
        )
         return false;
      prev = current;

Danach erzeugen wir Tensoren aus den Entitäten Query, Key und Value, um den mehrköpfigen Aufmerksamkeitsalgorithmus zu implementieren.

      //--- Query
      current = caQuery.At(l);
      if(!current ||
         !current.FeedForward(prev.AsObject())
        )
         return false;
      q = current.getOutput();
      //--- Key and Value
      current = caKV.At(l);
      if(!current ||
         !current.FeedForward(prev.AsObject())
        )
         return false;
      kv = current.getOutput();

Wir führen den Algorithmus des Aufmerksamkeits-Kernels für diese Ebene aus.

      //--- PAM
      current = caAttentionOut.At(l);
      if(!current || !AttentionOut(q, kv, caScore.At(l), current.getOutput(), iPAMLayers - l))
         return false;
      prev = current;

Beachten Sie, dass wir auf jeder weiteren Ebene das Aufmerksamkeitsfenster verkleinern, wodurch ein Pyramideneffekt entsteht. Hierfür verwenden wir die Differenz „iPAMLayers - l“.

Am Ende der Schleifeniterationen wird die Größe des mehrköpfigen Aufmerksamkeits-Ergebnissensors auf die Größe der Eingabedaten reduziert. 

      //--- W0
      current = caW0.At(l);
      if(!current ||
         !current.FeedForward(prev.AsObject())
        )
         return false;
      prev = current;
     }

Nachdem wir alle Stufen der pyramidalen Aufmerksamkeit erfolgreich abgeschlossen haben, summieren wir die Ergebnisse der Aufmerksamkeit und normalisieren sie mit den Eingabedaten.

//--- Residual
   current = caW0.At(iPAMLayers);
   if(!SumAndNormilize(NeuronOCL.getOutput(), prev.getOutput(), current.getOutput(), iWindowIn, true))
      return false;

Und der letzte in der pyramidalen Aufmerksamkeitsschicht ist der Vorwärtsdurchgangs-Block, ähnlich dem Vanilla Transformer.

//---FeedForward
   if(!cFF1.FeedForward(current.AsObject()) ||
      !cFF2.FeedForward(cFF1.AsObject())
     )
      return false;

Anschließend werden die Daten aus beiden Threads erneut summiert und normalisiert.

//--- Residual
   if(!SumAndNormilize(current.getOutput(), cFF2.getOutput(), getOutput(), iWindowIn, true))
      return false;
//---
   return true;
  }

Vergessen wir nicht, die Ausführung von Vorgängen zu kontrollieren. Am Ende der Methode geben wir das logische Ergebnis der Operationen an den Aufrufer zurück.

Wie üblich wird nach der Implementierung des Vorwärtsdurchgangs der Algorithmus des Rückwärtsdurchgangs entwickelt, der aus zwei Stufen besteht: Ausbreitung des Fehlergradienten und Optimierung der Modellparameter.

Die Weitergabe von Fehlergradienten ist in der Methode calcInputGradients implementiert.

bool CNeuronSPyrAttentionOCL::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
   if(!prevLayer)
      return false;

In den Parametern dieser Methode erhalten wir einen Zeiger auf das Objekt der vorherigen neuronalen Schicht. In den Puffer dieser Schicht müssen wir den Fehlergradienten entsprechend dem Einfluss der Eingangsdaten auf das Gesamtergebnis übertragen.

Als Nächstes erstellen wir einige lokale Variablen, um Zeiger auf interne Objekte vorübergehend zu speichern.

   CNeuronBaseOCL *next = NULL;
   CNeuronBaseOCL *current = NULL;
   CNeuronBaseOCL *q = NULL;
   CNeuronBaseOCL *kv = NULL;

Die Verteilung der Fehlergradienten erfolgt entsprechend den Operationen des Vorwärtsdurchgangs, jedoch in umgekehrter Reihenfolge. Zunächst propagieren wir den Fehlergradienten durch den FeedForward-Block.

//--- FeedForward
   current = caW0.At(iPAMLayers);
   if(!current ||
      !cFF1.calcHiddenGradients(cFF2.AsObject()) ||
      !current.calcHiddenGradients(cFF1.AsObject())
     )
      return false;
   next = current;

Dann müssen wir die Fehlergradienten aus den 2 Operationsfäden addieren.

//--- Residual
   current = caW0.At(iPAMLayers - 1);
   if(!SumAndNormilize(getGradient(), next.getGradient(), current.getGradient(), iWindowIn, false))
      return false;
   CBufferFloat *residual = next.getGradient();
   next = current;

Danach erstellen wir eine Rückwärtsschleife durch die Aufmerksamkeitsstufen mit einem sequentiellen Fehler-Gradientenabstieg.

   for(int l = int(iPAMLayers - 1); l >= 0; l--)
     {
      //--- W0
      current = caAttentionOut.At(l);
      if(!current ||
         !current.calcHiddenGradients(next.AsObject())
        )
         return false;

Im Hauptteil der Schleife propagieren wir zunächst den Fehlergradienten über die Aufmerksamkeitsköpfe. Dann wird es auf die Ebene von Query, Key und Value übertragen.

      //--- MH Attention
      q = caQuery.At(l);
      kv = caKV.At(l);
      if(!q || !kv ||
         !AttentionInsideGradients(q.getOutput(), q.getGradient(), kv.getOutput(), kv.getGradient(), 
                                                                   caScore.At(l), current.getGradient())
        )
         return false;

Der nächste Schritt ist die Weitergabe des Fehlergradienten an die Datenumlagerungsschicht. Hier müssen wir Daten aus den beiden Threads - Query und Key-Value - kombinieren. Dazu erhalten wir zunächst den Fehlergradienten aus Query und übertragen ihn in einen temporären Puffer.

      //--- Query
      current = caS3.At(l);
      if(!current ||
         !current.calcHiddenGradients(q.AsObject()) ||
         !Concat(current.getGradient(), current.getGradient(), residual, iWindowIn,0, iCount)
        )
         return false;

Dann nehmen wir den Gradienten von Key-Value und summieren die Ergebnisse der 2 Daten-Threads.

      //--- Key and Value
      if(!current ||
         !current.calcHiddenGradients(kv.AsObject()) ||
         !SumAndNormilize(current.getGradient(), residual, current.getGradient(), iWindowIn, false)
        )
         return false;
      next = current;

Wir propagieren den Fehlergradienten durch die Datenumlagerungsschicht und gehen zur nächsten Iteration der Schleife über.

      //--- S3
      current = (l == 0 ? prevLayer : caW0.At(l - 1));
      if(!current ||
         !current.calcHiddenGradients(next.AsObject())
        )
         return false;
      next = current;
     }

Am Ende der Methodenoperationen müssen wir nur noch den Fehlergradienten aus den beiden Threads kombinieren. Hier wird zunächst der Fehlergradient der Restverbindungen durch die Ableitung der Aktivierungsfunktion der vorherigen Schicht angepasst. Wenn der Fehlergradient direkt auf die Schichtebene absteigt, erfolgt die Anpassung des Fehlergradienten an die Aktivierungsfunktion automatisch.

   current = caW0.At(iPAMLayers - 1);
   if(!DeActivation(prevLayer.getOutput(), current.getGradient(), residual, prevLayer.Activation()) ||
      !SumAndNormilize(prevLayer.getGradient(), residual, prevLayer.getGradient(), iWindowIn, false)
     )
      return false;
//---
   return true;
  }

Und dann summieren wir die Fehlergradienten aus beiden Threads.

Nach der Verteilung der Fehlergradienten gehen wir zur Anpassung der Modellparameter über. Wir implementieren diese Funktionalität in der Methode updateInputWeights. Der Algorithmus dieser Methode ist recht einfach - wir rufen nacheinander die gleichnamigen Methoden der verschachtelten Objekte auf, die die lernbaren Parameter enthalten.

bool CNeuronSPyrAttentionOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   CNeuronBaseOCL *prev = NeuronOCL;
   CNeuronBaseOCL *current = NULL;
   for(uint l = 0; l < iPAMLayers; l++)
     {
      //--- S3
      current = caS3.At(l);
      if(!current ||
         !current.UpdateInputWeights(prev)
        )
         return false;
      //--- Query
      prev = current;
      current = caQuery.At(l);
      if(!current ||
         !current.UpdateInputWeights(prev)
        )
         return false;
      //--- Key and Value
      current = caKV.At(l);
      if(!current ||
         !current.UpdateInputWeights(prev)
        )
         return false;
      //--- W0
      prev = caAttentionOut.At(l);
      current = caW0.At(l);
      if(!current ||
         !current.UpdateInputWeights(prev)
        )
         return false;
      prev = current;
     }
//--- FeedForward
   prev = caW0.At(iPAMLayers);
   if(!cFF1.UpdateInputWeights(prev) ||
      !cFF2.UpdateInputWeights(cFF1.AsObject())
     )
      return false;
//---
   return true;
  }

Stellen Sie sicher, dass Sie die Ausführung aller Operationen der Methode kontrollieren und das logische Ergebnis der durchgeführten Operationen an den Aufrufer zurückgeben.

Damit ist unsere Arbeit zur Umsetzung der vorgeschlagenen Ansätze der Methode MSFformer abgeschlossen. Sie können den vollständigen Code der erstellten Klassen und ihrer Methoden im Anhang sehen. 

Schlussfolgerung

In diesem Artikel haben wir eine weitere interessante und vielversprechende Methode zur Prognose von Zeitreihen untersucht: MSFformer (Multi-Scale Feature Transformer). Die Methode wurde erstmals in der Veröffentlichung „Time Series Prediction Based on Multi-Scale Feature Extraction“ vorgestellt. Der vorgeschlagene Algorithmus basiert auf einer verbesserten pyramidalen Aufmerksamkeitsarchitektur und einem neuen Ansatz zur Extraktion von Merkmalen in verschiedenen Maßstäben aus den Eingabedaten.

Im praktischen Teil des Artikels haben wir zwei Hauptmodule des vorgeschlagenen Algorithmus implementiert. Die Ergebnisse dieser Arbeit werden wir im nächsten Artikel betrachten.

Referenzen

• Time Series Prediction Based on Multi-Scale Feature Extraction
• Andere Artikel aus dieser Reihe

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	Research.mq5	EA	EA-Beispielsammlung
2	ResearchRealORL.mq5	EA	EA zum Sammeln von Beispielen mit der Real-ORL-Methode
3	Study.mq5	EA	Trainings-EA des Modells
4	StudyEncoder.mq5	EA	Trainings-EA des Encoders
5	Test.mq5	EA	Modeltest-EA
6	Trajectory.mqh	Klassenbibliothek	Struktur der Systemzustandsbeschreibung
7	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
8	NeuroNet.cl	Code Base	Die Bibliothek des Programmcodes von OpenCL