Recursos do Assistente MQL5 que você precisa conhecer (Parte 49): Aprendizado por reforço e otimização proximal de política

Introdução

Damos continuidade à nossa série de artigos sobre o Assistente MQL5, na qual, recentemente, alternamos entre padrões simples de indicadores conhecidos e algoritmos de aprendizado por reforço. Depois de analisarmos os modelos baseados em indicadores (Alligator de Bill Williams) no artigo anterior, agora voltamos ao aprendizado por reforço. Desta vez, vamos explorar a otimização proximal de política (Proximal Policy Optimization, PPO). Relatos indicam que esse algoritmo, publicado pela primeira vez há 7 anos, é o preferido no aprendizado por reforço usado no ChatGPT. Atualmente, essa abordagem de aprendizado por reforço tem se tornado bastante popular. O algoritmo PPO tem como objetivo otimizar a política (a função que define as ações do agente) de forma a melhorar o desempenho geral, evitando mudanças bruscas que poderiam tornar o treinamento instável.

Ele não atua sozinho, mas funciona em conjunto com outros algoritmos de aprendizado por reforço, alguns dos quais já analisamos nesta série, e que em termos gerais podem ser divididos em duas categorias. Algoritmos baseados em política e algoritmos baseados em valor. Já estudamos exemplos de cada um deles nesta série de artigos. Entre os algoritmos baseados em política estavam Q-learning e SARSA. O algoritmo de diferenças temporais é um algoritmo baseado em valor. Então, o que exatamente é o PPO?

Como já mencionado, o "problema" que o PPO resolve é impedir alterações muito grandes na política durante as atualizações. A ideia principal é que, se não houver controle sobre a frequência e a escala das atualizações, o agente pode: esquecer o que aprendeu, tomar decisões equivocadas ou apresentar desempenho inferior no ambiente. Dessa forma, o PPO garante que as atualizações sejam pequenas, mas relevantes. O PPO funciona partindo de uma política previamente definida com seus parâmetros. Aqui, política nada mais é do que funções que determinam as ações do agente com base nas recompensas e nos estados do ambiente.

Quando existe uma política definida, a interação do agente com o ambiente será realizada com o objetivo de coletar dados. Essa "coleta de dados" fornece informações sobre o trio "estado-ação-recompensa", além das probabilidades associadas a diferentes ações tomadas de acordo com essa política. Em seguida, é necessário definir a função objetivo. Como mencionado na introdução, o PPO se ocupa em limitar a magnitude das atualizações no aprendizado por reforço e, para isso, utiliza a função de "clipping" (função de corte). Essa função é definida pela seguinte equação:

onde:

• r t (θ)=πθ(at∣st)/πθ old (at∣st) — a razão entre as probabilidades da nova política (com parâmetros θ) e da política anterior (com parâmetros θ old).
• Â t — estimativa de vantagem no instante t, que mede o quanto uma ação é melhor em comparação com a ação média nesse mesmo estado.
• ϵ — hiperparâmetro (geralmente 0,1 ou 0,2), que define o intervalo de corte, limitando o tamanho do passo na atualização da política.

A vantagem pode ser estimada de diferentes maneiras, mas, na nossa implementação, utilizamos o seguinte método:

onde:

• Q(s t ,a t ) é o valor Q (retorno esperado) da ação a t no estado s t.
• V(s t ) é a função de valor para o estado s t, que representa o retorno esperado caso a política seja seguida a partir desse estado.

Esse método de cálculo da função vantagem evidencia a interdependência entre algoritmos baseados em política e algoritmos baseados em valor, conforme já comentado. Depois de definida a função objetivo, passamos à atualização da política. A atualização ajusta os parâmetros da política com o objetivo de maximizar a função objetivo recortada. Isso garante que as mudanças na política sejam graduais e não baseadas apenas nos últimos dados coletados. Em seguida, o processo se repete através da interação com o ambiente usando a política atualizada, em um ciclo contínuo de coleta de dados e refinamento da política.

Por que o PPO é tão popular? Ele é mais simples de implementar em comparação com algoritmos como o trust region policy optimization. Ele garante atualizações estáveis graças ao clipping (cuja fórmula vimos acima), é altamente eficiente no sentido de funcionar bem com redes neurais modernas e consegue lidar com tarefas em grande escala. Ele também é versátil, pois pode ser aplicado tanto em espaços contínuos quanto discretos. Outra forma de entender a intuição por trás do PPO é imaginar uma pessoa aprendendo a jogar um jogo. Se você mudar drasticamente sua estratégia após cada tentativa, provavelmente perderá boas jogadas e táticas que poderia ter consolidado no início. O PPO atua justamente como um mecanismo para garantir que, durante o aprendizado do jogo, as mudanças sejam pequenas, graduais e bem pensadas, evitando alterações radicais que possam prejudicar o desempenho.

Em muitos aspectos, é justamente esse dilema entre diversificação e intensificação (en. exploration and exploitation) que o aprendizado por reforço busca resolver. Pode-se argumentar que, na fase inicial da maioria dos processos de aprendizado, são necessárias mudanças radicais na abordagem, favorecendo mais a diversificação do que a intensificação. Nesses estágios iniciais, o PPO, evidentemente, não é tão útil. No entanto, como se pode afirmar que, na maioria das áreas e disciplinas de aprendizado, os praticantes se encontram mais em fase de ajuste fino do que de descoberta inicial, o PPO se torna bastante popular. Nesse sentido, o PPO é amplamente usado em robótica, por exemplo, para treinar robôs a andar ou manipular objetos, além de ser aplicado em videogames, onde a IA aprende a jogar jogos complexos como xadrez ou Dota.

O papel do PPO no aprendizado por reforço para traders

O PPO, como algoritmo baseado em política que atua em conjunto com outros algoritmos fundamentais de aprendizado por reforço, não possui muitas alternativas diretas. Entre as poucas que valem ser mencionadas estão as Deep Q-Networks, que já analisamos aqui, o método do ator-crítico de vantagem assíncrona (Asynchronous Advantage Actor-Critic) e a otimização de política de região confiável (Trusted Region Policy Optimization). Vejamos em que pontos o PPO difere de cada uma dessas abordagens. Começando pelo DQN, ele utiliza o Q-learning e pode sofrer instabilidade devido a grandes atualizações de política, principalmente em cenários de ações contínuas. Por "espaços contínuos de ações" entendem-se ciclos de RL em que a escolha do agente não é limitada a opções enumeráveis como "comprar-vender-manter", mas sim definida por um número de ponto flutuante ou double, em aplicações como determinar o tamanho ideal da posição para a próxima operação.

Já o PPO, por sua vez, tende a ser mais estável e simples de implementar, pois não exige uma rede-alvo separada ou mesmo o uso de replay de experiência, conceito esse que será abordado em um próximo artigo. Graças ao processo de aprendizado mais simplificado, o PPO funciona diretamente tanto em espaços de ações discretos quanto contínuos, enquanto o DQN é mais indicado para espaços discretos.

O método do ator-crítico de vantagem assíncrona (A3C), que ainda vamos analisar nesta série, tende a utilizar vários ciclos de RL (ou agentes) para atualizar a política global em momentos diferentes. Isso normalmente aumenta a complexidade do modelo, que passa a envolver múltiplos ciclos de RL. O PPO, por outro lado, depende de atualizações síncronas e da limitação da política para manter o processo de aprendizado estável, evitando atualizações excessivamente agressivas que poderiam levar ao colapso da política.

A otimização de política de região confiável (TRPO) também apresenta algumas particularidades. A principal é que o TRPO utiliza um processo de otimização mais complexo para restringir as mudanças na política, processo esse que geralmente exige a solução de um problema de otimização com restrições. Já o PPO simplifica esse procedimento por meio do clipping, como mencionamos anteriormente, em que limitar as atualizações garante eficiência computacional, ao mesmo tempo em que mantém um nível semelhante de estabilidade e desempenho.

Na introdução, ainda vale destacar algumas outras características do PPO, por isso vamos observá-las antes de seguir para a parte principal. O PPO, como já enfatizado, utiliza o mecanismo de clipping para atualizar a política com o objetivo direto de evitar mudanças muito radicais. Contudo, um possível efeito colateral disso é que ele também favorece o equilíbrio entre intensificação e diversificação, que é o princípio central do aprendizado por reforço. Isso pode ser especialmente vantajoso para traders que atuam em cenários de alta volatilidade, onde explorar demais os ganhos imediatos pode ser uma estratégia ineficaz, e a melhor alternativa seria "manter a pólvora seca" para preservar uma visão de longo prazo sobre os mercados.

Ainda assim, em situações que exigem alguma diversificação, o PPO pode recorrer à regularização entrópica, que impede o algoritmo de se tornar excessivamente confiante em uma única ação, reduzindo assim a dependência exclusiva do clipping das atualizações de política. A regularização por entropia será abordada em detalhes no próximo artigo.

O PPO também demonstra eficiência ao lidar com grandes espaços de ação. Isso acontece porque sua estrutura de "ator-crítico" permite prever com mais precisão os valores no domínio do agente, mesmo em situações contínuas, como já foi mencionado. Mais importante ainda, a redução da variância nas atualizações de política, graças ao uso da função de perda substituta, pode resultar em um comportamento mais consistente nas operações, mesmo quando o RL é aplicado em ambientes altamente voláteis, como o mercado Forex.

O PPO também apresenta boa escalabilidade, já que não precisa armazenar grandes buffers de replay de experiência, que muitas vezes exigem alto consumo de recursos. Essa vantagem pode ser especialmente útil em cenários como trading de alta frequência com muitos instrumentos ou mesmo em configurações complexas de regras de negociação.

O PPO pode ser eficiente no aprendizado a partir de dados limitados. Essa eficiência no aproveitamento das amostras, em comparação a outros métodos, o torna extremamente valioso em situações em que a obtenção de dados de mercado é difícil ou muito custosa. Esse é um problema bastante delicado para muitos traders que precisam, por exemplo, testar suas estratégias em longos períodos históricos sob condições reais. Embora o testador de estratégias do MetaTrader consiga gerar dados de ticks quando os reais não estão disponíveis, na prática é muitas vezes preferível testar a estratégia sobre dados de ticks reais fornecidos pela corretora com a qual se pretende operar.

Para muitas corretoras, esse volume de dados em tempo real raramente está disponível em quantidade suficiente e, mesmo quando os anos necessários para o período de teste existem, uma verificação de qualidade pode revelar lacunas significativas no conjunto de dados. Esse é um problema particular no caso de dados financeiros porque, ao contrário de outras áreas, como desenvolvimento de videogames ou simulações, a geração de grandes volumes de dados e o posterior treinamento geralmente não representam uma dificuldade. Além disso, sinais cruciais muitas vezes estão ligados a eventos raros, como crashes ou grandes ralis de mercado, que não ocorrem com frequência suficiente para que os modelos aprendam adequadamente com eles.

O PPO "contorna" esses problemas, já que, por natureza, é eficiente em termos de amostragem e consegue aprender mesmo com volumes limitados de dados. Assim, a necessidade de grandes quantidades de dados para criar uma política eficaz não é um pré-requisito para o PPO. Isso é possível, em parte, graças ao cálculo da vantagem, que permite utilizar os dados de mercado disponíveis de forma mais eficiente, em lotes menores e em menos episódios. Esse pode ser um fator crucial na modelagem de eventos raros, mas altamente relevantes, já que o PPO consegue aprender gradualmente tanto com operações bem-sucedidas quanto com operações malsucedidas, mesmo em condições de escassez de dados.

Para a maioria dos sistemas de trading, as "recompensas", normalmente quantificadas como lucro ou prejuízo, podem estar significativamente atrasadas em relação a qualquer decisão tomada. Esse tipo de situação traz dificuldades, pois se torna problemático atribuir o mérito a uma ação específica executada anteriormente. Por exemplo, ao abrir uma posição de compra em determinado momento, a recompensa pode surgir apenas dias ou até semanas depois, o que claramente desafia os algoritmos de aprendizado por reforço a identificar quais ações ou estados do ambiente de fato levaram àquele resultado.

Esse cenário é ainda mais complicado pelo ruído de mercado e pela aleatoriedade, tão característicos de muitos movimentos de preços, tornando difícil determinar se um resultado positivo foi consequência de uma boa decisão ou de um movimento espontâneo do mercado. A função vantagem, cujo cálculo já apresentamos anteriormente, ajuda o PPO a estimar melhor a recompensa esperada de uma ação específica, considerando tanto o valor (peso de longo prazo V(st)) quanto a relação estado-ação que envolve os Q-valores (representados como Q(st, at)), de modo que as decisões tomadas fiquem mais equilibradas entre os dois extremos.

Configuração da classe de sinal PPO no MQL5

Para a implementação em MQL5, vamos utilizar a classe Cql, que tem sido nossa base em todos os artigos sobre aprendizado por reforço. Precisamos modificá-la para estender seu suporte ao PPO, e a primeira alteração é a introdução de uma estrutura de dados para lidar com as informações do PPO. O código necessário é mostrado abaixo:

//+------------------------------------------------------------------+
//| PPO                                                              |
//+------------------------------------------------------------------+
struct Sppo
{  matrix            policy[];
   matrix            gradient[];
};

Na estrutura de dados apresentada acima, existem duas matrizes cujo tamanho varia de acordo com a quantidade de ações disponíveis para o ator no ciclo de aprendizado por reforço. Cada uma das matrizes, tanto para gradiente quanto para política, tem dimensão igual ao número de estados, assumindo a forma de uma matriz quadrada. Assim, a matriz de política funciona como o equivalente ao nosso mapa Q, pois registra os pesos e, consequentemente, a probabilidade de escolha de cada ação em cada estado. Mantemos os mesmos estados simples do ambiente utilizados anteriormente nestas séries de tendências de mercado: de alta, de baixa e lateral. Em resumo, esses 3 estados são registrados tanto no horizonte de curto quanto no de longo prazo.

Na definição dos horizontes temporais, a maioria das pessoas costuma recorrer a timeframes e, por exemplo, verificar se o movimento de preços de um determinado título financeiro é de alta ou de baixa no timeframe diário e depois repetir o processo no timeframe horário para obter dois conjuntos de indicadores. Já nós utilizamos apenas um atraso em um número específico de barras de preço para separar a perspectiva de curto prazo da de longo prazo.

Esse valor de atraso é um parâmetro de entrada configurável, que denominamos Signal_PPO_RL_Scale ou m_scale no código da classe de sinal, e o processo de comparação entre duas tendências do movimento de preços é tratado na função get output, que será apresentada mais adiante neste artigo. No entanto, voltando ao PPO, a implementação dessa modificação na classe Cql implica, antes de tudo, a introdução de duas novas funções. Isso são as funções set-policy e get-clipping. Ao definir a próxima ação do ator, não chamamos nenhuma dessas funções; na prática, elas poderiam ser funções protegidas dentro da classe Cql.

A configuração da política é chamada nas funções dentro e fora da política (set on policy function e set-off policy function). O código necessário é o seguinte:

//+------------------------------------------------------------------+
//| PPO policy update function                                       | 
//+------------------------------------------------------------------+
void Cql::SetPolicy()
{  matrix _policies;
   _policies.Init(THIS.actions, Q_PPO.policy[acts[0]].Rows()*Q_PPO.policy[acts[0]].Cols());
   _policies.Fill(0.0);
   for(int ii = 0; ii < int(Q_PPO.policy[acts[0]].Rows()); ii++)
   {  for(int iii = 0; iii < int(Q_PPO.policy[acts[0]].Cols()); iii++)
      {  for(int i = 0; i < THIS.actions; i++)
         {  _policies[i][GetMarkov(ii, iii)] += Q_PPO.policy[i][ii][iii];
         }
      }
   }
   vector _probabilities;
   _probabilities.Init(Q_PPO.policy[acts[0]].Rows()*Q_PPO.policy[acts[0]].Cols());
   _probabilities.Fill(0.0);
   for(int ii = 0; ii < int(Q_PPO.policy[acts[0]].Rows()); ii++)
   {  for(int iii = 0; iii < int(Q_PPO.policy[acts[0]].Cols()); iii++)
      {  for(int i = 0; i < THIS.actions; i++)
         {  _policies.Row(i).Activation(_probabilities, AF_SOFTMAX);
            double _old = _probabilities[states[1]];
            double _new = _probabilities[states[0]];
            double _advantage = Q_SA[i][ii][iii] - Q_V[ii][iii];
            double _clip = GetClipping(_old, _new, _advantage);
            Q_PPO.gradient[i][ii][iii] = (_new - _old) * _clip;
         }
      }
   }
   for(int i = 0; i < THIS.actions; i++)
   {  for(int ii = 0; ii < int(Q_PPO.policy[i].Rows()); ii++)
      {  for(int iii = 0; iii < int(Q_PPO.policy[i].Cols()); iii++)
         {  Q_PPO.policy[i][ii][iii] += THIS.alpha * Q_PPO.gradient[i][ii][iii];
         }
      }
   }
}

Dentro dessa função, cobrimos essencialmente 3 etapas de atualização dos valores de política para nossa estrutura PPO, cujo código já mostramos acima. Esses valores de política determinam a escolha da próxima ação na função action. Essa é a função antiga, já mencionada em artigos anteriores. Seu uso aqui continua relevante porque realizamos mais alterações em sua listagem:

//+------------------------------------------------------------------+
//| Choose an action using epsilon-greedy approach                   |
//+------------------------------------------------------------------+
void Cql::Action(vector &E)
{  int _best_act = 0;
   if (double((rand() % SHORT_MAX) / SHORT_MAX) < THIS.epsilon)
   {  // Explore: Choose random action
      _best_act = (rand() % THIS.actions);
   }
   else
   {  // Exploit: Choose best action
      double _best_value = Q_SA[0][e_row[0]][e_col[0]];
      for (int i = 1; i < THIS.actions; i++)
      {  if (Q_SA[i][e_row[0]][e_col[0]] > _best_value)
         {  _best_value = Q_SA[i][e_row[0]][e_col[0]];
            _best_act = i;
         }
      }
   }
//update last action
   act[1] = act[0];
   act[0] = _best_act;
//markov decision process
   e_row[1] = e_row[0];
   e_col[1] = e_col[0];
   LetMarkov(e_row[1], e_col[1], E);
   int _next_state = 0;
   for (int i = 0; i < int(markov.Cols()); i++)
   {  if(markov[int(E[0])][i] > markov[int(E[0])][_next_state])
      {  _next_state = i;
      }
   }
   //printf(__FUNCSIG__+" next state is: %i, with best act as: %i ",_next_state,_best_act);
   int _next_row = 0, _next_col = 0;
   SetMarkov(_next_state, _next_row, _next_col);
   e_row[0] = _next_row;
   e_col[0] = _next_col;
   states[1] = states[0];
   states[0] = GetMarkov(_next_row, _next_col);
   td_value = Q_V[_next_row][_next_col];
   td_policies[1][0] = td_policies[0][0];
   td_policies[1][1] = td_policies[0][1];
   td_policies[1][2] = td_policies[0][2];
   td_policies[0][0] = _next_row;
   td_policies[0][1] = td_value;
   td_policies[0][2] = _next_col;
   q_sa_act = 1;
   q_ppo_act = 1;
   for (int i = 0; i < THIS.actions; i++)
   {  if(Q_SA[i][_next_row][_next_col] > Q_SA[q_sa_act][_next_row][_next_col])
      {  q_sa_act = i;
      }
      if(Q_PPO.policy[i][_next_row][_next_col] > Q_PPO.policy[q_ppo_act][_next_row][_next_col])
      {  q_ppo_act = i;
      }
   }
//update last acts
   acts[1] = acts[0];
   acts[0] = q_ppo_act;
}

Voltando à função de configuração da política e seus três passos, o primeiro deles quantifica o peso total da política para cada ação em todos os estados. Em essência, é uma forma de alinhar a matriz de estados do ambiente utilizando a função get-Markov, que retorna um índice a partir de dois valores de índice (que representam os padrões de curto e longo prazo). Uma vez obtidos esses pesos cumulativos para cada ação na matriz, que denominamos _policies, podemos passar ao cálculo dos gradientes que atualizarão os pesos das nossas políticas.

Os gradientes, armazenados na matriz de gradientes introduzida na estrutura PPO acima, atualizam os pesos da política de maneira semelhante ao processo usado em redes neurais. No entanto, a obtenção desses valores de gradiente, como acontece na maioria das redes neurais modernas, é um processo relativamente complexo. Primeiro, precisamos definir o vetor _probabilities, cujo tamanho corresponde ao índice suavizado dos estados do ambiente. Neste caso, trata-se de 3 x 3, resultando em 9. Outra modificação feita na classe Cql para integrar o PPO foi a introdução de uma matriz de estados com tamanho 2. Essa matriz simplesmente registra ou armazena em buffer os dois últimos índices de estados do ambiente que foram "experimentados" pelo agente, e o objetivo desse registro é auxiliar na atualização dos gradientes.

Assim, por meio da matriz _policies, onde para cada ação e índice de estado suavizado temos um peso cumulativo da política, obtemos a distribuição de probabilidades em todos os estados para cada ação. Agora, como o coeficiente de peso da política pode assumir valores negativos, precisamos normalizar esses valores brutos para o intervalo 0–1, e uma das formas mais simples de fazer isso é utilizando funções de ativação internas com ativação SoftMax. Essas ativações são aplicadas linha por linha e, após esse processo, obtemos as probabilidades tanto para o estado anterior quanto para o estado atual do ambiente. Mais uma vez, para simplificação, aqui utilizamos índices suavizados.

Outro elemento essencial que precisamos calcular nesse ponto é a vantagem. Como já mencionado anteriormente, essa vantagem nos ajuda a normalizar ou equilibrar as atualizações dos pesos da política, de modo a considerar tanto os pesos de curto prazo, baseados em ações de estados, quanto os pesos de longo prazo, baseados em valor — processo que torna a escolha de ações do PPO mais eficiente ao conectar movimentos de preço de curto prazo com recompensas de longo prazo, conforme já discutido. Essa vantagem é obtida pela subtração da matriz de pesos de Q-valores, que introduzimos no artigo sobre o algoritmo de diferenças temporais, da matriz de pares "estado-ação", apresentada no nosso primeiro artigo sobre aprendizado por reforço. Ambas foram renomeadas, mas seu funcionamento e seus princípios permanecem os mesmos.

Com a vantagem calculada, passamos então a definir o quanto precisamos aplicar o clipping nas atualizações. Como mencionado na introdução, o PPO se diferencia de outros algoritmos de controle de política pela forma como suaviza suas atualizações, garantindo que não sejam excessivamente radicais e que, na maioria dos casos, ocorram de forma gradual para alcançar sucesso a longo prazo. A definição do _clip é realizada pela função get-clipping, cujo código-fonte é mostrado abaixo:

//+------------------------------------------------------------------+
//| Helper function to compute the clipped PPO objective             |
//+------------------------------------------------------------------+
double Cql::GetClipping(double OldProbability, double NewProbability, double Advantage)
{  double _ratio = NewProbability / OldProbability;
   double _clipped_ratio = fmin(fmax(_ratio, 1 - THIS.epsilon), 1 + THIS.epsilon);
   return fmin(_ratio * Advantage, _clipped_ratio * Advantage);
}

O código dessa função é bastante curto, e a probabilidade anterior não deve ser igual a zero; caso contrário, pode-se adicionar o valor epsilon ao denominador para validação. Obtido o _clip, que basicamente é uma fração normalizada, multiplicamos esse valor pela diferença entre as duas probabilidades. Vale destacar aqui que tanto a vantagem quanto o produto entre o clipping e a diferença das probabilidades podem ser positivos ou negativos. Isso implica que os gradientes de atualização também podem ter sinal, ou seja, serem positivos ou negativos.

Isso leva à atualização efetiva dos pesos da política, que, como mencionado anteriormente, é muito semelhante ao processo de atualização dos pesos em uma rede neural. Esses valores, baseados nos gradientes descritos acima, também podem ser negativos ou positivos. O fato de os pesos da política do PPO poderem assumir sinais diferentes é a razão pela qual precisamos aplicar a ativação SoftMax às somas dos pesos de cada ação ao calcular as distribuições de probabilidade, como destacado na segunda etapa da configuração da política. Após a atualização dos pesos da política, eles passam a ser usados da seguinte forma na função action modificada, cujo novo código já apresentamos.

O ajuste feito na antiga função Action é bastante pequeno, já que apenas verificamos o valor do peso da política e escolhemos a ação com maior peso, de acordo com o regime de atualização PPO descrito acima. Uma vez definida a próxima ação, podemos obtê-la por meio da função get output, que também, como já observado, define as matrizes de estados do ambiente. Seu código é mostrado a seguir. 

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalPPO::GetOutput(Cql *QL, int RewardSign)
{  vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(m_scale) &&
      _in_row.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_row.Size() == m_scale
      &&
      _in_row_old.Init(m_scale) &&
      _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, 1, m_scale) &&
      _in_row_old.Size() == m_scale
      &&
      _in_col.Init(m_scale) &&
      _in_col.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_col.Size() == m_scale
      &&
      _in_col_old.Init(m_scale) &&
      _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale, m_scale) &&
      _in_col_old.Size() == m_scale
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      vector _in_e;
      _in_e.Init(m_scale);
      QL.Environment(_in_row, _in_col, _in_e);
      int _row = 0, _col = 0;
      QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
      double _reward_float = RewardSign*_in_row[m_scale - 1];
      double _reward_max = RewardSign*_in_row.Max();
      double _reward_min = RewardSign*_in_row.Min();
      double _reward = QL.GetReward(_reward_max, _reward_min, _reward_float, RewardSign);
      if(m_policy)
      {  QL.SetOnPolicy(_reward, _in_e);
      }
      else if(!m_policy)
      {  QL.SetOffPolicy(_reward, _in_e);
      }
   }
}

Assim como a função action mencionada acima, ela é muito semelhante à que utilizamos nos artigos anteriores sobre aprendizado por reforço, e as mudanças parecem quase insignificantes (com exceção de alguns pontos importantes), considerando que as funções principais agora chamadas pelo PPO ficam encapsuladas, ou seja: a função de configuração da política e a função de clipping. Evidentemente, trata-se de uma versão reduzida da função get output que utilizávamos antes. Em resumo, o m_scale pode ser entendido aqui como nosso atraso, que separa tendências de mercado de curto prazo das de longo prazo ao trabalhar com um único timeframe. O leitor pode considerar alternativas baseadas em diferentes timeframes, mas, nesse caso, o timeframe alternativo precisaria ser adicionado como parâmetro de entrada. As "mudanças significativas" no código da classe de sinais personalizados ocorreram nas funções de condição de compra e venda, cujos códigos são apresentados a seguir:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalPPO::LongCondition(void)
{  int result = 0;
   GetOutput(RL_BUY, 1);
   if(RL_BUY.q_ppo_act==0)
   {  result = 100;
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalPPO::ShortCondition(void)
{  int result = 0;
   GetOutput(RL_SELL, -1);
   if(RL_SELL.q_ppo_act==2)
   {  result = 100;
   }
   return(result);
}

Esse código é quase idêntico ao que utilizávamos anteriormente, exceto pela referência a q_ppo_act em vez da ação escolhida exclusivamente a partir do processo de decisão de Markov.

Relatórios e análise do testador de estratégias

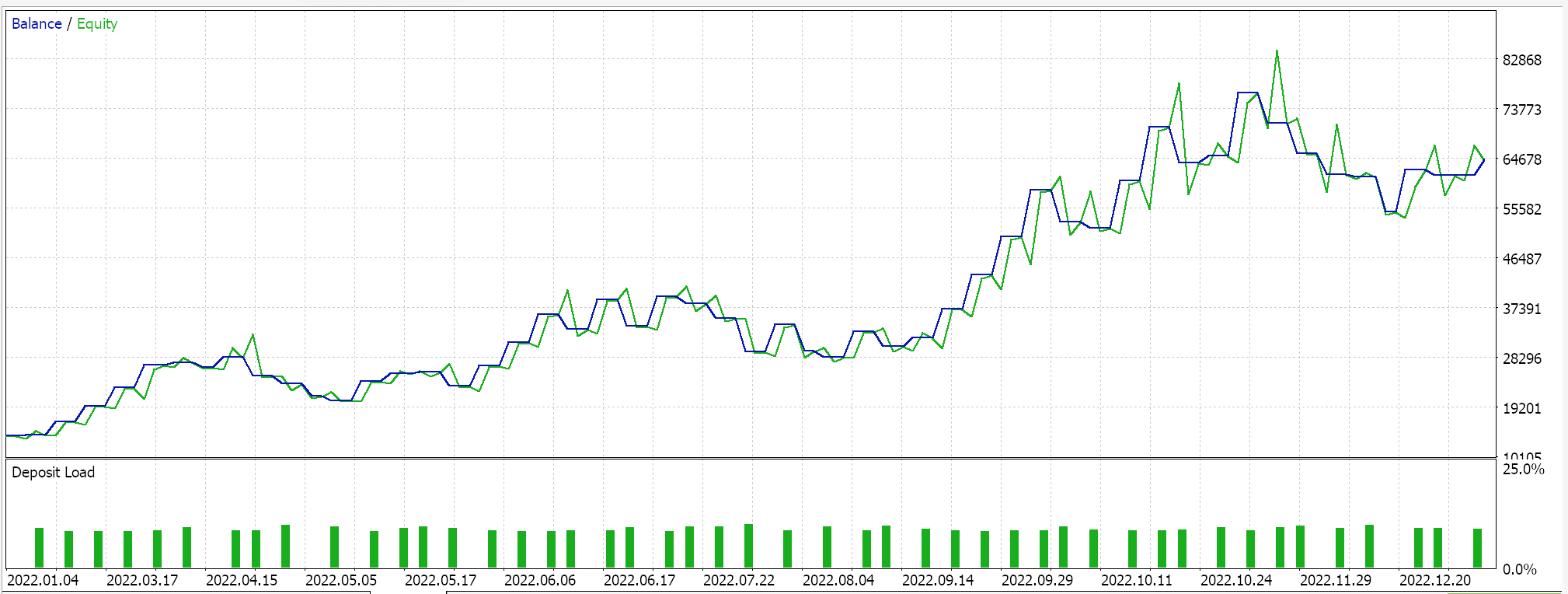
Vamos reunir a classe de sinais personalizada em um EA utilizando o Assistente MQL5. Os iniciantes podem encontrar guias de referência aqui e aqui. Se extraímos alguns parâmetros favoráveis da otimização do par GBPJPY durante o ano de 2022 no timeframe de 4 horas, obtemos os seguintes resultados:

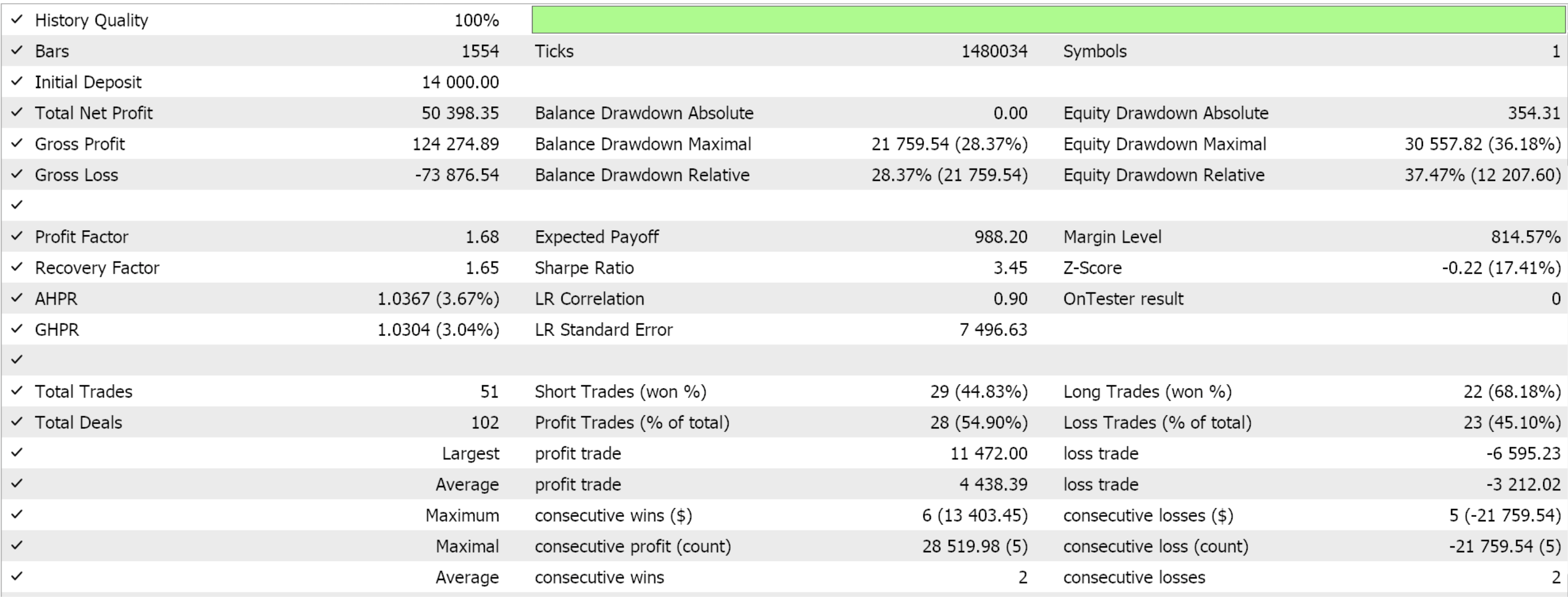
Como sempre, os resultados apresentados aqui têm o objetivo de demonstrar o potencial do sinal personalizado. Os parâmetros de entrada utilizados neste relatório não passaram por validação cruzada e, portanto, não devem ser considerados universais. O leitor é encorajado a adaptar o EA às suas próprias expectativas.

Minha filosofia é que qualquer EA, independentemente de ser usado de forma totalmente automática ou como suporte a um sistema de trading manual, nunca pode responder por mais de 50% do sucesso da "estratégia de trading". A outra metade está sempre ligada às emoções humanas. Por isso, mesmo que você apresente um "Santo Graal" a alguém que não esteja familiarizado com seus detalhes e princípios de funcionamento, essa pessoa inevitavelmente será guiada pelas próprias emoções e passará a duvidar de muitas de suas principais decisões de negociação. Assim, ao apresentar o sinal personalizado sem suas configurações "de Graal", o leitor pode não apenas entender por que o EA pode ter funcionado bem durante um curto período otimizado, mostrado nos artigos, mas também compreender por que ele pode ter resultados diferentes em outros períodos de teste, e essas duas peças de informação devem ajudar a iniciar o processo de identificação de parâmetros que funcionem em horizontes mais longos.

Acredito que o processo em que o trader desenvolve suas próprias configurações ou combina diferentes sinais personalizados para formar um EA funcional já representa metade do caminho para o sucesso.

Considerações finais

Exploramos mais um algoritmo de aprendizado por reforço, a otimização proximal de política. Esse é um método bastante popular e eficiente devido à sua capacidade de moderar as atualizações da política durante os episódios de aprendizado por reforço.

O algoritmo PPO representa uma abordagem inovadora para o aprendizado por reforço, combinando estabilidade da política e adaptabilidade, fatores cruciais para diferentes aplicações práticas, incluindo o trading. Sua estratégia especializada de clipping cobre tanto ações discretas quanto contínuas e garante eficiência escalável sem exigir forte dependência de recursos, o que o torna valioso para sistemas complexos que enfrentam uma ampla gama de condições de mercado.

Nome do arquivo	Descrição
Cql.mqh	Classe base de aprendizado por reforço
SignalWZ_49.mqh	Arquivo da classe de sinais personalizados
wz_49.mqh	EA construído no Assistente, cujo cabeçalho exibe os arquivos utilizados