
Нейросети — это просто (Часть 96): Многоуровневое извлечение признаков (MSFformer)
Введение
Данные временных рядов широко распространены в реальном мире и играют ключевую роль в различных областях, включая финансы. Эти данные представляют собой последовательности наблюдений, собранных в разные временные точки. Глубокий анализ и моделирование временных рядов позволяют исследователям прогнозировать будущие тенденции и паттерны, что используется в процессе принятия решений.
В последние годы многие исследователи сосредоточили свои усилия на изучении временных рядов с использованием моделей глубокого обучения. Эти методы доказали свою эффективность в захвате нелинейных взаимосвязей и обработке долгосрочных зависимостей, что особенно полезно для моделирования сложных систем. Однако, несмотря на значительные достижения, остаются значительные проблемы с эффективным извлечением и интеграцией долгосрочных зависимостей и краткосрочных характеристик. Понимание и правильное объединение этих двух типов зависимостей критично для построения точных и надежных предсказательных моделей.
Один из вариантов решения указанной проблемы был представлен в работе "Time Series Prediction Based on Multi-Scale Feature Extraction". В ней предлагается модель прогнозирования временных рядов MSFformer (Multi-Scale Feature Transformer), которая основывается на улучшенной архитектуре пирамидального внимания. Данная модель предназначена для эффективного извлечения и интеграции многоуровневых признаков.
Авторы метода выделяют следующие инновации MSFformer:
- Введение механизма Skip-PAM, позволяющего модели эффективно захватывать как долгосрочные, так и краткосрочные признаки в длинных временных рядах.
- Улучшенный модуль для создания пирамидальной структуры данных CSCM.
Авторы MSFformer представили результаты экспериментов на трех наборах данных временных рядов, которые демонстрируют превосходную производительность предложенной модели. Предложенные механизмы позволяют модели MSFformer более точно и эффективно обрабатывать сложные данные временных рядов, обеспечивая высокую точность и надежность прогнозов.
1. Алгоритм MSFformer
Авторы модели MSFformer предлагают инновационную архитектуру пирамидального механизма внимания на различных временных интервалах, которая и лежит в основе их метода. Кроме того, с целью построения многоуровневой временной информации в исходных данных они используют свертку признаков в модуле построения крупного масштаба CSCM (Coarser-Scale Construction Module). Что позволяет извлекать временную информацию на более грубом уровне.
В CSCM модуле происходит построение дерева признаков анализируемого временного ряда. Здесь вначале исходные данные проходят через полносвязный слой для преобразования размерности признаков до фиксированного размера. А затем используется несколько последовательных, специально разработанных, блоков свертки признаков FCNN.
В блоке FCNN сначала формируются векторы признаков путем извлечения данных из исходной последовательности с использованием заданного перекрестного шага. Затем эти векторы объединяются. И над ними выполняются операции свертки. Авторская визуализация FCNN блока представлена ниже.
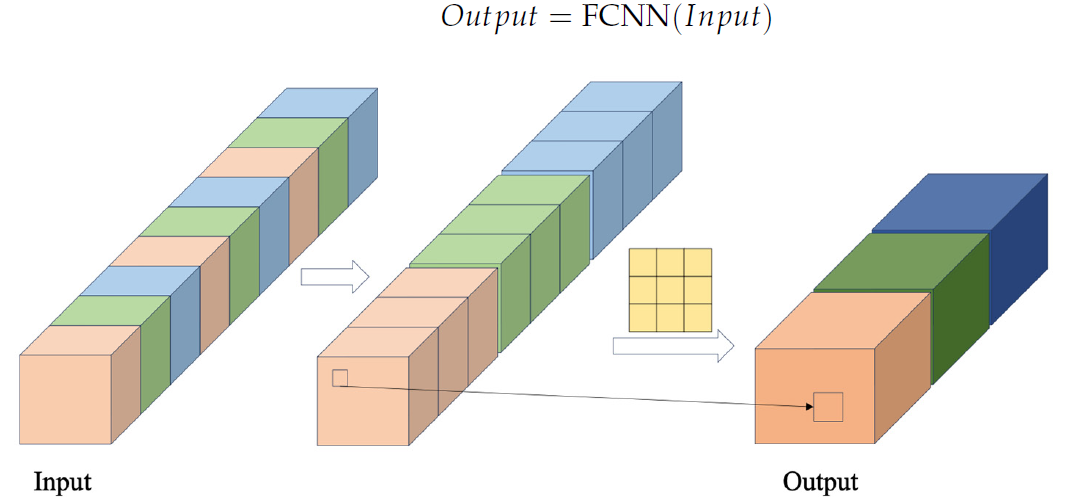
Предложенный авторами метода CSCM модуль использует несколько последовательных FCNN блоков. И каждый из них, используя в качестве исходных данных результаты работы предыдущего блока, извлекает признаки более крупного масштаба.
Полученные таким образом признаки различных масштабов объединяются в единый вектор, размер которого понижается линейным слоем до уровня исходных данных.
Авторская визуализация CSCM модуля представлена ниже.
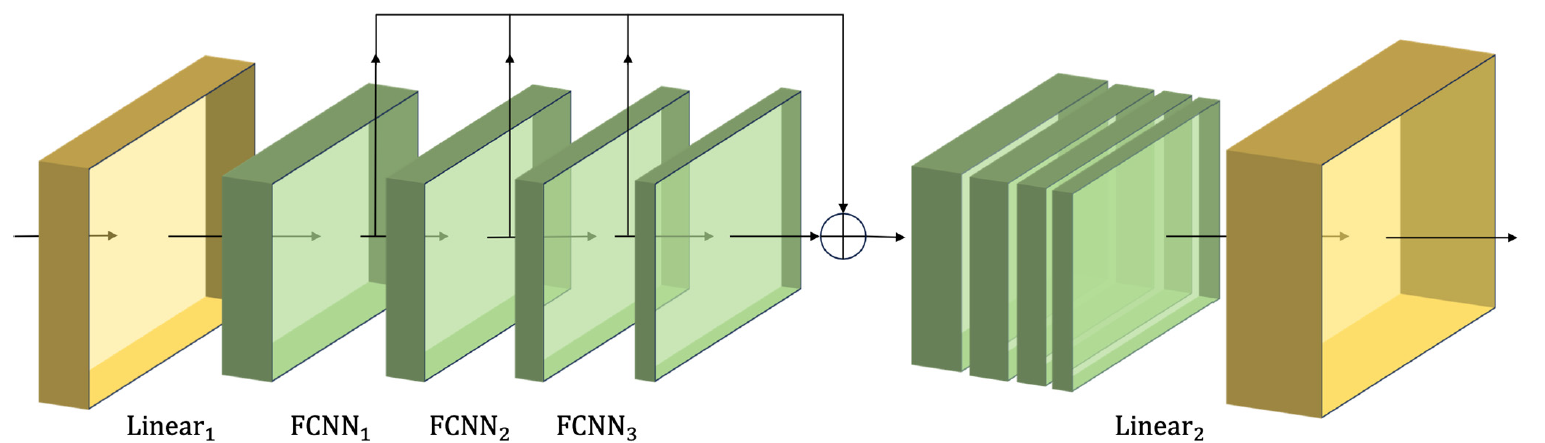
Пропуская данные анализируемого временного ряда через такой CSCM, мы получаем временную информацию о признаках на разных уровнях детализации. Мы строим пирамидальное дерево признаков, путем накладывания слоев FCNN. Что позволяет понять данные на нескольких уровнях и обеспечивает прочную основу для реализации инновационной структуры пирамидального внимания Skip-PAM (Skip-Pyramidal Attention Module).
Основная идея Skip-PAM заключается в обработке исходных данных на различных временных интервалах, что позволяет модели захватывать временные зависимости разных уровней детализации. В нижних уровнях модель может фокусироваться на краткосрочных, детализированных шаблонах. Тогда как верхние уровни способны захватывать более макроскопические тренды и периодичности. Предложенный Skip-PAM уделяет больше внимания таким периодическим зависимостям, как каждый понедельник или начало каждого месяца. Этот многоуровневый подход позволяет модели захватывать разнообразные временные взаимосвязи на разных уровнях.
Skip-PAM извлекает информацию из временных рядов на нескольких масштабах через механизм внимания, построенный на основе дерева временных признаков. Этот процесс включает внутримасштабные и межмасштабные соединения. Внутримасштабные соединения включают выполнение вычислений внимания между узлом и его соседними узлами в том же слое. Межмасштабные соединения включают вычисления внимания между узлом и его родительским узлом.
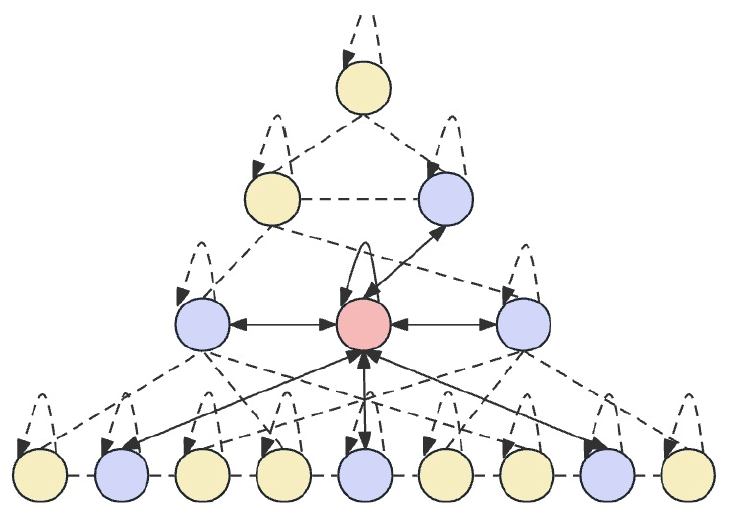
Через этот пирамидальный механизм внимания Skip-PAM, в сочетании с многоуровневой сверткой признаков в CSCM, формируется мощная сеть извлечения признаков, которая может адаптироваться к динамическим изменениям на различных временных масштабах, будь то краткосрочные колебания или долгосрочные эволюции.
Описанные выше 2 модуля авторы метода объединяют в одну мощную модель MSFformer, авторская визуализация которой представлена ниже.
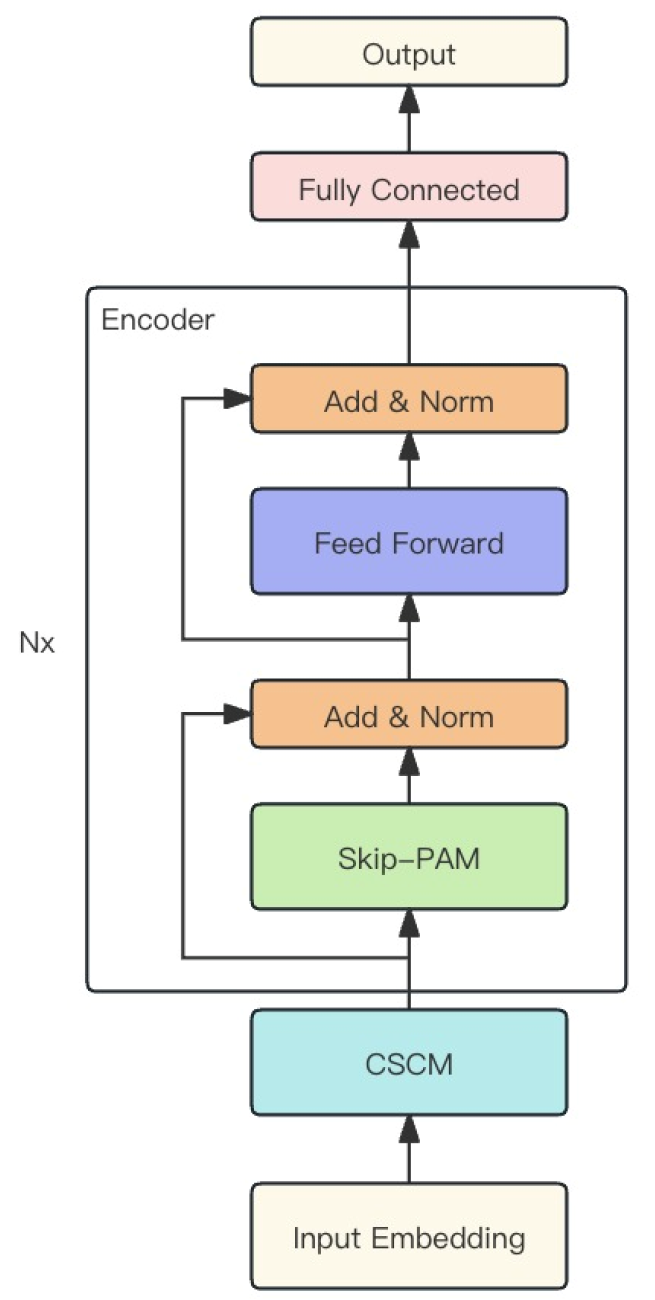
2. Реализация средствами MQL5
После ознакомления с теоретическими аспектами метода MSFformer, мы переходим к практической части нашей статьи, в которой реализуем свое видение предложенных подходов средствами MQL5.
Как было сказано выше, в основе предложенного метода MSFformer лежат 2 модуля: CSCM и Skip-PAM. Их нам и предстоит реализовать в рамках данной статьи. Работы предстоит много. Её мы раздели на 2 части, в соответствии с реализуемыми модулями.
2.1. Построение модуля CSCM
А начнем мы работу с построения модуля CSCM. Для реализации архитектуры данного модуля мы создадим класс CNeuronCSCMOCL, который унаследует основной функционал от базового класса нейронных слоев CNeuronBaseOCL. Структура нового класса представлена ниже.
class CNeuronCSCMOCL : public CNeuronBaseOCL { protected: uint i_Count; uint i_Variables; bool b_NeedTranspose; //--- CArrayInt ia_Windows; CArrayObj caTranspose; CArrayObj caConvolutions; CArrayObj caMLP; CArrayObj caTemp; CArrayObj caConvOutputs; CArrayObj caConvGradients; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); //--- virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronCSCMOCL(void) {}; ~CNeuronCSCMOCL(void) {}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint &windows[], uint variables, uint inputs_count, bool need_transpose, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronCSCMOCL; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
В представленной структуре класса CNeuronCSCMOCL можно заметить довольно стандартный набор переопределяемых методов и большое количество динамических массивов, которые помогут нам организовать многослойную структуру извлечения признаков. С назначением динамических массивов и объявленных переменных мы познакомимся в процессе реализации методов.
Все объекты класса объявлены статично, что позволяет нам оставить "пустыми" конструктор и деструктор класса. Непосредственная инициализация всех вложенных объектов и переменных осуществляется в методе Init.
Как обычно, в параметрах метода Init мы получаем основные константы, которые позволяют однозначно определить архитектуры создаваемого объекта.
С целью предоставить пользователю возможность гибко определять количество слоев извлечения признаков и размер окна свертки, мы используем динамический массив windows. Количество элементов в массиве указывает на число создаваемых блоков извлечения признаков FCNN. А значение каждого элемента укажет на размер окна свертки соответствующего блока.
Количество унитарных временных последовательностей в многомерном временном ряде исходных данных, а также размер исходной последовательности указаны в параметрах variables и inputs_count, соответственно.
Кроме того, мы добавим логическую переменную need_transpose, которая укажет на необходимость транспонировать исходные данные перед извлечением признаков.
bool CNeuronCSCMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint &windows[], uint variables, uint inputs_count, bool need_transpose, ENUM_OPTIMIZATION optimization_type, uint batch) { const uint layers = windows.Size(); if(layers <= 0) return false; if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, inputs_count * variables, optimization_type, batch)) return false;
В теле метода мы организуем небольшой контрольный блок. Здесь мы сначала проверяем необходимость создания хотя бы одного блока извлечения признаков. После чего взываем одноименный метод родительского класса, в котором уже реализована часть контрольных функций и инициализация унаследованных объектов. Результат выполнения операций метода родительского класса мы контролируем по возвращаемому логическому значению.
Следующим этапом мы сохраним полученные параметры в соответствующие внутренние переменные и массив.
if(!ia_Windows.AssignArray(windows)) return false; i_Variables = variables; i_Count = inputs_count / ia_Windows[0]; b_NeedTranspose = need_transpose;
После чего начинаем процесс инициализации вложенных объектов. И здесь в случае необходимости транспонирования исходных данных мы создадим 2 вложенных слоя транспонирования данных. Первый для транспонирования исходных данных.
if(b_NeedTranspose) { CNeuronTransposeOCL *transp = new CNeuronTransposeOCL(); if(!transp) return false; if(!transp.Init(0, 0, OpenCL, inputs_count, i_Variables, optimization, iBatch)) { delete transp; return false; } if(!caTranspose.Add(transp)) { delete transp; return false; }
А второй для транспонирования результатов, возвращая их к размерности исходных данных.
transp = new CNeuronTransposeOCL(); if(!transp) return false; if(!transp.Init(0, 1, OpenCL, i_Variables, inputs_count, optimization, iBatch)) { delete transp; return false; } if(!caTranspose.Add(transp)) { delete transp; return false; } if(!SetOutput(transp.getOutput()) || !SetGradient(transp.getGradient()) ) return false; }
И обратите внимание, что при необходимости транспонирования данных, мы переопределяем буферы результатов и градиентов нашего класса на соответствующие буферы слоя транспонирования результатов. Такой ход позволит нам исключить излишние операции копирования данных.
Затем мы создадим слой выравнивания размера исходных данных в рамках отдельных унитарных последовательностей.
uint total = ia_Windows[0] * i_Count; CNeuronConvOCL *conv = new CNeuronConvOCL(); if(!conv.Init(0, 0, OpenCL, inputs_count, inputs_count, total, 1, i_Variables, optimization, iBatch)) { delete conv; return false; } if(!caConvolutions.Add(conv)) { delete conv; return false; }
И в цикле создадим необходимое количество сверточных слоев извлечения признаков.
total = 0; for(uint i = 0; i < layers; i++) { conv = new CNeuronConvOCL(); if(!conv.Init(0, i + 1, OpenCL, ia_Windows[i], ia_Windows[i], (i < (layers - 1) ? ia_Windows[i + 1] : 1), i_Count, i_Variables, optimization, iBatch)) { delete conv; return false; } if(!caConvolutions.Add(conv)) { delete conv; return false; } if(!caConvOutputs.Add(conv.getOutput()) || !caConvGradients.Add(conv.getGradient()) ) return false; total += conv.Neurons(); }
Обратите внимание, что в массиве caConvolutions мы объединили слой выравнивания размера исходных данных и свертки извлечения признаков. Поэтому в нем на один объект больше, чем заданное количество блоков FCNN.
Напомню, что алгоритмом модуля CSCM предполагается конкатенация признаков всех анализируемых масштабов в единый тензор. Поэтому параллельно с созданием сверточных слоев мы посчитали суммарный размер тензора их результатов. Кроме того, мы сохранили в отдельные динамические массивы указатели на буферы данных результатов и градиентов ошибки созданных слоев извлечения признаков, что даст нам более быстрый доступ к их содержанию в процессе обучения и эксплуатации модели.
И теперь, имея необходимое нам значение, мы создадим слой для записи конкатенированного тензора.
CNeuronBaseOCL *comul = new CNeuronBaseOCL(); if(!comul.Init(0, 0, OpenCL, total, optimization, iBatch)) { delete comul; return false; } if(!caMLP.Add(comul)) { delete comul; return false; }
И тут же мы предусмотрим частный случай создания 1 слоя извлечения признаков. Не сложно догадаться, что в таком случае нам нечего объединять, и конкатенированный тензор будет полной копией единственного тензора извлечения признаков. Следовательно, для исключения излишних операций копирования мы переопределим буферы результатов и градиентов ошибки.
if(layers == 1) { comul.SetOutput(conv.getOutput()); comul.SetGradient(conv.getGradient()); }
После чего создадим слой для линейной корректировки размерности конкатенированного тензора признаков до размера исходной последовательности.
conv = new CNeuronConvOCL(); if(!conv.Init(0, 0, OpenCL, total / i_Variables, total / i_Variables, inputs_count, 1, i_Variables, optimization, iBatch)) { delete conv; return false; } if(!caMLP.Add(conv)) { delete conv; return false; }
Выше мы переопределили буферы исходных данных и результатов нашего класса при необходимости транспонирования исходных данных. А вот в противном случае мы переопределим их сейчас.
if(!b_NeedTranspose) { if(!SetOutput(conv.getOutput()) || !SetGradient(conv.getGradient()) ) return false; }
Таким образом мы исключили операции излишнего копирования данных в обоих случаях — нужно транспонировать исходные данные или нет.
В завершение работы метода мы создадим 3 вспомогательных буфера для хранения промежуточных данных, которые будем использовать при конкатенации признаков и деконкатенации соответствующих градиентов ошибки.
CBufferFloat *buf = new CBufferFloat(); if(!buf) return false; if(!buf.BufferInit(total, 0) || !buf.BufferCreate(OpenCL) || !caTemp.Add(buf)) { delete buf; return false; } buf = new CBufferFloat(); if(!buf) return false; if(!buf.BufferInit(total, 0) || !buf.BufferCreate(OpenCL) || !caTemp.Add(buf)) { delete buf; return false; } buf = new CBufferFloat(); if(!buf) return false; if(!buf.BufferInit(total, 0) || !buf.BufferCreate(OpenCL) || !caTemp.Add(buf)) { delete buf; return false; } //--- caConvOutputs.FreeMode(false); caConvGradients.FreeMode(false); //--- return true; }
Не забываем контролировать процесс создания всех вложенных объектов. И после успешной инициализации всех вложенных объектов, возвращаем логический результат выполнения операций вызывающей программе.
После построения метода инициализации объекта нашего класса CNeuronCSCMOCL, мы переходим к организации его метода прямого прохода. Здесь стоит сказать, что в рамках данного класса мы не осуществляем работу на стороне OpenCL программы. Вся реализация построена на использовании методов вложенных объектов, алгоритм которых уже реализован на стороне OpenCL. И в подобных условиях нам достаточно выстроить верхнеуровневый алгоритм из методов вложенных объектов и унаследованных от родительского класса.
Как вы знаете, прямой проход мы организовываем в методе feedForward, в параметрах которого вызывающая программа дала нам указатель на объект предшествующего слоя.
bool CNeuronCSCMOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { CNeuronBaseOCL *inp = NeuronOCL; CNeuronBaseOCL *current = NULL;
В теле метода мы объявим 2 переменные для хранения указателей на объекты нейронных слоев. На данном этапе в переменную исходных данных мы передадим указатель, полученный от вызывающей программы. А вторую переменную оставим пустой.
Далее мы проверяем необходимость транспонирования исходных данных. И в случае надобности осуществим данную операцию.
if(b_NeedTranspose) { current = caTranspose.At(0); if(!current || !current.FeedForward(inp)) return false; inp = current; }
После чего пропускаем исходный временной ряд через последовательные сверточные слои извлечения признаков разных масштабов, указатели на которые мы сохранили в массиве caConvolutions.
int layers = caConvolutions.Total() - 1; for(int l = 0; l <= layers; l++) { current = caConvolutions.At(l); if(!current || !current.FeedForward(inp)) return false; inp = current; }
Напомню, что первый слой в данном массиве предназначен для выравнивания размера последовательности исходных данных. И его результат мы не используем при конкатенации извлеченных признаков, которую мы осуществим на следующем этапе.
Надо сказать, что мы строим алгоритм без ограничения верхнего предела сверточных слоев извлечения признаков. При этом минимально допускается даже 1 слой извлечения признаков. И наверное, самый простой алгоритм, который мы можем использовать в данном случае — это создание цикла с последовательным добавлением в тензор по 1 массиву признаков. Но такой подход ведет к потенциальному многоразовому копированию одних и тех же данных. Что существенно увеличивает наши затраты вычислительных ресурсов при прямом проходе. С целью минимизации таких операций, мы создали разветвление алгоритма по количеству блоков извлечения признаков.
Как уже было сказано выше, должен быть хотя бы один слой извлечения признаков. Если его нет, то возвращаем вызывающей программе сигнал ошибки в виде негативного результата.
current = caMLP.At(0); if(!current) return false; switch(layers) { case 0: return false;
При использовании одного слоя извлечения признаков нам нечего конкатенировать. И как вы помните, в методе инициализации класса для такого случая мы переопределили буферы данных слоев извлечения признаков и конкатенации, что позволило нам сократить излишние операции копирования. И мы просто переходим к следующим операциям.
case 1: break;
Наличие от 2 до 4 слоев извлечения признаков приводит к выбору соответствующего метода конкатенации данных.
case 2: if(!Concat(caConvOutputs.At(0), caConvOutputs.At(1), current.getOutput(), ia_Windows[1], 1, i_Variables * i_Count)) return false; break; case 3: if(!Concat(caConvOutputs.At(0), caConvOutputs.At(1), caConvOutputs.At(2), current.getOutput(), ia_Windows[1], ia_Windows[2], 1, i_Variables * i_Count)) return false; break; case 4: if(!Concat(caConvOutputs.At(0), caConvOutputs.At(1), caConvOutputs.At(2), caConvOutputs.At(3), current.getOutput(), ia_Windows[1], ia_Windows[2], ia_Windows[3], 1, i_Variables * i_Count)) return false;
Если же таких слоев больше, то мы конкатенируем 4 первых слоя извлечения признаков, но результат записываем в буфер временного хранения данных.
default: if(!Concat(caConvOutputs.At(0), caConvOutputs.At(1), caConvOutputs.At(2), caConvOutputs.At(3), caTemp.At(0), ia_Windows[1], ia_Windows[2], ia_Windows[3], ia_Windows[4], i_Variables * i_Count)) return false; break; }
Обратите внимание, что при выполнении операций конкатенации мы обращаемся не к объектам сверточных слоев из массива caConvolutions, а напрямую к буферам их результатов, указатели на которые мы предусмотрительно сохранили в динамический массив caConvOutputs.
Далее мы организуем цикл, начиная с 4 слоя извлечения признаков и шагом в 3 слоя. В теле данного цикла мы сначала посчитаем размер окна данных, сохраненных во временном буфере.
uint last_buf = 0; for(int i = 4; i < layers; i += 3) { uint buf_size = 0; for(int j = 1; j <= i; j++) buf_size += ia_Windows[j];
А затем организуем алгоритм выбора функции конкатенации, аналогичный приведенному выше. Только в данном случае, на первом месте всегда будет временный буфер с ранее собранными данными, а к нему уже добавляется следующая партия извлеченных признаков.
switch(layers - i) { case 1: if(!Concat(caTemp.At(last_buf), caConvOutputs.At(i), current.getOutput(), buf_size, 1, i_Variables * i_Count)) return false; break; case 2: if(!Concat(caTemp.At(last_buf), caConvOutputs.At(i), caConvOutputs.At(i + 1), current.getOutput(), buf_size, ia_Windows[i + 1], 1, i_Variables * i_Count)) return false; break; case 3: if(!Concat(caTemp.At(last_buf), caConvOutputs.At(i), caConvOutputs.At(i + 1), caConvOutputs.At(i + 2), current.getOutput(), buf_size, ia_Windows[i + 1], ia_Windows[i + 2], 1, i_Variables * i_Count)) return false; break; default: if(!Concat(caTemp.At(last_buf), caConvOutputs.At(i), caConvOutputs.At(i + 1), caConvOutputs.At(i + 2), caTemp.At((last_buf + 1) % 2), buf_size, ia_Windows[i + 1], ia_Windows[i + 2], ia_Windows[i + 3], i_Variables * i_Count)) return false; break; } last_buf = (last_buf + 1) % 2; }
Обратите внимание, что при добавлении последних слоев признаков (от 1 до 3), результат операции сохраняется в буфер слоя конкатенации данных. В остальных же случаях мы используем еще один буфер временного хранения данных. При этом на каждой итерации цикла происходит чередование буферов с целью предотвращения искажения и потери данных.
После конкатенации всех признаков в единый тензор нам остается скорректировать размер тензора результатов.
inp = current; current = caMLP.At(1); if(!current || !current.FeedForward(inp)) return false;
И при необходимости, транспонировать их в размерность исходных данных.
if(b_NeedTranspose) { inp = current; current = caTranspose.At(1); if(!current || !current.FeedForward(inp)) return false; } //--- return true; }
Напомню, что в методе инициализации мы организовали подмену буферов данных. Поэтому копирование результатов операций в соответствующий унаследованный буфер нашего класса осуществляется "в автомате".
После построения метода прямого прохода, мы переходим к реализации алгоритмов обратного прохода. И первым мы создадим метод распределения градиента ошибки до всех объектов, в соответствии с их влиянием на общий результат (calcInputGradients). Как обычно, в параметрах данного метода мы получаем указатель на объект предшествующего нейронного слоя. В данном случае нам предстоит передать ему соответствующую долю градиента ошибки.
bool CNeuronCSCMOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!prevLayer) return false;
В теле метода мы сразу проверяем актуальность полученного указателя. После чего создадим локальные указатели 2 нейронных слоев, с которыми будем последовательно работать.
CNeuronBaseOCL *current = caMLP.At(0); CNeuronBaseOCL *next = caMLP.At(1);
Напомню, что в процессе распределения градиента ошибки мы двигаемся по алгоритму прямого прохода, но в обратном направлении. Следовательно, мы сначала проведем градиент через слой транспонирования данных, конечно, если есть необходимость такой операции.
if(b_NeedTranspose) { if(!next.calcHiddenGradients(caTranspose.At(1))) return false; }
Затем мы передадим градиент ошибки на конкатенированный слой извлеченных признаков различного масштаба.
if(!current.calcHiddenGradients(next.AsObject())) return false; next = current;
После чего, нам предстоит распределить градиент ошибки до соответствующих слоев извлечения признаков.
Не будем забывать про частный случай наличия 1 слоя извлечения признаков. Здесь нам надо лишь скорректировать градиент ошибки на производную функции активации.
int layers = caConvGradients.Total(); if(layers == 1) { next = caConvolutions.At(1); if(next.Activation() != None) { if(!DeActivation(next.getOutput(), next.getGradient(), next.getGradient(), next.Activation())) return false; } }
В общем же случае, мы сначала отделим градиент ошибки последнего слоя извлечения признаков и скорректируем его на производную функции активации.
else { int prev_window = 0; for(int i = 1; i < layers; i++) prev_window += int(ia_Windows[i]); if(!DeConcat(caTemp.At(0), caConvGradients.At(layers - 1), next.getGradient(), prev_window, 1, i_Variables * i_Count)) return false; next = caConvolutions.At(layers); int current_buf = 0;
После чего, организуем цикл обратного перебора слоев извлечения признаков, в теле которого мы сначала получаем градиент ошибки от последующего слоя извлечения признаков.
for(int l = layers; l > 1; l--) { current = caConvolutions.At(l - 1); if(!current.calcHiddenGradients(next.AsObject())) return false;
Затем выделим долю анализируемого слоя из буфера градиентов ошибки конкатенированного тензора признаков.
int window = int(ia_Windows[l - 1]); prev_window -= window; if(!DeConcat(caTemp.At((current_buf + 1) % 2), caTemp.At(2), caTemp.At(current_buf), prev_window, window, i_Variables * i_Count)) return false;
Скорректируем его на производную функции активации.
if(current.Activation() != None) { if(!DeActivation(current.getOutput(), caTemp.At(2), caTemp.At(2), current.Activation())) return false; }
И суммируем градиенты ошибки от 2 потоков данных.
if(!SumAndNormilize(current.getGradient(), caTemp.At(2), current.getGradient(), 1, false, 0, 0, 0, 1)) return false; next = current; current_buf = (current_buf + 1) % 2; } }
После чего, мы переходим к следующей итерации нашего цикла.
Таким образом мы распределим градиент ошибки по всем слоям извлечения признаков. И затем передадим градиент ошибки до слоя выравнивания размера исходных данных.
current = caConvolutions.At(0); if(!current.calcHiddenGradients(next.AsObject())) return false; next = current;
При необходимости, мы проведем градиент ошибки через слой транспонирования данных.
if(b_NeedTranspose) { current = caTranspose.At(0); if(!current.calcHiddenGradients(next.AsObject())) return false; next = current; }
И в завершение операций метода, передадим градиент ошибки на предшествующий нейронный слой, указатель которого мы получили в параметрах данного метода.
if(!prevLayer.calcHiddenGradients(next.AsObject())) return false; //--- return true; }
Как вы знаете, распределение градиента ошибки не является целью обучения модели. Это лишь средство для определения направления и объема корректировки параметров модели. Поэтому после успешного распределения градиента ошибки, нам предстоит скорректировать параметры модели таким образом, чтобы в целом минимизировать ошибку её работы. Данный функционал реализован в методе updateInputWeights.
bool CNeuronCSCMOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { CObject *prev = (b_NeedTranspose ? caTranspose.At(0) : NeuronOCL); CNeuronBaseOCL *current = NULL;
В параметрах метода мы, как и ранее, получаем указатель на объект предшествующего нейронного слоя. Однако в данном случае мы не осуществляем проверку актуальности полученного указателя. Мы просто сохраним его в локальную переменную. Хотя тут есть нюанс. Слой транспонирования данных не содержит параметров. Следовательно, мы не будем для него вызывать метод корректировки параметров модели. Только вот для слоя выравнивания размера исходных данных мы будем выбирать предшествующий слой в зависимости от параметра необходимости транспонирования исходных данных b_NeedTranspose.
Далее мы организуем цикл последовательного корректирования параметров сверточных слоев, включая слой корректировки размера исходной последовательности и блоков извлечения признаков.
for(int i = 0; i < caConvolutions.Total(); i++) { current = caConvolutions.At(1); if(!current || !current.UpdateInputWeights(prev) ) return false; prev = current; }
Затем нам предстоит скорректировать параметры слоя выравнивания размерности результатов.
current = caMLP.At(1); if(!current || !current.UpdateInputWeights(caMLP.At(0)) ) return false; //--- return true; }
Остальные вложенные объекты нашего класса CNeuronCSCMOCL не содержат обучаемых параметров.
На этом можно считать завершенной реализацию основных алгоритмов модуля CSCM. Конечно, функциональность нашего класса будет не полной без дополнительной реализации алгоритмов вспомогательных методов. Но с целью сокращения объема статьи мы оставим их для самостоятельного изучения. Полный код всех методов данного класса представлен во вложении. Там же Вы найдете полный код всех классов и программ, используемых при подготовке данной статьи. А мы переходим к построению алгоритмов следующего модуля — Skip-PAM.
2.2 Реализация алгоритмов модуля Skip-PAM
Вторая часть работы, которую нам предстоит выполнить, — это реализовать алгоритм пирамидального внимания. Инновацией авторов метода MSFformer является применение алгоритмов внимания к дереву признаков с различными интервалами. При этом авторы метода используют фиксированные шаги между признаками в рамках одного уровня внимания. Мы же в своей реализации поступим немного иначе. А что если позволить модели самостоятельно выучить, какие признаки будет анализировать каждая отдельная пирамида внимания на каждом отдельном уровне внимания? Звучит заманчиво. Да и реализация, на мой взгляд, очевидна и проста. Мы просто добавим перед каждым уровнем внимания слой S3.
Строить алгоритмы нашей реализации модуля Skip-PAM мы будем в рамках класса CNeuronSPyrAttentionOCL, структура которого представлена ниже.
class CNeuronSPyrAttentionOCL : public CNeuronBaseOCL { protected: uint iWindowIn; uint iWindowKey; uint iHeads; uint iHeadsKV; uint iCount; uint iPAMLayers; //--- CArrayObj caS3; CArrayObj caQuery; CArrayObj caKV; CArrayInt caScore; CArrayObj caAttentionOut; CArrayObj caW0; CNeuronConvOCL cFF1; CNeuronConvOCL cFF2; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool AttentionOut(CBufferFloat *q, CBufferFloat *kv, int scores, CBufferFloat *out, int window); virtual bool AttentionInsideGradients(CBufferFloat *q, CBufferFloat *q_g, CBufferFloat *kv, CBufferFloat *kv_g, int scores, CBufferFloat *gradient); //--- virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); virtual void ArraySetOpenCL(CArrayObj *array, COpenCLMy *obj); public: CNeuronSPyrAttentionOCL(void) {}; ~CNeuronSPyrAttentionOCL(void) {}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window_in, uint window_key, uint heads, uint heads_kv, uint units_count, uint pam_layers, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronSPyrAttentionMLKV; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
Как можно заметить в представленной структуре, новый класс содержит ещё больше динамических массивов и параметров. Их названия созвучны с объектами других классов внимания. И как вы понимаете, это не случайность. А с использованием создаваемых объектов и переменных мы познакомимся в процессе реализации.
Как и ранее, рассмотрение алгоритмов нового класса мы начинаем с метода инициализации объекта Init.
bool CNeuronSPyrAttentionOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window_in, uint window_key, uint heads, uint heads_kv, uint units_count, uint pam_layers, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_in * units_count, optimization_type, batch)) return false;
В параметрах метода мы получаем основные константы, определяющие архитектуры создаваемого объекта. А в теле метода сразу вызываем одноименный метод родительского класса, в котором реализованы минимально-необходимые контроли и инициализация унаследованных объектов.
Также следует обратить внимание, что в рамках данного метода мы будем анализировать отдельные временные шаги в рамках общей мультимодальной временной последовательности. Хотя в данном случае, наверное, сложно назвать исходные данные, подаваемые на вход модуля Skip-PAM, мультимодальным временным рядом. Ведь результаты работы предшествующего модуля CSCM представляют собой набор извлеченных признаков разного масштаба данных, а не временную последовательность.
После успешного выполнения метода инициализации объектов родительского класса, мы сохраняем полученные константы в локальные переменные.
iWindowIn = window_in; iWindowKey = MathMax(window_key, 1); iHeads = MathMax(heads, 1); iHeadsKV = MathMax(heads_kv, 1); iCount = units_count; iPAMLayers = MathMax(pam_layers, 2);
Здесь стоит обратить вынимание на появление нового параметра iPAMLayers, который определяет количество уровней пирамидального внимания. Остальные же параметры подразумевают тот же функционал, что и рассмотренные ранее методы внимания. Мы так же оставили параметр iHeadsKV для возможности использования количества голов Key-Value отличным от размерности голов внимания Query, как это рассматривалось в методе MLKV.
Затем мы очищаем динамические массивы.
caS3.Clear(); caQuery.Clear(); caKV.Clear(); caScore.Clear(); caAttentionOut.Clear(); caW0.Clear();
Создадим необходимые локальные переменные.
CNeuronBaseOCL *base = NULL; CNeuronConvOCL *conv = NULL; CNeuronS3 *s3 = NULL;
И организуем цикл инициализации объектов блока пирамидального внимания. Как не сложно догадаться, количество итераций цикла равно количество создаваемых уровней внимания.
for(uint l = 0; l < iPAMLayers; l++) { //--- S3 s3 = new CNeuronS3(); if(!s3) return false; if(!s3.Init(0, l, OpenCL, iWindowIn, iCount, optimization, iBatch) || !caS3.Add(s3)) return false; s3.SetActivationFunction(None);
В теле цикла мы первым создаем слой S3, в котором организована перестановка анализируемой последовательности. В данном случае мы используем только один слой перемешивания данных с окном, равным количеству анализируемых параметров в исходной мультимодальной последовательности.
Затем мы создаем объекты генерации сущностей Query, Key и Value. Обратите внимание, при формировании сущностей мы используем один объект исходных данных, но различные параметры голов внимания.
//--- Query conv = new CNeuronConvOCL(); if(!conv) return false; if(!conv.Init(0, 0, OpenCL, iWindowIn, iWindowIn, iWindowKey*iHeads, iCount, optimization, iBatch) || !caQuery.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(None); //--- KV conv = new CNeuronConvOCL(); if(!conv) return false; if(!conv.Init(0, 0, OpenCL, iWindowIn, iWindowIn, 2*iWindowKey*iHeadsKV, iCount, optimization, iBatch) || !caKV.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(None);
Матрицу коэффициентов зависимости мы создадим только на стороне контекста OpenCL. Здесь же мы сохраним только указатель на буфер.
//--- Score int temp = OpenCL.AddBuffer(sizeof(float) * iCount * iCount * iHeads, CL_MEM_READ_WRITE); if(temp < 0) return false; if(!caScore.Add(temp)) return false;
Следующим шагом мы создадим слой для записи результатов многоголового внимания.
//--- MH Attention Out base = new CNeuronBaseOCL(); if(!base) return false; if(!base.Init(0, 0, OpenCL, iWindowKey * iHeadsKV * iCount, optimization, iBatch) || !caAttentionOut.Add(conv)) { delete base; return false; } base.SetActivationFunction(None);
И завершает итерации цикла слой понижения размерности до уровня исходных данных.
//--- W0 conv = new CNeuronConvOCL(); if(!conv) return false; if(!conv.Init(0, 0, OpenCL, iWindowKey * iHeadsKV, iWindowKey * iHeadsKV, iWindowIn, iCount, optimization, iBatch) || !caW0.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(None); }
После успешного завершения всех итераций создания уровней пирамидального внимания, мы добавим слой, в буфере которого будем записывать сумму результатов блока пирамидального внимания и исходных данных.
//--- Residual base = new CNeuronBaseOCL(); if(!base) return false; if(!base.Init(0, 0, OpenCL, iWindowIn * iCount, optimization, iBatch) || !caW0.Add(conv)) { delete base; return false; } base.SetActivationFunction(None);
И теперь нам остается инициализировать слои блока FeedForward.
//--- FeedForward if(!cFF1.Init(0, 0, OpenCL, iWindowIn, iWindowIn, 4 * iWindowIn, iCount, optimization, iBatch)) return false; cFF1.SetActivationFunction(LReLU); if(!cFF2.Init(0, 0, OpenCL, 4 * iWindowIn, 4 * iWindowIn, iWindowIn, iCount, optimization, iBatch)) return false; cFF2.SetActivationFunction(None); if(!SetGradient(cFF2.getGradient())) return false;
В завершении метода мы принудительно уберем функцию активации нашего слоя.
SetActivationFunction(None); //--- return true; }
После инициализации объектов нашего класса, мы переходим к реализации алгоритмов прямого прохода. И надо сказать, что здесь нам необходимо провести небольшую подготовительную работу на стороне OpenCL программы. Мы создадим новый кернел MH2PyrAttentionOut, который по существу является скорректированной версией кернела MH2AttentionOut.
__kernel void MH2PyrAttentionOut(__global float *q, __global float *kv, __global float *score, __global float *out, const int dimension, const int heads_kv, const int window ) { //--- init const int q_id = get_global_id(0); const int k = get_global_id(1); const int h = get_global_id(2); const int qunits = get_global_size(0); const int kunits = get_global_size(1); const int heads = get_global_size(2);
Помимо названия кернела, от предыдущего его отличает наличие дополнительного параметра окна внимания window. Вызывать кернел мы планируем в 3-мерном пространстве задач. И как всегда, в начале кернела мы осуществляем идентификацию потока во всех измерениях пространства задач.
Далее мы осуществим расчет необходимых констант.
const int h_kv = h % heads_kv; const int shift_q = dimension * (q_id * heads + h); const int shift_k = dimension * (2 * heads_kv * k + h_kv); const int shift_v = dimension * (2 * heads_kv * k + heads_kv + h_kv); const int shift_s = kunits * (q_id * heads + h) + k; const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE); const int delta_win = (window + 1) / 2; float koef = sqrt((float)dimension); if(koef < 1) koef = 1;
И инициализируем локальный массив для записи промежуточных значений.
__local float temp[LOCAL_ARRAY_SIZE];
Вначале нам предстоит определить коэффициенты зависимостей для каждого элемента последовательности. Как вы знаете, в блоке внимания коэффициенты зависимости нормализуются функцией SoftMax. Для этого мы сначала посчитаем сумму экспонент коэффициентов зависимости.
На первом этапе каждый поток соберет свою часть суммы экспоненциальных значений в соответствующий элемент локального массива данных. И здесь следует обратить внимание на небольшое дополнение: коэффициенты зависимости мы считаем только в пределах окна внимания текущего элемента. Для остальных элементов коэффициент зависимости равен "0".
//--- sum of exp uint count = 0; if(k < ls) do { if((count * ls) < (kunits - k)) { float sum = 0; if(abs(count * ls + k - q_id) <= delta_win) { for(int d = 0; d < dimension; d++) sum = q[shift_q + d] * kv[shift_k + d]; sum = exp(sum / koef); if(isnan(sum)) sum = 0; } temp[k] = (count > 0 ? temp[k] : 0) + sum; } count++; } while((count * ls + k) < kunits); barrier(CLK_LOCAL_MEM_FENCE);
Для синхронизации потоков локальной группы мы используем барьер.
На следующем этапе нам предстоит собрать сумму значений всех элементов локального массива. Для этого мы организуем ещё один цикл, с синхронизацией локальных потоков на каждой итерации. Здесь следует быть внимательными, чтобы каждый поток посетил одинаковое количество барьеров. В противном случае можем получить "зависание" отдельных потоков.
count = min(ls, (uint)kunits); //--- do { count = (count + 1) / 2; if(k < ls) temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0); if(k + count < ls) temp[k + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
После определения суммы экспонент, мы можем посчитать нормализованные коэффициенты зависимости. И тут мы не забываем о наличии зависимостей только в пределах окна внимания.
//--- score float sum = temp[0]; float sc = 0; if(sum != 0 && abs(k - q_id) <= delta_win) { for(int d = 0; d < dimension; d++) sc = q[shift_q + d] * kv[shift_k + d]; sc = exp(sc / koef) / sum; if(isnan(sc)) sc = 0; } score[shift_s] = sc; barrier(CLK_LOCAL_MEM_FENCE);
И конечно, мы синхронизируем локальные потоки после вычисления коэффициентов зависимости.
Далее нам предстоит определить значение элементов с учетом зависимостей. Здесь мы воспользуемся тем же алгоритмом суммирования значений в параллельных потоках, как это было сделано при определении суммы экспоненциальных значений зависимостей. Мы сначала соберем суммы отдельных значений в элементах локального массива.
//--- out for(int d = 0; d < dimension; d++) { uint count = 0; if(k < ls) do { if((count * ls) < (kunits - k)) { float sum = 0; if(abs(count * ls + k - q_id) <= delta_win) { sum = kv[shift_v + d] * (count == 0 ? sc : score[shift_s + count * ls]); if(isnan(sum)) sum = 0; } temp[k] = (count > 0 ? temp[k] : 0) + sum; } count++; } while((count * ls + k) < kunits); barrier(CLK_LOCAL_MEM_FENCE);
А затем соберем сумму значений элементов массива.
//--- count = min(ls, (uint)kunits); do { count = (count + 1) / 2; if(k < ls) temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0); if(k + count < ls) temp[k + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); //--- out[shift_q + d] = temp[0]; } }
Полученную сумму мы сохраним в соответствующий элемент буфера результатов.
Таким образом, мы создали новый керненел внимания в рамках заданного окна. Обратите внимание, что для элементов вне окна внимания коэффициенты зависимости мы указали равными "0". Этот не сложный ход позволяет нам воспользоваться ранее созданным кернелом MH2AttentionInsideGradients для распределения градиента ошибки в рамках обратного прохода.
Для постановки указанных кернелов в очередь выполнения на стороне основной программы были созданы методы AttentionOut и AttentionInsideGradients, соответственно. Их алгоритм не сильно отличается от аналогичных методов, рассмотренных в предыдущих статьях данной серии, и мы не будем сейчас детально на них останавливаться. Я предлагаю вам ознакомиться с ними самостоятельно во вложении. А мы переходим к реализации алгоритмов метода прямого прохода feedForward.
В параметрах метод прямого прохода получает указатель на объект предшествующего нейронного слоя, который содержит исходные данные.
bool CNeuronSPyrAttentionOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { CNeuronBaseOCL *prev = NeuronOCL; CNeuronBaseOCL *current = NULL; CBufferFloat *q = NULL; CBufferFloat *kv = NULL;
В теле метода мы создадим ряд локальных переменных для хранения указателей на обрабатываемые объекты вложенных нейронных слоев.
Далее мы создадим цикл перебора уровней внимания. В теле цикла мы сначала перемешаем исходные данные.
for(uint l = 0; l < iPAMLayers; l++) { //--- Mix current = caS3.At(l); if(!current || !current.FeedForward(prev.AsObject()) ) return false; prev = current;
После чего сгенерируем тензоры сущностей Query, Key и Value для реализации алгоритма многоголового внимания.
//--- Query current = caQuery.At(l); if(!current || !current.FeedForward(prev.AsObject()) ) return false; q = current.getOutput(); //--- Key and Value current = caKV.At(l); if(!current || !current.FeedForward(prev.AsObject()) ) return false; kv = current.getOutput();
И выполним алгоритм кернела внимания для данного уровня.
//--- PAM current = caAttentionOut.At(l); if(!current || !AttentionOut(q, kv, caScore.At(l), current.getOutput(), iPAMLayers - l)) return false; prev = current;
Обратите внимание, что на каждом последующем уровне мы уменьшаем окно внимания, тем самым создавая эффект пирамиды. Для этого мы используем разницу "iPAMLayers - l".
В завершение итераций цикла мы понижаем размер тензора результатов многоголового внимания до уровня размера исходных данных.
//--- W0 current = caW0.At(l); if(!current || !current.FeedForward(prev.AsObject()) ) return false; prev = current; }
За успешным выполнением всех уровней пирамидального внимания, мы суммируем и нормализуем результаты внимания с исходными данными.
//--- Residual current = caW0.At(iPAMLayers); if(!SumAndNormilize(NeuronOCL.getOutput(), prev.getOutput(), current.getOutput(), iWindowIn, true)) return false;
И завершает слой пирамидального внимания блок FeedForward, аналогичный ванильному Transformer.
//---FeedForward if(!cFF1.FeedForward(current.AsObject()) || !cFF2.FeedForward(cFF1.AsObject()) ) return false;
После чего мы повторно суммируем и нормализуем данные от 2 потоков операций.
//--- Residual if(!SumAndNormilize(current.getOutput(), cFF2.getOutput(), getOutput(), iWindowIn, true)) return false; //--- return true; }
При этом не забываем контролировать процесс выполнения операций. А в завершении метода мы возвращаем логический результат выполнения операций вызывающей программе.
Как обычно, после реализации прямого прохода мы переходим к построению алгоритмов обратного прохода, который состоит из 2 этапов: распределение градиента ошибки и оптимизации параметров модели.
Распределение градиентов ошибки реализовано в методе calcInputGradients.
bool CNeuronSPyrAttentionOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!prevLayer) return false;
В параметрах данного метода мы получаем указатель на объект предшествующего нейронного слоя, в буфер которого нам предстоит передать градиент ошибки в соответствии с влиянием исходных данных на общий результат.
Затем мы создадим несколько локальных переменных для временного хранения указателей на внутренние объекты.
CNeuronBaseOCL *next = NULL; CNeuronBaseOCL *current = NULL; CNeuronBaseOCL *q = NULL; CNeuronBaseOCL *kv = NULL;
Распределение градиентов ошибки осуществляется в соответствии с операциями прямого прохода, но в обратном порядке. Вначале мы проведем градиент ошибки через блок FeedForward.
//--- FeedForward current = caW0.At(iPAMLayers); if(!current || !cFF1.calcHiddenGradients(cFF2.AsObject()) || !current.calcHiddenGradients(cFF1.AsObject()) ) return false; next = current;
Затем нам необходимо сложить градиенты ошибки от 2 потоков операций.
//--- Residual current = caW0.At(iPAMLayers - 1); if(!SumAndNormilize(getGradient(), next.getGradient(), current.getGradient(), iWindowIn, false)) return false; CBufferFloat *residual = next.getGradient(); next = current;
После чего, мы организуем цикл обратного перебора уровней внимания с последовательным спуском градиента ошибки.
for(int l = int(iPAMLayers - 1); l >= 0; l--) { //--- W0 current = caAttentionOut.At(l); if(!current || !current.calcHiddenGradients(next.AsObject()) ) return false;
В теле цикла мы сначала распределяем градиент ошибки по головам внимания. А затем распределим его до уровня сущностей Query, Key и Value.
//--- MH Attention q = caQuery.At(l); kv = caKV.At(l); if(!q || !kv || !AttentionInsideGradients(q.getOutput(), q.getGradient(), kv.getOutput(), kv.getGradient(), caScore.At(l), current.getGradient()) ) return false;
Следующим этапом нам предстоит спустить градиент ошибки до слоя перемешивания данных. И здесь нам предстоит объединить данные из 2 потоков — от Query и Key-Value. Для этого мы сначала получим градиент ошибки от Query. И перенесем его во временный буфер.
//--- Query current = caS3.At(l); if(!current || !current.calcHiddenGradients(q.AsObject()) || !Concat(current.getGradient(), current.getGradient(), residual, iWindowIn,0, iCount) ) return false;
Затем возьмем градиент от Key-Value и суммируем результаты 2 потоков данных.
//--- Key and Value if(!current || !current.calcHiddenGradients(kv.AsObject()) || !SumAndNormilize(current.getGradient(), residual, current.getGradient(), iWindowIn, false) ) return false; next = current;
Пропустим градиент ошибки через слой перемешивания данных и перейдем к следующей итерации цикла.
//--- S3 current = (l == 0 ? prevLayer : caW0.At(l - 1)); if(!current || !current.calcHiddenGradients(next.AsObject()) ) return false; next = current; }
В завершение операций метода нам остается лишь объединить градиент ошибки из 2 потоков. Здесь мы сначала скорректируем на производную функции активации предшествующего слоя градиент ошибки остаточных связей. При спуске градиента ошибки непосредственно до уровня слоя, корректировка градиента ошибки на функцию активации происходит автоматически.
current = caW0.At(iPAMLayers - 1); if(!DeActivation(prevLayer.getOutput(), current.getGradient(), residual, prevLayer.Activation()) || !SumAndNormilize(prevLayer.getGradient(), residual, prevLayer.getGradient(), iWindowIn, false) ) return false; //--- return true; }
И затем мы суммируем градиенты ошибок от обоих потоков.
После распределения градиентов ошибки, мы переходим к корректировке параметров модели. Данный функционал реализуем в методе updateInputWeights. Алгоритм данного метода довольно прозаичен и предсказуем — мы лишь последовательно вызываем одноименные методы вложенных объектов, которые содержат обучаемые параметры.
bool CNeuronSPyrAttentionOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { CNeuronBaseOCL *prev = NeuronOCL; CNeuronBaseOCL *current = NULL; for(uint l = 0; l < iPAMLayers; l++) { //--- S3 current = caS3.At(l); if(!current || !current.UpdateInputWeights(prev) ) return false; //--- Query prev = current; current = caQuery.At(l); if(!current || !current.UpdateInputWeights(prev) ) return false; //--- Key and Value current = caKV.At(l); if(!current || !current.UpdateInputWeights(prev) ) return false; //--- W0 prev = caAttentionOut.At(l); current = caW0.At(l); if(!current || !current.UpdateInputWeights(prev) ) return false; prev = current; } //--- FeedForward prev = caW0.At(iPAMLayers); if(!cFF1.UpdateInputWeights(prev) || !cFF2.UpdateInputWeights(cFF1.AsObject()) ) return false; //--- return true; }
В обязательном порядке не забываем контролировать процесс выполнения всех операций метода и вернуть логический результат выполненных операций вызывающей программе.
На этом мы завершаем работу по реализации предложенных подходов метода MSFformer. С полным кодом созданных классов и их методов вы можете ознакомиться во вложении.
Заключение
В данной статье мы познакомились с еще одним интересным и многообещающим методом прогнозирования временных рядов MSFformer (Multi-Scale Feature Transformer), который был представлен в статье "Time Series Prediction Based on Multi-Scale Feature Extraction". Предложенный алгоритм основывается на улучшенной архитектуре пирамидального внимания и нового подхода многоуровневого излечения признаков различного масштаба из исходных данных.
В практической части статьи мы реализовали 2 основных модуля предложенного алгоритма, а на результаты данной работы мы посмотрим в следующей статье.
Ссылки
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Research.mq5 | Советник | Советник сбора примеров |
| 2 | ResearchRealORL.mq5 | Советник | Советник сбора примеров методом Real-ORL |
| 3 | Study.mq5 | Советник | Советник обучения Моделей |
| 4 | StudyEncoder.mq5 | Советник | Советник обучения Энкодера |
| 5 | Test.mq5 | Советник | Советник для тестирования модели |
| 6 | Trajectory.mqh | Библиотека класса | Структура описания состояния системы |
| 7 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 8 | NeuroNet.cl | Библиотека | Библиотека кода программы OpenCL |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Введение в MQL5 (Часть 4): Структуры, классы и функции времени
Введение в MQL5 (Часть 4): Структуры, классы и функции времени
 Разработка системы репликации (Часть 41): Начало второй фазы (II)
Разработка системы репликации (Часть 41): Начало второй фазы (II)
 Алгоритм поиска в окрестности — Across Neighbourhood Search (ANS)
Алгоритм поиска в окрестности — Across Neighbourhood Search (ANS)
 Как разработать агент обучения с подкреплением на MQL5 с интеграцией RestAPI (Часть 4): Организация функций в классах в MQL5
Как разработать агент обучения с подкреплением на MQL5 с интеграцией RestAPI (Часть 4): Организация функций в классах в MQL5
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования