Redes neurais de maneira fácil (Parte 95): Redução do consumo de memória em modelos Transformer
101
0
Introdução
O surgimento da arquitetura Transformer em 2017 resultou no desenvolvimento de grandes modelos de linguagem (LLM), que apresentam alto desempenho na solução de tarefas de processamento de linguagem natural. Logo, as vantagens dos métodos Self-Attention foram adotadas por pesquisadores de quase todas as áreas de aprendizado de máquina.
Contudo, devido à sua natureza autorregressiva, o Decodificador Transformer é limitado pela capacidade da memória usada para carregar e armazenar as entidades Key e Value em cada passo temporal (o chamado cache KV). Como esse cache escala linearmente de acordo com o tamanho do modelo, do tamanho do lote e do comprimento do contexto, ele pode até mesmo superar a quantidade de memória utilizada pelos pesos do modelo.
Devo mencionar que esse problema não é novo. E há diferentes abordagens para resolvê-lo. O mais difundido é a redução direta do número de cabeças KV utilizadas. Em 2019, os autores do artigo "Fast Transformer Decoding:" "One Write-Head is All You Need" propuseram o algoritmo Multi-Query Attention (MQA), que usa apenas uma projeção Key e Value para todas as cabeças de atenção em um único nível. Isso reduz o consumo de memória para o cache KV em 1/heads. No entanto, essa significativa redução no uso de recursos leva a uma certa degradação na qualidade e estabilidade do modelo.
Os autores do método Grouped-Query Attention (GQA), descrito no artigo "GQA:" "Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints" (2023), apresentam uma solução intermediária que divide várias cabeças KV em vários grupos de atenção. A eficiência na redução do tamanho do cache KV ao usar o GQA é de groups/heads. Com um número razoável de cabeças, o GQA pode alcançar quase paridade com o modelo base em vários testes. No entanto, a redução no tamanho do cache KV ainda é limitada a 1/heads com o MQA, o que pode ser insuficiente para algumas aplicações.
Para superar essa limitação, os autores do artigo "MLKV:" "Multi-Layer Key-Value Heads for Memory Efficient Transformer Decoding" propõem o algoritmo de compartilhamento multinível de Key e Value (MLKV). Eles avançam ainda mais no compartilhamento de KV. O MLKV não apenas compartilha as cabeças KV entre as cabeças de atenção de um único nível, mas também entre as cabeças de atenção de outros níveis. As cabeças KV podem ser usadas para grupos de cabeças de atenção em um único nível e/ou em níveis posteriores. Em casos extremos, é possível usar uma única cabeça KV para todas as cabeças de atenção de todos os níveis. Os autores do método experimentam com várias configurações, que utilizam tanto Query agrupadas em um nível quanto entre diferentes níveis. Eles também testam configurações em que o número de cabeças KV é menor que o número de níveis. Os experimentos apresentados no artigo demonstram que essas configurações proporcionam um equilíbrio razoável entre desempenho e economia de memória. A redução prática do volume de memória utilizado para 2/layers em relação ao tamanho original do cache KV não leva a uma deterioração significativa da qualidade do modelo.
1. Método MLKV
O método MLKV é uma continuação lógica dos algoritmos MQA e GQA. Nesses métodos, o tamanho do cache KV é reduzido ao diminuir-se as cabeças KV compartilhadas por um grupo de cabeças de atenção dentro de um único nível de Self-Attention. O passo mais previsível é o uso compartilhado das entidades Key e Value entre os níveis de Self-Attention. Tal passo pode ser justificado por pesquisas recentes sobre o papel do bloco FeedForward no algoritmo Transformer. Supõe-se que esse bloco simula uma memória "Key-Value" que processa diferentes níveis de informação. No entanto, o mais notável para nós é a observação de que grupos de níveis sequenciais calculam coisas semelhantes. Mais precisamente, os níveis inferiores lidam com padrões superficiais, enquanto os superiores lidam com detalhes mais semânticos. Assim, pode-se concluir que a atenção pode ser delegada a grupos de níveis, mantendo os cálculos necessários no bloco FeedForward. Intuitivamente, é compreensível que as cabeças KV possam ser compartilhadas entre níveis com objetivos semelhantes.
Desenvolvendo essas ideias, os autores do método MLKV propõem o compartilhamento multinível de chaves. O MLKV não apenas compartilha as cabeças KV entre as cabeças de atenção para Query em um nível único de Self-Attention, mas também entre cabeças de atenção em outros níveis. Isso permite reduzir o número total de cabeças KV no Transformer e garantir um cache KV ainda menor.
O MLKV pode ser descrito da seguinte forma:
Abaixo está uma visualização feita pelos autores que compara os métodos de redução do tamanho do cache KV.
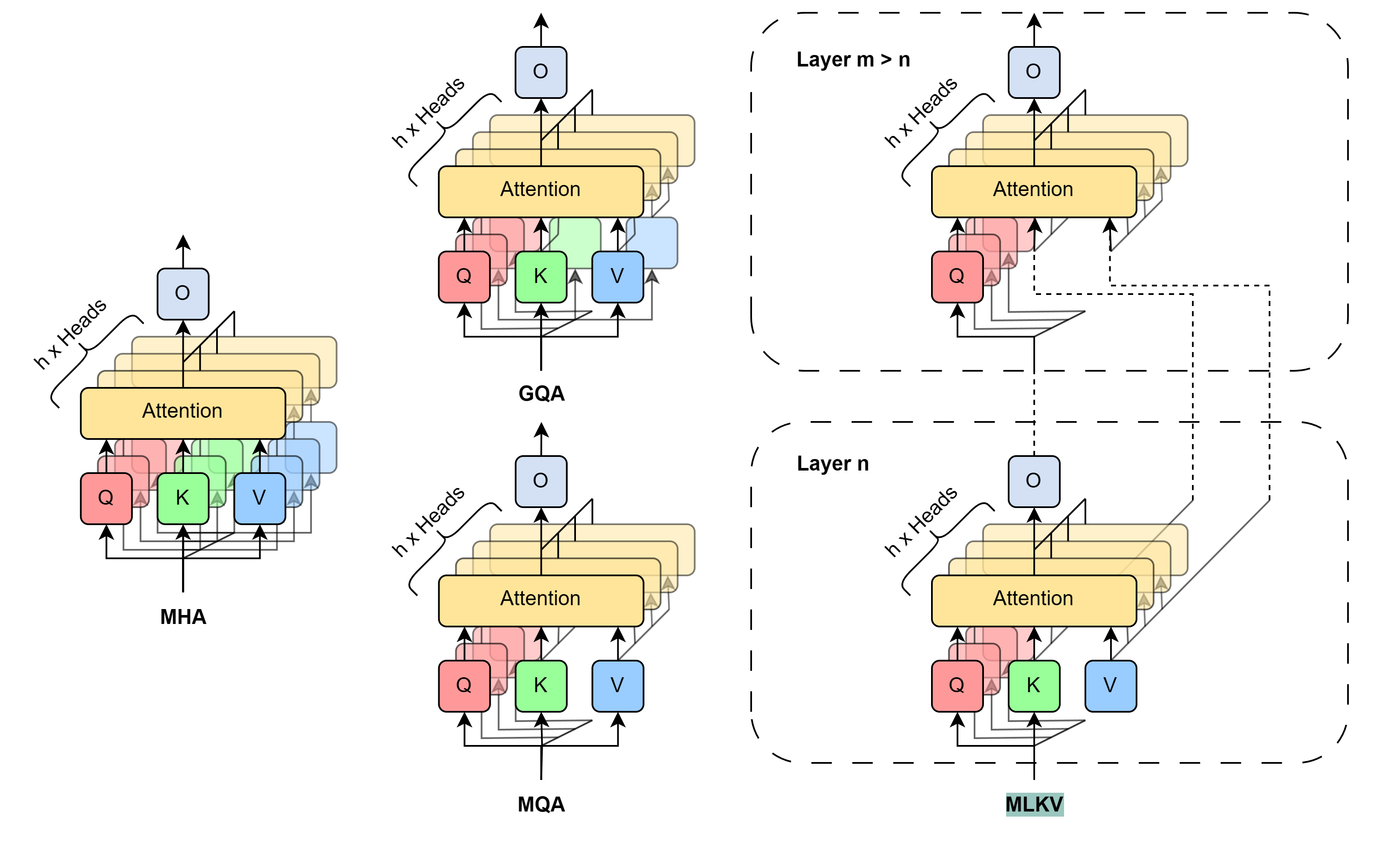
Os experimentos realizados pelos autores do método demonstram um claro compromisso entre memória e precisão. Cabe aos arquitetos decidir o que será sacrificado, considerando vários fatores. Para um número de cabeças KV maior ou igual ao número de níveis, é mais recomendável utilizar GQA/MQA em vez de MLKV. Os autores do método sugerem que ter múltiplas cabeças KV distribuídas em diversos níveis é mais vantajoso do que concentrar várias cabeças KV em um único nível. Em outras palavras, é preferível sacrificar as cabeças KV primeiramente no nível individual^[a-z] da camada (GQA/MQA) e, depois, no nível entre camadas (MLKV).
Para os casos que exigem requisitos de memória mais rigorosos, em que o número de cabeças KV precisa ser menor que o número de níveis, a única solução é o MLKV. Essa decisão de projeto é viável. Ao reduzir o número de cabeças de atenção para 2 vezes menos que o número de níveis, os autores do método descobriram que o MLKV funciona de maneira muito próxima ao MQA. Portanto, esta deve ser uma solução relativamente simples se for necessário um cache KV com metade do tamanho fornecido pelo MQA.
Para requisitos abaixo desse valor, é possível utilizar um número de cabeças KV até 6 vezes menor que o número de níveis sem uma degradação acentuada na qualidade. Qualquer coisa abaixo disso se torna questionável.
2. Implementação com MQL5
Após uma descrição teórica relativamente breve dos métodos propostos, passamos à sua implementação prática com MQL5. E aqui implementaremos o método MLKV. A meu ver, essa é a abordagem mais geral, enquanto o MQA e o GQA podem ser vistos como casos específicos do MLKV.
E a questão mais controversa da implementação iminente é a transmissão de informações entre os níveis neurais. Neste caso, optou-se por não complicar o algoritmo existente de troca de dados entre os objetos dos níveis neurais, utilizando-se o bloco de sequência em múltiplos níveis. Essa implementação já ocorreu anteriormente. Além disso, o CNeuronMLMHAttentionOCL foi escolhido como classe pai para a implementação futura.
2.1 Implementação no lado do OpenCL
Começaremos com a preparação dos kernels no lado do programa OpenCL. Aqui, deve-se destacar que, na classe pai escolhida para a geração paralela das entidades Query, Key e Value, utilizamos um único tensor concatenado. E todo o mecanismo de atenção foi construído com base nisso. No entanto, o uso de diferentes quantidades de cabeças para Query e Key-Value, assim como a utilização de Key-Value de outro nível, nos força a considerar a separação dessas entidades em 2 tensores distintos. Lembro que já fizemos algo semelhante ao construir os blocos de cross-attention.
Então, por que não aproveitar o que já foi desenvolvido e ajustar levemente o algoritmo dos kernels de cross-attention? Tudo o que precisamos fazer é adicionar um novo parâmetro ao kernel, destacando o número de KV-cabeças (marcado em vermelho no código).
__kernel void MH2AttentionOut(__global float *q, ///<[in] Matrix of Querys __global float *kv, ///<[in] Matrix of Keys __global float *score, ///<[out] Matrix of Scores __global float *out, ///<[out] Matrix of attention int dimension, ///< Dimension of Key int heads_kv )
No corpo do kernel, para determinar a cabeça KV a ser analisada, basta usar o resto da divisão da cabeça de atenção atual pelo número total de KV cabeças.
const int h_kv = h % heads_kv;
E faremos o ajuste do deslocamento no buffer do tensor Key-Value.
const int shift_k = 2 * dimension * (k + h_kv); const int shift_v = 2 * dimension * (k + heads_kv + h_kv);
O restante do código do kernel permaneceu inalterado. Alterações semelhantes foram feitas no código do kernel da propagação reversa MH2AttentionInsideGradients. O código completo de ambos os kernels pode ser consultado no anexo.
Concluímos, assim, o trabalho no lado do OpenCL e partimos para o código do programa principal. Primeiro, precisamos restaurar a funcionalidade do código anteriormente criado. Afinal, o parâmetro adicional nos kernels mencionados anteriormente causará erros ao ser chamado. Portanto, localizamos todas as chamadas desses kernels e adicionamos a transmissão de dados ao novo parâmetro.
Lembro que anteriormente utilizávamos o mesmo número de cabeças para Query и Key-Value.
if(!OpenCL.SetArgument(def_k_MH2AttentionOut, def_k_mh2ao_heads_kv, (int)iHeads)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgument(def_k_MH2AttentionInsideGradients, def_k_mh2aig_heads_kv, (int)iHeads)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
2.2 Criação da classe MLKV
Dando continuidade ao nosso trabalho. O próximo passo é criar a classe do bloco de atenção em múltiplos níveis usando a abordagem MLKV — CNeuronMLMHAttentionMLKV. Como mencionado anteriormente, essa nova classe herdará todas as características da classe CNeuronMLMHAttentionOCL. A seguir, é apresentada a estrutura da nova classe.
class CNeuronMLMHAttentionMLKV : public CNeuronMLMHAttentionOCL { protected: uint iLayersToOneKV; uint iHeadsKV; CCollection KV_Tensors; CCollection KV_Weights; CBufferFloat Temp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool AttentionOut(CBufferFloat *q, CBufferFloat *kv, CBufferFloat *scores, CBufferFloat *out); virtual bool AttentionInsideGradients(CBufferFloat *q, CBufferFloat *q_g, CBufferFloat *kv, CBufferFloat *kv_g, CBufferFloat *scores, CBufferFloat *gradient); //--- virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronMLMHAttentionMLKV(void) {}; ~CNeuronMLMHAttentionMLKV(void) {}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint heads_kv, uint units_count, uint layers, uint layers_to_one_kv, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronMLMHAttentionMLKV; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
Como pode ser visto, na estrutura apresentada da classe, introduzimos 2 variáveis para armazenar o número de cabeças KV (iHeadsKV) e a periodicidade de atualização do tensor Key-Value (iLayersToOneKV).
Também adicionamos coleções para armazenamento dos tensores Key-Value e a matriz de pesos para a sua formação (KV_Tensors e KV_Weights, respectivamente).
Além disso, incluímos um buffer Temp para registrar valores intermediários dos gradientes de erro.
O conjunto de métodos da classe é bastante padrão, e imagino que você já compreenda sua finalidade. Entraremos em detalhes sobre cada um deles durante a implementação.
Declaramos todos os objetos internos da classe como estáticos, o que nos permite deixar os construtores e destrutores da classe "vazios". A inicialização de todos os objetos e variáveis embutidas é realizada no método Init. Como de costume, os parâmetros desse método contêm todas as informações necessárias para a criação do objeto requerido.
bool CNeuronMLMHAttentionMLKV::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint heads_kv, uint units_count, uint layers, uint layers_to_one_kv, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
No corpo do método, chamamos imediatamente o método homônimo da classe base de todos os níveis neurais, CNeuronBaseOCL.
Observe que nos referimos ao objeto da classe base, e não diretamente ao pai imediato. Isso se deve à separação das entidades Query, Key e Value em 2 tensores, o que altera os tamanhos de alguns buffers de dados. No entanto, essa abordagem nos obriga a inicializar não apenas novos objetos, mas também os herdados da classe pai.
Após a execução bem-sucedida do método de inicialização da classe base, armazenamos os parâmetros recebidos em variáveis internas.
iWindow = fmax(window, 1); iWindowKey = fmax(window_key, 1); iUnits = fmax(units_count, 1); iHeads = fmax(heads, 1); iLayers = fmax(layers, 1); iHeadsKV = fmax(heads_kv, 1); iLayersToOneKV = fmax(layers_to_one_kv, 1);
O próximo passo é definir os tamanhos de todos os buffers a serem criados.
uint num_q = iWindowKey * iHeads * iUnits; //Size of Q tensor uint num_kv = 2 * iWindowKey * iHeadsKV * iUnits; //Size of KV tensor uint q_weights = (iWindow + 1) * iWindowKey * iHeads; //Size of weights' matrix of Q tenzor uint kv_weights = 2 * (iWindow + 1) * iWindowKey * iHeadsKV; //Size of weights' matrix of KV tenzor uint scores = iUnits * iUnits * iHeads; //Size of Score tensor uint mh_out = iWindowKey * iHeads * iUnits; //Size of multi-heads self-attention uint out = iWindow * iUnits; //Size of out tensore uint w0 = (iWindowKey + 1) * iHeads * iWindow; //Size W0 tensor uint ff_1 = 4 * (iWindow + 1) * iWindow; //Size of weights' matrix 1-st feed forward layer uint ff_2 = (4 * iWindow + 1) * iWindow; //Size of weights' matrix 2-nd feed forward layer
Então, criamos um laço com o número de iterações igual ao número de camadas internas no bloco de atenção que estamos criando.
for(uint i = 0; i < iLayers; i++) {
No corpo do laço, criamos outro loop aninhado, onde primeiro criamos os buffers para armazenar dados. E na segunda iteração do loop aninhado, criamos os buffers para gravar os respectivos gradientes de erro.
CBufferFloat *temp = NULL; for(int d = 0; d < 2; d++) { //--- Initilize Q tensor temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(num_q, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Tensors.Add(temp)) return false;
Primeiro, criamos os tensores das entidades Query. E em seguida, os tensores correspondentes para gravar as entidades Key-Value. Apenas os últimos serão criados uma vez a cada iLayersToOneKV iterações do loop.
//--- Initilize KV tensor if(i % iLayersToOneKV == 0) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(num_kv, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!KV_Tensors.Add(temp)) return false; }
Depois, seguindo o algoritmo Transformer, criamos os buffers para registrar os tensores da matriz de coeficientes de dependência, a atenção multi-cabeças e sua representação comprimida.
//--- Initialize scores temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(scores, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!S_Tensors.Add(temp)) return false;
//--- Initialize multi-heads attention out temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(mh_out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!AO_Tensors.Add(temp)) return false;
//--- Initialize attention out temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false;
Adicionamos também os buffers do bloco FeedForward.
//--- Initialize Feed Forward 1 temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(4 * out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false;
//--- Initialize Feed Forward 2 if(i == iLayers - 1) { if(!FF_Tensors.Add(d == 0 ? Output : Gradient)) return false; continue; } temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false; }
Preste atenção que, ao criar buffers para salvar os resultados e os gradientes de erro da 2ª camada do bloco FeedForward, verificamos o número da camada. Como não criaremos novos buffers para a última camada, preservamos os ponteiros para os buffers de resultados e gradientes de erro já criados na nossa classe CNeuronMLMHAttentionMLKV. Isso nos permite evitar a cópia excessiva de dados ao trocar informações com a camada subsequente.
Após a criação dos buffers para armazenar os resultados intermediários e os gradientes de erro correspondentes, procederemos com a criação dos buffers das matrizes de parâmetros treináveis da nossa classe. É importante mencionar que há um número considerável desses parâmetros. Primeiro, criaremos e inicializaremos a matriz de pesos para a geração da entidade Query com parâmetros aleatórios.
//--- Initilize Q weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(q_weights)) return false; float k = (float)(1 / sqrt(iWindow + 1)); for(uint w = 0; w < q_weights; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Weights.Add(temp)) return false;
Da mesma forma, geramos os parâmetros para a criação do tensor Key-Value. Esses parâmetros são criados apenas uma vez a cada iLayersToOneKV níveis internos.
//--- Initilize KV weights if(i % iLayersToOneKV == 0) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(kv_weights)) return false; float k = (float)(1 / sqrt(iWindow + 1)); for(uint w = 0; w < kv_weights; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!KV_Weights.Add(temp)) return false; }
Em seguida, geramos os parâmetros para a compressão dos resultados da atenção multi-cabeças.
//--- Initilize Weights0 temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(w0)) return false; for(uint w = 0; w < w0; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
Por último, mas não menos importante, geramos os parâmetros para o bloco FeedForward.
//--- Initilize FF Weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(ff_1)) return false; for(uint w = 0; w < ff_1; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(ff_2)) return false; k = (float)(1 / sqrt(4 * iWindow + 1)); for(uint w = 0; w < ff_2; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
Durante o treinamento do modelo, precisaremos de buffers para registrar os momentos de todos os parâmetros criados anteriormente. Esses buffers serão gerados em um loop aninhado, cujo número de iterações depende do método de otimização selecionado.
//--- for(int d = 0; d < (optimization == SGD ? 1 : 2); d++) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(q_weights, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Weights.Add(temp)) return false;
if(i % iLayersToOneKV == 0) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(kv_weights, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!KV_Weights.Add(temp)) return false; }
temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(w0, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
//--- Initilize FF Weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(ff_1, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(ff_2, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; } }
Depois de criarmos todas as coleções de buffers para o nosso bloco de atenção, inicializamos mais um buffer auxiliar, que usaremos para armazenar valores intermediários.
if(!Temp.BufferInit(MathMax(num_kv, out), 0)) return false; if(!Temp.BufferCreate(OpenCL)) return false; //--- return true; }
Em cada etapa, garantimos o controle do processo de execução das operações. E, ao final do método, retornamos um resultado lógico para a função chamadora, indicando o sucesso ou falha das operações.
Nos métodos AttentionOut e AttentionInsideGradients, ocorre o enfileiramento dos kernels que ajustamos. No entanto, não entraremos em detalhes sobre seus algoritmos neste momento. O algoritmo para enfileirar qualquer kernel permanece inalterado:
- Definição do espaço de tarefas.
- Transferência de todos os parâmetros necessários para o kernel.
- Enfileiramento do kernel para execução.
O código deste algoritmo já foi descrito várias vezes ao longo desta série de artigos, incluindo os métodos de enfileiramento da versão original dos kernels que modificamos, detalhados no artigo dedicado ao método ADAPT. Recomendo que você consulte esses métodos no anexo.
Agora, vamos analisar o algoritmo do método de propagação para frente feedForward. Nos parâmetros do método, recebemos um ponteiro para o objeto do nível anterior, que, neste caso, fornece os dados de entrada.
bool CNeuronMLMHAttentionMLKV::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(NeuronOCL) == POINTER_INVALID) return false;
No corpo do método, a primeira coisa que fazemos é verificar a validade do ponteiro recebido. Em seguida, declaramos um ponteiro local para o buffer do tensor Key-Value e criamos um laço para iterar por todos os níveis internos do nosso bloco.
CBufferFloat *kv = NULL; for(uint i = 0; (i < iLayers && !IsStopped()); i++) { //--- Calculate Queries, Keys, Values CBufferFloat *inputs = (i == 0 ? NeuronOCL.getOutput() : FF_Tensors.At(6 * i - 4)); CBufferFloat *q = QKV_Tensors.At(i * 2); if(IsStopped() || !ConvolutionForward(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)), inputs, q, iWindow, iWindowKey * iHeads, None)) return false;
Dentro do laço, primeiro geramos o tensor das entidades Query. Depois, geramos o tensor Key-Value. Observe que o último não é gerado em cada iteração do laço, mas apenas a cada iLayersToOneKV níveis. O controle matemático dessa condição é simples — o índice do nível atual deve ser divisível sem resto pelo número de níveis que utilizam o mesmo tensor Key-Value. Vale destacar que, para o primeiro nível com índice "0", o resto da divisão também é zero.
if((i % iLayersToOneKV) == 0) { uint i_kv = i / iLayersToOneKV; kv = KV_Tensors.At(i_kv * 2); if(IsStopped() || !ConvolutionForward(KV_Weights.At(i_kv * (optimization == SGD ? 2 : 3)), inputs, kv, iWindow, 2 * iWindowKey * iHeadsKV, None)) return false; }
O ponteiro para o buffer das entidades geradas é salvo na variável local que declaramos anteriormente, facilitando o acesso a esses dados nas iterações subsequentes do laço.
Após a geração de todas as entidades necessárias, realizamos as operações de propagação para frente do bloco de cross-attention, cujos resultados são registrados no buffer de saída da atenção multi-cabeças.
//--- Score calculation and Multi-heads attention calculation CBufferFloat *temp = S_Tensors.At(i * 2); CBufferFloat *out = AO_Tensors.At(i * 2); if(IsStopped() || !AttentionOut(q, kv, temp, out)) return false;
Em seguida, comprimimos os dados obtidos até o tamanho dos dados de entrada originais.
//--- Attention out calculation temp = FF_Tensors.At(i * 6); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), out, temp, iWindowKey * iHeads, iWindow, None)) return false;
Após isso, conforme o algoritmo Transformer, somamos os resultados do bloco Self-Attention com os dados de entrada e normalizamos os valores resultantes.
//--- Sum and normilize attention if(IsStopped() || !SumAndNormilize(temp, inputs, temp, iWindow, true)) return false;
Em seguida, passamos os dados pelo bloco FeedForward.
//--- Feed Forward inputs = temp; temp = FF_Tensors.At(i * 6 + 1); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), inputs, temp, iWindow, 4 * iWindow, LReLU)) return false; out = FF_Tensors.At(i * 6 + 2); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), temp, out, 4 * iWindow, iWindow, activation)) return false;
Depois, os dados provenientes dos dois fluxos são novamente somados e normalizados.
//--- Sum and normilize out if(IsStopped() || !SumAndNormilize(out, inputs, out, iWindow, true)) return false; } //--- return true; }
Após o término bem-sucedido de todas as iterações do laço que percorre os níveis internos do nosso bloco neural, retornamos um resultado lógico para a função chamadora, indicando o sucesso das operações realizadas.
Com a implementação dos métodos de propagação concluída, passamos à construção dos algoritmos de propagação reversa. Nessa etapa, otimizamos os parâmetros do modelo para maximizar a função de verossimilhança na amostra de treinamento. Como você sabe, o algoritmo de propagação reversa é dividido em duas etapas. Primeiro, propagamos o gradiente do erro por todos os elementos do modelo, considerando sua influência no resultado geral. Essa funcionalidade é realizada no método calcInputGradients. Na segunda etapa (método updateInputWeights), a otimização dos parâmetros é feita na direção do anti-gradiente.
Nossa implementação do algoritmo de propagação reversa começa com o método de propagação do gradiente de erro, calcInputGradients. Nos parâmetros, esse método recebe um ponteiro para o objeto do nível neural anterior. Enquanto na propagação para frente ele servia como dados de entrada, nesta etapa, os resultados das operações serão registrados no buffer de gradientes de erro desse objeto.
bool CNeuronMLMHAttentionMLKV::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer) == POINTER_INVALID) return false;
No corpo do método, verificamos a validade do ponteiro recebido. Em seguida, criamos duas variáveis locais para armazenar os ponteiros dos buffers de dados que são transmitidos entre os níveis internos.
CBufferFloat *out_grad = Gradient;
CBufferFloat *kv_g = KV_Tensors.At(KV_Tensors.Total() - 1);
Após uma breve preparação, criamos um laço que percorre os níveis internos do bloco neural em ordem reversa.
for(int i = int(iLayers - 1); (i >= 0 && !IsStopped()); i--) { if(i == int(iLayers - 1) || (i + 1) % iLayersToOneKV == 0) kv_g = KV_Tensors.At((i / iLayersToOneKV) * 2 + 1);
Dentro deste laço, determinamos a necessidade de trocar o buffer de gradientes de erro das entidades Key-Value.
Lembro que o método MLKV pressupõe o uso de um único tensor de entidades Key-Value para vários blocos Self-Attention. Durante a realização da propagação para frente, já implementamos os mecanismos apropriados. Agora, precisamos propagar o gradiente de erro até o nível correspondente de Key-Value. E, naturalmente, somaremos os gradientes de erro de diferentes níveis.
A estrutura do algoritmo deste método é muito semelhante à distribuição do gradiente de erro em objetos de cross-attention. Primeiro, passamos o gradiente de erro recebido do nível subsequente pelo bloco FeedForward.
//--- Passing gradient through feed forward layers if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), out_grad, FF_Tensors.At(i * 6 + 1), FF_Tensors.At(i * 6 + 4), 4 * iWindow, iWindow, None)) return false; CBufferFloat *temp = FF_Tensors.At(i * 6 + 3); if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), FF_Tensors.At(i * 6 + 4), FF_Tensors.At(i * 6), temp, iWindow, 4 * iWindow, LReLU)) return false;
Assim como somamos os dados de dois fluxos durante a propagação para frente, também somamos o gradiente de erro nesses mesmos fluxos de dados na direção reversa.
//--- Sum and normilize gradients if(IsStopped() || !SumAndNormilize(out_grad, temp, temp, iWindow, false)) return false; out_grad = temp;
No próximo estágio, realizamos a separação do gradiente de erro obtido entre as cabeças de atenção.
//--- Split gradient to multi-heads if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), out_grad, AO_Tensors.At(i * 2), AO_Tensors.At(i * 2 + 1), iWindowKey * iHeads, iWindow, None)) return false;
E então distribuímos o gradiente de erro entre as entidades Query, Key e Value. Aqui, fazemos uma pequena ramificação no algoritmo. Precisamos somar o gradiente de erro do tensor Key-Value de vários níveis internos. Se realizássemos a distribuição do gradiente de erro diretamente, acabaríamos apagando os dados previamente acumulados e substituindo-os por novos a cada vez. Por isso, gravaremos o gradiente de erro no buffer do tensor Key-Value apenas na primeira vez que for acessado.
//--- Passing gradient to query, key and value if(i == int(iLayers - 1) || (i + 1) % iLayersToOneKV == 0) { if(IsStopped() || !AttentionInsideGradients(QKV_Tensors.At(i * 2), QKV_Tensors.At(i * 2 + 1), KV_Tensors.At((i / iLayersToOneKV) * 2), kv_g, S_Tensors.At(i * 2), AO_Tensors.At(i * 2 + 1))) return false; }
Nos demais casos, primeiro registraremos o gradiente de erro em um buffer auxiliar. Em seguida, somaremos os valores obtidos aos dados anteriormente acumulados.
else { if(IsStopped() || !AttentionInsideGradients(QKV_Tensors.At(i * 2), QKV_Tensors.At(i * 2 + 1), KV_Tensors.At((i / iLayersToOneKV) * 2), GetPointer(Temp), S_Tensors.At(i * 2), AO_Tensors.At(i * 2 + 1))) return false; if(IsStopped() || !SumAndNormilize(kv_g, GetPointer(Temp), kv_g, iWindowKey, false, 0, 0, 0, 1)) return false; }
A seguir, precisamos transferir o gradiente de erro para o nível anterior. Aqui, o termo "nível anterior" refere-se, principalmente, ao nível interno anterior. No entanto, ao processar o nível mais inferior, o gradiente de erro será transferido para o buffer do objeto fornecido nos parâmetros do método.
Primeiro, definimos um ponteiro para o objeto que receberá o gradiente de erro.
CBufferFloat *inp = NULL; if(i == 0) { inp = prevLayer.getOutput(); temp = prevLayer.getGradient(); } else { temp = FF_Tensors.At(i * 6 - 1); inp = FF_Tensors.At(i * 6 - 4); }
Depois disso, propagamos o gradiente de erro da entidade Query.
if(IsStopped() || !ConvolutionInputGradients(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)), QKV_Tensors.At(i * 2 + 1), inp, temp, iWindow, iWindowKey * iHeads, None)) return false;
E somamos o gradiente de erro nos dois fluxos de dados (Query + "fluxo direto").
//--- Sum and normilize gradients if(IsStopped() || !SumAndNormilize(out_grad, temp, temp, iWindow, false, 0, 0, 0, 1)) return false;
No algoritmo descrito acima, faltam apenas os gradientes de erro das entidades Key e Value. Como você se lembra, essas entidades não são formadas em cada nível interno. Portanto, o gradiente de erro será transmitido apenas para os dados que foram utilizados na sua formação. Mas há um detalhe importante. Já registramos no buffer de gradientes dos dados de entrada o erro da entidade Query e do fluxo direto. Assim, primeiro gravaremos o gradiente de erro em um buffer auxiliar e, em seguida, o somaremos aos dados previamente coletados.
//--- if((i % iLayersToOneKV) == 0) { if(IsStopped() || !ConvolutionInputGradients(KV_Weights.At(i / iLayersToOneKV * (optimization == SGD ? 2 : 3)), kv_g, inp, GetPointer(Temp), iWindow, 2 * iWindowKey * iHeadsKV, None)) return false; if(IsStopped() || !SumAndNormilize(GetPointer(Temp), temp, temp, iWindow, false, 0, 0, 0, 1)) return false; }
Ao final das iterações do laço, passamos o ponteiro para o buffer de gradientes de erro para realizar as operações na próxima iteração.
if(i > 0) out_grad = temp; } //--- return true; }
Como sempre, monitoramos o resultado da execução das operações em cada etapa. E, após o sucesso de todas as iterações do laço, retornamos o resultado lógico da execução do método à função chamadora.
Distribuímos o gradiente de erro por todos os objetos internos e o nível anterior. O próximo passo é ajustar os parâmetros do modelo. Essa funcionalidade é realizada no método updateInputWeights. Assim como nos métodos mencionados anteriormente, recebemos um ponteiro para o objeto do nível anterior nos parâmetros.
bool CNeuronMLMHAttentionMLKV::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(NeuronOCL) == POINTER_INVALID) return false; CBufferFloat *inputs = NeuronOCL.getOutput();
No corpo do método, verificamos a validade do ponteiro recebido e, imediatamente, armazenamos o ponteiro para o buffer de resultados do objeto na variável local.
Em seguida, definimos o laço que percorre todos os níveis internos, atualizando os parâmetros do modelo.
for(uint l = 0; l < iLayers; l++) { if(IsStopped() || !ConvolutuionUpdateWeights(QKV_Weights.At(l * (optimization == SGD ? 2 : 3)), QKV_Tensors.At(l * 2 + 1), inputs, (optimization == SGD ? QKV_Weights.At(l * 2 + 1) : QKV_Weights.At(l * 3 + 1)), (optimization == SGD ? NULL : QKV_Weights.At(l * 3 + 2)), iWindow, iWindowKey * iHeads)) return false;
De forma similar ao método de propagação para frente, primeiro corrigimos os parâmetros de formação do tensor Query.
Depois, atualizamos os parâmetros de formação do tensor Key-Value. É importante notar que esses parâmetros não são corrigidos em todas as iterações do laço. No entanto, a correção dos parâmetros do tensor Key-Value no laço geral facilita a sincronização com o buffer correto dos dados de entrada e mantém o código o mais legível possível.
if(l % iLayersToOneKV == 0) { uint l_kv = l / iLayersToOneKV; if(IsStopped() || !ConvolutuionUpdateWeights(KV_Weights.At(l_kv * (optimization == SGD ? 2 : 3)), KV_Tensors.At(l_kv * 2 + 1), inputs, (optimization == SGD ? KV_Weights.At(l_kv*2 + 1) : KV_Weights.At(l_kv*3 + 1)), (optimization == SGD ? NULL : KV_Weights.At(l_kv * 3 + 2)), iWindow, 2 * iWindowKey * iHeadsKV)) return false; }
O bloco Self-Attention em si não contém parâmetros treináveis. No entanto, eles aparecem no nível de compressão dos resultados da atenção multi-cabeças para o tamanho dos dados de entrada. O próximo passo é corrigir esses parâmetros.
if(IsStopped() || !ConvolutuionUpdateWeights(FF_Weights.At(l * (optimization == SGD ? 6 : 9)), FF_Tensors.At(l * 6 + 3), AO_Tensors.At(l * 2), (optimization == SGD ? FF_Weights.At(l * 6 + 3) : FF_Weights.At(l * 9 + 3)), (optimization == SGD ? NULL : FF_Weights.At(l * 9 + 6)), iWindowKey * iHeads, iWindow)) return false;
Após isso, resta apenas ajustar os parâmetros do bloco FeedForward.
if(IsStopped() || !ConvolutuionUpdateWeights(FF_Weights.At(l * (optimization == SGD ? 6 : 9) + 1), FF_Tensors.At(l * 6 + 4), FF_Tensors.At(l * 6), (optimization == SGD ? FF_Weights.At(l * 6 + 4) : FF_Weights.At(l * 9 + 4)), (optimization == SGD ? NULL : FF_Weights.At(l * 9 + 7)), iWindow, 4 * iWindow)) return false; //--- if(IsStopped() || !ConvolutuionUpdateWeights(FF_Weights.At(l * (optimization == SGD ? 6 : 9) + 2), FF_Tensors.At(l * 6 + 5), FF_Tensors.At(l * 6 + 1), (optimization == SGD ? FF_Weights.At(l * 6 + 5) : FF_Weights.At(l * 9 + 5)), (optimization == SGD ? NULL : FF_Weights.At(l * 9 + 8)), 4 * iWindow, iWindow)) return false;
Passamos o ponteiro para o buffer de dados de entrada para o próximo ciclo interno do nível neural e seguimos para a próxima iteração do laço.
inputs = FF_Tensors.At(l * 6 + 2); } //--- return true; }
Completadas todas as iterações com sucesso, retornamos um resultado lógico para a função chamadora, indicando a execução bem-sucedida das operações.
Assim, concluímos a análise dos métodos de nosso novo bloco de atenção que utiliza as abordagens propostas pelos autores do método MLKV. O código completo desta classe e de todos os seus métodos pode ser consultado no anexo.
Como mencionado anteriormente, os métodos MQA e GQA são casos particulares do MLKV. Eles podem ser facilmente implementados com a classe criada, definindo o parâmetro "layers_to_one_kv=1" no método de inicialização da classe. Se o valor do parâmetro heads_kv for igual ao número de cabeças de atenção da entidade Query, obtemos o Transformer tradicional. Se for menor, temos o GQA. E, se heads_kv for igual a "1", temos a implementação do MQA.
Vale mencionar que, durante a elaboração deste artigo, também foi criado um bloco de cross-attention com as abordagens MLKV — CNeuronMLCrossAttentionMLKV. A estrutura dessa classe está apresentada abaixo.
class CNeuronMLCrossAttentionMLKV : public CNeuronMLMHAttentionMLKV { protected: uint iWindowKV; uint iUnitsKV; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context); virtual bool AttentionOut(CBufferFloat *q, CBufferFloat *kv, CBufferFloat *scores, CBufferFloat *out); virtual bool AttentionInsideGradients(CBufferFloat *q, CBufferFloat *q_g, CBufferFloat *kv, CBufferFloat *kv_g, CBufferFloat *scores, CBufferFloat *gradient); //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context); public: CNeuronMLCrossAttentionMLKV(void) {}; ~CNeuronMLCrossAttentionMLKV(void) {}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key,uint heads, uint window_kw, uint heads_kv, uint units_count, uint units_count_kv, uint layers, uint layers_to_one_kv, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronMLCrossAttentionMLKV; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); };
Essa classe é uma herança da classe CNeuronMLMHAttentionMLKV, com apenas pequenas correções nos algoritmos de seus métodos, as quais você pode explorar no anexo.
2.3 Arquitetura das Modelos
Acima, implementamos as abordagens propostas pelos autores do método MLKV usando MQL5, e agora podemos descrever a arquitetura dos modelos treináveis. Ao contrário de algumas das últimas discussões, desta vez não iremos modificar a arquitetura do Codificador de Estado do Ambiente. Em vez disso, adicionaremos novos objetos à arquitetura das modelos do Ator e do Crítico. Lembro que a arquitetura desses modelos é definida no método CreateDescriptions.
bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; }
Nos parâmetros, o método recebe ponteiros para dois arrays dinâmicos que registram a arquitetura sequencial das modelos. No corpo do método, verificamos os ponteiros recebidos e, se necessário, criamos novas instâncias dos objetos.
Começamos descrevendo a arquitetura do Ator. Planejamos fornecer ao modelo a descrição do estado da conta e das posições abertas como entrada.
//--- Actor actor.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = AccountDescr; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Os dados recebidos passam por um processamento inicial por meio de uma camada completamente conectada.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = EmbeddingSize; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Em seguida, introduziremos uma nova camada de cross-attention multinível usando as abordagens MLKV.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMLCrossAttentionMLKV; { int temp[] = {1, BarDescr}; ArrayCopy(descr.units, temp); } { int temp[] = {EmbeddingSize, NForecast}; ArrayCopy(descr.windows, temp); }
Essa camada irá associar o estado atual da conta com a previsão do movimento de preços futuro, gerada pelo Codificador de Estado do Ambiente.
Aqui, utilizaremos 8 cabeças de atenção para Query e apenas 2 para o tensor Key-Value.
{
int temp[] = {8, 2};
ArrayCopy(descr.heads, temp);
}
No total, criaremos 9 camadas aninhadas em nosso bloco, gerando um novo tensor Key-Value a cada 3 camadas.
descr.layers = 9; descr.step = 3;
Para otimizar os parâmetros do modelo, empregaremos o método Adam.
descr.window_out = 32; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Após o bloco de atenção, os dados serão processados por duas camadas totalmente conectadas.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Na saída do modelo, formaremos uma política estocástica do Ator, que permite ações dentro de um intervalo de valores ótimos.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 2 * NActions; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = NActions; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Além disso, aplicaremos as abordagens do método FreDF para alinhar as ações na área de frequência.
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = NActions; descr.count = 1; descr.step = int(false); descr.probability = 0.8f; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
De forma semelhante, construiremos o modelo do Crítico. No entanto, em vez do estado da conta, forneceremos ao modelo um vetor de ações gerado pela política do Ator.
//--- Critic critic.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = NActions; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Essas ações também passam por um processamento inicial em uma camada totalmente conectada.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = EmbeddingSize; descr.activation = SIGMOID; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Em seguida, há um bloco de cross-attention.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMLCrossAttentionMLKV; { int temp[] = {1, BarDescr}; ArrayCopy(descr.units, temp); } { int temp[] = {EmbeddingSize, NForecast}; ArrayCopy(descr.windows, temp); } { int temp[] = {8, 2}; ArrayCopy(descr.heads, temp); } descr.window_out = 32; descr.step = 3; descr.layers = 9; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Os resultados do processamento no bloco de cross-attention passam por três camadas totalmente conectadas.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Na saída do modelo, formamos um vetor de recompensas esperadas.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NRewards; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Adicionamos também uma camada FreDF para garantir a consistência das recompensas na área de frequência.
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = NRewards; descr.count = 1; descr.step = int(false); descr.probability = 0.8f; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- return true; }
Os Expert Advisors de coleta de dados e treinamento dos modelos permaneceram inalterados. O código completo deles pode ser consultado no anexo. No mesmo lugar, você encontrará o código completo de todas as classes e programas utilizados na preparação deste artigo.
3. Testes
Após a implementação dos métodos propostos, passamos à etapa final do nosso trabalho: verificar a eficácia das abordagens sugeridas com dados reais.
Como de costume, usamos dados históricos reais do par EURUSD no timeframe H1 durante todo o ano de 2023 para treinar os modelos. A coleta de dados para o conjunto de treinamento é feita executando os Expert Advisors que interagem com o ambiente no testador de estratégias do MetaTrader 5.
Não é segredo que, na primeira execução, nossos modelos são inicializados com parâmetros aleatórios. Consequentemente, obtemos execuções de políticas completamente aleatórias, longe do ideal. Para incluir dados de execuções lucrativas no conjunto de treinamento inicial, recomendo usar as abordagens do método Real-ORL ao coletar os dados primários.
Depois de coletar o conjunto de treinamento inicial, começamos treinando o Codificador de Estado do Ambiente, executando o Expert Advisor ".../MLKV/StudyEncoder.mq5" em tempo real no gráfico do terminal MetaTrader 5. Este Expert Advisor trabalha apenas com o conjunto de treinamento, analisando as dependências nos dados históricos de movimento de preços. E, essencialmente, para o treinamento, um único ciclo é suficiente, independentemente dos resultados de negociação. Portanto, treinamos o Codificador de Estado da Conta até que ocorra uma estabilização na redução do erro de previsão, sem atualizar o conjunto de treinamento.
Vale mencionar que os modelos do Ator e do Crítico treinados posteriormente utilizam as previsões obtidas de maneira indireta. Para alcançar o melhor desempenho, é necessário extrair as tendências atuais do estado do ambiente e sua intensidade no estado oculto do Codificador, ao qual as modelos do Ator e do Crítico recorrem.
Após alcançar o resultado desejado no treinamento do Codificador de Estado do Ambiente, passamos ao treinamento da política do Ator e à avaliação precisa das ações pelo Crítico. A segunda etapa do treinamento dos modelos é iterativa. Isso se deve à alta variabilidade da interação com o ambiente dos mercados financeiros. E não é possível cobrir todos os cenários de interação do Agente com o ambiente. Portanto, após algumas iterações de treinamento dos modelos do Ator e do Crítico, realizamos uma iteração adicional para coletar mais dados de treinamento. Esse processo visa complementar o conjunto de dados coletado anteriormente com interações recentes do Agente com o ambiente dentro do escopo da política atual do Ator, o que ajuda a refiná-la e otimizá-la.
Como mencionado anteriormente, várias iterações de treinamento dos modelos do Ator e do Crítico são alternadas com operações de atualização do conjunto de dados de treinamento. Este processo se repete algumas vezes até que a política desejada do Ator seja obtida.
O teste dos modelos treinados é feito com dados de janeiro de 2024, que não fazem parte do conjunto de treinamento. Todos os outros parâmetros permanecem inalterados desde as iterações de coleta do conjunto de treinamento.
Devo admitir que, durante o treinamento dos modelos para esta parte do artigo, não consegui desenvolver uma política capaz de gerar lucro na amostra de teste. Isso parece ser uma consequência do processo de degradação do modelo, mencionado no artigo original.
Os resultados dos testes estão apresentados abaixo.
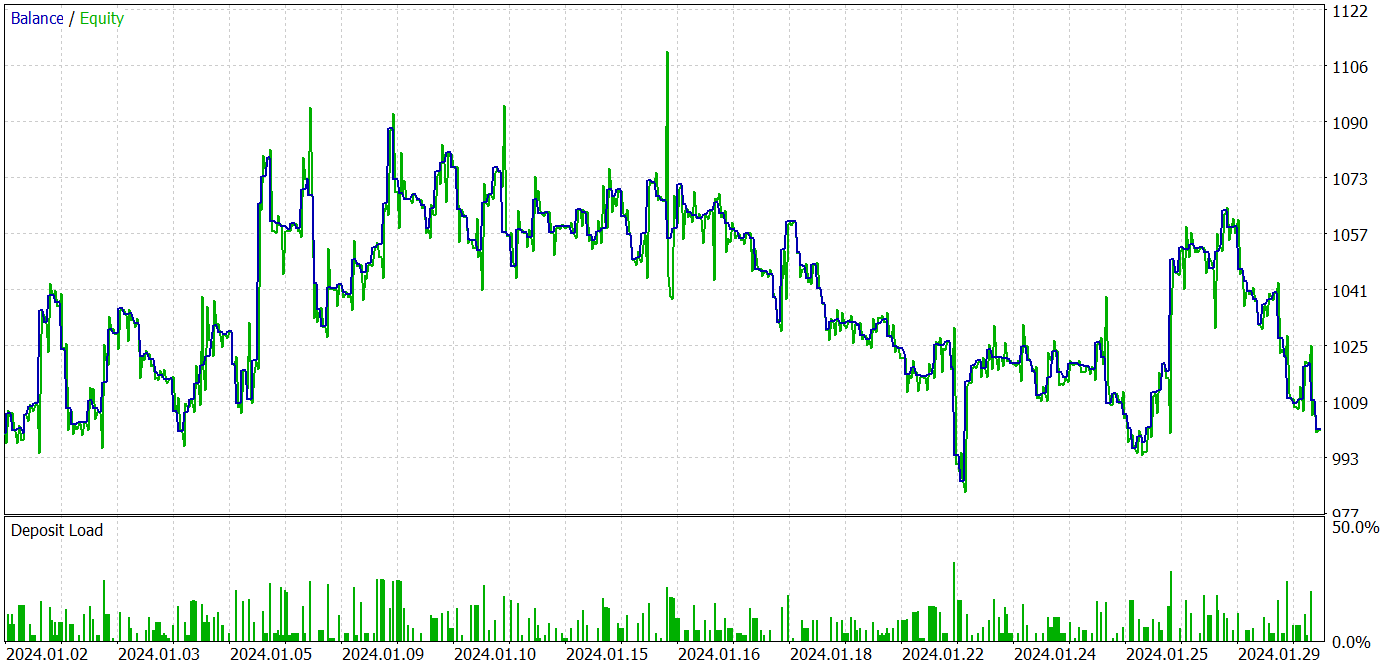
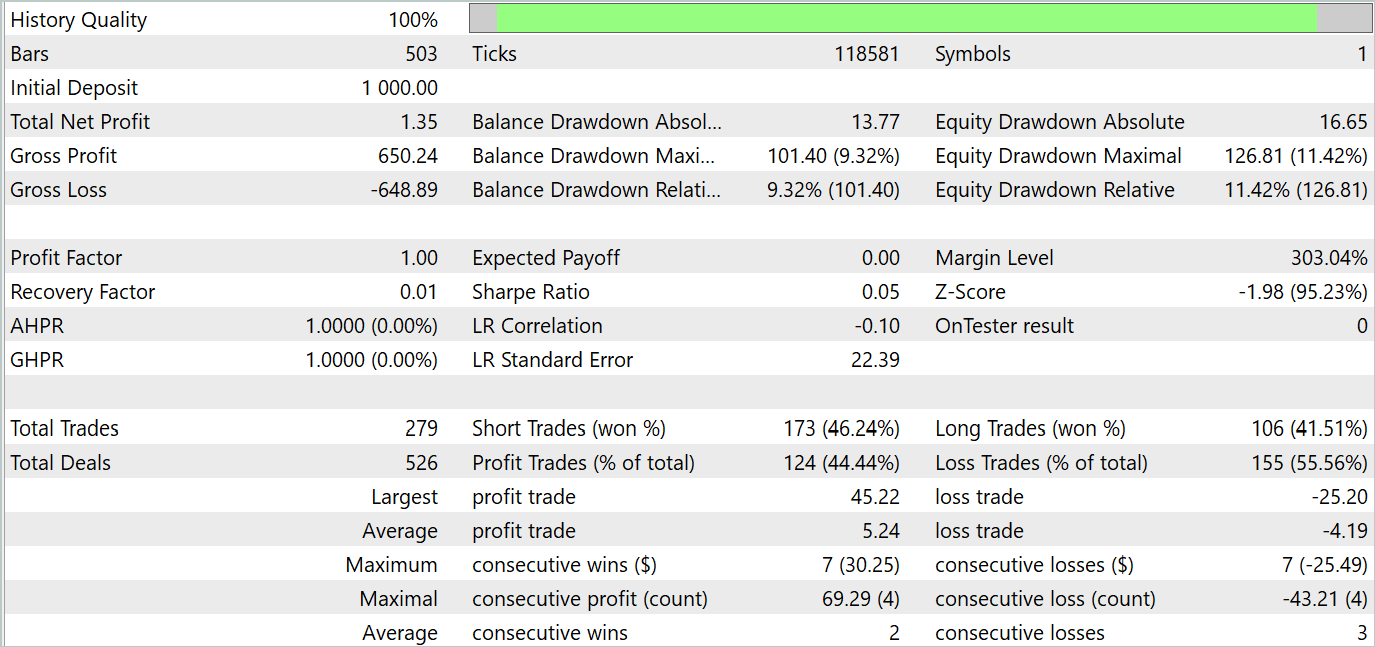
Os resultados dos testes mostram oscilações de rentabilidade próximas a "0" nos novos dados. De modo geral, a rentabilidade máxima e a média foram superiores aos valores das perdas, mas a proporção de 44,4% de negociações lucrativas não foi suficiente para gerar lucro durante o período de teste.
Considerações finais
Neste artigo, exploramos o novo método MLKV (Multi-Layer Key-Value), uma abordagem inovadora para o uso mais eficiente de memória em Transformers. A ideia central é estender o cache KV para vários níveis, o que permite uma redução significativa no uso de memória.
Na parte prática do artigo, implementamos as abordagens propostas usando MQL5. Treinamos e testamos os modelos com dados reais. Nossos testes indicaram que as abordagens propostas podem reduzir consideravelmente os custos de treinamento e execução do modelo. No entanto, isso exige um sacrifício na eficiência do desempenho do modelo. Portanto, é necessário encontrar um equilíbrio ponderado entre os custos e a eficácia do modelo.
Referências
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA de coleta de exemplos |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA de coleta de exemplos pelo método Real-ORL |
| 3 | Study.mq5 | Expert Advisor | EA de treinamento de Modelos |
| 4 | StudyEncoder.mq5 | Expert Advisor | EA de treinamento do Codificador |
| 5 | Test.mq5 | Expert Advisor | EA para testar o modelo |
| 6 | Trajectory.mqh | Biblioteca de classe | Estrutura de descrição do estado do sistema |
| 7 | NeuroNet.mqh | Biblioteca de classe | Biblioteca de classes para criar redes neurais |
| 8 | NeuroNet.cl | Biblioteca | Biblioteca de código para OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/15117
Desenvolvimento de robô em Python e MQL5 (Parte 3): Implementação do algoritmo de negociação baseado em modelo
Algoritmo de otimização por reações químicas — Chemical Reaction Optimisation, CRO (Parte II): Montagem e resultados
Do básico ao intermediário: União (II)
Algoritmo de otimização por reações químicas — Chemical Reaction Optimization, CRO (Parte I): A química dos processos na otimização
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso