強化学習におけるランダム決定フォレスト

ランダムフォレストアルゴリズムの抽象的な記述

バギングを使用するランダムフォレスト（RF）は最も強力な機械学習方法の1つですが、グラジエントブースティングには若干劣ります。 

ランダムフォレストは決定木（同じ名前のタスクを解決するための分類木または「CART」回帰木とも呼ばれます）の委員会で構成されています。これらは、統計、データマイニング、機械学習に使用されます。個々の木は、分岐、ノード、および葉を持つかなり単純なモデルです。ノードには、目的関数が依存する属性が含まれています。その後、目的関数の値は枝を通って葉に向かいます。新しい事例の分類過程では、論理的原理「IF-THEN」に従ってすべての属性値を通過しながら枝を通って葉へ下りていくことが必要です。これらの条件に応じて、目的変数には特定の値またはクラスが割り当てられます（目的変数は特定の葉に分類されます）。決定木を構築する目的は、いくつかの入力変数に応じて目的変数の値を予測するモデルを作成することです。

ランダムフォレストは、バギングアルゴリズムを使用した決定木の単純な投票によって構築されます。バギング（bagging）は、ブートストラップ集約（bootstrap aggregating）の単語の組み合わせから形成された人工的な単語です。この用語は1994年にLeo Breimanによって紹介されました。

ブートストラップは統計であり、選択されたオブジェクトの数がオブジェクトの初期数と同じサンプル生成の方法です。しかし、これらのオブジェクトは繰り返しで選択されます。 つまり、ランダムに選択されたオブジェクトが返され、再び選択されることができます。 この場合、選択されたオブジェクトの数はソースサンプルの約63％を占め、オブジェクトの残りの部分（約37％）は決して訓練サンプルになりません。この生成されたサンプルは、基本アルゴリズム（この場合は決定木）の訓練に使用されます。これはランダムにも起こります。指定された長さのランダムサブセット（サンプル）は、特徴（属性）の選択されたランダムサブセットで訓練されます。 サンプルの残りの37％は、構築されたモデルの一般化能力をテストするために使用されます。

その後、すべての訓練された木は、すべてのサンプルの平均誤差を使用して、簡単な投票で合成されます。 ブートストラップアグリゲーションの使用によって、平均二乗誤差が減少し、訓練された分類器の分散が減少します。誤差はサンプルが異なってもあまり変わりません。著者によると、この結果モデルの過剰適合が減少します。バギングの有効性は、基本的なアルゴリズム（決定木）が様々な無作為なサンプルに対して訓練され、それらの結果が大幅に異なり、その誤差が投票で相互に補償されることにあります。

決定木が基盤として使われている場合、ランダムフォレストはバギングの特別なケースであると言えます。同時に、従来の決定木の構築方法とは異なり、プルーニングは使用されません。この方法は、できるだけ速く大きなデータサンプルから構成を作成することを目的としています。それぞれの木は特定の方法で構築されています。木ノードを構築するための特徴（属性）は、特徴の総数から選択されるのではなく、そのランダムな部分集合から選択されます。 回帰モデルを構築する場合、特徴の数はn/3です。分類の場合は√nです。これらはすべて実証的な勧告であり、無相関化と呼ばれています。特徴の異なるセットは異なるツリーに分類され、ツリーは異なるサンプルで訓練されます。

図1　ランダムフォレスト操作のスキーム

ランダムフォレストのアルゴリズムは非常に効果的で実用的な問題を解決することができました。モデルを構築するプロセスに導入された、多少のランダム性を伴う高品質の訓練が提供されます。他の機械学習モデルを上回る利点は、訓練サンプルに含まれていないセットの一部についてのOOB(Out-Of-Bag)推定値です。したがって、単一のサンプルに対する相互検証またはテストは、決定木には必要ありません。モデルの更なる「チューニング」のために、OOB(Out-Of-Bag)推定値に限定することで十分です。これは、決定木の数と正規化コンポーネントの選択です。 

標準のМetaТrader 5パッケージに含まれるALGLIBライブラリには、RDF(Random Decision Forest)アルゴリズムが含まれています。それは、Leo BreimanとAdele Cutlerが提案した元のランダムフォレストアルゴリズムを変更したものです。このアルゴリズムは、投票によって結果を得る決定木の委員会を使用し、学習プロセスをランダム化するという2つのアイデアを組み合わせます。アルゴリズムの変更の詳細については、ALGLIBのWebサイトを参照してください。

アルゴリズムの長所

• 学習速度の速さ
• 非反復学習 - アルゴリズムは一定数の操作で完了する
• スケーラビリティ(大量のデータを処理する能力)
• 得られたモデルの高品質(ニューラルネットワークとニューラルネットワークのアンサンブルに匹敵）
• 無作為抽出によるデータの急上昇に対する感受性の欠如
• 設定可能なパラメータ数の少なさ
• ランダムな部分空間の選択による特徴値のスケーリング（および一般的な単調な変換）に敏感ではない
• パラメータを慎重に設定する必要なしですぐに使用できる。パラメータを調整することで、タスクやデータに応じて精度を0.5％から3％に上げることができる。
• 欠落しているデータにも効果があり、データの大部分が欠落していても、正確な精度を保持する
• モデルの一般化能力の内部評価
• 前処理なしで生データを処理する能力

アルゴリズムの短所

• 構築されたモデルは、大量のメモリを占有します。委員会がサイズNの訓練セットに基づいてK本の木から構築される場合、メモリ要件はO(K·N)です。たとえば、K=100でN=1000の場合、ALGLIBで構築されたモデルは約1 MBのメモリを必要とします。しかし、最新のコンピュータのRAM容量は十分に大きいので、これは大きな欠陥ではありません。
  
• 訓練されたモデルは、他のアルゴリズムよりもやや遅く動作します（モデルに100本の木がある場合は、結果を得るためにすべてを繰り返し処理する必要があります）。しかし現代の機械では、これはそれほど顕著ではありません。
• セットにたくさんの疎な特徴（テキスト、単語の単語）があったり分類されるオブジェクトが線形に分離できる際には、このアルゴリズムは、ほとんどの線形方法ほどよく機能しません。
• このアルゴリズムには、特にノイズの多いタスクの場合、過適合の傾向があります。この問題の一部はrパラメータを調整することで解決できます。元のランダムフォレストアルゴリズムにも同様の、しかし顕著な問題が存在します。しかし、著者は、このアルゴリズムは過適合の影響を受けないと主張しました。この誤解は、機械学習実践者や理論家によって共有されています。
• レベル数が異なるカテゴリ変数を含むデータの場合、ランダムフォレストは、より多くのレベルの特徴を優先して偏っています。ツリーは、最適化された特徴（情報ゲインの種類）のより高い値を受け取ることができるように、そのような特徴のために強く調整されます。
• 決定木同様、アルゴリズムは絶対的に外挿できません（ただしスパイクの場合は極端な値がないため、プラスと見なすことができます）

取引における機械学習の使い方の特殊性

機械学習を知ったばかりの人たちの間には、これは、プログラムがトレーダーのためのすべてのことを行い、トレーダーは単に受け取った利益を楽しんむという、ある種のおとぎ話の世界だという一般的な考えがあります。これは部分的にのみ真実です。最終結果は、以下に述べる問題がどの程度うまく解決されたかによって変わります。

• 特徴の選択

最初の主な問題は、模型が何を教える必要があるかの選択です。価格は多くの要因の影響を受けます。市場を研究する科学的アプローチは一つしかありません 。それは、計量経済学です。回帰分析、時系列分析、パネル分析の3つの主要な方法があります。この分野の別の興味深いセクションは、利用可能なデータのみに基づくノンパラメトリック計量経済学であり、それを形成する原因の分析はありません。ノンパラメトリック計量経済学の方法は、最近、応用研究で普及しています。例えば、カーネル法やニューラルネットワークがあります。同じセクションには、非数値概念の数学的分析が含まれています。たとえば、ファジー集合などです。機械の訓練を真剣にしたい場合は、計量経済学的方法の導入が役立ちます。本稿では、ファジーセットに焦点を当てます。

• モデル選択

第2の問題は、訓練モデルの選択です線形モデルと非線形モデルは多くあります。その一覧と特性の比較は、マイクロソフトのサイトなどにあります。

例として、さまざまなニューラルネットワークがあります。それらを使用するときは、ネットワークアーキテクチャを試し、レイヤーとニューロンの数を選択する必要があります。同時に、古典的なMLP型ニューラルネットワークは、ゆっくりと訓練され（特に固定ステップでの勾配降下）、それらを用いた実験には多くの時間がかかります。近代的な高速学習の深層学習ネットワークは現在、端末の標準ライブラリでは利用できず、DLL形式のサードパーティライブラリもあまり便利ではありません。私はまだそのようなパッケージを十分に研究していません。

ニューラルネットワークとは異なり、線形モデルは高速で動作しますが、近似を常にうまく処理するとは限りません

ランダムフォレストにはこれらの短所はありません。必要なのは、訓練サンプルに含まれるオブジェクトのパーセンテージを担当する木の数とパラメータrを選択するだけです。Microsoft Azure Machine Learning Studioの実験では、ほとんどの場合、ランダムなフォレストがテストデータの予測誤差を最小限に抑えることが示されています。

• モデルのテスト

一般に、1つの厳格な推奨事項があります。訓練サンプルが大きく、特徴に情報があるほど、新しいデータにシステムを安定させる必要があります。 しかし、トレーディングのタスクを解決するとき、予測変数の相互の変動があまりにも少なく情報も少ない場合、システム能力が不十分な場合があります。その結果、予測変数からの同じ信号が売買シグナルを両方生成します。出力モデルは一般化能力が低く、その結果、将来的に信号品質が悪くなります。 さらに、大きなサンプルの訓練が遅くなり、最適化中に複数回の実行が不可能になります。しかも、肯定的な結果は保証されません。これらの問題に、相場の混沌とした性質、非定常性、市場パターンの絶え間ない変化、または（もっとひどい場合）完全な欠如が伴います。

モデル訓練法の選択

ランダムフォレストは、さまざまな回帰、分類、クラスタリングの問題を解決するために使用されます。

これらの方法は、以下のように表すことができます。

• 教師なし学習。 クラスタリング、異常の検出。これらの手法は、自動的に決定された特有の違いを持つ特徴をプログラムによってグループに分けるために適用されます。
• 教師付き学習。分類と回帰。以前に知られている一連の訓練例（ラベル）が入力として供給され、ランダムフォレストはすべてのケースの学習（近似）を試みます。
• 強化学習。これは、おそらく最も珍しくて有望な機械学習であり、残りから際立っています。ここでは、仮想エージェントが環境とやりとりするときに学習が行われ、エージェントはこの環境内のアクションから受け取った報酬を最大化を試みます。このアプローチを使ってみましょう。

トレーディングシステム開発タスクにおける強化学習

人工知能のトレーダーを想像してみてください。それは環境と相互作用し、環境からのその行動への一定の応答を受けます。たとえば、収益性の高い取引が推奨され、不採算取引の場合は罰が課せられます。最終的に、市場との相互作用を繰り返した後、人工トレーダーは独自の経験を開発し、その「脳」に刻印します。ランダムフォレストは「脳」として機能します。

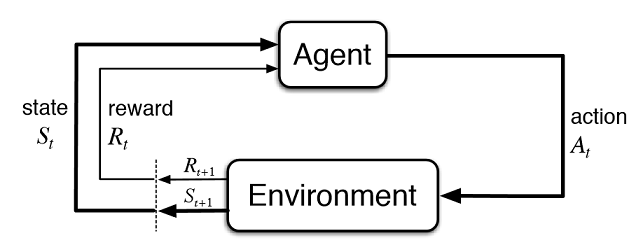
図2　仮想トレーダーと市場との相互作用

図2は、エージェント（人工トレーダー）と環境（市場）との相互作用スキームを示しています。エージェントは、状態St にある間に、時刻tにアクションAを実行することができます。その後、前の動作の成功度に応じて、それに対する報酬Rtを環境から受け取る状態St+1になります。これらのアクションは、調査されたシーケンス全体（またはエージェントのゲームエピソード）が完了するまで、t+n回続くかもしれません。このプロセスは繰り返し実行され、エージェントは複数回学習し、常に結果を改善します。

エージェントのメモリ（または経験）はどこかに保存される必要があります。強化学習の古典的な実装では、状態行動行列が使用されます。特定の状態に入ると、エージェントは次の決定のために行列を参照しなければなりません。この実装は、非常に限られた状態のセットを持つタスクに適しています。そうしないと、行列が非常に大きくなる可能性があります。したがって、票はランダムフォレストで置き換えられます。

図3　ポリシーの近似のためのディープニューラルネットワークまたはランダムフォレスト

エージェントの確率的パラメータ化方程式は、（s、a）対の集合で、θは各状態のパラメータのベクトルです。最適なポリシーは、特定のタスクに対して最適なアクションのセットです。エージェントが最適なポリシーを策定しようとしているとします。このアプローチは、以前に未知数の状態を持つ連続的なタスクでうまく機能し、強化学習のモデルフリーのActor-Criticメソッドです。強化学習には他にも多くのアプローチがあります。それらはRichard S. SuttonとAndrew G. Bartoの"Reinforcement Learning: An Introduction"（強化学習: はじめに）に記載されています。

自己学習エキスパート（エージェント）のソフトウェア実装

私は自分の記事での継続性を目指しているので、ファジー論理システムをエージェントとして仕様します。前の記事では、マムダニファジー推論のためにガウスメンバーシップ関数が最適化されました。しかし、そのアプローチには、環境の現在の状態（指標値）に関係なく、ガウス分布がすべての場合で変わらないという、大きな欠点がありました。今度は、ファジー出力 "out"の "ニュートラル"な期間のガウス分布の位置を自動的に選択します。エージェントは、値を選択し、3つの値の値と[0; 1]の範囲に応じて、ガウスの中心の関数を近似することによって、最適な方針の開発を担当します。

エキスパートのグローバル変数のメンバシップ関数へのポインタを作成します。これにより、学習過程でパラメータを自由に変更することができます。

CNormalMembershipFunction *updateNeutral=new CNormalMembershipFunction(0.5,0.2);

ランダムなフォレストと行列のクラスオブジェクトを作成して値を入力します。

//RDFシステム。ここではすべてのRFオブジェクトを作成する。
CDecisionForest      RDF;                                     // ランダムフォレストオブジェクト
CMatrixDouble        RDFpolicyMatrix;                         // RF出入力の行列
CDFReport            RDF_report;                              // RFがこのオブジェクトにエラーを返し、それを確認する

ランダムフォレストの主な設定は、木の数と正規化コンポーネントの入力パラメータに移動されます。これにより、次のパラメータを調整することでモデルを少し改善できます。

sinput int number_of_trees=50;
sinput double regularization=0.63;

モデルの状態を確認するサービス関数を記述しましょう。ランダムフォレストがすでに現在の時間枠で訓練されている場合、それは取引シグナルに使用され、そうでない場合はランダムな値でポリシーを初期化します（無作為に取引します）。

void checkBeforeLearn()
  {
   if(clear_model)
     {
      int clearRDF=FileOpen("RDFNtrees"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      FileWrite(clearRDF,0);
      FileClose(clearRDF);
      ExpertRemove();
      return;
     }

   int filehnd=FileOpen("RDFNtrees"+ _Symbol + (string)_Period +".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
   int ntrees =  (int)FileReadNumber(filehnd);
   FileClose(filehnd);

   if(ntrees>0)
     {
      random_policy=false;

      int setRDF=FileOpen("RDFBufsize"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      RDF.m_bufsize=(int)FileReadNumber(setRDF);
      FileClose(setRDF);

      setRDF=FileOpen("RDFNclasses"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      RDF.m_nclasses=(int)FileReadNumber(setRDF);
      FileClose(setRDF);

      setRDF=FileOpen("RDFNtrees"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      RDF.m_ntrees=(int)FileReadNumber(setRDF);
      FileClose(setRDF);

      setRDF=FileOpen("RDFNvars"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      RDF.m_nvars=(int)FileReadNumber(setRDF);
      FileClose(setRDF);

      setRDF=FileOpen("RDFMtrees"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_BIN|FILE_ANSI|FILE_COMMON);
      FileReadArray(setRDF,RDF.m_trees);
      FileClose(setRDF);
     }
   else Print("Starting new learn");

   checked_for_learn=true;
  }

コードからわかるように、訓練されたモデルは、以下を含むファイルから読み込まれます。

• 訓練サンプルのサイズ
  
• クラス数（回帰モデルの場合は1）
  
• 木の数
  
• 特徴の数
• 訓練された木の配列

訓練は、ストラテジーテスターの最適化モードで行われます。テスターの各パスの後、モデルは新たに形成された行列で訓練され、後の使用のために上記のファイルに記憶されます。

double OnTester()
  {
   if(clear_model) return 0;

   if(MQLInfoInteger(MQL_OPTIMIZATION)==true)
     {
      if(numberOfsamples>0)
        {
         CDForest::DFBuildRandomDecisionForest(RDFpolicyMatrix,numberOfsamples,3,1,number_of_trees,regularization,RDFinfo,RDF,RDF_report);
        }

      int filehnd=FileOpen("RDFBufsize"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      FileWrite(filehnd,RDF.m_bufsize);
      FileClose(filehnd);

      filehnd=FileOpen("RDFNclasses"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      FileWrite(filehnd,RDF.m_nclasses);
      FileClose(filehnd);

      filehnd=FileOpen("RDFNtrees"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      FileWrite(filehnd,RDF.m_ntrees);
      FileClose(filehnd);

      filehnd=FileOpen("RDFNvars"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      FileWrite(filehnd,RDF.m_nvars);
      FileClose(filehnd);

      filehnd=FileOpen("RDFMtrees"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_BIN|FILE_ANSI|FILE_COMMON);
      FileWriteArray(filehnd,RDF.m_trees);
      FileClose(filehnd);
     }

   return 0;
  }

前の記事にあった取引シグナルを処理する関数は実質的に変更されていませんが、注文を出した後に次の関数が呼び出されます。 

void updatePolicy(double action)
  {
   if(MQLInfoInteger(MQL_OPTIMIZATION)==true)
     {
      numberOfsamples++;
      RDFpolicyMatrix.Resize(numberOfsamples,4);

      RDFpolicyMatrix[numberOfsamples-1].Set(0,arr1[0]);
      RDFpolicyMatrix[numberOfsamples-1].Set(1,arr2[0]);
      RDFpolicyMatrix[numberOfsamples-1].Set(2,arr3[0]);
      RDFpolicyMatrix[numberOfsamples-1].Set(3,action);
     }
  }

3つの指標値を持つ状態ベクトルを行列に加え、出力値はマムダニファジー推論から得られた現在のシグナルで満たされます。

あと１つの関数:

void updateReward()
  {
   if(MQLInfoInteger(MQL_OPTIMIZATION)==true)
     {
      int unierr;
      if(getLAstProfit()<0) RDFpolicyMatrix[numberOfsamples-1].Set(3,MathRandomUniform(0,1,unierr));
     }
  }

は、注文が決済されるたびに呼び出されます。取引が不採算であると判明した場合、エージェントの報酬はランダムな一様分布から選択され、そうでなければ報酬は変わりません。

図4　ランダムな報酬値を選択するための一様分布

したがって、現在の実装では、代理人によって行われた収益性の高い取引が推奨され、不利益な取引の場合、代理人は最適な解を探してランダムな行動（ガウスの中心のランダムな位置）をとるよう強制されます。

シグナル処理関数の完全なコードは次のようになります。

void PlaceOrders(double ts)
  {
   if(CountOrders(0)!=0 || CountOrders(1)!=0)
     {
      for(int b=OrdersTotal()-1; b>=0; b--)
         if(OrderSelect(b,SELECT_BY_POS)==true)
            if(OrderSymbol()==_Symbol && OrderMagicNumber()==OrderMagic)

               switch(OrderType())
                 {
                  case OP_BUY:
                     if(ts>=0.5)
                     if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red))
                       {
                        updateReward();
                        if(ts>0.6)
                          {
                           lots=LotsOptimized();
                           if(OrderSend(Symbol(),OP_SELL,lots,SymbolInfoDouble(_Symbol,SYMBOL_BID),0,0,0,NULL,OrderMagic,Red)>0)
                             {
                              updatePolicy(ts);
                             };
                          }
                       }
                     break;

                  case OP_SELL:
                     if(ts<=0.5)
                     if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red))
                       {
                        updateReward();
                        if(ts<0.4)
                          {
                           lots=LotsOptimized();
                           if(OrderSend(Symbol(),OP_BUY,lots,SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,Green)>0)
                             {
                              updatePolicy(ts);
                             };
                          }
                       }
                     break;
                 }
      return;
     }

   lots=LotsOptimized();

   if((ts<0.4) && (OrderSend(Symbol(),OP_BUY,lots,SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,INT_MIN) > 0))
      updatePolicy(ts);
   else if((ts>0.6) && (OrderSend(Symbol(),OP_SELL,lots,SymbolInfoDouble(_Symbol,SYMBOL_BID),0,0,0,NULL,OrderMagic,INT_MIN) > 0))
      updatePolicy(ts);
   return;
  }

マムダニのファジー推論を計算する関数が変更されました。エージェントのポリシーがランダムに選択されなかった場合、訓練されたランダムフォレストを使用して、X軸に沿ったガウスの位置の計算を呼び出します。ランダムフォレストには3つのオシレータ値を持つベクトルとして現在の状態が与えられ、得られた結果でガウスの位置が更新されます。EAがオプティマイザで最初に実行される場合、ガウスの位置は各状態ごとにランダムに選択されます。

double CalculateMamdani()
  {
   CopyBuffer(hnd1,0,0,1,arr1);
   NormalizeArrays(arr1);

   CopyBuffer(hnd2,0,0,1,arr2);
   NormalizeArrays(arr2);

   CopyBuffer(hnd3,0,0,1,arr3);
   NormalizeArrays(arr3);

   if(!random_policy)
     {
      vector[0]=arr1[0];
      vector[1]=arr2[0];
      vector[2]=arr3[0];

      CDForest::DFProcess(RDF,vector,RFout);
      updateNeutral.B(RFout[0]);
     }
   else
     {
      int unierr;
      updateNeutral.B(MathRandomUniform(0,1,unierr));
     }
   
   //Print(updateNeutral.B());
   firstTerm.SetAll(firstInput,arr1[0]);
   secondTerm.SetAll(secondInput,arr2[0]);
   thirdTerm.SetAll(thirdInput,arr3[0]);

   Inputs.Clear();
   Inputs.Add(firstTerm);
   Inputs.Add(secondTerm);
   Inputs.Add(thirdTerm);

   CList *FuzzResult=OurFuzzy.Calculate(Inputs);
   Output=FuzzResult.GetNodeAtIndex(0);
   double res=Output.Value();
   delete FuzzResult;

   return(res);
  }

モデルの訓練とテストのプロセス

エージェントはオプティマイザで逐次訓練されます。つまり、ファイルに書き込まれた以前の訓練の結果は、次の実行に使用されます。これを行うには、すべてのテストエージェントとクラウドを無効にして、コアを1つだけ残します。 

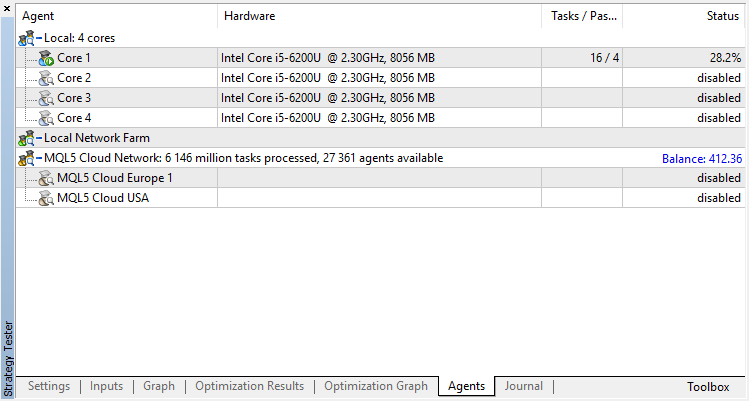
遺伝的アルゴリズムを無効にします（遅い完全アルゴリズムを使用します）。EAが新しいバーの開きを明示的に制御するため、訓練/テストは始値を使用して実行されます。

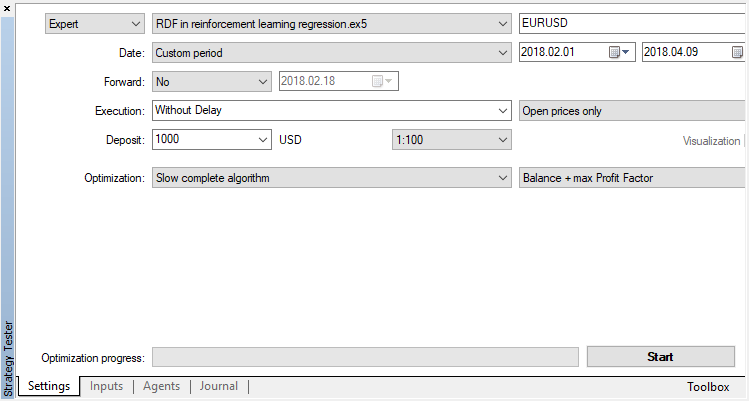
最適化可能なパラメータは、オプティマイザのパス数の1つだけです。アルゴリズム操作を説明するために、15反復を設定します。

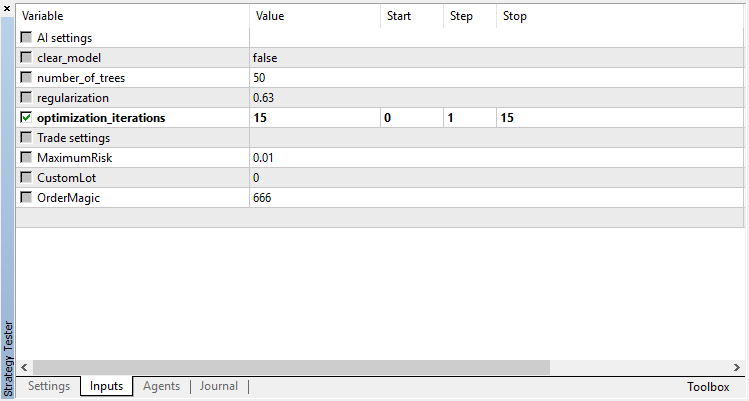
回帰モデル（1つの出力変数を持つ）の最適化結果を以下に示します。訓練されたモデルはファイルに保存されるので、最後の実行結果のみが保存されることに注意してください。

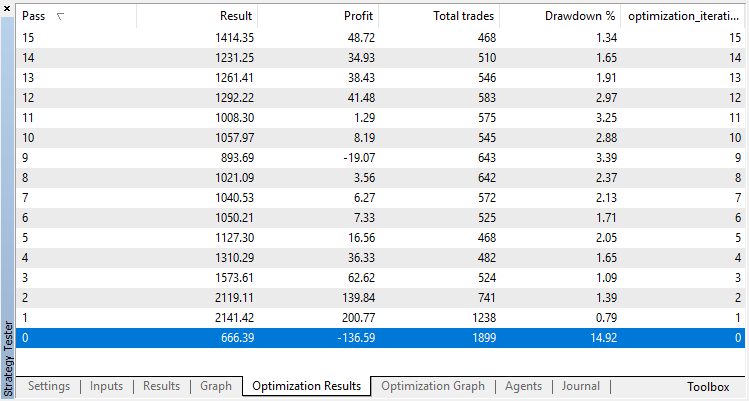
ゼロランはエージェントのランダムポリシー（最初の実行）に対応しているため、最大の損失をもたらしました。逆に、最初の実行は最も生産的であることが判明しました。その後もは利益は得られず、停滞しました。その結果、第15回目の実行後の成長チャートは次のようになります。

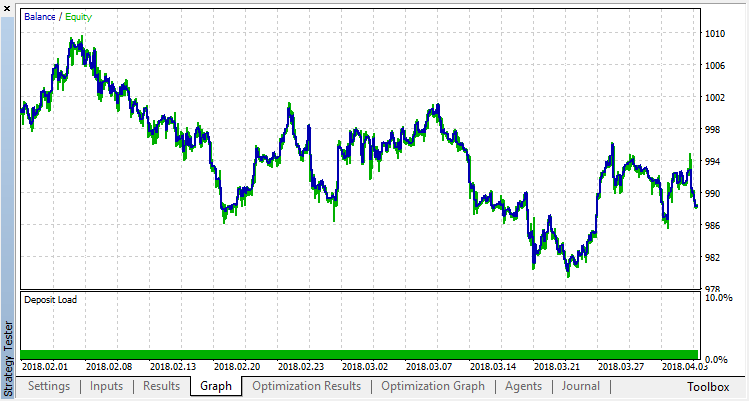
分類モデルについても同じ実験を行いましょう。この場合、報酬はプラスとマイナスの2つのクラスに分類されます。

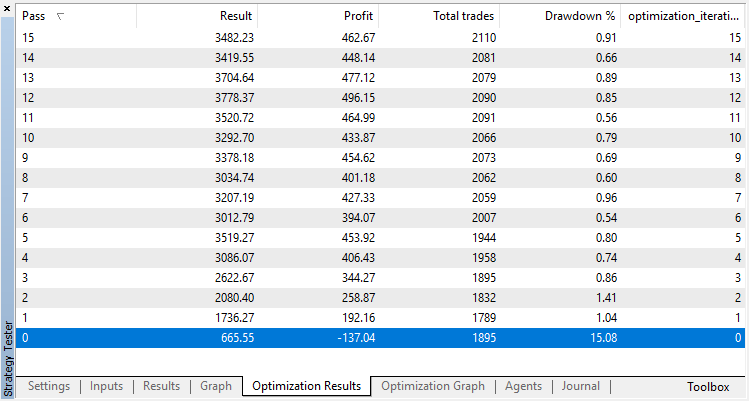
分類はこの作業をはるかによく実行します。少なくともランダムなポリシーに対応してゼロランから15回目まで安定した伸びがあります。伸びはここで止まり、ポリシーは最適化を中心に変動し始めます。

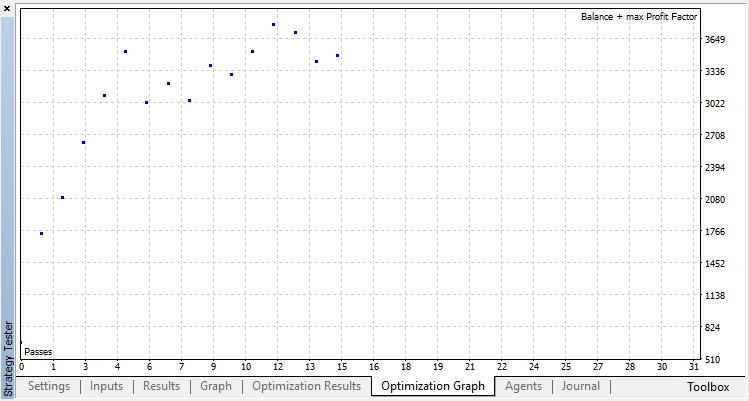
下記はエージェントの訓練の最終結果です。

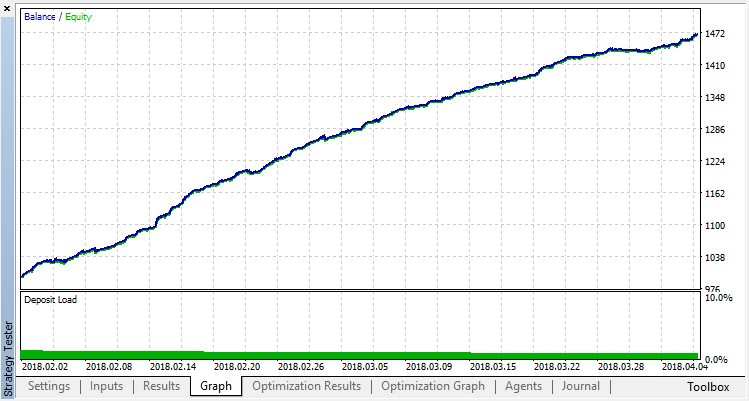
訓練範囲外のサンプルでシステム操作の結果を確認してください。モデルは著しく過剰適合されています。

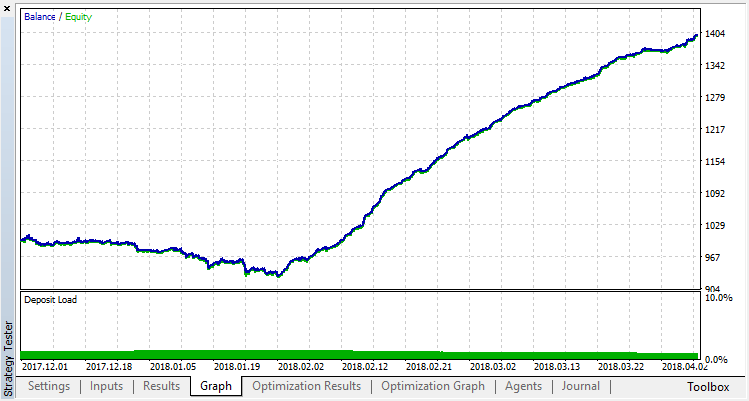
過剰適合を取り除いてみましょう。パラメータr（正則化）を0.25に設定すると、訓練にはサンプルのわずか25％が使用されます。同じ訓練範囲を使用します。

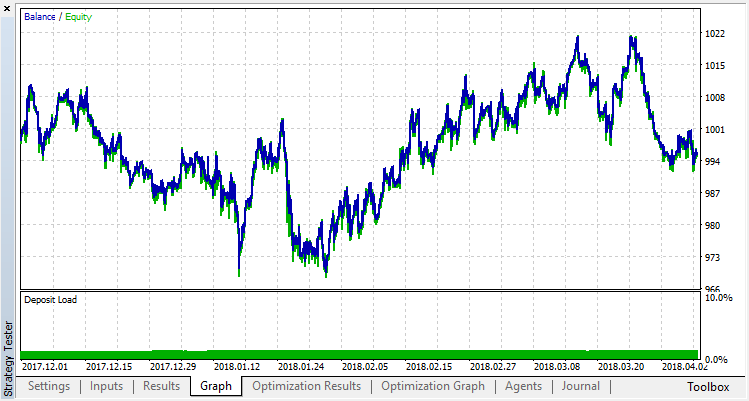
モデルは悪化し（より多くの騒音が追加されました）、全体的過剰適合を取り除くことはできませんでした。この正則化法が、規則性が経時的に変化しない定常的なプロセスにのみ適していることは明らかです。別の明らかな負の要因は、モデルの入力にある3つのオシレータで、これらのオシレータは、お互いに相関しています。

本稿の要約

目的は、関数を近似するためにランダムフォレストを使用する可能性を示すことでした。この場合、指標値は売買シグナルとして機能しました。また、分類と回帰の2つのタイプの教師あり学習が考慮されました。学習には、最適化プロセス中に自動的に選択された、以前に知られていなかった訓練例を使用した非標準的アプローチを適用しました。一般に、このプロセスは、テスター（クラウド）における従来の最適化と同様で、アルゴリズムは数回の反復で収束し、最適化されたパラメータの数を心配する必要はありません。これは、適用されるアプローチの明確な利点です。このモデルの欠点は、戦略が誤って選択されたときに過大適合の傾向があり、これがパラメータの過剰最適化に相当することです。 

伝統によって、戦略を改善するための可能な方法を提供します（結局のところ、現在の実装は大まかな枠組みです）。

• 最適化されたパラメータの数を増やす（複数のメンバシップ関数の最適化）
• さまざまな重要な予測変数を追加する
• エージェントに報酬を与えるさまざまな方法を適用する
• 複数のライバルエージェントを作成してバリアントのスペースを増やす

自己学習エキスパートのソースファイルは下記に添付されています。

エキスパートがコンパイルして作業するためには、 MT4Ordersライブラリと更新されたFuzzyライブラリをダウンロードしてください。