取引戦略におけるファジー論理

MetaTrader 5 — 例 | 24 11月 2017, 09:32

1 385

はじめに

トレーダーはよく、機械学習を通じて取引システムを改善する方法や新しい取引方法を作成する方法について考えます。出版物は豊富なのにもかかわらず、コンピューターによる計算に頼らずに解析的に見積もることができるモデルを作成するための単純で直観的な方法は、いまだに見いだされていません。ファジー論理は、機械学習の世界への窓です。遺伝的アルゴリズムと組み合わせることで、ファジー論理は自己学習型または簡単に最適化可能な取引システムを構築する機能を拡張することができます。同時に、ファジー論理は、人間が思考の過程で行うように、クリスプな数値情報を曖昧な（ぼやけた）用語でカプセル化するため直観的です。

ここに例があります。クリスプなロジックの観点から、移動する車の速度は測定装置によって、例えば時速60kmのように決定されます。しかし、測定装置を持たないカジュアルな観察者は、経験や知識ベースに頼って、車の速度を概算することしかできません。例えば、自動車は速く進むことができ、「速い」はおよそ時速100km以上と定義されていることが知られています。また、車は時速5-10kmで遅く進むこともできることも知られています。そして最後に、近づいてくる車のサイズが適度に大きくなると、速度は視覚的に平均的（時速約60km）だと評価されます。したがって、時速60kmは以下の4つの異なる表現で特徴付けることができます。

平均速度
平均に近い速度
「速い」というよりは平均
「遅い」というよりは平均

これは情報が人間の意識の中でカプセル化され、たとえば、「車が非常に速く動いていないとしたら道を渡る時間があるだろうか？」のように、現在の瞬間に必要な情報だけを把握するかです。すべてを一度に細かく考えると、道路を走ってわたるか車を先に行かせるかの特定の決定を下す前に、膨大な時間とエネルギーを費やすことになります。同時に、現在の状況は徹底的に研究したとしても、将来的にはまったく同じことが繰り返されることはなく、似ているのはアウトラインだけです。機械学習では、このような状況は過適合と呼ばれます。

本稿はファジー論理理論を掘り下げません。このトピックに関する情報は、インターネットやMQL5サイトで広く掲載されています。すぐさま実践で始め、これを理論の抜粋と興味深い事実で説明します。

モデルを構築するには、標準のMetaTrader 5ターミナルパッケージのファジーライブラリが使用されます。

結果的にファジー論理に基づいた既製のエキスパートアドバイザーができ、カスタムシステムを構築するための例になります。

取引システムプロトタイプの作成

クリスプなTSロジックの作成に移ります。これはさらなる研究の基盤として使用されます。次に、2つの同一システムを比較することができます。2番目のシステムはファジー論理を利用します。

期間の異なる3つのRSIオシレータが基本として使用されます。

hnd1 = iRSI(_Symbol,0,9,PRICE_CLOSE);
hnd2 = iRSI(_Symbol,0,14,PRICE_CLOSE);
hnd3 = iRSI(_Symbol,0,21,PRICE_CLOSE);

シグナルのクリスプな状態を定式化し、関数内で定義します。

double CalculateSignal()
{
 double res =0.5;
 CopyBuffer(hnd1,0,0,1,arr1);
 CopyBuffer(hnd2,0,0,1,arr2);
 CopyBuffer(hnd3,0,0,1,arr3);
 
 if(arr1[0]>70 && arr2[0]>70 && arr3[0]>70) res=1.0;                    // 全指標が買われ過ぎ領域にある場合は売る
 if(arr1[0]<30 && arr2[0]<30 && arr3[0]<30) res=0.0;                    // 全指標が売られ過ぎ領域にある場合は買う
 
 if(arr1[0]<30 && arr2[0]<30 && arr3[0]>70) res=0.5;                    // 2つが売られ過ぎ、1つが買われ過ぎ、シグナルなし
 if(arr1[0]<30 && arr2[0]>70 && arr3[0]<30) res=0.5;
 if(arr1[0]>70 && arr2[0]<30 && arr3[0]<30) res=0.5;
 
 if(arr1[0]>70 && arr2[0]>70 && arr3[0]<30) res=0.5;                    // 2つが買われ過ぎ、1つが売られ過ぎ、シグナルなし
 if(arr1[0]>70 && arr2[0]<30 && arr3[0]>70) res=0.5;
 if(arr1[0]<30 && arr2[0]>70 && arr3[0]>70) res=0.5;
 
 if(arr1[0]<30 && arr2[0]<30 && (arr3[0]>40 && arr3[0]<60)) res=0.0;    // 2つが売られ過ぎで3番目が40~60、買いシグナル
 if(arr1[0]<30 && (arr2[0]>40 && arr2[0]<60) && arr3[0]<30) res=0.0;
 if((arr1[0]>40 && arr1[0]<60) && arr2[0]<30 && arr3[0]<30) res=0.0;
 
 if(arr1[0]>70 && arr2[0]>70 && (arr3[0]>40 && arr3[0]<60)) res=1.0;    // 2つが買われ過ぎで3番目が40~60、売りシグナル
 if(arr1[0]>70 && (arr2[0]>40 && arr2[0]<60) && arr3[0]>70) res=1.0;
 if((arr1[0]>40 && arr1[0]<60) && arr2[0]>70 && arr3[0]>70) res=1.0;
 
 return(res);
}

次に、他のすべてのサービス機能を記述し、エキスパートを2017年の初めからEURUSD、時間枠М15とМ5でテストします（エキスパートのフルコードはは本稿末尾に添付されています）。

EURUSD M15

EURUSD M5

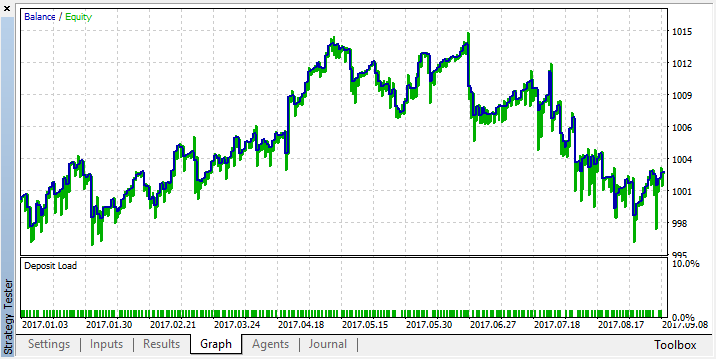
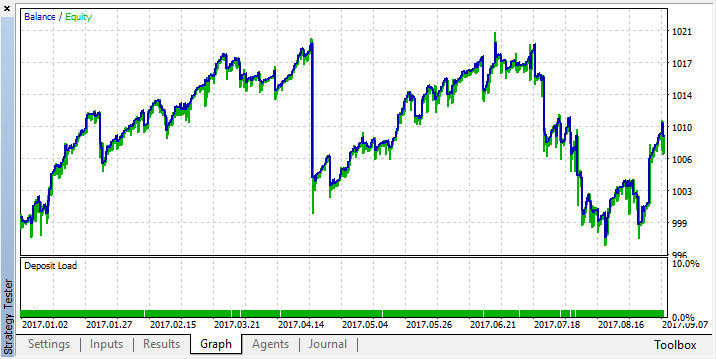
3つの指標の組み合わせに対するクリスプな条件が定義されており、その条件が論理的で一貫性があるにもかかわらず、このアプローチはあまりにも単純で柔軟性に欠けていることが判明しました。システムには平均して8ヶ月の間損益がありません。収益を得るためには、多数の条件を組み合わせて、多分さらに多くのオシレータを追加する必要があります。しかし、条件がきわめて正確に設定されているため、最適化する余地はあまりありません。

ファジー論理を使ってこの取引システムを有益にする条件についてのアイデアをぼかしてみましょう。

ファジー論理モデルの作成

初めに、ファジーライブラリをインクルードすることが必要です。正確に言うとマムダニまたは菅野の2つのうち1つのファジー論理モデルをインクルードします。それらの違いは、菅野がファジー用語セットの形での出力変数を作成せずに線形モデルを出力する一方、マムダニはこの要素を提供することです。本稿はファジートレーダーのために書かれているので、ここではマムダニを使用します。しかし、これは、菅野モデルがいくつかの特定のタスクには適していないことを意味するものでありません。ファジー論理の基本的な理解に頼って実験することは常に可能であり、必要です。

#include <Math\Fuzzy\MamdaniFuzzySystem.mqh>
CMamdaniFuzzySystem *OurFuzzy=new CMamdaniFuzzySystem();

ライブラリがインクルードされ、Mamdaniクラスへの参照が宣言されます。始めるのに必要なのはこれですべてです。

ここで、ファジー推論を構成する主な段階について考えてみましょう。これはファジーモデリングシステムの中核です。ファジー推論過程は、ファジ－論理の基本的な操作を用いてファジー仮定に基づいてファジー結論を得るための特定の手順またはアルゴリズムです。

ファジー推論は7つの段階で構成されます。

ファジー推論システムの構造の決定

入力と出力の数、メンバシップ関数は設計段階で定義されます。ここでは、4つの入力と1つの出力があり、それぞれに3つのメンバシップ関数があります。

ファジー推論システムのルールベースの作成

開発過程では、取引システムのエキスパートの判断に基づいてファジー推論のカスタムルールを作成します。

入力変数のファジー化

ファジー推論システムの入力変数の数値と、言語変数の対応する用語のメンバシップ関数の値との対応を設定します。

集計

ファジー推論システムの各ルールに対する条件の真理度を決定する手順です。

アクティブ化

すべてのあいまいな生産ルールのカーネルの結果を構成する基本命題（副節）のそれぞれの真理度を見つける過程です。

累積

出力言語変数のそれぞれについてメンバシップ関数を見つける過程です。

非ファジー化

出力言語変数のメンバシップ関数からクリスプな値への遷移過程です。出力値は0〜1の範囲を持ちます。

実行する必要があるのはポイント1とポイント2のみで、他はすべて介入なしにシステムによって実行されることには留意すべきです。ファジー論理演算の微妙な操作に関心のある方は、ここで全段階の詳細を見つけることができます。

ファジー推論システム構造の決定

モデルの作成を続けましょう。3つの入力と1つの出力のオブジェクトと辞書の補助オブジェクトを定義して、ロジックの作業を容易にします。

CFuzzyVariable *firstInput=new CFuzzyVariable("rsi1",0.0,1.0);
CFuzzyVariable *secondInput=new CFuzzyVariable("rsi2",0.0,1.0);
CFuzzyVariable *thirdInput=new CFuzzyVariable("rsi3",0.0,1.0);
CFuzzyVariable *fuzzyOut=new CFuzzyVariable("out",0.0,1.0);

CDictionary_Obj_Double *firstTerm=new CDictionary_Obj_Double;
CDictionary_Obj_Double *secondTerm=new CDictionary_Obj_Double;
CDictionary_Obj_Double *thirdTerm=new CDictionary_Obj_Double;
CDictionary_Obj_Double *Output;

期間が異なる3つのRSIが入力として使用されます。RSIオシレータの範囲は常に0〜100であるため、変数は同じく作成する必要があります。ただし、便宜上、指標値は0〜1の範囲に正規化されます。作成された変数は、入力ベクトルの次元に等しい次元を持つ必要があります。つまり、すべての値を保持する必要があります。0〜1の範囲は出力にも設定されます。

ファジー論理作成のポイント1によれば、メンバシップ関数を定義して構成することも必要です。これは OnInit()イベントハンドラで行われます。

firstInput.Terms().Add(new CFuzzyTerm("buy", new CZ_ShapedMembershipFunction(0.0,0.6)));
firstInput.Terms().Add(new CFuzzyTerm("neutral", new CNormalMembershipFunction(0.5, 0.2)));
firstInput.Terms().Add(new CFuzzyTerm("sell", new CS_ShapedMembershipFunction(0.4,1.0)));
OurFuzzy.Input().Add(firstInput);
   
secondInput.Terms().Add(new CFuzzyTerm("buy", new CZ_ShapedMembershipFunction(0.0,0.6)));
secondInput.Terms().Add(new CFuzzyTerm("neutral", new CNormalMembershipFunction(0.5, 0.2)));
secondInput.Terms().Add(new CFuzzyTerm("sell", new CS_ShapedMembershipFunction(0.4,1.0)));
OurFuzzy.Input().Add(secondInput);
   
thirdInput.Terms().Add(new CFuzzyTerm("buy", new CZ_ShapedMembershipFunction(0.0,0.6)));
thirdInput.Terms().Add(new CFuzzyTerm("neutral", new CNormalMembershipFunction(0.5, 0.2)));
thirdInput.Terms().Add(new CFuzzyTerm("sell", new CS_ShapedMembershipFunction(0.4,1.0)));
OurFuzzy.Input().Add(thirdInput);
   
fuzzyOut.Terms().Add(new CFuzzyTerm("buy", new CZ_ShapedMembershipFunction(0.0,0.6)));
fuzzyOut.Terms().Add(new CFuzzyTerm("neutral", new CNormalMembershipFunction(Gposition, Gsigma)));
fuzzyOut.Terms().Add(new CFuzzyTerm("sell", new CS_ShapedMembershipFunction(0.4,1.0)));
OurFuzzy.Output().Add(fuzzyOut);

メンバシップ関数とは何であり、どのような目的を果たすのかを見てみましょう。

それぞれの入力（および1つの出力）変数に対して、独自のメンバシップ関数を持つ "buy"、 "neutral"、 "sell"という3つの用語が作成されています。言い換えれば、オシレータ値は3つのファジーグループに分割することができ、各グループにはメンバシップ関数を使用して値の範囲を割り当てることができます。ファジー論理の言葉で言えば、4つの用語セットが作成されており、それぞれに3つの用語があります。上記を説明するために、用語とそのメンバシップ関数を視覚化するために使用できる簡単なスクリプトを記述します。

//+------------------------------------------------------------------+ 
//|                                      Our MembershipFunctions.mq5 | 
//|                        Copyright 2016, MetaQuotes Software Corp. | 
//|                                             https://www.mql5.com | 
//+------------------------------------------------------------------+ 
#include <Math\Fuzzy\membershipfunction.mqh> 
#include <Graphics\Graphic.mqh> 
//--- メンバシップ関数を作成する 
CZ_ShapedMembershipFunction func2(0.0, 0.6);
CNormalMembershipFunction func1(0.5, 0.2); 
CS_ShapedMembershipFunction func3(0.4, 1.0);

//--- メンバシップ関数のラッパーを作成する 
double NormalMembershipFunction1(double x) { return(func1.GetValue(x)); } 
double ZShapedMembershipFunction(double x) { return(func2.GetValue(x)); }
double SShapedMembershipFunction(double x) { return(func3.GetValue(x)); }
 
//+------------------------------------------------------------------+ 
//| スクリプトプログラム開始関数                                   | 
//+------------------------------------------------------------------+ 
void OnStart() 
  { 
//--- グラフィックを作成する 
   CGraphic graphic; 
   if(!graphic.Create(0,"Our MembershipFunctions",0,30,30,780,380)) 
     { 
      graphic.Attach(0,"Our MembershipFunctions"); 
     } 
   graphic.HistoryNameWidth(70); 
   graphic.BackgroundMain("Our MembershipFunctions"); 
   graphic.BackgroundMainSize(16); 
//--- 曲線を作成する 
   graphic.CurveAdd(NormalMembershipFunction1,0.0,1.0,0.01,CURVE_LINES,"[0.5, 0.2]"); 
   graphic.CurveAdd(ZShapedMembershipFunction,0.0,1.0,0.01,CURVE_LINES,"[0.0, 0.6]"); 
   graphic.CurveAdd(SShapedMembershipFunction,0.0,1.0,0.01,CURVE_LINES,"[0.4, 1.0]"); 
//--- X軸プロパティを設定する 
   graphic.XAxis().AutoScale(false); 
   graphic.XAxis().Min(0.0); 
   graphic.XAxis().Max(1.0); 
   graphic.XAxis().DefaultStep(0.1); 
//--- Y軸プロパティを設定する 
   graphic.YAxis().AutoScale(false); 
   graphic.YAxis().Min(0.0); 
   graphic.YAxis().Max(1.1); 
   graphic.YAxis().DefaultStep(0.1); 
//--- プロットする 
   graphic.CurvePlotAll(); 
   graphic.Update(); 
  }

チャートでのスクリプトの実行：

図1　メンバシップ関数

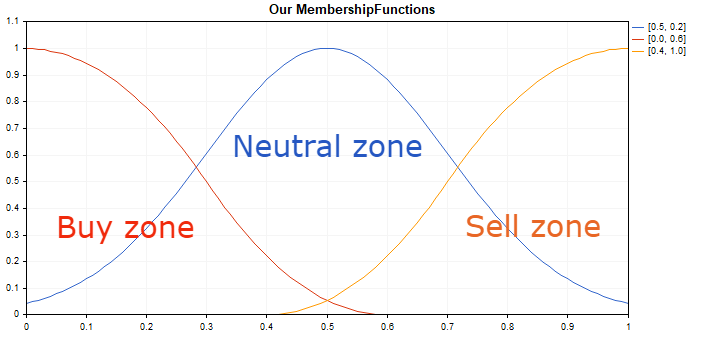
これらのメンバシップ関数は、2つの最適化可能な入力パラメータしか持たないため選択されています（これは後でシステムテスト段階で行われます）。また、システムの極端な位置と中央の位置についても説明します。Fuzzyライブラリの利用可能なメンバシップ関数から任意のメンバシップ関数を適用できます。

オシレータの極値が今後の方向性の変化を示し、その結果、今後の動向の逆転を示すというルールを採用しましょう。したがって、オシレータがゼロに近づいたら、成長がいつ始まるかのヒントです。オシレータが0.5マークに移動すると、CZ_ShapedMembershipFunctionまたは「買い領域」が徐々に減少します。同時に、「中立領域」の CNormalMembershipFunctionの不確定性が高まり、オシレータが1に近づくと最終的にCS_ShapedMembershipFunctionまたは「売り領域」が増加します。入力と出力すべてで同じ原則が使用され、指標値がファジー境界を持つ特定の領域に属しているかどうかを確認します。

各変数のメンバシップ関数の数に制限はありません。3ではなく5、7、15の関数を設定できますが、もちろん、常識内またファジーロジックの範囲内でです。

ファジー推論システムのルールベースの作成

この段階では、ファジー決定を行う際に使用する知識ベースをシステムに追加します。

   rule1 = OurFuzzy.ParseRule("if (rsi1 is buy) and (rsi2 is buy) and (rsi3 is buy) then (out is buy)");
   rule2 = OurFuzzy.ParseRule("if (rsi1 is sell) and (rsi2 is sell) and (rsi3 is sell) then (out is sell)");
   rule3 = OurFuzzy.ParseRule("if (rsi1 is neutral) and (rsi2 is neutral) and (rsi3 is neutral) then (out is neutral)"); 
   
   rule4 = OurFuzzy.ParseRule("if (rsi1 is buy) and (rsi2 is sell) and (rsi3 is buy) then (out is neutral)");
   rule5 = OurFuzzy.ParseRule("if (rsi1 is sell) and (rsi2 is sell) and (rsi3 is buy) then (out is neutral)");
   rule6 = OurFuzzy.ParseRule("if (rsi1 is buy) and (rsi2 is buy) and (rsi3 is sell) then (out is neutral)"); 
   
   rule7 = OurFuzzy.ParseRule("if (rsi1 is buy) and (rsi2 is buy) and (rsi3 is neutral) then (out is buy)");
   rule8 = OurFuzzy.ParseRule("if (rsi1 is sell) and (rsi2 is sell) and (rsi3 is neutral) then (out is sell)");
   rule9 = OurFuzzy.ParseRule("if (rsi1 is buy) and (rsi2 is neutral) and (rsi3 is buy) then (out is buy)");
   rule10 = OurFuzzy.ParseRule("if (rsi1 is sell) and (rsi2 is neutral) and (rsi3 is sell) then (out is sell)");
   rule11 = OurFuzzy.ParseRule("if (rsi1 is neutral) and (rsi2 is buy) and (rsi3 is buy) then (out is buy)");
   rule12 = OurFuzzy.ParseRule("if (rsi1 is neutral) and (rsi2 is sell) and (rsi3 is sell) then (out is sell)");

   OurFuzzy.Rules().Add(rule1);
   OurFuzzy.Rules().Add(rule2);
   OurFuzzy.Rules().Add(rule3);
   OurFuzzy.Rules().Add(rule4);
   OurFuzzy.Rules().Add(rule5);
   OurFuzzy.Rules().Add(rule6);
   OurFuzzy.Rules().Add(rule7);
   OurFuzzy.Rules().Add(rule8);
   OurFuzzy.Rules().Add(rule9);
   OurFuzzy.Rules().Add(rule10);
   OurFuzzy.Rules().Add(rule11);
   OurFuzzy.Rules().Add(rule12);

知識ベースには少なくとも1つの論理条件を追加する必要があります。少なくとも1つの用語が論理演算に関与していない場合、知識ベースは不完全と見なされます。論理条件は限りなく存在する可能性があります。

提示された例は12の論理条件を設定し、これらは満たされるとファジー推論に影響を及ぼします。したがって、すべての用語が論理演算に関与します。デフォルトでは、すべての論理演算には1に等しい同じ重み係数が割り当てられます。この例ではデフォルトが使われます。

3つの指標がすべてファジー領域内にある場合、ファジー買いシグナルが出力されます。売りシグナルと中立シグナルにも同じことが当てはまります（ルール1~3）。

2つの指標が買いを示し、1つが売りを示す場合、出力値は中立、つまり不確実です（ルール4~6）。

2つの指標が買いまたは売りを示し、1つが中性である場合、買いまたは売りが出力値に割り当てられます（ルール7~12）。

明らかに、これはルールベースを作成する唯一のやり方ではなく、実験するのは自由です。このルールベースは、システムがどのように機能すべきかという私の「エキスパート」判断とビジョンに基づいています。

非ファジー化後のクリスプな出力値の取得

残るのは、モデルを計算して結果を0から1までの値として取得することです。0に近い値は強い買いシグナルを示し、0.5に近いものは中立であり、1に近い値は強い売りシグナルを示します。

double CalculateMamdani()

{
 CopyBuffer(hnd1,0,0,1,arr1);
 NormalizeArrays(arr1);
   
 CopyBuffer(hnd2,0,0,1,arr2);
 NormalizeArrays(arr2);
    
 CopyBuffer(hnd3,0,0,1,arr3);
 NormalizeArrays(arr3);
     
 firstTerm.SetAll(firstInput,arr1[0]);
 secondTerm.SetAll(secondInput,arr2[0]);
 thirdTerm.SetAll(thirdInput,arr2[0]);
       
 Inputs.Clear(); 
 Inputs.Add(firstTerm);
 Inputs.Add(secondTerm);
 Inputs.Add(thirdTerm);
      
 CList *FuzzResult=OurFuzzy.Calculate(Inputs);
 Output=FuzzResult.GetNodeAtIndex(0);
 double res = Output.Value();
 delete FuzzResult;

 return(res);
}

この関数は、期間の異なる3つのRSIオシレータの値を取得し、0~1の範囲で正規化します（値は単純に100で割ることができます）。ファジー辞書オブジェクトでリストを更新し（最新の指標値）、て計算に送り、出力変数のリストを作成してその結果を 'res'変数に入れます。

サービス機能の追加と結果システムの最適化/テスト

機械学習（少なくともその基礎）が考慮されているため、一部のパラメータは入力に移動されて最適化されます。

input string Fuzzy_Setings;        // ファジー最適化設定
input double Gsigma = 0.5;         // シグマは0.05~0.5でステップは0.05
input double Gposition=0.5;        // ポジションは0.0~1.0でステップは0.1
input double MinNeutralSignal=0.4; // MinNeutralSignalは0.3~0.5でステップは0.1
input double MaxNeutralSignal=0.6; // MaxNeutralSignalは0.5~0.7でステップは0.1

Gaussian（メンバシップ関数）のパラメータは、ファジー論理の出力で最適化されます。その中心はX軸に沿ってシフトされ（パラメータGposition）、そのシグマが変更されます（ベルの縮小と圧縮、パラメータGsigma）。これは、売買RSIシグナルが非対称である場合にシステムのより良く微調整します。

さらに、中立シグナルの最小値と最大値（シグナルが定義されていないため、これらの値の間の範囲では新しいポジションは開かれない）を取引の条件として最適化します。

下記はファジー論理の出力におけるシグナルの処理を示します。

void OnTick()
  {
//---
   if(!isNewBar())
     {  
      return;
     }
     
   double TradeSignal=CalculateMamdani(); 
   
   if(CountOrders(0)!=0 || CountOrders(1)!=0)                                           // ポジションがある場合
      {
       for(int b=OrdersTotal()-1; b>=0; b--)
         {
          if(OrderSelect(b,SELECT_BY_POS)==true)
           {
            if(OrderSymbol()==_Symbol && OrderMagicNumber()==OrderMagic)
             {
              if(OrderType()==OP_BUY && TradeSignal>=MinNeutralSignal)                  // 買い注文が選択され取引シグナルが中立シグナルの左境界を上回る
               {                                                                        // つまり中立シグナルか売りシグナルが存在する場合は
                if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red))       // 買いポジションを決済する
                 {
                  if(TradeSignal>MaxNeutralSignal)                                      // 注文が決済されて売りシグナルが存在する（中立シグナルの右境界を上回る）場合、売りポジションを開く
                  {
                   lots = LotsOptimized(); 
                   if(OrderSend(Symbol(),OP_SELL,lots,SymbolInfoDouble(_Symbol,SYMBOL_BID),0,0,0,NULL,OrderMagic,Red)){
                     };
                  }
                 }
               }
               if(OrderType()==OP_SELL && TradeSignal<=MaxNeutralSignal)                 // 買い注文が選択され....///.... 買いポジションも同じですが、すべての条件は反対です。
               {
                if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red))
                 {
                  if(TradeSignal<MinNeutralSignal)
                  {
                   lots = LotsOptimized(); 
                   if(OrderSend(Symbol(),OP_BUY,lots,SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,Green)){
                    };
                  }
                 }
               }
             }
            }
          }
         return;
        }
                 // ポジションがなければ、シグナルに応じてポジションを開く
   lots = LotsOptimized(); 
   if(TradeSignal<MinNeutralSignal && CheckMoneyForTrade(_Symbol,lots,ORDER_TYPE_BUY))
     { 
      if(OrderSend(Symbol(),OP_BUY,lots,SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,Green)){
       };
     }
   else if(TradeSignal>MaxNeutralSignal && CheckMoneyForTrade(_Symbol,lots,ORDER_TYPE_SELL))
     {
      if(OrderSend(Symbol(),OP_SELL,lots,SymbolInfoDouble(_Symbol,SYMBOL_BID),0,0,0,NULL,OrderMagic,Red)){
       };
     }
   return;
     
  }

デモを加速するために、計算は新しいバーで実行されます。ロジックは自由にカスタマイズしてください。たとえば、新しいバーの確認をやめるだけで、すべてのティックを取引することができます。

ポジションがあってシグナルが現在のポジションと矛盾するまたは定義されていない場合は、ポジションを決済します。反対のポジションを開くための条件が満たされている場合は、それを開きます。

このシステムは、取引の決済/再開がシグナルに基づいているため、ストップロスば取引の逆転ではないので利用しません。

エキスパートアドバイザーはMT4Ordersライブラリを使用するので、注文操作は容易で、コードはMQL4に簡単に変換できます

テスト過程

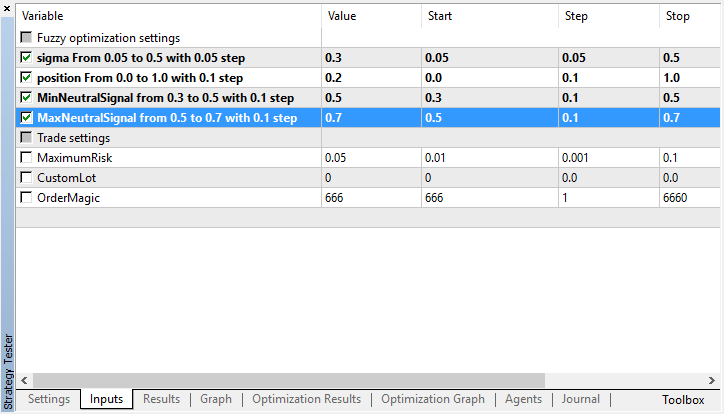
システムはスクリーンショットに示された設定を使用して8ヶ月間のM15時間枠で、始値に基づいて最適化されています。 高速遺伝的アルゴリズムが使用され残高+最大利益による最適化基準が使われます。

最良の最適化結果を選択します。

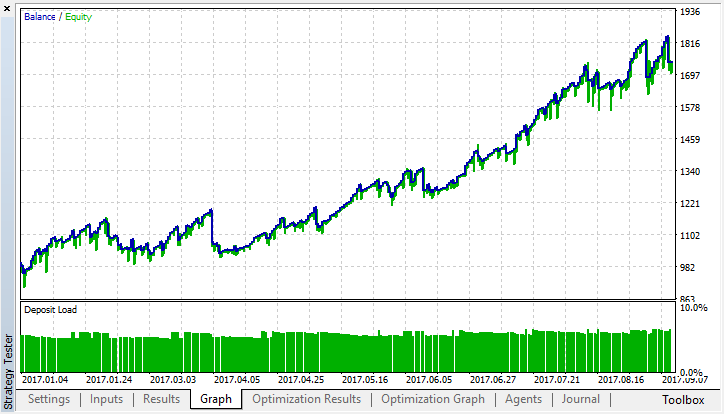
厳密なモデルのテスト結果と比較します。

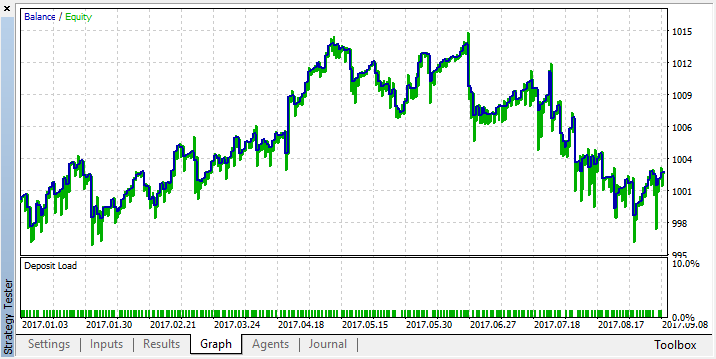
最適化後の出力での得られたメンバシップ関数（入力は最適化されていないので変更されない）。

変更前：

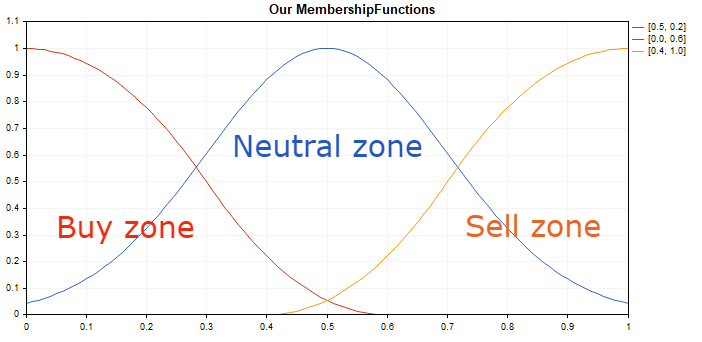
変更後：

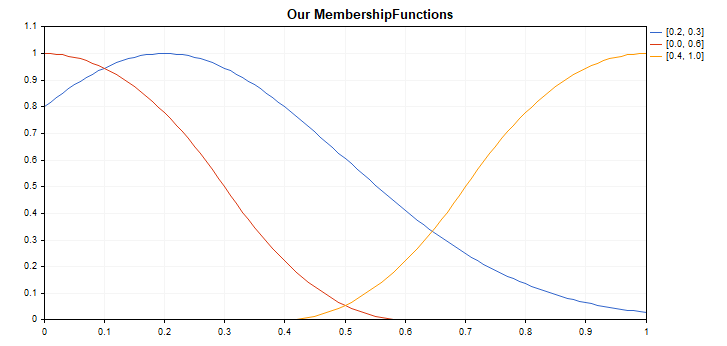
同じ設定を使ってM5時間枠でシステムを最適化します。

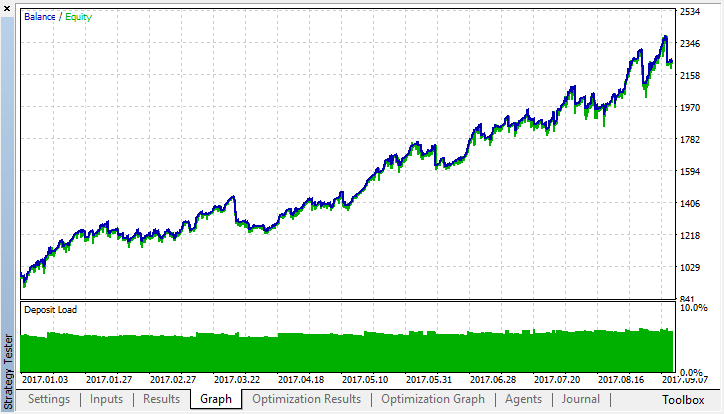
厳密なモデルのテスト結果と比較します。

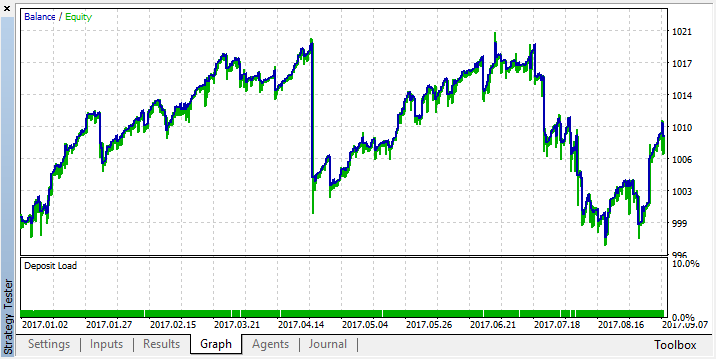
最適化後の出力での得られたメンバシップ関数（入力は最適化されていないので変更されない）。

変更前：

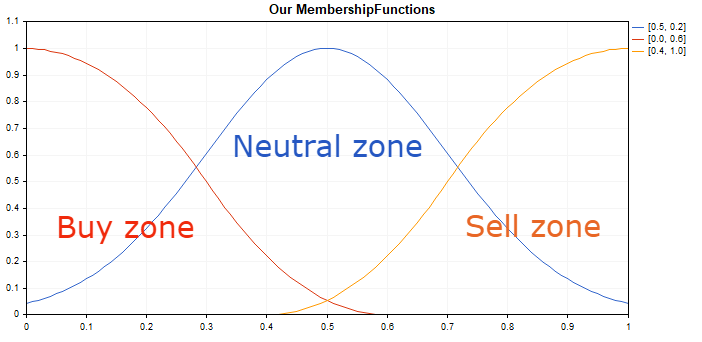
変更後：

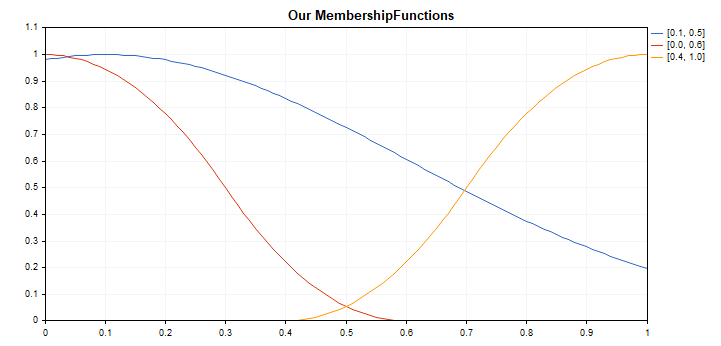
どちらの場合も、Gaussian（中立領域）は売りにシフトし、売りポジションの数よりも買いポジションの数が多くなっています。これは、買売シグナルはこの特定の履歴範囲では非対称で、これは実験なしでは発見できなかったということです。3つのRSIで構成されるシステムは、買われ過ぎ領域（領域0）よりも頻繁に売られ過ぎ領域（領域1）にあり、Gaussianの最適化がこの不均衡を平滑化するのを助けた可能性があります。最もクリスプな出力については、なぜ、そのような出力構成が取引システムの結果の改善に寄与したのかを分析するのは困難です。ファジー集合への入力の全てのマッピングに関連して、重力の重心法を用いた非ファジー化の過程が、すでにそれ自体が複雑なシステムだからです。

システムは、4つのパラメータのみが最適化されていても、8ヶ月間安定していました。Gsigma及びGposition以外の2つは結果にほとんど影響を及ぼさず常に0.5付近にあるため、パラメータは簡単にGsigmaとGpositionの2つに減らすことができます。これは、ファジー論理の要素を取引システムに導入することによって最適化されたパラメータの数をどのように減らすことができるかを示すことを目的とした、実験システムにとって満足のいく結果であると思われます。対照的に、厳しいルールに対しては多数の最適化基準を作成する必要があり、システム開発の複雑さと最適化されたパラメータの数を増やすことになったでしょう。

これは、ストップロスさえも使用せずに原始的なRSIベースの戦略を使用しており、ファジー論理に基づいた取引システム構築の非常に大まかな例でしかないことは留意されるべきです。しかし、これは、取引システム作成へのファジー論理の適用可能性を理解するのには十分であるはずです。

終わりに

ファジー論理を使うと、最適化するのが非常に簡単なファジールールを持つシステムを素早く作成することができます。同時に、取引システムのパラメータを選択する複雑な過程は、遺伝的最適化を通じ、開発者を取引戦略の検索、取引システムの多数のルールの開発、アルゴリズム化から解放します。他の機械学習方法（例えば、ニューラルネットワーク）と共に、このアプローチは印象的な結果の達成を可能にします。過適合の可能性と入力データの次元は減少します（期間が異なる3つのRSI指標が1つのシグナルに絞り込まれ、各指標よりも市場状況をより完全かつ一般化します）。

ファジー論理がどのように機能するかを理解するのにまだ苦しんでいる場合は、あなたの考え方、あなたが操作する用語、そして意思決定がどのようなルールベースに基づいているのかを自問してください。

ここに補強的な例があります。たとえばあなたに、パーティーに行く、家で映画を見る、世界を救う、という3つの願いがあるとします。あなたがすでに家にいてそれ以上の努力は必要ないので、「家で映画を見る」は最大の重さを持ちます。誰かがあなたを招待して迎えに来てくれるならばパーティーに行くことは実行可能ですが、これはまだ起こっていないので、行くチャンスはほどほどです。そして最後に、世界を救うためには、持っている超自然能力をすべて動員してスーパーマンの衣装を着て宇宙モンスターと戦わなければなりません。今日これをすることはまずないので、このチャンスはごくわずかです。

ファジー推論は次のようなものになります：私は家にいる可能性が高く、パーティに行くかもしれませんが、今日世界を救うつもりはありません。チャンスは非ファジー化の後で0〜10のスケールで評価することができ、0は「家にいる」、5は「パーティに行く」、10は「モンスターと戦う」となります。明らかに、クリスプな出力は0~3の範囲にあります。つまり、自宅にいる可能性が最も高いです。お見せした取引システムでは同じ原理が使用されます。3つの指標の値を比較し、論理的条件を使用して現時点で最も良いオプションが買う、売る、または何もしないことかを決定します。

下記はこの例を改善するための可能な方法です（自習用）。