MetaTrader 5 / トレーディング
English Русский 中文 Español Deutsch Português
ディープニューラルネットワーク(その4)ニューラルネットワーク分類器のアンサンブル: バギング

ディープニューラルネットワーク(その4)ニューラルネットワーク分類器のアンサンブル: バギング

MetaTrader 5 — トレーディング | 17 9月 2018, 10:12
2 269 1
Vladimir Perervenko
Vladimir Perervenko

内容


はじめに

本シリーズの前の記事ではDNNモデルの超パラメータについてお話しし、複数の例で訓練し、検証しました。結果として得られたモデルの品質はかなり高いものでした。

また、分類品質を改善する方法の可能性も検討しました。それらの1つは、ニューラルネットワークのアンサンブルを使用することです。この増幅の変法については、この記事で説明します。


1. ニューラルネットワーク分類器のアンサンブル

研究によると、分類器のアンサンブルは通常、個々の分類器よりも正確です。そのようなアンサンブルの1つを図1aに示します。これは、複数の分類器を使用し、それぞれが入力として入力されたオブジェクトに関する決定を行います。次に、これらの個々の決定は結合器で集約されます。アンサンブルは、オブジェクトのクラスラベルを出力します。

分類器のアンサンブルを厳密に定義することができないのは直感的にわかります。この一般的な不確かさは図1b-dに示されています。基本的には、アンサンブル自体は分類器です(図1b)。それを含む基本分類器は(しばしば暗黙の)規則性の複雑な機能を抽出し、結合器はこれらの機能を集約する単純な分類器になります。

一方、従来の標準ニューラルネットワーク分類器をアンサンブルと呼べない理由はありません(図1c)。その最後から2番目の層のニューロンは、別個の分類器と考えることができます。それらの決定は結合器で「解読」されなければならず、その役割は最上位層が果たします。

最後に、機能は原始的な分類器、分類器はその複雑な結合器として考えることができます(図1d)。

ここでは、シンプルな訓練可能な分類器を組み合わせて、分類に関する正確な決定を得ます。しかしこれは正しい方法でしょうか。

2002年に公開された重要なレビュー記事"Multiple Classifier Combination: Lessons and Next steps"(複数の分類器の組み合わせ: レッスンと次のステップ)で、Tin Kam Hoは次のように書いています。

「最良の分類器と最良の分類器を探すのではなく、最良の分類器セットを探し、次に最良の組み合わせ法を探すのです。そのうち、最良の組み合わせ法を探して、それらをすべて使う最良の方法を探していきます。この挑戦から生じる根本的な問題を見直すチャンスがなければ、ますます複雑な組み合わせスキームや理論と無限の再発に巻き込まれ、徐々に元の問題を見失ってしまうでしょう。」

分類器アンサンブルとは

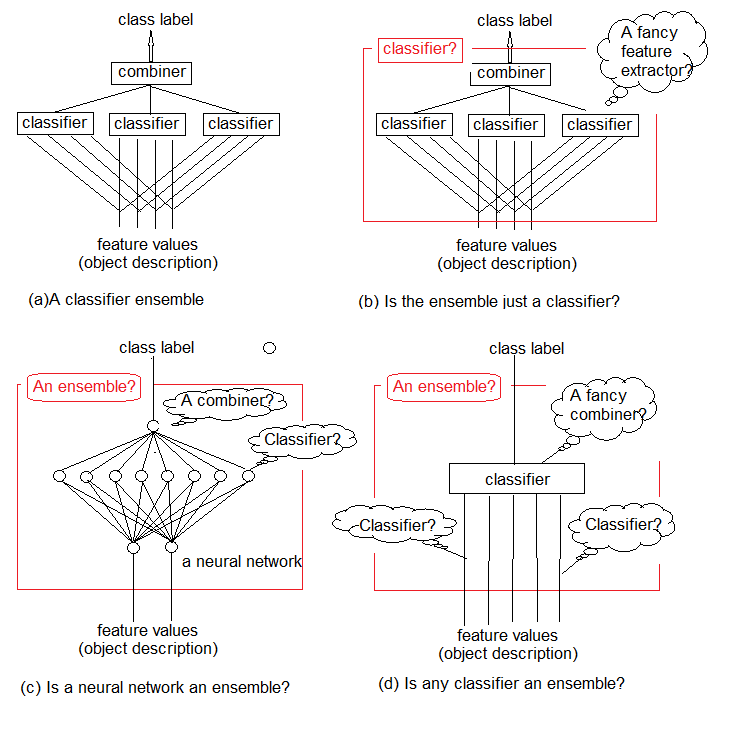
図1　分類器アンサンブル

ここでの教訓は、複雑なプロジェクトを新しく作成する前に、既存のツールや方法を使う最適な方法を見つけなければならないということです。

ニューラルネットワークの分類器は「普遍的な近似」であることが知られています。これは、どのような分類境界も、その複雑さにかかわらず、必要な精度を有する有限のニューラルネットワークによって近似することができることを意味します。しかし、この知識を持っても、そのようなネットワークを作り、訓練する方法はわかりません。分類器を組み合わせるという考え方は、管理されたビルディングブロックのネットワークを構成することによって問題を解決する試みです。

アンサンブルを構成する方法は、いくつかの機械学習方法を1つの予測モデルに組み合わせたメタアルゴリズムです。

  • 分散を減らす — バギング
  • バイアスを減らす — ブースティング
  • 予測を改善する — スタッキング

これらの方法は、2つのグループに分けることができます。

  • アンサンブルを並列に構築する方法ではベースモデルが並行して生成されます(例: ランダムフォレスト)。ここでのアイディアはベースモデル間の独立性を使用し、平均化によって誤差を減らすことです。したがって、モデルの主な要件は、相互相関の低さと多様性の高さです。
  • シーケンシャルアンサンブル法では、ベースモデルが順次生成されます(AdaBoost、XGBoostなど)。ここでの主なアイデアは、ベースモデル間の依存関係を使用することです。ここでは、以前に誤って分類された例に高い重みを割り当てることによって全体の品質を高めることができます。

ほとんどのアンサンブル手法は、均質なベースモデルを作成する際に単一の基本学習アルゴリズムを使用します。これは均質なアンサンブルにつながります。異種モデル(異なるタイプのモデル)を使用する方法もあります。その結果、異種のアンサンブルが形成されます。アンサンブルが個々のメンバーよりも正確であるためには、ベースモデルは可能な限り多様でなければなりません。言い換えれば、より多くの情報が基本分類器から来るほど、アンサンブルの精度は高くなります。

図2は、分類器のアンサンブルを作成する4つのレベルを示しています。それぞれについて疑問がありますが、それらについては後述します。

図2　分類器のアンサンブルを作成する4つのレベル

もっと詳しくお話ししましょう。

1. 結合器


結合器はアンサンブル法の一部では定義されません。しかし、定義される場合、3種類あります。 

  • 訓練不可: この方法の例は「多数決」です。
  • 訓練可: このグループには、「重み付け多数決」、「単純ベイズ」、特定のオブジェクトに関する決定がアンサンブルの1つの分類器によって行われる「分類器選択」アプローチが含まれます。
  • メタ分類器: 基本分類器の出力は、新しい分類器が訓練される入力として考慮され、これは結合器になります。このアプローチは、「複雑な一般化」、「訓練による一般化」、または単に「スタッキング」と呼ばれています。メタ分類器の訓練セットを構築することは、この結合器の主な問題の1つです。

2. アンサンブルの構築


基本分類器は(独立して)並列に訓練されるべきでょうか。それとも逐次訓練されるべきでょうか。逐次訓練の例はAdaBoostで、追加された各分類器の訓練セットは、前に作成されたアンサンブルに依存します。

3. 多様性


アンサンブルの違いを生み出す方法としては、次のオプションが提案されています。

  • 取引パラメータを操作: 個々の基本分類器を訓練する場合は、異なるアプローチとパラメータを使用します。 例えば、各基本分類器のニューラルネットワークの隠れ層におけるニューロン重みを異なる確率変数で初期化することが可能です。超パラメータをランダムに設定することもできます。
  • サンプルを操作: アンサンブルの各メンバーの訓練セットからカスタムブートストラップサンプルを取得します。
  • 予測子を操作: 各基本分類器のためのランダムに決定された予測子のカスタムセットを準備します。これは、訓練セットのいわゆる垂直分割です。

4. アンサンブルサイズ


アンサンブルの分類器数はどのように決定するのでしょうか。アンサンブルは、必要な数の分類器を同時に訓練して構築されたでのしょうか。それとも分類器を追加/削除することによって反復的に構築されたのでしょうか。可能なオプションは次の通りです。

  • 数が事前に予約されている
  • 数は訓練の過程で設定される
  • 分類器が過剰生成されて選択される

5. 汎用性(基本分類器に相対)


アンサンブルアプローチの一部は、任意の分類器モデルと共に使用されますが、他のアプローチは、特定の種類の分類器に関連付けられます。「分類器固有の」アンサンブルの一例は、ランダムフォレストです。その基本分類器は決定木です。したがって、アプローチには2つのバリエーションがあります。

  • 特定モデルの基本分類器のみの使用が可能
  • 任意モデルの基本分類器の使用が可能

分類器アンサンブルのパラメータを訓練して最適化する際は、解の最適化とカバレッジの最適化とを区別しなければなりません。

  • 意思決定の最適化: 基本分類器(図2のレベルA)の固定されたアンサンブルに対して結合器を選択
  • 代替カバレッジの最適化: 固定結合器(図2のレベルB、C、D)を用いて多様な基本分類器を作成

このようにアンサンブル設計を分解することは、問題の複雑さが軽減するために合理的です。

アンサンブル法の非常に詳細で深い分析は以下の書籍で考察されています。Combining Pattern Classifiers. Ludmila Kuncheva著、Methods and Algorithms第2版(英語)、Ensemble Methods. Foundations and Algorithms(英語)。お読みになってください。

2. バギング

この手法の名前(Bagging)は、Bootstrap AGGregatINGという語句から来ています。バギングアンサンブルは次のように作成されます。

  1. ブートストラップサンプルが訓練セットから抽出されます。
  2. 各分類器がそれ自身のサンプルで訓練されます。
  3. 別々の分類器からの個々の出力が、1つのクラスラベルに結合されます。個々の出力がクラスラベルの形式を持つ場合、単純な多数決が使用されます。分類器の出力が連続変数である場合、平均化が適用されるか、変数がクラスラベルに変換されてから単純多数決が行われます。

図2に戻り、バギング法に適用される分類器のアンサンブルを作成するすべてのレベルを分析しましょう。

A: 集計レベル

このレベルでは、分類器から得られたデータが結合され、単一の出力が集計されます。

個々の出力をどのように組み合わせるのでしょうか。これには、訓練不可な結合器を使用します(平均、単純多数決)。

B: 分類器のレベル

すべての分類器作業はレベルBで行われます。ここではいくつかの疑問がわきます。

  • 異なる分類器を使用するか、同じ分類器を使用するか: バギングでは同じ分類器が使用されます。
  • 基本分類器にはどの分類器を使用するか: ELM (エクストリーム・ラーニング・マシン)を使用します。

これについてもっと詳しく説明しましょう。分類器の選択とその推論は、作業の重要な部分です。高品質のアンサンブルを作成するための基本分類器の主な要件を挙げてみましょう。 

まず、分類器は単純でなければなりません。ディープニューラルネットワークは推奨されません。 

第2に、分類器は異なるものでなければなりません。初期化、学習パラメータ、訓練セット等が異ならなければなりません。

第3に、分類器の速度が重要です。モデルの訓練に数時間もかかってはいけません。

第4に、分類モデルは弱く、50％よりわずかに良い予測結果を与えるべきです。

そして、最終的には、分類器の不安定性が重要であるため、予測結果には広い範囲があります。

これらの要件をすべて満たすオプションがあります。それは、特別なタイプのニューラルネットワークであるELM(クストリーム・ラーニング・マシン)であり、MLPの代わりに代替学習アルゴリズムとして提案されています。正式には、それは1つの隠れ層を持つ全結合ニューラルネットワークですが、重み(訓練)が反復的に決定されないため、例外的に高速です。初期化中に隠れ層のニューロンの重みが一度ランダムに選択され、選択された活性化関数に従って出力重みが解析的に決定されます。ELMアルゴリズムの詳細な説明とその多くの種類の概要は、添付のアーカイブに記載されています。

  • 必要な分類器の数: 500にして、後でアンサンブルを刈り込みしましょう。
  • 分類器は並列で訓練されるか連続的に訓練されるか: 並列訓練が使用され、すべての分類器で同時に実行されます。
  • どの基本分類器パラメータを調整できるか: 隠れ層の数、活性化関数、訓練セットのサンプルサイズです。これらのパラメータはすべて最適化の対象となります。

C: 特定された規則性の機能レベル

  • すべての予測子が使用されるか、各分類器の個別のサブセットのみが使用されるか: すべての分類器は、予測子のサブセットを1つ使用しますが、予測子の数は最適化することができます。
  • サブセットの選択法: この場合、特別なアルゴリズムが使用されます。

D: 入力データとその操作のレベル

このレベルでは、訓練のためにソースデータがニューラルネットワークの入力に供給されます。

入力データを操作して高い多様性と高い精度を実現する方法: ブートストラップのサンプルは各分類器ごとに個別に使用されます。ブートストラップのサンプルサイズは、すべてのアンサンブルメンバーで同じですが、最適化されます。

ELMアンサンブルで実験を行うには、R(elmNN、ELMR) とPython(hpelm)の2つのパッケージがあります。今のところ、従来のELMを実装しているelmNNパッケージの機能をテストしてみましょう。elmNNパッケージは、ELMバッチ法を使用して作成、訓練、テストするために設計されています。したがって、訓練およびテストサンプルは、訓練前にそろっており、一度モデルに供給されます。パッケージはとてもシンプルです。

実験は次の段階で構成されます。

  1. ソースデータセットの生成
  2. 情報の重要度による予測子の配置
  3. アンサンブル分類器の訓練とテスト
  4. 分類器の個々の出力の結合(平均/投票)
  5. アンサンブルの刈り込みとその手法
  6. アンサンブル分類の品質指標の検索
  7. アンサンブルメンバーの最適パラメーターの特定手法
  8. 最適のパラメータを使ったアンサンブルの訓練とテスト

ソースデータセットの生成

実験にはMRO 3.4.3の最新版が使用されます。そこでは、ここでの作業に適したいくつかの新しいパッケージが実装されています。

RStudioを実行し、GitHub/Part_Iに移動して、ターミナルから取得されたクオーツを持つCotir.RDataファイルをダウンロードし、データ準備関数を持つFunPrepareData.RファイルをGitHub/Part_IVからダウンロードします。

補完された外れ値と正規化データを持つデータセットは、事前訓練を使用した訓練でより良い結果を得ることが以前にわかりました。これを使用します。前に考えた他の前処理オプションもテストすることができます。

pretrain/train/val/test(事前訓練/訓練/検証/テスト)サブセットに分割する際には、分類の質を向上させるための最初の機会を使用します。つまり、訓練のサンプル数を増やします。「事前訓練」サブセットのサンプル数は4000に増やされます。

#---- 準備する -------------
library(anytime)
library(rowr)
library(elmNN)
library(rBayesianOptimization)
library(foreach)
library(magrittr)
library(clusterSim)
#source(file = "FunPrepareData.R")
#source(file = "FUN_Ensemble.R")
#--- 準備する ----
evalq({
  dt <- PrepareData(Data, Open, High, Low, Close, Volume)
  DT <- SplitData(dt, 4000, 1000, 500, 250, start = 1)
  pre.outl <- PreOutlier(DT$pretrain)
  DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl)
  preproc <- PreNorm(DTcap, meth = meth)
  DTcap.n <- NormData(DTcap, preproc = preproc)
}, env)

startパラメータをSplitData()関数で変更することで、'start'の分だけ右にシフトしたセットを得ることができます。これにより、将来の価格帯のさまざまな部分の品質を確認し、履歴の変化を判断することができます。

訓練用およびテスト用のデータセット(pretrain/train/test/test1)を作成して、Xリストに集めます。目的を因子から数値型(0.1)に変換します。

#---データX-------------
evalq({
  list(
    pretrain = list(
      x = DTcap.n$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
      y = DTcap.n$pretrain$Class %>% as.numeric() %>% subtract(1) 
    ),
    train = list(
      x = DTcap.n$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
      y = DTcap.n$train$Class %>% as.numeric() %>% subtract(1) 
    ),
    test = list(
      x = DTcap.n$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
      y = DTcap.n$val$Class %>% as.numeric() %>% subtract(1) 
    ),
    test1 = list(
      x = DTcap.n$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), 
      y = DTcap.n$test$Class %>% as.numeric() %>% subtract(1) 
    )
  ) -> X
}, env)

情報の重要度による予測子の配置

clusterSim::HINoV.Mod()関数をテストします(詳細はパッケージを参照)。この関数は、異なる距離と方法でクラスタリングに基づいて変数をランク付けします。ここでは、デフォルトのパラメータを使用しますが、他のパラメータを使ってご自由に実験してください。numFeature <- 10定数を使用すると、モデルに供給される最良の予測子の数(bestF)を変更することができます。

計算はX$pretrainセットで行われます。

require(clusterSim)
evalq({
  numFeature <- 10
  HINoV.Mod(x = X$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4, 
            distance =  NULL, # "d1" - Manhattan, "d2" - Euclidean, 
            #"d3" - Chebychev (max), "d4" - squared Euclidean, 
            #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
            method = "kmeans" ,#"kmeans" (default) , "single", 
            #"ward.D", "ward.D2", "complete", "average", "mcquitty", 
            #"median", "centroid", "pam"
            Index = "cRAND") -> r
  r$stopri[ ,1] %>% head(numFeature) -> bestF
}, env)
print(env$r$stopri)
      [,1]      [,2]
 [1,]    5 0.9242887
 [2,]   11 0.8775318
 [3,]    9 0.8265240
 [4,]    3 0.6093157
 [5,]    6 0.6004115
 [6,]   10 0.5730556
 [7,]    1 0.5722479
 [8,]    7 0.4730875
 [9,]    4 0.3780357
[10,]    8 0.3181561
[11,]    2 0.2960231
[12,]   12 0.1009184

予測子の順位付けの結果は、上のコードに示されています。トップ10は以下のとおりで、将来使用されます。 

> colnames(env$X$pretrain$x)[env$bestF]
 [1] "v.fatl" "v.rbci" "v.ftlm" "rbci"   "v.satl" "v.stlm" "ftlm"  
 [8] "v.rftl" "pcci"   "v.rstl"

実験のためのセットの用意ができました。

テスト結果から指標を計算するためのEvaluate()関数は、このシリーズの前の記事から取ります。mean(F1)の値は最適化(最大化)基準として使用されます。この関数を'env'環境に読み込みます。

アンサンブルの作成、訓練、テスト

ニューラルネットワークのアンサンブル(n <- 500単位)を訓練し、Ensで結合します。各ニューラルネットワークは、独自のサンプルで訓練されています。サンプルは、訓練セットからの7/10の例をランダムに置換して抽出し、生成されます。モデルでは 'nh'(隠れ層ニューロンの数)と 'act'(活性化関数)の2つのパラメータを設定する必要があります。パッケージの活性化関数には次のオプションがあります。

  1. - sig: sigmoid
  2. - sin: sine
  3. - radbas: radial basis
  4. - hardlim: hard-limit
  5. - hardlims: symmetric hard-limit
  6. - satlins: satlins
  7. - tansig: tan-sigmoid
  8. - tribas: triangular basis
  9. - poslin: positive linear
  10. - purelin: linear

入力変数が10個あることを考慮して、まずnh = 5とします。活性化関数は、actfun = "sin"とみなされます。アンサンブルはすばやく学びます。私はニューラルネットワークに関する経験に基づいて直感的にパラメータを選択しましたが、他のオプションを試すこともできます。 

#---3-----訓練----------------------------
evalq({
  n <- 500
  r <- 7
  nh <- 5
  Xtrain <- X$pretrain$x[ , bestF]
  Ytrain <- X$pretrain$y 
  Ens <- foreach(i = 1:n, .packages = "elmNN") %do% {
    idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr
    elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], 
             nhid = nh, actfun = "sin")
  }
}, env)

スクリプトの計算について簡単に触れてみましょう。定数n(アンサンブル内のニューラルネットワークの数)とr(ニューラルネットワークの学習に使用するブートストラップサンプルのサイズで、このサンプルは、アンサンブル内の各ニューラルネットワークごとに異なります)を定義します。nhは隠れ層でのニューロンの数です。次に、メインセットXtrainを使用して入力データセットXtrainを定義し、特定の予測子bestFだけを残します。

これにより、500個の個々のニューラルネットワーク分類器からなるアンサンブルEns[[500]]が生成されます。最良の予測子bestFを使用してメインセットX$trainから取得したテストセットXtestでテストします。生成された結果は、500個の連続予測変数のデータフレームy.pr[1001, 500]です。

#---4-----予測-------------------
evalq({
  Xtest <- X$train$x[ , bestF]
  Ytest <- X$train$y
  foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% {
    predict(Ens[[i]], newdata = Xtest)
  } -> y.pr #[ ,n]
}, env)

分類器の個々の出力の結合方法(平均化/投票)

アンサンブルの基本分類器は、次の出力タイプを持つことができます。

  • クラスラベル
  • 2クラス以上で分類された場合のクラスランキングラベル
  • 継続的な数値予測/サポートの程度

基本分類器には、出力に連続的な数値変数(サポートの程度)があります。この入力Xのサポートの程度は、さまざまな方法で解釈できます。これは、提案されたラベルの信頼性またはクラスのための可能性の評価であり得ます。ここでの場合では、提案された分類ラベルの信頼性が出力として役立ちます。

結合の最初のバリエーションは平均化で、個々の出力の平均値を取得します。これが、変換のしきい値を0.5として、クラスラベルに変換されます。

結合の2番目のバリエーションは多数決です。これを行うために、各出力はまず連続変数からクラスラベル[-1, 1]に変換されます(変換しきい値は0.5です)。次に、すべての出力が合計され、結果が0より大きい場合はクラス1が割り当てられ、それ以外の場合はクラス0が割り当てられます。

得られたクラスラベルを使用して、指標(正確度、精度、再現率、F1)を決定します。

アンサンブルの刈り込み手法

余分な数の基本分類器から、最良のものを選択します。これを行うには、次の手法が適用されます。

  • 順序ベースの刈り込み - ある品質スコアによって順位付けされたアンサンブルから選択します。
    • エラー削減刈り込み — 分類器を分類エラーによって並び替え、いくつかの最良(エラーが最小)のものを選択します。
    • kappa刈り込み - kappaの統計に基づいてアンサンブルのメンバーを順位付けし、最小のスコアをもつ必要数を選択します。
  • クラスタリングベースの刈り込み - アンサンブルの予測結果は任意の手法でクラスタリングされ、その後、各クラスタのいくつかの代表を選択します。クラスタリング法には下記があります。
    • パーティショニング(例: SOM、k平均)
    • 階層
    • 密度ベース(例: dbscan)
    • GMMベース
  • 最適化ベースの刈り込み - 最良のものを選択するために進化的アルゴリズムまたは遺伝的アルゴリズムが使用されます。

アンサンブルの刈り込みは、予測子の選択と同じなので、予測子を選択するときと同じ方法を適用することができます(これについては、前回の記事で説明しました)。

分類誤差(縮小誤差剪定)によって順序付けられたアンサンブルからの選択は、さらなる計算に使用されます。

合計で、以下の方法を実験に使用します。

  • 結合器法 - 平均化と単純多数決
  • 指標 — 正確度、精度、再現率、F1
  • 刈り込み — mean(F1)に基づく分類誤差によって順序付けられたアンサンブルからの選択

連続変数の個々の出力をクラスラベルに変換するためのしきい値は0.5です。これは最良の選択肢ではなく、最も簡単な選択肢で、後で改善することができます。

a) アンサンブルの最良分類器の特定

500個のニューラルネットワークのmean(F1)を特定し、最高スコアを持ついくつかの'bestNN'を選択します。多数決のための最良のニューラルネットワークの数は奇数でなければならないので、(numEns*2 + 1)として定義されます。

#---5-----最良----------------------
evalq({
  numEns <- 3
  foreach(i = 1:n, .combine = "c") %do% {
    ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred
    Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>%
      mean() 
  } -> Score
  Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN
  Score[bestNN] %>% round(3)
}, env)
[1] 0.720 0.718 0.718 0.715 0.713 0.713 0.712

スクリプトの計算について簡単に触れてみましょう。foreach()ループで、各ニューラルネットワークの連続予測y.pr[ ,i]を数値[0,1]に変換します。この予測のmean(F1)を特定し、値をベクトルScore[500]として出力します。次に、ベクトルScoreのデータを降順で並び替え、最良(最高)スコアを持つbestNNニューラルネットワークのインデックスを決定します。Score[bestNN]の最良メンバーの指標値を小数点第3位まで四捨五入して出力します。ご覧のとおり、個々の結果はあまり高くありません。

注: サンプルとニューラルネットワークの初期設定が異なるため、訓練とテストの実行ごとに異なる結果が生成されます。

さて、アンサンブルの中で最も優れた個々の分類器が特定されました。平均化と単純多数決の組み合わせ法を使って、サンプルX$testとX$test1でテストしましょう。

b) 平均化

#---6---- averaging(test)をテスト--------
evalq({
  n <- len(Ens)
  Xtest <- X$test$x[ , bestF]
  Ytest <- X$test$y
  foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:%
    when(i %in% bestNN) %do% {
    predict(Ens[[i]], newdata = Xtest)} %>%
    divide_by(length(bestNN)) -> ensPred
  ifelse(ensPred > 0.5, 1, 0) -> ensPred
  Evaluate(actual = Ytest, predicted = ensPred)$Metrics[ ,2:5] %>%
    round(3)
}, env)
Accuracy Precision Recall    F1
0     0.75     0.723  0.739 0.731
1     0.75     0.774  0.760 0.767

スクリプトでの計算についての一言です。メインセットX$testを使ってアンサンブルnのサイズ、入力Xtestと目的Ytestを決定します。次に、foreachループ(インデックスが 'bestNN'インデックスに等しいときのみ)で、これらの最良のニューラルネットワークの予測を計算し、合計し、最良のニューラルネットワークの数で除算します。出力を連続変数から数値変数(0,1)に変換し、指標を計算します。ご覧のように、分類品質スコアは個々の分類器のスコアよりもはるかに高いです。

X$testの横にあるX$test1セットに対して同じテストを実行します。質を見積もります。 

#--6.1 ---averaging(test1)をテスト---------
evalq({
  n <- len(Ens)
  Xtest <- X$test1$x[ , bestF]
  Ytest <- X$test1$y
  foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:%
    when(i %in% bestNN) %do% {
      predict(Ens[[i]], newdata = Xtest)} %>%
    divide_by(length(bestNN)) -> ensPred
  ifelse(ensPred > 0.5, 1, 0) -> ensPred
  Evaluate(actual = Ytest, predicted = ensPred)$Metrics[ ,2:5] %>%
    round(3)
}, env)
Accuracy Precision Recall    F1
0    0.745     0.716  0.735 0.725
1    0.745     0.770  0.753 0.761

分類の質は実質的に変わっておらず、かなり高いままです。この結果は、ニューラルネットワーク分類器のアンサンブルが、前の記事で得られたDNNよりもはるかに長い期間(この例では750バー)の訓練と刈り込み後に高品質の分類を保持することを示しています。

c) 単純多数決

アンサンブルの最良の分類器から得られ、単純な投票で結合される予測の指標を特定しましょう。まず、最良の分類器の連続予測をクラスラベル(-1/+1)に変換し、すべての予測ラベルを合計します。合計が0より大きい場合、クラス1が出力され、それ以外の場合はクラス0が出力されます。まず、すべてをX$testセットでテストします。

#--7 --テスト--voting(test)--------------------
evalq({
  n <- len(Ens)
  Xtest <- X$test$x[ , bestF]
  Ytest <- X$test$y
  foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:% 
    when(i %in% bestNN) %do% {
    predict(Ens[[i]], newdata = Xtest)
  } %>% 
    apply(2, function(x) ifelse(x > 0.5, 1, -1)) %>%
    apply(1, function(x) sum(x)) -> vot
  ifelse(vot > 0, 1, 0) -> ClVot
  Evaluate(actual = Ytest, predicted = ClVot)$Metrics[ ,2:5] %>%
    round(3)
}, env)
Accuracy Precision Recall    F1
0    0.745     0.716  0.735 0.725
1    0.745     0.770  0.753 0.761

結果は平均化の結果と実質的に同じです。下記はX$test1セットでのテストです。

#--7.1 --テスト--voting(test1)--------------------
evalq({
  n <- len(Ens)
  Xtest <- X$test1$x[ , bestF]
  Ytest <- X$test1$y
  foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:% 
    when(i %in% bestNN) %do% {
      predict(Ens[[i]], newdata = Xtest)
    } %>% 
    apply(2, function(x) ifelse(x > 0.5, 1, -1)) %>%
    apply(1, function(x) sum(x)) -> vot
  ifelse(vot > 0, 1, 0) -> ClVot
  Evaluate(actual = Ytest, predicted = ClVot)$Metrics[ ,2:5] %>%
    round(3)
}, env)
Accuracy Precision Recall    F1
0    0.761     0.787  0.775 0.781
1    0.761     0.730  0.743 0.737

予想外に、結果は以前のものよりも優れていることが判明しました。これはX$test1がX$testの後に位置しているにもかかわらずです。 

これは、同じデータの同じアンサンブルでも、組み合わせ法が異なると、分析の質が非常に違うことがあるということです。

アンサンブル内の個々の分類器の超パラメータが直感的に選択され、明らかに最適ではないという事実にもかかわらず、平均化と単純多数決を使用することにより、質の高く安定した分類が得られました。

上記をすべて要約してみます。図式的に示すと、ニューラルネットワークのアンサンブルを作成してテストするプロセス全体は4段階に分けることができます。

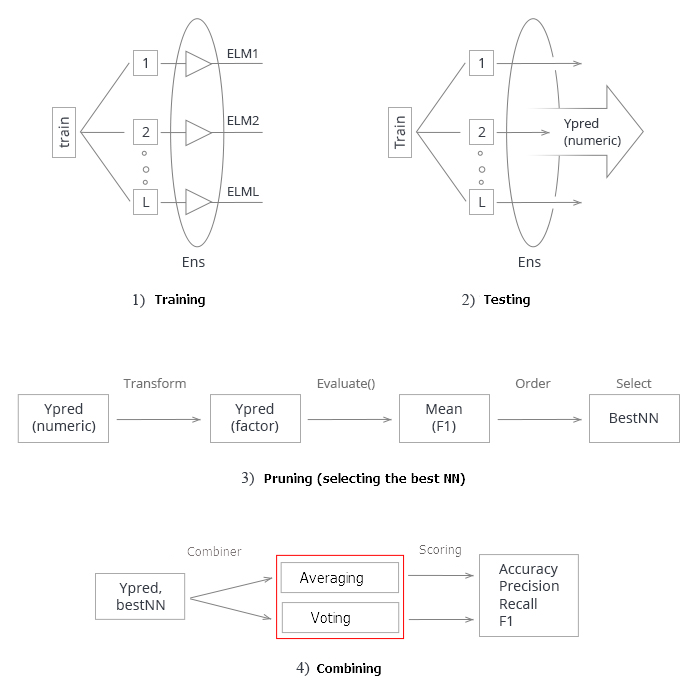
図3　平均化/投票結合器によるニューラルネットワークのアンサンブルの訓練およびテストの構造

1. アンサンブルの訓練: 訓練セットからランダムサンプル(ブートストラップ)上のL個のニューラルネットワークを訓練します。訓練されたニューラルネットワークのアンサンブルを得ます。

2. テストセットでニューラルネットワークのアンサンブルをテストします。個々の分類器の連続予測を取得します。

3. アンサンブルを刈り込み、特定の分類品質基準によって最良のnを選びます。この場合、それはmean(F1)です。

4. 個々の最良分類器の連続予測を使って、平均化または単純多数決の助けを借りて結合します。その後、指標を決定します。

最後の2つのステップ(刈り込みと結合)には複数の実装オプションがあります。同時に、アンサンブルの刈り込みに成功(最良のものを正しい識別)すると、パフォーマンスを大幅に向上させる可能性があります。この場合、それは、連続予測から数値への変換の最適なしきい値を見つけることです。したがって、これらの段階で最適なパラメータを見つける作業は面倒です。これらの段階は自動的されるべきで、最適な結果が得られるべきです。私たちに、これを行い、アンサンブルの品質スコアを向上させる能力はあるのでしょうか。それには、少なくとも2つの方法があるので、確認しましょう。

  • アンサンブルの個々の分類器の超パラメータを最適化する(ベイズ最適化)。
  • DNNをアンサンブルの個々の出力の結合器として使用する。一般化は学習を通じて行われる。

アンサンブルの個々の分類器の最適なパラメータの特定: 手法

ここでのアンサンブルの個々の分類器はELMニューラルネットワークです。ELMの主な特徴は、その特性と品質が主に隠れ層のニューロン重みのランダム初期化に依存していることです。他(ニューロン数と活性化関数の数)は同じで、各訓練は新しいニューラルネットワークを生成します。

ELMのこの特徴はアンサンブルを作成するのに最適です。アンサンブルでは、各分類器の重みをランダムな値で初期化するだけでなく、各分類器に別々のランダムに生成された訓練サンプルを提供します。

しかし、ニューラルネットワークの最良の超パラメータを選択するためには、その品質は、与えられた超パラメータの変化のみに依存しなければなりません。さもないと、検索の意味が失われます。

できるだけ多様なメンバーを持つアンサンブルが必要な一方、多様で永久的なメンバーを持つアンサンブルが必要だという矛盾が生じます。

再現可能な永続的なバリエーションが必要なのです。

これが可能かどうかを示すために、アンサンブル訓練の例を使用しましょう。"doRNG" (再現可能な乱数生成RNG)パッケージが使用されます。結果を再現するには、単一のスレッドで計算を実行する方がよいです。

クリーンなグローバル環境で新しい実験を始めます。クオーツと必要なライブラリを再度読み込み、ソースデータを定義してもう一度並び替え、numFeatureの最良の予測子を再度選択します。1つのスクリプトですべてを実行します。

#---- 準備する -------------
library(anytime)
library(rowr)
library(elmNN)
library(rBayesianOptimization)
library(foreach)
library(magrittr)
library(clusterSim)
library(doRNG)
#source(file = "FunPrepareData.R")
#source(file = "FUN_Ensemble.R")
#--- 準備する ----
evalq({
  dt <- PrepareData(Data, Open, High, Low, Close, Volume)
  DT <- SplitData(dt, 4000, 1000, 500, 250, start = 1)
  pre.outl <- PreOutlier(DT$pretrain)
  DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl)
  preproc <- PreNorm(DTcap, meth = meth)
  DTcap.n <- NormData(DTcap, preproc = preproc)
#--1-Data X-------------
  list(
    pretrain = list(
      x = DTcap.n$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
      y = DTcap.n$pretrain$Class %>% as.numeric() %>% subtract(1) 
    ),
    train = list(
      x = DTcap.n$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
      y = DTcap.n$train$Class %>% as.numeric() %>% subtract(1) 
    ),
    test = list(
      x = DTcap.n$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
      y = DTcap.n$val$Class %>% as.numeric() %>% subtract(1) 
    ),
    test1 = list(
      x = DTcap.n$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), 
      y = DTcap.n$test$Class %>% as.numeric() %>% subtract(1) 
    )
  ) -> X
#---2--bestF-----------------------------------
#require(clusterSim)
  numFeature <- 10
  HINoV.Mod(x = X$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4, 
            distance =  NULL, # "d1" - Manhattan, "d2" - Euclidean, 
            #"d3" - Chebychev (max), "d4" - squared Euclidean, 
            #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
            method = "kmeans" ,#"kmeans" (default) , "single", 
            #"ward.D", "ward.D2", "complete", "average", "mcquitty", 
            #"median", "centroid", "pam"
            Index = "cRAND") %$% stopri[ ,1] -> orderX
  orderX %>% head(numFeature) -> bestF
}, env)

必要な初期データはすべてそろっているので、ニューラルネットワークのアンサンブルを訓練します。

#---3-----訓練----------------------------
evalq({
  Xtrain <- X$pretrain$x[ , bestF]
  Ytrain <- X$pretrain$y 
  setMKLthreads(1)
  n <- 500
  r <- 7
  nh <- 5
  k <- 1
  rng <- RNGseq(n, 12345)
  Ens <- foreach(i = 1:n, .packages = "elmNN") %do% {
    rngtools::setRNG(rng[[k]])
    k <- k + 1
    idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr
    elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], 
             nhid = nh, actfun = "sin")
  }
  setMKLthreads(2)
}, env)

実行中には何が起こるのでしょう。(Xtrain, Ytrain)を訓練するための入力データと出力データを定義し、MKLライブラリをシングルスレッドモードに設定します。乱数列rngを作成して一定の定数を初期化し、foreach()が反復されるごとに乱数生成器を初期化します。

反復を完了したら、MKLの設定をマルチスレッドモードに戻すことを忘れないでください。シングルスレッドモードでは、計算結果が若干悪化します。

したがって、個々の分類器が異なるアンサンブルが得られますが、これらのアンサンブルの分類器は訓練の再実行を通して同じです。これは、4段階の計算(train/predict/best/test)を数回繰り返すことによって容易に確認することができます。計算順は、train/predict/best/test_averaging/test_votingです。

#---4-----予測-------------------
evalq({
  Xtest <- X$train$x[ , bestF]
  Ytest <- X$train$y
  foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% {
    predict(Ens[[i]], newdata = Xtest)
  } -> y.pr #[ ,n]
}, env)
#---5-----最良----------------------
evalq({
  numEns <- 3
  foreach(i = 1:n, .combine = "c") %do% {
    ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred
    Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>%
      mean() 
  } -> Score
  Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN
  Score[bestNN] %>% round(3)
}, env)
# [1] 0.723 0.722 0.722 0.719 0.716 0.714 0.713
#---6----averaging(test)をテスト--------
evalq({
  n <- len(Ens)
  Xtest <- X$test$x[ , bestF]
  Ytest <- X$test$y
  foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:%
    when(i %in% bestNN) %do% {
      predict(Ens[[i]], newdata = Xtest)} %>%
    divide_by(length(bestNN)) -> ensPred
  ifelse(ensPred > 0.5, 1, 0) -> ensPred
  Evaluate(actual = Ytest, predicted = ensPred)$Metrics[ ,2:5] %>%
    round(3)
}, env)
# 正確度　制度　再現率　F1
# 0 0.75 0.711 0.770 0.739
# 1 0.75 0.790 0.734 0.761
#--7 --テスト--voting(test)--------------------
evalq({
  n <- len(Ens)
  Xtest <- X$test$x[ , bestF]
  Ytest <- X$test$y
  foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:% 
    when(i %in% bestNN) %do% {
      predict(Ens[[i]], newdata = Xtest)
    } %>% 
    apply(2, function(x) ifelse(x > 0.5, 1, -1)) %>%
    apply(1, function(x) sum(x)) -> vot
  ifelse(vot > 0, 1, 0) -> ClVot
  Evaluate(actual = Ytest, predicted = ClVot)$Metrics[ ,2:5] %>%
    round(3)
}, env)
# 正確度　制度　再現率　F1
# 0 0.749 0.711 0.761 0.735
# 1 0.749 0.784 0.738 0.760

これらの計算が何回繰り返されても(もちろん同じパラメータで)、結果は変わりません。これはまさにアンサンブルを構成するニューラルネットワークの超パラメータを最適化するために必要なものです。

まず、最適化する超パラメータのリストを定義し、それらの値の範囲を見つけ、最適化(最大化)基準とアンサンブルの予測を返す適応度関数を作成します。個々の分類器の品質は、4つのパラメータの影響を受けます。

  • 入力データ内の予測子の数
  • 訓練に使用されるサンプルのサイズ
  • 隠れ層でのニューロンの数
  • 活性化関数

超パラメータとその値の範囲を一覧してみましょう。

evalq({
  #活性化関数の種類 
  Fact <- c("sig", #: sigmoid
            "sin", #: sine
            "radbas", #: radial basis
            "hardlim", #: hard-limit
            "hardlims", #: symmetric hard-limit
            "satlins", #: satlins
            "tansig", #: tan-sigmoid
            "tribas", #: triangular basis
            "poslin", #: positive linear
            "purelin") #: linear
  bonds <- list(
    numFeature = c(3L, 12L),
    r = c(1L, 10L),
    nh <- c(1L, 50L),
    fact = c(1L, 10L)
  )
}, env)

上記のコードをより詳細に考えてみましょう。ここで、Factは可能な活性化関数のベクトルです。リストbondsは最適化するパラメータとその値の範囲を定義します。

  • numFeature — 入力として供給される予測子の数(最小3、最大12)
  • r — ブートストラップで使用される訓練セットの割合で、計算の前に10で割ります
  • nh — 隠れ層のニューロンの数(最小1、最大50)
  • fact — Factベクトル内の活性化関数のインデックス

適合関数を決定します。

#---Fitnes -FUN-----------
evalq({
  Ytrain <- X$pretrain$y
  Ytest <- X$train$y
  Ytest1 <- X$test$y
  n <- 500
  numEns <- 3
fitnes <- function(numFeature, r, nh, fact){
    bestF <- orderX %>% head(numFeature)
    Xtrain <- X$pretrain$x[ , bestF]
    setMKLthreads(1)
    k <- 1
    rng <- RNGseq(n, 12345)
    #---訓練---
    Ens <- foreach(i = 1:n, .packages = "elmNN") %do% {
      rngtools::setRNG(rng[[k]])
      idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr
      k <- k + 1
      elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], 
               nhid = nh, actfun = Fact[fact])
    }
    setMKLthreads(2)
    #---予測---
    Xtest <- X$train$x[ , bestF]
    foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% {
      predict(Ens[[i]], newdata = Xtest)
    } -> y.pr #[ ,n]
   #---最良---
    foreach(i = 1:n, .combine = "c") %do% {
      ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred
      Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>%
        mean() 
    } -> Score
    Score %>% order(decreasing = TRUE) %>% 
      head((numEns*2 + 1)) -> bestNN
    #---test-aver--------
    Xtest1 <- X$test$x[ , bestF]
    foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:%
      when(i %in% bestNN) %do% {
        predict(Ens[[i]], newdata = Xtest1)} %>%
      divide_by(length(bestNN)) -> ensPred
    ifelse(ensPred > 0.5, 1, 0) -> ensPred
    Evaluate(actual = Ytest1, predicted = ensPred)$Metrics$F1 %>%
      mean() %>% round(3) -> Score
    return(list(Score = Score, Pred = ensPred))
   }
}, env)  

スクリプトの詳細は次のとおりです。パラメータ検索中に変更されていないので、目的関数(Ytrain, Ytest, Ytest1)の計算を適合関数から外します。定数を初期化します。

n — アンサンブル内のニューラルネットワークの数

numEns — 予測が結合される最良の個体分類器の数(numEns*2 + 1)

fitnes()関数には4つの仮パラメータがあり、これらは最適化されるべきです。この関数の後半で、アンサンブルを訓練し、predictを計算し、最良のbestNN個のものを段階的に決定します。最後に、平均化を使用してこれらの最良の予測を結合し、指標を計算します。この関数は、最適化基準Score = mean(F1)と予測を含むリストを返します。平均化によって結合を使用するアンサンブルを最適化します。単純多数決を用いてアンサンブルの超パラメータを最適化するための適合関数は、最終部分を除いて同様です。最適化は自分で行うことができます。

適合関数の操作性とその実行時間を確認しましょう。

#----------
evalq(
  system.time(
   res <- fitnes(numFeature = 10, r = 7, nh = 5, fact = 2)
  )
, env)
 user  system elapsed 
   8.65    0.19    7.86

すべての計算結果を得るのに約9秒かかりました。 

> env$res$Score
[1] 0.761

これで、10個のランダムな初期化点と20個の反復で超パラメータを最適化することができます。私たちは最高の結果を探しています。

#------
evalq(
  OPT_Res <- BayesianOptimization(fitnes, bounds = bonds,
                                   init_grid_dt = NULL, init_points = 10, 
                                   n_iter = 20, acq = "ucb", kappa = 2.576, 
                                   eps = 0.0, verbose = TRUE)
, envir = env)
見つかった最良のパラメータは下記の通りです。 
  Round = 23  numFeature = 8.0000  r = 3.0000 nh = 3.0000  fact = 7.0000        Value = 0.7770

Valueで最適化履歴を順位付け、最良の10スコアを選択します。

evalq({
  OPT_Res %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
    dplyr::select(-Round) -> best.init
  best.init
}, env)
 numFeature r nh fact Value
1           8 3  3    7 0.777
2           8 1  5    7 0.767
3           8 3  2    7 0.760
4          10 7  9    8 0.759
5           8 5  4    7 0.758
6           8 2  7    8 0.756
7           8 6  9    7 0.755
8           8 3  4    8 0.754
9           9 2 13    9 0.752
10         11 2 24    4 0.751

得られた最良の結果の超パラメータを解釈します。予測子数は8、サンプルサイズは0.3、隠れ層のニューロン数は3、活性化関数は"radbas"です。これは、ベイズ最適化が多様なモデルの広いスペクトルを与え、直感的に導出される可能性は低いことを再度証明します。最適化を何度も繰り返し、最良の結果を選択する必要があります。

したがって、最適な訓練の超パラメータが見つかりました。アンサンブルをテストします。

最適のパラメータを使ったアンサンブルの訓練とテスト

上で得られた最適なパラメータで訓練されたアンサンブルをテストセットでテストします。アンサンブルの最良のメンバーを決定し、その結果を平均化して最終的な指標を見ます。下記にスクリプトを示します。

ニューラルネットワークのアンサンブルを訓練するときは、最適化時と同じ方法で作成します。

#--1-Train--optEns-predict--best--test-average------------------------
evalq({
  Ytrain <- X$pretrain$y
  Ytest <- X$train$y
  Ytest1 <- X$test$y
  n <- 500
  numEns <- 3
  #--BestParams--------------------------
  best.par <- OPT_Res$Best_Par %>% unname 
  numFeature <- best.par[1] # 8L
  r <- best.par[2]          # 3L
  nh <- best.par[3]         # 3L
  fact <- best.par[4]       # 7L
  bestF <- orderX %>% head(numFeature)
  Xtrain <- X$pretrain$x[ , bestF]
  setMKLthreads(1)
  k <- 1
  rng <- RNGseq(n, 12345)
  #---訓練---
  OptEns <- foreach(i = 1:n, .packages = "elmNN") %do% {
    rngtools::setRNG(rng[[k]])
    idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr
    k <- k + 1
    elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], 
             nhid = nh, actfun = Fact[fact])
  }
  setMKLthreads(2)
  #---予測---
  Xtest <- X$train$x[ , bestF]
  foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% {
    predict(OptEns[[i]], newdata = Xtest)
  } -> y.pr #[ ,n]
  #---最良---
  foreach(i = 1:n, .combine = "c") %do% {
    ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred
    Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>%
      mean() 
  } -> Score
  Score %>% order(decreasing = TRUE) %>% 
    head((numEns*2 + 1)) -> bestNN
  #---test-aver--------
  Xtest1 <- X$test$x[ , bestF]
  foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:%
    when(i %in% bestNN) %do% {
      predict(OptEns[[i]], newdata = Xtest1)} %>%
    divide_by(length(bestNN)) -> ensPred
  ifelse(ensPred > 0.5, 1, 0) -> ensPred
  Evaluate(actual = Ytest1, predicted = ensPred)$Metrics[ ,2:5] %>%
    round(3) -> OptScore
  caret::confusionMatrix(Ytest1, ensPred) -> cm
}, env)

アンサンブルの7つの最良ニューラルネットワークの結果を見てみましょう。

> env$Score[env$bestNN]
[1] 0.7262701 0.7220685 0.7144137 0.7129644 0.7126606 0.7101981  0.7099502

下記は最良ニューラルネットワークを平均した結果です。

> env$OptScore
  Accuracy Precision Recall    F1
0    0.778     0.751  0.774 0.762
1    0.778     0.803  0.782 0.793
> env$cm
Confusion Matrix and Statistics

          Reference
Prediction   0   1
         0 178  52
         1  59 212
                                          
               Accuracy : 0.7784          
                 95% CI : (0.7395, 0.8141)
    No Information Rate : 0.5269          
    P-Value [Acc > NIR] : <2e-16          
                                          
                  Kappa : 0.5549          
 Mcnemar's Test P-Value : 0.569           
                                          
            Sensitivity : 0.7511          
            Specificity : 0.8030          
         Pos Pred Value : 0.7739          
         Neg Pred Value : 0.7823          
             Prevalence : 0.4731          
         Detection Rate : 0.3553          
   Detection Prevalence : 0.4591          
      Balanced Accuracy : 0.7770          
                                          
       'Positive' Class : 0      

この結果は、アンサンブル内の個々のニューラルネットワークの結果よりも顕著に優れており、 このシリーズの前の記事で得られた最適なパラメータを持つDNNの結果と同等です。

終わりに

  1. 簡単で高速なELMニューラルネットワークで構成されたニューラルネットワーク分類器のアンサンブルは、より複雑なモデル(DNN)に匹敵する分類品質を示します。
  2. アンサンブルにおける個々の分類器の超パラメータの最適化は、Acc = 0.77(95% CI = 0.73 - 0.81)までの分類品質の向上をもたらします。
  3. 平均化されたアンサンブルと多数決のアンサンブルの分類品質はほぼ同じです。
  4. 訓練後、アンサンブルは訓練セットサイズの半分以上の長さで分類品質を保持します。ここでは、品質は最大750バーまで維持されます。これは、DNNで得られたもの(250バー)よりも大幅に高いものです。 
  5. 連続予測変数の変換しきい値を数値(較正、最適なCutOff、遺伝子検索)に最適化することによって、アンサンブルの分類品質を大幅に向上させることが可能です。
  6. アンサンブルの分類品質は、訓練可能なモデル(スタッキング)を結合器として使用することによっても増やすことができます。これは、ニューラルネットワークまたはニューラルネットワークのアンサンブルとすることができます。記事の次の部分では、スタッキングのこれら2つのバリエーションがテストされます。ニューラルネットワークの構築には、ライブラリのTensorFlowグループによって提供される新しい機能をテストします。

添付ファイル

GitHub/PartVIには下記が含まれます。

  1. FUN_Ensemble.R — この記事で説明するすべての計算を実行するために必要な関数
  2. RUN_Ensemble.R — アンサンブルを作成、訓練、テストするスクリプト
  3. Optim_Ensemble.R — アンサンブル内のニューラルネットワークの超パラメータを最適化するスクリプト
  4. SessionInfo_RunEns.txt — アンサンブルの作成とテストに使用されるパッケージ
  5. SessionInfo_OptEns.txt — NNアンサンブルの超パラメータの最適化に使用されるパッケージ
  6. ELM.zip — ELMニューラルネットワーク記事のアーカイブ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/4227

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

最後のコメント | ディスカッションに移動 (1)
Vladimir Perervenko
Vladimir Perervenko | 24 2月 2019 において 16:50

Обсуждение и вопросы по коду можно сделать в ветке

Удачи

14,000自動売買ロボットがMetaTraderマーケットに 14,000自動売買ロボットがMetaTraderマーケットに
最大級のアルゴリズム取引既成アプリストアでは13,970件の製品があります。これには4,800件のロボット、6,500件の指標、2,400件のユーティリティその他のソルーションが含まれます。半分以上のアプリケーション (6,000) はレンタルもできます。全製品の4分の1(3,800)は無料でダウンロードできます。
取引口座モニタリングは不可欠なトレーダーツールです。 取引口座モニタリングは不可欠なトレーダーツールです。
取引口座モニタリングでは、完了したすべての取引に関する詳細なレポートが提供されます。すべての取引統計は自動的に収集され、わかりやすい図やグラフとして提供されます。
通貨ペアパターンのテスト: 実用的なアプリケーションと実際のトレードの視点 第４部 通貨ペアパターンのテスト: 実用的なアプリケーションと実際のトレードの視点 第４部
この記事では、トレーディング通貨ペアバスケットのシリーズに結論付けを行います。 ここでは、残りのパターンをテストし、実際のトレードでの適用について説明します。 相場におけるエントリーと決済、パターンを分析し、複合インジケータの使用を考察します。
強化学習におけるランダム決定フォレスト 強化学習におけるランダム決定フォレスト
バギングを使用するランダムフォレスト（RF）は最も強力な機械学習方法の1つですが、グラジエントブースティングには若干劣ります。本稿では、市場との相互作用から得られた経験に基づいて意思決定を行う自己学習型取引システムの開発を試みます。