
マーケット価格予測に対する汎用回帰モデル
はじめに
マーケット価格は需要と供給の間の安定したバランスから形作られ、それは逆に経済、政治、心理要因の多様性に依存します。
ただし現況における商品、通貨、株式の売買に従った正しい判断ができるためには一定レベルの正確性をもった将来的7マーケット価格の振る舞いを見、予測できることが必要です。この問題はひとつの方法または他の方法で処理されるすべての種類の資源からくる異なる性質の大きな情報量を用いて解決することができます。
研究者の目的、資格、性質に応じた効果的なマーケット動向の戦略と戦術を開発するのに有用な分析方法 /1/が4とおりあります。
- マーケット価格がそれに影響をあたえる事柄を考慮したテクニカル分析それは進んだ数学的方法を取り入れます。 /2/
- マーケット価格に関して異なる経済的要因を使った基本的な分析それはマクロ経済モデルを取り入れます。 /3-5/
- 主要なマーケット指数と指標知識に代用される直感的分析、将来の動向を予測する手法。その結果は初期前提に対する理論的ルールと数学を直接適用することで証明することはできませんが、それでもなお不思議なことにそれはしばしば真実であると判ります。
- 各消費者個別のマーケット条件分析、または全体として多様な成功の結果となる心理分析を基にした心理分析
問題に対する知識状態
マーケと価格予測に対する新規に提案される新しい手法を含む技術はどんなものもれわれの意見で考慮され、幸運な状況の組合せにおいてダウ理論/6,7/ として知られる3つの公理に基づいて客観的に存在する法律を説明します。それは以下のように短く形成されます。
- マーケット価格は需要と供給の法則に従いすべての影響ある要因を考慮し、それを予測するには時間の流れに従い変動するデータがあれば十分です。
- マーケット価格の時間への依存は主にS字型の傾向を洗わります。その高値と安値は水平(平らな)線でつながれ、サイドウェイトレンドと呼ばれるか、あるいは何もなしです。
- 「歴史は繰り返す」または「過去に働き、今に働き、将来に働く」という原理として知られる、時間の経過の中で変わらず残る客観的な既存のマーケット価格の変化パターンがあります。
ただし、例えば通貨レートといったマーケット価格時系列の残りの動的段階には、ひじょうに複雑なため、自己組織化の過程で再び秩序を産み出す完全に予測不可能な混沌の印象を得る段階が続きます。
しかし、ある一定のポイントで安定によって弱められた動的システムはふたたび経済インディケータの時系列の性質は混合していると信じる根拠をあたえる混沌を再び生み出します。これは、マーケット価格時系列にはある点において決定性があり分析可能であるが、別の点では信頼性ある予測がす可能で、それに正規分布法則/8/が続き、また別のポイントでランダム変数としてふるまう、ということを意味します。
よって、科学会ではいまだにマーケット価格を明確に定義し実用化する根拠を見つけることを阻むマーケット価格の動向性質についての共通認識はありません。
ブラックボックスのシングルセルモデルに対するトランジェント関数
処理にあいまいさがあるので、まずときとして課題/1/ の問題に帰属するブラックボックスのシングルセルモデルに注目し、マテリアルのバランス式を適用することを提案します。
前述の公理を詳しく述べるため、平衡マーケット価格は外力D(t)、価格同様のディメンションで計測される量と値によって影響されるとき変化すると仮定します。
また、時間の経過 t においてマーケット価格P(t) の変化が指定の力の影響当初から、無限遠においてP(∞) = D0 値に到達しようとするまた知られていないある法則によって継続的にゼロ値から増加しています。言い換えると、D0 は性質や影響力のサインに依存するマーケット価格の有限増分または減少であります。
またD(t=0) = D0でもあります。また、無限小期間dtでは、影響力は時間 t 分残っている力D(t) に比例する値dD(t) 分減少します。
![]()
その結果として、以下のように時間 t において指数関数的依存性D(t) を取得します。
![]() (1)
(1)
ここで ![]()
t は不安定化の影響の最初からの時間で、単位は時系列の秒(分、時間、日、週、10年、月、年)です。
τ (tau) は処理時間定数、秒分、時間、日、週、10年月、年)に数値的に等しい比例因子です。
マーケット価格P(t) 変化スピードV(t) が値D(t) および時間 t に比例していると仮定します。
![]()
ここで![]() (2)
(2)
k はディメンション 1/(time)^2 を持つ比例因子です。
β = k*τ*D0 はマーケット価格変化スピードのディメンションをもつ比例因子です。
H(t)として表される既定の時間 t による単位時間あたりの価格の絶対インクリメントまたはデクリメントは数値的にV(t)と等しくなります。
H(t) = V(t) = β*m
疑いなく、時間 t の変化の全範囲に渡り統合 H(t) によって、マーケット価格が不安定になり始めたときから時間 t によtマーケット価格 P(t) の変化のトータル値を取得します。
![]()
ここで![]() (3)
(3)
(3) に基づき t = ∞ s = 1のときそれは現れるので、以下のような結論に至ります。
P(∞) = β*τ = D0;
or: β = D0/τ;
ここで得た結果を伴 β の前回表記と比べると、以下となります。
k = 1/τ^2;
そして、以下の関係が真となります。
H(t) = D0*m;
P(t) = D0*s.
係数 τ および β が決定されると、初期段階も含め、あらゆる価格変化の段階において価格変化の限界値 D0 を試算し予測することが可能となります。ただし、この考えは対象のバランス条件が満たされているときのみ真となります。
D(t) + H(t) + P(t) = D0 (4)
または ![]()
よって正規化要件は満たされました。
ℓ + m + s = 1; (5)
関係(1-3)を用いてこの事実を確認します。
![]()
対象のバランス条件を正確に満たし (4) 、また正規化要件を満たす(5) ことはわれわれの仮定と提案されている関係が真であることを指します。
マルチプルセルモデルに対するトランジェント関数
n 個のセルで構成されているブラックボックスマルチプルセルモデル従い似た方法で判断すると、関数 D(t)、H(t)、P(t) に対して以下の関係を得ます。
- D(t) = D0 * L;
- H(t) = D0 * M;
- P(t) = D0 * S;
ここで
![]() (6)
(6)
これをここでは「2パラメータ累積指数分布関数」と呼びました。
![]() (7)
(7)
はガンマ分布の確率密度関数、またはアーラン分布の確率密度関数です。
![]() (8)
(8)
はガンマ分布の累積分布関数、またはアーラン分布の累積分布関数の一種です。
- t/τ, n は分布パラメータ
- 1 は "true"に対して判定されるブール式
- 0 は "false"に対して判定されるブール式
積分 (8) は次の点を証明します。
または
![]()
その結果 (6-8) によると正規化要件はこの場合にも正確に満たされます。
L+M+S = 1; (9)
私は L 関数を「将来期間の関数」と呼びました。その理由は将来のマーケット価格はその値に依存するからです。 M 関数を「現在の関数」と呼びました。その理由はそれは既定の単位時間内におけるマーケット価格の変化を判断するためです。そして S 関数を「過去の関数」と呼びました。なぜなら、価格が混乱し始めて以来全期間を通して達成されたマーケット価格レベルはトランジェントの考えと矛盾せず、問題の方向に関する現状についてわれわれの考えを大きく広げます。
n = 1 を (6-8) に代入することで関数 L、M 、 Sは関数 ℓ、m 、 s fになり、ゆえにそれぞれただ関数L、M 、 Sを予測という目的についてこのクラスの関数のもっとも一般的ケースであるとみなします。
解明したトランジェント関数に基づくマーケット価格予測に対する汎用レグレッションモデル作成
観測の初めからの時間 t におけるマーケット価格レベル P(h) の依存関係は以下のように表します。
シングルセルモデルで
マルチプルセルモデルで
![]() (10b)
(10b)
ここで、 P0 不安定になる直前の価格レベルで、すなわち時間による t = 0です。
パラメータ n および τ は、計数 β 同様にマーケットにおける混乱状態の初めからの実マーケット価格値を用いて決定されます。そこではof (10b)のデリバティブ値として取ることのできる単位時間 t ごとのマーケット価格 f が決定されます。この仮定を受け入れるエラーは、価格変化値のパーセントの数100分の1と些少です。この仮定を受け入れることで前述のパラメータおよび係数 β の決定を大きく促します。
関数 S を分析することで関数 M の分析に進むことができます。
![]() (11)
(11)
(11) by t^n の両パートを分割し、取得した関係の対数を取ると、半対数座標の直線方程式を得ます。
![]()
時間 t の対応する点に対する関数 f の値が判り、パラメータ n、 τ 、および係数 β は以下のように決定されます。
![]() (12)
(12)
![]() (13)
(13)
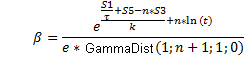 (14)
(14)
ここで
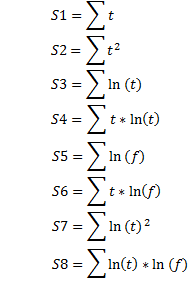
時間 t の対応する点に対する関数 f の値は時間 t 同様、マーケット価格が混乱し始めたときから時間һ0, һ1,…, һк の点での実マーケット価格値 Р0, Р1,…, Рк を基にし、区間の中間で数値微分および積分を用いて決定されます。
f1 = (P1 - P0)/(һ1 – һ0);
f2 = (P2 – P1)/( һ2– һ1);
f3 = (P3 – P2)/( һ3– һ2); and so forth;
t1 = (һ0 + һ1)/2;
t2 = (һ1 + һ2)/2;
t3 = (һ3 + һ2)/2; and so forth.
モデルの修正および調整
回帰モデルとしての方程式 (10a) および (10b) の実用検証は、実データの使用により値 Р(0) と D0 が正しいと示されるとき、以下のようなものです。
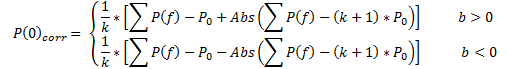 (15)
(15)
![]() (16)
(16)
ここでSf と Sr はそれぞれ実際の領域および理論曲線です。
∑Pf = P0+ P1 + P2 + …+ Pk は実価格値の合計です。
![]() (17)
(17)
i = 0, 1,2,......k;
k>2 は価格分散が決定される時間区間数です。
b は線形回帰方程式の係数 ![]() 実データのトレンド方向を決定します。
実データのトレンド方向を決定します。
マーケット価格の予測する回帰方程式 (10b) は以下のような最終形式を取ります。
![]() (18)
(18)
モデル検証
この方法で計算されたマーケット価 P(t) と、下記の外為マーケットで提供される実価格値 Pf はつねに完全に正確マテリアルのバランス条件を満たします。
∑ P(t) = ∑ Pf. (19)
調査対象のパラメータの実地および理論値、特にマーケット価格は絶対で、特定の時間においてあらゆる引数値と一致しており、計算、変換、関数アウトプットで受け付けられた仮定は正しいことを証明し、提案の回帰モデルの汎用性は示されています。
次の絵は、指定の方法で行った外為マーケットの実データ処理(1分足の時間枠)を示しています。EUR/USDクオートの実価格 (Pf) (赤い点のある黄色い線)、理論値、予測値( (P1) (ブルーの線)、計算では考慮されなかった将来の実値 (Pff) (赤い点を含むブルーの線)の間の対応を満たす方程式(18)を使っています。
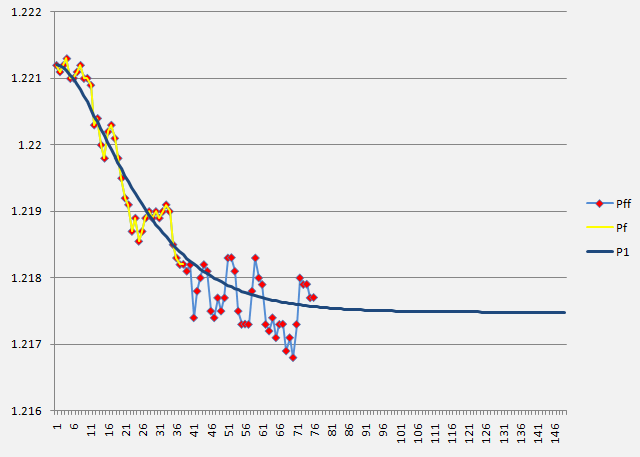
おわりに
3つの動的トランジェンとを記述する3つの関数を特定し、提案してきました。それらはそれぞれガンマ分布関数の様々な変更を決定し、調査対象パラメータし、特に将来の時間依存し、不安定化の初めから現在、過去ほマーケット価格の振る舞いを決定するものです。
指定の処理に続いて、マーケット価格予測のための汎用回帰モデルを取り上げました。それは開発の基本となりえ、たとえば多様な目的のためのマーケットインディケータ、トレーダーの処理を最適化するExpert Advisors、自動化されたトレーディングシステム、売買ロボット、他人に変わって自立的にトレーディングを行うROBOTRADERの開発さえも行わせるものです。
追記本稿における関係、式、主な仮定と結論は確認され、詳細に述べられ、紹介され、初めて公に公表されるものです。
参照資料
- A. E. Kotenko. On Methods of Technical and Fundamental Analysis in the Forex Market Study. Electronic Magazine "INVESTIGATED IN RUSSIA", http://zhurnal.ape.relarn.ru/articles/2003/151.pdf
- V. N. Yakimkin. Forex Market – Your Way to Success, М., "Akmos-Media", 2001.
- V. N. Likhovidov. Fundamental Analysis of the Currency Markets: Methods for Prediction and Decision-Making. Vladivostok, 1999.
- M. K. Bunkina. A. M. Semenov. Principles of Currency Relations, М., Urait, 2000.
- Jeffrey D. Sachs, Felipe B. Larrain. Macroeconomics in the Global Economy. М., Delo, 1996.
- Rhea, Robert. Dow Theory,- New York; Barrons, 1932.
- Greiner, P. and H. C. Whitcomb: Dow Theory, New York: Investor’s Intelligence, 1969.
- O. S. Gulyaeva. Foreign Exchange Risk Management on the Basis of Currency Rate Pre-Prediction Analysis Using Fractal Methods. Ph.D. thesis, Moscow-Tver, TvGU, 2008.
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/250
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 時系列予測に対する ENCOG マシン学習へのMetaTrader 5インディケータ使用
時系列予測に対する ENCOG マシン学習へのMetaTrader 5インディケータ使用
 C plus plus テンプレートの代用としての疑似テンプレート使用
C plus plus テンプレートの代用としての疑似テンプレート使用
 ランダムウォーク理論とトレンドインディケータ
ランダムウォーク理論とトレンドインディケータ
 価格 Correlationの統計データを基にしたシグナルのフィルタリング
価格 Correlationの統計データを基にしたシグナルのフィルタリング
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
指標は有料か何か? コードベースに公開されているので、思う存分使ってください!
新しい記事「市場価格予測のためのユニバーサル回帰モデル」が掲載されました:
著者Юсуфходжа
良い記事だ。
非常に印象的
残念なことだが、冒頭に間違いがある。
まず、ある時刻tにおける価格の増分はもちろん何らかの値を持ち、それをD0とする。と仮定しよう。
次にt=0の時点では、価格への影響はなく、外部からの影響による価格上昇もないらしいことは理解できる。しかし、我々は再びデルタをD0と呼びました。
そして、dt/tauを式に入れましたが、これはいずれにせよ1/C^2です。 つまり、インパクトに加速度を与え、幾何学的 回帰を動かすことになります。 なぜそうしなければならないのでしょうか?結局のところ、我々はまだ定義していない。
まあ、一般的には。
残念なことだが、冒頭に間違いがある。
まず、ある時刻tにおける価格の増分はもちろん何らかの値を持ち、それをD0とする。と仮定しよう。
次にt=0の時点では、価格への影響はなく、外部からの影響による価格上昇もないらしいことは理解できる。しかし、我々は再びデルタをD0と呼びました。
そして、dt/tauを式に入れましたが、これはいずれにせよ1/C^2です。 つまり、インパクトに加速度を与え、幾何学的回帰を動かすことになります。 なぜそうしなければならないのでしょうか?結局のところ、私たちはまだ定義していない。
まあ、一般的には...
1.Doは価格の増分ではなく、時間t=0における価格に影響を与える力の初期ポテンシャルである。
2.記事より:"...均衡状態にある市場価格は、ある外力D(t)の作用下でのみ変化しうると仮定する。
また、この力の影響の始まりから時間tの経過に伴う市場価格の変化P(t)は、まだ知られていない何らかの規則性によってゼロ値から連続的に増加し、無限大の値P(∞)=D0に達する傾向があると仮定しよう。すなわち、D0とは、この影響力の性質と符号に応じて、市場価格の有限の増加または減少を意味する。
さらに、D(t=0) = D0と仮定する。さらに、無限小の時間dtの間に、影響力は、時間tの瞬間までに残っている力D(t)に比例して、値dD(t)だけ減少すると仮定しよう:
したがって、D(t)の時間tに対する指数関数的な依存性が得られる:
ここで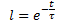
t - 不安定化力の影響開始からの時間、時系列単位、秒(分、時、日、週、数十年、月、年);
τ(tau)-比例係数、数値的にはプロセスの時定数に等しい、sec.(min,hours,days,weeks,decades,month,years)"。
どこから1/s^2の次元性を見つけたのですか?その比に次元性はない。私は、ある過程に作用する力の変化(減少)速度は、力そのものに比例する、という仮説を立てた。比例係数として、時間の逆数次元を持つ比a(α)=1/tauを導入した。a (α)とは、システムのインピーダンス、つまりプロセスの流れに対するシステムの抵抗を意味し、tauとは、後に判明するように、ラプラス変換における時間のイメージであり、プロセスの分析を微分領域から通常の領域へと移行させるものである。つまり、どのような過程にも私たちとは異なる独自の時間が存在し、タウは時間の「翻訳者」として機能するのである。記事の中で、タウを推定する方法を紹介した:
さて、時間tの対応する瞬間に対する関数fの値がわかっていれば、この式からパラメータn、τ、係数βは次のように決定される:
ここで
時間tと時間tの対応する瞬間に対する関数fの値は、区間の中間を参照した数値微分による不安定化の始まりから時間h0、h1、...、kの瞬間までの市場価格P0、P1、...、Pkの実際の値によって決定される:
f1 = (P1 - P0)/(ch1 - ch0); f2 = (P2 - P1)/( ch2- ch1); f3 = (P3 - P2)/( ch3- ch2); など;
t1 = (ch0 + ch1)/2; t2 = (ch1 + ch2)/2; t3 = (ch3 + ch2)/2; など。