Random Decision Forest в обучении с подкреплением

Тезисное описание алгоритма Random Forest

Random Forest (RF) с применением бэггинга — один из самых сильных методов машинного обучения, который немного уступает градиентному бустингу. 

Случайный лес состоит из комитета деревьев решений (которые также называются деревьями классификации или регрессионными деревьями "CART" и решают одноименные задачи). Они применяются в статистике, анализе данных и машинном обучении. Каждое отдельное дерево — достаточно простая модель, которая имеет ветви, узлы и листья. В узлах записаны атрибуты, от значений которых зависит целевая функция. Далее по ветвям в листья попадают значения целевой функции. В процессе классификации нового случая нужно спуститься по дереву через ветви до листа, пройдя через все значения атрибутов по логическому принципу "ЕСЛИ-ТО". В зависимости от этих условий, целевой переменной будет присвоено то или иное значение или класс (целевая переменная попадет в конкретный лист). Цель построения дерева решений — создание модели, которая предсказывает значение целевой переменной в зависимости от нескольких переменных на входе.

Случайный лес строится путем простого голосования деревьев решений по алгоритму Bagging (Бэггинг). Bagging — это искусственное слово, образованное от английского словосочетания bootstrap aggregating. Этот термин ввел Лео Брейман в 1994 году.

Bootstrap в статистике — это такой способ формирования выборки, когда выбирается ровно столько же объектов, сколько их исходно и было. Но объекты эти выбираются с повторениями. Иными словами, выбранный случайный объект возвращается обратно и может быть выбран повторно. При этом число объектов, которое будет выбрано, составит примерно 63% от исходной выборки, а оставшаяся доля объектов (примерно 37%) ни разу не попадет в обучающую выборку. По этой сформированной сэмплированной выборке обучаются базовые алгоритмы (в нашем случае деревья решений). Это тоже происходит случайным образом: берутся случайные подмножества (сэмплы) заданной длины и обучаются на выбранном случайном подмножестве признаков (атрибутов). Оставшиеся 37% выборки используются для проверки обобщающей способности построенной модели.

Затем все обученные деревья объединяются в композицию при помощи простого голосования, с использованием усредненной ошибки для всех сэмплов. В результате применения bootstrap aggregating уменьшается средний квадрат ошибки, снижается дисперсия обучаемого классификатора. На разных выборках ошибка будет отличаться не так сильно. В результате модель, по заявлениям авторов, будет меньше переобучаться. Эффективность бэггинга заключается в том, что базовые алгоритмы (деревья решений) обучаются по различным случайным подвыборкам и их результаты могут сильно отличаться, но их ошибки взаимно компенсируются при голосовании.

Можно сказать, что Random forest — это специальный случай бэггинга, когда в качестве базового семейства используются решающие деревья. При этом, в отличие от обычного способа построения решающих деревьев, не используется усечение дерева (pruning). Метод настроен на то, чтобы можно было построить композицию как можно быстрее по большим выборкам данных. Каждое дерево строится специфическим образом. Признак (атрибут) для построения узла дерева выбирается не из общего числа признаков, а из их случайного подмножества. Если мы строим регрессионную модель, то число признаков равно n/3. В случае классификации это √n. Все это является эмпирическими рекомендациями и называется декорреляцией: в разные деревья попадают разные наборы признаков, и деревья обучаются на разных выборках.

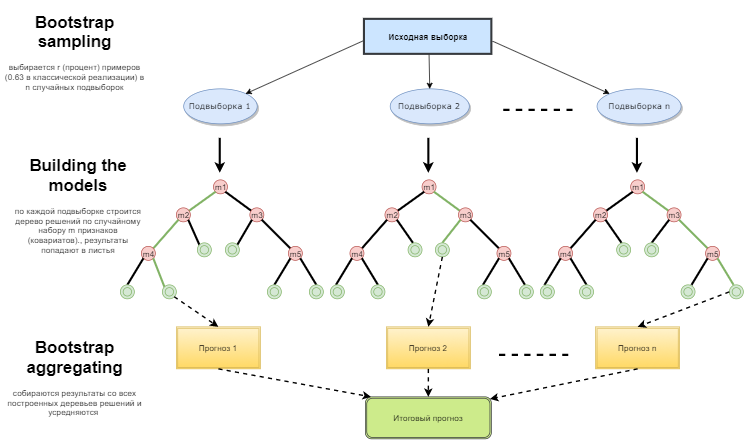
Рис. 1. Схема функционирования случайного леса

Алгоритм случайного леса оказался чрезвычайно эффективным, способным решать практические задачи. Он дает высокую точность обучения при, казалось бы, большом количестве случайностей, внесенных в процесс построения модели. Преимущество перед другими моделями машинного обучения — оценка out of bag для части множества, не попавшей в обучающую выборку. Поэтому для деревьев решений не обязательно проводить кросс-валидацию или тестирование на отдельной выборке. Достаточно ограничиться оценкой out of bag для дальнейшего "тюнинга" модели: подбора количества решающих деревьев и регуляризующей составляющей. 

В библиотеке ALGLIB, включенной в стандартную поставку терминала МetaТrader 5, есть алгоритм Random Decision Forest (RDF). Это модификация оригинального алгоритма Random Forest, предложенного Лео Брейманом и Адель Катлер. Этот алгоритм сочетает в себе две идеи: использование комитета деревьев решений, получающего результат путем голосования, и идею рандомизации процесса обучения. Более подробную информацию о модификациях алгоритма можно найти на сайте ALGLIB.

Достоинства алгоритма

• Высокая скорость обучения
• Неитеративное обучение — алгоритм завершается за фиксированное число операций
• Масштабируемость (способность обрабатывать большие объемы данных)
• Высокое качество получаемых моделей (сравнимое с нейронными сетями и ансамблями нейронных сетей)
• Отсутствие чувствительности к выбросам в данных из-за случайного сэмплирования
• Малое количество настраиваемых параметров
• Отсутствие чувствительности к масштабированию (и вообще к любым монотонным преобразованиям) значений признаков, благодаря выбору случайных подпространств
• Не требует тщательной настройки параметров, хорошо работает «из коробки». С помощью «тюнинга» параметров можно достичь прироста от 0.5 до 3% точности в зависимости от задачи и данных
• Хорошо работает с пропущенными данными — сохраняет хорошую точность, даже если большая часть данных пропущена
• Внутренняя оценка способности модели к обобщению
• Возможность работы с сырыми данными, без препроцессинга

Недостатки алгоритма

• Построенная модель занимает большое количество памяти. Если мы строим комитет из K деревьев на основе обучающего множества размером N, то требования к памяти составят O(K·N). Например, для K=100 и N=1000 модель, построенная ALGLIB, займет порядка 1 Мб памяти. Но объем оперативной памяти у современных ПК достаточно велик, так что это не самый серьезный недостаток.
  
• Обученная модель работает несколько медленнее других алгоритмов (если в модель входит 100 деревьев, мы должны пройтись по всем, чтобы получить результат). Но на современных быстрых машинах и это не столь заметно.
• Алгоритм работает хуже многих линейных методов, когда в выборке очень много разреженных признаков (тексты, Bag of words) или когда классифицируемые объекты заведомо могут быть разделены линейно.
• Алгоритм склонен к переобучению, особенно  на зашумленных задачах. Отчасти эту проблему можно решить, настроив параметр r. Аналогичная, но еще более выраженная проблема есть и у оригинального алгоритма Random Forest. Однако авторы алгоритма, напротив, заявляли, что склонности к переобучению нет. Это заблуждение разделяют некоторые практики и теоретики машинного обучения.
• Для данных, включающих категориальные переменные с различным количеством уровней, случайные леса предвзяты в пользу признаков с большим количеством уровней.  Дерево будет сильнее подстраиваться именно под такие признаки, поскольку на них можно получить более высокое значение оптимизируемого функционала (типа прироста информации).
• Как и деревья решений, алгоритм абсолютно не способен к экстраполяции (но это можно считать и плюсом, так как не будет экстремальных значений в случае попадания выброса)

Особенности применения машинного обучения в трейдинге

Среди неофитов машинного обучения бытует мнение, что это какой-то сказочный мир, где программы все делают за трейдера, а он просто радуется полученной прибыли. Это так, но лишь отчасти. Конечный результат будет зависеть от того, насколько качественно будут решены нижеописанные проблемы.

• Feature selection (выбор признаков)

Первая и основная проблема — выбор того, чему конкретно нужно обучать модель. На цену воздействует множество факторов. Есть только один научный подход изучения рынка — эконометрика. В ней три основных метода: регрессионный анализ, анализ временных рядов и панельный анализ. Отдельный интересный раздел этой науки — непараметрическая эконометрика, которая основывается исключительно на имеющихся данных, без анализа причин, их формирующих. Методы непараметрической эконометрики в последнее время популярны в прикладных исследованиях: к примеру, это ядерные методы и нейронные сети. К этому же разделу относится математический анализ нечисловых понятий — например, нечеткие множества. Если вы собираетесь заниматься машинным обучением всерьез, то вам пригодится ознакомление с эконометрическими методами. В этой статье я остановлюсь на нечетких множествах.

• Model selection (выбор модели)

Вторая проблема — выбор модели обучения. Существует множество линейных и нелинейных моделей. С их списком и сравнительными характеристиками вы можете ознакомиться, например, на сайте Microsoft.

К примеру, есть огромное множество разновидностей нейронных сетей. Используя их, приходится экспериментировать с архитектурой сети, подбирая количество слоев и нейронов. В то же время классические нейросети типа MLP обучаются медленно (особенно на градиентном спуске с фиксированным шагом), эксперименты с ними занимают массу времени. Современные быстрообучающиеся Deep Learning сети на данный момент не представлены в стандартной библиотеке терминала, а подключать сторонние библиотеки в виде dll не совсем удобно. Такие пакеты я пока еще недостаточно изучил.

В отличие от нейронных сетей, линейные модели работают быстро, но не всегда хорошо справляются с аппроксимацией.

Random Forest лишен этих недостатков. Нам нужно всего лишь подобрать количество деревьев и параметр r, отвечающий за процент объектов, попавших в обучающую выборку. Мои эксперименты в Microsoft Azure Machine Learning Studio показали, что случайные леса в большинстве случаев дают наименьшую ошибку предсказания на тестовых данных.

• Model testing (тестирование полученной модели на новых данных)

В общем случае есть только одна строгая рекомендация: чем больше обучающая выборка и информативнее признаки, тем стабильнее должна быть система на новых данных. Но при решении задач трейдинга может возникнуть случай недостаточной емкости системы, когда взаимных вариаций предикторов очень мало и они неинформативны. В результате одни и те же сигналы предикторов будут давать сигналы и на покупку, и на продажу. На выходе получится низкая обобщающая способность модели и, как следствие, плохое качество сигналов в будущем. К тому же, обучение на большой выборке будет медленным, а значит, не будет возможности множественных прогонов при оптимизации. При этом гарантии положительного результата у нас не будет. Добавим к этим проблемам хаотичную природу котировок, с их нестационарностью, с постоянно меняющимися рыночными закономерностями или (что хуже) с полным их отсутствием.

Выбор способа обучения модели

Случайный лес используется для решения широкого спектра задач регрессии, классификации и кластеризации.

Условно эти методы можно представить следующим образом.

• Обучение без учителя (unsupervised). Кластеризация, выявление аномалий. Эти методы применяются, чтобы программно разделять признаки на группы с характерными отличиями, которые определяются автоматически.
• Обучение с учителем (supervised). Классификация и регрессия. На выход подается набор заранее известных обучающих примеров (меток), и случайный лес пытается выучить (аппроксимировать) все случаи.
• Обучение с подкреплением (reinforcement). Пожалуй, это самый необычный и перспективный вид машинного обучения, который стоит особняком от остальных. Здесь обучение происходит при взаимодействии виртуального агента со средой, при этом агент пытается максимизировать вознаграждения, получаемые от действий в этой среде. Давайте применим такой подход.

Обучение с подкреплением в задачах разработки ТС

Представим создание трейдера с искусственным интеллектом. Он будет взаимодействовать со средой и получать от нее какой-то отклик на свои действия. Например, прибыльные сделки будут поощряться а за убыточные он будет штрафоваться. В итоге, после некоторого количества эпизодов взаимодействия с рынком, искусственный трейдер выработает собственный уникальный опыт, который отложится в его "мозге". Роль "мозга" будет выполнять случайный лес.

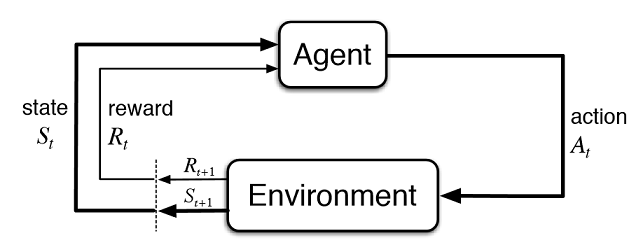
Рис. 2. Взаимодействие виртуального трейдера с рынком

На рис. 2 представлена схема взаимодействия агента (искусственного трейдера) со средой (рынком). Агент может совершать действия A в момент времени t, находясь при этом в состоянии St. После этого он переходит в состояние St+1, получая вознаграждение Rt от среды за предыдущее действие, в зависимости от того, насколько оно оказалось успешным. Эти действия могут продолжаться t+n число раз, пока не закончится вся исследуемая последовательность (или игровой эпизод для агента). Можно сделать этот процесс итеративным, заставив агента обучаться несколько раз, постоянно улучшая результаты.

Память агента (или его опыт) должна где-то храниться. В классической реализации обучения с подкреплением используются матрицы состояние-действие. Попадая в определенное состояние, агент вынужден обращаться к матрице за очередным решением. Такая реализация подходит для задач с очень ограниченным набором состояний. В ином случае матрица может стать очень большой. Поэтому таблицу мы заменим на случайный лес:

Рис. 3. Глубокая нейросеть или случайный лес для аппроксимации политики

Стохастической параметризированной политикой Πθ (policy) агента называется совокупность пар (s,a), где θ — вектор параметров для каждого состояния. Оптимальной политикой называется оптимальная совокупность действий для конкретной задачи. Условимся, что агент стремится выработать оптимальную политику. Этот подход хорошо работает для непрерывных задач с заранее неизвестным количеством состояний и является model-free actor-critic методом в обучении с подкреплением. Есть еще много других подходов к обучению с подкреплением. Они описаны в книге Richard S. Sutton и Andrew G. Barto "Reinforcement Learning: An Introduction"

Программная реализация самообучающегося эксперта (агента)

Я стремлюсь к преемственности в своих статьях, поэтому в роли агента будет выступать система нечеткой логики. Напомню, что в предыдущей статье я оптимизировал гауссовскую функцию принадлежности для нечеткого вывода Мамдани. Но тот подход имел существенный недостаток — гауссиана оставалась неизменной для всех случаев, вне зависимости от текущего состояния среды (показаний индикаторов). Теперь наша задача — автоматический подбор положения гауссианы терма "neutral" нечеткого вывода "out". Задачей агента будет выработка оптимальной политики через подбор значений и аппроксимацию фунции положения центра гауссианы, в зависимости от показаний трёх индикаторов, в диапазоне [0;1].

Создадим отдельный указатель на функцию принадлежности в глобальных переменных эксперта. Это позволит произвольно изменять ее параметры в процессе обучения:

CNormalMembershipFunction *updateNeutral=new CNormalMembershipFunction(0.5,0.2);

Создадим объекты классов случайного леса и матрицы, для заполнения ее значениями:

//RDF system. Here we create all RF objects.
CDecisionForest      RDF;                                     //Random forest object
CMatrixDouble        RDFpolicyMatrix;                         //Matrix for RF inputs and output
CDFReport            RDF_report;                              //RF return errors in this object, then we can check it

В инпуты вынесем основные настройки случайного леса: количество деревьев и регуляризующую составляющую. Это позволит немного улучшить модель путем тюнинга этих параметров:

sinput int number_of_trees=50;
sinput double regularization=0.63;

Напишем сервисную функцию проверки состояния модели. Если случайный лес уже обучен для текущего таймфрейма, то будем использовать его для торговых сигналов, если же нет — инициализируем политику случайными значениями (будем торговать случайным образом):

void checkBeforeLearn()
  {
   if(clear_model)
     {
      int clearRDF=FileOpen("RDFNtrees"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      FileWrite(clearRDF,0);
      FileClose(clearRDF);
      ExpertRemove();
      return;
     }

   int filehnd=FileOpen("RDFNtrees"+ _Symbol + (string)_Period +".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
   int ntrees =  (int)FileReadNumber(filehnd);
   FileClose(filehnd);

   if(ntrees>0)
     {
      random_policy=false;

      int setRDF=FileOpen("RDFBufsize"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      RDF.m_bufsize=(int)FileReadNumber(setRDF);
      FileClose(setRDF);

      setRDF=FileOpen("RDFNclasses"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      RDF.m_nclasses=(int)FileReadNumber(setRDF);
      FileClose(setRDF);

      setRDF=FileOpen("RDFNtrees"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      RDF.m_ntrees=(int)FileReadNumber(setRDF);
      FileClose(setRDF);

      setRDF=FileOpen("RDFNvars"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      RDF.m_nvars=(int)FileReadNumber(setRDF);
      FileClose(setRDF);

      setRDF=FileOpen("RDFMtrees"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_BIN|FILE_ANSI|FILE_COMMON);
      FileReadArray(setRDF,RDF.m_trees);
      FileClose(setRDF);
     }
   else Print("Starting new learn");

   checked_for_learn=true;
  }

Как видно из листинга, обученная модель загружается из файлов, содержащих:

• размер обучающей выборки,
  
• количество классов (1 в случае регрессионной модели),
  
• количество деревьев,
  
• количество признаков
• и массив обученных деревьев.

Обучение будет происходить в тестере терминала, в режиме оптимизации. После каждого прохода тестера модель будет обучаться на вновь сформированной матрице и сохраняться в вышеуказанные файлы для последующего использования:

double OnTester()
  {
   if(clear_model) return 0;

   if(MQLInfoInteger(MQL_OPTIMIZATION)==true)
     {
      if(numberOfsamples>0)
        {
         CDForest::DFBuildRandomDecisionForest(RDFpolicyMatrix,numberOfsamples,3,1,number_of_trees,regularization,RDFinfo,RDF,RDF_report);
        }

      int filehnd=FileOpen("RDFBufsize"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      FileWrite(filehnd,RDF.m_bufsize);
      FileClose(filehnd);

      filehnd=FileOpen("RDFNclasses"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      FileWrite(filehnd,RDF.m_nclasses);
      FileClose(filehnd);

      filehnd=FileOpen("RDFNtrees"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      FileWrite(filehnd,RDF.m_ntrees);
      FileClose(filehnd);

      filehnd=FileOpen("RDFNvars"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      FileWrite(filehnd,RDF.m_nvars);
      FileClose(filehnd);

      filehnd=FileOpen("RDFMtrees"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_BIN|FILE_ANSI|FILE_COMMON);
      FileWriteArray(filehnd,RDF.m_trees);
      FileClose(filehnd);
     }

   return 0;
  }

Функция обработки торговых сигналов из предыдущей статьи осталаcь практически без изменений, но теперь, после открытия нового ордера, вызывается функция: 

void updatePolicy(double action)
  {
   if(MQLInfoInteger(MQL_OPTIMIZATION)==true)
     {
      numberOfsamples++;
      RDFpolicyMatrix.Resize(numberOfsamples,4);

      RDFpolicyMatrix[numberOfsamples-1].Set(0,arr1[0]);
      RDFpolicyMatrix[numberOfsamples-1].Set(1,arr2[0]);
      RDFpolicyMatrix[numberOfsamples-1].Set(2,arr3[0]);
      RDFpolicyMatrix[numberOfsamples-1].Set(3,action);
     }
  }

Она добавляет в матрицу новый вектор состояния из значений трех индикаторов, а выходное значение заполняется текущим сигналом, полученным из нечеткого вывода Мамдани.

Другая функция:

void updateReward()
  {
   if(MQLInfoInteger(MQL_OPTIMIZATION)==true)
     {
      int unierr;
      if(getLAstProfit()<0) RDFpolicyMatrix[numberOfsamples-1].Set(3,MathRandomUniform(0,1,unierr));
     }
  }

вызывается каждый раз после закрытия ордера. Если сделка оказалась отрицательной, то вознаграждение агента выбирается из случайного равномерного распределения, в ином случае вознаграждение остается без изменений.

Рис. 4.  Равномерное распределение для выбора случайного значения реворда

Таким образом, в текущей реализации прибыльные сделки агента поощряются, а в случае убыточных мы заставим его совершать случайное действие (случайное положение центра гауссианы), в поиске оптимального решения.

Полный код функции обработки сигналов выглядит так:

void PlaceOrders(double ts)
  {
   if(CountOrders(0)!=0 || CountOrders(1)!=0)
     {
      for(int b=OrdersTotal()-1; b>=0; b--)
         if(OrderSelect(b,SELECT_BY_POS)==true)
            if(OrderSymbol()==_Symbol && OrderMagicNumber()==OrderMagic)

               switch(OrderType())
                 {
                  case OP_BUY:
                     if(ts>=0.5)
                     if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red))
                       {
                        updateReward();
                        if(ts>0.6)
                          {
                           lots=LotsOptimized();
                           if(OrderSend(Symbol(),OP_SELL,lots,SymbolInfoDouble(_Symbol,SYMBOL_BID),0,0,0,NULL,OrderMagic,Red)>0)
                             {
                              updatePolicy(ts);
                             };
                          }
                       }
                     break;

                  case OP_SELL:
                     if(ts<=0.5)
                     if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red))
                       {
                        updateReward();
                        if(ts<0.4)
                          {
                           lots=LotsOptimized();
                           if(OrderSend(Symbol(),OP_BUY,lots,SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,Green)>0)
                             {
                              updatePolicy(ts);
                             };
                          }
                       }
                     break;
                 }
      return;
     }

   lots=LotsOptimized();

   if((ts<0.4) && (OrderSend(Symbol(),OP_BUY,lots,SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,INT_MIN) > 0))
      updatePolicy(ts);
   else if((ts>0.6) && (OrderSend(Symbol(),OP_SELL,lots,SymbolInfoDouble(_Symbol,SYMBOL_BID),0,0,0,NULL,OrderMagic,INT_MIN) > 0))
      updatePolicy(ts);
   return;
  }

Функция расчета нечеткого вывода Мамдани претерпела изменения. Теперь, если политика агента выбрана не случайной, то вызывается расчет значения положения гауссианы по оси x через уже обученный случайный лес. На вход лесу подается текущее состояние в виде вектора из 3 значений осцилляторов, а полученный результат обновляет положение гауссианы. Если эксперт запускается в оптимизаторе впервые, положение гауссианы выбирается случайным образом для каждого состояния.

double CalculateMamdani()
  {
   CopyBuffer(hnd1,0,0,1,arr1);
   NormalizeArrays(arr1);

   CopyBuffer(hnd2,0,0,1,arr2);
   NormalizeArrays(arr2);

   CopyBuffer(hnd3,0,0,1,arr3);
   NormalizeArrays(arr3);

   if(!random_policy)
     {
      vector[0]=arr1[0];
      vector[1]=arr2[0];
      vector[2]=arr3[0];

      CDForest::DFProcess(RDF,vector,RFout);
      updateNeutral.B(RFout[0]);
     }
   else
     {
      int unierr;
      updateNeutral.B(MathRandomUniform(0,1,unierr));
     }
   
   //Print(updateNeutral.B());
   firstTerm.SetAll(firstInput,arr1[0]);
   secondTerm.SetAll(secondInput,arr2[0]);
   thirdTerm.SetAll(thirdInput,arr3[0]);

   Inputs.Clear();
   Inputs.Add(firstTerm);
   Inputs.Add(secondTerm);
   Inputs.Add(thirdTerm);

   CList *FuzzResult=OurFuzzy.Calculate(Inputs);
   Output=FuzzResult.GetNodeAtIndex(0);
   double res=Output.Value();
   delete FuzzResult;

   return(res);
  }

Процесс обучения и тестирования модели

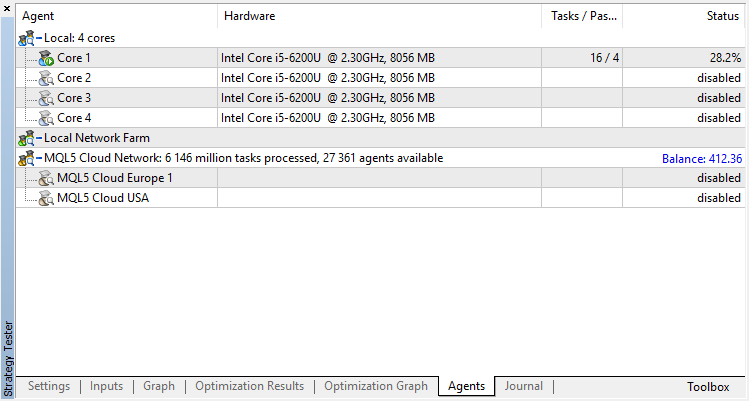
Агент будет обучаться в оптимизаторе последовательно. То есть результаты предыдущего обучения, записанные в файлы, будут использоваться для следующего прогона. Для этого просто выключим всех агентов тестирования и облако, оставив только одно ядро. 

Отключим генетический алгоритм (используем полный перебор). Обучение/тестирование проводится по ценам открытия, потому что в советнике будет явный контроль открытия нового бара.

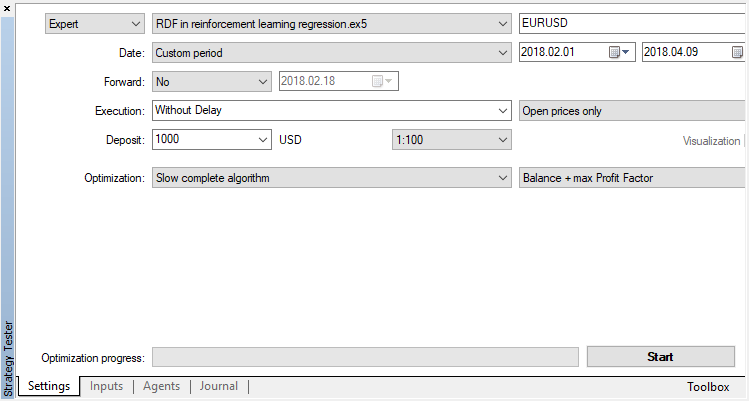
Оптимизируемый параметр всего один — количество проходов в оптимизаторе. Для демонстрации работы алгоритма установим 15 итераций.

Результаты оптимизации регрессионной модели (с одной выходной переменной) представлены ниже. Не забывайте, что обученная модель сохраняется в файл, поэтому сохранен будет только результат последнего прогона.

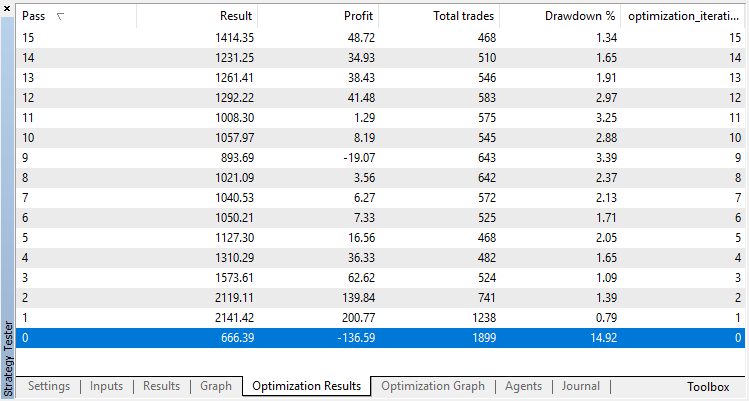
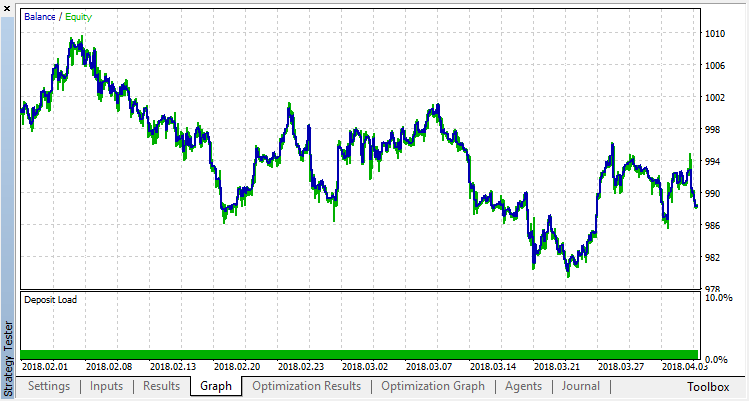
Нулевой прогон соответствует случайной политике Агента (первый запуск), поэтому он принес самый большой убыток. Первый прогон, напротив, получился самым результативным. Следующие игры уже не дали прироста, а стагнировали. В итоге, после 15-го прогона, график прироста выглядит следующим образом:

Проведем точно такой же эксперимент для классификационной модели. В этом случае реворды разделяются на 2 класса — позитивные и негативные.

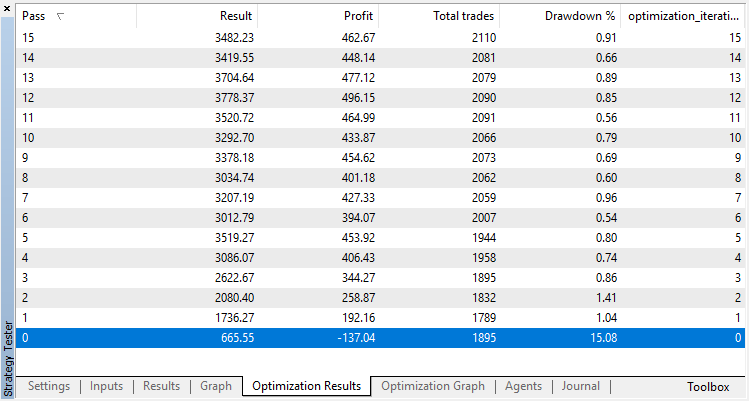
Классификация для нашей задачи работает значительно лучше. По крайней мере, наблюдается устойчивый рост от нулевого прогона, соответствующего случайной политике, до 15-го, на котором рост прекратился, а политика начала флуктуировать вокруг оптимума.

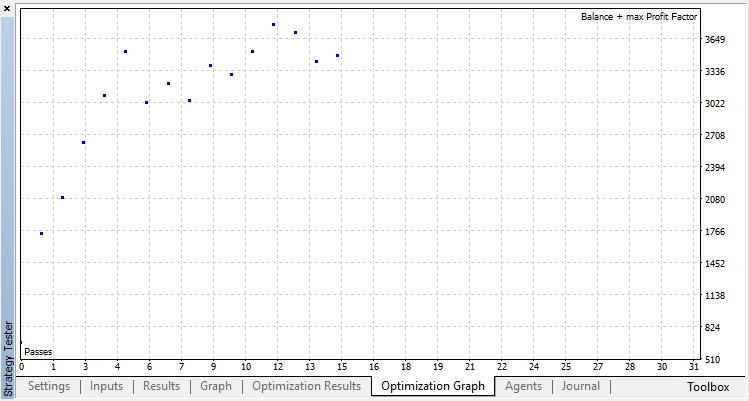
Итоговый результат обучения Агента:

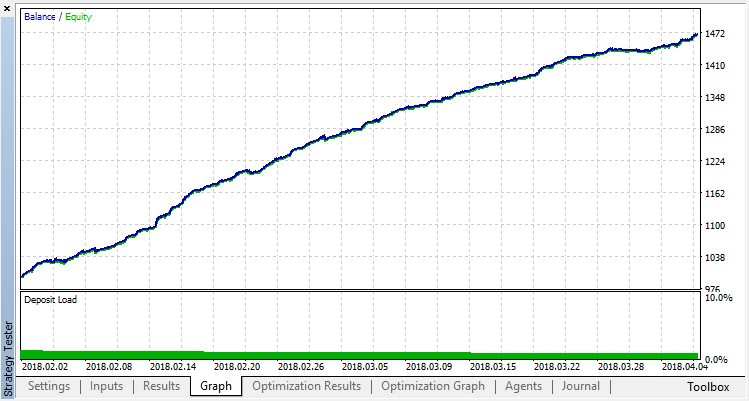
Проверим результаты работы системы на выборке вне участка обучения. Модель сильно переобучилась:

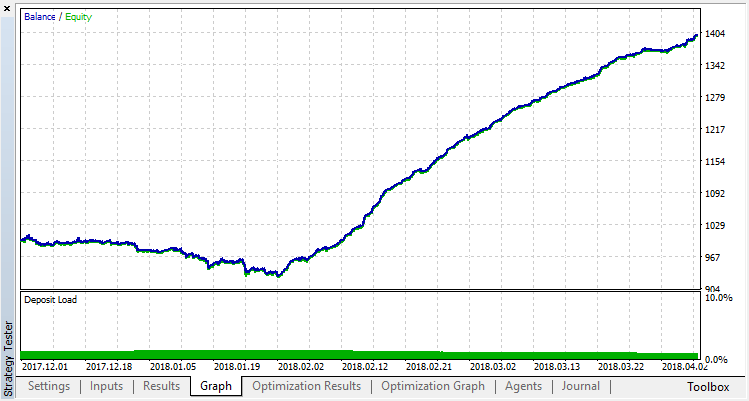
Попробуем избавиться от переобучения. Установим параметр r (regularization), равный 0.25: в обучении будет участвовать только 25% выборки. Обучимся на том же временном промежутке.

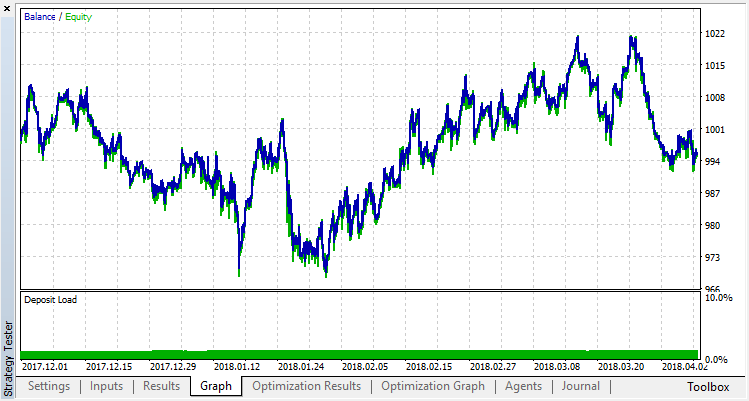
Модель обучилась хуже (добавлено больше шума), но от глобальной переобученности избавиться не удалось. Очевидно, что этот способ регуляризации подходит только для стационарных процессов, в которых закономерности не меняются со временем. Другой очевидный негативный фактор — 3 осциллятора на входе модели, которые, к тому же, коррелируют между собой.

Подведение итогов статьи

Моей целью было показать возможности применения случайного леса для аппроксимации какой-либо функции. В нашем случае функцией от показаний индикаторов был сигнал на покупку или продажу. Также были рассмотрены 2 вида обучения с учителем — классификация и регрессия, и применен нестандартный подход к обучению с заранее неизвестными обучающими примерами, которые подбирались автоматически, в процессе оптимизации. В целом, процесс похож на обычную оптимизацию в тестере (облаке), при этом алгоритм сходится всего за несколько итераций и нам не стоит заботиться о количестве оптимизируемых параметров. Это несомненный плюс примененного подхода. Минус модели — сильный оверфит при неправильно выбранной стратегии, который эквивалентен переоптимизации параметров. 

По традиции, приведу возможные пути улучшения стратегии (ведь текущая реализация — только грубый каркас).

• Увеличение числа оптимизируемых параметров (оптимизация нескольких функций принадлежности).
• Добавление разнообразных значимых предикторов.
• Применение других способов вознаграждения агента.
• Создание нескольких конкурирующих между собой агентов для увеличения пространства вариантов.

Ниже приложены файлы исходников самообучающегося эксперта.

Для работы и компиляции эксперта необходимо загрузить библиотеку MT4Orders и обновленную библиотеку Fuzzy.